Как составить таблицу значений функции y ax2 - Исправление недочетов и поиск решений вместе с Examum.ru

Определение:

Квадратичной
называют функцию вида:

Графиком
квадратичной функции является парабола. Она состоит из двух ветвей и имеет
вершину.

Ветви
могут быть направлены вверх:

Ветви
могут быть направлены вниз:

Квадратичная
функция имеет свои свойства. Поговорим о них. В своей вершине квадратичная
функция сменяет своё поведение с убывания на возрастание и с возрастания на
убывание. Понятно, что областью определения в обоих случаях будет множество
всех действительных чисел. Если говорим о нулях функции, то мы имеем ввиду те значения, при которых
функция у=0. Когда находят нули функции по графику, то ищут точки
пересечения графика с осью х. Если же находят нули функции по уравнению,
то значение функции принимают равное 0. Тем самым получаем квадратное
уравнение. Оно может иметь 2, 1 корень или не иметь корней. Соответственно,
график может иметь 2 точки пересечения с осью х, 1 точку пересечения с
осью х или не пересекать её. Понятно, что нулями квадратичной функции
являются корни соответствующего квадратного уравнения. По графику удобно
находить промежутки знакопостоянства и промежутки
монотонности функции.

Пример:
по графику квадратичной функции опишите её свойства.

На
рисунке изображена парабола, ветви которой направлены вверх, значит a>0.
Опишем её свойства.

Областью определения и областью значений являются:

Нулями
функции являются:

Промежутки
знакопостоянства:

Промежутки
монотонности:

Заметим,
что описать свойства функции по её графику проще, чем по формуле. Поэтому очень
важно уметь изображать график функции.

Рассмотрим
частный случай квадратичной функции:

Изобразим
график этой функции схематично и обратим внимание на некоторые её свойства.
Возможны два случая изображения графика.

Областью
определения в обоих случаях является:

Область
значений:

Функция
такого вида обращается в ноль только при х=0, график будет пересекать
ось х в одной точке. Первым свойством мы запишем, что если:

Другими
словами график такой функции всегда проходит через точку начала координат.
Причём эта точка является вершиной параболы.

Если
же

то
график расположен выше или ниже оси Х.

Если
взять противоположные значения аргумента, то видно, что им соответствуют
одинаковые значения функции. Противоположным значениям аргумента соответствуют
равные значения функции. Другими словами график функции симметричен
относительно оси у.

Промежутки
монотонности:

Заметим,
что:

Пример.

В
одной координатной плоскости изобразим графики функций:

Составим
таблицу значений для первой функции.

Составим
таблицу значений для второй функции

Получим
два графика, они симметричны относительно оси х.

Рассмотрим
пример: изобразим в одной координатной плоскости графики функции:

Составим
таблицу значений для функции:

Изобразим
графики этих функций:

График
функции у=ах² можно получить из
параболы у=х² растяжением от оси х в а раз,
если а>0, и сжатием к оси х в 1/а раз к оси х,
если 0<а<1.

Источник

Функция y=ax2, её график и свойства

План урока

Квадратичная функция;
Функция y=ax2 и её график в зависимости от значения a;
Свойства функции y=ax2.

Цели урока

Знать определение квадратичной функции;
Уметь строить график функции y=ax2;
Знать свойства функции y=ax2.

Разминка

Как называется график функции y=x2?
В чем отличие графиков функций y=x2 и y=-x2?
Как построить график функции y=x2?

Квадратичная функция

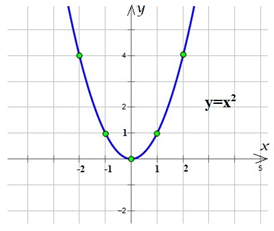
Рис. 1. График функции y=x²

С несколькими функциями и их графиками вы уже знакомы. Парабола, которая служит графиком функции y=x2 (рис. 1), — одна из них. Параболу можно встретить везде и не только в объектах, созданных человеком, как, например, в фонтанах, бокалах и даже сёдлах для лошади, но и в самой природе, где не касалась рука человека: в виде горных хребтов, морских заливов и в другом большом количестве знакомых нам объектов.

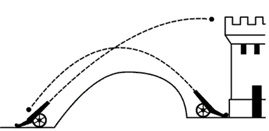
Рис. 2. Параболическая траектория

Квадратичная функция (парабола) задает форму изгиба спутниковых тарелок. Также по параболической траектории летят в воздухе пушечные ядра, лыжники фристайлеры и взмывают из воды дельфины (рис. 2). Поэтому изучение квадратичной функции очень важно.

Квадратичной функцией
называется функция, которую можно задать формулой вида:

y=ax2+bx+c,

где x — независимая переменная, a, b и c — некоторый числа, причём a≠0.

Областью определения квадратичной функции является множество всех чисел x∈-∞; +∞.

Одним из самым популярных примеров квадратичной функции является зависимость координаты тела от времени при равноускоренном движении. Эта зависимость выражается формулой:

x(t)=at22+v0t+x0,

где a (м/c²) —ускорение тела, v0 (м/c) — начальная скорость движения, x0 (м) — начальная координата, t (c) время, x (м) — координата тела.

Если, например, a=8, v0=7, x0=1, то

x(t)=4t2+7t+1.

Функция y=ax2 и её график в зависимости от значения a

Изучение квадратичной функции начнем с частного случая – функции y=ax2.

При a=1 формула y=ax2 принимает вид y=x2. Об этой функции и её графике мы поговорили в самом начале (рис.1).

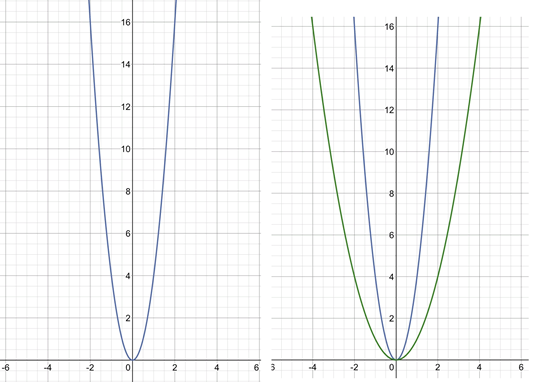
Построим график функции y=4×2 (рис.3а).

Составим таблицу значений этой функции:

x	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2
y	16	9	4	1	0	1	4	9	16

При любом x≠0 значения функции y=4×2 больше соответствующего значения функции y=x2 в 4 раза. Получаем, что все точки графика функции y=4×2 можно получить путем перемещения точек графика функции y=x2 вверх так, чтобы расстояние от оси x до каждой точки увеличилось в 4 раза. Иными словами, график функции y=4×2 можно получить из параболы y=x2 растяжением от оси x в 4 раза (рис. 3. б).

Рис. 3. а) График функции y=4x², б) График функции y=4x² и y=x²

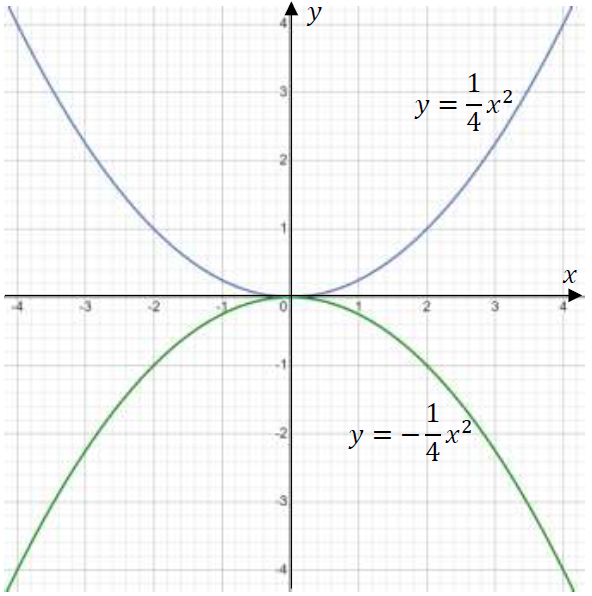
Теперь построим график функции y=14×2 и y=-14×2. Для этого составим таблицу значений для первой функции:

x	-4	-3	-2	-1	0	1	2	3	4
y	4	2.25	1	0.25	0	0.25	1	2.25	4

Составим таблицу значений для второй функции:

x	-4	-3	-2	-1	0	1	2	3	4
y	-4	-2.25	-1	-0.25	0	-0.25	-1	-2.25	-4

Рис. 4. Графики функций

Построим оба графика в одной координатной плоскости (рис. 4).

Сравнив таблицы значений и графики функций y=14×2 и y=-14×2, можно увидеть, что при любом x≠0 значения этих функций являются противоположными числами. Таким образом, можно сделать вывод, что графики этих функций симметричны относительно оси x.

Графики функций y=ax2 и y=-ax2 (при a≠0) симметричны относительно оси x.

График функции y=ax2 где a≠0, как и график функции y=x2 называется
параболой
.

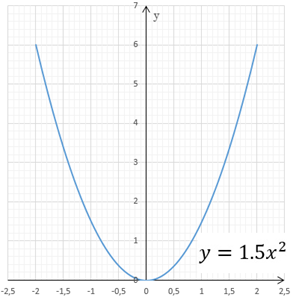
Построить график функции y=1.5×2.
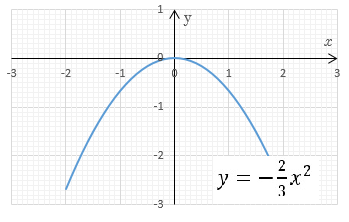
Построить график функции y=-23×2.

Свойства функции y=ax2

Сформулируем свойства функции y=ax2 при a>0.

1. Если x=0, то y=0 График функции проходит через начало координат.

2. Если x≠0, то y>0 График расположен в верхней полуплоскости.

3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси y.

4. Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0; +∞).

5. Наименьшее значение, равное нулю, функция принимает при x=0, наибольшего значения функция не имеет.

6. Областью значений функции является промежуток [0; +∞).

Теперь сформулируем свойства функции y=ax2 при a<0.

1. Если x=0 то y=0. График функции проходит через начало координат.

2. Если x≠0, то y<0 График расположен в нижней полуплоскости.

4. Функция возрастает в промежутке (-∞; 0] и убывает в промежутке [0; +∞).

5. Наибольшее значение, равное нулю, функция принимает при x=0, наименьшего значения функция не имеет.

6. Областью значений функции является промежуток (-∞; 0].

Из перечисленных свойств следует, что при a>0 ветви параболы y=ax2 направлены вверх, а при a<0 — вниз. Ось y является осью симметрии параболы.

Точку пересечения параболы с её осью симметрии называют
вершиной параболы
.

График функции y=-f(x) можно получить из графика функции y=f(x) с помощью симметрии относительно оси x.

График функции y=af(x) можно получить из графика функции y=f(x) с помощью растяжения от оси x в a раз, если a>1, и с помощью сжатия к оси x в 1a раза, если 0<a<1.

Опишите свойства функции y=1.5×2;
Опишите свойства функции y=-23×2.

Контрольные вопросы:

1. Что называют квадратичной функцией?

2. Какие свойства функции y=ax2 являются одинаковыми для положительных и отрицательных значений коэффициента a?

3. Как получить график функции y=-4×2 из графика функции y=x2, используя симметрию и растяжение/сжатие?

Ответы

Упражнение 1

Упражнение 2

1. x=0 — Нуль функции; область определения x∈-∞; +∞; область значений y∈[0; +∞); функция возрастает в [0; +∞); функция убывает в (-∞; 0];

наименьшее значение функции y=0 при x=0; наибольшего значения нет.

2. x=0 — Нуль функции; область определения x∈-∞; +∞; область значений y∈(-∞; 0]; функция возрастает в (-∞; 0] функция убывает в [0; +∞);

наибольшее значение функции y=0, при x=0; наименьшего значения нет.

Источник

Функция

y=ax2

и её график

В (7)-м классе мы изучали функции (у = m), (у = kx), (у = kx + m),

y=x2

. В общем виде функция (у = f(x)) является математической моделью зависимости значений функции (зависимой переменной (y)) от заданных значений аргумента (независимой переменной (x)).

Действительно, функция

y=ax2

в одном случае нам немного знакома. Смотри: при (a = 1), получаем

y=x2

; эту функцию мы изучили в (7)-м классе, и ты, скорее всего, помнишь, что график этой функции — парабола.

Посмотрим, что получится при иных значениях коэффициента (a).

Проведём анализ двух функций:

y=4×2

y=0,25×2

. Составим таблицу значений для первой функции

y=4×2

(x)	(0)	(1)	(-1)	(2)	(-2)	(1.5)	(-1.5)
(y)	(0)	(4)	(4)	(16)	(16)	(9)	(9)

Нанесём точки ((0; 0), (1; 4), (-1; 4), (2; 16), (-2; 16), (1,5; 9), (-1,5; 9)) и соединим их плавной линией.

Заполним таблицу значений для функции

y=0,25×2

(x)	(0)	(1)	(-1)	(2)	(-2)	(4)	(-4)
(y)	(0)	(0.25)	(0.25)	(1)	(1)	(4)	(4)

Нанесём точки ((0; 0), (1; 0,25), (-1; 0,25), (2; 1), (-2; 1), (4; 4), (-4; 4)) и соединим их плавной линией.

Сравни полученные рисунки. Заметно, что оба графика похожи. График такого вида называют параболой.

У каждой параболы есть вершина и ось симметрии (говорят ось параболы). У данных парабол это точка ((0; 0))) и ось (y).

Обрати внимание!

Коэффициент (a) определяет, как быстро изменяется значение функции при изменении аргумента. Чем больше коэффициент (a), тем более круто направлены вверх ветви параболы.

Возьмём отрицательный коэффициент (a=-1) и построим график функции

y=−x2

. Заполним таблицу:

(x)	(0)	(1)	(-1)	(2)	(-2)	(3)	(-3)
(y)	(0)	(-1)	(-1)	(-4)	(-4)	(-9)	(-9)

Отметим точки ((0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; — 9)) и соединим плавной линией.

Эта парабола имеет вершину в точке ((0; 0)), ось симметрии — ось (y). Коэффициент (a<0), поэтому ветви идут вниз.

График функции

y=ax2

— парабола с вершиной в точке ((0; 0)), с симметричными относительно оси ординат ветвями, идущими вверх (если (a>0)) или вниз (если (a<0)).

Графики функций, имеющие противоположные значения коэффициента (a), симметричны друг другу относительно оси абсцисс. Например, графики функций

y=x2

y=−x2

Точно так же симметричны друг другу относительно оси (x) параболы

y=4×2

y=−4×2

Обрати внимание!

График функции (у = — f(x)) симметричен графику функции (у = f(x)) относительно оси абсцисс.

Источник

График функции ${displaystyle y=x^{2}}$

График функции ${displaystyle y=ax^{2}}$ называется параболой.
При a = 1, функция имеет вид ${displaystyle y=x^{2}}$ .

Составим таблицу значений этой функции:

x	-5	-4	-3	-2	-1	0	1	2	3	4	5
y = x²	25	16	9	4	1	0	1	4	9	16	25

Отметив полученные точки на координатной плоскости, соединим их плавной кривой — параболой (см. рисунок).

Если а > 1, график функции ${displaystyle y=ax^{2}}$ получается из графика функции ${displaystyle y=x^{2}}$ растяжением вдоль оси ординат в a раз.

Если 0 < а < 1, т.е. ${displaystyle a={frac {1}{b}}quad (b>1)}$ , график функции ${displaystyle y=ax^{2}}$ получается из графика функции ${displaystyle y=x^{2}}$ сжатием вдоль оси ординат в b раз.

Если а < 0, т.е. , график функции ${displaystyle y=ax^{2}}$ получается из графика функции ${displaystyle y=cx^{2}}$ отражением относительно оси абсцисс.

Эта статья слишком короткая.

Пожалуйста, дополните её ещё несколькими предложениями и уберите это сообщение. Если статья останется недописанной, она может быть выставлена к удалению. Для указания на продолжающуюся работу над статьёй используйте шаблон {{редактирую}}.

Источник

Функция y = ах2, ее график и свойства — Квадратичная функция и ее
график — Квадратичная функция

Цель: рассмотреть свойства и график простейшей квадратичной
функции у = ах2.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных
задач).

III. Изучение нового материала

Одной из наиболее распространенных и изученных функций является
квадратичная функция у = ах2 + bх + с, где х — независимая переменная; а, b и
с- некоторые числа (причем а ≠ 0).

Например, перемещение х тела при движении с ускорением а
описывается квадратичной функций где
x0 и V0 — положение и скорость тела в начальный момент времени t = 0.

С частным случаем квадратичной функции у = х2 (где а = 1, b = 0, с
= 0) школьники уже знакомы. Графиком этой функции является парабола. Продолжим
изучение квадратичных функций. Сначала ограничимся изучением функции у = ах2.

Пример 1

Составим таблицу значений и в одной системе координат построим
графики функций

x	-2	-1,5	-1	-0,5	0,5	1	1,5	2
у = 1/2х2	2	1,12	0,5	0,12	0,12	0,5	1,12	2
у = х2	4	2,25	1	0,25	0,25	1	2,25	4
y = 2х2	8	4,5	2	0,5	0,5	2	4,5	8

Отметив на координатной плоскости точки, приведенные в таблице,
построим графики данных функций. Видно, что при каждом значении х значения
функции у = 1/2х2 в два раза меньше значений функции у = х2, а значения функции
у = 2х2 в два раза больше значений функции у = х2. Другими словами, график
функции у = 1/2х2 можно получить сжатием в два раза вдоль оси ординат графика
функции у = х2. График функции у = 2х2 можно получить растяжением в два раза
вдоль оси ординат графика функции у = х2.

Вообще говоря, график функции у = ах2 можно получить из параболы у
= х2 растяжением вдоль оси ординат в а раз при а > 1 и сжатием вдоль оси
ординат в 1/a раз при 0 < а < 1. График функции у = ах2 так же, как и
график функции у = х2, называют параболой.

Приведем свойства функции у = ах2 при а > 0:

1. Область определения функции — промежуток (-∞; ∞).

2. Если х = 0, то у = 0. Следовательно, график проходит через
начало координат.

3. Если х ≠ 0, то у > 0. Поэтому график расположен в верхней
полуплоскости.

4. Функция четная, т. е. противоположным значениям аргумента
соответствуют равные значения функции у(-х) = у(х). График функции симметричен
относительно оси ординат.

5. Функция убывает в промежутке (-∞; 0] и возрастает в промежутке
[0; ∞).

6. Функция ограничена снизу, у ≥ 0. Наименьшее значение у = 0
функция принимает при х = 0, наибольшего значения функция не имеет.

7. Область значений функции — промежуток [0; +∞).

Обсудим теперь свойства и график квадратичной функции у = ах2 при
a < 0.

Пример 2

Составим таблицу значений и в одной системе координат построим
графики функций у = 1/2х2 и у = -1/2х2.

x	-2	-1,5	-1	-0,5	0,5	1	1,5	2
у = 1/2х2	2	1,12	0,5	0,12	0,12	0,5	1,12	2
у = -1/2х2	-2	-1,12	-0,5	-0,12	-0,12	-0,5	-1,12	-2

Отметим точки, приведенные в таблице, и построим графики данных
функций. Видно, что при каждом значении х значения функции у = -1/2х2
противоположны по знаку значениям функции у = 1/2х2. Поэтому график функции у =
-1/2х2 получается из графика функции у = 1/2х2 с помощью симметрии относительно
оси абсцисс.

Теперь легко сформулировать свойства функции у = ах2 при а < 0:

1. Область определения функции — промежуток (-∞; ∞).

2. Если х = 0, то у = 0. Следовательно, график проходит через
начало координат.

3. Если х ≠ 0, то у < 0. Поэтому график расположен в нижней
полуплоскости.

4. Функция четная, у(-х) = y(x). График функции симметричен
относительно оси ординат.

5. Функция возрастает в промежутке (-∞; 0] и убывает в промежутке
[0; ∞).

6. Функция ограничена сверху, у ≤ 0. Наибольшее значение у = 0
функция принимает при х = 0, наименьшего значения функция не имеет.

7. Область значений функции — промежуток (-∞; 0].

Пример 3

Обсудим монотонность функции у(х) = ах2.

Область определения такой функции — все значения х. Рассмотрим два
произвольных значения х2 и х1, такие, что х2 > x1. Найдем значения функции в
этих точках: у(х2) = ах22 и у(х1) = ах12 и сравним их. Для этого определим знак
разности у(х2) — у(х1) = ах22 – ах12 = а(х2 + х1)(х2 – х1).

Так как х2 > x1, то разность х2 – х1 положительна. Поэтому
разность у(х2) — у(х1) определяется знаком произведения а(х2 + х1). Так как
сумма х2 + х1 может иметь различный знак, то в области определения выделим два
промежутка.

а) Для промежутка х ∈ [0;
+∞) сумма х2 + х1 > 0. Поэтому знак разности у(х2) — y(х1) совпадает со
знаком коэффициента а.

При а > 0 разность у(х2) — y(x1) > 0, т. е. у(х2) > у(х1)
и функция возрастает.

При а < 0 разность у(х2) – y(х1) < 0 т. е. у(х2) < у(х1)
и функция убывает.

б) Для промежутка х ∈ (-∞;
0] сумма х2 + x1 < 0. Поэтому знак разности у(х2) — y(х1) противоположен
знаку коэффициента а.

При а > 0 разность у(х2) — y(х1) < 0, т. е. у(х2) < y(х1)
и функция убывает.

При а > 0 разность у(х2) — y(х1) > 0, т. е. у(х2) > y(х1)
и функция возрастает.

Ads by optAd360

Пример 4

Построим график функции

Область определения функции задается условием 2х — 4 ≠ 0, т. е. х
≠ 2. Разложим числитель и знаменатель дроби на множители и сократим ее.
Получаем:

Построим параболу у = 1/2х2 и удалим из нее точку с абсциссой х =
2 (показана стрелками).

Пример 5

При каких значениях а парабола у = -1/2х2 и прямая у = 3х + а не
имеют общих точек?

Предположим, что данные линии имеют общую точку. Тогда ее
координаты удовлетворяют системе уравнений

Попробуем решить эту систему. Так как в уравнениях левые части
одинаковы, то равны и правые.

Получаем уравнение -1/2х2 = 3х + а, или 0 = х2 + 6х + 2а. На самом
деле данные линии общих точек не имеют. Это означает, что полученное квадратное
уравнение решений не имеет. Поэтому его дискриминант D = 36 — 8а < 0, откуда
а > 36/8 = 4,5.

На рисунке приведена иллюстрация задачи. Очевидно, прямая у = 3х +
а пересекает ось ординат в точке у = а. При увеличении а прямая смещается вверх
параллельно самой себе. Выполненные расчеты показывают, что прямая при а <
4,5 пересекает параболу в двух точках (линия 1), при а = 4,5 касается параболы
в одной точке (линия 2), при а > 4,5 не имеет общих точек с параболой (линия
3).

IV. Контрольные вопросы

1. Какая функция называется квадратичной?

2. Как называют график квадратичной функции?

3. Приведите основные свойства и график функции у = ах2 при а >
0.

4. Приведите основные свойства и график функции у = ах2 при а <
0.

5. Как из графика функции у = x2 получить график функции у = ах2
при а > 0.

V. Задание на уроке

№215,217,218,219

VI. Задание на дом

П. 2.2 № 216

VII. Творческие задания

1. Постройте график функции.