Как составит теорему по геометрии 7 класс - Исправление недочетов и поиск решений вместе с Examum.ru

«Краткий курс геометрии 7 класс» — это краткие теоретические сведения по курсу геометрии за 7 класс (определения, теоремы, основные свойства).

☑ 1. Простейшие геометрические фигуры и их свойства

Аксиома. Основное свойство прямой: Через любые две точки можно провести прямую, и притом только одну.
Определение. Пересекающиеся прямые: Две прямые, имеющие общую точку, называют пересекающимися.
ТЕОРЕМА. О двух пересекающихся прямых: Любые две пересекающиеся прямые имеют только одну общую точку.
Два отрезка называют равными, если их можно совместить наложением.
Аксиома. Основное свойство длины отрезка: Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и т. е. АВ = АС + СВ.
Расстоянием между точками называют длину отрезка АВ.
Два луча, имеющие общее начало и лежащие на одной прямой, называют дополнительными.

☑ 2. Углы

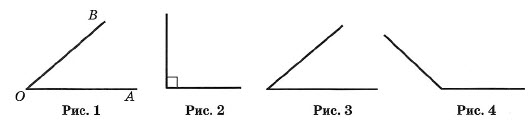
Углом называется геометрическая фигура (рис. 1), образованная двумя лучами, исходящими из одной точки.
Точка О — вершина угла, а лучи ОА и ОБ — стороны угла. Обозначение: ∠AOB или ∠ab.
Угол в 90° называется прямым (рис. 2).
Угол, меньший прямого, называется острым (рис. 3).
Угол, больший прямого, но меньший развернутого, называется тупым (рис. 4).

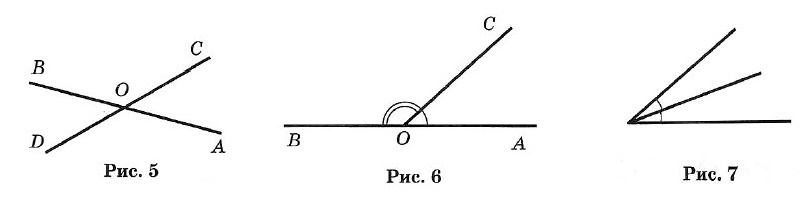
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого (рис. 5).
∠AOC и ∠DOB; ∠BOC и ∠AOD — вертикальные.
Вертикальные углы равны: ∠AOC = ∠DOB и ∠BOC = ∠AOD.
Два угла называются смежными, если у них одна сторона общая, а две другие составляют прямую линию (рис. 6), ∠AOC и ∠BOC — смежные.

Сумма смежных углов равна 180°.
Биссектрисой угла называется луч, проходящий между сторонами угла и делящий его пополам (рис. 7).
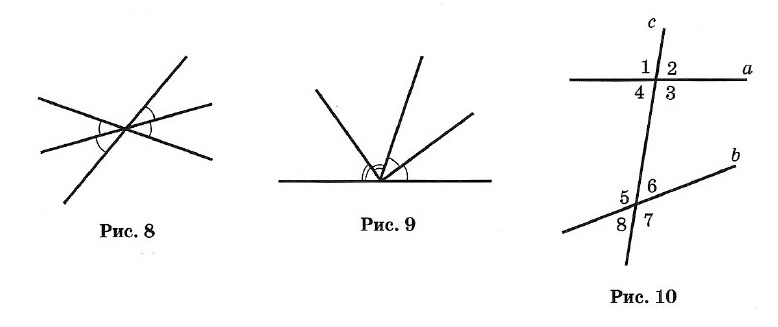
Биссектрисы вертикальных углов составляют продолжение друг друга (рис. 8).
Биссектрисы смежных углов взаимно перпендикулярны (рис. 9).

При пересечении двух прямых a и b третьей с (секущей) образуется 8 углов (рис. 10):

соответственные углы: ∠1 и ∠5, ∠2 и ∠6, ∠4 и ∠8, ∠3 и ∠7;
внутренние накрест лежащие: ∠4 и ∠6, ∠3 и ∠5;
внешние накрест лежащие: ∠1 и ∠7, ∠2 и ∠8;
внутренние односторонние: ∠4 и ∠5, ∠3 и ∠6;
внешние односторонние: ∠1 и ∠8, ∠2 и ∠7.

☑ 3. Параллельные прямые

Две прямые называют параллельными, если они не пересекаются.
Аксиома параллельности прямых: Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Признаки параллельности двух прямых:
• Две прямые, перпендикулярные третьей прямой, параллельны.
• Если накрест лежащие углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
• Если сумма односторонних углов, образующихся при пересечении двух прямых секущей, равна 180°, то прямые параллельны.
• Если соответственные углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
Свойства параллельных прямых:
• Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.
• Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.
• Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180°.
Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

☑ 4. Треугольник

Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, последовательно соединяющих эти точки.
Точки А, В, С — вершины треугольника АВС.
Отрезки АВ, ВС и АС — стороны, ∠A, ∠B и ∠C — углы. ∠A + ∠B + ∠C = 180°.
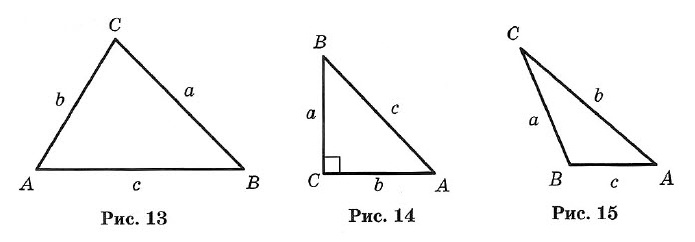
Стороны треугольника часто обозначают малыми буквами (рис. 13): АВ = с, ВС = а, АС = b.
Р = а + b + с — периметр треугольника.

Треугольник, у которого все углы острые, называется остроугольным (см. рис. 13).
Треугольник, у которого есть прямой угол, называется прямоугольным (рис. 14).
Стороны, образующие прямой угол, называются катетами (а и b), а сторона, лежащая против прямого угла, — гипотенузой (с).
Треугольник с тупым углом называется тупоугольным (рис. 15).

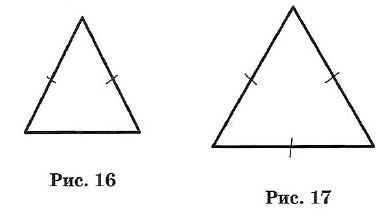
Треугольник, у которого две стороны равны, называется равнобедренным (рис. 16).
Равные стороны называются боковыми, а третья сторона — основанием равнобедренного треугольника.
Треугольник, у которого все стороны равны, называется равносторонним (рис. 17).
Каждый угол равностороннего треугольника равен 60°.
Свойства равнобедренного треугольника:
1. Углы при основании равны.
2. Биссектриса, проведенная к основанию, является одновременно медианой и высотой.
3. Высота, проведенная к основанию, является одновременно медианой и биссектрисой.
4. Медиана, проведенная к основанию, является одновременно высотой и биссектрисой.

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника (рис. 18). ∠CBD — внешний угол треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним (см. рис. 18): ∠CBD = ∠A + ∠C.
Отрезок, соединяющий середины двух сторон, называется средней линией треугольника (рис. 19).

☑ 5. Признаки равенства треугольников

I признак (признак равенства по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 20). АВ = А₁В₁, АС = А₁С₁, ∠A = ∠A₁

II признак (признак равенства по стороне и прилежащим к ней углам).
Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 21). АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁

III признак (признак равенства по трем сторонам).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 22). АВ = А₁В₁, ВС = B₁C₁, АС =А₁С₁.

Вы смотрите:
Краткий курс геометрии 7 класс

☑ 6. Соотношения между сторонами и углами треугольника

ТЕОРЕМА о сумме углов треугольника. Сумма углов треугольника равна 180°. ∠A + ∠B + ∠C = 180°.
ТЕОРЕМА о соотношениях между сторонами и углами треугольника. В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.
Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.
Следствие 2. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
ТЕОРЕМА о неравенстве треугольника. Каждая сторона треугольника меньше суммы двух других сторон: а < b + с, b < а + с, с < а + b.

☑ 7. Определение вида треугольника по его сторонам

Пусть с — наибольшая сторона, тогда:
а) если с² < а² + b², то треугольник остроугольный;
б) если с² > а² + b², то треугольник тупоугольный;
в) если с² = а² + b², то треугольник прямоугольный.

☑ 8. Прямоугольные треугольники (некоторые свойства)

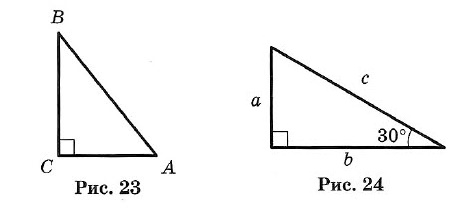
1. Сумма острых углов равна 90° (рис. 23). ∠A + ∠B = 90°.
2. Катет, лежащий против угла в 30°, равен половине гипотенузы (рис. 24). a = c/2
3. Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° (рис. 24).

☑ 9. Признаки равенства прямоугольных треугольников

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис. 25). АС = А₁С₁, ВС = В₁С₁.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны (рис. 26). АС = А₁С₁, ∠A = ∠A₁.

3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны (рис. 27). АВ = А₁В₁, ∠A = ∠A₁.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис. 28). АВ = А₁В₁, АС = А₁С₁

Краткий курс геометрии 7 класс

☑ 10. Четыре замечательные точки треугольника

С каждым треугольником связаны 4 точки:
1) точка пересечения медиан;
2) точка пересечения биссектрис;
3) точка пересечения высот (или их продолжений);
4) точка пересечения серединных перпендикуляров к сторонам.
Эти четыре точки называются замечательными точками треугольника.
Высотой треугольника называется длина перпендикуляра, опущенного из любой его вершины на противолежащую сторону или ее продолжение.

В тупоугольном треугольнике (рис. 29) две высоты падают на продолжение сторон и лежат вне треугольника, а третья внутри.
В остроугольном треугольнике (рис. 30) все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты одновременно служат и высотами (рис. 31).
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном треугольнике он совпадает с вершиной прямого угла.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

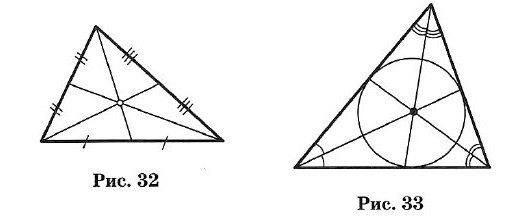
Три медианы треугольника пересекаются в одной точке, которая является центром тяжести треугольника (рис. 32).
Эта точка делит каждую медиану в отношении 2 : 1 (считая от соответствующей вершины).
Биссектрисой треугольника называется отрезок биссектрисы угла от вершины до пересечения с противолежащей стороной.
Три биссектрисы треугольника пересекаются в одной точке, которая является центром вписанного круга (рис. 33).
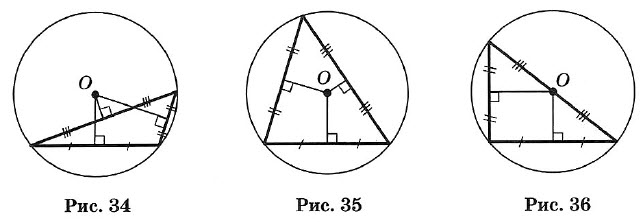
Три перпендикуляра к сторонам треугольника, проведенные через их середины (рис. 34, 35, 36), пересекаются в одной точке, которая является центром описанной окружности.

В тупоугольном треугольнике (рис. 34) эта точка лежит вне треугольника, в остроугольном (рис. 35) — внутри, в прямоугольном — на середине гипотенузы (рис. 36).
Ортоцентр, центр тяжести, центр вписанной и описанной окружностей совпадают друг с другом только в равностороннем треугольнике.

☑ 11. Окружность

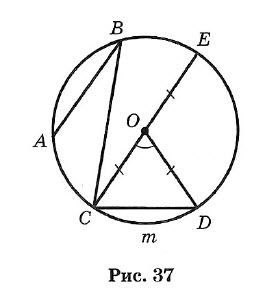
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R. На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр. Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

☑ 12. Свойства касательных к окружности

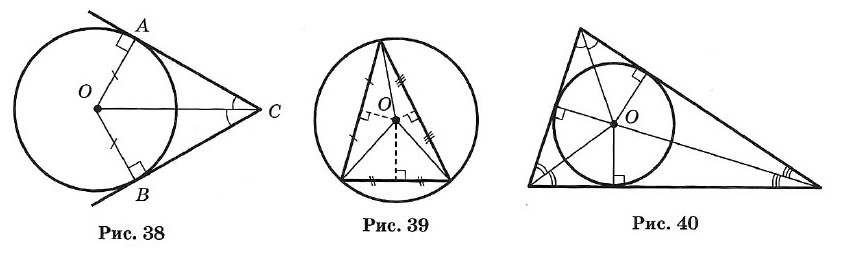
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.

☑ 13. Окружность и треугольник

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

Вы смотрели «Краткий курс геометрии 7 класс» — все определения, теоремы и основные свойства из Геометрии за 7 класс. Выберите дальнейшие действия:

Посмотреть Краткий курс алгебры за 7 класс
Посмотреть Краткий курс геометрии за 8 класс
Вернуться к Списку конспектов по геометрии

(с) В учебных целях использованы цитаты из следующих пособий:
— «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ (базовый уровень): 7 класс / Э.Н.Бабаян. — Ростов н/Д: Феникс»;
— «Геометрия. 7-9 классы : учеб. для общеобразоват. организаций / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — М. : Просвещение»;
— «Геометрия 7 класс : учебник для учащихся общеобразовательных организаций /А.Г.Мерзляк, В.Б.Полонский, М.С.Якир — М.: Вентана-Графт».

Источник

«Если две стороны и угол между
ними одного треугольника равны двум сторонам и углу между ними другого
треугольника, то эти треугольники равны.»

Сокращенно его называют равенство «по
двум сторонам и углу между ними».

Прежде чем перейти к доказательству теоремы необходимо
вспомнить, что называют треугольником и в каком случае можно утверждать, что
два треугольника равны.

Что такое
треугольник и когда они считаются равными?

Треугольник –
это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии,
что они не лежат на одной прямой. Эти точки считаются вершинами треугольника.
А соединяющие их отрезки – сторонами).

На рисунке 1 представлен треугольник ABС. Который имеет три
вершины (А, В и С). И стороны – АВ, АС и ВС.

Рисунок
1

Треугольники считаются равными, когда все их стороны и углы
соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны,
треугольники называются подобными).
Таким образом очевидно, что равные треугольники можно наложить друг на друга –
и они полностью совпадут.

Доказательство первого
признака равенства треугольников

Дано:

Два
треугольника: ABC и DEF (рисунок 2).

Рисунок 2

По условию
теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ =
EF). Углы между отрезками также равны (т.е. ∠АСВ
= ∠EFD).

Доказать,
что треугольник ABC равен треугольнику DEF.

Доказательство:

1.
Поскольку имеется равенство углов (∠АСВ
= ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина
С совпадала с вершиной F.

2.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.

3.
А поскольку отрезки двух треугольников равны между собой (АС = FD
и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.

4.
Это в свою очередь даст совмещение вершин А и D, В и Е.

5.
Следовательно, треугольники полностью совместятся, а значит, они
равны.

Теорема
доказана.

Второй
признак равенства треугольников

Если
сторона и два прилежащих к ней угла одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого треугольника, то такие
треугольники равны.

MN=PR∡N=∡R∡M=∡P

Как
и в доказательстве первого признака, нужно убедиться, достаточно ли этого
для равенства треугольников, можно ли их полностью совместить?

1. Так какMN=PR, то эти отрезки совмещаются, если совместить их конечные точки.

2.
Так как∡N=∡R и∡M=∡P, то лучи MK и NK наложатся соответственно на лучи PT и RT.

3. Если
совпадают лучи, то совпадают точки их пересечения K и T.

4. Совмещены
все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит они
равны.

Третий
признак равенства треугольников

Если три
стороны одного треугольника соответственно равны трём сторонам другого треугольника,
то такие треугольники равны.

MN=PRKN=TRMK=PT

Опять
попробуем совместить треугольникиΔMNK и ΔPRT наложением и убедится, что
соответственно равные стороны гарантирует и равенство соответственных углов
этих треугольников и они полностью совпадут.

Совместим,
например, одинаковые отрезки MK иPT. Допустим, что точки N и R при этом не совмещаются.

Пусть O — середина отрезка NR.
Соответственно данной информацииMN=PR, KN=TR. Треугольники MNR и KNR равнобедренные с общим основанием NR.

Поэтому
их медианы MO и KO являются
высотами, значит перпендикулярны NR.
Прямые MO и KO не
совпадают, так как точки M, K, O не
лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы
пришли к противоречию.

Доказано,
что должны совместиться и вершины N и R.

Третий
признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда
говорят, что треугольник — жёсткая фигура.
Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника
такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.

Теорема
4.6. Из любой точки, не лежащей на данной прямой, можно опустить на эту
прямую перпендикуляр, и только один.

Доказательство.
Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через
какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через
точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как
прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна
и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к
прямой а.

Докажем
единственность перпендикуляра АВ. Допустим,

существует
другой перпендикуляр АС. Тогда у треугольника ABC будут два прямых угла. А это,
как мы знаем, невозможно. Теорема доказана.

Медианы,
биссектрисы и высоты треугольника

Медиана треугольника —
это отрезок, соединяющий вершину треугольника с серединой противолежащей
стороны.

Поэтому
для построения медианы необходимо выполнить следующие действия:
1. Найти середину стороны;
2. Соединить точку, являющуюся серединой стороны треугольника, с противолежащей
вершиной отрезком — это и будет медиана.

У
треугольника три стороны, следовательно, можно построить три медианы.

Все
медианы пересекаются в одной точке.

Биссектриса треугольника —
это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на
противоположной стороне.

Поэтому,
для построения биссектрисы необходимо выполнить следующие действия:
1. Построить биссектрису какого-либо угла треугольника (биссектриса
угла — это луч, выходящий из вершины угла и делящий его на две равные
части);
2. Найти точку пересечения биссектрисы угла треугольника с противоположной
стороной;
3. Соединить вершину треугольника с точкой пересечения на противоположной
стороне отрезком — это и будет биссектриса треугольника.

У
треугольника три угла и три биссектрисы.

Все
биссектрисы пересекаются в одной точке.

Высота треугольника —
это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей
противоположную сторону.

Поэтому,
для построения высоты необходимо выполнить следующие действия:
1. Провести прямую, содержащую одну из сторон треугольника (в
случае, если проводится высота из вершины острого угла в тупоугольном
треугольнике);
2. Из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к
ней (перпендикуляр — это отрезок, проведённый из точки к прямой,
составляющей с ней угол 90°) —
это и будет высота.

Также
как медианы и биссектрисы, треугольник имеет три высоты.

Высоты треугольника
пересекаются в одной точке.

Но,
как выше упомянуто, для некоторых видов треугольников построение высот и точки
их пересечения отличается.

Если
треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать
высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот
является общая вершина перпендикулярных сторон.

Если
треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят
вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты,
пересекаются вне треугольника.

Обрати внимание!

Если из одной и той же
вершины провести медиану, биссектрису и высоту, то медиана окажется самым
длинным отрезком, а высота — самим коротким отрезком.

Равнобедренный
треугольник

Если
у треугольника две стороны равны, то такой треугольник называют равнобедренным.

Равные
стороны называют боковыми, а
третью сторону — основанием.

AB=BC — боковые стороны , AC —
основание.

Если
у треугольника все три стороны равны, то такой треугольник является равносторонним.

Равнобедренный
треугольник имеет некоторые свойства, которые не имеют треугольники с разными
сторонами.

1.
В равнобедренном треугольнике углы при основании равны.

2.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является
медианой и высотой.

3.
В равнобедренном треугольнике медиана, проведённая к основанию, является
биссектрисой и высотой.

4. В
равнобедренном треугольнике высота, проведённая к основанию, является
биссектрисой и медианой.

Первое
и второе свойство можно доказать, если докажем равенство двух
треугольников, которые образуются, когда углу напротив основания провести
биссектрису BD.

Рассмотрим
равнобедренный треугольник ABC с
основанием AC и докажем, чтоΔABD=ΔCBD.

Пусть BD — биссектриса треугольника ABC. ΔABD=ΔCBD по
первому признаку равенства треугольников (AB=BC по условию, BD —
общая сторона, ∡ABD=∡CBD, так как BD —
биссектриса).

У
равных треугольников равны все соответствующие элементы:

1. ∡A=∡C — доказано, что прилежащие основанию углы равны.

2. AD=DC — доказано, что биссектриса является медианой.

3. ∡ADB=∡CDB —
так как смежные углы, сумма которых180°, равны,
то каждый из них равен90°, то есть медиана является
высотой.

Можно
очень легко самостоятельно доказать и третье и четвёртое свойство.

1. Первый признак параллельности.

Если при
пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти
прямые параллельны.

Пусть прямые АВ и СD
пересечены прямой ЕF и / 1 = / 2. Возьмём
точку О — середину отрезка КL секущей ЕF (черт. 189).

Опустим из точки О
перпендикуляр ОМ на прямую АВ и продолжим его до пересечения с прямой СD,
АВ_|_МN. Докажем, что и СD_|_МN.
Для этого рассмотрим два треугольника: МОЕ и NОК. Эти треугольники равны между
собой. В самом деле: / 1 = / 2 по условию
теоремы; ОK = ОL — по построению;
/ МОL = / NОК, как вертикальные углы. Таким
образом, сторона и два прилежащих к ней угла одного треугольника соответственно
равны стороне и двум прилежащим к ней углам другого треугольника;
следовательно, / МОL = / NОК, а
отсюда и
/ LМО = / КNО, но / LМО прямой,
значит, и / КNО тоже прямой. Таким образом, прямые АВ
и СD перпендикулярны к одной и той же прямой МN, следовательно, они
параллельны (§ 33), что и требовалось доказать.

Примечание. Пересечение прямых МО и СD
может быть установлено путём поворота треугольника МОL вокруг точки О на 180°.

2. Второй признак параллельности.

Посмотрим, будут ли
параллельны прямые АВ и СD, если при пересечении их третьей прямой ЕF равны
соответственные углы.

Пусть какие-нибудь
соответственные углы равны, например / 3 = / 2
(черт. 190);
/ 3 = / 1, как углы вертикальные; значит, / 2
будет равен / 1. Но углы 2 и 1 — внутренние накрест лежащие
углы, а мы уже знаем, что если при пересечении двух прямых третьей внутренние
накрест лежащие углы равны, то эти прямые параллельны. Следовательно, АВ || СD.

Если при
пересечении двух прямых третьей соответственные углы равны, то эти две прямые
параллельны.

На этом свойстве основано
построение параллельных прямых при помощи линейки и чертёжного треугольника.
Выполняется это следующим образом.

Приложим треугольник к
линейке так, как это показано на чертеже 191. Будем передвигать треугольник
так, чтобы одна его сторона скользила по линейке, а по какой-либо другой
стороне треугольника проведём несколько прямых. Эти прямые будут параллельны.

3. Третий признак параллельности.

Пусть нам известно, что
при пересечении двух прямых АВ и СD третьей прямой сумма каких-нибудь
внутренних односторонних углов равна 2d (или 180°). Будут ли в этом
случае прямые АВ и СD параллельны (черт. 192).

Пусть / 1
и / 2—внутренние односторонние углы и в сумме составляют 2d.
Но / 3 + / 2 = 2d, как углы смежные.
Следовательно, / 1 + / 2 = / 3+ / 2.

Отсюда / 1
= / 3, а эти углы внутренние накрест лежащие. Следовательно,
АВ || СD.

Если при
пересечении двух прямых третьей сумма внутренних односторонних углов
равна 2d,
то эти две прямые параллельны.

Признак —
это некоторый факт, благодаря которому мы устанавливаем справедливость
интересующего нас суждения о некотором объекте.

Если при
пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две
прямые параллельны.

Свойство —
если мы уверены в справедливости суждения, мы формулируем свойство
объекта.

Если две
прямые параллельны, то при пересечении их с третьей секущей накрест лежащие
углы равны.

Аксиома,
в свою очередь, такая истина, которую не надо доказывать. В каждой науке есть
свои аксиомы, на справедливость которых строят все дальнейшие суждения и
их доказательства.

Аксиома
параллельных прямых.

В одной
плоскости с заданной прямой через точку, не лежащую на этой прямой, можно
провести только одну прямую, параллельную заданной прямой.

Иногда
эту аксиому называют как одно из свойств параллельных прямых, но на
справедливости этой аксиомы строятся многие доказательства в геометрии.

Другие
свойства параллельных прямых.

1.
Если одна из пары параллельных прямых параллельна третьей прямой, то и другая
прямая параллельна третьей прямой.

2. Если
некая прямая пересекает одну из двух параллельных прямых, то она пересекает и
вторую параллельную прямую.

Эти
свойства в отличии от аксиомы нужно доказать.

Докажем
1. Свойство.

Даны
две параллельные прямые a и b. Верно ли, если прямая c параллельна
прямой a, то она параллельна и прямой b?

Используем
противоположное суждение.

Допустим,
что возможна ситуация, когда прямая c параллельна
одной из параллельных прямых — прямой a,
пересекает другую прямую b в
некоторой точке K.

Получается
противоречие с аксиомой параллельных прямых. Мы имеем ситуацию, когда через
точку проходят две пересекающиеся прямые, которые параллельны одной и той же
прямой a. Такого не может быть, значит прямые b и cпересекаться не могут.

Мы
доказали, что верно — если одна из пары параллельных прямых параллельна третьей
прямой, то и другая прямая параллельна третьей прямой.

Попробуй доказать самостоятельно 2. Свойство.

Если
некая прямая c пересекает
одну из двух параллельных прямых a,
то она пересекает и вторую параллельную прямую b.

Таким
же методом от противоположного суждения попробуй представить, что возможно
ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает
другую.

Свойства
углов, которые образуются при пересечении двух параллельных прямых с третьей
секущей мы уже назвали в первой части теории.

При
пересечении двух параллельных прямых третьей секущей:

—
накрест лежащие углы равны,

—
соответственные углы равны,

— сумма
односторонних углов равна 180°.

Теорема об
углах, образованных двумя параллельными прямыми и секущей

Теорема об углах, образованных двумя параллельными прямыми и
секущей

Теоремы

1.
Если две параллельные прямые пересечены секущей, накрест лежащие
углы равны.

2.
Если две параллельные прямые пересечены секущей, то
соответственные углы равны.

3.
Если две параллельные прямые пересечены секущей, то сумма односторонних
углов равна 180°.

4.
Если при пересечении двух прямых секущей накрест лежащие углы
равны, топрямые параллельны.

Доказательство

1. Пусть параллельные прямые a и b пересечены
секущей MN (c). Докажем, что накрест лежащие углы 3 и 6
равны. Допустим, что углы 3 и 6 не равны. Отложим от луча MN угол PMN,
равный углу 6, так, чтобы угол PMN и угол 6 были накрест
лежащими углами при пересечении прямых МР и b секущей MN.
По построению эти накрест лежащие углы равны, поэтому МР||b.
Мы выяснили, что через точку М проходят две прямые
(прямые a и МР), параллельные прямой b.
Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно
и угол 3 равен углу 6.

3.4.
Углы с соответственно параллельными и перпендикулярными сторонами

Теорема 1

Если стороны
одного угла соответственно параллельны сторонам другого угла, то такие углы
равны или в сумме составляют .

Дано: || , || .

Требуется доказать , , =, =.

Доказательство:

(соответственные при
параллельных  и  и секущей ). (соответственные при
параллельных  и  и секущей ). . (вертикальные), поэтому . = и = (по свойству смежных углов). Эти
два равенства останутся верными, если  заменим равным углом . Тогда = и =. Что и требовалось доказать.

Теорема 2

Если стороны
одного угла соответственно перпендикулярны сторонам другого угла, то такие углы
равны или в сумме составляют .

Дано: , , и .

Требуется доказать: ,,,=, =.

Доказательство:

=— и =—, поэтому . || и ||. (по теореме 1). Отсюда . Тогда , =, =.

1. Сумма углов треугольника

Теория:

Сумма
углов треугольника равна 180°.

Доказательство.

Рассмотрим
произвольный треугольник KLM и докажем, что ∡K+∡L+∡M=180°.

Проведём
через вершину L прямую a, параллельную стороне KM.

Углы, обозначенные 1, являются накрест лежащими углами при пересечении
параллельных прямых a и KMсекущей KL, а углы, обозначенные 2 — накрест лежащими углами при пересечении тех же
параллельных прямых секущей ML.

Очевидно,
сумма углов 1, 2 и 3 равна развёрнутому углу с вершиной L, т. е.
∡1+∡2+∡3= 180°или ∡K+∡L+∡M=180°.

Теорема
доказана.

Следствия
из теоремы о сумме углов треугольника

Следствие 1. Сумма
острых углов прямоугольного треугольника равна 90°.

Следствие 2. В равнобедренном
прямоугольном треугольнике каждый острый угол равен 45°.

Следствие 3. В
равностороннем треугольнике каждый угол равен 60°.

Следствие 4. В любом
треугольнике либо все углы острые, либо два угла острые, а третий — тупой или
прямой.

Следствие 5. Внешний
угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство.

Из
равенств ∡KML+∡BML= 180° и ∡K+∡L+∡KML=180° получаем, что ∡BML=∡K+∡L.

Остроугольный,
прямоугольный и тупоугольный треугольники

Как
гласит четвёртое следствие из теоремы о сумме углов треугольника, можно
выделить три вида треугольников в зависимости от углов.

У
треугольника KLM все углы острые.

У
треугольника KMN угол K=90°.

У
прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.

На рисунке MN — гипотенуза, MK и KN — катеты.

У
треугольника KLM один угол тупой.

Соотношения
между сторонами и углами треугольника. Неравенство треугольника

Теорема 1. В
треугольнике против большей стороны лежит больший угол.

Доказательство. Пусть
в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).

Рис.1

Докажем, что ∠ С > ∠
В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD
< АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является
частью угла С и, значит, ∠ C > ∠
1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2
равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠
С > ∠ 1, ∠ 1 = ∠
2, ∠ 2 > ∠ B. Отсюда следует, что ∠
С > ∠ В.

Справедлива и обратная теорема (ее доказательство проводится
методом от противного).

Теорема 2. В
треугольнике против большего угла лежит большая сторона.

Из теоремы 1 вытекает

Следствие 1. Если два угла треугольника равны, то
треугольник равнобедренный (признак равнобедренного
треугольника).

Доказательство следствия проводится методом от противного.

Из следствия 1 следует, что если три угла треугольника равны, то
треугольник равносторонний.

Из теоремы 2 получаем

Следствие 3. В прямоугольном треугольнике гипотенуза
больше катета.

С использованием теоремы 2 устанавливается следующая теорема.

Теорема 3. Каждая
сторона треугольника меньше суммы двух других сторон.

Следствие 4. Для любых трех точек А, В и С, не
лежащих на одной прямой, справедливы неравенства:
АВ < АС + СВ, АС <
АВ + ВС, ВС < ВА + АС.

Каждое из этих неравенств называется неравенством треугольника.

1. Прямоугольные треугольники

Теория:

Свойства
прямоугольного треугольника

Сумма
двух острых углов прямоугольного треугольника равна 90°.

Сумма
углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника∡1+∡2=90°.

Катет
прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее
катета против угла в 30°).

Рассмотрим
прямоугольный треугольник ABC, в котором∡A — прямой, ∡B=30°и значит, что ∡C=60°.

Докажем,
что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD как показано на рисунке.

Получим
треугольник BCD, в котором∡B=∡D=60°, поэтому DC=BC. Но DC=2AC. Следовательно, BC=2AC.

Справедливо
и обратное суждение.

Если
катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в
два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства
прямоугольных треугольников

В прямоугольном треугольнике угол между катетами прямой, а
любые два прямых угла равны. Поэтому согласно теоремам о первом и втором
признаках равенства треугольников справедливы следующие утверждения:

если катеты одного
прямоугольника соответственно равны катетам другого прямоугольного
треугольника, то такие треугольники равны (рис. 101);

если катет и
прилежащий к нему острый угол одного прямоугольного треугольника соответственно
равны катету и прилежащему к нему острому углу другого прямоугольного
треугольника, то такие треугольники равны (рис. 102).

Учитывая, что сумма двух острых углов прямоугольного треугольника равна 90°,
получаем еще два признака равенства прямоугольных треугольников:

если гипотенуза и
острый угол одного прямоугольного треугольника соответственно равны гипотенузе
и острому углу другого прямоугольного треугольника, то такие треугольники равны
(рис. 103);

если катет и
противолежащий ему угол одного прямоугольного треугольника соответственно
равны катету и противолежащему углу другого прямоугольного треугольника, то
такие треугольники равны (рис. 104).

В самом деле, в таких треугольниках два других острых угла
также равны, поэтому указанные треугольники равны по второму признаку равенства
треугольников.

Рассмотрим еще один признак равенства прямоугольных
треугольников.

Теорема. Если
гипотенуза и катет одного прямоугольного треугольника соответственно равны
гипотенузе и катету другого прямоугольного треугольника, то такие треугольники
равны.

Доказательство. Рассмотрим прямоугольные треугольники ABC и A₁B₁C₁, у которых
углы A и A₁ прямые, BC = B₁C₁ и AB = A₁B₁ (рис.
105, а). Докажем, что эти треугольники равны.

Приложим треугольник ABC к треугольнику A₁B₁C₁ так, чтобы
вершина A совместилась с вершиной A₁, вершина B
– с вершиной B₁, а вершины C и C₁ оказались
по разные стороны от прямой A₁B₁ (рис.
105, б). Поскольку ∠CA₁C₁ = 90° +
90° = 180°, то точки C, A₁ и C₁ будут лежать на одной прямой. Треугольник CB₁C₁
равнобедренный, поэтому ∠C = ∠C₁. Следовательно, прямоугольные треугольники ABC и A₁B₁C равны по
гипотенузе (BC = B₁C₁) и острому углу (∠C = ∠C₁). Теорема
доказана.

Расстояние
между двумя параллельными прямыми – определение.

Определение расстояния
между двумя параллельными прямыми дается через расстояние от точки до прямой.

Определение.

Расстояние
между двумя параллельными прямыми – это расстояние
от произвольной точки одной из параллельных прямых до другой прямой.

Для наглядности
изобразим две параллельные прямые a и b,
отметим на прямой апроизвольную
точку М₁, опустим перпендикуляр из
точки М₁ на прямую b,
обозначив его H₁.
Отрезок М₁H₁ соответствует
расстоянию между параллельными прямыми a и b.

Приведенное определение
расстояния между двумя параллельными прямыми справедливо как для параллельных
прямых на плоскости, так и для прямых в трехмерном пространстве. Более того,
такое определение расстояния между двумя параллельными прямыми принято не
случайно. Оно тесно связано со следующей теоремой.

Теорема.

Все
точки одной из двух параллельных прямых удалены на одинаковое расстояние от
другой прямой.

Доказательство.

Рассмотрим параллельные
прямые a и b.
Отметим на прямой a точку М₁,
опустим из нее перпендикуляр на прямую b.
Основание этого перпендикуляра обозначим как H₁.
Тогда длина перпендикуляра М₁H₁ есть
расстояние между параллельными прямыми a и b по
определению. Докажем, что равно ,
где М₂ – произвольная точка
прямой a, отличная от точки M₁,
а H₂ – основание
перпендикуляра, проведенного из точки М₂ на
прямую b. Доказав этот факт, мы докажем и саму
теорему.

Так как
внутренние накрест лежащие углы, образованные при пересечении двух параллельных
прямых секущей, равны (об этом говорилось в статье параллельные прямые, параллельность прямых),
то , а прямая M₂H₂,
перпендикулярная прямой b по
построению, перпендикулярна и прямой a.
Тогда треугольники М₁H₁H₂ и М₂М₁H₂ прямоугольные,
и, более того, они равны по гипотенузе и острому углу: М₁H₂ –
общая гипотенуза, . Из равенства треугольников следует
равенство их соответствующих сторон, поэтому, . Теорема
доказана.

Источник

Середина отрезка- точка, делящая отрезок пополам.

Биссектриса- луч, исходящий из вершины угла и делящий его на два равных угла.

Медиана- отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Высота- перпендикуляр, проведенный из вершины угла к прямой, содержащей противолежащую сторону.

Равнобедренный треугольник, если две его стороны равны.

Окружность- геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от одной единственной точки-центр окружности.

Хорда- отрезок, соединяющий две точки, лежащие на окружности.

Диаметр- хорда, проходящая через центр окружности.

Дуга- часть окружности, полученная делением этой окружности двумя точками.

Параллельные прямые- две не пересекающиеся на плоскости прямые.

Секущая к двум прямым-прямая, пересекающая данные прямые в двух точках.

Гипотенуза- сторона прямоугольного треугольника, лежащая напротив прямого угла. Две другие стороны прямоугольного треугольника-катеты.

Неравенства треугольника: АВ

Расстояние между прямыми- расстояние от любой точки одной из параллельных прямых до другой прямой.

1.1. Через любые две точки можно провести только одну прямую.

1.2. Две прямые имеют либо одну общую точку, либо ни одной.

1.3. Две геометрические фигуры называются равными, если их можно совместить наложением.

1.4. Равные отрезки имеют равные длины.

1.6. Вертикальные углы равны.

1.8. Две прямые, перпендикулярные к третьей, не пересекаются.

2.1. Признаки равенства треугольников:

Теорема 1 (по двум сторонам и углу). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

Теорема 2 (по стороне и двум углам). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

Теорема 3 (по трём сторонам). Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то эти треугольники равны.

2.3. Медиана делит сторону на два равных отрезка.

2.4. Свойства равнобедренного треугольника:

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

3.1. Признаки параллельности двух прямых (обратные теоремы тоже справедливы):

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то данные прямые параллельны.

Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3.2. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствия из аксиомы:

4.2. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

4.5. Теорема (о соотношении между сторонами и углами треугольника). В треугольнике против большей стороны лежит больший угол и против большего угла лежит большая сторона.

Следствия из теоремы:

4.6. Каждая сторона треугольника меньше суммы двух других сторон.

4.7. Свойства прямоугольного треугольника:

4.8. Признаки равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то эти треугольники равны.

2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого треугольника, то эти треугольники равны.

Теорема 1. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузы и острому углу другого прямоугольного треугольника, то эти треугольники равны.

Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

4.9. Угол падения равен углу отражения.

4.10. Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Источник

Геометрия 7 класс все правила и теоремы и доказательства определения

Точка — самая простая геометрическая фигура. Это единственная фигура, которую нельзя разбить на части. Прямая — это геометрическая фигура, обладающая определёнными свойствами.

$ 2. Отрезок и его длина.

$ 3. Луч. Угол. Измерение углов.

Проведём прямую АВ и отметим на ней произвольную точку О. Эта точка разбивает прямую на две части. Каждую из этих частей вместе с точкой О называют лучом или полупрямой. Точку О называют началом луча.

На рисунке 46 изображена фигура, состоящая из двух лучей ОА и ОВ, имеющих общее начало. Эта фигура делит плоскость на две части, выделенные разными цветами. Каждую из этих частей вместе с лучами ОА и ОВ называют углом. Лучи ОА и ОВ называют сторонами угла, а точку О — вершиной угла.

$ 4. Смежные и вертикальные углы.

$ 5. Перпендикулярные прямые

$ 6. Аксиомы.

Аксиомы используют не только в математике. Нередко в обыденной жизни любое истинное утверждение называют аксиомой. Например, говорят: «После марта наступит апрель. Это аксиома». Аксиомы возникают не только из практики или наблюдений. Для любого гражданина России Конституция — это список аксиом. Поэтому аксиому можно рассматривать как закон или правило.

Из истории геометрии.

Геометрия стала называться наукой лишь тогда, когда её истины начали устанавливать путём доказательства.

Появление доказательной геометрии связано с именем первого из «семи мудрецов» — Фалеса Милетского (ок. 625-547 гг. до н. э.) — философа, учёного, купца и государственного деятеля. Задолго до Фалеса было известно, что вертикальные углы равны, диаметр делит крут на две равные части. Никто в истинности этих фактов не сомневался. А Фалес доказал их, тем самым прославив себя.

Книгу, по которой учили геометрию более 2000 лет, без преувеличения можно назвать великой. Её название «Начала», автор — Евклид (ок. 365-300 гг. до п. э.). В фундаменте науки — список простейших фактов. Их называют постулатами (от латинского «требование») и аксиомами. Затем на их основе путём логических рассуждений доказывают все другие свойства — теоремы. Постулатов у Евклида пять.

На протяжении многих веков с «Началами» Евклида по популярности могла сравниться разве что Библия. Так, ещё в конце XIX в. в ряде европейских стран геометрию преподавали по упрощённым изданиям «Начал».

ИТОГИ ГЛАВЫ 1.

Аксиома. Основное свойство прямой
Через любые две точки можно провести прямую, и притом только одну.

Определение. Пересекающиеся прямые
Две прямые, имеющие общую точку, называют пересекающимися.

ТЕОРЕМА 1.1. О двух пересекающихся прямых
Любые две пересекающиеся прямые имеют только одну общую точку.

Равные отрезки
Два отрезка называют равными, если их можно совместить наложением.

Аксиома. Основное свойство длины отрезка
Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и т. е. АВ = АС + СВ.

Расстояние между точками
Расстоянием между точками называют длину отрезка АВ.

Дополнительные лучи
Два луча, имеющие общее начало и лежащие на одной прямой, называют дополнительными.

Развёрнутый угол
Угол, стороны которого являются дополнительными лучами, называют развёрнутым.

Равные углы
Два угла называют равными, если их можно совместить наложением.

Биссектриса угла
Биссектрисой угла называют луч с началом в вершине угла, делящий этот угол на два равных угла.

Острый, прямой, тупой углы
Угол, градусная мера которого меньше 90°, называют острым.
Угол, градусная мера которого равна 90°, называют прямым.
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Аксиома. Основное свойство величины угла
Если луч ОС делит угол АОВ на два угла АОС и СОВ, то ∠АОВ = ∠АОС + ∠COB.

Смежные углы
Два угла называют смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.

ТЕОРЕМА 4.1. Свойство смежных углов.
Сумма смежных углов равна 180°.

Вертикальные углы
Два угла, отличных от развёрнутого, называют вертикаль-ными, если стороны одного угла являются дополнительными лучами сторон другого.

ТЕОРЕМА 4.2. Свойство вертикальных углов.
Вертикальные углы равны.

Перпендикулярные прямые
Две прямые называют перпендикулярными, если при их пересечении образовался прямой угол.

ТЕОРЕМА 5.1. О единственности прямой, перпендикулярной данной
Через каждую точку прямой проходит только одна прямая, перпендикулярная данной.

Это конспект по теме «Мерзляк Геометрия 7 Глава 1». Выберите дальнейшие действия:

Источник

Геометрия 7 класс все правила и теоремы и доказательства определения

1. Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
2.В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
3. Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
4. Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
5. Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
6. Две геометрические фигуры называются равными, если их можно совместить наложением.
7. Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
8. Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
9.Угол называется прямым, если он равен 90°.
10. Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
11. Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
12. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
13. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
14. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
15 Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
16. Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
17. Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
18.Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
19.Треугольник называется равносторонним, если все его стороны равны.
20.Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.
21.(Аксиома) Через любые две точки проходит прямая, и притом только одна.
22. Если все три угла треугольника острые, то треугольник называется остроугольным.
23. Если один из углов треугольника тупой, то треугольник называется тупоугольным.
24. Если один из углов треугольника прямой, то треугольник называется прямоугольным.

Теоремы

Теорема 2
Первый признак равенства треугольников ( по двум сторонам и углу между ними)

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство:

Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить на треугольник ABC так, чтобы
точка A1 совместилась с точкой A,
луч A1C1 наложился на луч AC,
луч A1B1 — на луч AB.
Так как AB=A1B1, то при таком наложении сторона A1B1 совместится со стороной AB, а значит, точка B1 совместится с точкой B.
Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C.
Следовательно, сторона B1C1 совместится со стороной BC.
Значит, при наложении треугольники полностью совместятся, поэтому ΔABC= ΔA1B1C1 (по определению).
Что и требовалось доказать.

Теорема 3
Теорема единственности перпендикуляра, проведенного из произвольной точки к заданной прямой
Из любой точки А, не лежащей на данной прямой, можно провести перпендикуляр к прямой. К тому же этот перпендикуляр единственный.

Дано: точка А не принадлежит прямой a.

Доказать: существует единственный отрезок АН, где АН- перпендикуляр к a из точки A.

1. Построим 2 равных угла. ∠АВС =∠МВС или ∠1 = ∠2.

2. Равные углы можно совместить наложением. При этом точка А перейдет в точку A1. ВА = ВA1(перегибание по прямой ВС).

3. Соединим точки А и A1. Получим точку Н. Углы ∠ВНА = ∠3, ∠ВНA1 = ∠4.

4. Так как ∠1 = ∠2,ВА = ВA1, BC- общая,то треугольники ВНА = ВНA1 по первому признаку равенства треугольников, то есть по углу и двум прилежащим сторонам. Из равенства треугольников следует равенство всех элементов. А значит, ∠3 = ∠4. Эти углы лежат против равных сторон. Два смежных равны только в случае, если каждый из них равен по 90°. А значит, АН ⊥ ВС. Мы доказали, что из точки А можно провести перпендикуляр к прямой a.

Единственность перпендикуляра, проведенного из точки А к прямой, докажем методом «от противного».

5. Предположим, что из точки А можно провести к прямой a два разных перпендикуляра.

Это невозможно, поскольку из разных точек прямой a проведены 2 перпендикуляра, которые имеют общую точку А. Мы получили противоречие, значит, наше предположение неверно. Из точки А можно провести лишь один перпендикуляр к прямой a. Теорема доказана.

Источник

Теория по геометрии 7-9 класс

Виды углов:

· острый угол – от 0 до 90 градусов;

· прямой угол – равен 90 градусам;

· тупой угол – от 90 до 180 градусов;

· развернутый угол (прямая) – равен 180 градусам.

Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжением друг друга.

Свойство смежных углов:

· сумма смежных углов равна 180 градусам.

Вертикальные углы – два угла, у которых стороны являются продолжением друг друга.

Свойство вертикальных углов:

· вертикальные углы равны.

Перпендикулярные прямые – прямые пересекающиеся под углом 90 градусов.

Перпендикуляр – отрезок, проведенный из точки к прямой под углом 90 градусов.

Теорема о перпендикуляре: из точки, не лежащей на прямой можно провести перпендикуляр к этой прямой и при том только один.

Периметр многоугольника – сумма длин всех его сторон.

Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов.

Виды треугольников:

· остроугольный треугольник – все три угла острые;

· прямоугольный треугольник – один угол прямой и два угла острые;

· тупоугольный треугольник – один угол тупой и два угла острые.

Равные треугольники – треугольники, которые можно совместить наложением.

Свойства равных треугольников:

· если два треугольника равны, то их элементы (углы и стороны) попарно равны;

· в равных треугольниках напротив равных сторон лежат равные углы и наоборот, напротив равных углов лежат равные стороны.

Признаки равенства треугольников:

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны;

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны;

3. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Биссектриса – отрезок, выходящий из вершины треугольника к противоположной стороне и делящий угол пополам.

Медиана – отрезок, выходящий из вершины треугольника к противоположной стороне и делящий эту сторону пополам.

Высота – отрезок, выходящий из вершины треугольника к прямой, содержащей противоположную сторону, под углом 90 градусов.

Равнобедренный треугольник – треугольник, у которого две стороны равны, а третья является основанием.

Свойства равнобедренного треугольника:

· углы при основании равны;

· биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Равносторонний треугольник – треугольник, у которого все стороны равны.

Свойства равностороннего треугольника:

· углы равны по 60 градусов;

· биссектриса равностороннего треугольника, проведенная к любой стороне, является медианой и высотой.

Параллельные прямые – прямые, которые не пересекаются.

Секущая – прямая, пересекающая параллельные прямые.

Виды углов, образованных при пересечении параллельных прямых секущей:

Свойства параллельных прямых:

· при пересечении параллельных прямых секущей накрест-лежащие углы равны;

· при пересечении параллельных прямых секущей соответственные углы равны;

· при пересечении параллельных прямых секущей сумма односторонних углов равна 180 градусам.

Признаки параллельности прямых:

· если при пересечении двух прямых секущей накрест-лежащие углы равны, то прямые параллельны;

· если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;

· если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусам, то прямые параллельны.

Аксиома о параллельных прямых: через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и при том только одну.

Следствия из аксиомы:

· если секущая пересекает одну из параллельных прямых, то она пересечет и вторую параллельную прямую;

· если каждая из двух прямых параллельна третьей, то они параллельны между собой.

Теорема о сумме углов треугольника: сумма углов треугольника равна 180 градусам.

Внешний угол треугольника – угол, смежный с одним из углов треугольника.

Свойство внешнего угла треугольника:

· внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.

Теорема о соотношении между сторонами и углами треугольника: в треугольнике напротив бОльшей стороны лежит бОльший угол и наоборот, напротив бОльшего угла лежит бОльшая сторона.

Теорема о сторонах треугольника: каждая сторона треугольника меньше суммы двух других сторон.

Прямоугольный треугольник – треугольник, у которого один угол равен 90 градусам.

Свойства прямоугольного треугольника:

· сумма острых углов треугольника равна 90 градусам;

· в прямоугольном треугольнике катет, лежащий на против угла 30 градусов, равен половине гипотенузы;

· если в прямоугольном треугольнике катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 градусов.

Признаки равенства прямоугольных треугольников:

1. если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны;

2. если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны;

3. если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны;

4. если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Расстояние от точки до прямой – перпендикуляр, проведенный от этой точки к данной прямой.

Расстояние между параллельными прямыми – перпендикуляр, проведенный от произвольной точки на одной прямой ко второй прямой.

Четырехугольник – геометрическая фигура, состоящая из 4 сторон и 4 углов.

Сумма углов выпуклого многоугольника равна (n-2)*180, где n – количество углов.

Сумма углов любого четырехугольника равна 360 градусов.

Параллелограмм – четырехугольник, у которого стороны попарно параллельны.

Свойства параллелограмма:

· противоположные углы и стороны равны;

· диагонали пересекаются и точкой пересечения делятся пополам.

Диагональ – отрезок, соединяющий две противоположные вершины четырехугольника.

Признаки параллелограмма:

· если в четырехугольнике стороны попарно равны, то данный четырехугольник – параллелограмм;

· если в четырехугольнике две стороны равны и параллельны, то данный четырехугольник параллелограмм;

· если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то данный четырехугольник параллелограмм.

Трапеция – четырехугольник, у которого две стороны параллельны (основания) а две другие – нет (боковые стороны).

Виды трапеций:

· прямоугольная – трапеция, у которой два прямых угла;

· равнобедренная – трапеция, у которой боковые стороны равны.

Свойства равнобедренной трапеции:

· углы при основаниях равны;

Ромб – частный случай параллелограмма, у которого все стороны равны.

Свойство ромба:

· у ромба диагонали перпендикулярны и делят углы, из которых они исходят, пополам.

Прямоугольник – частный случай параллелограмма, у которого все углы по 90 градусов.

Свойство прямоугольника:

· у прямоугольника диагонали равны

Признак прямоугольника:

· если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник.

Квадрат – частный случай прямоугольника, у которого все стороны равны.

Теорема Фалеса – если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

Площадь многоугольника – часть плоскости, ограниченная сторонами многоугольника.

Свойство площадей:

· равные многоугольники имеют равные площади;

· если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей многоугольников, из которых он состоит.

Площадь квадрата равна квадрату его стороны: S =

Площадь прямоугольника равна произведению двух его смежных сторон: S =

Площадь трапеции равна половине произведения основания на высоту: S =

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне: S =

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними: S =

Площадь ромба равна половине произведения его диагоналей: S =

Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне: S =

Площадь ромба равна произведению двух его смежных сторон на синус угла между ними:

S =

Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне: S =

Площадь треугольника равна половине произведения двух его смежных сторон на синус угла между ними: S =

Площадь треугольника равна произведению его сторон, деленное на 4 радиуса описанной окружности: S =

Формула Герона, где р – полупериметр: S =

Площадь прямоугольного треугольника равна половине произведения его катетов: S =

Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе из вершины прямого угла: S =

Площадь равностороннего треугольника, где а – сторона треугольник: S =

Высота, медиана, биссектриса равностороннего треугольника, где а – сторона треугольника: h =

Площадь круга, где r – радиус: S =

Длина окружности, где r – радиус: C = 2

Длина дуги окружности, где r – радиус, α – грудасная мера дуги:

Площадь кругового сектора, где r – радиус, α – грудасная мера дуги:

Площадь правильного шестиугольника, где а – сторона шестиугольника: S =

Если в многоугольник можно вписать окружность, то его площадь можно найти как половина произведения периметра на радиус этой окружности: S =

Свойства площадей треугольников:

· если два треугольника имеют равные высоты, то их площади относятся как основания;

· если два треугольника имеют пару равных углов, то их площади относятся как произведение сторон, заключающих эти углы.

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Обратная теорема Пифагора: если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то данный треугольник – прямоугольный.

Формула для нахождения гипотенузы равнобедренного прямоугольного треугольника: , где х – катет равнобедренного прямоугольного треугольника.

Формула для нахождения диагонали квадрата: , где х – сторона квадрата.

Отношение двух величин – деление одной величины на другую (дробь).

Пропорция – равенство нескольких дробей.

Основное свойство пропорции: *d = c*b

Подобные треугольники – треугольники, у которых углы равны, а стороны одного треугольника пропорциональны сходственным сторонам другого.

Сходственные стороны – стороны двух подобных треугольников, расположенные напротив равных углов.

Коэффициент подобия – отношение двух сходственных сторон подобных треугольников.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

Коэффициент подобия равных треугольников равен единице.

Теорема о биссектрисе треугольника: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Признаки подобия треугольников:

1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны;

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами, равны, то такие треугольники подобны;

3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Теорема о средней линии треугольника: средняя линия треугольника параллельна противоположной стороне и равна ее половине.

Среднее арифметическое для нескольких величин равно сумме этих величин, деленной на их количество.

Среднее геометрическое (пропорциональное) для нескольких величин равно квадратному корню из их произведения.

Свойства среднего геометрического в прямоугольных треугольниках:

· высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое для отрезков, на которые гипотенуза делится этой высотой;

· катет прямоугольного треугольника есть среднее геометрическое для гипотенузы и отрезка гипотенузы, заключенного между этим катетом и высотой, проведенной к гипотенузе.

Синус острого угла прямоугольного треугольника – отношение противолежащего катета к гипотенузе.

Косинус острого угла прямоугольного треугольника – отношение прилежащего катета к гипотенузе.

Тангенс острого угла прямоугольного треугольника – отношение противолежащего катета к прилежащему.

Котангенс острого угла прямоугольного треугольника – отношение прилежащего катета к прилежащему.

Основное тригонометрическое тождество: sin 2 (a) + cos 2 (a) = 1

Тригонометрические формулы:

Табличные углы:

30 0	45 0	60 0
sin
cos
tg
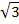ctg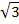

В прямоугольном треугольнике синус одного острого угла равен косинусу другого

В прямоугольном треугольнике косинус одного острого угла равен синусу другого

В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого

В прямоугольном треугольнике котангенс одного острого угла равен тангенсу другого

Синусы смежных углов равны

Косинусы смежных углов равны с противоположными знаками

Тангенсы смежных углов равны с противоположными знаками

Котангенсы смежных углов равны с противоположными знаками

Окружность – множество точек, равноудаленных от одной точки (центр окружности).

Радиус – отрезок, соединяющий центр окружности с любой точкой на окружности.

Хорда – отрезок, соединяющий любые две точки на окружности.

Диаметр – хорда, проходящая через центр окружности.

Соотношение диаметра и радиуса – диаметр равен двум радиусам.

Секущая – прямая, имеющая с окружностью две общих точки.

Касательная – прямая, имеющая с окружностью одну общую точку.

Теоремы о касательных:

1) Радиус, проведенный в точку касания, перпендикулярен касательной.

2) Отрезки касательных, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Теорема о хордах:

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Вписанный угол – угол, вершина которого лежит на окружности, а его стороны пересекают окружность.

Центральный угол – угол, вершина которого лежит в центре окружности, а его стороны пересекают окружность.

Дуга – часть окружности, ограниченная с двух сторон.

Вписанный угол равен половине дуги, на которую он опирается.

Центральный угол равен дуге, на которую он опирается.

Следствия из измерений центрального и вписанного углов:

1) вписанный угол равен половине центрального угла, опирающегося на ту же дугу;

2) если вписанные углы опираются на одну и ту же дугу, то они равны;

3) вписанный угол, опирающийся на диаметр равен 90 градусов.

Серединный перпендикуляр – прямая, проходящая через середину отрезка под углом 90 градусов.

Четыре замечательные точки треугольника:

· биссектрисы треугольника пересекаются в одной точке;

· медианы треугольника пересекаются в одной точке;

· высоты треугольника пересекаются в одной точке;

· серединные перпендикуляры треугольника пересекаются в одной точке.

Теорема о биссектрисе:

Любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

Теорема о медианах:

Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины.

Теорема о серединном перпендикуляре:

Любая точка, лежащая на серединном перпендикуляре, проведенному к отрезку, равноудалена от концов этого отрезка.

Вписанная окружность – окружность, касающаяся всех сторон фигуры.

Описанная окружность – окружность, проходящая через каждую вершину фигуры.

Источник

Основные правила математики. Геометрия. Теоремы, определения. 7 класс | Сайт учителя математики Косыхиной Н.В.

Основные правила математики. Геометрия. Теоремы, определения. 7 класс

Геометрия — одна из самых древних наук, она возникла очень давно, еще до нашей эры .В переводе с греческого слово геометрия означает землемерие (гео- по-гречески земля, а метрео — мерить)
Школьный курс геометрии делится на планиметрию и стереометрию
В планиметрии рассматриваются свойства фигур на плоскости. Примерами таких фигур являются отрезки ,треугольники, прямоугольники.
В стереометрии изучаются свойства фигур в пространстве ,таких ,как параллелепипед ,шар, цилиндр.
Через любые две точки можно провести прямую и притом только одну

Взаимное расположение прямых:

Если нет общих точек, то прямые параллельны
Есть общая точка, то прямые пересекаются.

Отрезок, луч

Отрезком называют часть прямой, ограниченную двумя точками(концы отрезка)
Луч — это часть прямой ,имеющая начало, но не имеющая конца. Луч имеет направление.
Угол -это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла.
Угол называется развернутым, если обе его стороны лежат на одной прямой.
Любой угол разделяет плоскость на две части(полуплоскости).
Если угол неразвернутый, то одна из частей называется внутренней, а другая внешней областью этого угла.
Если угол развернутый, то любую из двух частей ,на которые он разделяет плоскость ,можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
Если луч исходит из вершины неразвернутого угла и проходит внутри угла, то он делит этот угол на два угла.

Равные фигуры, середина отрезка, биссектриса

Равными называют две фигуры, имеющие одинаковую форму и одинаковые размеры.
Две геометрические фигуры оказываются равными, если их можно совместить наложением.

Серединой отрезка называется точка отрезка, равно удаленная от концов отрезка ,т.е. это точка разбивает исходный отрезок на два равных.
Биссектрисой угла называют луч, исходящий из вершины угла и делящий его на два равных угла.

Единицы измерения отрезков, углов

Измерение отрезков основано на сравнении их с некоторыми отрезками. Выбрав единицу измерения , можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.
Стандартной международной единицей измерения отрезков является метр.
При измерении небольших расстояний, например расстояния между точками, изображенными на листе бумаги ,за единицу измерения принимают сантиметр и миллиметр. Расстояния между отдельными объектами в реальном мире измеряются в метрах, километрах и т.д.
Измерение углов аналогично измерению отрезков. Оно основано на сравнений их с углом, принятым за единицу измерения.
Обычно за единицу измерения углов применяют градус.
Градусной мерой угла называют положительное число, которое показывает, сколько раз градус и его части укладываются в данном угла.
Часть градуса называется минутой, часть минуты называется секундой.

Равные углы имеют равные градусные меры.
Меньший угол имеет меньшую градусную меру.
Развернутый угол равен 180 градусов.
Неразвернутый угол — меньше 180 градусов
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов
Угол называется прямым, если он равен 90 градусов.
Острым углом называют, если он меньше 90 градусов.
Тупым углом называют, если он больше 90 градусов.

Смежные и вертикальные углы

Cмежными углами называются два угла, у которого одна сторона общая ,а две другие являются продолжениями сторон друг друга.
Сумма смежных углов равна 180 градусов.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого

Перпендикулярные прямые

Две пресекающиеся прямые называются перпендикулярными, если они пересекаются под прямым углом.

Треугольник

Фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков попарно соединяющих их, называется треугольником.
Сумма длин трех сторон треугольника называется периметром.

Теоремой называют утверждение, справедливость которого устанавливается путем рассуждения.

Медиана, биссектриса, высота треугольника

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Отрезок биссектрисы угла треугольника ,соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Перпендикуляр ,проведенный из вершины треугольника к прямой ,содержащей противоположную сторону, называется высотой треугольника.

Равнобедренный, равносторонний треугольники

Треугольник называется равнобедренным, если две его стороны равны.
Треугольник, все стороны которого равны, называется равносторонним.
В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

Три признака равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольник, то такие треугольники равны
Теорема 2. Если сторона и 2 прилежащих к ней угла одного треугольника равны стороне и 2 прилежащим к ней углам другого треугольник, то такие треугольники равны
Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Окружность

Для изображении окружности на чертеже пользуются циркулем.

Окружностью называют геометрическая фигура ,состоящая из всех точек плоскости, расположенных на заданном расстоянии от заданной точки.
Отрезок ,соединяющий две точки окружности ,называется хордой
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности.

Формула длины окружности

Формула площади круга

Источник

Конспект по учебнику Л.С. Атанасяна.

Нумерация правил и теорем соответствует номеру главы из данного учебника, т.е. теорема 3.10 из главы 3. Это поможет быстрее найти доказательства или приложения к конкретной теореме.

Пригодится детям при подготовке к ОГЭ (особенно для части 2).

opr-te.docx
opr-te.pdf

Определения

Отрезок — часть прямой, ограниченная двумя точками.

Концы отрезка- точки, ограничивающие прямую.

Луч-прямая, имеющая начало в точке, но не имеющая конца.

Угол-геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки.

Стороны угла — лучи, составляющие угол.

Вершина угла — точка, из которой берут начало стороны угла.

Развернутый угол, если обе его стороны лежат на одной прямой.

Середина отрезка — точка, делящая отрезок пополам.

Прямой угол=900. Острый угол<900. 1800>Тупой угол>900.

Смежные-два угла, у которых одна сторона общая, а две другие-это продолжения друг друга.

Вертикальные — два угла, если стороны одного угла-это продолжение сторон другого.

Перпендикулярные-две пересекающиеся прямые, образующие четыре прямых угла.

Периметр — сумма длин всех сторон фигуры.

Перпендикуляр АН-отрезок, соединяющий точку А с точкой Н, лежащей на прямой. Этот отрезок с прямой образует прямой угол.

Биссектриса — луч, исходящий из вершины угла и делящий его на два равных угла.

Медиана — отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Высота — перпендикуляр, проведенный из вершины угла к прямой, содержащей противолежащую сторону.

Равнобедренный треугольник, если две его стороны равны.

Окружность — геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от одной единственной точки-центр окружности.

Радиус r — отрезок, соединяющий центр окружности с любой точкой, лежащей на этой окружности.

Хорда — отрезок, соединяющий две точки, лежащие на окружности.

Диаметр — хорда, проходящая через центр окружности.

Дуга — часть окружности, полученная делением этой окружности двумя точками.

Параллельные прямые-две не пересекающиеся на плоскости прямые.

Параллельные отрезки, если они лежат на параллельных прямых.

Секущая к двум прямым-прямая, пересекающая данные прямые в двух точках.

Гипотенуза — сторона прямоугольного треугольника, лежащая напротив прямого угла. Две другие стороны прямоугольного треугольника-катеты.

Неравенства треугольника: АВ<АС+СВ, АС<АВ+ВС, ВС<ВА+АС.

Расстояние от точки до прямой-длина перпендикуляра, проведенного из точки к прямой.

Расстояние между прямыми-расстояние от любой точки одной из параллельных прямых до другой прямой.

Автор: Маенкова Маргарита Васильевна.

Источник

☑ 1. Простейшие геометрические фигуры и их свойства

☑ 2. Углы

☑ 3. Параллельные прямые

☑ 4. Треугольник

☑ 5. Признаки равенства треугольников

☑ 6. Соотношения между сторонами и углами треугольника

☑ 7. Определение вида треугольника по его сторонам

☑ 8. Прямоугольные треугольники (некоторые свойства)

☑ 9. Признаки равенства прямоугольных треугольников

☑ 10. Четыре замечательные точки треугольника

☑ 11. Окружность

☑ 12. Свойства касательных к окружности

☑ 13. Окружность и треугольник

Что такое треугольник и когда они считаются равными?

Теорема об углах, образованных двумя параллельными прямыми и секущей

Теоремы

Доказательство

1. Сумма углов треугольника

Теория:

Соотношения между сторонами и углами треугольника. Неравенство треугольника

1. Прямоугольные треугольники

Теория:

Признаки равенства прямоугольных треугольников

Геометрия 7 класс все правила и теоремы и доказательства определения

$ 2. Отрезок и его длина.

$ 3. Луч. Угол. Измерение углов.

$ 4. Смежные и вертикальные углы.

$ 5. Перпендикулярные прямые

$ 6. Аксиомы.

Из истории геометрии.

ИТОГИ ГЛАВЫ 1.

Геометрия 7 класс все правила и теоремы и доказательства определения

Теоремы

Теория по геометрии 7-9 класс

Основные правила математики. Геометрия. Теоремы, определения. 7 класс

Взаимное расположение прямых:

Отрезок, луч

Равные фигуры, середина отрезка, биссектриса

Единицы измерения отрезков, углов

Смежные и вертикальные углы

Перпендикулярные прямые

Треугольник

Медиана, биссектриса, высота треугольника

Равнобедренный, равносторонний треугольники

Три признака равенства треугольников

Окружность

Что такое
треугольник и когда они считаются равными?

Теорема об
углах, образованных двумя параллельными прямыми и секущей

Соотношения
между сторонами и углами треугольника. Неравенство треугольника

Признаки равенства
прямоугольных треугольников