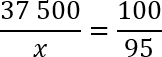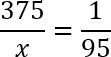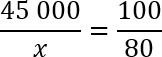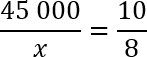Как составить уравнение чтобы найти процент - Исправление недочетов и поиск решений вместе с Examum.ru

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все — 100%
часть — часть в %

которые можно записать в виде пропорции

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Примеры решения задач на проценты

Пример 1.

Найти число B составляющее 15% от числа 30.

Решение:

30 соответствует 100%
x соответствует 15%

Запишим пропорцию

решим полученное уравнение

Ответ: 15% от 30 равно 4.5.

Пример 2.

Найти сколько процентов составляет число 35 от числа 20.

Решение:

20 соответствует 100%
35 соответствует x

Запишим пропорцию

решим полученное уравнение

Ответ: 35 составляет 175% от 20.

Пример 3.

Найти число, 5% которого равны 20.

Решение:

x соответствует 100%
20 соответствует 5%

Запишим пропорцию

решим полученное уравнение

Ответ: 400.

При изучении процентов вам также будут полезны:

Источник

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все — 100% часть — часть в %

которые можно записать в виде пропорции

все	=	100%
часть	часть в %

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Примеры решения задач на проценты

30 соответствует 100% x соответствует 15%

решим полученное уравнение

Ответ: 15% от 30 равно 4.5.

20 соответствует 100% 35 соответствует x

решим полученное уравнение

Ответ: 35 составляет 175% от 20.

x соответствует 100% 20 соответствует 5%

решим полученное уравнение

Ответ: 400.

При изучении процентов вам также будут полезны:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как решать задачи с процентами

О чем эта статья:

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

40 : 0,16 = 40 · 100 : 16 = 250

Ответ: 250 задач собрано в этом учебнике.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

Ответ: в классе 40% девочек.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

А можно воспользоваться формулой:

a = b · (1 + с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?

Как решаем: можно найти 12% от 110:

Прибавить к исходному числу:

110 + 13,2 = 123,2 рубля.

Или можно воспользоваться формулой, тогда:

110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.

Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

А можно воспользоваться формулой:

a = b · (1 − с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Как решаем: можно найти 25% от 100:

Вычесть из исходного числа 100 − 25 = 75 человек.

Или можно воспользоваться формулой, тогда:

100 · (1 − 25 : 100) = 75/p>

Ответ: 75 выпускников в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а · (1 + у · х : 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?

Как решаем: подставим в формулу данные из условий задачи.

70 000 · (1 + 12 · 8 : 100) = 137 200

Ответ: 137 200 рублей вернет Мария через год.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а · (1 + х : 100) y ,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?

Как решаем: просто подставим в формулу данные из условий задачи:

10000 · (1 + 10 : 100)3 = 13 310

Ответ: 13 310 рублей снимет Антон через год.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.

10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем:

100 — 25 = 75,
значит нужно заплатить 75% от первоначальной цены.
Используем правило соотношения чисел:
8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х — 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Задачи на проценты: 3 способа решения с примерами

Как решать задачи на проценты? Есть 3 способа, выбирай тот, который для тебя проще и понятнее.

Умение быстро и правильно решать задачи на проценты важно, как для успешной сдачи ЕГЭ, так и для повседневной жизни. И если в ЕГЭ вы можете встретить такую задачу в задании 11, то в повседневной жизни такие задачи повсюду.

Зарплату повысили на 15%, а потом оштрафовали на 10%, после этого из зарплаты удержали налог 13% — сколько же мы получим в конце месяца? Коммунальные услуги повысили на 15%, сколько они теперь будут стоить? При возврате ж/д билета вернут только 20% стоимости, какую сумму мы получим? Все это задачи на проценты, которые нам приходится решать каждый день.

Поэтому умение быстро и правильно решать задачи на проценты – это полезно.

Задачи на проценты: вся суть

Задачи на проценты, как правило, описывают жизненную ситуацию. В ней присутствует какая-то величина, которая увеличивается или уменьшается на сколько-то процентов. Таким образом, в задаче на проценты упоминается такие данные, как первоначальная величина, конечная величина и процент, на который эта величина изменилась. Чаще всего в задаче требуется найти либо первоначальную величину, либо конечную величину, реже – процент, на который эта величина изменилась.

Решение задач на проценты с помощью формулы простого процента

Формула, которой мы пользуемся при решении задач на проценты, называется формула простого процента:

Х_{конечное} – конечная величина

Х_{первоначальное} – первоначальная величина

k – процент, на который первоначальная величина изменилась

Из этой формулы всегда можно найти первоначальную величину или процент, на который происходит изменение.

Знак стоящий перед k зависит от того, увеличивается первоначальная величина или уменьшается. Так, если величина увеличивается на сколько-то процентов, то ставим знак плюс. Если уменьшается – минус.

Для наглядности приведем несколько простых примеров.

Задача 1

В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?

Решение: Очевидно, что в этой задаче нам известна первоначальная величина – 30 000 человек и процент, на который она увеличилась +6% Нужно найти конечную величину.

30 000 * ((100 + 6)/100) = х

х = 31 800 человек

Ответ: 31 800 человек

Задача 2

Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?

Решение: В этой задаче нам известна конечная величина – 5 килограмм и процент, на который происходит изменение -90%. Нужно найти первоначальную величину:

5 = х * ((100 – 90) / 100)

Задача 3

Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?

Решение: В данной задаче нам известна первоначальная (20 000 рублей) и конечная величина (22 000 рублей), а найти нужно процент, на который данная величина изменилась.

22 000 = 20 000 * ((100 + х) / 100)

22 000 / 20 000 = 1 + х/100

Решение задач на проценты: метод пропорции

Еще один способ решения задач на проценты – это метод пропорции. Это наиболее простой способ решения таких задач.

Напомним, что пропорция – это равенство двух отношений:

Для нас важно основное свойство пропорции, которое заключается в том, что произведение крайних членов пропорции равно произведению средних членов. Проще запомнить, что мы можем перемножить члены пропорции крест-накрест:

При решении задач на проценты с помощью метода пропорции необходимо руководствоваться следующим правилом:

Далее записываем пропорцию:

Давайте решим приведенные выше примеры задач на проценты с помощью метода пропорции.

Задача 4

Решение: Итак, в городе проживало 30 000 человек и это всё его население, т.е. 100%. Так и запишем:

Далее население выросло на 6%, т.е. всё его население стало составлять 100% + 6% = 106% и нам неизвестно, сколько это человек, т.е. Х человек. Запишем:

Таким образом, получаем:

Составим пропорцию: Правую дробь пропорции можно сократить на 2, получим: Теперь воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

30 000 * 53 = 50х

Далее обе части полученного уравнения мы можем разделить на 50, получим:

Ответ: 31 800 человек

Задача 5

Решение: Нам неизвестно первоначальное количество всех яблок (всё количество), т.е. это Х, которое составляет 100%. Количество сушеных яблок (часть от первоначального количества яблок) составляет 5 кг. Причем известно, что количество сушеных яблок на 90% меньше от первоначального количества яблок (т.к. 90% — это вода, которая из них испарилась). Следовательно, количество сушеных яблок составит 100% — 90% = 10%. Запишем наши рассуждения:

Запишем наши рассуждения: Сократим правую дробь на 10, получим:Воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

Задача 6

Решение: Нам известно, что исходная цена – 20 000 рублей, следовательно, 20 000 рублей – это 100%. Тогда конечная цена 22 000 рублей – это неизвестное количество процентов, т.е. Х%. Так и запишем:

Теперь запишем пропорцию: Сократим левую дробь на 2 000, получим: Воспользуемся основным свойством пропорции, то есть перемножим ее члены крест-накрест:

В результате решения мы получили результат 110%, но он не является ответом! Ведь нам нужно найти, на сколько процентов изменилась стоимость холодильника. Чтобы это узнать, нужно из полученного числа процентов отнять 100%:

Решение задач на проценты методом коэффициентов

Можно назвать еще один метод решения задач на проценты, который является следствием из формулы простого процента. Так, формулу простого процента можно переписать следующим образом:

Таким образом, мы получили формулу для решения задач на проценты методом коэффициентов. Полученная формула удобна тем, что при достаточной практике простые задачи на проценты можно решать в уме, даже не задумываясь.

Например, яблоки стоили 150 рублей, затем они подорожали на 20%. Найдите новую стоимость яблок.

Применим полученную формулу и получим:

150 * 1,2 = 180 рублей

То есть мы интуитивно 20% превращаем в 0,2 прибавляем единицу, так как происходит увеличение на данное количество процентов, и умножаем на первоначальную стоимость.

Или другой пример. Зарплата работника составляла 25 000 рублей в месяц, в результате применения штрафа за опоздания зарплата сократилась на 10%. Найти сумму зарплаты, которую получит оштрафованный работник.

25 000 * 0,9 = 22 500 рублей

Опять же мы сразу понимаем, что 10% — это 0,1. Т.к. происходит уменьшение первоначальной величины на это количество процентов, то мы вычитаем из единицы этот процент и получаем 0,9. Затем умножаем полученное значение на первоначальную величину. Готово!

Давайте решим этим методом задачу про зарплату и налоги.

Задача 7

В России налог на доходы физических лиц составляет 13%. Зарплата Марии Ивановны после удержания налога на доходы составила 60 900 рублей. Найти сумму зарплаты Марии Ивановны до удержания налога.

Решение: Итак, 13% — это 0,13. Первоначальная зарплата уменьшилась на этот процент, значит, вычитаем из единицы и получаем 1 – 0,13 = 0,87. Подставляем в формулу:

Ответ: 70 000 рублей

Задача 8

В школе 1000 учеников, из них 20% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучают?

Решение: Для начала из общего количества учеников исключим тех, кто французский язык точно не изучает, т.е. учеников начальной школы. Ученики начальной школы – это 20%, т.е. 0,2, мы уменьшаем на этот процент, следовательно, вычитаем из единицы и получаем 1 – 0,2 = 0,8.

Из 800 полученных учеников французский язык изучают только 30%.

Обратите внимание, что здесь идет речь о проценте от числа. Т.е. мы не уменьшаем на 30% (в этом случае мы вычитаем значение процента в долях из единицы) и не увеличиваем на 30% (в этом случае мы прибавляем к значению процента в долях к единице), а берем 30% от заданного числа (в этом случае мы умножаем заданное число на значение процента в долях). Всегда внимательно читайте условия задачи!

В нашем случае нам нужно найти 30% от 800:

Это и есть ответ. 240 учеников изучают французский язык в школе.

Ответ: 240 учеников.

Задача 9

Разберем еще одну задачу на проценты, которая часто встречается на ЕГЭ и в которой легко можно допустить ошибку.

Задача: Зарплата рабочего составляла 30 000 рублей, затем зарплату повысили на 30%, а потом понизили на 30%. Какую зарплату стал получать рабочий?

Решение: быстро прочитав условие задачи, сходу хочется дать ответ – зарплата останется прежней, ее размер не изменился. Но это не так! Давайте разбираться.

Будем решать по формуле простого процента.

Первое событие – зарплату повысили на 30%. Следовательно, первоначальную сумму мы увеличиваем на 30%:Второе событие – зарплату понизили на 30%. Следовательно, нашу увеличенную зарплату мы теперь уменьшаем на 30%:Таким образом, рабочий теперь будет получать зарплату 27 300 рублей.

Данную задачу мы могли бы решить в одно действие, применяя формулу для вычисления сложного процента. Напомним ее:

S = P (1 + i) n , где

S – это конечная сумма;

P – это первоначальная сумма;

i – это процент/100;

n – количество периодов.

Т.к. 30% — это 0,3, то, применяя формулу для вычисления сложного процента к нашей задаче, мы получим:

30 000 * (1 + 0,3) 1 (1 – 0,3) 1 = 27 300 рублей

Результат получился тот же.

Ответ: 27 300 рублей

В этой статье были разобраны достаточно простые примеры задач на проценты, чтобы максимально доступно продемонстрировать методы решения задач на проценты. В профильном ЕГЭ с процентами вы можете столкнуться в задаче с экономическим содержанием по вкладам и кредитам. Такие задачи гораздо сложнее и подробное их решение вы можете посмотреть на нашем сайте.

Итак, надеюсь, что данная статья помогла вам понять, как решать задачи на проценты. Мы увидели, что задачи на проценты можно решать тремя способами – с помощью формулы простого процента, методом пропорции и методом коэффициентов. Выбирайте тот, который вам наиболее понятен, и которым вам решать такие задачи проще.

источники:

http://skysmart.ru/articles/mathematic/kak-reshat-zadachi-s-procentami

http://yourrepetitor.ru/kak-reshat-zadachi-na-procenty/

Источник

Один из способов решения задач на проценты — это использование пропорций.

Как правильно составлять и решать подобные пропорции?

Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции.

В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% — это его четвёртая часть, 20% — это пятая часть, 10% -это 10 часть , 5 % — 20 часть, 1% — 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30.

А можно использовать универсальный способ — понятие пропорции.

Предположим надо найти 13% от 180.

Тогда составим:

180 — 100%

Х — 13 %

Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали — делим.

У нас получаем 180*13/100=23,4

система выбрала этот ответ лучшим

Ксарфакс
[156K]

4 года назад

Пропорция с процентами составляется по следующему принципу:

Исходное число (обозначим его буквой A) принимается за 100%. Первым членом пропорции будет цифровая запись числа A, ему будет соответствовать 100%.
Остальными членами пропорции будут часть от этого числа (обозначим его буквой B) и проценты, соответствующие этой части (обозначим их буквой p).

Вот как выглядет такая пропорция:

A / B = 100% / p%

Например:

1000 / 50 = 50% / 5%.

Или можно записать по-другому:

1000 — 100%.

50 — 5%.

При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x.

Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест).

Исходное число будет равно: A = 100% * B / p%.
Часть от числа будет равна: B = A * p% / 100%.
Проценты от числа можно найти по формуле: p% = 100% * B / A.

Далее рассмотрим несколько простых примеров.

Пример 1.

Зарплата составляет 30000 рублей, а премия — 10% от зарплаты. Нужно определить размер премии.

30000 — 100%.

x — 10%.

Вспоминаем, что произведение крайних членов равно произведению средних:

30000 * 10 = 100 * x.

x = (30000 * 10) / 100 = 3000.

Значит, премия равна 3000 рублей.

Пример 2.

Сделано 20 выстрелов, 4 из них — мимо мишени. Нужно определить процент попадания.

20 — 100%.

4 — x%.

Умножаем крест-накрест и приравниваем:

20 * x = 100* 4.

x = (100 * 4) / 20 = 20.

Здесь нужно учесть, что 20% — это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи).

Процент попадания в свою очередь равен 100% — 20% = 80%.

Пример 3.

За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально.

x — 100%.

30 — 20%.

Умножаем крест-накрест:

20 * x = 100 * 30.

x = (100 * 30) / 20 = 150.

Таким образом, изначально в продаже было 150 ноутбуков.

Zummy out off
[226K]

3 года назад

Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал.

Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство — нужно наглядно записывать это. Это не страшно — бумага всегда под рукой.

Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х.

Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х.

Пример: нужно найти 5% от числа 420.

Пишу пропорцию.

420 — 100 %

Х — 5 %

Х = 5 • 420 : 100 = 21%

Вот моя запись с крестом

Ещё пример: сколько процентов от 200 составляет число 20.

Составляю пропорцию.

200 — 100 %

20 — Х %

Решение: X = 20 • 100 : 200 = 10%

Алиса в Стране
[364K]

3 года назад

Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая:

90 — 100 %

18 — х %, откуда х = 100 х 18 / 90 = 20 процентов.

Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция:

24 — х

250 — 100

х = 24 х 100 /250 = 9,6 %.

Go Green
[537K]

3 года назад

Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них.

Для простоты давайте приведем примеры с числом 100.

1 % от ста — это одна сотая часть или один процент.

2% от ста — две сотых части от ста.

7% от ста — семь сотых части от ста и так далее.

То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение.

Например, нам нужно найти, сколько будет равно 7 процентам от 200.

Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14.

Итого: 7% от 200 будет равняться числу 14.

СТА 1106
[295K]

3 года назад

Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово.

Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем.

250 штук — 100 %

262 штуки — х %

Решение: 262 × 100:250= 104,8 %.

Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%.

Решение.

Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100.

20 тонн — 82 %

Х тонн — 100 %.

20 × 100:82= 24,4 тонны.

Бекки Шарп
[71.2K]

3 года назад

Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 — это 100%, а неизвестной х — 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так:

Бархатные лапки
[382K]

3 года назад

Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%.

Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х — сколько рублей 38%. Из пропорции находим х = 95 %.

Точно в цель
[110K]

3 года назад

Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% — это половина от числа, 25% — одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент.

Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 — получаю 46.

50 процентов является половиной от числа, 25 является четвертой частью, 20 — пятой, 10 — 10, 5 является 20, а 1 процент — 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30.

Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4.

[пользователь заблокирован]
[3.3K]

4 года назад

Всё очень просто. Всегда нужно начинать с того, что процент — это одна сотая часть. Ну, а далее — пропорция составляется исходя из этой посылки.

Знаете ответ?

Источник

Как решать задачи на проценты? Есть 3 способа, выбирай тот, который для тебя проще и понятнее.

Поэтому умение быстро и правильно решать задачи на проценты – это полезно.

Задачи на проценты: вся суть
Решение задач на проценты: формула простого процента
Решение задач на проценты: метод пропорции
Решение задач на проценты: метод коэффициентов

Задачи на проценты: вся суть

Решение задач на проценты с помощью формулы простого процента

Формула, которой мы пользуемся при решении задач на проценты, называется формула простого процента:

Х_{конечное} – конечная величина

Х_{первоначальное} – первоначальная величина

k – процент, на который первоначальная величина изменилась

Из этой формулы всегда можно найти первоначальную величину или процент, на который происходит изменение.

Для наглядности приведем несколько простых примеров.

Задача 1

30 000 * ((100 + 6)/100) = х

30 000 * 1,06 = х

х = 31 800 человек

Ответ: 31 800 человек

Задача 2

5 = х * ((100 – 90) / 100)

5 = 0,1х

х = 50 кг

Ответ: 50 кг

Задача 3

22 000 = 20 000 * ((100 + х) / 100)

22 000 / 20 000 = 1 + х/100

1,1 = 1 + х/100

0,1 = х/100

х = 10%

Ответ: 10%

Решение задач на проценты: метод пропорции

Напомним, что пропорция – это равенство двух отношений:

При решении задач на проценты с помощью метода пропорции необходимо руководствоваться следующим правилом:

всё – 100%

часть – часть в %

Далее записываем пропорцию:

Давайте решим приведенные выше примеры задач на проценты с помощью метода пропорции.

Задача 4

Решение: Итак, в городе проживало 30 000 человек и это всё его население, т.е. 100%. Так и запишем:

30 000 – 100%

Х – 106%

Таким образом, получаем:

30 000 – 100%

Х – 106%

30 000 * 53 = 50х

Далее обе части полученного уравнения мы можем разделить на 50, получим:

600 * 53 = Х

Х = 31 800

Ответ: 31 800 человек

Задача 5

Х – 100%

5 – 10%

Х = 10 * 5

Х = 50

Ответ: 50 кг

Задача 6

20 000 – 100%

22 000 – Х%

10Х = 1 100

Х = 110

110% — 100% = 10%

Ответ: 10%

Решение задач на проценты методом коэффициентов

Например, яблоки стоили 150 рублей, затем они подорожали на 20%. Найдите новую стоимость яблок.

Применим полученную формулу и получим:

150 * 1,2 = 180 рублей

25 000 * 0,9 = 22 500 рублей

Давайте решим этим методом задачу про зарплату и налоги.

Задача 7

0,87х = 60 900

х = 70 000

Ответ: 70 000 рублей

Задача 8

1000 * 0,8 = 800

Из 800 полученных учеников французский язык изучают только 30%.

В нашем случае нам нужно найти 30% от 800:

800 * 0,3 = 240

Это и есть ответ. 240 учеников изучают французский язык в школе.

Ответ: 240 учеников.

Задача 9

Будем решать по формуле простого процента.

S = P (1 + i)ⁿ, где

S – это конечная сумма;

P – это первоначальная сумма;

i – это процент/100;

n – количество периодов.

Т.к. 30% — это 0,3, то, применяя формулу для вычисления сложного процента к нашей задаче, мы получим:

30 000 * (1 + 0,3)¹ (1 – 0,3)¹ = 27 300 рублей

Результат получился тот же.

Ответ: 27 300 рублей

Источник

Задачи на проценты: стандартный расчет с помощью пропорций

12 ноября 2013

Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.

Итак, первая задача:

Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?

На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:

Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?

Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:

37 500 — 100%
X — 95%

Нужно составить пропорцию и найти x. Получаем:

Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:

По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:

x = 375 · 95

Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:

x = 35 625

Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.

Задача на проценты №2

Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?

Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:

45 000 — 100%
x — 80%

Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:

Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:

45 000 · 8 = x · 10

Это простейшее линейное уравнение. Выразим из него переменную x:

x = 45 000 · 8 : 10

Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:

x = 4500 · 8

Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:

x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000

А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!

Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:

45 000 − 36 000 = 9000

Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.

Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)

Смотрите также:

Процент: налоги и зарплата. Считаем с помощью коэффициентов
Задачи на проценты: считаем проценты с помощью пропорции
Тест к уроку «Что такое числовая дробь» (легкий)
Тест: простейшие показательные уравнения (1 вариант)
Изюм и виноград (смеси и сплавы)
ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром

Источник