Как составить уравнение диагоналей прямоугольника

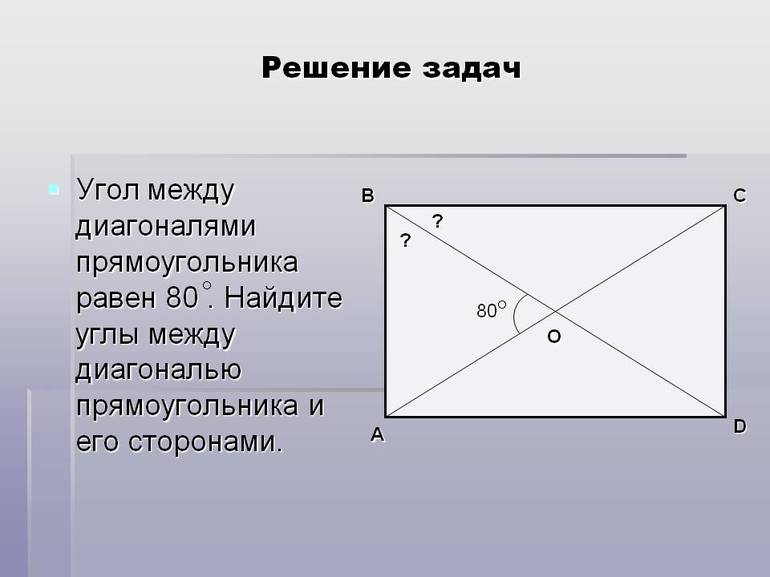
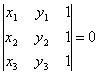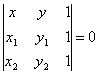Свойства и признаки диагоналей прямоугольника — формулы и примеры расчетов

Общая информация

В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.

Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.

Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.

Сведения о прямоугольнике

Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.

Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.

Идентификация или признаки

Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:

• Вычислить значение четвертого угла: D = 360 — (90 * 3) = 90 (градусов).
• Сопоставить сведения, полученные при вычислении, с определением.

Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:

• Равенство сторон, которые противоположны между собой.
• Внутренние углы между собой равны, а их градусная мера соответствует 90 градусам.
• Диагонали равны между собой.
• Сумма квадратов двух сторон, которые не противоположны, равна квадрату одной диагонали. Это следует из теоремы Пифагора, по которой находится одна из сторон прямоугольного треугольника.
• Если прямоугольник не является квадратом, то его стороны не равны одному значению.

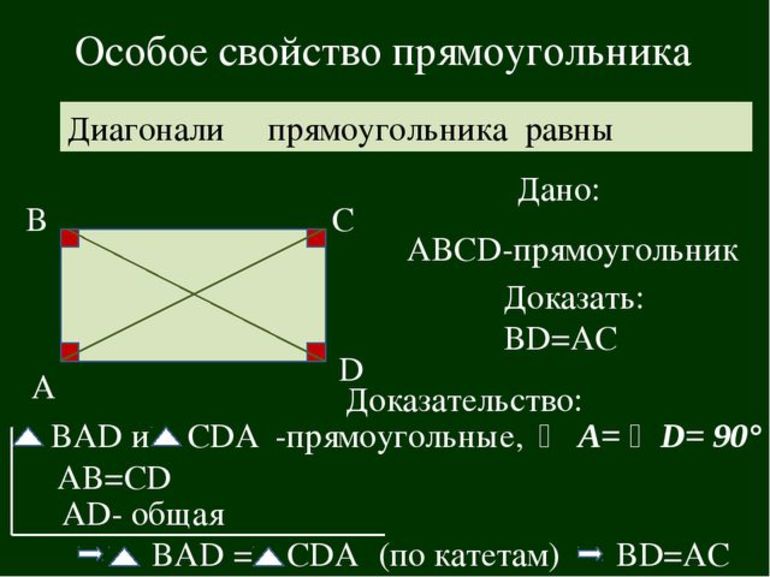
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.

Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.

Четвертый признак также доказывается. Следует рассматривать прямоугольный треугольник ABC. Используя теорему Пифагора, нужно выразить гипотенузу, которая является диагональю фигуры, через катеты (стороны фигуры): AC 2 = AB 2 + BC 2 . Таким способом доказывается данный признак. Последнее утверждение получается из частного случая: если у прямоугольника все стороны равны, то он является квадратом.

Свойства фигуры

Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB 2 + BC 2 )^(½). При решении задач применяются свойства прямоугольника:

• Каждый из углов равен 90 градусам.
• Стороны, которые являются противолежащими и параллельными, равны.
• Сумма углов внутри фигуры составляет 360.
• Пересечение диагоналей в точке, которая делит их пополам, также является центром окружности, описанной вокруг фигуры и центром симметрии.
• Треугольники, полученные в результате проведения диагоналей, равны.
• Суммарное значение квадратичных значений всех сторон эквивалентно двойному квадрату диагонали.
• Большой и маленький треугольники, образованные диагоналями, подобны. Следует обратить внимание на коэффициент подобия.
• Диагональ эквивалентна диаметру окружности, описанной около фигуры.
• Геометрическая характеристика фигуры (сумма противоположных углов составляет 180) позволяет описать вокруг нее окружность.
• Вписать круг в прямоугольник можно тогда, когда он является правильным, т. е. ширина эквивалентна длине (квадрат).
• Угол между смежными сторонами равен 90.
• В любом прямоугольнике диагонали взаимно перпендикулярны, когда он является квадратом.
• Диагонали, пересекаясь между собой, образуют не разносторонние, а прямоугольные и равносторонние треугольники.
• Половина диагонали, проведенная из любой вершины фигуры, является медианой и высотой.
• Диагональ является биссектрисой (прямоугольник — квадрат).
• Средняя линия прямоугольника проходит через точку пересечения диагоналей.

Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).

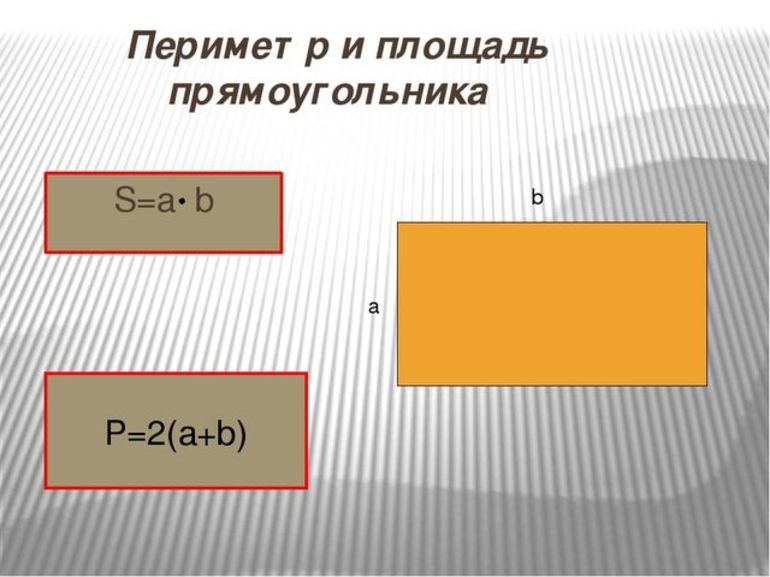
Периметр и площадь

Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:

• Величина площади и сторона, которая известна: P = (2S + 2a 2 ) / a или P = (2S + 2b 2 ) / b.
• Диагональ и a (b): P = 2(a + (d 2 — a 2 )^(0.5)) = 2(b + (d 2 — b 2 )^(0.5)).
• a (b) и R: P = 2(a + (4 * R 2 — a 2 )^(0.5)) = 2(b + (4 * R 2 — b 2 )^(0.5)).
• D и a (b): P = 2(a + sqrt(D 2 — a 2 )) = 2(b + sqrt(D 2 — b 2 )).

Площадь — характеристика размерности двумерной фигуры. Ее обозначают литерой S, и измеряют в метрических единицах в квадрате (мм 2 , см 2 , м 2 и т. д.). Следует отметить, что она вычисляется интегральным методом. Однако для частных случаев существуют соотношения. Формула, которая является основанием для всех остальных соотношений, называется базовой. Она имеет такой вид: S = a * b. Площадь находится в зависимости от параметров, которые известны:

P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.

a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].

Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.

R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].

D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].

Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.

Диагонали и стороны

Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:

• d и a (b): a = sqrt[d 2 — b 2 ] и b = sqrt[d 2 — a 2 ].
• S и a (b): a = S / b и b = S / a.
• P и a (b): a = (P — 2b) / 2 и b = (P — 2a) / 2.

Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:

a и b: d = [a 2 + b 2 ]^(1/2).

S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.

P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.

Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.

Другие соотношения

Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:

a и b: R = (a 2 + b 2 )^(1/2) / 2.

P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.

S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.

d: R = d / 2.

sin(F), прилегающего к диагонали и стороне, и a: R = a / 2sin (F).

cos(F) и b: R = b / 2cos (F).

Для нахождения угла F следует воспользоваться такой формулой: sin (F) = a / d и cos (F) = b / d. Острый угол между двумя диагоналями определяется при помощи такого соотношения: sin (Y) = 2S / d 2 .

Пример решения

Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:

• Другие стороны.
• Значения диагоналей.
• Площадь.
• R описанной окружности через площадь и периметр.
• Выяснить возможность укладки плитки в форме квадрата на такую поверхность.
• Вычислить значения всех углов между смежными сторонами.

Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.

У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.

Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:

R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).

R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).

Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.

Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.

Свойства и признаки диагоналей прямоугольника — формулы и примеры расчетов

Во время ремонта или решения геометрических задач возникает необходимость определения основных параметров прямоугольника. Свойства диагоналей фигуры иногда могут играть важную роль, поскольку заметно облегчают решение. В интернете существует множество информации, но возникает некоторая проблема. Она состоит в полном отсутствии систематизации знаний, которые следует искать по всей сети.

Общая информация

В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.

Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.

Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.

Сведения о прямоугольнике

Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.

Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.

Идентификация или признаки

Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:

• Вычислить значение четвертого угла: D = 360 — (90 * 3) = 90 (градусов).
• Сопоставить сведения, полученные при вычислении, с определением.

Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:

• Равенство сторон, которые противоположны между собой.
• Внутренние углы между собой равны, а их градусная мера соответствует 90 градусам.
• Диагонали равны между собой.
• Сумма квадратов двух сторон, которые не противоположны, равна квадрату одной диагонали. Это следует из теоремы Пифагора, по которой находится одна из сторон прямоугольного треугольника.
• Если прямоугольник не является квадратом, то его стороны не равны одному значению.

Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.

Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.

Четвертый признак также доказывается. Следует рассматривать прямоугольный треугольник ABC. Используя теорему Пифагора, нужно выразить гипотенузу, которая является диагональю фигуры, через катеты (стороны фигуры): AC 2 = AB 2 + BC 2 . Таким способом доказывается данный признак. Последнее утверждение получается из частного случая: если у прямоугольника все стороны равны, то он является квадратом.

Свойства фигуры

Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB 2 + BC 2 )^(½). При решении задач применяются свойства прямоугольника:

• Каждый из углов равен 90 градусам.
• Стороны, которые являются противолежащими и параллельными, равны.
• Сумма углов внутри фигуры составляет 360.
• Пересечение диагоналей в точке, которая делит их пополам, также является центром окружности, описанной вокруг фигуры и центром симметрии.
• Треугольники, полученные в результате проведения диагоналей, равны.
• Суммарное значение квадратичных значений всех сторон эквивалентно двойному квадрату диагонали.
• Большой и маленький треугольники, образованные диагоналями, подобны. Следует обратить внимание на коэффициент подобия.
• Диагональ эквивалентна диаметру окружности, описанной около фигуры.
• Геометрическая характеристика фигуры (сумма противоположных углов составляет 180) позволяет описать вокруг нее окружность.
• Вписать круг в прямоугольник можно тогда, когда он является правильным, т. е. ширина эквивалентна длине (квадрат).
• Угол между смежными сторонами равен 90.
• В любом прямоугольнике диагонали взаимно перпендикулярны, когда он является квадратом.
• Диагонали, пересекаясь между собой, образуют не разносторонние, а прямоугольные и равносторонние треугольники.
• Половина диагонали, проведенная из любой вершины фигуры, является медианой и высотой.
• Диагональ является биссектрисой (прямоугольник — квадрат).
• Средняя линия прямоугольника проходит через точку пересечения диагоналей.

Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).

Периметр и площадь

Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:

• Величина площади и сторона, которая известна: P = (2S + 2a 2 ) / a или P = (2S + 2b 2 ) / b.
• Диагональ и a (b): P = 2(a + (d 2 — a 2 )^(0.5)) = 2(b + (d 2 — b 2 )^(0.5)).
• a (b) и R: P = 2(a + (4 * R 2 — a 2 )^(0.5)) = 2(b + (4 * R 2 — b 2 )^(0.5)).
• D и a (b): P = 2(a + sqrt(D 2 — a 2 )) = 2(b + sqrt(D 2 — b 2 )).

Площадь — характеристика размерности двумерной фигуры. Ее обозначают литерой S, и измеряют в метрических единицах в квадрате (мм 2 , см 2 , м 2 и т. д.). Следует отметить, что она вычисляется интегральным методом. Однако для частных случаев существуют соотношения. Формула, которая является основанием для всех остальных соотношений, называется базовой. Она имеет такой вид: S = a * b. Площадь находится в зависимости от параметров, которые известны:

P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.

a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].

Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.

R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].

D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].

Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.

Диагонали и стороны

Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:

• d и a (b): a = sqrt[d 2 — b 2 ] и b = sqrt[d 2 — a 2 ].
• S и a (b): a = S / b и b = S / a.
• P и a (b): a = (P — 2b) / 2 и b = (P — 2a) / 2.

Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:

a и b: d = [a 2 + b 2 ]^(1/2).

S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.

P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.

Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.

Другие соотношения

Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:

a и b: R = (a 2 + b 2 )^(1/2) / 2.

P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.

S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.

d: R = d / 2.

sin(F), прилегающего к диагонали и стороне, и a: R = a / 2sin (F).

cos(F) и b: R = b / 2cos (F).

Для нахождения угла F следует воспользоваться такой формулой: sin (F) = a / d и cos (F) = b / d. Острый угол между двумя диагоналями определяется при помощи такого соотношения: sin (Y) = 2S / d 2 .

Пример решения

Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:

• Другие стороны.
• Значения диагоналей.
• Площадь.
• R описанной окружности через площадь и периметр.
• Выяснить возможность укладки плитки в форме квадрата на такую поверхность.
• Вычислить значения всех углов между смежными сторонами.

Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.

У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.

Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:

R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).

R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).

Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.

Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

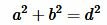(1)

Из равенства (1) найдем d:

.

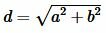(2)

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

( small R=frac<large d> <large 2>)

(3)

Подставляя (3) в (2), получим:

( small R=frac<large sqrt> <large 2>)

(4)

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

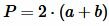(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

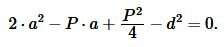(10)

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

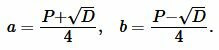(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

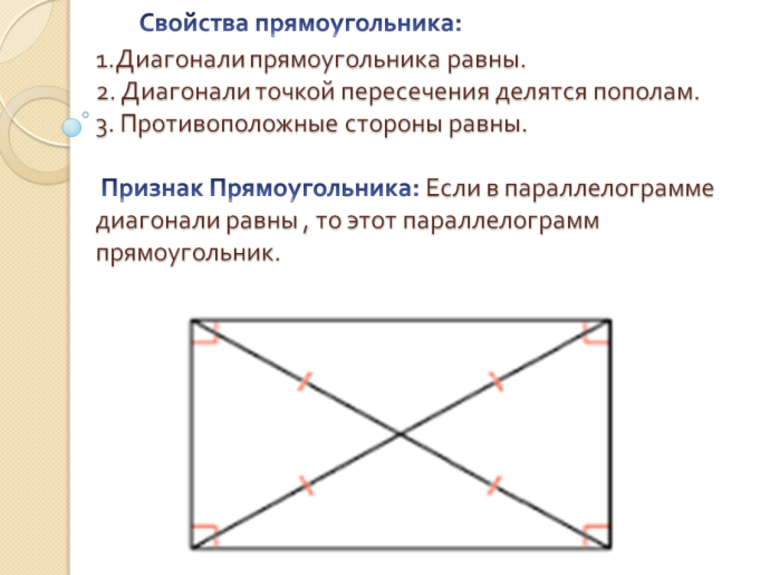
Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

В общем виде прямоугольник , действительно задаётся (описывается системой четырёх уравнений , два из которых представляет собой прямые линии , параллельные оси ОХ , но с разными значениями ординат : у1 = a ,y2 = b , , а два уравнения параллельны оси ОУ . И также два эти уравнения отличаются только значениями абцисс : х1 = с , х2 = d .При таком задании стороны прямоугольника равны соответственно a-b ).(a>b) , и ( c-d ),(c>d). Отсюда зная параметры обоих сторон прямоугольника , найдём и периметр , и площадь прямоугольника.

Конечно , есть другие возможности описать уравнением прямоугольник.При этом описываются уравнения диагоналей , допустим.

Данные стороны параллельны:

1. Пусть $%5x+2y−7=0$% — это $%DC$%:
   http://www.wolframalpha.com/input/?i=5x%2B2y%3D7
2. Пусть $%5x+2y−15=0$% — это $%AB$%:
   http://www.wolframalpha.com/input/?i=5x%2B2y%3D15

Тогда для сторон $%DC$% и $%AB$% дана диагональ $%DB$% ($%x+2y=1$%): http://www.wolframalpha.com/input/?i=5x%2B2y%3D7%3B+5x%2B2y%3D15%3B+x%2B2y%3D1

Схематичный чертёж:

Нужно найти стороны $%DA$%, $%BC$% и диагональ $%AC$%.

Искомые стороны $%DA$% и $%BC$% должны быть перпендикулярны данным $%DC$% и $%AB$% (параллельны друг другу) и проходить через $%D$% и $%B$% — точки пересечения данных сторон с данной диагональю.

Искомая диагональ пройдёт через $%A$% и $%C$% — точки пересечения данных сторон $%DC$% и $%AB$% с найденными сторонами $%DA$% и $%BC$%.

Т.е.:

1. Нужно найти $%B$% и $%D$% (найти точки пересечения данных сторон с данной диагональю).
2. Опустить перпендикуляр из $%B$% на $%CD$%, из $%D $% на $%AD$% (построить две прямые перпендикулярные к данным так, чтобы каждая проходила через одну из точек пересечения с данной диагональю).
3. Получить точки пересечения $%A $% и $%C$%.
4. Построить прямую проходящую через точки $%A$% и $%C$%.

210

Определить, какие из точек M₁(3; 1), M₂(2; 3), M₃(6; 3), M₄(-3;
-3), M₅(3; -1), M₆(-2; 1) лежат
на прямой и какие на ней не лежат. 211 Точки P₁,
P₂, P₃, P₄, P₅ расположены
на прямой ; их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 212 Точки Q₁,
Q₂, Q₃, Q₄, Q₅ расположены
на прямой ; их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 213 Определить точки
пересечения прямой с координатными
осями и построить эту прямую на чертеже. 214 Найти точку
пересечения двух прямых , . 215 Стороны АВ, ВС и АС
треугольника АВС даны соответственно
уравнениями , , . Определить
координаты его вершин. 216 Даны уравнения двух
сторон параллелограмма , и уравнение одной из
его диагоналей .
Определить координаты вершин
этого параллелограмма. 217 Стороны
треугольника лежат на прямых , , . Вычислить его площадь S. 218 Площадь
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой . Определить координаты вершины С. 219 Площадь
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой .
Определить координаты третьей
вершины С. 220 Составить
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy: 220.1 k=2/3, b=3; 220.2 k=3, b=0; 220.3 k=0, b=-2; 220.4 k=-3/4, b=3; 220.5 k=-2, b=-5; 220.6 k=-1/3, b=2/3. 221 Определить угловой
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых: 221.1 ; 221.2 ; 221.3 ; 221.4 ; 221.5 . 222 Дана прямая . Определить угловой коэффициент k
прямой: 222.1 Параллельной
данной прямой; 222.2 Перпендикулярно к
данной прямой. 223 Дана прямая . Составить уравнение прямой,
проходящей через точку М₀(2; 1): 223.1 Параллельно данной
прямой; 223.2 Перпендикулярно
данной прямой. 224 Даны уравнения двух
сторон прямоугольника , и одна из его вершин
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника. 225 Даны уравнения двух
сторон прямоугольника , и уравнение одной из
его диагоналей .
Найти вершины прямоугольника. 226 Найти проекцию
точке Р(-5; 13) относительно прямой . 227 Найти точку Q,
симметричную точке Р(-5; 13) относительно прямой . 228 В каждом из
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними: 228.1 , ; 228.2 , ; 228.3 , ; 228.4 , ; 228.5 , . 229 Вычислить угловой
коэффициент k прямой, проходящей через две данные
точки: 229.1 M₁(2;
-5), M₂(3; 2); 229.2 P(-3, 1), Q(7; 8); 229.3 A(5; -3), B(-1; 6). 230 Составить
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам. 231 Даны середины
сторон треугольника M₁(2; 1), M₂(5;
3), M₃(3; -4). Составить
уравнение его сторон. 232 Даны две точки P(2; 3),
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку . 233 Составить
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую. 234 Даны вершины
треугольника M₁(2; 1), M₂(-1; -1),
M₃(3; 2). Составить уравнения
его высот. 235 Стороны
треугольника даны уравнениями , , . Определить точку пересечения его
высот. 236 Даны вершины
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В. 237 Даны вершины
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А. 238 Составить
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0). 239 Через точки M₁(-1; 2), M₂(2; 3) проведена
прямая. Определить точки пересечения этой прямой
с осями координат. 240

Доказать,
что условие, при котором три точки M₁(x₁,
y₁), M₂(x₂, y₂), M₃(x₃,
y₃) лежат на одной прямой,
может быть записано в следующем виде:

241

Доказать,
что уравнение прямой, проходящей через две
данные точки M₁(x₁, y₁),
M₂(x₂, y₂), может
быть записано в следующем виде:

242 Даны
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей. 243 Даны две смежные
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма. 244 Даны уравнения двух
сторон прямоугольника , и уравнение его
диагонали . Составить уравнения остальных
сторон и второй диагонали этого прямоугольника. 245 Даны вершины
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А. 246 Составить
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15). 247 Найти проекцию
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1). 248 Найти точку M₁, симметричную точке М₂(8;
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2). 249 На оси абсцисс
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей. 250 На оси ординат
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей. 251 На прямой найти такую точку Р, сумма
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей. 252 На прямой найти такую точку Р, разность
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей. 253 Определить угол между двумя прямыми: 253.1 , ; 253.2 , ; 253.3 , ; 253.4 , . 254 Дана прямая . Составить уравнение прямой,
проходящей через точку M₀(2; 1) под углом 45⁰ к данной прямой. 255 Точка А(-4; 5)
является вершиной квадрата, диагональ которого
лежит на прямой . Составить
уравнения сторон и второй диагонали этого
квадрата. 256 Даны две
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон. 257 Точка E(1; -1) является
центром квадрата, одна из сторон которого лежит
на прямой . Составить уравнения
прямых, на которых лежат остальные стороны этого
квадрата. 258 Из точки M₀(-2; 3) под углом к оси
Ox направлен луч света. Известно, что . Дойдя
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи. 259 Луч света направлен
по прямой , луч от нее отразился.
Составить уравнение прямой, на которой лежит
отраженный луч. 260 Даны уравнения
сторон треугольника , , . Доказать, что этот треугольник
равнобедренный. Решить задачу при помощи
сравнения углов треугольника. 261 Доказатть, что
уравнение прямой, проходящей через точку M₁(x₁; y₁) параллельно
прямой , может быть записано в виде . 262 Составить
уравнение прямой, проходящей через точку М₁(2: -3) параллельно
прямой: 262.1 ; 262.2 ; 262.3 ; 262.4 ; 262.5 . 263 Доказать, что
условие перпендикулярности прямых ; может быть записано
в следующем виде: . 264 Установить, какие
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 264.1  , ; 264.2 , ; 264.3 , ; 264.4 , ; 264.5 , ; 264.6 , . 265

Доказать,
что формула для определения угла между
прямыми , может
быть записана в следующей форме:

266 Определить угол , образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 266.1 , ; 266.2  , ; 266.3  , . 267 Даны две вершины
треугольника M₁(-10; 2), M₂(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M₃. 268 Даны две вершины A(3;
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника. 269 В треугольнике АВС
даны: уравнение стороны АВ: , уравнения
высот АМ: и BN: . Составить уравнения двух
других сторон и третьей высоты этого
треугольника. 270 Составить
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан , . 271 Составить
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот , . 272 Составить
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис , . 273 Составить
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты и
биссектрисы , проведенных из одной вершины. 274 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты и биссектрисы , проведенных из
различных вершин. 275 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты и медианы , проведенной из
одной вершины. 276 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты и медианы , проведенных из
различных вершин. 277 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы и медианы , проведенных из
одной вершины. 278 Составить
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы и медианы , проведенных из
различных вершин. 279 Составить
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми , образует
треугольник с площадью, равной 1,5. 280 Среди прямых,
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми , , делится в точке Р
пополам. 281 Через точку Р(-3; -1)
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми , , делится
в точке Р пополам. 282 Через точку Р(0; 1)
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми , , делился бы в точке Р
пополам. 283 Составить
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми , , равна . 284 Составить
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми , , равна 5.

Based on Raskolnikov’s answer here, one can build an implicit Cartesian equation for a $2p times 2q$ rectangle:

$$left(frac{x}{p}right)^2+left(frac{y}{q}right)^2=secleft(arctanleft(frac{x}{p},frac{y}{q}right)-frac{pi}{2}leftlfloorfrac2{pi}arctanleft(frac{x}{p},frac{y}{q}right)+frac12rightrfloorright)^2$$

Another one is based on modifying the implicit equation of a Lamé curve:

$$left|frac{x}{p}+frac{y}{q}right|+left|frac{x}{p}-frac{y}{q}right|=2$$

---

For purposes of plotting with a computer, the implicit equation isn’t terribly convenient to handle, so I’ll throw in a set of parametric Cartesian equations for free, based on the parametric equations of the Lamé curve:

$$begin{align*}x&=pleft(|cos,t|cos,t+|sin,t|sin,tright)\y&=qleft(|cos,t|cos,t-|sin,t|sin,tright)end{align*}$$

Here’s another one, based on a special case of the parametric equations given in this answer:

$$begin{align*}x&=pleft(cosleft(frac{pi}{2}lfloor urfloorright)-(2u-2lfloor urfloor-1)sinleft(frac{pi}{2}lfloor urfloorright)right)\y&=qleft(sinleft(frac{pi}{2}lfloor urfloorright)+(2u-2lfloor urfloor-1)cos left(frac{pi}{2}lfloor urfloorright)right)end{align*}$$

…and another one:

$$begin{align*}x&=pmaxleft(-1,minleft(frac4{pi}arcsinleft(sinleft(frac{pi u}{2}+frac{pi}{4}right)right),1right)right)\y&=qmaxleft(-1,minleft(-frac4{pi}arcsinleft(cosleft(frac{pi u}{2}+frac{pi}{4}right)right),1right)right)end{align*}$$

…and I suppose I should stop here.