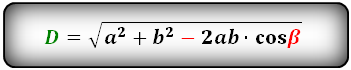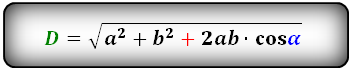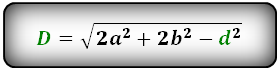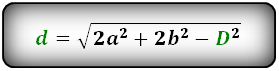Как составить уравнение диагонали параллелограмма

Задача 59148 Подскажите как правильно решать! Найти.

Условие

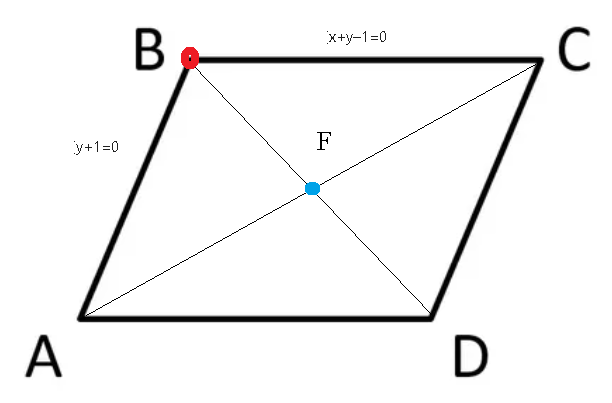
Подскажите как правильно решать! Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x+y-1=0 если у+1=0 если известно что диагональ параллелограмма пересекается в точке F(-1, 0) И надо ли в этой задаче чертить рисунок?

Решение

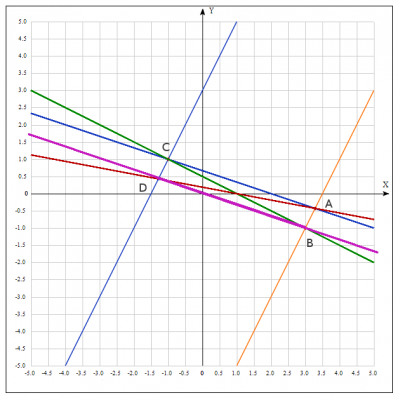
Можно нарисовать схематический чертеж, чтобы понять как решать задачу ( cм. рис)

Противоположные стороны параллелограмма параллельны.

Даны уравнения смежных сторон. Это может быть АВ и ВС

1) чтобы найти точку пересечения сторон АВ и ВС

Это и есть координаты точки B.

2)
Составить уравнение прямой, проходящей через две точки:
(2;-1) и F(–1, 0)

Это можно сделать двумя способами:

Уравнение прямой с угловым коэффициентом имеет вид:
y=kx+b

Подставляем координаты точек:
-1=k*2+b
0=k*(-1)+b
находим k и b

[b]x+3y+1=0[/b] — это ответ.

Второй способ
Уравнение прямой, проходящей через две точки имеет вид: ( cм. скрин)

Подставляем координаты точек

и получаем пропорцию:

[b]x+3y+1=0[/b]- ответ.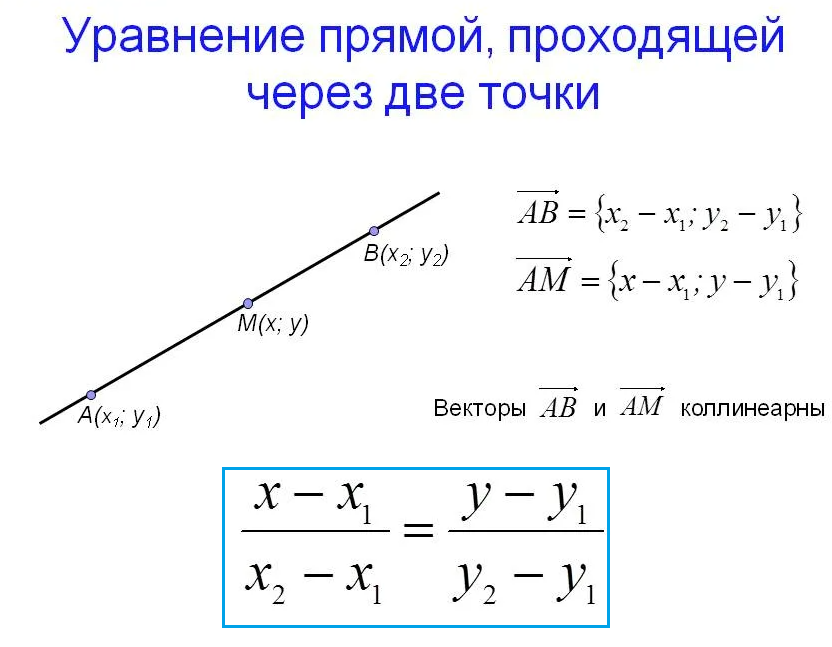

Параллелограмм. Формулы, признаки и свойства параллелограмма

Признаки параллелограмма

AB||CD, AB = CD (или BC||AD, BC = AD)

∠DAB = ∠BCD, ∠ABC = ∠CDA

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Основные свойства параллелограмма

∠ABC = ∠CDA, ∠BCD = ∠DAB

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:

AO = CO =	d 1
2
BO = DO =	d 2
2

AC 2 + BD 2 = 2AB 2 + 2BC 2

Стороны параллелограмма

Формулы определения длин сторон параллелограмма:

1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и другую сторону:

a =	√ 2 d 1 2 + 2 d 2 2 — 4 b 2
2

b =	√ 2 d 1 2 + 2 d 2 2 — 4 a 2
2

3. Формула сторон параллелограмма через высоту и синус угла:

4. Формула сторон параллелограмма через площадь и высоту:

Диагонали параллелограмма

Формулы определения длины диагонали параллелограмма:

d ₁ = √ a 2 + b 2 — 2 ab·cosβ

d ₂ = √ a 2 + b 2 + 2 ab·cosβ

d ₁ = √ a 2 + b 2 + 2 ab·cosα

d ₂ = √ a 2 + b 2 — 2 ab·cosα

d ₁ = √ 2 a 2 + 2 b 2 — d ₂ 2

d ₂ = √ 2 a 2 + 2 b 2 — d ₁ 2

4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:

d 1 =	2S	=	2S
d 2· sinγ	d 2· sinδ

d 2 =	2S	=	2S
d 1· sinγ	d 1· sinδ

Периметр параллелограмма

Формулы определения длины периметра параллелограмма:

P = 2 a + 2 b = 2( a + b )

P = 2 a + √ 2 d ₁ 2 + 2 d ₂ 2 — 4 a 2

P = 2 b + √ 2 d ₁ 2 + 2 d ₂ 2 — 4 b 2

3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:

Площадь параллелограмма

Формулы определения площади параллелограмма:

3. Формула площади параллелограмма через две диагонали и синус угла между ними:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Написать уравнение сторон и диагоналей параллелограмма

Вопрос по геометрии:

Даны точки О(0;0) и А(-3; 0). На отрезке ОА построен параллелограмм , диагонали которого пересекаются в точке В (0;2). Написать уравнение сторон и диагоналей параллелограмма

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Обозначим параллелограмм АОСР, где диагонали АС и ОР пересекаются в точке В. Найдем координаты точек С и Р.

Точка P(0;4)
Точки А и О лежат на оси Ох, т е уравнение прямой АО у=0, С и Р лежат на прямой у=4, т е уравнение прямой РС у=4.
Точки А и Р лежат на прямой у=kx+b, для A: 0=-3k+b, для P: 4=0*k+b , отсюда b=4, k=4/3, т е уравнение прямой АР у=4/3х+4.
Точки О и С лежат на прямой у=kx+b, для О: 0=0*k+b, для С: 4=3*k+b , отсюда b=0, k=4/3, т е уравнение прямой ОС у=4/3х.
Ответ: уравнения сторон параллелограмма у=0, у=4, у=4/3х+4,

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Задача 59148 Подскажите как правильно решать! Найти.

Условие

Подскажите как правильно решать! Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x+y-1=0 если у+1=0 если известно что диагональ параллелограмма пересекается в точке F(-1, 0) И надо ли в этой задаче чертить рисунок?

Решение

Можно нарисовать схематический чертеж, чтобы понять как решать задачу ( cм. рис)

Противоположные стороны параллелограмма параллельны.

Даны уравнения смежных сторон. Это может быть АВ и ВС

1) чтобы найти точку пересечения сторон АВ и ВС

Это и есть координаты точки B.

2)
Составить уравнение прямой, проходящей через две точки:
(2;-1) и F(–1, 0)

Это можно сделать двумя способами:

Уравнение прямой с угловым коэффициентом имеет вид:
y=kx+b

Подставляем координаты точек:
-1=k*2+b
0=k*(-1)+b
находим k и b

[b]x+3y+1=0[/b] — это ответ.

Второй способ
Уравнение прямой, проходящей через две точки имеет вид: ( cм. скрин)

Подставляем координаты точек

и получаем пропорцию:

[b]x+3y+1=0[/b]- ответ.

Помогите, пожалуйста, решить задачу по геометрии.

1. Даны две противоположные вершины квадрата А (1;3) и С (-1;1). Найти коорди-наты В и D.

2.Две стороны параллелограмма заданы уравнениями у = х — 2 и 5у = х + 6. Его диа-гонали пересекаются в начале координат. Написать уравнения диагоналей.

1) Уравнение диагонали АС:
(у-ус) /(уА-уС) = (х-хС) /(хА-хС)
(у-1)/2 = (х+1)/2
у = х+2
Диагональ BD перпендикулярна АС (угловой коэффициент равен -1) и проходит через середину АС, т. е. через точку О (0;2).
Уравнение диагонали BD
y = 2 — х
Искомые координаты вершин могут быть найдены, например, из условий
АO=OВ и AO=OD
(1-0)^2 + (3-2)^2 = x^2 + (2-x-2)^2
2 = 2*x^2
x = 1; y = 2-1=1 — координаты т. В
x = -1; y = 2+1 = 3 — координаты т. D
2) Одна из вершин параллелограмма — точка пересечения данных прямых. Решение системы линейных уравнений
у = х — 2
х = 5*у — 6
даст точку вершины с координатами А (4; 2).
Начало координат — точка пересечения диагоналей, поэтому противоположная вершина С (-4; -2) — центрально симметрична точке А относительно начала координат.
Собственно, сразу можно было найти уравнение диагонали АС (то же, что и прямой АО) :
у = 2*х/4 = х/2
Для нахождения второй диагонали достаточно найти третью вершину параллелограмма, например, как точку пересечения стороны, задаваемой уравнением
х = 5*у — 6
и стороны, параллельной прямой
у = х — 2
и проходящей через точку С.
уравнение этой стороны будет иметь вид:
у = -2 + х + 4
у = х + 2
Координаты вершины В найдем из решения системы:
х = 5*у — 6
у = х + 2
Вершина В (-1; 1)
Уравнение диагонали BD (то же, что и прямой ОВ)
у = -х

Все формулы диагонали параллелограмма

Свойства параллелограмма:

1. Противоположные стороны равны и параллельны

2. Противоположные углы равны

3. Точка пересечения диагоналей, делит их пополам

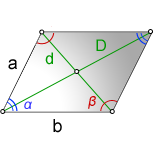
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.

a , b — стороны параллелограмма

D — большая диагональ

d — меньшая диагональ

α , β — углы параллелограмма

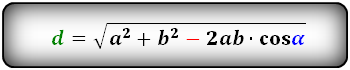
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), ( D , d ):

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), ( D , d ):

2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.

D — большая диагональ

d — меньшая диагональ

α , β — углы между диагоналями

S — площадь параллелограмма

Формулы диагонали через площадь, известную диагональ и угол между диагоналями, ( D , d ):

Условие

Решение

Написать комментарий

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---