Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые.
В этой статье собрана информация, необходимая для нахождения уравнения плоскости, проходящей через две заданные пересекающиеся или параллельные прямые. Сначала разобран принцип составления уравнения плоскости, которая проходит через две заданные прямые, после этого приведены подробные решения характерных примеров.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через две пересекающиеся прямые.
Прежде чем приступать к нахождению уравнения плоскости, проходящей через две заданные пересекающиеся прямые, напомним одну теорему: в трехмерном пространстве через две пересекающиеся прямые проходит единственная плоскость. Это утверждение является следствием из двух аксиом геометрии:
- через три различные и не лежащие на одной прямой точки проходит единственная плоскость;
- если две несовпадающие точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Таким образом, конкретную плоскость в трехмерном пространстве можно задать, указав две пересекающиеся прямые, лежащие в этой плоскости.
Теперь покажем, что плоскость, проходящая через две заданные пересекающиеся прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных прямых, а третья – на другой прямой.
Пусть заданные прямые a и b пересекаются в точке М . Отметим на прямой a две различные точки М1 и М2 (одна из них может совпадать с точкой M ), а на прямой b точку М3 , отличную от точки М . Покажем, что плоскость М1М2М3 есть плоскость, проходящая через заданные пересекающиеся прямые a и b .
Так как в плоскости М1М2М3 лежат две точки прямой a (точки М1 и М2 ), то из озвученной в начале этого пункта аксиомы следует, что все точки прямой a лежат в плоскости М1М2М3 , в частности, точка М . Тогда в плоскости М1М2М3 лежат все точки прямой b , так как две несовпадающие точки прямой b (точки М и М3 ) лежат в указанной плоскости. Следовательно, плоскость, проходящая через пересекающиеся прямые a и b , и плоскость, проходящая через три точки М1 , М2 и М2 , совпадают.
Итак, поставим перед собой следующую задачу.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , заданы две пересекающиеся прямые a и b , и требуется написать уравнение плоскости, проходящей через пересекающиеся прямые a и b .
Сведем решение этой задачи к нахождению уравнения плоскости, проходящей через три точки. Для этого нужно определить координаты двух различных точек M1 и M2 , лежащих на одной из заданных пересекающихся прямых, и координаты точки M3 , лежащей на другой прямой и не являющейся точкой пересечения заданных прямых. Для нахождения координат точек М1 , М2 и М3 все средства хороши. Например, можно получить параметрические уравнения прямой a в пространстве вида . Из них видны координаты точки М1 (они получаются при ), а координаты точки М2 можно вычислить, придав параметру любое ненулевое действительное значение (к примеру, ). После этого можно получить параметрические уравнения прямой b и при некотором значении параметра вычислить координаты точки М3 , не забыв удостовериться, что она не является точкой пересечения заданных прямых (что она не лежит на прямой a ).
Будем считать, что координаты точек М1 , М2 и М3 найдены. После этого мы можем написать уравнение плоскости, проходящей через три точки и в виде . Вычислив определитель матицы вида , мы получим общее уравнение плоскости М1М2М3 , которое и будет уравнением плоскости, проходящей через две пересекающиеся прямые a и b .
Нахождение уравнения плоскости, проходящей через две параллельные прямые.
Прежде чем получить уравнение плоскости, проходящей через две заданные параллельные прямые, вспомним теорему: через две параллельные прямые проходит единственная плоскость. Эта теорема доказывается на основе аксиомы о единственной плоскости, проходящей через три заданные точки, с использованием утверждения: если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
Таким образом, мы можем задать конкретную плоскость в трехмерном пространстве, указав две параллельные прямые, лежащие в этой плоскости.
Очевидно, что плоскость, проходящая через две заданные параллельные прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных параллельных прямых, а третья лежит на другой прямой.
Теперь можно приступать к нахождению уравнения плоскости, проходящей через две заданные параллельные прямые.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , заданы две параллельные прямые a и b и требуется составить уравнение плоскости, которая проходит через параллельные прямые a и b .
Эта задача, также как и задача о нахождении уравнения плоскости, проходящей через две заданные пересекающиеся прямые, сводится к составлению уравнения плоскости, проходящей через три точки. Действительно, мы можем определить координаты двух точек М1 и М2 , лежащих на одной из заданных параллельных прямых, и координаты точки М3 , лежащей на другой прямой. После этого нам лишь нужно написать уравнение плоскости, проходящей через три точки и , в виде . Это уравнение является искомым уравнением плоскости, проходящей через две заданные параллельные прямые.
Примеры составления уравнения плоскости, проходящей через две прямые.
Итак, чтобы написать уравнение плоскости, проходящей через две заданные параллельные или пересекающиеся прямые, нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки. Покажем применение этого алгоритма при решении примеров.
Известно, что прямая a в прямоугольной системе координат Oxyz в трехмерном пространстве проходит через точку и пересекает координатную прямую Oy в точке . Напишите уравнение плоскости, проходящей через пересекающиеся прямые a и Oy .
Из условия нам известны координаты двух точек М1 и М2 , лежащих на прямой a . Очевидно, что точка лежит на координатной прямой Oy и не совпадает с точками М1 и М2 . Тогда плоскость, проходящая через три точки , и , есть плоскость, проходящая через пересекающиеся прямые a и Oy . Напишем ее уравнение:
.
Рассмотрим еще один пример, в котором координаты точек, лежащих на заданных пересекающихся прямых, не так очевидны.
Составьте уравнение плоскости, которая проходит через две пересекающиеся прямые a и b , заданные уравнениями и соответственно.
Сначала найдем координаты двух точек, лежащих на прямой a , и координаты точки, лежащей на прямой b .
Прямая, которую в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида , проходит через точку . Перейдем к параметрическим уравнениям этой прямой, чтобы определить координаты еще одной точки (обозначим ее М2 ), лежащей на ней. Имеем , примем и из параметрических уравнений прямой вычислим координаты точки М2 : . Следовательно, .
Очевидно, что прямая проходит через точку . Проверим, не является ли точка точкой пересечения заданных прямых, подставив ее координаты в уравнения прямой a : . Канонические уравнения прямой a обратились в тождества, следовательно, точка М3 лежит на прямой a и является точкой пересечения заданных прямых. Таким образом, нам нужно взять другую точку М3 , лежащую на прямой b , так как сейчас найденные точки М1 , М2 и М3 лежат на одной прямой. Для этого мы также переходим к параметрическим уравнениям прямой b : , и вычисляем координаты точки М3 , приняв : .
Теперь мы можем получить уравнение плоскости, проходящей через три точки , и , которое является искомым уравнением плоскости, проходящей через две заданные пересекающиеся прямые:
.
Не правда ли, что нахождение координат точек, лежащих на заданных прямых, является самым трудоемким процессом при составлении уравнения плоскости, проходящей через две пересекающиеся прямые?
Осталось рассмотреть пример составления уравнения плоскости, проходящей через две заданные параллельные прямые.
Напишите уравнение плоскости, проходящей через две параллельные прямые и .
По параметрическим уравнениям прямой при и вычислим координаты двух точек М1 и М2 :
Очевидно, что прямая проходит через точку .
Найдем уравнение плоскости, проходящей через три точки М1 , М2 и М3 :
Это уравнение и есть искомое уравнение плоскости, проходящей через две заданные параллельные прямые.
.
Точка пересечения двух прямых на плоскости
Пересечение прямых
Для создания компьютерных игр, программ математических графиков, расчетов движения объектов и т.п. очень часто требуется найти точку пресечения прямых. Сначала необходимо на бумаге вывести и упростить формулы вычисления и далее эти формулы перевести в программный код.
Прямые это бесконечные линии, поэтому на плоскости они всегда пересекаются. Если прямые не пересекаются значит они параллельны. Частные случаи поведения прямых на плоскости: прямые неопределенны, прямые параллельны, прямые совпадают, одна из прямых параллельна оси X или Y. Общие случаи «нормального» пересечения прямых и частные случаи учитываются в программном коде класса Intersections прикрепленного исходника.
Прямые пересекаются
Даны две прямые AB и CD расположенные на одной плоскости. Они пересекаются и необходимо найти точку пересечения. За основу берем классическое уравнение прямой и подставляя данные получаем систему уравнений для двух прямых.
Точку пересечения можно найти, решая совместно уравнения прямых. Два уравнения — две неизвестных величины. Если количество уравнений больше или равно количеству неизвестных, то система решаема. Точка пересечения двух прямых это такая точка, которая принадлежит обеим прямым.
Классическое уравнение прямой: Запишем уравнение в одну строчку: Вычислим коэффициенты и свободные члены: В итоге получаем уравнение прямой с коэффициентами:
Уравнение с линейными коэффициентами отличается от уравнения с угловым коэффициентом отсутствием операции деления. Минимум операций деления упрощает создание устойчивого программного кода.
Точка пересечения прямых
Координаты точки пересечения это числа которые являются решением для каждого из уравнений прямых. Решая систему из двух уравнений находим в какой точке пересекаются прямые AB и CD.
Подставляем известные данные: Получаем два уравнения: Решаем систему уравнений: Найдено, прямые пересекаются в точке с координатами:
Прямые параллельны
Если прямые параллельны и лежат друг от друга на расстоянии, то у них нет общих точек. Совместная система уравнений не имеет решений. Эти уравнения существуют как бы сами по себе. В точности как их параллельные прямые.
Две прямые могут полностью совпадать, в таком случае у них бесконечное количество общих точек. Совпадение прямых означает равность коэффициентов и свободных членов уравнений. Совпадающие прямые имеют идентичные уравнения.
Применяя формулу у.2 выведем уравнения прямых: Получаем систему уравнений:
Итог: система уравнений параллельных прямых не имеет решений.
Уравнение в программный код
На бумаге всё славненько, надо также сделать и в программном коде. Но программы не разбираются в уравнениях, им подавай переменные, постоянные и функции. Программный код не терпит неопределенности, он требует точные данные. Очень желательно строить выражения без операций деления. Преобразуем в программный код уравнение с коэффициентами (у.3) описанное выше. Для каждой прямой своё уравнение и переменные.
Точки определяющие прямые запишем в структуры Point. У каждой прямой две точки и они являются входными данными:
Определяем коэффициенты и свободные члены уравнений. Записываем их в соответствующие переменные:
Точка пересечения также будет храниться в структуре Point:
Вывод результата
В выражениях присутствует деление. Но знаменатель только тогда и только тогда будет равен нулю, когда обе прямые будут параллельны или оси X или оси Y. В этом случае они не пересекаются или совпадают. Это отслеживаемые состояния в классе Intersections , и вывод информации заканчивается до выбрасывания исключения при делении на ноль.
Проверка параллельности и совпадения
Проверка на перпендикулярность
Класс Intersections
Исходник представляет собой два класса: класс вычисления точки пересечения прямых и информационный класс выдающий множество дополнительных сведений о свойствах исследуемых прямых.
Краткий листинг исходника дающий представление о структуре классов:
Применение класса Intersections
Класс class Intersections легко встраивается в любой исходный код. Точки определяющие прямые являются входными данными. На выходе получаем результат пересечения, координаты точки пересечения. Для дальнейшей обработки результатов можно использовать идентификатор свойства пересечения и дополнительную текстовую информацию.
Прикрепленный файл
Прикрепленный файл архива содержит исходник классов Intersections, Info и программу демонстрирующую работу класса Intersections в режиме вычисления точки пересечения прямых на плоскости. Исходный код написан на языке C#, но его легко можно преобразовать в код на другом языке программирования. Для работы демонстрационной программы необходима установка платформы. .NET Core 3.1.
Скачать исходник
- Файл: IntersectionsLineLine.zip
- Размер: 84 Кбайт
- Загрузки: 547
Похожая тематика
Пересечение луча и прямой на плоскости »
Пересечение прямых. Точка пересечения двух прямых
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x — 1 y = -3 x + 1
Вычтем из первого уравнения второе
y — y = 2 x — 1 — (-3 x + 1) y = -3 x + 1 => 0 = 5 x — 2 y = -3 x + 1
Из первого уравнения найдем значение x
5 x = 2 y = -3 x + 1 => x = 2 5 = 0.4 y = -3 x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x — 1 x = 2 t + 1 y = t
В первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2 t + 1) — 1 x = 2 t + 1 y = t => t = 4 t + 1 x = 2 t + 1 y = t =>
-3 t = 1 x = 2 t + 1 y = t => t = — 1 3 x = 2 t + 1 y = t
Подставим значение t во второе и третье уравнение
t = — 1 3 x = 2·(- 1 3 ) + 1 = — 2 3 + 1 = 1 3 y = — 1 3
Ответ. Точка пересечения двух прямых имеет координаты ( 1 3 , — 1 3 )
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2 x + 3 y = 0 x — 2 3 = y 4
Из второго уравнения выразим y через x
2 x + 3 y = 0 y = 4· x — 2 3
Подставим y в первое уравнение
2 x + 3·4· x — 2 3 = 0 y = 4· x — 2 3 => 2 x + 4·( x — 2) = 0 y = 4· x — 2 3 =>
2 x + 4 x — 8 = 0 y = 4· x — 2 3 => 6 x = 8 y = 4· x — 2 3 =>
x = 8 6 = 4 3 y = 4· x — 2 3 => x = 8 6 = 4 3 y = 4· 4/3 — 2 3 = 4· -2/3 3 = — 8 9
Ответ. Точка пересечения двух прямых имеет координаты ( 4 3 , — 8 9 )
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2 x — 1 y = 2 x + 1
Вычтем из первого уравнения второе
y — y = 2 x — 1 — (2 x + 1) y = -3 x + 1 => 0 = -2 y = -3 x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).
Решение: Подставим координаты точки N в уравнения прямых.
Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Решение: Составим систему уравнений
x — 1 = a y — 1 = a z — 1 = a x — 3 -2 = b 2 — y = b z = b => x = a + 1 y = a + 1 z = a + 1 x — 3 -2 = b 2 — y = b z = b =>
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1 y = a + 1 z = a + 1 a + 1 — 3 -2 = b 2 — ( a + 1) = b a + 1 = b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 + (1 — a ) = b + b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b b = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = 1 1 — a = 1 b = 1 => x = a + 1 y = a + 1 z = a + 1 a — 2 = -2 a = 0 b = 1 =>
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2 t — 3 y = t z = — t + 2 x = a + 1 y = 3 a — 2 z = 3
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2 t — 3 y = t z = — t + 2 2 t — 3 = a + 1 t = 3 a — 2 — t + 2 = 3 => x = 2 t — 3 y = t z = — t + 2 2 t = a + 4 t = 3 a — 2 t = -1 =>
Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) — 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3 a — 2 t = -1 => x = -5 y = -1 z = 3 a = -6 a = 1 3 t = -1
Ответ. Так как -6 ≠ 1 3 , то прямые не пересекаются.
http://www.interestprograms.ru/source-codes-tochka-peresecheniya-dvuh-pryamyh-na-ploskosti
http://ru.onlinemschool.com/math/library/analytic_geometry/lines_intersection/
5.4.4. Прямая, заданная пересечением двух плоскостей
Если плоскости пересекаются, то система линейных уравнений

То есть прямая задана уравнениями двух плоскостей. Типовая и
распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Задача 151
Записать канонические уравнения прямой
Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух
плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим
какую-нибудь координату, например, . Тогда получается система двух линейных
уравнений с двумя неизвестными: . Почленно складываем уравнения и находим
решение системы:
Таким образом, точка принадлежит данной прямой. Но принадлежит ли?
Выполним проверку – подставим её координаты в исходную систему уравнений:
Получены верные равенства, значит, действительно .
В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в
системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует
проводить мысленно или на черновике.
2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух
плоскостей 

В нашей задаче:
Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: и
, поэтому вектор «пэ» можно найти как векторное произведение векторов нормали:
.

«снимаем» их векторы нормали:
и находим направляющий вектор прямой:
Проверим результат с помощью скалярного произведения:
, ч.т.п.
И, наконец, завершающий этап:
3) Составим канонические уравнения прямой по точке и
направляющему вектору :
Ответ:
Аналогичная задача для самостоятельного решения:
Задача 152
Записать канонические уравнения прямой
Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения
и подставьте в моё уравнение (или наоборот).
Полное решение и ответ в конце книги.
И сейчас самое время перейти к простейшим задачам с пространственной прямой:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Пересечение прямых. Точка пересечения двух прямых
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x — 1 y = -3 x + 1
Вычтем из первого уравнения второе
y — y = 2 x — 1 — (-3 x + 1) y = -3 x + 1 => 0 = 5 x — 2 y = -3 x + 1
Из первого уравнения найдем значение x
5 x = 2 y = -3 x + 1 => x = 2 5 = 0.4 y = -3 x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x — 1 x = 2 t + 1 y = t
В первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2 t + 1) — 1 x = 2 t + 1 y = t => t = 4 t + 1 x = 2 t + 1 y = t =>
-3 t = 1 x = 2 t + 1 y = t => t = — 1 3 x = 2 t + 1 y = t
Подставим значение t во второе и третье уравнение
t = — 1 3 x = 2·(- 1 3 ) + 1 = — 2 3 + 1 = 1 3 y = — 1 3
Ответ. Точка пересечения двух прямых имеет координаты ( 1 3 , — 1 3 )
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2 x + 3 y = 0 x — 2 3 = y 4
Из второго уравнения выразим y через x
2 x + 3 y = 0 y = 4· x — 2 3
Подставим y в первое уравнение
2 x + 3·4· x — 2 3 = 0 y = 4· x — 2 3 => 2 x + 4·( x — 2) = 0 y = 4· x — 2 3 =>
2 x + 4 x — 8 = 0 y = 4· x — 2 3 => 6 x = 8 y = 4· x — 2 3 =>
x = 8 6 = 4 3 y = 4· x — 2 3 => x = 8 6 = 4 3 y = 4· 4/3 — 2 3 = 4· -2/3 3 = — 8 9
Ответ. Точка пересечения двух прямых имеет координаты ( 4 3 , — 8 9 )
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2 x — 1 y = 2 x + 1
Вычтем из первого уравнения второе
y — y = 2 x — 1 — (2 x + 1) y = -3 x + 1 => 0 = -2 y = -3 x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).
Решение: Подставим координаты точки N в уравнения прямых.
Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Решение: Составим систему уравнений
x — 1 = a y — 1 = a z — 1 = a x — 3 -2 = b 2 — y = b z = b => x = a + 1 y = a + 1 z = a + 1 x — 3 -2 = b 2 — y = b z = b =>
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1 y = a + 1 z = a + 1 a + 1 — 3 -2 = b 2 — ( a + 1) = b a + 1 = b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b a + 1 + (1 — a ) = b + b => x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = b 1 — a = b b = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a — 2 -2 = 1 1 — a = 1 b = 1 => x = a + 1 y = a + 1 z = a + 1 a — 2 = -2 a = 0 b = 1 =>
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2 t — 3 y = t z = — t + 2 x = a + 1 y = 3 a — 2 z = 3
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2 t — 3 y = t z = — t + 2 2 t — 3 = a + 1 t = 3 a — 2 — t + 2 = 3 => x = 2 t — 3 y = t z = — t + 2 2 t = a + 4 t = 3 a — 2 t = -1 =>
Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) — 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3 a — 2 t = -1 => x = -5 y = -1 z = 3 a = -6 a = 1 3 t = -1
Ответ. Так как -6 ≠ 1 3 , то прямые не пересекаются.
Исследование уравнений второго порядка
Преобразование координат в уравнении второго порядка.
В общей декартовой системе координат линия второго порядка может быть задана уравнением
$$
Ax^ <2>+ 2Bxy + Cy^ <2>+ 2Dx + 2Ey + F = 0,label
$$
в котором коэффициенты (A), (B) и (C) не равны нулю одновременно. Исследуем множество точек, которые ему удовлетворяют, не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид уравнения eqref не изменится.
При повороте базиса декартовой прямоугольной системы координат на угол (varphi) старые координаты точки (x), (y) будут связаны с ее новыми координатами (x’), (y’) формулами
$$
x = x’cos varphi-y’sin varphi,\ y = x’sin varphi + y’cos varphi.nonumber
$$
В новых координатах уравнение eqref примет вид
$$
A(x’cos varphi-y’sin varphi)^ <2>+ 2B(x’cos varphi-y’sin varphi) times \ times (x’sin varphi + y’cos varphi) + C(x’sin varphi + y’cos varphi) + … = 0.nonumber
$$
Здесь многоточием обозначены члены первой степени относительно (x’), (y’) и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением (x’y’) в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэффициента при (x’y’) есть
$$
B’ = -Asin varphi cos varphi + B(cos^<2>varphi-sin^<2>varphi) + Csin varphi cos varphi.nonumber
$$
Если (B = 0), то поворачивать систему координат не будем. Если же (B neq 0), то выберем угол (varphi) так, чтобы (B’) обратилось в нуль.
Это требование приведет к уравнению
$$
2B cos 2varphi = (A-C)sin 2varphi.label
$$
Если (A = C), то (cos 2varphi = 0), и можно положить (varphi = pi/4). Если же (A neq C), то выбираем (varphi = displaystylefrac<1> <2>operatorname left[frac<2B>right]). Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота системы координат на этот угол линия будет иметь уравнение
$$
A’x’^ < 2>+ C’y’^ < 2>+ 2D’x’ + 2E’y’ + F’ = 0.label
$$
Выражения для коэффициентов уравнения eqref через коэффициенты eqref подсчитать не трудно, но это не нужно. Теперь коэффициент при произведении переменных равен нулю, а остальные члены мы по-прежнему считаем произвольными.
Если в уравнение eqref входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.
В самом деле, пусть, например, (A’ neq 0). Перепишем eqref в виде
$$
A’left(x’^ < 2>+ frac<2D’>x’ + frac>>right) + C’y’^ < 2>+ 2E’y’ + F’-frac = 0.nonumber
$$
Если мы сделаем перенос начала координат, определяемый формулами (x″ = x’ + D’/A’), (y″ = y’), то уравнение приведется к виду
$$
A’x″^ < 2>+ C’y″^ < 2>+ 2E’y″ + F″ = 0,nonumber
$$
как и требовалось.
Канонические виды уравнений второго порядка.
Предположим, что (A’C’ neq 0), то есть оба коэффициента отличны от нуля. Согласно утверждению 1 при помощи переноса начала координат уравнение приведется к виду
$$
A’x″^ < 2>+ C’y″^ < 2>+ F″ = 0.label
$$
Могут быть сделаны следующие предположения относительно знаков коэффициентов в этом уравнении.
Случай A’C’ > 0.
Если (A’C’ > 0), то коэффициенты (A’) и (C’) имеют один знак. Для (F″) имеются следующие три возможности.
- Знак (F″) противоположен знаку (A’) и (C’). Перенесем (F″) в другую часть равенства и разделим на него. Уравнение примет вид
$$
frac>> + frac>> = 1,label
$$
где (a^ <2>= -F″/A’), (b^ <2>= -F″/C’). Можно считать, что в этом уравнении (a > 0), (b > 0) и (a geq b). Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат
$$
x^ <*>= y″, y^ <*>= x″.label
$$
Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref при условии (a geq b), называется эллипсом, уравнение называется каноническим уравнением эллипса, а система координат — его канонической системой координат.
При (a = b) уравнение eqref есть уравнение окружности радиуса (a). Таким образом, окружность — частный случай эллипса.
$$
frac>> + frac>> = -1,label
$$
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, которое приводится к каноническому виду eqref, называется уравнением мнимого эллипса.
$$
a^<2>x″^ < 2>+ c^<2>y″^ < 2>= 0.label
$$
Ему удовлетворяет только одна точка (x″ = 0), (y″ = 0). Уравнение, приводящееся к каноническому виду eqref, называется уравнением пары мнимых пересекающихся прямых. Основанием для этого названия служит сходство с приведенным ниже уравнением eqref.
Случай A’C’ Определение.
Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref, называется гиперболой, уравнение называется каноническим уравнением гиперболы, а система координат — ее канонической системой координат.
Случай (A’C’ = 0).
Допустим теперь, что (A’C’ = 0), и, следовательно, один из коэффициентов (A’) или (C’) равен нулю. В случае необходимости, делая замену eqref, мы можем считать, что (A’ = 0). При этом (C neq 0), так как иначе порядок уравнения был бы меньше двух. Используя утверждение 1, мы приведем уравнение к виду
$$
C’y″^ < 2>+ 2D’x″ + F″ = 0.nonumber
$$
Пусть (D’ neq 0). Сгруппируем члены следующим образом:
$$
C’y″^ < 2>+ 2D’left(x″ + frac<2D’>right) = 0.nonumber
$$
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода (x^ <*>= x″ + F″/2D’), (y^ <*>= y″). Тогда уравнение примет вид
$$
C″y^ <*2>+ 2D’x^ <*>= 0,nonumber
$$
или
$$
y^ <*2>= 2px^<*>,label
$$
где (p = -D’/C″). Мы можем считать, что (p > 0), так как в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: (tilde = -x^<*>), (tilde = y^<*>).
Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref при условии (p > 0), называется параболой, уравнение называется каноническим уравнением параболы, а система координат — ее канонической системой координат.
Допустим, что (D’ = 0). Уравнение имеет вид (C’y″^ < 2>+ F″ = 0). Относительно (F″) есть следующие три возможности.
- Если (C’F″ 0) знаки (C’) и (F″) совпадают. Разделив на (C’), приведем уравнение к виду
$$
y″^ < 2>+ a^ <2>= 0.label
$$
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническому виду eqref, называют уравнением пары мнимых параллельных прямых. - Остался последний случай (F″ = 0). После деления на (C’) уравнение принимает вид
$$
y″^ < 2>= 0.label
$$
Это уравнение эквивалентно уравнению (y″ = 0), и потому определяет прямую линию. Уравнение, приводящееся к каноническому виду eqref, называется уравнением пары совпавших прямых.
Теперь мы можем объединить всё вместе.
Пусть в декартовой системе координат задано уравнение второго порядка eqref.
Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:
- Уравнение эллипса.
$$
frac>> + frac>> = 1;nonumber
$$ - Мнимый эллипс. Данному уравнению не удовлетворяет ни одна точка.
$$
frac>> + frac>> = -1;nonumber
$$ - Уравнение пары мнимых пересекающихся прямых (точка).
$$
a^<2>x^ <2>+ c^<2>y^ <2>= 0;nonumber
$$ - Уравнение гиперболы.
$$
frac>>-frac>> = 1;nonumber
$$ - Пересекающиеся прямые.
$$
a^<2>x^<2>-c^<2>y^ <2>= 0;nonumber
$$ - Уравнение параболы.
$$
y^ <2>= 2px;nonumber
$$ - Пара параллельных прямых.
$$
y^<2>-a^ <2>= 0;nonumber
$$ - Пара мнимых параллельных прямых. Данному уравнению не удовлетворяет ни одна точка.
$$
y^ <2>+ a^ <2>= 0;nonumber
$$ - Прямая (пара совпавших прямых).
$$
y^ <2>= 0.nonumber
$$
Пересечение прямых, угол и координаты пересечения
IP76 > Пересечение прямых, угол и координаты пересечения
Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x1-x2) никак не разделить и т.д.
Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.
Коэффициенты А, B, C
Все помним со школы формулу:
Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):
Те же фаберже, только сбоку.
В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.
Загвоздка в том, что мы не знаем коэффициенты для обеих линий.
В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:
Путем несложных операций приходим к следующей записи:
Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:
Пока все идет отлично, нигде вероятного деления на ноль не встретилось.
Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.
Система уравнений
Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.
Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.
Сразу же запишем метод под нашу систему.
Имеем следующую систему:
Исходя из метода, решение выглядит так:
Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.
Практика 1
Частные случаи
- Прямые параллельны: ∆ab = 0
- (A1B2 – B1A2 = 0);
- Прямые совпадают: ∆ab = ∆X = ∆Y = 0
- (A1B2 – B1A2 = 0) И (A1C2 — A2C1 = 0) И (C1B2 -B1C2 = 0);
- Прямые перпендикулярны:
- (A1 A2 + B1 B2 = 0).


Принадлежность точки отрезку
В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:
- Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
- Проверить факт нахождения точки между концами отрезка.
Займемся пунктом 2. Данный факт можно установить двумя способами:
- Логически, т.е. (x1 = x >= x2). На случай «вертикальности» линии добавить проверку на Y:
- (y1 = y >= y2).
- Арифметически. Сумма отрезков |x-x1| + |x-x2| должна быть равна длине отрезка |x1-x2|. Аналогично, на случай «вертикальности» , добавить проверку:
- |y-y1| + |y-y2| = |y1-y2|
Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.
Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.
Угол пересечения прямых
Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p1 и p2, получим направляющий вектор V(p1,p2), и аналогично второй вектор M(p3,p4). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.
Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:

α — угол наклона вектора к оси X, который можно найти, как:
Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…
Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.

Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.

По рисунку явно видно, что угол между векторам это γ = (β — α).
В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.
От теории к практике
Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.
Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.
Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:
источники:
http://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/second-order-equation/
http://ip76.ru/theory-and-practice/cross-lines/
Уравнение прямой как результат пересечения плоскостей
| Коэффициенты первой плоскости | |
| Коэффициенты второй плоскости | |
| Уравнение первой плоскости |
| Уравнение второй плоскости |
| Уравнение прямой как пересечение двух плоскостей |
Определяем уравнение прямой в пространстве если нам известны общие уравнения двух плоскостей.
Обновление от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений
Если первая плоскость задана уравнением вида
а другая плоскость уравнением вида
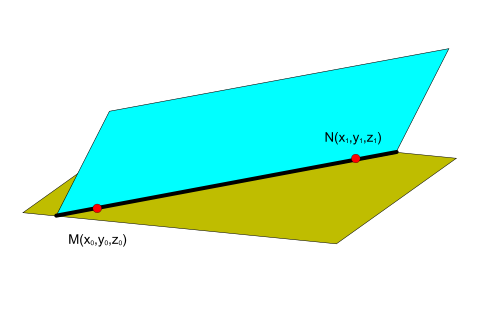
и они перескаются, то уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям.
Прямая в пространстве, проходящая через две точки )
)
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z-z_0}{z_1-z_0})
B принципе этого достаточно что бы решить уравнение. Положим что z=0 ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид
Получили систему линейных уравнений которая легко решается.
Определили таким образом точку
Теперь пусть z=1 и решаем систему
и получаем вторую точку
Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z}{1})
Есть еще второй способ, использующий вектора. Рассмотрим и его.
Если известна точка в пространстве )
то уравнение прямой имеет вид
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
Узнав координаты точки )
Для этого вычислим векторное произведение
(begin{pmatrix}i&j&k\A_1&B_1&C_1\A_2&B_2&C_2end{pmatrix}=im+jn+kp)
и подставив вычисленные значения в уравнение
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.
Созданный онлайн калькулятор позволяет автоматически находить уравнение прямой по двум заданным общим уравнениям плоскостей.
Условие параллельности плоскостей
Две плоскости заданные уравнениями вида
лишь тогда параллельны, когда верным становится соотношение
(cfrac{A_1}{A_2}=cfrac{B_1}{B_2}=cfrac{C_1}{C_2})
Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле
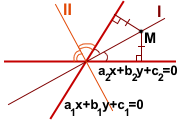
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
Это равенство можно записать в виде
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Пример.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
Решение:
В формулу уравнения биссектрис подставляем данные прямых:
Ответ: 3x+3y-23=0; 21x-21y-37=0.






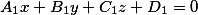
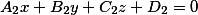
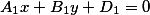
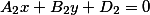
)
=0)
=0)
)
)