Как составить уравнение кривой безразличия

Понятие, сущность и значение кривых безразличия

Понятие кривых безразличия было введено в научных оборот двумя учеными – Вильфредо Парето и Френсисом Эджвортом. Сегодня оно довольно часто используется в различных отраслях экономической науки.

По большому счету кривые безразличия служат отражением наборов безразличия, под которыми обычно понимаются наборы вариантов потребительского выбора, имеющие одинаковую полезность, а потому – не имеющие предпочтения перед другими наборами. Товары «Х» и «У» формируют набор безразличия в том случае, если все соотношения этих благ будут равноценны для потребителя, которому будет все равно, какой из их наборов выбрать. Таким образом, кривые безразличия отражают собой совокупность наборов благ, приносящих потребителю одинаковую полезность, то есть обеспечивающих равный объем удовлетворения его потребностей.

Кривые безразличия отражают предпочтения потребителей и позволяют найти ответ на вопрос о том, как можно обеспечить максимально полное удовлетворение от покупки в условиях ограниченности бюджета. Иначе говоря, с их помощью можно узнать, какой из наборов продуктов окажется наиболее предпочтителен для потребителя.

Основополагающими свойствами кривых безразличия считаются:

• отрицательный наклон кривых безразличия;
• выпуклость кривых безразличия по отношению к началу координат;
• непересекаемость кривых безразличия;
• равенство абсолютной величины наклона кривой безразличия и предельной нормы замещения;
• возможность построения кривой безразличия, проходящей через любой набор благ.

Кривые безразличия двух товаров, расположенные на одной плоскости и построенные для одного потребителя, формируют карту безразличия. Таким образом, под картами безразличия следует понимать совокупность кривых безразличия, которые соответствуют различным уровням полезности для одной пары благ и для одного потребителя. Предпочтения и вкусы потребителей представляются картой кривых безразличия. При этом каждая следующая кривая безразличия, которая проходит дальше т начала координат, будет нести в себе большую величину полезности для потребителя.

«Кривые безразличия: суть, построение, точки на кривых» 👇

Основы построения кривых безразличия

Для того, чтобы разобраться в основах построения кривых безразличия, для начала подытожим их суть, а затем – рассмотрим конкретный пример их построения.

Итак, кривые безразличия представляют собой одинаковую для потребителя совокупную полезность различных благ. Для их построения рекомендуется придерживаться следующего плана:

• выбрать (составить) массив исходных данных;
• построить ось координат;
• на сторонах оси координат (X и Y соответственно) отметить различное количество товара X (Qx)и Y (Qy);
• соединить точки кривой, отражающей возможные комбинации благ, дающих одинаковое удовлетворение;
• проанализировать полученные результаты.

Таким образом, в основе построения карты кривых безразличия лежит необходимость группировки благ и выделения целевой группы, определение выборов каждого потребителя, агрегирование и исключение возможных ошибок, проведение статистического анализа данных, а также интер и экстраполяция. Рассмотрим данный алгоритм на конкретном примере.

Предположим, что Иван получает полезность и удовлетворение от яблок и апельсинов и, соответственно, приобретает наборы, состоящие из этих благ. Для Ивана одинаковую полезность несут в себе следующие наборы благ: 10 яблок и 25 апельсинов, 14 яблок и 20 апельсинов, 20 яблок и 15 апельсинов, 28 яблок и 10 апельсинов, 38 яблок и 5 апельсинов.

Для построения кривой безразличия используем двухмерное пространство. В рамках системы координат Х Y на осях отложим единицы обоих товаров, входящих в наборы. Полученный результат представим на рисунке 1.

Таким образом, наборы яблок и апельсинов, представленные точками А, В, С, D, E имеют одинаковую полезность для потребителя – ему все равно, какой из них выбрать.

Точки на кривых безразличия

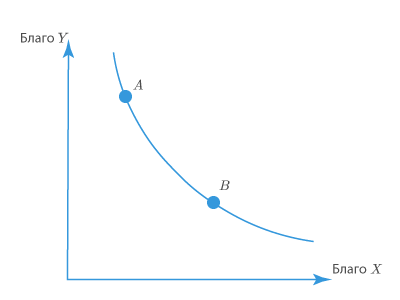
Каждая точка, расположенная на кривой безразличия, является комбинацией двух товаров, имеющих одинаковую для потребления общую полезность. Соответственно, потребителям безразлично, какой из наборов выбрать. В общем виде пример кривых безразличия представлен на рисунке 2. Рассмотрим кривую безразличия и точки на ней представленные более подробно.

Предположим, что существует два товара — «Х» и «Y». Допустим, что набор, состоящий из двух товаров «Х» и трех товаров «Y», имеет такую же общую полезность, как набор, состоящий из трех товаров «Х» и двух товаров «Y». В этом случае отказ от одного из товаров будет компенсирован получением другого.

К представленным комбинациям товаров «Х» и «Y» потребитель в равной степени безразличен. Это означает, что вне зависимости от того, какой из наборов будет им приобретен, он получит равное (одинаковое) удовлетворение своих потребностей, то есть любые комбинации, отмеченные на кривой безразличия, одинаково хороши для потребителя, поскольку способны принести ему одинаковую полезность.

В том случае, если наборы благ равноценны с точки зрения потребителя, то точки А и В будут лежать на одой кривой безразличия. Так кривая безразличия, что расположена правее и выше другой кривой, а также точки на не расположенные, отражает более предпочтительные для данного потребителя наборы благ. Так, например, набор С содержит в себе то же самое количество товара «Y», что и набор «А», однако в него входит большее количество товара «Х».

В целом справедливо говорить о том, что те кривые безразличия, которые сильнее удалены от начала координат, соответствуют более высокому уровню удовлетворения потребностей. В виду того, что кривая U2 находится справа от кривой U1, всякий набор благ, находящийся на кривой безразличия U2 будет более предпочтителен для потребителя, нежели набор, находящийся на кривой U1.

Понятия «кривая безразличия», «бюджетное ограничение» используются в экономической теории в рамках ординалистической теории полезности. Их появление было связано с необходимостью устранить недостаток кардинатистической теории, которая измеряла полезность в абсолютном выражении, тогда как при ординалистическом подходе используется относительное измерение полезности благ, сравнение их друг с другом. Теорию развивали Ф. Эджуорт, В. Парето, И. Фишер.

Кривые безразличия

Кривая безразличия (КБ) представляет собой графическое изображение выбора потребителя между двумя благами.

Положение каждой точки этой кривой характеризует такую комбинацию из двух товаров или услуг (по оси х и у), которая приносит одинаковую полезность индивиду.

Другими словами, полезность комбинации А равна полезности комбинации В, и потребителю безразлично, какую из них выбрать. Например, ученик использует карандаши и ручки, и ему будет не важно, выбрать пенал А, в котором лежат 3 ручки и 7 карандашей, или пенал В, где 4 ручки и 6 карандашей.

Свойства кривых безразличия

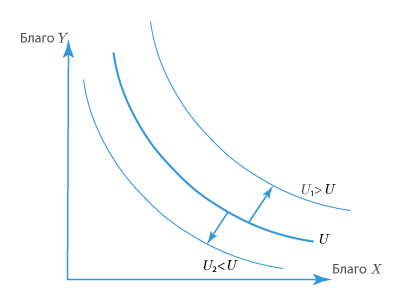
Кривые безразличия не пересекаются. Это связано с тем, что каждая КБ описывает свой уровень полезности. Математически они представляют собой линии уровня функции полезности, то есть, зафиксировав U, строят ту или иную кривую, форма которой не меняется, а будет изменяться только положение.

Чем больше расстояние от кривой до начала координат, тем выше полезность наборов, которым она соответствует. При увеличении общей полезности набора благ происходит сдвиг КБ вверх вправо, а при уменьшении – вниз влево. На основании приведенного ниже графика это свойство можно описать так: набор благ на U более предпочтителен, чем на U₂, но менее предпочтителен, чем на U₁.

Кривая безразличия вогнута к началу координат, вследствие этого любая касательная, проведенная к ней, будет иметь отрицательный наклон. Такая форма КБ связана с тем, что при увеличении количества потребляемого блага, полезность каждой дополнительной единицы убывает. Также в силу рациональности индивида предпочтение всегда отдается большему количеству товаров и услуг, чем меньшему.

Бюджетное ограничение и потребительский выбор

Каждый индивид имеет в своем распоряжении определенный размер денежных средств, которые он тратит на ту комбинацию товаров или услуг, которые изображаются кривой безразличия. Эта сумма денег и есть бюджетное ограничение, которое накладывается на выбор потребителя.

Например, у Васи есть 200 д.е., цена пирожка с капустой 50 д.е., а пирожка с мясом 100 д.е. На свои деньги он сможет купить следующие наборы пирожков (4 с капустой; 0 с мясом), (2К; 1М), (0К;2М). Эти точки и будут лежать на прямой, описывающей бюджетное ограничение.

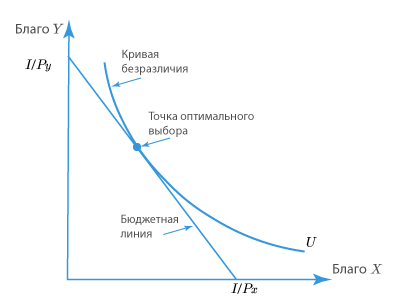
Представим это на графике.

Оптимальный выбор потребителя будет находиться в точке касания бюджетной линии к кривой безразличия.

Если рассматривать математическую интерпретацию задачи оптимального выбора, то необходимо использовать понятие предельной полезности.

Пусть U=f(x,y)U=f(x,y) – функция полезности.
MUx=fx′MU_x= f’_x

MUy=fy′MU_y= f’_y

Тогда оптимум будет достигаться при

MUxPx=MUyPyfrac{MU_x}{P_x}=frac{MU_y}{P_y}

Примеры решения

Пример 1

Сидоров Степан Сергеевич вышел на пенсию и решил, что 1000 руб. из нее он будет тратить только на творог и сыр. Стоимость пачки творога составляет 20 руб., сыра — 50 руб. Также, имея за плечами опыт экономиста, он определил, что функция полезности этих продуктов U=x⋅yU=xcdot y. Теперь перед ним стоит задача, в каком объеме покупать творог и сыр, чтобы достичь максимальной полезности и потратить всю выделенную для этого сумму.

Решение

Находим предельные полезности.

MUx=yMU_x= y

MUy=xMU_y= x

Тогда

y20=x50frac{y}{20}=frac{x}{50}

x=2,5yx=2,5y

С учетом максимальных трат на эти продукты Степана Сергеевича в размере одной тысячи рублей:

20x+50y=100020x+50y=1000

50y+50y=100050y+50y=1000

y=10y=10

x=2,5⋅10=25x=2,5cdot10=25

То есть он будет покупать 10 пачек сыра и 25 пачек творога.

Пример 2

Доход Клавдии Петровны составляет 7500 руб., из них 450 руб. она выделяет на покупку корма коту Барсику и собаке Джеку. Цена корма для котов составляет 20 руб. за 1 кг, а для собак — 15 руб. за кг. Составить уравнение бюджетного ограничения.

Решение

Если Клавдия Петровна всю сумму потратит на кошачий корм, то она купит

x=450/20=22,5x=450/20=22,5 кг

Значит, прямая бюджетного ограничения будет проходить через точку (22,5;0)
Аналогично по собачьему корму

y=450/15=30y=450/15=30 кг

То есть прямая проходит через (0;30)
Из математики мы знаем уравнение прямой, проходящей через две точки

x−x1x2−x1=y−y1y2−y1frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}

x−22.50−22.5=y−030−0frac{x-22.5}{0-22.5}=frac{y-0}{30-0}

y=30−4/3xy=30-4/3x

Тест по теме «Кривые безразличия и их свойства»

Однако
уверены ли мы в том, что вообще существует
какой-либо способ приписывания товарным
наборам порядковых полезностей? Допустим,
имеется некое ранжирование предпочтений.
Всегда ли можно найти функцию полезности,
располагающую товарные наборы в том же
порядке, в каком располагаются эти
предпочтения? Существует ли функция
полезности, описывающая любое рациональное
ранжирование предпочтений?

Не
все виды предпочтений можно представить
с помощью функции полезности. Предположим,
например, что предпочтения некоего
индивида нетранзитивны, так что A

B

C

A.
Тогда функция полезности, соответствующая
этим предпочтениям, должна была бы
состоять из чисел u(A),
u(B)
и u(C)
таких, что u(A) > u(B) > u(C)
> u(A).
Но это невозможно.

Если,
однако, исключить из рассмотрения
аномальные случаи вроде нетранзитивных
предпочтений, то окажется, что практически
всегда можно найти некую функцию
полезности, которая бы представляла
данные предпочтения. Поясним построение
функции полезности наглядными примерами,
рассмотрев один из них здесь, а другой
— в гл. 14.

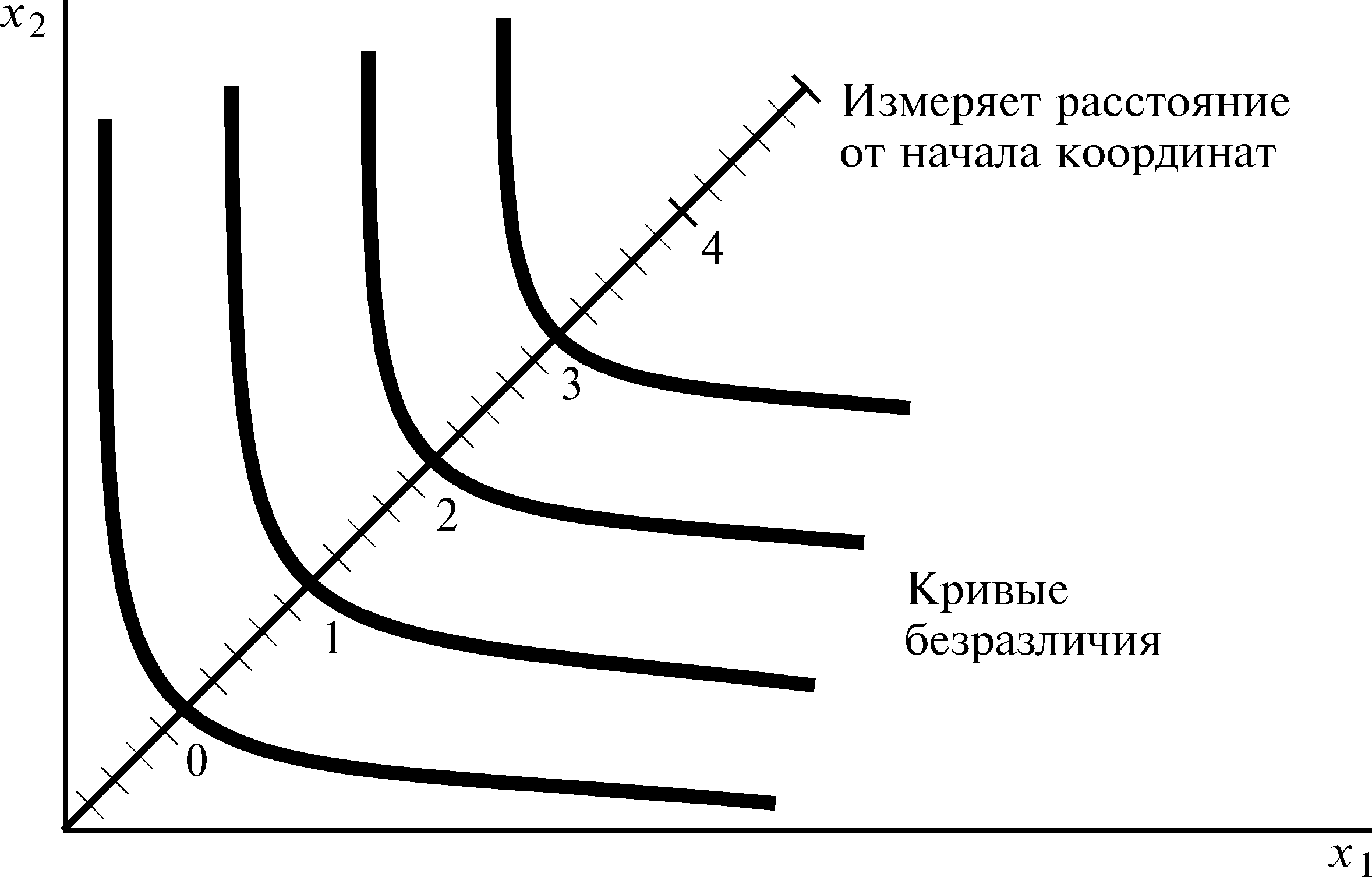
Допустим,
что нам дана карта кривых безразличия,
такая, как на рис. 4.2. Мы знаем, что функция
полезности есть способ обозначения
кривых безразличия, при котором более
высоким кривым безразличия ставятся в
соответствие бóльшие
числа. Как это можно сделать?

Рис. 4.2

Построение функции полезности на основе кривых безразличия. Нарисуйте диагональную линию и обозначьте каждую кривую безразличия числом, соответствующим расстоянию от нее до начала координат, измеренному вдоль этой линии.

Один
из простых способов — провести диагональ,
как показано на рисунке, и обозначить
каждую кривую безразличия числом,
соответствующим ее расстоянию от начала
координат, измеренному вдоль этой
диагонали.

Откуда
мы знаем, что в результате этого получим
функцию полезности? Нетрудно заметить,
что если предпочтения монотонны, то
луч, проходящий через начало координат,
должен пересечь каждую кривую безразличия
в точности один раз. Таким образом,
каждый набор благ получает свое
обозначение, и наборы, находящиеся на
более высоких кривых безразличия,
обозначаются бóльшими
числами, а только это и требуется, чтобы
построить функцию полезности.

Это
дает нам один из способов обозначения
кривых безразличия по крайней мере для
случая монотонных предпочтений. Данный
способ не всегда будет самым подходящим
для любого заданного случая, но он
показывает достаточно общий характер
идеи, заложенной в функции порядковой
полезности: «разумные» предпочтения
почти любого вида можно представить с
помощью функции полезности.

4.3. Некоторые примеры функций полезности

В
гл. 3 мы рассмотрели несколько примеров
предпочтений и представляющих их кривых
безразличия. Эти предпочтения можно
представить также с помощью функций
полезности. Если дана функция полезности
u(x₁, x₂),
нарисовать соответствующие кривые
безразличия сравнительно несложно:
надо нанести на график все точки (x₁, x₂),
для которых u(x₁, x₂)
постоянна. В математике множество всех
(x₁, x₂),
для которых u(x₁, x₂)
постоянна, называется упорядоченным
множеством.
Для каждого другого значения константы
мы получаем другую кривую безразличия.

ПРИМЕР:
Кривые безразличия, получаемые на основе
функции полезности

Предположим,
что функция полезности имеет вид:
u(x₁, x₂) = x₁x₂.
Как выглядят тогда кривые безразличия?
Нам известно, что типичная кривая
безразличия есть просто множество всех
x₁
и x₂,
таких, что k = x₁x₂
для некой константы k.
Выразив x₂
как функцию от x₁,
мы видим, что типичной кривой безразличия
в данном случае будет соответствовать
формула:

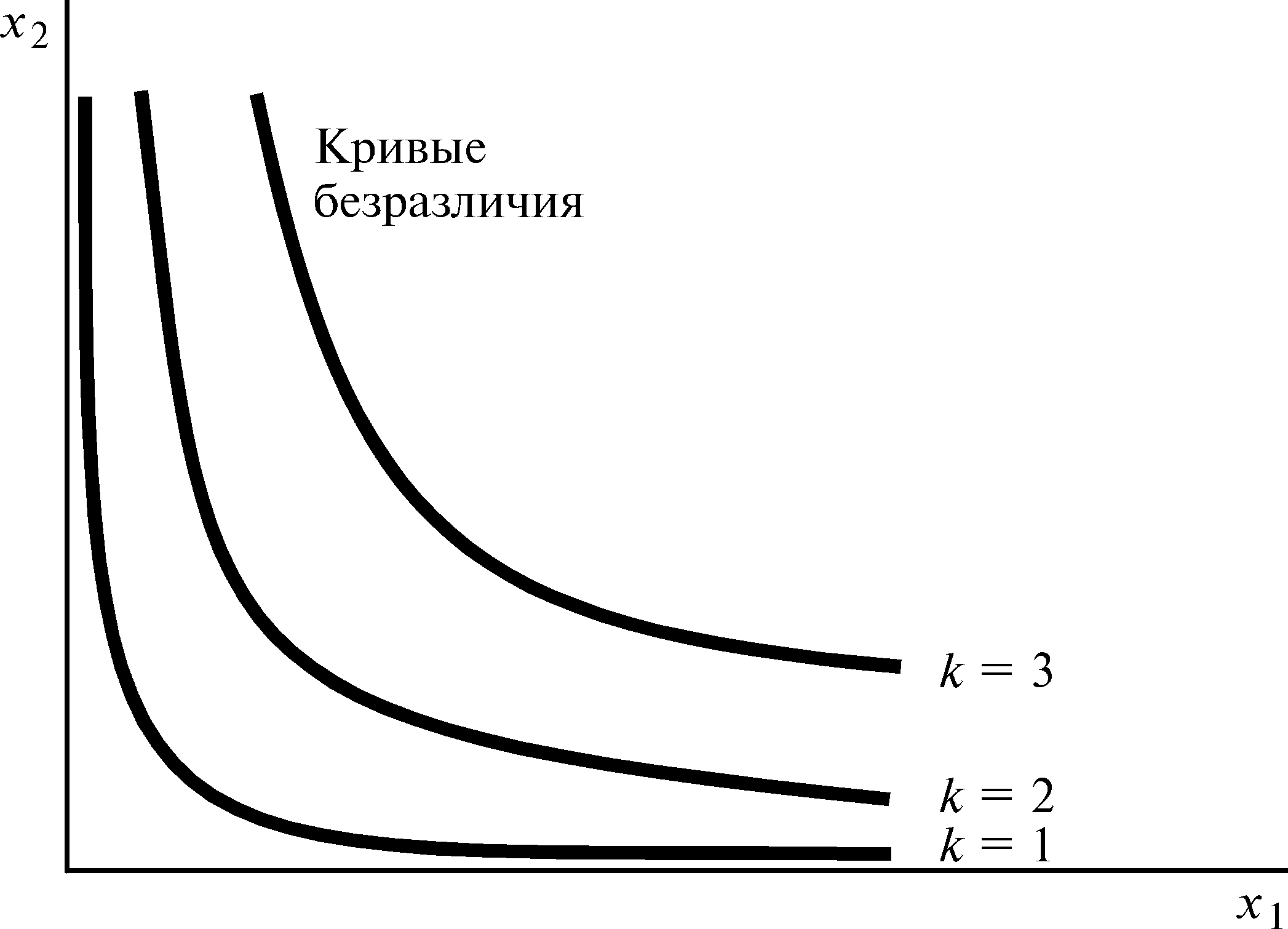
Эта
кривая изображена на рис. 4.3 для k = 1,
2, 3...

Кривые безразличия. Кривые безразличия k = x1x2 для любых значений k.

Рис. 4.3

Рассмотрим
еще один пример. Допустим, нам задана
функция полезности вида
Как выглядят ее кривые безразличия?
Согласно стандартным правилам алгебры:

Иными
словами, функция полезности v(x₁, x₂)
есть просто квадрат функции полезности
u(x₁, x₂).
Поскольку u(x₁, x₂) 
не может быть отрицательной величиной,
отсюда следует, что v(x₁, x₂) 
является монотонным преобразованием
исходной функции полезности u(x₁, x₂).
Это означает, что функции полезности
должны соответствовать кривые безразличия
в точности такой же формы, как у
представленных на рис.4.3. Обозначения
кривых безразличия будут другими —
обозначения 1, 2, 3 теперь станут
обозначениями 1, 4, 9, …, но множество
наборов, имеющее полезностьv(x₁, x₂) = 9,
в точности такое же, что и множество
наборов, имеющее полезность v(x₁, x₂) = 3.
Следовательно, v(x₁, x₂)
описывает в точности те же предпочтения,
что и u(x₁, x₂),
поскольку она ранжирует
все наборы таким же образом.

Идти
в обратном направлении — находить
функцию полезности, представляющую
определенные кривые безразличия, —
несколько сложнее. Для этого можно
прибегнуть к двум способам. Первый
способ — математический. Исходя из
заданных кривых
безразличия мы хотим найти функцию,
которая принимала бы постоянные значения
вдоль каждой кривой безразличия и
приписывала бы бóльшие
численные значения более высоким кривым
безразличия.

Второй
способ — несколько более интуитивный.
Исходя из описания предпочтений, мы
пытаемся представить себе, что именно
стремится максимизировать потребитель
— какая комбинация товаров описывает
его потребительский выбор. Хотя на
данной стадии рассмотрения этот способ
может показаться несколько неясным,
после обсуждения нескольких примеров
его смысл станет понятнее.

Совершенные
субституты

Помните
пример с красными и синими карандашами?
Для потребителя имело значение только
общее число карандашей. Таким образом,
вполне естественно измерять полезность
общим числом карандашей. Поэтому
предварительно выберем функцию полезности
вида
u(x₁, x₂) = x₁ + x₂.
Подойдет ли она? Достаточно задать себе
два вопроса: принимает ли эта функция
полезности постоянные значения при
перемещении вдоль кривых безразличия?
Приписывает ли она более высокие
численные значения более предпочитаемым
наборам? Поскольку на оба эти вопроса
следует дать утвердительный ответ,
перед нами — функция полезности.

Разумеется,
это не единственная функция полезности,
которую мы могли бы использовать в
данном случае. Можно было бы также
использовать
квадрат
числа карандашей. Таким образом, функция
полезности
тоже представляет предпочтения для
случая совершенных субститутов, как,
впрочем, и любая другая функция, являющаяся
монотонным преобразованием функцииu(x₁, x₂).

Что,
если потребитель хочет заместить товар
1 товаром 2 в соотношении, отличном от
соотношения «один к одному»?
Предположим, например, что потребителю
потребуются две
единицы товара 2, чтобы компенсировать
отказ от одной единицы товара 1. Это
означает, что товар 1 вдвое
ценнее для потребителя, чем товар 2.
Функция полезности, следовательно,
принимает вид u(x₁, x₂) 
= 2x₁ + x₂.
Заметьте, что эта функция полезности
дает кривые безразличия с наклоном –2.

Вообще
предпочтения в отношении совершенных
субститутов можно представить функцией
вида

u(x₁, x₂) 
= ax₁ + bx₂.

Здесь
a
и b
— некие положительные числа, измеряющие
«ценность» товаров 1 и 2 для
потребителя. Обратите внимание на то,
что наклон типичной кривой безразличия
задан — a/b.

Совершенные
комплементы

Это
случай левого и правого башмаков. При
предпочтениях такого рода потребителя
заботит только число имеющихся у него
пар
обуви, поэтому естественно выбрать
число пар обуви в качестве функции
полезности. Число имеющихся у вас полных
пар обуви есть минимум
числа имеющихся у вас правых x₁
и левых x₂
башмаков. В соответствии с этим функция
полезности для совершенных комплементов
принимает вид u(x₁, x₂) 
= min{x₁, x₂}.

Чтобы
проверить, действительно ли эта функция
полезности подходит в данном случае,
выберем, скажем, товарный набор (10, 10).
Добавив еще одну единицу товара 1,
получаем набор (11, 10), потребляя который,
мы должны были бы остаться на той же
самой кривой безразличия. Так ли это?
Да, поскольку min{10, 10} = min{11, 10} = 10.

Итак,
u(x₁, x₂) 
= min{x₁, x₂}
— функция полезности, с помощью которой
можно описать совершенные комплементы.
Как обычно, для этого подойдет и любая
функция, являющаяся монотонным
преобразованием данной .

Что
можно сказать о случае, когда потребитель
хочет потреблять товары не в пропорции
«один к одному»? Например, как насчет
потребителя, всегда потребляющего 2
ложки сахара с чашкой чая? Если x₁
— число имеющихся чашек чая, а x₂
— число имеющихся ложек сахара, то число
должным образом чашек подслащенного
чая составит

Это
несколько сложно для понимания, так что
немного поразмыслим об этом. Ясно, что
если число чашек чая будет больше
половины числа ложек сахара, то мы не
сможем положить в каждую чашку чая по
2 ложки сахара. В этом случае у нас в
итоге окажется только
чашек должным образом подслащенного
чая. (Чтобы убедиться в этом, подставьте
вместоx₁
и x₂
какие-нибудь числа.)

Разумеется,
те же самые предпочтения могут быть
описаны любой функцией, которая является
монотонным преобразованием указанной
функции полезности. Например, можно
произвести умножение на 2, чтобы избавиться
от дроби. В результате этого получим
функцию полезности u(x₁, x₂) =
min{2x₁, x₂}.

Вообще,
функция полезности, описывающая
предпочтения для случая совершенных
комплементов, имеет вид

u(x₁, x₂) 
= min{ax₁, bx₂},

где
a
и b
— положительные числа, показывающие
пропорции, в которых потребляются
товары.

Квазилинейные
предпочтения

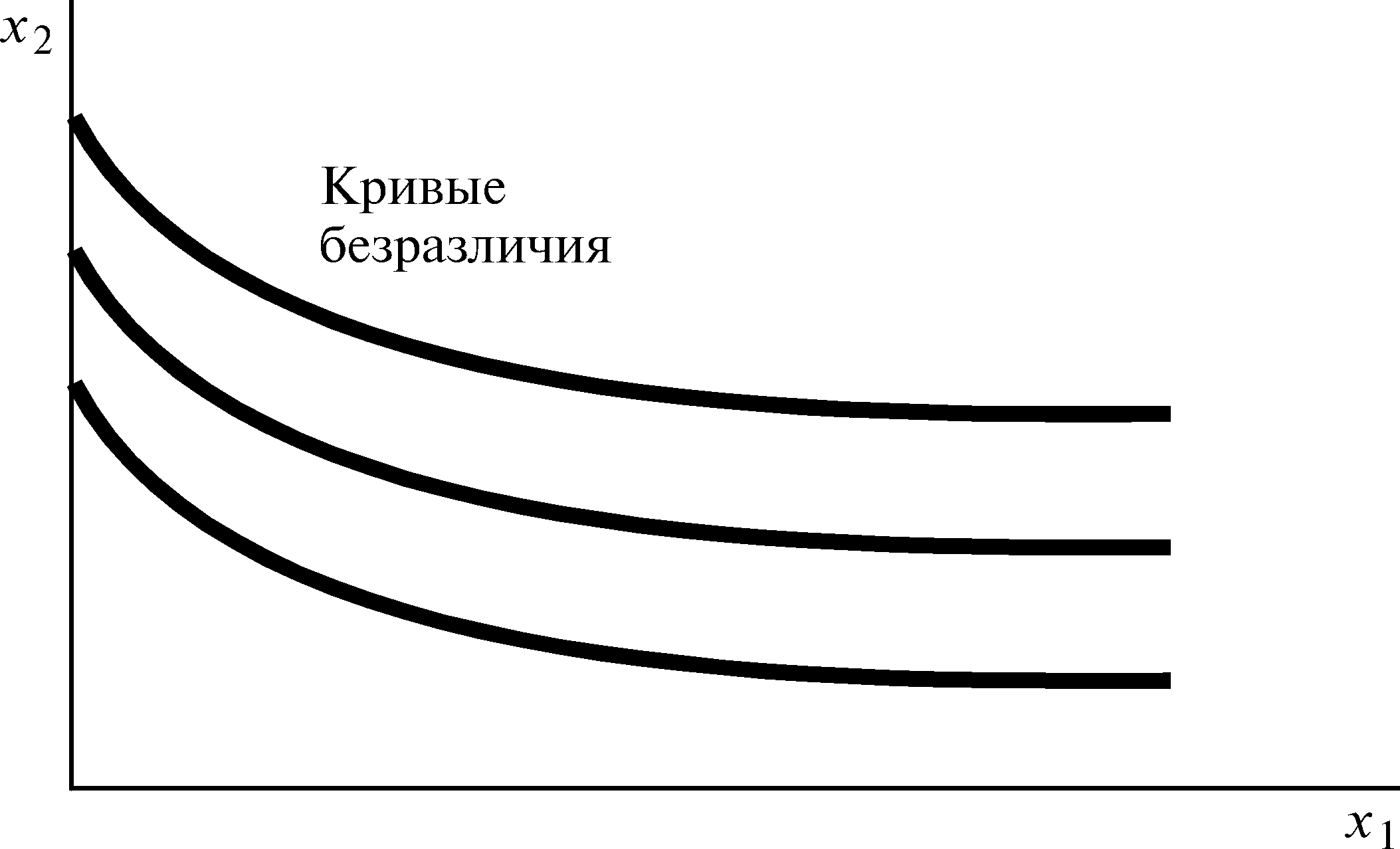
Перед
нами форма кривых безразличия, с которой
мы раньше не сталкивались. Предположим,
что кривые безразличия потребителя
представляют собой, как на рис. 4.4,
вертикальные смещения одной кривой по
отношению к другой. Это означает, что
все кривые безразличия являются просто
вертикально «смещенными» копиями
одной и той же кривой безразличия. Отсюда
следует, что уравнение кривой безразличия
принимает вид x₂ = k – v(x₁),
где k
— константа, имеющая для каждой кривой
безразличия свои значения. Чем
больше значения k,
тем выше располагаются кривые безразличия.
(Знак «минус» здесь — не более, чем
условность; почему он удобен, мы увидим
ниже.)

В
этой ситуации вполне естественным
является ранжирование кривых безразличия
по k,
или по «высоте» вдоль вертикальной
оси. Выразив k
и приравняв его к полезности, получаем

u(x₁, x₂) = k = v(x₁) + x₂.

В
данном случае функция полезности линейна
по товару 2, но нелинейна (возможно) по
товару 1; отсюда и название квазилинейная,
означающее частично линейную полезность.
Конкретные примеры квазилинейной
функции полезности:
илиu(x₁, x₂) = lnx₁ + x₂.
Квазилинейные функции полезности не
особенно реалистичны, но с ними легко
работать, в чем мы убедимся на нескольких
примерах, рассматриваемых далее в этой
книге.

Предпочтения
Кобба — Дугласа

Другая
широко используемая функция полезности
— функция полезности Кобба
— Дугласа:

где
c
и d
— положительные числа, описывающие
предпочтения потребителя¹.

Квазилинейные предпочтения. Каждая кривая безразличия есть вертикально смещенная копия одной-единственной кривой безразличия.

Рис. 4.4

Функция
полезности Кобба — Дугласа будет полезна
нам при рассмотрении нескольких примеров.
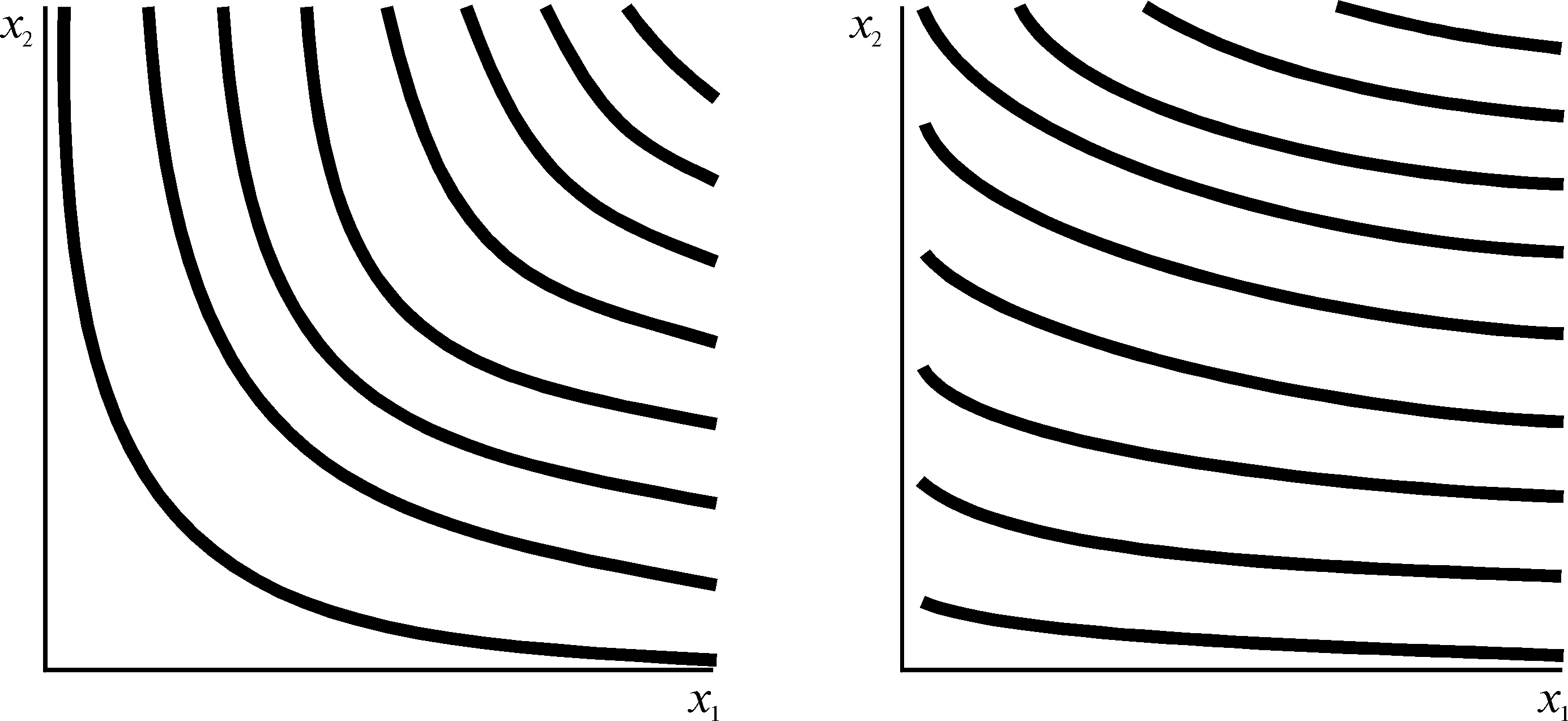
Предпочтения, представленные функцией
полезности Кобба — Дугласа, в общем
виде характеризуются формой кривых
безразличия, изображенной на рис. 4.5. На
рис.4.5A изображены кривые безразличия
для с = 1/2,
d = 1/2,
на рис.4.5B соответственно для c = 1/5,
d = 4/5.
Обратите внимание на то, что разные
значения параметров c
и d
обусловливают различие форм кривых
безразличия.

A

c = 1/2
d = 1/2
B

c = 1/5
d = 4/5

Кривые безразличия Кобба — Дугласа. На рис.A показан случай c = 1/2, d = 1/2, а на рис.B — случай c = 1/5, d = 4/5.

Рис. 4.5

Кривые
безразличия Кобба — Дугласа выглядят
в точности так же, как симпатичные
выпуклые к началу координат монотонные
кривые безразличия, которые в гл.3 мы
называли стандартными кривыми безразличия.
Предпочтения Кобба — Дугласа дают нам
типовой пример таких стандартных с виду
кривых безразличия, и, действительно,
описывающая их формула — это, пожалуй,
простейшее алгебраическое выражение,
соответствующее стандартным предпочтениям.
Предпочтения Кобба — Дугласа окажутся
весьма полезными для представления на
алгебраических примерах некоторых
экономических идей, которые мы рассмотрим
позднее.

Разумеется,
те же самые предпочтения могут быть
представлены и с помощью функции,
являющейся монотонным преобразованием
функции полезности Кобба — Дугласа, и
пару примеров таких преобразований
стоит рассмотреть.

Во-первых,
если взять натуральный логарифм
полезности, то произведение членов
превратится в сумму, так что:

Кривые
безразличия для этой функции полезности
будут выглядеть совершенно так же, как
и для первой функции Кобба — Дугласа,
поскольку логарифмирование — это
монотонное преобразование. (Краткий
обзор натуральных логарифмов вы найдете
в математическом приложении в конце
книги.)

В
качестве второго примера предположим,
что вначале у нас была функция Кобба —
Дугласа вида

Возведя
полезность в степень 1/(c + d),
получим:

Определим
новый член:

Теперь
можно записать нашу функцию полезности
как

Это
означает, что всегда можно произвести
такое монотонное преобразование функции
полезности Кобба — Дугласа, при котором
сумма показателей степени станет равной
1. Позднее станет ясно, что этот факт
может иметь полезную интерпретацию.

Функция
полезности Кобба — Дугласа может быть
представлена различными способами;
следует научиться их распознавать, так
как данное семейство предпочтений очень
полезно для использования в качестве
примеров.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  05.03.2016568.83 Кб40G3.doc

• #
• #

  05.03.2016717.82 Кб11G5.doc

• #

  05.03.2016680.96 Кб23G6.doc

• #
• #
• #

Как построить кривую безразличия

Понятие кривой безразличия ввели Фрэнсис Эджворт и Вильфредо Парето. Кривая безразличия есть набор комбинаций из двух благ, полезность которых одинаково равна для экономического субъекта, и одно благо не имеет предпочтений перед другим.

Инструкция

Начните с построения координатной оси. На сторонах X и Y отметьте количество товара X (Qx)и Y (Qy) соответственно. X и Y в данном случае обозначают каждый набор благ.

Множество кривых безразличия, характеризующих наборы благ для одного потребителя, представляют собой карту безразличия. Карта безразличия представляет различные уровни полезности, удовлетворяющие потребности одного конкретного человека, при наличии одной пары благ. Чем дальше от осей координат расположена кривая безразличия на карте, тем наиболее полно удовлетворяются потребности потребителя с помощью данного набора благ.

На кривой безразличия нетрудно найти участок, в любой точке которого возможно эффективное замещение одной полезности на другую. Этот отрезок (в данном случае AB) называется зоной замещения (субституции). Взаимное замещение благ произойдет только на отрезке AB. Самое минимальное значение товара X находится в точке X1, а товара Y — в Y1. Эти значения минимальны, но их потребление необходимо даже в таком количестве, поскольку заменить полностью одно благо на другой невозможно, сколько бы много при этом ни предлагалось другого блага. Здесь предельным порогом замещения выступает такое значение одного блага, при котором присутствие другого равнозначного блага не требуется. Таким образом, предельной нормой замещения является отношение количества блага X, от которого потребитель может полностью отказаться, к выбору единицы блага Y и наоборот.

Определяя предельную норму замещения, следует учитывать ее как величину отрицательную. Это происходит потому, что увеличивая потребление одного блага соответственно сокращается потребление другого.

Обратите внимание

Кривые безразличия никогда не могут пересечься, а сама кривая имеет отрицательный наклон. Последнее следует из правил обратной связи переменных между кривыми: при увеличении одного блага, происходит сокращение другого.

Полезный совет

По любой паре благ можно построить кривую безразличия, а при их совмещении на одной плоскости (построении карты безразличия) возможно выявить всю систему предпочтения потребителя.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?