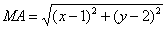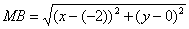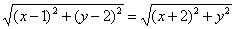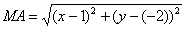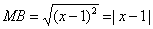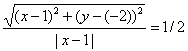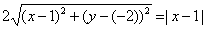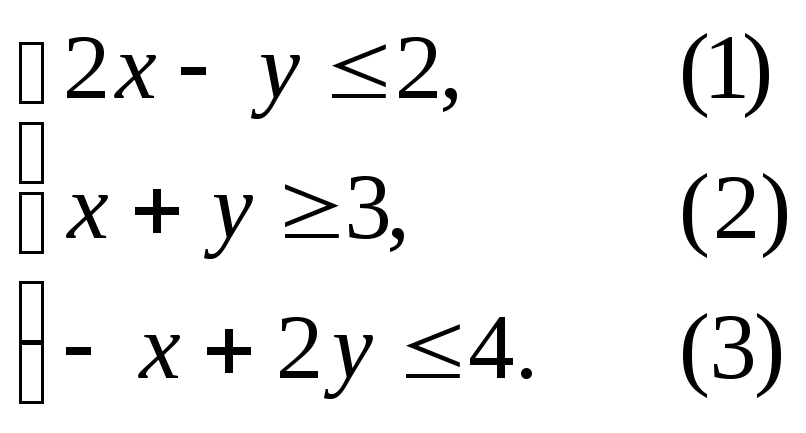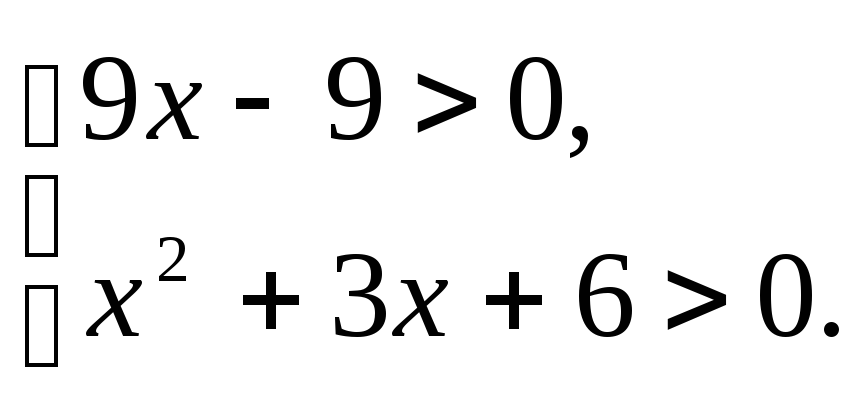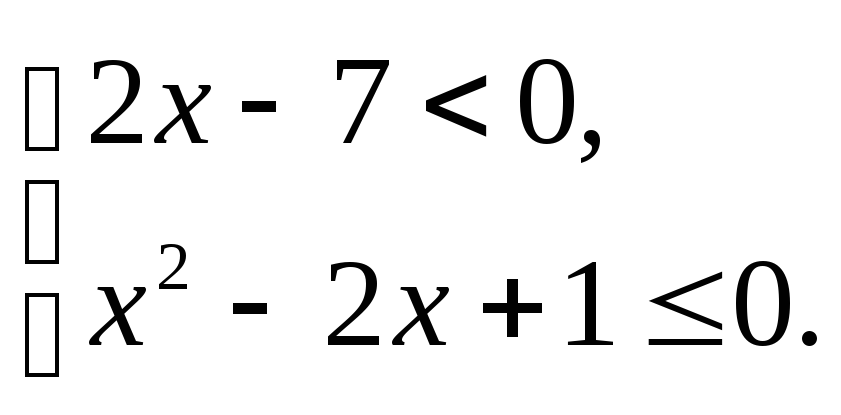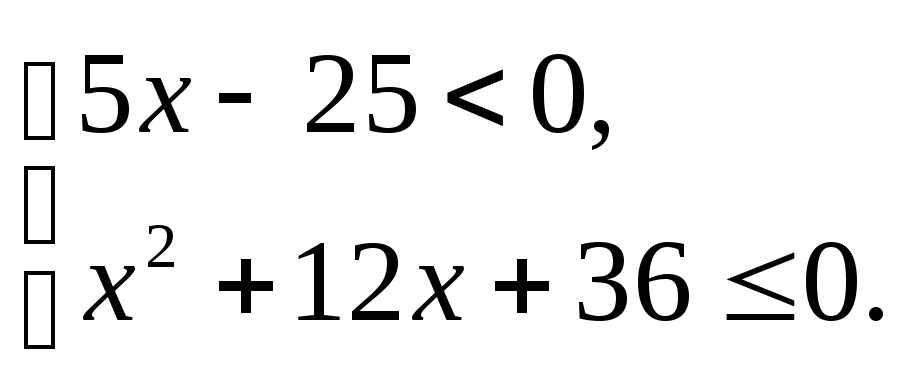Как составить уравнение множества точек на плоскости - Исправление недочетов и поиск решений вместе с Examum.ru

Множество точек на плоскости

Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как

то

После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.

Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /₂.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /₂. Так как:

то

или

Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.

Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.

Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.

Множества точек на плоскости и их уравнения

На этом занятии вы познакомитесь с тем, как в аналитической геометрии с помощью уравнений можно найти то или иное множество точек на плоскости.

Такими множествами могут быть: одна или несколько точек, линия или область на плоскости.

Тот факт, что числа х и у являются координатами точек, принадлежащих некоторому множеству точек, аналитически записывается в виде уравнения.

Во многих задачах требуется найти множество точек (х;у), координаты которых удовлетворяют заданному уравнению. Ответами в таких задачах являются, как правило, фигуры, хорошо известные из школьного курса геометрии. Главное — установить, какая это фигура, и выяснить, какими свойствами она обладает.

Определение уравнения линии

Примеры на отыскание множеств точек

Автор: Вяликова Мария Владимировна — учитель математики и информатики высшей квалификационной категории МАОУ Пролетарская СОШ Новгородского района Новгородской области

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

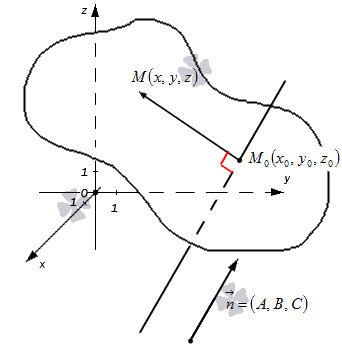
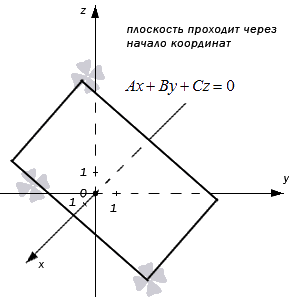
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

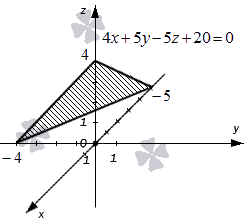
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Решение

Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

источники:

http://analit-geometr.5311pro2.edusite.ru/p10aa1.html

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/

Источник

Урок 5

оПределение уравнения линии.

Примеры на отыскание множеств точек.

оПределение уравнения линии.

рассмотрим соотношение вида: F(x,y)=0 (1)

связывающее Переменные величины х и у. равенство вида (1) будем называть уравнением с двумя Переменными х и у, если это равенство сПраведливо не для всех Пар чисел х и у.

Примеры уравнений: 2х+3у=0, х 2 +у 2 -25=0.

если равенство (1) сПраведливо для всех Пар чисел х и у, то оно называется т ождеством .

Примеры тождеств: (х+у) 2 — х 2 -2ху -у 2 =0, (х-у)(х+у) — х 2 +у 2 =0.

уравнение (1) будем называть уравнением множества точек (х;у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координатам никакой точки, не Принадлежащей этому множеству.

важным Понятием аналитической геометрии является Понятие уравнения линии. Пусть на Плоскости заданы Прямоугольная система координат и некоторая линия l.

оПределение. уравнение (1) называется уравнением линии l (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии l , и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

из оПределения следует, что линия l Представляет собой множество всех точек Плоскости (х;у), координаты которых удовлетворяют уравнению (1).

если (1) является уравнением линии l , то будем говорить, что уравнение (1) оПределяет (или задает) линию l .

Понятие уравнения линии дает возможность сводить геометрические задачи к алгебраическим. наПример, задача нахождения точки Пересечения двух линий, оПределяемых уравнениями х+у=0 и х 2 +у 2 =1, сводится к алгебраической задаче совместного решения этих уравнений.

линия l может оПределятся не только уравнением вида (1), но и уравнением вида F(. )=0, содержащим Полярные координаты.

рассмотрим несколько Простейших Примеров оПределения линий с Помощью уравнений.

1) х — у=0 . заПисав это уравнение в виде у=х, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, Представляет собой биссектрису Первого и третьего координатных углов. это и есть линия, оПределенная данным уравнением.

2) х 2 — у 2 =0. Представив уравнение в виде (х-у)(х+у)=0, заключаем, что множество точек, координаты которых удовлетворяют данному уравнению, — это две Прямые, содержащие биссектрисы четырех координатных углов. (см рисунок — гиПерссылка)

3) х 2 +у 2 =0. множество точек, координаты которых удовлетворяют этому уравнению, состоит из одной точки (0;0). в данном случае уравнение оПределяет, как говорят, вырожденную линию.

4) х 2 +у 2 +1=0. так как При любых х и у числа х 2 и у 2 неотрицательны, то х 2 +у 2 +1>0. значит, нет ни одной точки, координаты которой удовлетворяют данному уравнению, т.е. никакого геометрического образа на Плоскости данное уравнение не оПределяет. оно оПределяет «Пустое» множество точек.

5) p=а cOSf , где а — Положительное число, Переменные p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f), через а — точку с Полярными координатами (а;0). если p=а cOSf , где 0

6) p=аf , где а — Положительное число, p и f — Полярные координаты. обозначим через м точку с Полярными координатами (p;f). если p=0, то и f=0. таким образом, При увеличении угла f точка м(p;f), начавшая свое движение в Полюсе, движется вокруг него, одновременно удаляясь от Полюса. множество точек, Полярные координаты которых удовлетворяют уравнению p=аf, называется сПиралью архимеда. При этом ПредПолагается, чтоf? может Принимать любые неотрицательные значения.

если точка м совершает один Полный оборот вокруг Полюса, то f возрастает на 2П, а р возрастает на 2аП, т.е. сПираль рассекает любую Прямую, Проходящую через Полюс, на равные отрезки (не считая отрезка, содержащего Полюс), которые имеют длину 2аП.

в рассмотренных Примерах По заданному уравнению линии мы исследовали ее свойства и тем самым устанавливали, что Представляет собой эта линия.

рассмотрим теПерь обратную задачу для заданного (какими-то его свойствами) множества точек, т.е. для заданной линии l , требуется найти его уравнение F (х;у)=0.

Примеры на отыскание множеств точек.

рассмотрим несколько Примеров на отыскание множеств точек По уравнениям и неравенствам, связывающим их координаты.

Пример 1. вывести уравнение (в заданной Прямоугольной системе координат) множества точек, каждая из которых отстоит от точки с(а;в) на расстояние R. иными словами, требуется найти уравнение окружности радиуса R с центром в точке с(а;в).

решение. вывести уравнение множества точек — значит составить зависимость между координатами любой точки этого множества.

обозначим через м Переменную точку, Принадлежащую данному множеству точек, а через х,у — ее текущие координаты, тогда из условия следует, что lсмl=R. Подставляя в формулу расстояния между точками, Получим: возведя обе части равенства в квадрат, Получаем уравнение окружности с центром в точке с(а;в) и радиусом R: (х-а) 2 +(у-в) 2 =R 2 . оно встречается во многих геометрических задачах. Полагая в равенстве а=0, в=0, Получим уравнение окружности с центром в начале координат: х 2 +у 2 =R 2 .

Пример 2. найти уравнение множества точек, равноудаленных от точек а(1;1) и в(3;3).

решение. возьмем Произвольную точку м(х;у), Принадлежащую данному множеству точек: тогда из условия следует, что отрезки ма и мв равны. исПользуя формулу расстояния между двумя точками, находим: , таким образом,

После Преобразования Приходим к искомому уравнению множества точек, равноудаленных от точек а(1;1) и в(3;3): х+у-4=0. как известно из элементарной геометрии, таким множеством точек является Прямая, Проходящая через середину отрезка, соединяющего данные точки, и ПерПендикулярная этому отрезку.

даны точки о(2;-2), а(2;2), в(2;-1), с(3;-3), м(5;-5) и к(3;-2). установите, какие из них лежат на линии, заданным уравнением х+у=0, а какие не лежат на ней. (ответ: точки о, с и м лежат на линии, а точки а, в и к не лежат на ней)
даны точки а(1;п / 3), в(2;0), с(2;п / 4), м(v3;п / 6) и к(1;2?п3). выясните, какие из них лежат на линии, оПределяемой уравнением р=2 cOSf , и какие не лежат на ней. (ответ: точки а, в и м — лежат на данной линии, точки с и к — не лежат на ней. уравнение оПределяет окружность с диаметром ов)
составьте уравнение линии, По которой движется точка м(х;у), равноудаленная от точек а(0;2) и в(4;-2). (ответ: х-у-2=0)
составьте уравнение линии, расстояние каждой точки которой от точки а(0;0,25) равно расстоянию этой же точки от Прямой у=-0,25. (ответ: у=х 2 )
найдите уравнение множества точек, сумма расстояний каждой из которых от точек а(2;0) и в(-2;0) равна 2v5. (ответ: 0,2х 2 +у 2 =1)
найдите уравнение множества точек, равноудаленных от точки а(2;2) и оси ох. (ответ: у=0,25х 2 -х+2)
найдите уравнение множества точек, равноудаленных от оси оу и точки а(4;0). (ответ: у 2 =8х-16)
составьте уравнение линии, оПисываемой серединой отрезка с длиной, равной D , один из концов которого Перемещается По оси абсцисс, а другой конец — По оси ординат. (ответ: х 2 +у 2 =0,25 D 3 )

Множество точек на плоскости

Уравнение множества точек на плоскости

Пример 15. Построим множество точек ( x , y ) (x, y) , удовлетворяющих уравнению x 2 + x y = 0 x^2 + xy = 0 .

Построим множество точек ( x , y ) (x, y) таких, что

x 2 + 4 x + 4 + 4 y 2 = 0 x^2 + 4x + 4 + 4y^2 = 0 .

Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.

т. е. уравнению снова будет удовлетворять единственная точка ( 0,5 ; – 0,5 ) (0,5; – 0,5) (см. рис. 39).

Множеством точек может быть область на плоскости. Рассмотрим пример.

Построим множество точек ( x , y ) (x, y) таких, что

Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.

Построим множество точек, удовлетворяющих | y | = | x | |y| = |x| .

источники:

http://math.semestr.ru/line/points.php

http://zftsh.online/articles/4712

Источник

и неравенствами
с двумя переменными

Пусть на плоскости
выбрана система координат. Тогда любое
уравнение с двумя переменными F(x;y) = 0 задает множество
точек на плоскости, а именно множество
точекM(x;y), координатыкоторых
удовлетворяют этому уравнению.

Например, точка
M(– 3; 4) принадлежит
множеству, заданному уравнениемx²+y²= 25, а точкаN(1; 6) не принадлежит
этому множеству, так как (–3)²+ 4²= 25, а 1²+ 6²≠ 25. В этом легко
убедиться, если построить график данного
уравнения в декартовой системе координат
(рис. 7.1). Геометрическим местом всех
точек, принадлежащих этому множеству,
является окружностьR= 5 с центром в начале координат.

Рис. 7.1

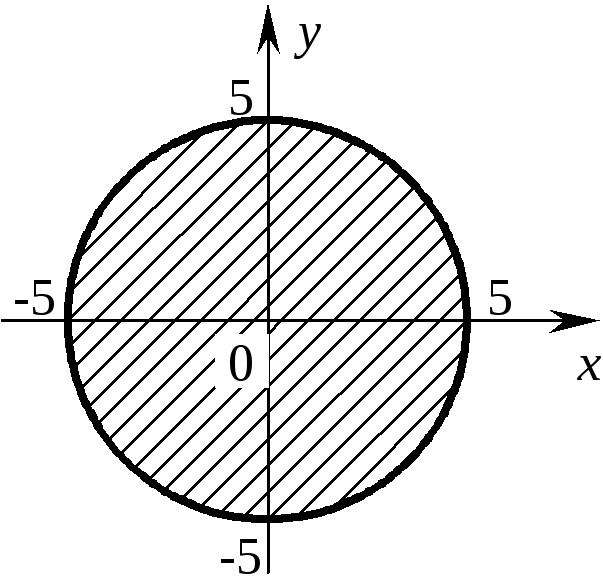
Если мы рассмотрим
множество, заданное в виде неравенства
x²+y²< 25, то множеством будут являться все
точки, находящиеся внутри этой окружности
(рис.7.2). Сама окружность изображена
пунктиром, чтобы показать, что точки,
принадлежащие самой окружности (границе
области) в данном случае на нее не
попадают и точкаM(–
3; 4)множествуx²+y²< 25 (области),
в чем легко убедится, а точкаN(1;
2){x²+y²< 25}.

Рис.
7.2

Если же x²+y²≤ 25, то здесь
уже войдет и граница (сама окружность).
Изобразим ее жирной линией (рис. 7.3).

Рис.
7.3

То же касается
систем линейных неравенств.

Пример.Построить область допустимых решений
системы линейных неравенств.

Решение.Нумеруем ограничения задачи

В прямоугольной
декартовой системе координат (рис. 7.4)
строим прямую 2x
– y = 2,
соответствующую ограничению (1).

Рис.
7.4

Находим, какая
из двух полуплоскостей, на которые эта
прямая делит всю координатную плоскость,
является областью решения неравенства
(1). Для этого достаточно координаты
какой-либо точки, не лежащей на прямой,
подставить в неравенство. Так как прямая
(1) не проходит через начало координат,
подставляем координаты точки О (0,
0) в первое ограничение: 2·0 – 0 < 2.
Получаем строгое неравенство 0 < 2.
Следовательно, точкаОлежит в
полуплоскости решений. Таким образом,
стрелки на концах прямой (1) должны быть
направлены в полуплоскость, содержащую
точкуО.

Аналогично
строим прямые x+y= 3 и –x+ 2y= 4 и области решений ограничений (2) и
(3).

Находим общую
часть полуплоскостей решений. Полученную
область допустимых решений отмечаем
на рис. 7.4 штриховкой. В этой области
находятся все точки M(x;y), в которых выполняются
все три неравенства системы. ◄

Задание 3

Решить неравенство
(а) и систему неравенств (б).

3.1.а);

б)

3.2.а);

б)

3.3.а);

б)

3.4.а);

б)

3.5.а);

б)

3.6.а);

б)

3.7.а);

б)

3.8.а);

б)

3.9.а);

б)

3.10.а);

б)

3.11.а);

б)

3.12.а);

б)

3.13.а);

б)

3.14.а);

б)

3.15.а);

б)

3.16.а);

б)

3.17.а);

б)

3.18.а);

б)

3.19.а);

б)

3.20.а);

б)

3.21.а);

б)

3.22.а);

б)

3.23.а);

б)

3.24.а);

б)

3.25.а);

б)

3.26.а);

б)

3.27.а);

б)

3.28.а);

б)

3.29.а);

б)

3.30.а);

б)

Источник

Общие уравнения геометрических мест точек

Уравнением множества точек (уравнением г.м.т.) координатной плоскости называется равенство, связывающее координаты точек, верное для координат точек, принадлежащих множеству , и неверное для координат точек, не принадлежащих . Например, уравнение множества в аффинной системе координат Ox_1x_2 имеет вид:

F(x_1,x_2)=0,

(3.1)

в частности, в прямоугольной системе координат Oxycolon~ F(x,y)=0 , а в полярной системе координат Orvarphi,colon

G(r,varphi)=0,

(3.2)

где и — некоторые функции двух аргументов.

Уравнения (3.1), (3.2) представляют собой аналитическую запись функциональной зависимости между координатами точек на плоскости, образующих геометрическое место точек. В частных случаях одна из координат может быть выражена через другую, т.е. одна координата задается как явная функция другой координаты. Тогда получается уравнение, разрешенное относительно этой координаты, например: y=f(x),,r=g(varphi).

Заметим, что уравнениями вида y=f(x) в прямоугольной системе координат Oxy могут быть заданы графики элементарных функций: степенных, тригонометрических, показательных, логарифмических.

Пример 3.1. Изобразить на координатной плоскости Oxy (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим уравнениям:

$begin{array}{*{20}l} mathsf{1)}~x-y=0;&qquad mathsf{2)}~x^2-y^2=0;&qquad mathsf{3)}~x^2+y^2=0;\[5pt] mathsf{4)}~x^2+y^2-1=0;&qquad mathsf{5)}~|x|-x=0;&qquad mathsf{6)}~x^2+y^2+1=0. end{array}$

Решение. а) Уравнению x-y=0 удовлетворяют только те точки плоскости, у которых равны абсциссы и ординаты (y=x) . Эти точки лежат на биссектрисах и III координатных углов (рис. 3.1, а).

б) Разлагая левую часть уравнения на множители, получаем уравнение (x-y)(x+y)=0 , которое равносильно совокупности уравнений

$left[!begin{aligned}y&=x,\y&=-x.end{aligned}right.$

Первому уравнению отвечают биссектрисы нечетных координатных углов, второму — биссектрисы четных координатных углов. Следовательно, заданному уравнению удовлетворяют только те точки, которые принадлежат хотя бы одной из указанных биссектрис (рис. 3.1, 6).

в) Уравнение x^2+y^2=0 равносильно системе уравнений $begin{cases} x=0,\y=0,end{cases}$
которая определяет единственную точку (начало координат) на плоскости (рис. 3.1, в).

Множества точек, координаты которых удовлетворяют уравнениям

г) Выражение x^2+y^2 есть квадрат расстояния от точки (x,y) до начала координат. Поэтому уравнению x^2+y^2-1=0 (или x^2+y^2=1 ) удовлетворяют только те точки, которые удалены от точки на расстояние, равное 1. Это множество точек является окружностью с центром в начале координат и радиусом 1 (рис.3.1,г).

д) Уравнению |x|+x=0 удовлетворяет каждая точка с неположительной абсциссой. Следовательно, множество решений этого уравнения представляет собой полуплоскость xleqslant0 , ограниченную осью ординат (рис.3.1,д).

е) Уравнение x^2+y^2+1=0 не имеет действительных решений, поэтому на координатной плоскости нет точек, удовлетворяющих этому уравнению.

Пример 3.2. На координатной плоскости Oxy (в прямоугольной системе координат) отмечены точки A(2,0) и B(0,4) . Вывести уравнения заданных множеств:

а) прямой (рис.3.2,а);

б) серединного перпендикуляра к отрезку (рис.3.2,б);

в) окружности с диаметром (рис.3.2,в).

Уравнения и графики прямой, серединного перпендикуляра и окружности с диаметром

Решение. а) Точка M(x,y) принадлежит прямой тогда и только тогда, когда ее радиус-вектор overrightarrow{OM} удовлетворяет условию overrightarrow{OM}=t,overrightarrow{OA}+(1-t),overrightarrow{OB} , где — некоторое действительное число (см. Применение векторов в задачах). Записывая это векторное равенство в координатной форме, получаем

$begin{pmatrix}x\yend{pmatrix}=tbegin{pmatrix}2\0end{pmatrix}+(1-t)begin{pmatrix} 0\4end{pmatrix}!~ Leftrightarrow~ begin{cases} x=2t,\y=4-4t.end{cases}$

Исключая параметр из этой системы (например, подставляя во второе уравнение t=x/2 ), приходим к уравнению y=4-2x или 2x+y-4=0 .

б) Пусть M(x,y) произвольная точка плоскости. Эта точка принадлежит серединному перпендикуляру к отрезку тогда и только тогда, когда MA=MB . Записывая это равенство в координатной форме, получаем

$sqrt{(x-2)^2+y^2}=sqrt{x^2+(y-4)^2}.$

Возводя в квадрат и приводя подобные члены, приходим к уравнению x-2y+3=0 .

в) Найдем радиус заданной окружности:

$r=frac{AB}{2}=frac{1}{2}sqrt{(2-0)^2+(0-4)^2}=sqrt{5}$

и координаты центра окружности — середины отрезка ABcolon Q(1;2) , так как $Q!left(frac{2+0}{2};,frac{0+4}{2}right)$ . По определению точка M(x,y) принадлежит этой окружности тогда и только тогда, когда MQ=r . Записывая это равенство в координатной форме, получаем

Спираль Архимеда (график в полярных координатах)

$sqrt{(x-1)^2+(y-2)^2}=sqrt{5}.$

Возводя в квадрат и перенося все члены в левую часть равенства, получаем (x-1)^2+(y-2)^2-5=0 .

Пример 3.3. Изобразить на плоскости в полярной системе координат Orvarphi множества точек, координаты которых удовлетворяют следующим уравнениям:

а) r=varphi (спираль Архимеда);

б) r=1+cosvarphi (кардиоида);

в) r^2=cos2varphi (лемниската Бернулли).

Решение. а) Построение выполняется по точкам при 0leqslantvarphileqslant2pi . Далее учитывается, что при каждом полном обороте полярный радиус увеличивается на 2pi (рис.3.3-1).

б) Построение выполняется по точкам при 0leqslantvarphileqslantpi , а затем продолжается симметрично полярной оси, так как замена varphi на -varphi не изменяет уравнения (рис.3.3-2,а).

в) Построение выполняется по точкам при $0leqslantvarphileqslantfrac{pi}{2}$ , а затем продолжается симметрично полярной оси и полюса (рис.3.3-2,б).

Кардиоида и Лемниската Бернулли (графики в полярных координатах)

Уравнения пересечений и объединений геометрических мест точек

Рассмотрим основные операции с множествами точек на координатной плоскости, заданными своими уравнениями.

Пусть множества и в аффинной системе координат Ox_1x_2 заданы общими уравнениями F(x_1,x_2)=0 и G(x_1,x_2)=0 соответственно.

Пересечение Fcap G множеств и состоит из точек, координаты которых удовлетворяют системе уравнений

$begin{cases}F(x_1,x_2)=0,\G(x_1,x_2)=0.end{cases}$

Можно составить одно уравнение, равносильное этой системе, например:

(F(x_1,x_2))^2+(G(x_1,x_2))^2=0.

Объединение Fcup G множеств и состоит из точек, координаты которых удовлетворяют совокупности уравнений

$left[!begin{aligned}F(x_1,x_2)=0,\G(x_1,x_2)=0.end{aligned}right.$ равносильной одному уравнению, например: F(x_1,x_2)cdot G(x_1,x_2)=0 .

Включение Fsubset G с алгебраической точки зрения означает, что уравнение G(x_1,x_2)=0 является следствием уравнения F(x_1,x_2)=0 , то есть

F(x_1,x_2)=0 quad Rightarrow quad G(x_1,x_2)=0.

Равенство F=G означает, что уравнения F(x_1,x_2)=0 и G(x_1,x_2)=0 равносильны (эквивалентны), то есть

F(x_1,x_2)=0 quad Leftrightarrow quad G(x_1,x_2)=0.

В частности, равносильные уравнения, описывающие одно и то же геометрическое место точек, получаются при тождественных алгебраических преобразованиях равенств, например, при умножении обеих частей уравнения на отличное от нуля число, при приведении подобных членов, при переносе членов из одной части уравнения в другую с изменением знака на противоположный и т.п.

Полученные соотношения, сводящие операции с множествами на плоскости к алгебраическим операциям с уравнениями этих геометрических мест точек, не зависят от выбора системы координат. Например, в прямоугольной системе координат Oxy аналогичные соотношения получаем, полагая x_1=x и x_2=y , а в полярной системе координат Orvarphi при x_1=r и x_2=varphi .

Параметрические уравнения геометрических мест точек

Функциональная зависимость между координатами точек плоскости, например в прямоугольной системе координат Oxy , может быть задана в параметрической форме, в которой обе координаты выражаются в виде функций вспомогательной переменной, называемой параметром:

$begin{cases}x=f(t),\[2pt]y=g(t),end{cases}$

(3.3)

где — параметр, принимающий действительные значения. Систему (3.3) называют параметрическим уравнением геометрического места точек.

Пример 3.4. Изобразить на координатной плоскости Oxy (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим параметрическим уравнениям:

$mathsf{1)}~begin{cases}x=cos{t},\y=sin{t};end{cases} quad mathsf{2)}~begin{cases}x=t-cos{t},\y=1-sin{t};end{cases} quad mathsf{3)}~begin{cases}x=cos^3{t},\y=sin^3{t}.end{cases}$

Решение. 1) Исключим из заданной системы уравнений параметр . Возведя обе части каждого уравнения в квадрат и сложив почленно результаты, получим уравнение окружности x^2+y^2=1 (см. пример 3.1 ,г). Параметром служит величина угла поворота радиус-вектора изображающей точки, измеряемого от положительного направления оси абсцисс (рис.3.4,а).

2) Уравнения задают циклоиду — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по прямой (оси абсцисс). Построение одной арки циклоиды выполняется по точкам при 0leqslant tleqslant2pi . Затем эта арка «переносится» вдоль оси абсцисс (рис.3.4,б). Параметром служит величина угла поворота радиуса катящейся окружности.

Графики окружности, циклоиды и астроиды

3) Уравнения задают астроиду (гипоциклоиду) — линию, которую описывает точка, принадлежащая окружности при качении этой окружности (без проскальзывания) по другой неподвижной окружности, касаясь ее внутренним образом. Астроида и обе окружности изображены на рис.3.4,в (астроида полужирной линией, неподвижная окружность сплошной, а подвижная — штриховой). Построение выполняется по точкам при $0leqslant tleqslantfrac{pi}{2}$ , а затем продолжается симметрично координатным осям.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Построение множеств точек на плоскости

Пример 15. Построим множество точек (x,y)(x, y), удовлетворяющих уравнению x2+xy=0x^2 + xy = 0.

Преобразуем уравнение: x(x+y)=0x(x + y) = 0. Таким образом, заданное уравнение равносильно совокупности двух уравнений x=0x = 0 или x+y=0x + y = 0 (y=−x)(y = − x). Поэтому искомым множеством точек будет объединение этих двух прямых.

Построим множество точек (x,y)(x, y) таких, что

x2+4x+4+4y2=0x^2 + 4x + 4 + 4y^2 = 0.

Преобразуем уравнение с помощью выделения полного квадрата: (x+2)2+4y2=0(x + 2)2 + 4y^2 = 0. Поскольку точные квадраты неотрицательны, то такому уравнению может удовлетворять лишь одна точка (–2,0)(–2, 0).

Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.

Построим множество точек (x,y)(x, y) таких, что |x−y−1|+x2+2xy+y2=0|x − y − 1| + x^2 + 2xy + y^2 = 0. Преобразуем уравнение: |x−y−1|=−(x+y)2|x − y − 1| = −(x + y)^2. Так как модуль равен неотрицательному числу, то

x−y−1=0,−(x+y)2=0; x−y=1,x+y=0,left{begin{array}{l}x-y-1=0,\-{(x+y)^2}=0;end{array}right.;;left{begin{array}{l}x-y=1,\x+y=0,end{array}right.

т. е. уравнению снова будет удовлетворять единственная точка (0,5;–0,5)(0,5; – 0,5) (см. рис. 39).

Множеством точек может быть область на плоскости. Рассмотрим пример.

Построим множество точек (x,y)(x, y) таких, что

(x−3)(y+2)=3−x−y−2sqrt{(x − 3)(y + 2)} = sqrt{3 − x} sqrt{−y − 2}.

Равенство (x−3)(y+2)=3−x−y−2sqrt{(x − 3)(y + 2)} = sqrt{3 − x} sqrt{−y − 2} будет верно для всяких xx и yy, удовлетворяющих ОДЗ. Поэтому искомым множество точек будет ОДЗ, т. е. часть плоскости, ограниченная двумя прямыми y=−2y = −2 и x=3x = 3 (рис. 40).

Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.

Построим множество точек, удовлетворяющих |y|=|x||y| = |x|.

По определению модуля получаем: y=±xy = ±x. Поэтому множество точек – объединение двух прямых линий (рис. 41).

Источник