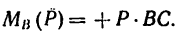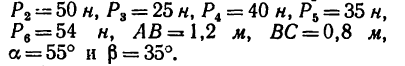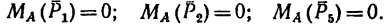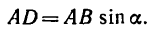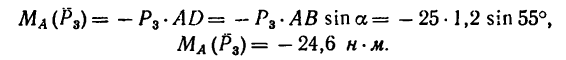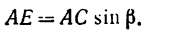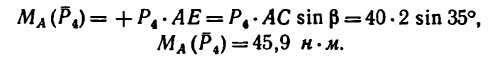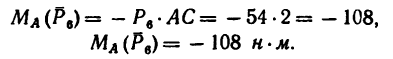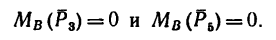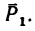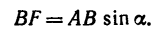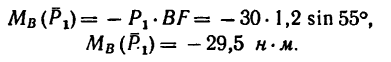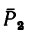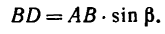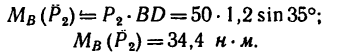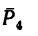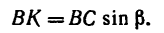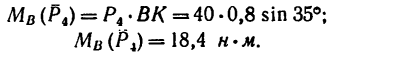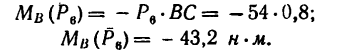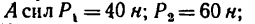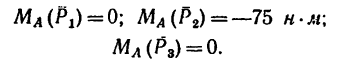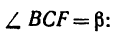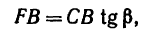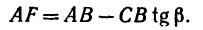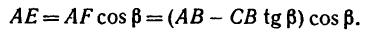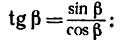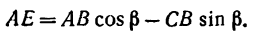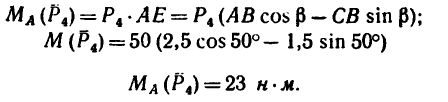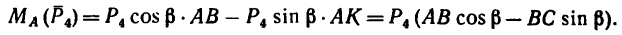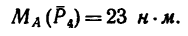iSopromat.ru
Правила знаков для моментов и проекций сил на оси координат:
Правило знаков проекций сил
То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.
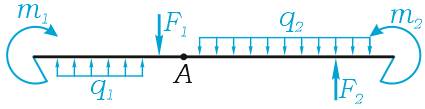
Например, для такой схемы нагружения:
уравнение суммы сил имеет вид
А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:
Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.
Правило знаков для моментов
Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

Например, для суммы моментов относительно точки A
или, что одно и то же
Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.
При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Теоретическая механика. В помощь студенту
Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.
Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.
Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.
Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.
Статика твердого тела
Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.
-
Основные понятия и законы статики
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон.
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
Размерность распределенной нагрузки – Н/м 3 (Н/м 2 , Н/м).
Принятое обозначение:
 .
. .
. .
.Принятое обозначение:
 .
. Под действием пары сил тело будет совершать вращательное движение.
Проекция положительна, если направление отрезка совпадает с положительным направлением оси.
Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси.
Эти две силы называются уравновешивающимися.
Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое.
Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.
Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.
диагонали.
По модулю равнодействующая равна:

Следует иметь в виду, что действие — сила, приложенная к телу Б, и противодействие — сила, приложенная к телу А, не уравновешиваются, так как они приложены к разным телам.
Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела.
-
Связи и их реакции
- Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
- Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
- Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
- Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
- Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.
-
Момент силы относительно точки
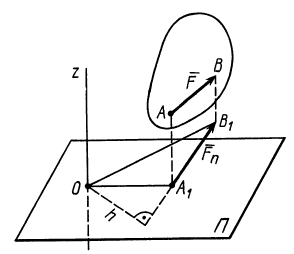
- Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы.
- Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.
- Свойства момента силы относительно точки:
1) Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы.
2) Момент силы равен нулю, если линия действия силы проходит через точку приложения силы.
3) Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.,
где
-
Момент силы относительно оси
- Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки. - Чтобы найти момент силы относительно оси, нужно:
1) Провести плоскость перпендикулярную оси z.
2) Спроецировать силу на эту плоскость и вычислить величину проекции.
3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силыи вычислить его длину.
4) Найти произведение этого плеча и проекции силы с соответствующим знаком. - Свойства момента силы относительно оси.
Момент силы относительно оси равен нулю, если:
1), то есть сила параллельна оси.
2) h=0, то есть линия действия силы пересекает ось.
-
Момент пары сил
- Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
,
где:— силы, составляющие пару;
h — плечо пары.
Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки. - Свойства пары сил.
1) Сумма проекций сил пары на любую ось равна нулю.
2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.
-
Преобразование произвольной системы сил
- Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.
В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.
Суммарный вектор— это главный вектор системы сил.
Суммарный момент— это главный момент системы сил.
Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил. - Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат:
,
-
Условия равновесия систем сил
- Равновесие системы сходящихся сил
Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.
Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю.
Из формулыследует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
- Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:
-
Равновесие произвольной системы сил.
- Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия:
.
- Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
- Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:
Кинематика
Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.
-
Основные понятия кинематики
-
Способы задания движения точки
- Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
- В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
Закон движения: . - В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
Закон движения: x = x(t), y = y(t); z = z(t). - В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
Закон движения: .
Движение точки, при естественном способе задания движения, определено если известны:
1) Траектория движения.
2) Начало и направление отсчета дуговой координаты.
3) Уравнение движения.
При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
Главная нормаль (n) – направлена в сторону вогнутости кривой.
Бинормаль (b) – направлена перпендикулярно к осям τ, n.
-
Определение кинематических характеристик точки
- Траектория точки
В векторной системе отсчета траектория описывается выражением: .
В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости.
В естественной системе отсчета траектория задается заранее. - Определение скорости точки в векторной системе координат
При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
Вывод:скорость точки – векторная величина, равная производной от закона движения по времени.
Свойство производной:производная от какой либо величины по времени определяет скорость изменения этой величины. - Определение скорости точки в координатной системе отсчета
Скорости изменения координат точки:
.
Модуль полной скорости точки при прямоугольной системе координат будет равен:
.
Направление вектора скорости определяется косинусами направляющих углов:
,
где — углы между вектором скорости и осями координат. - Определение скорости точки в естественной системе отсчета
Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .
-
Ускорение точки
- По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
- Ускорения точки в векторной системе отсчета
На основании свойства производной:
.
Вектор скорости может изменяться по модулю и направлению.
Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории. - Ускорение точки в координатной системе отсчета
Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:
.
Полное ускорение в прямоугольной системе координат будет определяться выражением:
.
Направляющие косинусы вектора ускорения:
. - Ускорение точки в естественной системе отсчета Приращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат:
.
Разделив левую и правую части равенства на dt, получим:
,
где — тангенциальное ускорение;
— нормальное ускорение;
R — радиус кривизны траектории в окрестности точки.
-
Кинематика твердого тела
- В кинематике твердых тел решаются две основные задачи:
1) задание движения и определение кинематических характеристик тела в целом;
2) определение кинематических характеристик точек тела. - Поступательное движение твердого тела
Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
Теорема:при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
Вывод:поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки. - Вращательное движение твердого тела вокруг неподвижной оси
Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
Закон вращательного движения тела вокруг неподвижной оси .
Угловую скорость и угловое ускорение тела определим методом дифференцирования:
— угловая скорость, рад/с;
— угловое ускорение, рад/с².
Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
Модуль линейной скорости:
.
Ускорение точки М при известной траектории определяется по его составляющим :
,
где .
В итоге, получаем формулы
тангенциальное ускорение: ;
нормальное ускорение: .
-
Плоско-параллельное движение твердого тела
- Плоско-параллельное движение твердого тела — это движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости.
Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений:
1) поступательного и вращательного;
2) вращательного относительно подвижного (мгновенного) центра. - В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса.
В качестве полюса может быть принята любая точка сечения.
Уравнения движения запишутся в виде:
.
Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса. - Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P.
В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения:
.
Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.
. - Положение мгновенного центра вращения может быть определено на основании следующих свойств:
1) вектор скорости точки перпендикулярен радиусу;
2) модуль скорости точки пропорционален расстоянию от точки до центра вращения ();
3) скорость в центре вращения равна нулю. - Теорема:проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.
Доказательство: расстояние АВ изменяться не может, следовательно, не может быть больше или меньше .
Вывод:.
-
Сложное движение точки
- Относительное движение — это движение точки относительно подвижной системы.
Переносное движение — это движение точки вместе с подвижной системой.
Абсолютное движение — это движение точки относительно неподвижной системы.
Соответственно называют скорости и ускорения:
— относительные;
— переносные;
— абсолютные. - Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (согласно теореме о сложении скоростей):
.
Абсолютное значение скорости определяется по теореме косинусов:
. - Ускорение по правилу параллелограмма определяется только при поступательном переносном движении
.
. - При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.
,
где .
Кориолисово ускорение численно равно:
,
где – угол между векторами и .
Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.
Динамика
Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.
-
Основные понятия динамики
где mk, xk, yk, zk — масса и координаты k-той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:
где — ускорение центра масс тела.
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов:
.
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
,
где α — угол между направлениями векторов перемещения и силы.
.
Единица измерения работы — Джоуль (1 Дж = 1 Н·м).
.
или
,
где m — масса механической системы, — вектор скорости центра масс системы.
.
.
-
Аксиомы динамики
- Первая аксиома — это закон инерции.
Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения. - Вторая аксиома — закон пропорциональности ускорения.
Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы: — это основной закон динамики. - Третья аксиома — это закон противодействия.
Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны:
. - Четвертая аксиома — закон независимости действия сил.
При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы:
-
Дифференциальные уравнения динамики
- Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме.
Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид:
. - Векторное уравнение может быть записано в проекциях на оси прямоугольной инерциальной системы координат:
- При известной траектория движения точки уравнение может быть записано в проекциях на оси естественной системы координат:
С учетом того, что ,
где — тангенциальное ускорение;
— нормальное ускорение,
уравнения примут вид:
-
Общие теоремы динамики
- Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.
- Теорема об изменении количества движения: изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени — для материальной точки;
— для механической системы. - Теорема об изменении кинетической энергии: изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении — для материальной точки;
— для механической системы. - Кинетическая энергия механической системы определяется в соответствии с , при этом для твердых тел выведены следующие зависимости:
— при поступательном движении тела;
— при вращательном движении тела;
— при плоско-параллельном движении тела. - Момент инерции цилиндра относительно его оси:
. - Момент инерции стержня относительно оси z:
. - Момент инерции прямоугольной пластины относительно осей х и y: .
- Момент инерции шара определяется по формуле:
. - Работа силы тяжести:
,
где P — сила тяжести;
h — изменение положения тела по вертикали. - Работа силы при вращательном движении тела
,
где M — момент силы,
w — угловая скорость тела.
Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.
-
Принцип Даламбера
- Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
. - Для механической системы:
.
Примеры решения задач
Решение примеров по теме: «Статика твердого тела»
Пример 1. Условия равновесия
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.
Дано: P = 10 Н; α = 45°
Найти: N, T — ?
Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.
Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).
Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).
При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).
В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:
После подстановки в формулы числовых значений, получим:
.
Ответ: .
Решение примеров по теме: «Кинематика»
Пример 2. Уравнение траектории точки
Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.
Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.
Опуская промежуточные выражения, получаем уравнение траектории:
.
Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).
Ответ: .
Решение примеров по теме: «Динамика»
Пример 3. Основной закон динамики точки
Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.
Дано: m = 10 кг; a = 0,5 м/с 2 .
Найти: F — ?
Решение.
Согласно основному закону динамики: .
Подставив значения в формулу, получим:
Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с 2 , равна 5 Н.
В помощь студенту
-
Формулы, правила, законы, теоремы, уравнения, примеры решения задач
Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Архив рубрики: Пара сил и моменты сил
Понятие о вращающих и крутящих моментах
Часто в прикладных задачах механики приходится определять моменты сил, приложенных к телу, относительно его оси. Покажем, что в сечениях тела под действием внешних сил всегда возникают внутренние силы.
Рассмотрим устройство для подъема грузов, состоящее из вала ABC, на который насажены барабан АВ с радиусом r и зубчатое колесо С с радиусом R.
Вал приводится во вращение от электродвигателя D через зубчатую передачу. Вес поднимаемого груза Q передается через трос на обод барабана, а от шестерни K, насаженной на вал электродвигателя, передается движущая сила Р.
При равномерном подъеме груза моменты внешних сил, приложенных к валу, должны уравновешиваться, т. е.
Реакции опор А и В не войдут в уравнение моментов, так как они пересекают ось z и, следовательно, не создают относительно этой оси моментов.
Из составленного уравнения равновесия следует, что PR = Qr или Мz (Р) = Мz (Q), т. е. на концы участка вала, расположенного между сечением приложения груза Q и зубчатым колесом С, действуют равные и противоположно направленные моменты внешних сил. Эти моменты называют вращающими моментами.
Участок вала между сечениями приложения вращающих моментов, как уже отмечалось, находится в равновесии. Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение Е.
Чтобы отсеченная часть ЕС находилась в равновесии, в сечении Е должен действовать какой-то момент, равный и противоположный по направлению вращающему моменту, приложенному к колесу С. Этот момент называется крутящим (его обозначают Мк ) и является моментом внутренних сил, возникающих в сечении тела.
Использованный здесь метод установления внутренних сил в сечении вала называется методом сечений (более подробно о методе сечений — см. здесь).
Момент внутренних сил в сечении —крутящий момент— равен алгебраической сумме моментов внешних сил, т. е. вращающих моментов, приложенных к отсеченной части вала:
где n — число вращающих моментов, приложенных к отсеченной части рассматриваемого вала.
Знак крутящего момента в поперечном сечении вала можно установить, исходя из направления внешних вращающих моментов. Условимся считать крутящий момент положительным, когда внешние моменты, приложенные к валу, вращают отсеченную часть по часовой стрелке (если смотреть со стороны внешней нормали к проведенному сечению). На рассматриваемом рисунке сила Р вызывает вращение отброшенной части вала против часовой стрелки, если смотреть со стороны внешней нормали на проведенное сечение Е. Таким образом, в рассмотренном сечении Е возникает отрицательный крутящий момент.
При возрастании веса поднимаемого груза соответственно увеличиваются вращающие моменты. Будут возрастать также крутящие моменты в сечениях вала. Очевидно, что при данных размерах вала нельзя допускать безграничного возрастания вращающего, а следовательно, и крутящего моментов, так как вал может разрушиться или сильно деформироваться. Поэтому определение крутящих моментов имеет очень большое практическое значение для расчетов на прочность.
Равновесие рычага
Во многих задачах механики приходится рассматривать равновесие тела, шарнирно закрепленного на некоторой неподвижной оси. Такое тело называют рычагом.
Рычаг обладает способностью вращаться вокруг оси закрепления (рис. а).
Равновесие рычага будет обеспечено только в том случае, когда алгебраическая сумма моментов всех действующих на рычаг сил относительно его неподвижной точки равна нулю.
Неподвижной точкой рычага, относительно которой мы будем составлять уравнение моментов, является точка пересечения оси вращения рычага с плоскостью чертежа (рис.а)
Рычаг можно использовать для подъема грузов, для создания больших давлений с помощью небольшого усилия и т. п. Рычаги двух видов показаны на рис.б и в.
Момент силы относительно оси
Рассмотрим, как определяется момент силы относительно оси. Стремление силы вращать тело вокруг неподвижной оси зависит от величины силы, ее наклона и расстояния от оси.
Из опыта известно, что силы, проходящие через ось, и силы, параллельные оси, НЕ МОГУТ ВЫЗВАТЬ ВРАЩЕНИЯ ТЕЛА вокруг этой оси. Посмотрим на рисунок.
Ни сила Р1, линия действия которой пересекает ось Oz, ни сила Р2, параллельная оси, не смогут повернуть тело вокруг этой оси.
Для вращательного эффекта силы относительно закрепленной оси вводится понятие момента силы относительно оси Мz (Р). Вращательный эффект силы относительно оси и выражается ее моментом.
Пусть на тело в какой-то точке действует произвольная сила Р, не параллельная оси вращения Oz и не пересекающая эту ось. Проведем плоскость H, перпендикулярную оси Oz и проходящую через начало вектора силы. Разложим заданную силу Р на две составляющие: Р1, расположенную в плоскости H, и Р2, параллельную оси Oz.
Составляющая Р2, параллельная оси Oz момента относительно этой оси не создает. Составляющая Р1, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы Р1 измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.
В выражение момента силы относительно оси входит не вся сила, а только ее составляющая, лежащая в плоскости, перпендикулярной оси вращения.
Знак момента по общему правилу определяется направлением вращения тела: (+) при движении по часовой стрелке, (—) при движении против часовой стрелки (правило условно). При определении знака момента наблюдатель должен непременно находиться со стороны положительного направления оси. На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.
На рисунке внизу момент силы Р относительно оси Oz — величина отрицательная.
Рассмотрим частный случай.
В частном случае момент силы Р, расположенной в плоскости H, относительно оси Oz, перпендикулярной этой плоскости, определится произведением полной величины силы Р на ее плечо l относительно точки пересечения оси Oz и плоскости H
Итак, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы на плоскость относительно точки пересечения оси с этой плоскостью.
Момент силы относительно точки
Моментом силы относительно точки называется произведение величины силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. а).
Если бы тело было закреплено в точке О, то сила Р стремилась бы вращать тело вокруг этой точки. Точка О, относительно которой берется момент, называется центром
момента, а перпендикуляр а называется плечом силы относительно центра момента.
М = сила×плечо.
Момент силы Р относительно О обозначается
Моменты сил измеряют в ньютонометрах (Нм) или килограммометрах (кГм) или в соответствующих кратных и дольных единицах, как и моменты пар.
Принято считать момент положительным, если сила стремится вращать тело по часовой стрелке (рис. а), и отрицательным — против часовой стрелки (рис. б).
Установленное правило знаков для моментов сил, как и для моментов пар, условно.
Когда линия действия силы проходит через данную точку, ее момент относительно этой точки равен нулю, так как в рассматриваемом случае плечо равно нулю а = 0 (рис. в).
Между моментом пары и моментом силы есть одно существенное различие. У момента пары сил величина и направление не зависят от положения этой пары в пространстве. У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Сложение пар
Пары, подобно силам, можно складывать.
Пара, заменяющая собой действие данных пар, называется результирующей. Результирующая нескольких пар эквивалентна заданным парам.
Определение по данным парам их результирующей пары называется сложением пар.
Сложим две пары, расположенные в одной плоскости.
Имеем пары P1 P‘1 и Р2 Р’2 с плечами а и b (см. рис.), т. е.
М1 = — P1а,
М2 = P2b
Приведем данные пары к одному плечу, не изменяя величины моментов каждой пары. Некоторый отрезок АВ = с (см. рис.выше) примем за общее плечо преобразованных пар.
Обозначим силы эквивалентных пар как Q1 ,Q’1 и Q2 ,Q’2 ; тогда
М1 = — P1а = —Q1c;
М2 = P2b = Q2c
Складывая силы, приложенные в точках А и В, найдем их равнодействующие
Обозначим эти уравнения буквой (а)
Равнодействующие R и R’, равные по величине и направленные в противоположные стороны, образуют пару сил RR’ ; момент которой
М = —Rc. (б)
Пара RR’ представляет результирующую пару. Подставив в уравнение (б) значение R из уравнения (а), получим
М = —Rc = — ( Q1 — Q2)с = Q2c —Q1c,
М2 = Q2c и М1 = —Q1c,
Таким образом, приходим к заключению, что момент результирующей пары равен алгебраической сумме моментов составляющих пар.
Аналогичное доказательство применимо к любому количеству пар, лежащих в одной плоскости. Поэтому при произвольном числе слагаемых пар, лежащих в одной плоскости или параллельных плоскостях, момент результирующей пары определится по формуле
На основании приведенного правила сложения пар устанавливается условие равновесия системы пар, лежащих в одной плоскости, а именно:
для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:
Эквивалентность пар
В соответствии с определением эквивалентных систем сил (см. — здесь), две пары сил считают эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.
Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.
Рассмотрим еще одно свойство пары сил, которое является основой для сложения пар.
Не нарушая состояния тела, можно как угодно изменять величины сил и плечо пары, только бы момент пары оставался неизменным.
Рассмотрим пару сил РР’ плечом а (рис. а).
Заменим эту пару новой парой QQ’ с плечом b (рис. 6) так, чтобы момент пары остался тем же.
Момент заданной пары сил M1 = Ра. Момент новой пары сил М2 = Qb. По определению пары сил эквивалентны, т. е. производят одинаковые действия, если их моменты равны.
Если, изменив величину сил и плечо новой пары, мы сохраним равенство их моментов M1 = М2 или Ра = Qb, то состояние тела от такой замены не нарушится.
Итак, вместо заданной пары РР’ с плечом а мы получили эквивалентную пару QQ’ с плечом b.
Пара сил и ее действие на тело
Система двух равных и параллельных сил, направленных в противоположные стороны и не лежащих на одной прямой, называется парой сил. Примером такой системы сил могут служить усилия, передаваемые от рук шофера на рулевое колесо автомобиля.
Пара сил имеет очень большое значение в практике. Именно поэтому свойства пары как специфической меры механического взаимодействия тел изучается отдельно.
Сумма сил пары равна нулю
Р — Р’ = 0 (рис. а),
т. е. пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил не находится в равновесии.
Действие пары сил на твердое тело, как показывает опыт, состоит в том, что она стремится вращать это тело.
Способность пары сил производить вращение количественно определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил.
Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютная величина момента (рис. а)
М = Ра = Р’а.
Кратчайшее расстояние между линиями действия сил называется плечом пары, поэтому можно сказать, что момент пары сил по абсолютной величине равен произведению одной из сил пары на ее плечо.
Эффект действия пары сил полностью определяется ее моментом. Поэтому пару сил можно изображать дугообразной стрелкой, указывающей направление вращения (см.рис.).
Так как пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой.
В Международной системе единиц (СИ) силу измеряют в ньютонах, а плечо в метрах. Соответственно момент пары в системе СИ измеряется в ньютонометрах (н·м) или в единицах, кратных ньютонометру: кн·м, Мн·м и т. д.
Будем считать момент пары сил положительным, если пара стремится повернуть тело по направлению хода часовой стрелки (рис. а) и отрицательным, если пара стремится вращать тело против хода часовой стрелки (рис. б).
Принятое правило знаков для моментов пар условно; можно было бы принять противоположное правило. При решении задач во избежание путаницы всегда нужно принимать одно определенное правило знаков.
http://prosopromat.ru/category/texnicheskaya-mexanika/statika/para-sil-i-momenty-sil
Содержание:
Моменты силы относительно точки и оси:
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
Алгебраический момент силы относительно точки
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки.
Рис. 19
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
Плечом 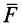

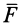
Обозначим 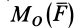
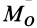
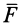

Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке — знак минус.
Алгебраический момент силы представляет собой произведение силы на длину (в 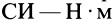
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе 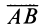
Векторный момент силы относительно точки
При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
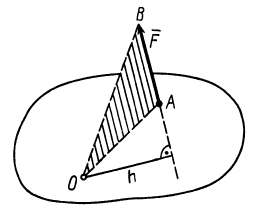
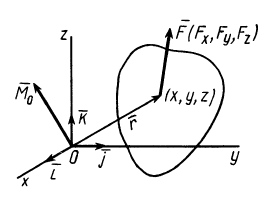
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
Плечом 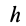

Рис. 20
Условимся векторный момент силы 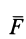


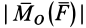
Как и для алгебраического момента, векторный момент силы относительно точки равен удвоенной площади треугольника, построенного на силе и моментной точке:
Справедлива формула
где 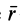

Чтобы убедиться в справедливости формулы (3), достаточно показать, что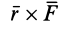

Как показано на рис. 20, 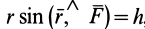
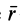
что совпадает с векторным моментом силы относительно точки 
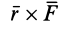
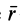
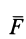
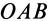

Направление 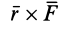

Векторный момент силы относительно точки не изменяется от переноса силы вдоль ее линии действия. Он станет равным
нулю, если линия действия силы пройдет через моментную точку.
Рис. 21
Если сила 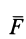
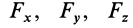
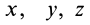
где 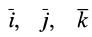
Используя формулу (4), можно выделить проекции 
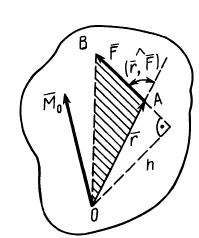
Модуль векторного момента 
В формулах (6) числовую величину 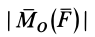
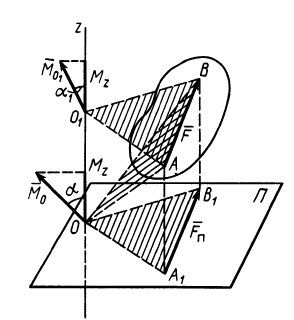
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 22). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси 
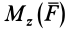
Рис. 22
По определению,
где 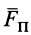
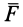





Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь треугольника, построенного на проекции силы 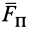

Из формулы (8) можно получить следующие важные свойства момента силы относительно оси:
- Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
- Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы
относительно точки
.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
Используя формулу (8), имеем (рис. 23)
Векторный момент силы 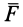



Векторный момент 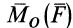
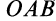
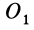
причем векторный момент 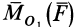
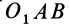
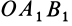
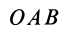
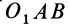

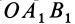

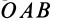
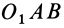
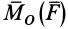
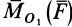
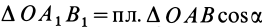
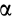
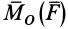

причем знак 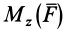
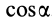
Аналогично,
т. е.
где 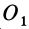

Формулы (11) и (12) отражают искомую связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.
Эту зависимость между моментом силы относительно оси и векторным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
Рис. 23
Формулы для моментов силы относительно осей координат
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы. Для оси 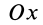
Согласно (5),
следовательно,
Аналогично, для осей 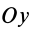
Окончательно
По формулам (13) можно вычислить моменты силы относительно прямоугольных осей координат.
По этим формулам получаются необходимые знаки для 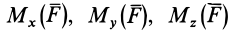
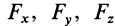
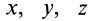
При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т. е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плоскостью.
Момент пары сил. Сложение пар сил. Равновесие пар сил
При изучении теоретической механики необходимо совершенно отчетливо уяснить, что в статике рассматриваются два простейших элемента: сила и пара сил. Любые две силы, кроме сил, образующих пару, всегда можно заменить одной —сложить их (найти равнодействующую). Пара сил нс поддается дальнейшему упрощению, она не имеет равнодействующей и является простейшим элементом.
Действие пары сил на тело характеризуется ее моментом — произведением одной из сил пары на ее плечо (на кратчайшее расстояние между линиями действия сил, образующих пару).
Единицей момента пары сил в Международной системе служит 1 нм (ньютон-метр = 1 н-1ж), а в системе МКГСС (технической)— 1 кГ-м.
Несколько пар сил, действующих на тело в одной плоскости, можно заменить одной парой сил (равнодействующей парой), момент которой равен алгебраической сумме моментов данных пар:
При равновесии пар сил
Если пары сил действуют в одной плоскости, то при решении задач достаточно рассматривать моменты пар как алгебраические величины. Причем знак момента определяется в зависимости от направления вращающего действия пары сил.
Дальнейшее изложение основано на правиле, т. е. считается момент положительным, если пара сил действует против хода часовой стрелки, если же пара сил действует на тело но ходу часовой стрелки, то момент считается отрицательным.
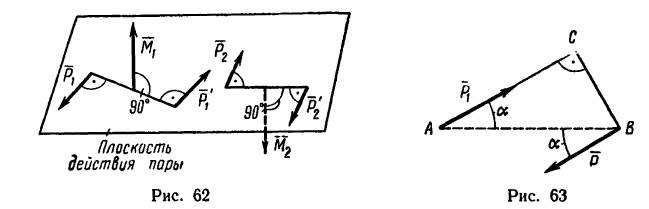
В том случае когда пары сил действуют на тело будучи расположенными в различных плоскостях, гораздо удобнее рассматривать пару сил как вектор, направленный перпендикулярно
к плоскости действия пары сил (рис. 62). Направление вектора в зависимости от направления вращательного действия пары определяется по направлению движения винта с правой нарезкой.
Задача 1.
Определить момент пары сил (рис. 63), если 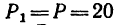
Решение.
1. При определении момента пары сил нужно прежде всего правильно определить плечо пары. При этом необходимо различать следующие понятия: плечо пары сил и расстояние между точками приложения сил нары.
Так как в механике твердого тела сила—скользящий вектор, то действие силы не изменяется при переносе точки ее приложения вдоль линии ее действия. Значит расстояние между точками приложения сил, образующих пару, можно изменять неограниченно. Но плечо пары при этом переносе остается неизменным.
В частном случае расстояние между точками приложения сил, образующих пару, может быть равно плечу.
Чтобы определить плечо данной пары из точки приложения одной из сил, например из точки В, восставим перпендикуляр ВС к линии действия другой силы. Расстояние ВС и есть плечо данной пары сил. Расстояние между точками приложения сил, образующих пару, АВ=0,5 м.
Легко видеть, что
2. Найдем момент пары сил:
Задача 2.
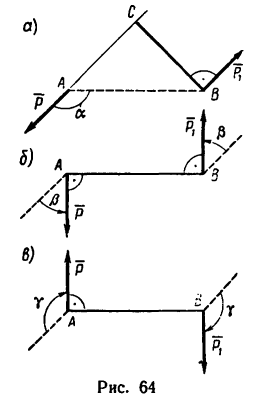
Как изменится момент пары сил 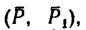
повернуть силы 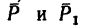
1. Найдем момент пары при заданном положении ее сил (рис. 64, а).
Из точки В восставим перпендикуляр ВС к линиям действия сил 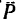
Момент пары при заданном положении сил
2. Повернем силы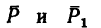
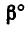
3. Сравнивая полученные результаты, видим, что после поворота сил момент пары увеличивается на 20—14,5 = 5,85 н-м.
4. Легко заметить, что силы 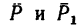
Момент пары сил изменяет свой знак.
Задача 3.
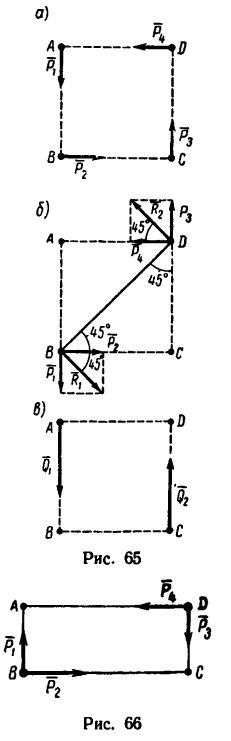
К точкам А, С и В, D, образующим вершины квадрата со стороной 0,5 м (рис. 65, а), приложены равные по модулю силы (Р = 12н) таким образом, что они образуют две пары сил
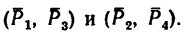
Решение 1.
Плечи у обеих пар сил равны стороне квадрата поэтому
Решение 2.
1. Перенесем силы 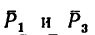
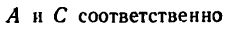
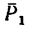
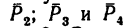
2. Сложим попарно эти силы у каждой из точек В и D. В обоих случаях
3. Силы R, модули которых теперь известны, направлены перпендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил 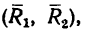
4. Найдем момент пары
и, следовательно,
Эту пару в соответствии со вторым решением можно представить в виде пары 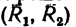
Но можно равнодействующую пару представить и в любом другом виде, например в виде сил Q = 24 и, приложенных к двум любым вершинам квадрата ABCD (рис. 65, в)
- Заказать решение задач по теоретической механике
Задача 4.
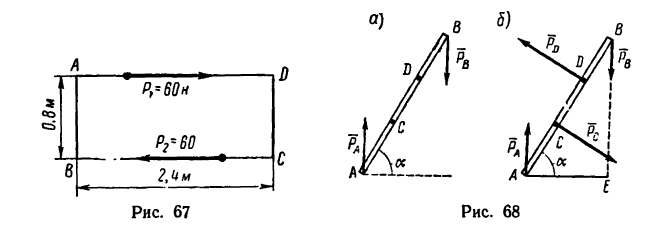
На прямоугольник ABCD (рис. 67) вдоль его длинных сторон действует пара сил 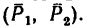
Решение.
1. Момент данной пары сил
необходимо уравновесить парой, момент которой обозначим Л1м. Тогда, согласно условию равновесия,
Откуда
2. Обозначив силы, образующие искомую пару 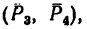
Отсюда
•Значит к прямоугольнику необходимо приложить пару сил с положительным (направленным против хода часовой стрелки) моментом, равным 48 н м. Силы, образующие эту пару, равняются
20 н каждая и одна из них должна действовать вдоль стороны АВ от А к В, вторая — вдоль стороны CD от С к D.
Задача 5.
Прямолинейный стержень АВ должен находиться в равновесии в положении, показанном на рис. 68, а (угол а = 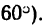
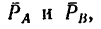
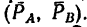
Решение.
1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары 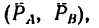
Так как пара 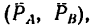
2. Применяем условие равновесия:
Или, подставив значения моментов,
где
Отсюда
Следовательно, в точках С и D необходимо приложить силы 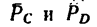
Момент силы относительно точки
Момент силы относительно точки при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.
Чтобы не допускать ошибок при определении моментов сил относительно точки, рекомендуется придерживаться следующего порядка:
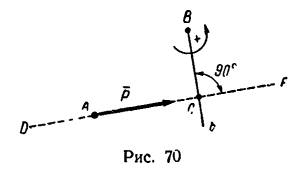
- Прежде всего нужно научиться «видеть» силу, момент которой определяем, и центр моментов — точку, относительно которой определяем момент (рис. 70 — сила
и центр моментов — точка В).
- Затем из центра момента проводим прямую ВЬ перпендикулярно к линии действия силы DF. Длина перпендикуляра ВС от центра момента до линии действия силы и есть плечо.
- Потом находим знак момента. При этом если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным (тоже правило, что и при определении знака момента пары сил).
- Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.
По рис. 70
В частном случае момент силы может равняться нулю. Это происходит тогда, когда центр моментов лежит на линии действия силы, при этом плечо равняется нулю. По рис. 70 момент силы 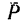
Задача 6.
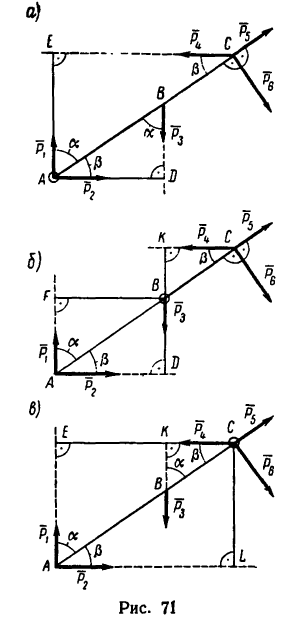
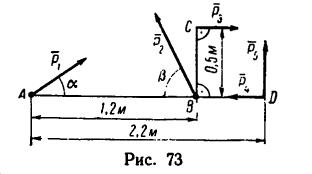
Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если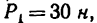
Решение 1 — определение моментов гнести заданных сил относительно точки А (рис. 71, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 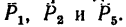
2. Находим момент силы 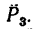
силы 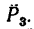
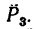
3. Величина момента отрицательная (сила 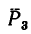
4. Находим момент силы 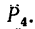
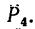
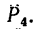
Величина момента положительная (плечо АЕ поворачивается около точки А силой 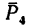
5. Находим момент силы 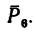
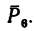
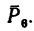
Решение 2 — определение моментов сил относительно точки В (рис. 71, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: 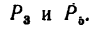
3. Находим момент силы 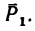
Величина момента отрицательная:
4. Находим момент силы 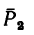
Момент отрицательный:
5. Находим момент силы 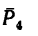
Величина момента положительная:
6. Находим момент силы 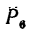
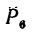
Решение 3 — определение моментов сил относительно точки С (рис. 71, в) рекомендуется выполнить самостоятельно.
Ответ.
В задаче силы расположены так, что либо их плечи определяются очень просто — как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
Задача 7.
Определить моменты относительно точки 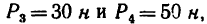

Решение.
1. Относительно точки А моменты сил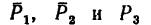
2. Находим момент силы 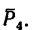
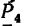
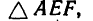
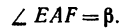
AF = AB — FB.
Величину FB находим из 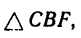
следовательно,
И теперь можем определить плечо АЕ:
Раскрываем скобки и заменяем
Момент положительный, следовательно:
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы 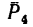
Разложим силу 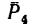
Модуль первой составляющей 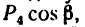
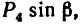
Применяя теорему Вариньона, получаем
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
- Аксиомы и теоремы статики
- Система сходящихся сил
- Плоское движение тела
- Принцип виртуальных перемещений
Моменты импульса и силы связаны между
собой важным соотношением, которое
называется уравнением моментов. Вначале
получим это соотношение для одной
материальной точки. С этой целью
продифференцируем момент импульса
(5.5) по времени
.
(5.9)
Учитывая, что
и
,
с учетом (5.1), получим
.
(5.10)
Это и есть уравнение моментов для одной
материальной точки.
Распространим теперь уравнение (5.10) на
систему материальных точек. Для этого
сложим все уравнения (5.10) для каждой
точки, понимая под М момент всех
действующих на нее сил, как внешних, так
и внутренних
.
(5.11)
Суммарный момент всех внутренних сил
равен нулю. Действительно, внутренние
силы входят в систему попарно. Эти силы
направлены противоположно и действуют
вдоль одной и той же прямой, поэтому
момент таких двух сил, а значит и момент
всех внутренних сил равны нулю. В
результате получаем уравнение моментов
для системы материальных точек:
,
(5.12)
где
— суммарный момент всех внешних сил,
—
момент импульса системы.
Таким образом, скорость изменения
момента импульса системы относительно
неподвижной точки (полюса) равна
результирующему моменту относительно
той же точки всех внешних сил, действующих
на систему.
Соотношение (5.12) справедливо, в частности,
для твердого тела, закрепленного в одной
точке. В этом случае оно выражает основной
закон динамики для тела, вращающегося
вокруг неподвижной точки. Из него
следует, что момент импульса является
основной динамической характеристикой
тела, вращающегося вокруг неподвижной
точки.
Из уравнения моментов (5.12) непосредственно
вытекает закон сохранения момента
импульса механической системы. Если
момент внешних сил равен нулю (),
то момент импульса системы остается
постоянным ().
Таким образом, момент импульса замкнутой
системы относительно произвольного
центра остается постоянным во времени.
Такова формулировка закона сохранения
момента импульса механической системы.
Этот закон, наряду с законами сохранения
импульса и энергии, является одним из
фундаментальных законов природы. В
теоретической механике, изучающей самые
общие законы движения, закон сохранения
момента импульса связывается с
изотропностью пространства, т.е. с
инвариантностью относительно вращений
пространства.
5.3. Момент силы и момент импульса относительно неподвижной оси
Следует различать и никоим образом не
смешивать понятия момента импульса и
момента силы относительно точки и
относительно оси. Момент вектора
относительно точки сам есть вектор,
тогда как момент вектора относительно
оси уже не является вектором.
М
Рис.5.4
оментом импульса
и моментом силы
относительно произвольной оси Z
называют проекции векторов
и
на эту ось в предположении, что точка О
(полюс) лежит на рассматриваемой оси
(рис.5.4).
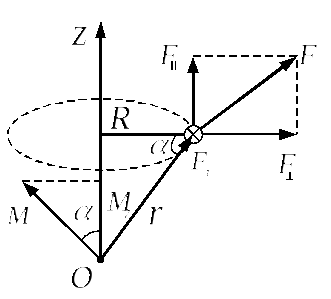
Покажем на примере момента силы, что
выбор точки на оси влияет на значение
,
но не влияет на значение
.
Будем полагать, что точка О, относительно
которой определен момент силы
,
расположена в произвольной точке на
оси вращения (рис.5.5). Разложим вектор
силы на три взаимно перпендикулярные
составляющие, две из которых,
||
и
,
параллельная и перпендикулярная оси
вращения, лежат в плоскости, проходящей
через ось вращения и точку приложения
силы, а третья
— перпендикулярна к этой плоскости
(обозначена на рисунке крестиком). Момент
силы
относительно
точки О равен сумме моментов составляющих:
.
В
Рис.5.5
екторное произведение направлено
перпендикулярно плоскости, в которой
лежат образующие его векторы. Векторы
||
и
перпендикулярны оси, и следовательно,
их проекции на эту ось равны нулю. Поэтому
.
(5.13)
Здесь
,
а
.
Окончательно, для момента силы относительно
оси вращения получаем:
,
(5.14)
где
—
радиус окружности с центром на оси OZ,
а
— касательная составляющая силы к этой
окружности.
Таким образом, момент силы относительно
оси характеризует способность силы
вращать тело вокруг этой оси. В соответствии
с правилом винта величина
положительна,
когда сила приводит к вращению тела
вокруг направления оси против часовой
стрелки, и отрицательна – при вращении
в противоположном направлении.
Проектируя векторное уравнение (5.12) на
ось ОZ, получим
.
(5.15)
Это уравнение называется уравнением
моментов относительно неподвижной оси.
Когда момент внешних сил относительно
какой-либо оси равен нулю, то момент
импульса системы относительно той же
оси остается постоянным. Это закон
сохранения момента импульса относительно
неподвижной оси.
Этот закон в сочетании с законом
сохранения механической энергии
эффективно используется при решении
задач на вращательное движение твердого
тела (см.5.8).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
Правила знаков для моментов и проекций сил на оси координат:
Правило знаков проекций сил
То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.
Другие видео
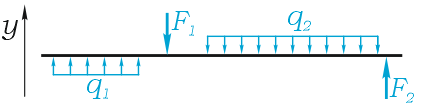
Например, для такой схемы нагружения:
уравнение суммы сил имеет вид
А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:
Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.
Правило знаков для моментов
Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.
Другие видео
Например, для суммы моментов относительно точки A
получаем
или, что одно и то же
Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.
При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее


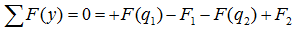
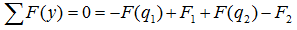
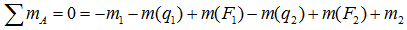
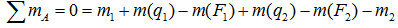

 ,
, 

 .
.  , то есть сила параллельна оси.
, то есть сила параллельна оси.  ,
,  — силы, составляющие пару;
— силы, составляющие пару;  — это главный вектор системы сил.
— это главный вектор системы сил.  — это главный момент системы сил.
— это главный момент системы сил.  ,
, 
 .
.  следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю: 

 .
.


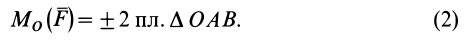
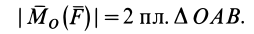

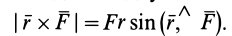
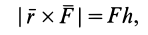
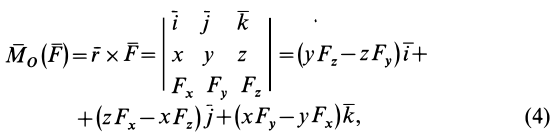
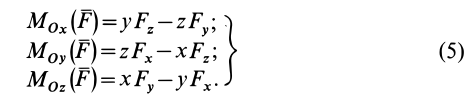
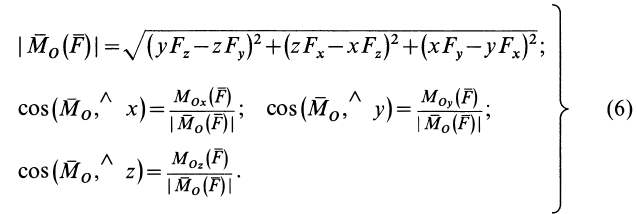
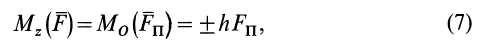
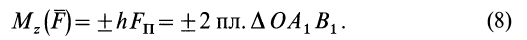
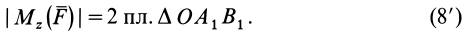
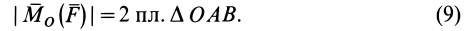
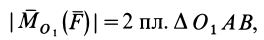
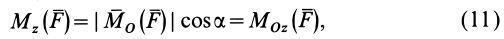
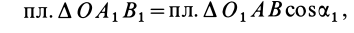
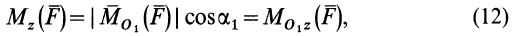
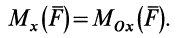
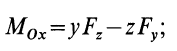
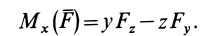
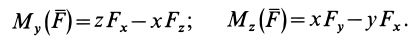
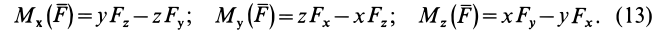
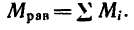
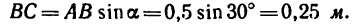
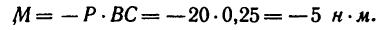
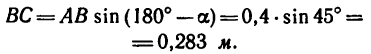
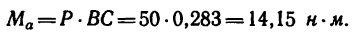
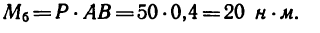
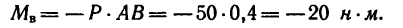
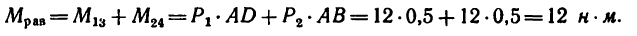
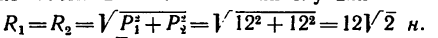
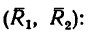
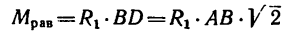
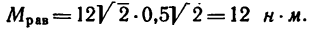
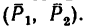
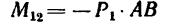
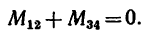
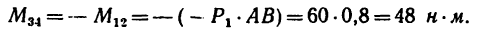
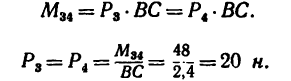
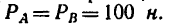
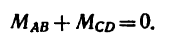
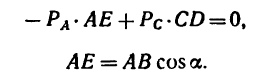
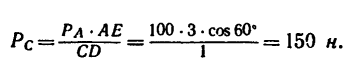
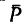 и центр моментов — точка В).
и центр моментов — точка В).