Как составить уравнение окружности проходящей через две точки - Исправление недочетов и поиск решений вместе с Examum.ru

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Уравнение окружности проходящей через две точки

Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).

Искомое уравнение имеет вид (x — a) 2 + (y — b) 2 = r 2 . Поскольку окружность проходит через заданные точки, координаты каждой из этих точек удовлетворяют уравнению окружности. Подставляя поочередно в искомое уравнение координаты данных точек, получим три уравнения для определения a, b и r. Вот эти уравнения:

Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем

Раскрывая скобки и упрощая, будем иметь

Отсюда . Подставляя эти значения a и b в первое из уравнений системы, получим . Искомое уравнение имеет вид

или после упрощений x 2 + y 2 + 3x + 9y — 10 = 0.

источники:

Написать уравнение окружности

http://www.pm298.ru/reshenie/iyfdg.php

Источник

Как составить уравнение окружности, проходящей через две заданные точки

Окружность — это геометрическая фигура, которая представляет собой множество точек на плоскости, находящихся на одинаковом расстоянии от определенной точки, называемой центром. Уравнение окружности позволяет определить все точки этой фигуры.

Для того чтобы составить уравнение окружности, проходящей через две заданные точки, необходимо решить систему уравнений, состоящую из уравнения окружности и уравнения прямой, проходящей через эти две точки.

Уравнение окружности

Уравнение окружности можно представить в виде:

(x-a)^2 + (y-b)^2 = r^2

где (a,b) — координаты центра окружности, а r — радиус окружности.

Уравнение прямой

Уравнение прямой можно представить в виде:

y = kx + b

где k — коэффициент наклона прямой, а b — свободный член.

Решение системы уравнений

Для того чтобы решить систему уравнений, необходимо подставить уравнение прямой в уравнение окружности, получив тем самым квадратное уравнение относительно x.

Далее необходимо решить это уравнение, получив два значения x и соответствующие им значения y. Эти две точки будут являться точками пересечения прямой и окружности.

Затем необходимо найти координаты центра окружности, используя формулы:

a = (x1 + x2) / 2

b = (y1 + y2) / 2

где (x1, y1) и (x2, y2) — координаты найденных точек пересечения.

Наконец, необходимо найти радиус окружности, используя формулу:

r = sqrt((x1-a)^2 + (y1-b)^2)

или r = sqrt((x2-a)^2 + (y2-b)^2)

Пример

Пусть даны две точки: (1,2) и (4,5). Необходимо найти уравнение окружности, проходящей через эти точки.

Решение

Найдем уравнение прямой, проходящей через эти точки:

k = (5-2)/(4-1) = 1

b = 2 - 1*1 = 1

y = x + 1

Подставим уравнение прямой в уравнение окружности:

(x-a)^2 + (y-b)^2 = r^2

(x-a)^2 + (x+1-1)^2 = r^2

x^2 - 2ax + a^2 + x^2 = r^2 - 2x + 1

2x^2 - 2ax + (a^2 - r^2 + 1) = 0

Решим полученное квадратное уравнение:

x1 = (2a + sqrt(8a-4(a^2-1)))/4 = 0.5a + 0.5sqrt(2a^2-1)

x2 = (2a - sqrt(8a-4(a^2-1)))/4 = 0.5a - 0.5sqrt(2a^2-1)

Найдем координаты центра окружности:

a = (1+4) / 2 = 2.5

b = (2+5) / 2 = 3.5

Найдем радиус окружности:

r = sqrt((0.5a + 0.5sqrt(2a^2-1) - a)^2 + (0.5a + 0.5sqrt(2a^2-1) + 1 - b)^2) = sqrt(18)/2

или r = sqrt((0.5a - 0.5sqrt(2a^2-1) - a)^2 + (0.5a - 0.5sqrt(2a^2-1) + 1 - b)^2) = sqrt(18)/2

Таким образом, уравнение окружности, проходящей через точки (1,2) и (4,5), будет:

(x-2.5)^2 + (y-3.5)^2 = 9

Источник

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Решение:

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

$[{(x - a)^2} + {(y - b)^2} = {R^2}]$

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

$[{(x - 5)^2} + {(y - ( - 1))^2} = {7^2},]$

$[{(x - 5)^2} + {(y + 1)^2} = 49.]$

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Решение:

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

$[R = AC = sqrt {{{({x_C} - {x_A})}^2} + {{({y_C} - {y_A})}^2}} ]$

$[R = AC = sqrt {{{(3 - 8)}^2} + {{( - 6 - ( - 3))}^2}} = sqrt {25 + 9} = sqrt {34} ,]$

$[{R^2} = 34.]$

Следовательно, уравнение данной окружности

$[{(x - 8)^2} + {(y + 3)^2} = 34.]$

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Решение:

$[{x_O} = frac{{{x_A} + {x_B}}}{2},{y_O} = frac{{{y_A} + {y_B}}}{2}]$

$[{x_O} = frac{{ - 4 + 6}}{2} = 1,{y_O} = frac{{ - 9 + 5}}{2} = - 2]$

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

$[R = OA = sqrt {{{({x_A} - {x_O})}^2} + {{({y_A} - {y_O})}^2}} ]$

$[R = OA = sqrt {{{( - 4 - 1)}^2} + {{( - 9 - ( - 2))}^2}} = sqrt {25 + 49} = sqrt {74} ,]$

$[{R^2} = 74.]$

Таким образом, уравнение окружности с диаметром AB —

$[{(x - 1)^2} + {(y + 2)^2} = 74.]$

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Решение:

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

получаем систему уравнений:

$[left{ begin{array}{l} {(4 - a)^2} + {( - 5 - b)^2} = {R^2}\ {(8 - a)^2} + {(3 - b)^2} = {R^2}\ {( - 8 - a)^2} + {(11 - b)^2} = {R^2} end{array} right.]$

$[{(4 - a)^2} + {( - 5 - b)^2} = {(8 - a)^2} + {(3 - b)^2}]$

$[16 - 8a + {a^2} + 25 + 10b + {b^2} = 64 - 16a + {a^2} + 9 - 6b + {b^2}]$

Приравняем правые части 2-го и 3-го уравнений:

$[{(8 - a)^2} + {(3 - b)^2} = {( - 8 - a)^2} + {(11 - b)^2}]$

$[64 - 16a + {a^2} + 9 - 6b + {b^2} = 64 + 16a + {a^2} + 121 - 22b + {b^2}]$

Умножив уравнение

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

$[{(4 + 2)^2} + {( - 5 - 3)^2} = {R^2}]$

$[{(4 + 2)^2} + {( - 5 - 3)^2} = {R^2},]$

получаем R²=100.

Следовательно, уравнение окружности, проходящей через три данные точки —

$[{(x + 2)^2} + {(y - 3)^2} = 100.]$

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

$[{(x - 5)^2} + {(y - 2)^2} = 25.]$

Источник

Уравнение окружности с радиусом R и с центром в точке O(( x_0;y_0)) имеет вид: (( x-x_0 )^2 + ( y-y_0)^2 = R^2 ).

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается: (x^2+y^2=R^2).

Пример 1. Дано уравнение окружности: ((x-1)^2+(y+2)^2=4). Найдем центр и радиус.

Решение: Центр этой окружности – точка (C(1;-2)), радиус (R=2).

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида (Ax + By + C = 0), где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при (b≠0) можно привести к виду:

(y = kx + b), где (k) – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами ((a; 0) и (0; b)), то она может быть найдена, используя формулу уравнения прямой в отрезках: (frac{x}{a}+frac{y}{b}=1).

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки (A(x_1;y_1)) и (B(x_2; y_2)), такие, что (x_1 ≠ x_2 и y_1 ≠ y_2), то уравнение прямой можно найти, используя следующую формулу: (frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}).

Пример 2. Составим общее уравнение прямой, которая в прямоугольной системе координат проходит через две точки (M_1(1;1)) и (M_2(4;2)).

Решение: Сначала напишем уравнение прямой, проходящей через две заданные точки. Оно имеет вид (frac{x-1}{4-1}=frac{y-1}{2-1} Leftrightarrow frac{x-1}3=frac{y-1}1). Теперь приведем полученное уравнение к требуемому виду: (frac{x-1}3=frac{y-1}1 Leftrightarrow 1cdot (x-1)=3cdot(y-1) Leftrightarrow x-3y+2=0).

Источник

Уравнение окружности

Пусть
окружность имеет радиус
,
а ее центр находится в точке
.
Точка
лежит на окружности тогда и только
тогда, когда модуль вектораравен,
то есть.
Последнее равенство выполнено тогда и
только тогда, когда

(1)

Уравнение
(1) и является искомым уравнением
окружности.

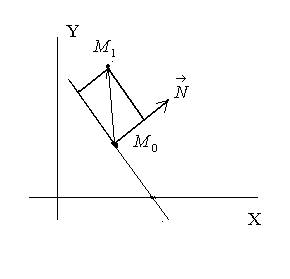
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору

Пусть
прямая проходит через точку

перпендикулярно вектору
.

Точка
лежит на прямой тогда и только тогда,
когда векторы
иперпендикулярны. Векторыиперпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю, то есть.
Используя формулу вычисления скалярного
произведения векторов, заданных своими
координатами, уравнение искомой прямой
записываем в виде

(2)

Рассмотрим
пример. Найти
уравнение прямой, проходящей через

середину
отрезка АВ перпендикулярно этому отрезку
если координаты точек соответственно
равны А(1;6), В(5;4).

Будем
рассуждать следующим образом. Чтобы
найти уравнение прямой мы должны знать
точку, через которую эта прямая проходит,
и вектор перпендикулярный этой прямой.
Вектором, перпендикулярным данной
прямой, будет вектор
,
поскольку, по условию задачи, прямая
перпендикулярна отрезку АВ. Точкуопределим
из условия, что прямая проходит через
середину АВ. Имеем
.
Таким образоми уравнение примет вид.

Выясним
вопрос, проходит ли эта прямая через
точку М(7;3).

Имеем
,
значит, эта прямая не проходит через
указанную точку.

Уравнение прямой, проходящей через данную точку, параллельно данному вектору

Пусть
прямая проходит через точку

параллельно вектору
.

Точка
лежит на прямой тогда и только тогда,
когда векторы
иколинеарны. Векторыиколинеарны тогда и только тогда, когда
их координаты пропорциональны, то есть

(3)

Полученное
уравнение и является уравнением искомой
прямой.

Уравнение
(3) представим в виде

,
где
принимает любые значения.

Следовательно,
можем записать

,
где
(4)

Система
уравнений (4) называется параметрическими
уравнениями прямой.

Рассмотрим
пример. Найти
уравнение прямой, проходящей через
точки
.
Мы можем построить уравнение прямой,
если знаем точку и параллельный или
перпендикулярный ей вектор. Точек в
наличии целых две. Но если две точки
лежат на прямой, то вектор, их соединяющий
будет параллелен этой прямой. Поэтому
воспользуемся уравнением (3), взяв в
качестве вектора
вектор.
Получаем

(5)

Уравнение
(5) называется уравнением прямой,
проходящей через две данные точки.

Общее уравнение прямой

Определение.
Общим
уравнением линии первого порядка на
плоскости называется уравнение вида
,
где.

Теорема.
Всякая прямая на плоскости может быть
задана в виде уравнения линии первого
порядка, и всякое уравнение линии первого
порядка является уравнением некоторой
прямой на плоскости.

Первая
часть этой теоремы доказывается просто.
На всякой прямой можно указать некоторую
точку
перпендикулярный
ей вектор
.
Тогда, согласно (2), уравнение такой
прямой имеет вид.
Обозначим.
Тогда уравнение примет вид
.

Теперь
перейдем ко второй части теоремы. Пусть
имеется уравнение

,
где.
Будем считать для определенности.

Перепишем
уравнение в виде:

;

Рассмотрим
на плоскости точку
,
где.
Тогда полученное уравнение имеет вид
,
и является уравнением прямой, проходящей
через точку
перпендикулярно вектору
.
Теорема доказана.

В
процессе доказательства теоремы мы
попутно доказали

Утверждение.
Если имеется уравнение прямой вида
,
то вектор
перпендикулярен данной прямой.

Уравнение
вида
называется общим уравнением прямой на
плоскости.

Далее
выведем формулу
вычисления расстояния от произвольной
точки плоскости до прямой, заданной
общим уравнением.

Пусть
имеется прямая
и точка.
Требуется определить расстояние от
указанной точки до прямой.

Рассмотрим
произвольную точку
на прямой. Имеем.
Расстояниеот точкидо прямой равно модулю проекции векторана вектор
,
перпендикулярный данной прямой. Имеем

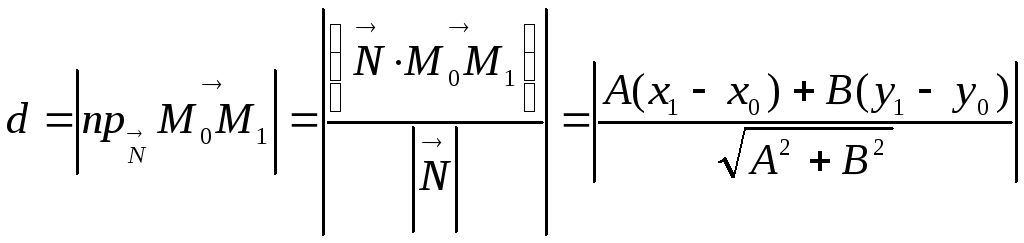
преобразуя,
получаем
формулу:

Пусть
даны две прямые, заданные общими
уравнениями

,
. Тогда векторы
перпендикулярны первой и второй прямой
соответственно. Уголмежду прямыми равен углу между векторами,.

Тогда
формула для определения угла между
прямыми имеет вид:

Условие
перпендикулярности прямых имеет вид:

Прямые
параллельны или совпадают тогда и только
тогда, когда векторы
колинеарны. При этомусловие
совпадения прямых имеет вид:
,

а
условие отсутствия пересечения
записывается в виде:
.
Последние два условия докажите
самостоятельно.

Исследуем
характер поведения прямой по ее общему
уравнению.

Пусть
дано общее уравнение прямой
.
Если,
то прямая проходит через начало координат.

Рассмотрим
случай, когда ни один из коэффициентов
не равен нулю
.
Уравнение перепишем в виде:

Где
.
Выясним смысл параметров
.
Найдем точки пересечения прямой с осями
координат. Приимеем,
а приимеем.
То есть— это отрезки, которые отсекает прямая
на координатных осях.Поэтому
уравнение
называется
уравнением прямой в отрезках.

В
случае
имеем
.
То есть прямая будет параллельна оси.
В случае
имеем
.
То есть прямая будет параллельна оси.

Напомним,
что угловым
коэффициентом прямой
называется тангенс угла наклона этой
прямой к оси.
Пусть прямая отсекает на осиотрезоки имеет угловой коэффициент.
Пусть точкалежит на данной

прямой.

Тогда
==.
И уравнение прямой запишется в виде

Пусть
прямая проходит через точку
и имеет угловой коэффициент.
Пусть точкалежит на этой прямой.

Тогда
=.

Полученное
уравнение называется уравнением прямой,
проходящей через данную точку с заданным
угловым коэффициентом.

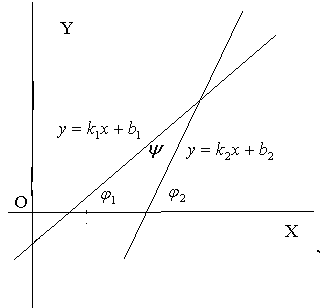
Пусть
даны две прямые
,.
Обозначим— угол между ними. Пусть,углы наклона к оси Х соответствующих
прямых

Тогда
=,.

Тогда
условие параллельности прямых имеет
вид
,
а условие перпендикулярности

В
заключение рассмотрим две задачи.

Задача.
Вершины треугольника АВС имеют координаты:
A(4;2),
B(10;10),
C(20;14).

Найти:
а) уравнение и длину медианы, проведенной
из вершины А;

б)
уравнение и длину высоты, проведенной
из вершины А;

в)
уравнение биссектрисы, проведенной из
вершины А;

Определим
уравнение медианы АМ.

Точка
М()
середина отрезка ВС.

Тогда

.
Следовательно, точка М имеет координаты
M(15;17).
Уравнение медианы на языке аналитической
геометрии это уравнение прямой, проходящей
через точку А(4;2) параллельно вектору
={11;15}.
Тогда уравнение медианы имеет вид.
Длина медианы АМ=.

Уравнение
высоты AS
— это уравнение прямой, проходящей через
точку А(4;2) перпендикулярно вектору
={10;4}.
Тогда уравнение высоты имеет вид
10(x-4)+4(y-2)=0,
5x+2y-24=0.

Длина
высоты — это расстояние от точки А(4;2) до
прямой ВС. Данная прямая проходит через
точку B(10;10)
параллельно вектору
={10;4}.
Ее уравнение имеет вид,
2x-5y+30=0.
Расстояние AS
от точки А(4;2) до прямой ВС, следовательно,
равно AS=.

Для
определения уравнения биссектрисы
найдем вектор
параллельный
этой прямой. Для этого воспользуемся
свойством диагонали ромба. Если от точки
А отложить единичные векторы одинаково
направленные с векторамии,
то вектор, равный их сумме, будет
параллелен биссектрисе. Тогда имеем=+.

={6;8},

,
={16,12},
.

Тогда
=В качестве направляющего вектора искомой
прямой может служить вектор={1;1},
коллинеарный данному. Тогда уравнение
искомой прямой имеет видилиx-y-2=0.

Задача.
Река протекает по прямой линии, проходящей
через точки А(4;3) и В(20;11). В точке С(4;8)
живет Красная Шапочка, а в точке D(13;20)
ее бабушка. Каждое утро Красная Шапочка
берет пустое ведро из дома, идет на реку,
черпает воду и относит ее бабушке. Найти
самую короткую дорогу для Красной
Шапочки.

Найдем точку Е,
симметричную бабушке, относительно
реки.

Для
этого сначала найдем уравнение прямой,
по которой течет река. Это уравнение
можно рассматривать, как уравнение
прямой, проходящей через точку А(4;3)
параллельно вектору
.
Тогда уравнение прямой АВ имеет вид.

Далее
найдем уравнение прямой DE,
проходящей через точку D
перпендикулярно АВ. Его можно рассматривать,
как уравнение прямой, проходящей через
точку D,
перпендикулярно вектору
.
Имеем

Теперь
найдем точку S
— проекцию точки D
на прямую АВ, как пересечение прямых АВ
и DE.
Имеем систему уравнений

Следовательно,
точка S
имеет координаты S(18;10).

Поскольку
S
середина отрезка DE,
то
.

Аналогично
.

Следовательно,
точка Е имеет координаты Е(23;0).

Найдем
уравнение прямой СЕ, зная координаты
двух точек этой прямой

Точку
М найдем как пересечение прямых АВ и
СЕ.

Имеем
систему уравнений

Следовательно,
точка М имеет координаты
.

Тема
2. Понятие
об уравнении поверхности в пространстве.
Уравнение сферы. Уравнение плоскости,
проходящей через данную точку,
перпендикулярно данному вектору. Общее
уравнение плоскости и его исследование
Условие параллельности двух плоскостей.
Расстояние от точки до плоскости. Понятие
об уравнении линии. Прямая линия в
пространстве. Канонические и параметрические
уравнения прямой в пространстве.
Уравнения прямой, проходящей через две
данные точки. Условия параллельности
и перпендикулярности прямой и плоскости.

Вначале,
дадим определение понятия уравнения
поверхности
в пространстве.

Пусть
в
пространстве
задана некотораяповерхность