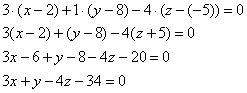Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения
Пусть задана точка M0(x0, y0, z0) и уравнение плоскости
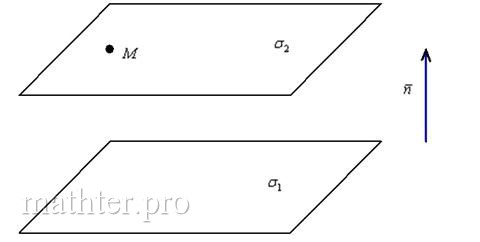
Наша задача найти уравнение плоскости, проходящей через точку M0 и параллельной плоскости (1)(Рис.1).
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (1):
Решим (2) относительно D:
Подставляя значение D из (3) в (1), получим:
Уравнение (4) можно представить также в следующем виде:
Уравнение (5) является уравнением плоскости, проходящей через точку M0(x0, y0, z0) и параллельной плоскости (1).
Пример 1.
Найти уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости :
Решение.
Запишем коэффициенты нормального вектора плоскости (6):
Подставляя координаты точки M0 и координаты нормального вектора в (3), получим:
Подставляя значения A, B, C, D в уравнение плоскости (1), получим:
Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:
Ответ.
Уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:
5.3.1. Как найти плоскость, параллельную данной?
Задача 137
Найти плоскость, проходящую через точку параллельно плоскости
.
Решение: Обозначим известную плоскость через . По условию требуется найти плоскость
, которая параллельна плоскости
и проходит через точку
. …Какие есть идеи? Немножко подумайте …
А ещё лучше выполнить схематический чертёж, который сразу поможет с идеей:
У параллельных плоскостей один и тот же вектор нормали. Добавить нечего =) Осталось оформить мат в два хода:
1) Из уравнения найдём нормальный вектор
.
2) Уравнение плоскости составим по точке
и вектору
:
Ответ:
Как выполнить проверку, я уже рассказал. Продолжаем раскидывать стог сена пространственной геометрии:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Уравнение плоскости, проходящей через заданную точку параллельно заданной плоскости.
В этой статье детально разобран процесс нахождения уравнения плоскости, проходящей через заданную точку трехмерного пространства параллельно заданной плоскости. После изложения необходимых теоретических основ приведены подробные решения характерных задач, в которых находится уравнение плоскости, проходящей через заданную точку пространства параллельно заданной плоскости.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную точку пространства параллельно заданной плоскости.
Задача нахождения уравнения плоскости, проходящей через заданную точку пространства параллельно заданной плоскости, возникает из следующей теоремы: через любую точку пространства, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной. Доказательство этой теоремы можно найти в учебнике геометрии для 10 — 1 1 классов, указанном в конце статьи.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней задана плоскость и точка , не лежащая в плоскости . Поставим перед собой задачу: написать уравнение плоскости , проходящей через точку параллельно плоскости .
Нам известно, что общее уравнение плоскости, проходящей через точку и имеющей нормальный вектор плоскости , имеет вид . Таким образом, мы сможем записать требуемое уравнение плоскости , если определим координаты ее нормального вектора.
При изучении темы «нормальный вектор плоскости» мы отметили, что нормальный вектор одной из двух параллельных плоскостей является нормальным вектором второй плоскости. Следовательно, в силу параллельности плоскостей и , нормальным вектором плоскости является любой нормальный вектор заданной плоскости . Таким образом, задача составления уравнения плоскости , проходящей через заданную точку М1 параллельно заданной плоскости , сводится к определению координат нормального вектора плоскости . В свою очередь координаты нормального вектора плоскости проще всего получить, если иметь перед глазами общее уравнение плоскости вида . В этом случае коэффициенты A , B , C перед переменными x , y , z являются соответствующими координатами нормального вектора плоскости .
Итак, запишем алгоритм нахождения уравнения плоскости , проходящей через заданную точку параллельно заданной плоскости :
- получаем общее уравнение плоскости в виде (если оно нам уже не дано в условии) и записываем ее нормальный вектор ;
- принимаем этот вектор в качестве нормального вектора плоскости ;
- записываем уравнение плоскости, проходящей через точку и имеющей нормальный вектор , в виде — это и есть искомое уравнение плоскости , проходящей через заданную точку параллельно заданной плоскости.
Следует заметить, что если точка М1 лежит в плоскости , то, действуя по записанному алгоритму, мы получим уравнение плоскости , которая совпадает с плоскостью .
Примеры составления уравнения плоскости, проходящей через заданную точку параллельно заданной плоскости.
Разберем решения нескольких примеров, в которых требуется составить уравнение плоскости, проходящей через заданную точку пространства параллельно заданной плоскости.
Начнем с самого простого случая, когда координаты нормального вектора плоскости очень легко находятся.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения
Наша задача найти уравнение плоскости, проходящей через точку M0 и параллельной плоскости (1)(Рис.1).
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (1):
Решим (2) относительно D:
Подставляя значение D из (3) в (1), получим:
| Ax+By+Cz−(Ax0+By0+Cz0)=0 | (4) |
Уравнение (4) можно представить также в следующем виде:
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (5) |
Уравнение (5) является уравнением плоскости, проходящей через точку M0(x0, y0, z0) и параллельной плоскости (1).
Найти уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости :
Запишем коэффициенты нормального вектора плоскости (6):
Подставляя координаты точки M0 и координаты нормального вектора в (3), получим:
Подставляя значения A, B, C, D в уравнение плоскости (1), получим:
Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:
Уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:
Помогите , пожалуйста : Напишите уравнение плоскости, если она проходит через точку B(3, — 2, 2) и : а) параллельна плоскости Oyz ; б) перпендикулярна оси Ox?
Алгебра | 10 — 11 классы
Помогите , пожалуйста : Напишите уравнение плоскости, если она проходит через точку B(3, — 2, 2) и : а) параллельна плоскости Oyz ; б) перпендикулярна оси Ox.
а) параллельна плоскости Oyz.
Уравнение плоскости, параллельной плоскостиyOz, имеет вид : Ax + D = 0.
Подставляя в него координаты точкиA, получим 3A + D = 0, илиD = — 3A.
Подставляя это значение вAx + D = 0, получимAx — 3A = 0, а сокращая наA, будем иметь окончательноx — 3 = 0.
Б) перпендикулярна оси Ox.
Так как плоскость перпендикулярна осиOx, то она параллельна плоскостиyOz, а потому ее уравнение имеет видAx + D = 0.
Подставляя в это уравнение координаты точкиA, получим, чтоD = — 3A.
Это значениеDподставим вAx + D = 0 и, сокращая наA, будем иметь окончательноx — 3 = 0.
Составить уравнение плоскости, которая проходит через точку М (3, 4, — 3) параллельно плоскости x + y + 7z = 0?
Составить уравнение плоскости, которая проходит через точку М (3, 4, — 3) параллельно плоскости x + y + 7z = 0.
Напишите уравнение прямой, параллельной оси ординат и проходящей через точку (3 ; 7)?
Напишите уравнение прямой, параллельной оси ординат и проходящей через точку (3 ; 7).
Составить уравнение плоскости проходящей через точки а( — 3 ; 2 ; 1) и в(4 ; — 1 ; 2) перпендикулярно плоскости 2x + 3y — 4z + 2 = 0?
Составить уравнение плоскости проходящей через точки а( — 3 ; 2 ; 1) и в(4 ; — 1 ; 2) перпендикулярно плоскости 2x + 3y — 4z + 2 = 0.
Если одна прямая параллельна плоскости а другая прямая параллельна этой же плоскости, необходимо ли, чтобы они были параллельны между собой?
Если одна прямая параллельна плоскости а другая прямая параллельна этой же плоскости, необходимо ли, чтобы они были параллельны между собой?
Нужна помощь?
1)Точка M не лежит в плоскости прямоугольника abcd.
Доказать что прямая CD параллельна плоскости ABM.
Помогите пожалуйста : Составить уравнение плоскости, проходящей через точки A(−3 ; 2 ; 1) и B(4 ; −1 ; 2) перпендикулярно плоскости 2x + 3y − 4z + 2 = 0?
Помогите пожалуйста : Составить уравнение плоскости, проходящей через точки A(−3 ; 2 ; 1) и B(4 ; −1 ; 2) перпендикулярно плоскости 2x + 3y − 4z + 2 = 0.
Даны плоскость α и точка A, не принадлежащая этой плоскости?
Даны плоскость α и точка A, не принадлежащая этой плоскости.
Как через точку A провести прямую a, параллельную плоскости α?
Запишите уравнение плоскости, если известно, что точка M0(1, 8, 1) является основанием перпендикуляра, опущенного из начала координат на эту плоскость?
Запишите уравнение плоскости, если известно, что точка M0(1, 8, 1) является основанием перпендикуляра, опущенного из начала координат на эту плоскость.
В ответ введите длину отрезка, отсекаемого найденной плоскостью от оси OX.
Уравнение прямой в декартовой плоскости : 2x — 3y + 5 = 0 Дайте уравнение линии, перпендикулярной к ней и проходящей через точку (5 ; — 4)?
Уравнение прямой в декартовой плоскости : 2x — 3y + 5 = 0 Дайте уравнение линии, перпендикулярной к ней и проходящей через точку (5 ; — 4).
1. ) График уравнения у + 12 = 0 на координатной плоскости расположен а) параллельно оси у и проходит через точку х = 12 б) параллельно оси у и проходит через точку х = — 12 в) параллельно оси х и про?
1. ) График уравнения у + 12 = 0 на координатной плоскости расположен а) параллельно оси у и проходит через точку х = 12 б) параллельно оси у и проходит через точку х = — 12 в) параллельно оси х и проходит через точку у = 12 г) параллельно оси х и проходит через точку у = — 12 2.
) Известно, что пара чисел (2 ; — 6) является решением уравнения 7х + ву — 2 = 0.
На этой странице находится ответ на вопрос Помогите , пожалуйста : Напишите уравнение плоскости, если она проходит через точку B(3, — 2, 2) и : а) параллельна плоскости Oyz ; б) перпендикулярна оси Ox?, из категории Алгебра, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Алгебра. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.
http://matworld.ru/analytic-geometry/uravnenie-ploskosti2-online.php
http://algebra.my-dict.ru/q/4798385_pomogite-pozalujsta-napisite-uravnenie-ploskosti-esli/
Задача 10598 Написать уравнение плоскости,…
Условие

Написать уравнение плоскости, параллельной плоскости 2х+у+3z+1=0 и проходящей через точку А(1;1;1).
математика 10-11 класс
1903
Решение
Ясно, что эта плоскость, действительно, параллельна данной, так как коэффициенты при переменных пропорциональны с k=1, но отношение свободных членов 1:(-6) не равно 1.
Ответ: 2x+y+3z-6=0
Написать комментарий
Материал из ALL
Перейти к: навигация, поиск
Уравнение плоскости, проходящей через точку параллельно плоскости, задаётся равенством нулю скалярного произведения вектора-разности радиусов-векторов точек и нормали к плоскости.
Обозначения
Введём обозначения:
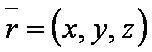
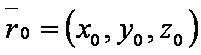
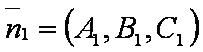
— уравнение плоскости.
Формулы:
Векторная форма:
Координатная форма:
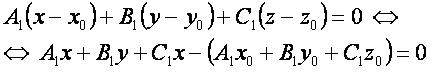
Другие уравнения:
- уравнение плоскости, проходящей через три точки;
- уравнение плоскости, равноудалённой от двух точек;
- уравнение плоскости, равноудалённой от двух прямых;
- уравнение плоскости, проходящей через две точки параллельно прямой;
- уравнение плоскости, проходящей через две точки перпендикулярно плоскости;
- уравнение плоскости, проходящей через точку и прямую;
- уравнение плоскости, проходящей через точку перпендикулярно прямой;
- уравнение плоскости, проходящей через точку параллельно плоскости;
- уравнение плоскости, проходящей через точку параллельно двум прямым;
- уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям;
- уравнение плоскости, проходящей через прямую параллельно прямой;
- уравнение плоскости, проходящей через прямую перпендикулярно плоскости.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Выгодский М. Я. Справочник по высшей математике. М.: Наука, 1964, стр.160.
- Участник:Logic-samara