Как составить уравнение плоскости по трем точкам онлайн калькулятор - Исправление недочетов и поиск решений вместе с Examum.ru

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Источник

Калькулятор онлайн.
Составить уравнение плоскости

Этот калькулятор онлайн составляет (находит) уравнение плоскости по трем точкам, лежащим на плоскости или по нормали и одной точке лежащей на плоскости.

Онлайн калькулятор для нахождения уравнения плоскости не просто даёт ответ задачи, он приводит подробное
решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )

Наши игры, головоломки, эмуляторы:

Немного теории.

Общее уравнение плоскости

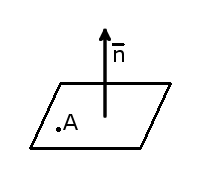
Пусть заданы:
прямоугольная система координат Oxyz,
произвольная плоскость ( pi );
точка ( M_0(x_0;y_0;z_0) in pi );
вектор ( vec{N}(A;B;C) ), перпендикулярный плоскости ( pi ) (смотри рисунок).

Рассмотрим произвольную точку М(х; у; z). Точка М лежит на плоскости ( pi ) тогда и только тогда, когда векторы
( vec{M_0M} ) и ( vec{N} ) взаимно перпендикулярны. Так как координаты вектора ( vec{M_0M} )
равны ( x-x_0, ; y-y_0, ; z-z_0 ) , то в силу условия перпендикулярности двух векторов (скалярное произведение
должно быть равно нулю) получаем, что точка М (х; у; z) лежит на плоскости ( pi ) тогда и только тогда, когда

( A(x-x_0)+B(y-y_0)+C(z-z_0)=0 tag{1} )

Это и есть искомое уравнение плоскости ( pi ), так как ему удовлетворяют координаты х; у; z любой точки М, лежащей на плоскости ( pi ),
и не удовлетворяют координаты никакой точки, не лежащей на этой плоскости.

Раскрывая скобки, приведем уравнение (1) к виду
( Ax+By+Cz+(-Ax_0-By_0-Cz_0)=0 )

Далее, обозначая число ( -Ax_0-By_0-Cz_0 ) через ( D ), получаем

( Ax +By+Cz+D=0 tag{2} )

Уравнение (2) называется общим уравнением плоскости. Таким образом, плоскость является поверхностью первого порядка, так как
определяется уравнением первой степени.

Верно и обратное: всякое уравнение первой степени вида (2) определяет в заданной прямоугольной системе координат плоскость.
Действительно, пусть заданы прямоугольная система координат Oxyz и уравнение ( Ax+By+Cz+D=0 ) с произвольными коэффициентами
А, В, С и D, причем из коэффициентов А, В и С хотя бы один отличен от нуля. Данное уравнение заведомо имеет хотя бы одно решение
( x_0, ; y_0, ; z_0 ) ( если, например, ( C neq 0 ), то, взяв произвольные х₀, и y₀, из уравнения получим:
( z_0 = -frac{A}{C}x_0 — frac{B}{C}y_0-frac{D}{C} ) ).

Таким образом, существует хотя бы одна точка M₀(x₀; y₀; z₀), координаты которой
удовлетворяют уравнению, т.е. Ax₀+By₀+Cz₀+D=0. Вычитая это числовое равенство из уравнения
Ax+By+Cz+D=0, получаем уравнение
A(x-x₀) + B(y-y₀) + C(z-z₀) + D=0,
эквивалентное данному. Полученное уравнение (а стало быть, и уравнение Ax+By+Cz+D=0 ) совпадает с уравнением (1) и, значит, определяет
плоскость ( pi ), проходящую через точку M₀(x₀ и перпендикулярную вектору ( vec{N}(A;B;C) ).

Вектор ( vec{N}(A;B;C) ), перпендикулярный плоскости, называется нормальным вектором или нормалью этой плоскости.

Теорема
Если два уравнения ( A_1x+B_1y+C_1z+D_1=0 ) и ( A_2x+B_2y+C_2z+D_2=0 ) определяют одну и ту же плоскость, то их коэффициенты
пропорциональны, т.е.
$$ frac{A_2}{A_1} = frac{B_2}{B_1} = frac{C_2}{C_1} = frac{D_2}{D_1} $$

Угол между двумя плоскостями

Рассмотрим две плоскости ( pi_1 ), и ( pi_2 ), заданные соответственно уравнениями

( A_1x+B_1y+C_1z+D_1=0, ;; A_2x+B_2y+C_2z+D_2=0 )

При любом расположении плоскостей ( pi_1 ), и ( pi_2 ) в пространстве один из углов ( varphi )
между ними равен углу между их нормалями ( vec{N_1}(A_1;B_1;C_1) ) и ( vec{N_2}(A_2;B_2;C_2) ) и вычисляется по
следующей формуле:
$$ cos varphi = frac{ vec{N_1} cdot vec{N_2}}{ |vec{N_1}| |vec{N_2}| } =
frac{A_1 A_2 + B_1 B_2 + C_1 C_2}{sqrt{A_1^2 + B_1^2 + C_1^2} ; sqrt{A_2^2 + B_2^2 + C_2^2} } tag{3} $$

Второй угол равен ( 180^circ -cos varphi )

Условие параллельности плоскостей

Если плоскости ( pi_1 ) и ( pi_2 ) параллельны, то коллинеарны их нормали ( vec{N_1} ) и
( vec{N_2} ), и наоборот. Но тогда
$$ frac{A_1}{A_2} = frac{B_1}{B_2} = frac{C_1}{C_2} tag{4} $$
Условие (4) является условием параллельности плоскостей ( pi_1 ) и ( pi_2 )

Условие перпендикулярности плоскостей

Если плоскости ( pi_1 ) и ( pi_2 ) взаимно перпендикулярны, то их нормали ( vec{N_1} ) и
( vec{N_2} ) также перпендикулярны, и наоборот. Поэтому из формулы (3) непосредственно получаем условие
перпендикулярности плоскостей ( pi_1 ) и ( pi_2 ):
( A_1 A_2 + B_1 B_2 + C_1 C_2 = 0 )

Источник

Уравнение плоскости по координатам трех точек: онлайн-калькулятор

Любая плоскость может быть проведена через три точки, не принадлежащие одной прямой. Автоматический сервис находит уравнение плоскости, которая проходит через эти три точки.

x-xay-yaz-zaxb-xayb-yazb-zaxc-xayc-yazc-za=0.

Чтобы решить уравнение плоскости по трем точкам онлайн, выполните простые действия:

впишите значения точек A, B, C в соответствующие пустые поля;
для получения решения воспользуйтесь кнопкой «Рассчитать».

Zaochnik предоставляет пошаговые вычисления и точный ответ бесплатно.

Уравнение плоскости онлайн по 3 точкам

Построить плоскость по уравнению онлайн понадобится:

студентам университетов при выполнении заданий по математическим дисциплинам;
школьникам, которые готовятся к поступлению в технические ВУЗы и участникам олимпиад;
преподавателям, проверяющим работы учащихся и составляющим задачи;
инженерам для облегчения процесса расчетов.

Цель сервиса – помощь в самостоятельных вычислениях учащимся. Автоматическая формула ускоряет получение ответа на задачу, позволяет избежать ошибок и не требует многократной перепроверки одних и тех же действий. Онлайн-калькулятор позволяет осуществлять подготовку к занятиям с усвоением непонятого ранее материала, запоминать и применять готовые алгоритмы решений.

Если возникла необходимость заказать услуги опытных преподавателей по решению уравнений или заданий на другие темы, обратитесь к консультанту. Мы гарантируем оперативный ответ и выгодное предложение.

Источник

В математике, плоскость — это плоская, двумерная поверхность, которая простирается бесконечно далеко

Общее уравнение плоскости выглядит так:

Плоскость может быть проведена через три не коллинеарные точки ( точки не лежат на одной прямой). И калькулятор ниже может это сделать. Вы вводите координаты трех точек, и калькулятор вычисляет уравнение плоскости, проходящей через эти три точки. Как всегда, объяснения и теорию вы можете найти ниже под калькулятором.

Уравнение плоскости по трем точкам

Первая точка

Вторая точка

Третья точка

Точность вычисления

Знаков после запятой: 2

Плоскость, проходящая через три точки

Зная три точки плоскости, мы знаем, что они удовлетворяют уравнению плоскости. Мы можем выразить это математически:
$ax_1+by_1+cz_1+d=0 \ ax_2+by_2+cz_2+d=0 \ ax_3+by_3+cz_3+d=0$

Точки нам даны, и коэффициенты a, b, c, d нужно найти. Это значит, что мы составляем систему из трех линейных уравнений с четырьмя переменными a, b, c, d:

$x_1a+y_1b+z_1c+d=0 \ x_2a+y_2b+z_2c+d=0 \ x_3a+y_3b+z_3c+d=0$

Или в матричной форме это будет выглядеть так:
$begin{array}{|cccc|} x_1 & y_1 & z_1 & 1 \ x_2 & y_2 & z_2 & 1 \ x_3 & y_3 & z_3 & 1\ end{array} * begin{array}{|c|} a \ b \ c \ d \ end{array} = begin{array}{|c|} 0 \ 0 \ 0 \ end{array}$

Хоть мы и имеем только три уравнения для трех неизвестных, это означает, что система уравнений имеет бесконечное множество решений; тем не менее мы все еще можем использовать этот калькулятор — Решение системы линейных алгебраических уравнений методом Гаусса для получения решения в стандартной форме с неизвестными переменнами ( это значит, что переменные могу принимать любое значение).

В нашем случае, мы имеет только одну независимую переменную. Если все координаты — целые числа, то калькулятор выбирает значение неизвестной переменной так, чтобы оно было наименьшим общим кратным (НОК) из всех знаменателей с другими коэффициентами, чтобы избавиться от фракций в ответе. Если координаты — не целые числа, значение независимой переменной нужно принять за 1.

Источник

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через три точки

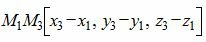
Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

Решение.

Уравнение плоскости, проходящей через точки A(x₁, y₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃) имеет следующий вид:

Подставляя координаты точек A, B, C в (1), получим:

Упростим:

Разложим определитель по первому столбцу:

Упростим выражение:

или

Ответ:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

Уравнение плоскости, проходящей через одну точку и имеющий нормаль n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

Решение.

Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) и имеющей нормаль n(A, B, C) имеет следующий вид:

Подставляя координаты векторов M₀ и n в (2), получим:

или

Источник