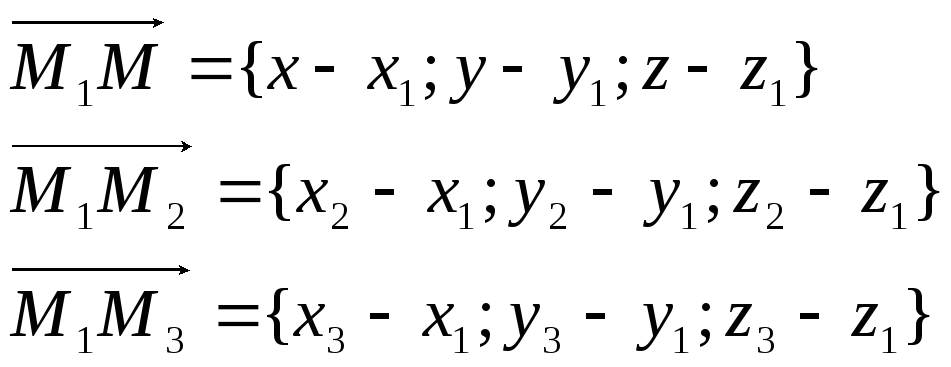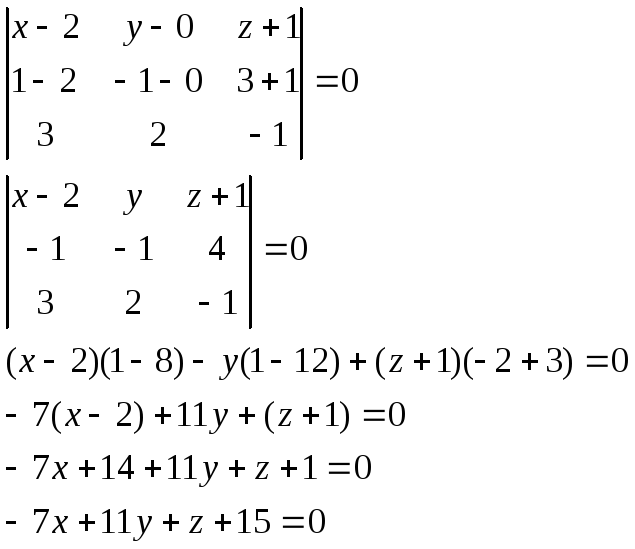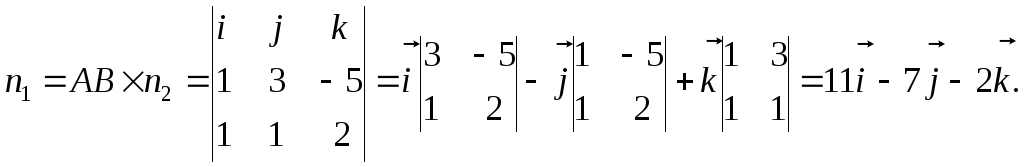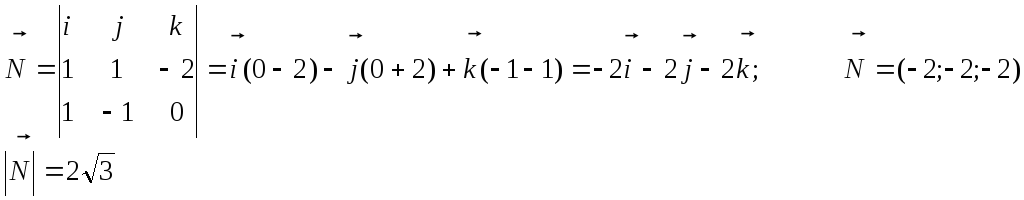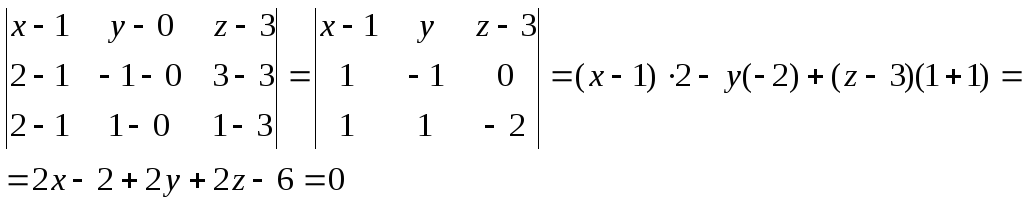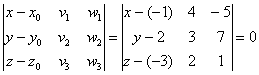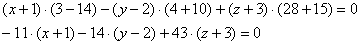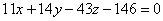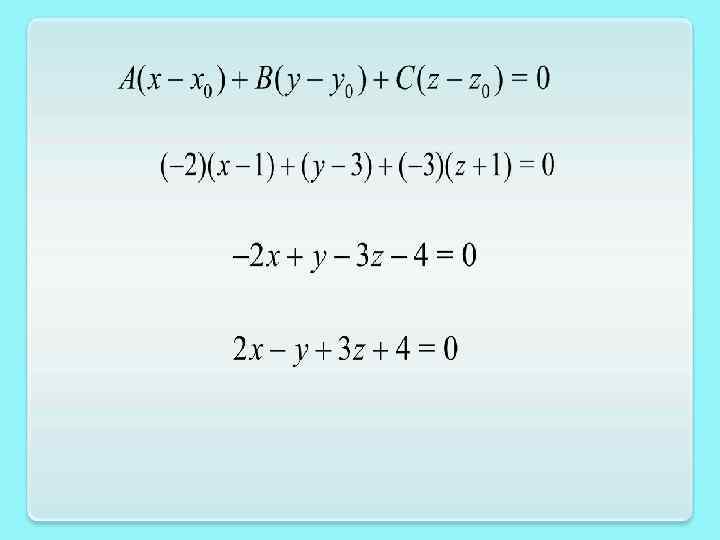Как составить уравнение плоскости проходящей через две точки параллельно вектору

6

Лекция
9.

Аналитическая
геометрия в пространстве.

Общее
уравнение плоскости.

Определение.
Плоскостью
называется
поверхность, все точки которой
удовлетворяют общему уравнению:

Ax
+ By
+ Cz
+ D
= 0,

где
А, В, С – координаты вектора
-вектор
нормали
к плоскости.

Возможны
следующие частные случаи:

А
= 0 – плоскость параллельна оси Ох

В
= 0 – плоскость параллельна оси Оу

С
= 0 – плоскость параллельна оси Оz

D
= 0 – плоскость проходит через начало
координат

А
= В = 0 – плоскость параллельна плоскости
хОу

А
= С = 0 – плоскость параллельна плоскости
хОz

В
= С = 0 – плоскость параллельна плоскости
yOz

А
= D
= 0 – плоскость проходит через ось Ох

В
= D
= 0 – плоскость проходит через ось Оу

С
= D
= 0 – плоскость проходит через ось Oz

А
= В = D
= 0 – плоскость совпадает с плоскостью
хОу

А
= С = D
= 0 – плоскость совпадает с плоскостью
xOz

В
= С = D
= 0 – плоскость совпадает с плоскостью
yOz

Уравнение
плоскости, проходящей через три точки.

Для
того, чтобы через три какие- либо точки
пространства можно было провести
единственную плоскость, необходимо,
чтобы эти точки не лежали на одной
прямой.

Рассмотрим
точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂),
M₃(x₃,
y₃,
z₃)
в декартовой системе координат.

Для
того, чтобы произвольная точка М(x,
y,
z)
лежала в одной плоскости с точками М₁,
М₂,
М₃
необходимо, чтобы векторы

были компланарны т.е. их смешанное
произведение:

()
= 0

Таким
образом,

Уравнение
плоскости, проходящей через три точки:

Уравнение
плоскости проходящей через две точки
параллельно вектору.

Пусть
заданы точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂)
и вектор
.

Составим
уравнение плоскости, проходящей через
данные точки М₁
и М₂
и произвольную точку М(х, у, z)
параллельно вектору
.

Векторы

и вектор

должны быть компланарны, т.е.

()
= 0

Уравнение
плоскости:

Уравнение
плоскости проходящей через точку
параллельно двум векторам.

Пусть
заданы два вектора

и
,
коллинеарные плоскости и точка М₁(х₁,
у₁,
z₁).
Тогда для произвольной точки М(х, у, z),
принадлежащей плоскости, векторы

должны быть компланарны.

Уравнение
плоскости:

Уравнение
плоскости проходящей через точку
перпендикулярной вектору.

Теорема.
Если в
пространстве задана точка М₀(х₀,
у₀,
z₀),
то уравнение плоскости, проходящей
через точку М₀
перпендикулярно вектору нормали
(A,
B,
C)
имеет вид:

A(x
– x₀)
+ B(y
– y₀)
+ C(z
– z₀)
= 0.

Доказательство.
Для произвольной точки М(х, у, z),
принадлежащей плоскости, составим
вектор
.
Т.к. вектор

— вектор нормали, то он перпендикулярен
плоскости, а, следовательно, перпендикулярен
и вектору
.
Тогда скалярное произведение

=
0

Таким
образом, получаем уравнение плоскости

Теорема
доказана.

Уравнение
плоскости в отрезках.

Если
в общем уравнении Ах + Ву + Сz
+ D
= 0 поделить обе части на -D

,

заменив
,
получим уравнение плоскости в отрезках:

Числа
a,
b,
c
отрезки отсекаемые плоскостью при
пересечении соответственно осей х, у,
z
декартовой прямоугольной системы
координат.

Уравнение
плоскости в векторной форме.

где

—
радиус- вектор текущей точки М(х, у, z),

— единичный вектор,
имеющий направление, перпендикуляра,
опущенного на плоскость из начала
координат.

,

и 
— углы, образованные этим вектором с
осями х, у, z.

p
– длина этого перпендикуляра.

В
координатах это уравнение имеет вид:

xcos
+ ycos
+ zcos
— p
= 0.

Параметрическое
уравнение плоскости

Пусть
в пространстве задана точка М₀(х₀,
у₀,
z₀)
и два неколлинеарных вектора

(p₁,
p₂,
p₃)
и
(q₁,
q₂,
q₃).
Пусть М(х, у, z)
текущая точка плоскости. Так как векторы

и

неколлинеарны, то они на плоскости
составляют базис, по которому разложим
вектор
=t+s,
где t,s
– параметры. Поместим произвольно на
плоскость декартову прямоугольную
систему координат так, что бы оси Ох и
Оу лежали в плоскости. Из центра О
проведем в точки М₀
и M
радиусы векторы

и
.
Тогда
=—и

=+t+s
.

Это
параметрическое уравнение плоскости
в векторной форме, а в скалярной форме

x=x₀
+p₁t
+ q₁
s

y=y₀
+p₂t
+ q₂
s

z=z₀
+p₃t
+ q₃
s

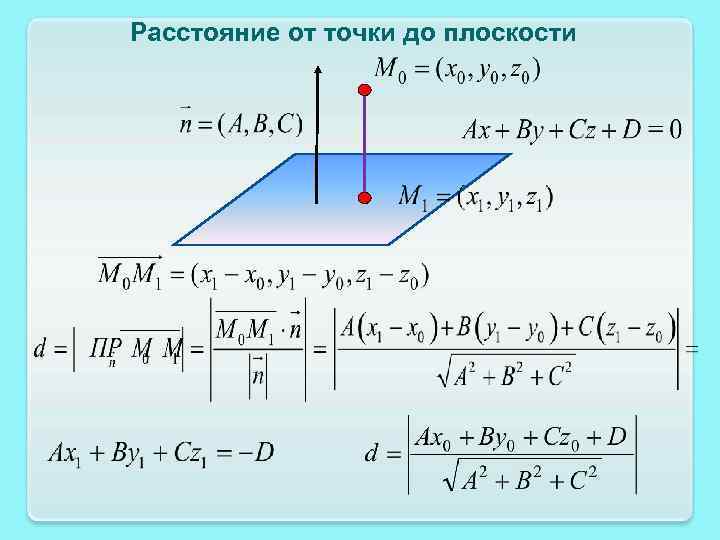
Расстояние от
точки до плоскости.

Расстояние
от произвольной точки М₀(х₀,
у₀,
z₀)
до плоскости Ах+Ву+Сz+D=0
равно:

Пример.
Найти уравнение плоскости, зная, что
точка Р(4; -3; 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Таким
образом, A
= 4/13; B
= -3/13; C
= 12/13, воспользуемся формулой:

A(x
– x₀)
+ B(y – y₀)
+ C(z – z₀)
= 0.

Пример.
Найти уравнение плоскости, проходящей
через две точки

P(2;
0; -1) и Q(1;
-1; 3) перпендикулярно плоскости 3х + 2у –
z
+ 5 = 0.

Вектор
нормали к плоскости 3х + 2у – z
+ 5 = 0
параллелен
искомой плоскости.

Получаем:

Пример.
Найти уравнение плоскости, проходящей
через точки А(2, -1, 4) и

В(3,
2, -1) перпендикулярно плоскости х
+ у
+ 2z
– 3 = 0.

Искомое
уравнение плоскости имеет вид: Ax
+ By
+ Cz
+ D
= 0, вектор нормали к этой плоскости
(A,
B,
C).
Вектор
(1,
3, -5) принадлежит плоскости. Заданная
нам плоскость, перпендикулярная искомой
имеет вектор нормали
(1,
1, 2). Т.к. точки А и В принадлежат обеим
плоскостям, а плоскости взаимно
перпендикулярны, то

Таким
образом, вектор нормали
(11,
-7, -2). Т.к. точка А принадлежит искомой
плоскости, то ее координаты должны
удовлетворять уравнению этой плоскости,
т.е. 112
+ 71
— 24
+ D
= 0; D
= -21.

Итак,
получаем уравнение плоскости: 11x
— 7y
– 2z
– 21 = 0.

Пример.
Найти уравнение плоскости, зная, что
точка Р(4, -3, 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Находим
координаты вектора нормали
=
(4, -3, 12). Искомое уравнение плоскости
имеет вид: 4x
– 3y
+ 12z
+ D
= 0. Для нахождения коэффициента D
подставим в уравнение координаты точки
Р:

16
+ 9 + 144 + D
= 0

D
= -169

Итак,
получаем искомое уравнение: 4x
– 3y
+ 12z
– 169 = 0

Пример.
Даны координаты вершин пирамиды

А₁(1;
0; 3), A₂(2;
-1; 3), A₃(2;
1; 1), A₄(1;
2; 5).

1. Найти
   длину ребра А₁А₂.

1. Найти
   угол между ребрами А₁А₂
   и А₁А₄.

Найти
угол между ребром А₁А₄
и гранью А₁А₂А₃.

Сначала
найдем вектор нормали к грани А₁А₂А₃
—
как векторное произведение векторов
и.

=
(2-1;
1-0; 1-3) = (1; 1; -2);

Найдем
угол между вектором нормали и вектором
.

-4
– 4 = -8.

Искомый
угол 
между вектором и плоскостью будет равен

= 90⁰
— .

1. Найти
   площадь грани А₁А₂А₃.

1. Найти
   объем пирамиды.

(ед³).

1. Найти
   уравнение плоскости А₁А₂А₃.

Воспользуемся
формулой уравнения плоскости, проходящей
через три точки.

2x
+ 2y
+ 2z
– 8 = 0

x
+ y
+ z
– 4 = 0;

5.2.1. Как составить уравнение плоскости
по точке и двум неколлинеарным векторам?

Конструировать уравнение будем с помощью векторов и точек. Их должно быть как можно меньше, но достаточно, чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность.

Казалось бы, плоскость можно однозначно определить с помощью двух неколлинеарных векторов. Но нет – векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка:

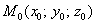
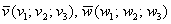
Уравнение плоскости, которая проходит через точку параллельно неколлинеарным векторам , выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так:
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (они будут «вертеться» вокруг точки и зададут целый «пучок» плоскостей).

Задача 130

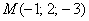
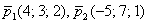
Составить уравнение плоскости по точке и неколлинеарным векторам .

Решение: искомое уравнение составим по формуле:

Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:

На первом месте у нас нарисовался знак «минус», и хорошим тоном считается его убрать (точно так же, как и у общего уравнения «плоской» прямой).

Меняем у каждого слагаемого знак и проводим дальнейшие упрощения:

, сократить здесь ничего нельзя, поэтому:

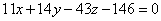
Ответ:

Как проверить задание? Для проверки пока не хватает информации, но мы обязательно выполним её чуть позже. Решаем самостоятельно:

Задача 131

Составить уравнение плоскости по векторам и принадлежащей ей точке .

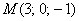
Кстати, если векторы коллинеарны, то и на этот случай есть корректный ответ

Уравнение плоскости, проходящей через две точки компланарно данному вектору

Согласно уравнению плоскости, проходящей через данную точку компланарно двум неколлинеарным векторам, уравнение плоскости, проходящей через M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂) компланарно вектору a=1, a₂, a₃>, который неколлинеарен вектору M₁M₂=2-x₁, y₂-y₁, z₂-z₁> имеет вид:

x-x1	y-y1	z-z1
x2-x1	y2-y1	z2-z1
a1	a2	a3

=0

Всё для учебы » Аналитическая геометрия » Уравнение плоскости, проходящей через две точки компланарно данному вектору

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Уравнения плоскости, компланарной двум неколлинеарным векторам

Напомним, что три или более векторов называются компланарными , если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам .

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим — радиус-векторы точек и (рис.4.16).

Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

Параметрическое уравнение плоскости

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и компланарны (см. разд. 1.3.2). Запишем условие компланарности: где — некоторые действительные числа (параметры). Учитывая, что получим векторное параметрическое уравнение плоскости :

где — направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

где и — координаты направляющих векторов и соответственно. Параметры в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины пропорциональны расстоянию от заданной точки до точки принадлежащей плоскости. При точка совпадает с заданной точкой . При возрастании (или ) точка перемещается в направлении вектора (или ), а при убывании (или ) — в противоположном направлении.

1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.

2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору для этой плоскости. Поэтому их скалярное произведение равно нулю:

Следовательно, координаты и направляющих векторов и плоскости и ее нормали связаны однородными уравнениями:

3. Направляющие векторы плоскости определяются неоднозначно.

4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:

1) найти любое решение уравнения определяя тем самым координаты точки принадлежащей плоскости;

2) найти любые два линейно независимых решения однородного уравнения определяя тем самым координаты решения и направляющих векторов и плоскости;

3) записать параметрическое уравнение (4.20).

5. Чтобы перейти от параметрического уравнения плоскости к общему , достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:

и записать общее уравнение плоскости в форме (4.14):

6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.

Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки и (см. рис.4.11). Требуется:

а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам и

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:

1) находим любое решение уравнения , например, следовательно, точка принадлежит плоскости;

2) находим два линейно независимых (непропорциональных) решения однородного уравнения например и следовательно, векторы являются направляющими для плоскости;

3) записываем параметрическое уравнение плоскости (4.20):

б) Координаты середины отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов и

Составляем уравнение (4.14):

Тот же результат можно получить, записывая уравнение (4.18):

Условие

Решение

Написать комментарий

Аналитическая геометрия в пространстве

Уравнения плоскости в пространстве 1) Общее уравнение плоскости -нормальный вектор плоскости 2) Уравнение плоскости, проходящей через заданную точку перпендикулярно вектору 3) Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой

4) Уравнение плоскости, проходящей через заданную точку параллельно двум неколлинеарным векторам

Исследование общего уравнения плоскости -плоскость проходит через начало координат -плоскость параллельна оси Ох -плоскость параллельна (перпендикулярна Oz) осям Ох и Оу

Пример. Плоскость описана уравнением Определить ее расположение в ДСК -плоскость параллельна оси Оz и проходит через начало координат Вывод: плоскость проходит через ось Оz Пример. Написать уравнение плоскости, проходящей через точку и ось Ox

Уравнения прямой в пространстве 1) Общие уравнения прямой 2) Параметрические и канонические уравнения прямой, проходящей через точку параллельно вектору 3) Уравнение прямой через две точки и

Угол между плоскостями: любой из смежных двугранных углов, образованных этими плоскостями Условие параллельности плоскостей: Условие перпендикулярности плоскостей:

Угол между прямыми в пространстве: угол между их направляющими векторами Условие параллельности прямых: Условие перпендикулярности прямых :

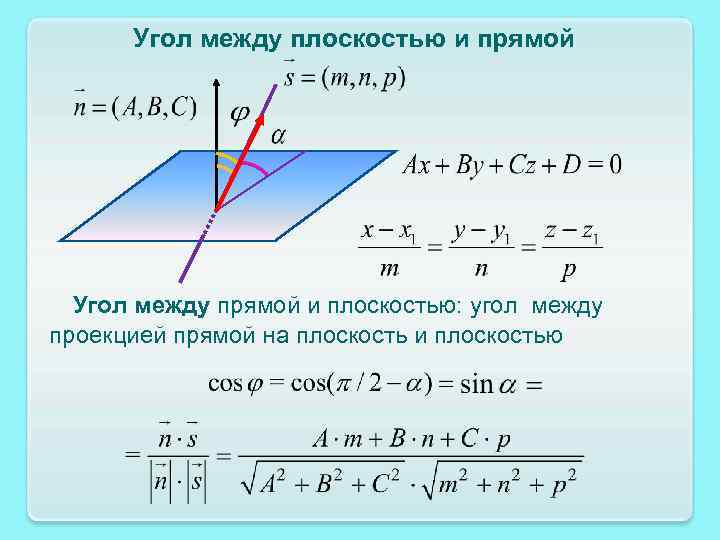
Угол между плоскостью и прямой Угол между прямой и плоскостью: угол между проекцией прямой на плоскость и плоскостью

Расстояние от точки до плоскости

Расстояние от точки до прямой

Пример. Найти уравнение плоскости, проходящей через точку и перпендикулярно отрезку , где

Пример. Найти уравнение плоскости, проходящей через точки

Пример. Найти координаты точки М пересечения плоскости прямой, проходящей через точку параллельно вектору и

Пример. Написать уравнение плоскости , проходящей через прямую и параллельно вектору

Пример. Найти величину угла между прямыми и

Пример. Найти расстояние между параллельными плоскостями 2 x-3 y+4 z-6=0 и -2 x+3 y-4 z+35=0.

Пример. Написать уравнение плоскости, проходящей через линию пересечения плоскостей и перпендикулярно к плоскости

Пример. Найти точку пересечения двух прямых

Пример. Записать уравнение прямой, проходящей через точку А(0, 2, 1) и образующей равные углы с векторами

Пример. Найти проекцию точки M(2, 3, -4) на прямую

Пример. Доказать, что прямые и параллельны и написать уравнение плоскости, в которой они расположены.

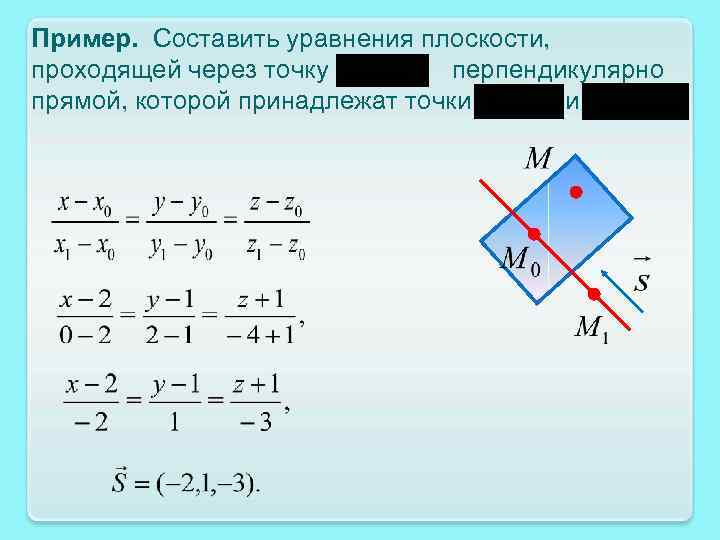
Пример. Составить уравнения плоскости, проходящей через точку перпендикулярно прямой, которой принадлежат точки и

• 
  
  

Составить уравнение плоскости, проходящей через точки М1(2;-1;3), М2(3;1;2), параллельно вектору а={3;-1;-4}