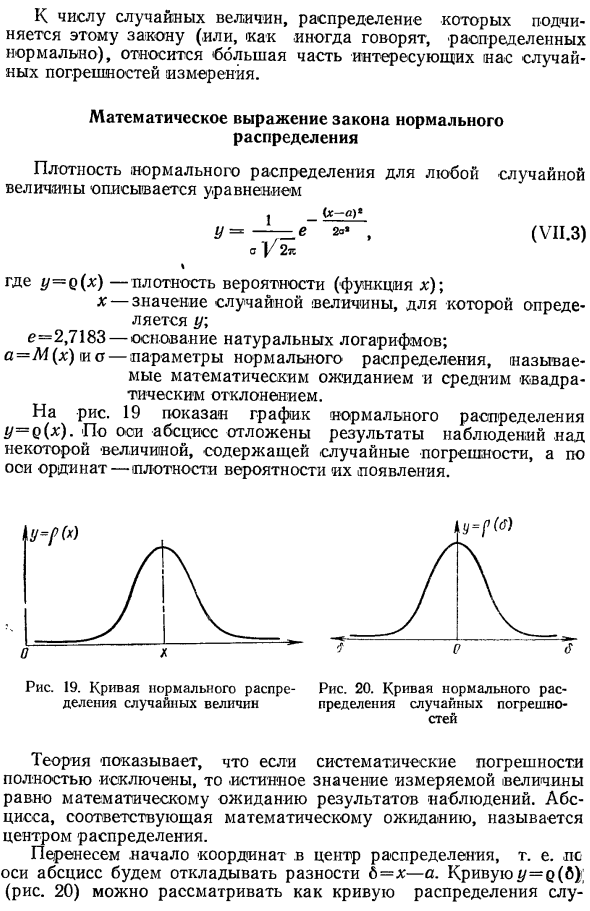
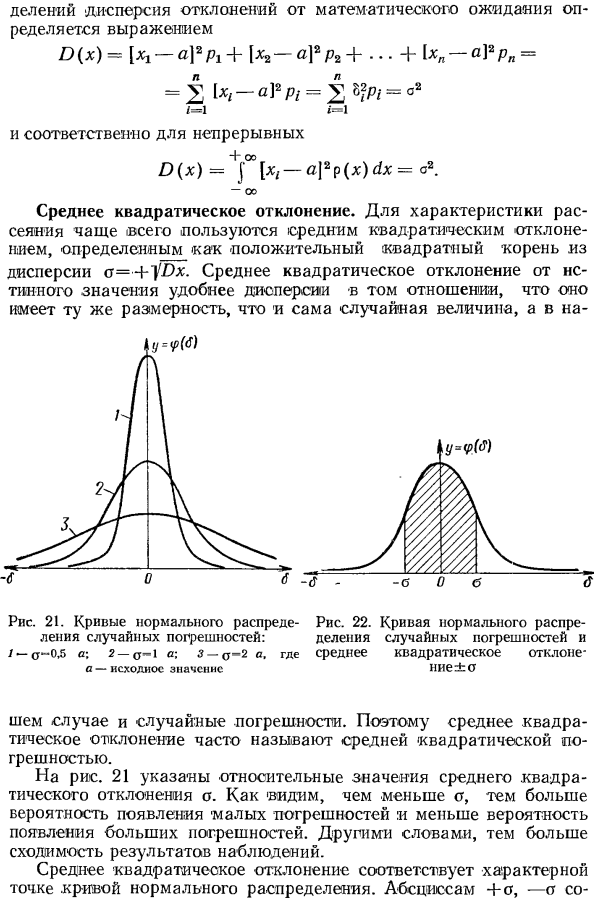
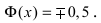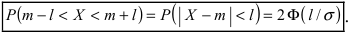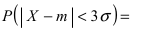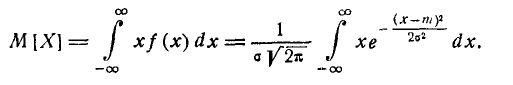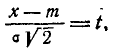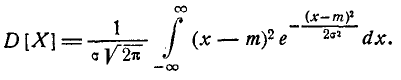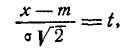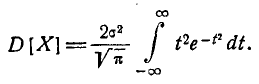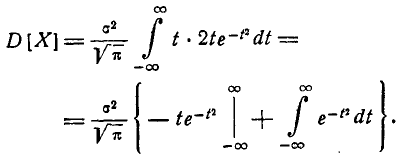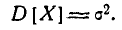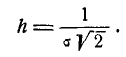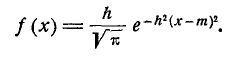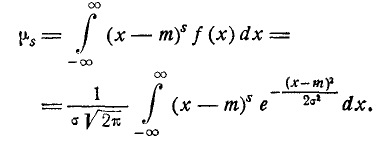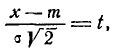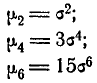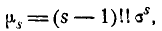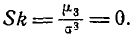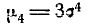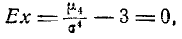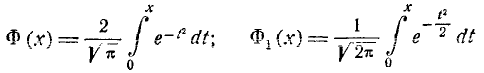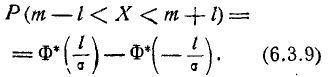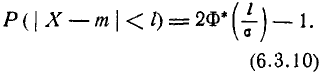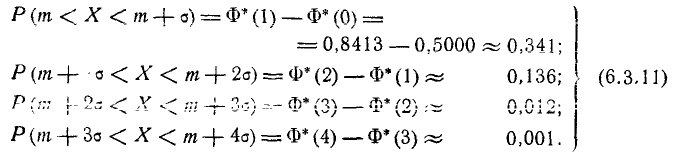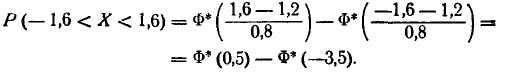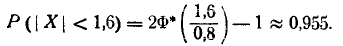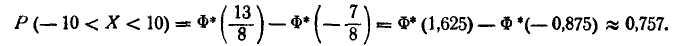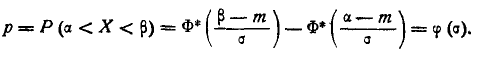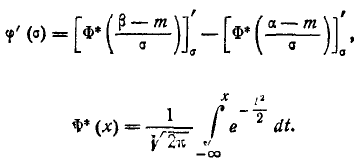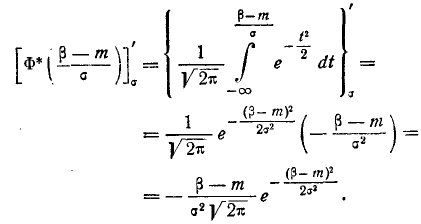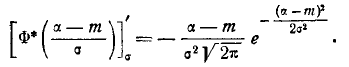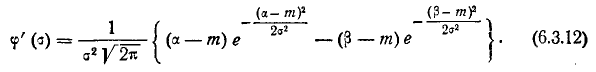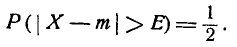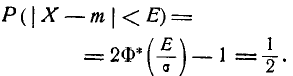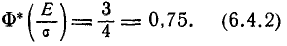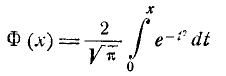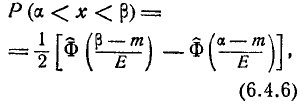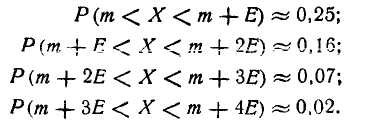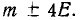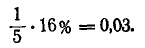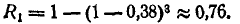Нормальное распределение
Время на прочтение
7 мин
Количество просмотров 36K
Автор статьи: Виктория Ляликова
Нормальный закон распределения или закон Гаусса играет важную роль в статистике и занимает особое положение среди других законов. Вспомним как выглядит нормальное распределение
где a -математическое ожидание, — среднее квадратическое отклонение.
Тестирование данных на нормальность является достаточно частым этапом первичного анализа данных, так как большое количество статистических методов использует тот факт, что данные распределены нормально. Если выборка не подчиняется нормальному закону, тогда предположении о параметрических статистических тестах нарушаются, и должны использоваться непараметрические методы статистики
Нормальное распределение естественным образом возникает практически везде, где речь идет об измерении с ошибками. Например, координаты точки попадания снаряда, рост, вес человека имеют нормальный закон распределения. Более того, центральная предельная теорема вообще утверждает, что сумма большого числа слагаемых сходится к нормальной случайной величине, не зависимо от того, какое было исходное распределение у выборки. Таким образом, данная теорема устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведет к распределению, отличному от нормального.
Можно выделить следующие этапы проверки выборочных значений на нормальность
-
Подсчет основных характеристик выборки. Выборочное среднее, медиана, коэффициенты асимметрии и эксцесса.
-
Графический. К этому методу относится построение гистограммы и график квантиль-квантиль или кратко QQ
-
Статистические методы. Данные методы вычисляют статистику по данным и определяют, какая вероятность того, что данные получены из нормального распределения
При нормальном распределении, которое симметрично, значения медианы и выборочного среднего будут одинаковы, значения эксцесса равно 3, а асимметрии равно нулю. Однако ситуация, когда все указанные выборочные характеристики равны именно таким значениям, практически не встречается. Поэтому после этапа подсчета выборочных характеристик можно переходить к графическому представлению выборочных данных.
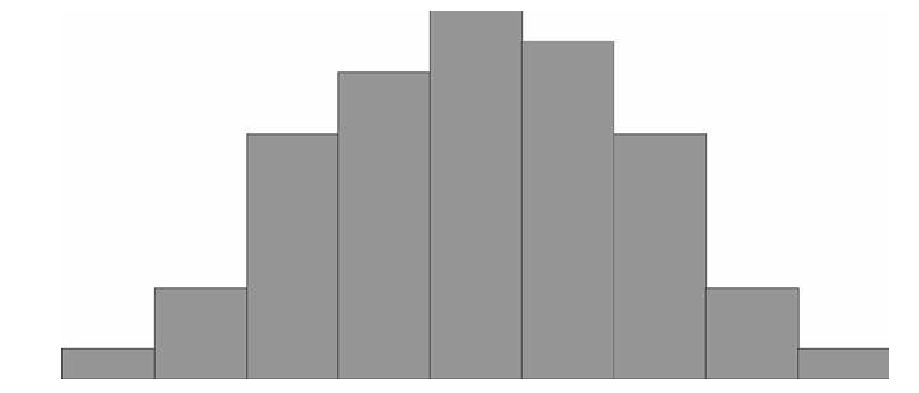
Гистограмма позволяет представить выборочные данные в графическом виде – в виде столбчатой диаграммы, где данные делятся на заранее определенное количество групп. Вид гистограммы дает наглядное представление функции плотности вероятности некоторой случайной величины, построенной по выборке.
График QQ (квантиль-квантиль) является графиком вероятностей, который представляет собой графический метод сравнения двух распределений путем построения их квантилей. QQ график сравнивает наборы данных теоретических и выборочных (эмпирических) распределений. Если два сравниваемых распределения подобны, тогда точки на графике QQ будут приблизительно лежать на линии y=x. Основным шагом в построении графика QQ является расчет или оценка квантилей.
Существует множество статистических тестов, которые можно использовать для проверки выборочных значений на нормальность. Каждый тест использует разные предположения и рассматривает разные аспекты данных.
Чтобы применять статистические критерии сформулируем задачу. Выдвигаются две гипотезы H0 и H1, которые утверждают
H0 — Выборка подчиняется нормальному закону распределения
H1 — Выборка не подчиняется нормальному распределению
Установи уровень значимости alpha=0,05.
Теперь задача состоит в том, чтобы на основании какого-то критерия отвергнуть или принять основную нулевую гипотезу при уровне значимости
Критерий Шапиро-Уилка
Критерий Шапиро-Уилка основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид
Числитель является квадратом оценки среднеквадратического отклонения Ллойда. Коэффициенты и критические
значения статистики являются табулированными значениями. Если
, то нулевая гипотеза нормальности распределения отклоняется на уровне значимости
.
В Python функция содержится в библиотеке scipy.stats и возвращает как статистику, рассчитанную тестом, так и значение p. В Python можно использовать выборку до 5000 элементов. Интерпретация вывода осуществляется следующим образом
Если значение , тогда принимается гипотеза H0, в противном случае, т.е. если,
, тогда принимается гипотеза H1, т.е. что выборка не подчиняется нормальному закону.
Критерий Д’Агостино
В данном критерии в качестве статистики для проверки нормальности распределения используется отношение оценки Даутона для стандартного отклонения к выборочному стандартному отклонению, оцененному методом максимального правдоподобия
В качестве статистики критерия Д’Агостино используется величина
значение которой рассчитывается на основе центральной предельной теоремы, которая утверждает, что при
гдестандартная нормальная случайная величина.
Критические значения являются табулированными значениями. Гипотеза нормальности принимается, если значение статистики лежит в интервале критических значений. Данный критерий показывает хорошую мощность против большого спектра альтернатив, по мощности немного уступая критерию Шапиро-Уилка.
В Python функция normaltest() также содержится в библиотеке scipy.stats и возвращает статистику теста и значение p. Интерпретация результата аналогична результатам в критерии Шапиро-Уилка.
Критерий согласия— Пирсона
Данный критерий является одним из наиболее распространенных критериев проверки гипотез о виде закона распределения и позволяет проверить значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Таким образом, данный критерий позволяет проверить гипотезу о принадлежности наблюдаемой выборки некоторому теоретическому закону. Можно сказать, что критерий является универсальным, так как позволяет проверить принадлежность выборочных значений практическому любому закону распределения.
Для решения задачи используется статистика — Пирсона
где — эмпирические частоты (подсчитывается число элементов выборки, попавших в интервал),
— теоретические частоты. Подсчитывается критическое значение
. Если
, отклоняется гипотеза о принадлежности выборки нормальному распределению и принимается, если
.
Теперь перейдем к практической части. Для демонстрации функций будем использовать Dataset, взятый с сайта kaggle.com по прогнозированию инсульта по 11 клиническим характеристикам.
Загружаем необходимые библиотеки
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as npЗагружаем датасет
data_healthcares = pd.read_csv('E:/vika/healthcare-dataset-stroke-data.csv')Набор состоит из 5110 строк и 12 столбцов.
Посмотрим на основные характеристики, каждого признака.data_healthcares.describe()
Из данных характеристик можно увидеть, что есть пропущенные значения в показателях индекс массы тела. Посчитаем количество пропущенных значений.
Если бы нам необходимо было делать модель для прогноза, то пропущенные значения bmi являются достаточно большой проблемой, в которой возникает вопрос как их восстановить. Поэтому будем предполагать, что значения столбца bmi (индекс массы тела) подчиняются нормальному закону распределения (предварительно был построен график распределения, поэтому сделано такое предположение). Но так как, на данный момент, у нас нет необходимости в построении модели для прогноза, то удалим все пропущенные значения
new_data=data_healthcares.dropna()
Теперь можем приступать к проверке выборочных значений показателя bmi на нормальность. Вычислим основные выборочные характеристики
|
Выборочная характеристика |
Код в python |
Значение характеристики |
|
Выборочное среднее |
new_data.bmi.mean() |
28,89 |
|
Выборочная медиана |
new_data.bmi.median() |
28,1 |
|
Выборочная мода |
new_data.bmi.mode() |
28,7 |
|
Выборочное среднеквадратическое отклонение |
new_data.bmi.std() |
7.854066729680458 |
|
Выборочный коэффициент асиметрии |
new_data.bmi.skew() |
1.0553402052962928 |
|
Выборочный эксцесс |
new_data.bmi.kurtosis() |
3.362659165623678 |
После вычислений основных характеристик мы видим, что выборочное среднее и медиана можно сказать принимают одинаковые значения и коэффициент эксцесса равен 3. Но, к сожалению коэффициент асимметрии равен 1, что вводить нас в некоторое замешательство, т.е. мы уже можем предположить, что значения bmi не подчиняются нормальному закону. Продолжим исследования, перейдем к построению графиков.
Строим гистограмму
fig = plt.figure
fig,ax= plt.subplots(figsize=(7,7))
sns.distplot(new_data.bmi,color='red',label='bmi',ax=ax)
plt.show()Гистограмма достаточно хорошо напоминает нормальное распределение, кроме конечно, небольшого выброса справа, но смотрим дальше. Тут скорее, можно предположить, что значения bmi подчиняются распределению .
Строим QQ график. В python есть отличная функция qqplot(), содержащаяся в библиотеке statsmodel, которая позволяет строить как раз такие графики.
from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
qqplot(new_data.bmi, line=’s’)
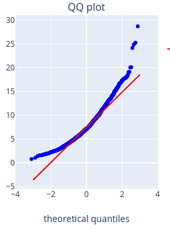
Pyplot.showЧто имеем из графика QQ? Наши выборочные значений имеют хвосты слева и справа, и также в правом верхнем углу значения становятся разреженными.
На основе данных графика можно сделать вывод, что значения bmi не подчиняются нормальному закону распределения. Рядом приведен пример QQ графика распределения хи-квадрат с 8 степенями свободы из выборки в 1000 значений.
Для примера построим график QQ для выборки из нормального распределения с такими же показателями стандартного отклонения и среднего, как у bmi.
std=new_data.bmi.std() # вычисляем отклонение
mean=new_data.bmi.mean() #вычисляем среднее
Z=np.random.randn(4909)*std+mean # моделируем нормальное распределение
qqplot(Z,line='s') # строим график
pyplot.show()Продолжим исследования. Перейдем к статистическим критериям. Будем использовать критерий Шапиро-Уилка и Д’Агостино, чтобы окончательно принять или опровергнуть предположение о нормальном распределении. Для использования критериев подключим библиотеки
from scipy.stats import shapiro
from scipy.stats import normaltest
shapiro(new_data.bmi)
ShapiroResult(statistic=0.9535483717918396, pvalue=6.623218133972133e-37)
Normaltest(new_data.bmi)
NormaltestResult(statistic=1021.1795052962864, pvalue=1.793444363882936e-222)После применения двух тестов мы имеем, что значение p-value намного меньше заданного критического значения alpha , значит выборочные значения не принадлежат нормальному закону.
Конечно, мы рассмотрели не все тесты на нормальности, которые существуют. Какие можно дать рекомендации по проверке выборочных значений на нормальность. Лучше использовать все возможные варианты, если они уместны.
На этом все. Еще хочу порекомендовать бесплатный вебинар, который 15 июня пройдет на платформе OTUS в рамках запуска курса Математика для Data Science. На вебинаре расскажут про несколько часто используемых подходов в анализе данных, а также разберут, какие математические идеи работают у них под капотом и почему эти подходы вообще работают так, как нам нужно. Регистрация на вебинар доступна по этой ссылке.
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
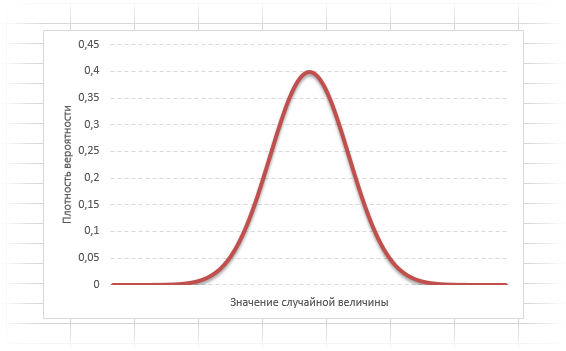
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
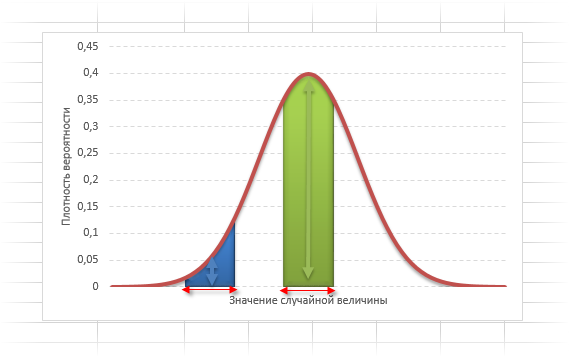
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
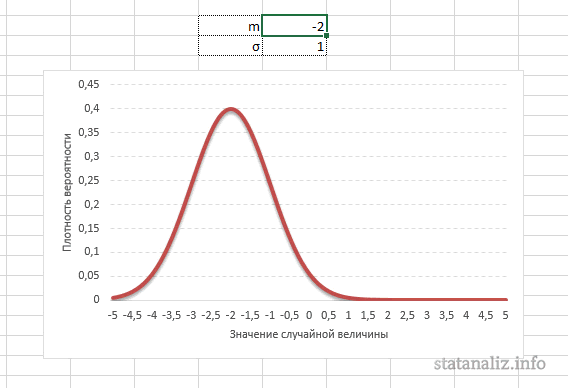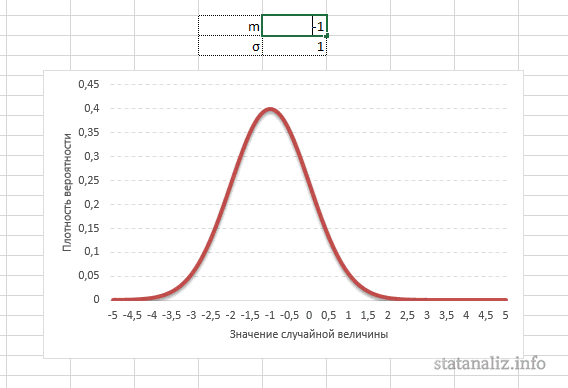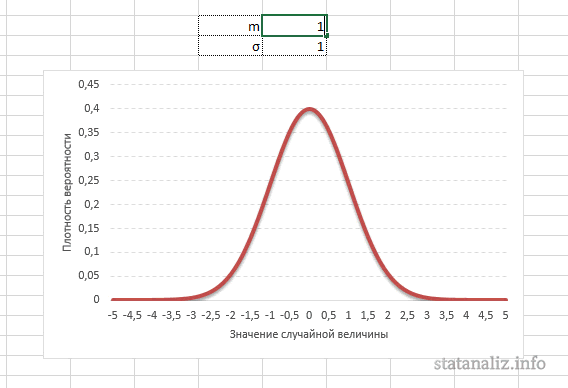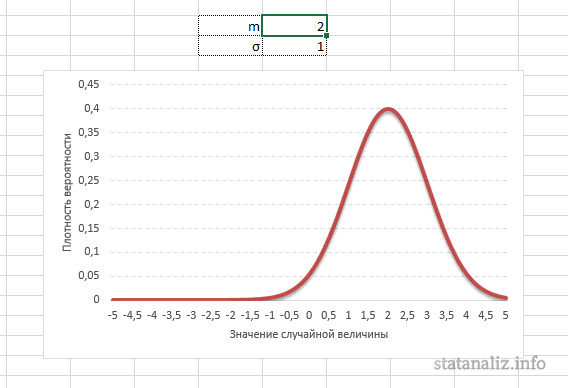
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
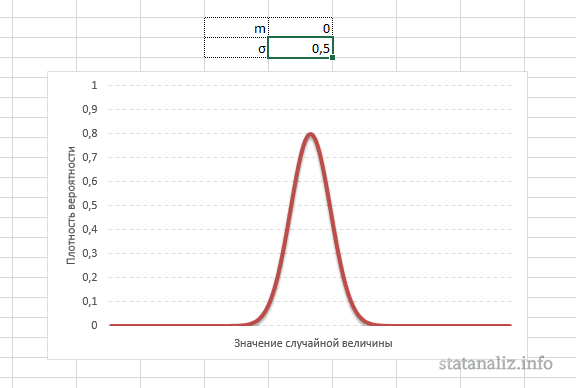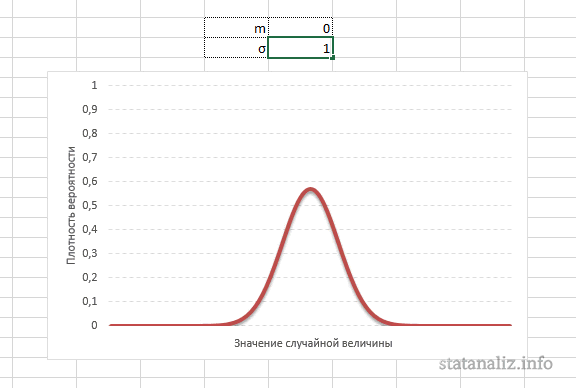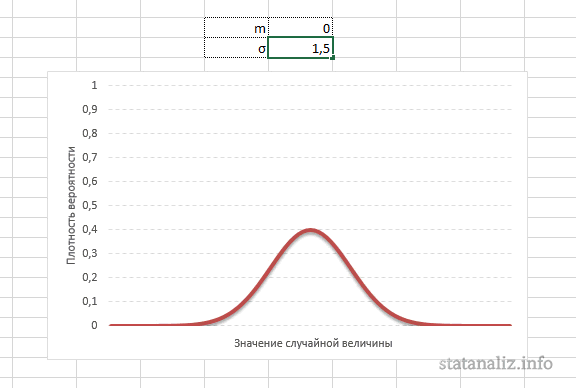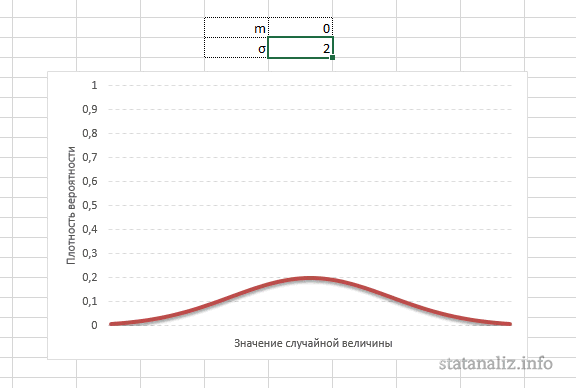
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
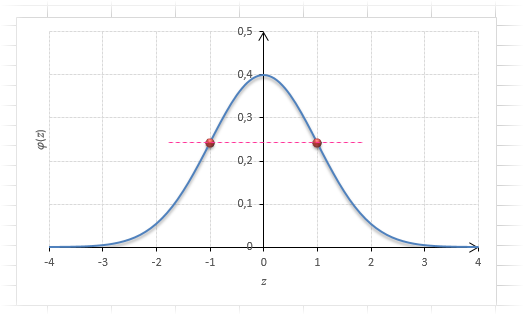
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
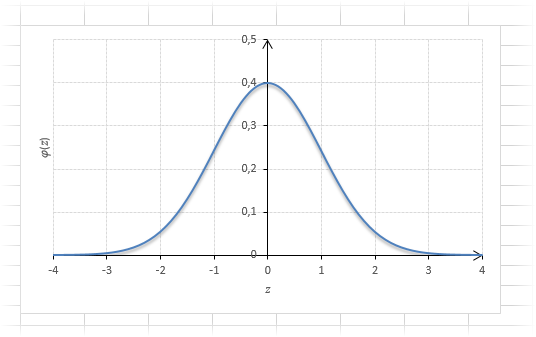
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
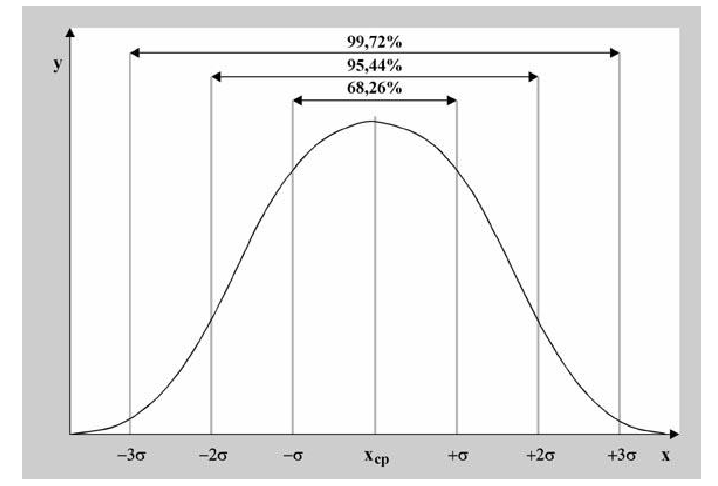
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
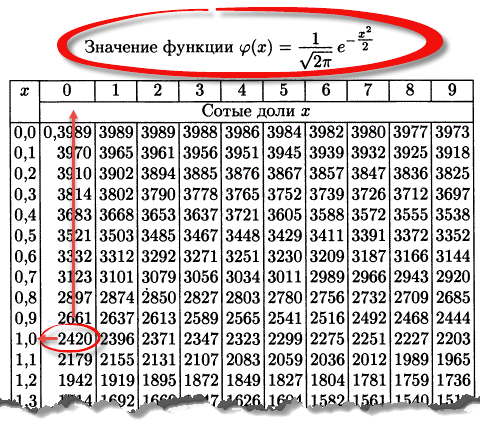
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
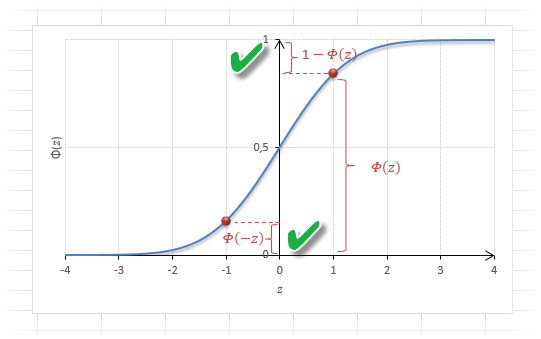
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
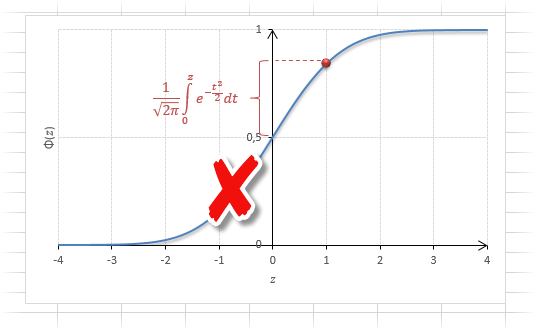
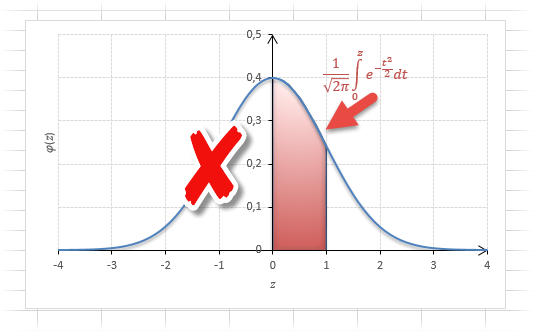
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
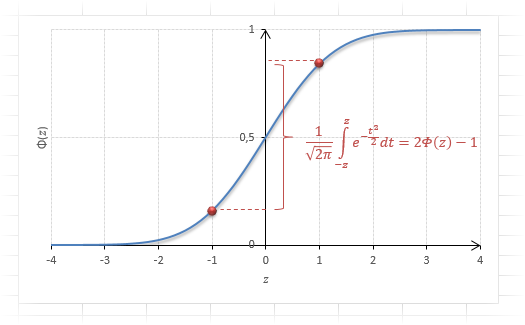
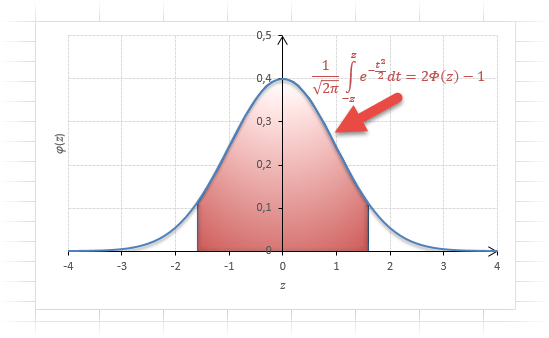
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
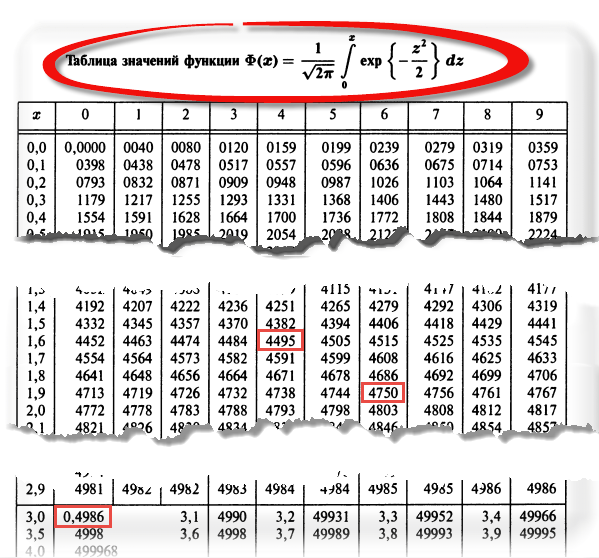
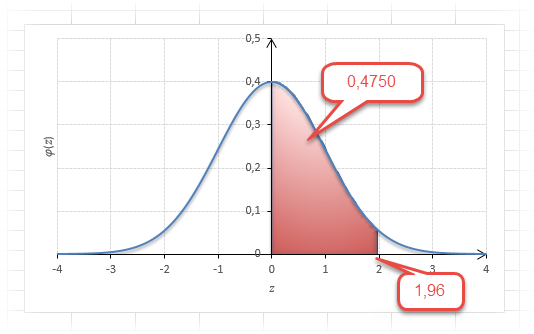
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
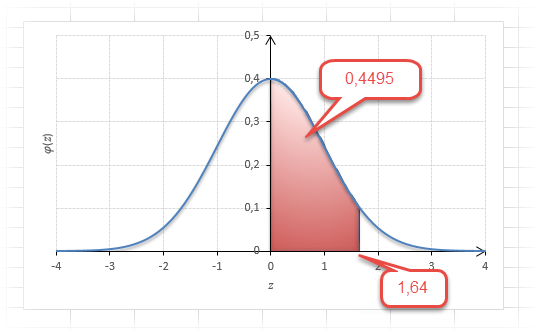
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
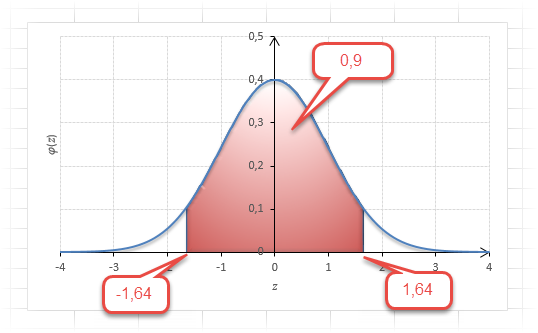
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
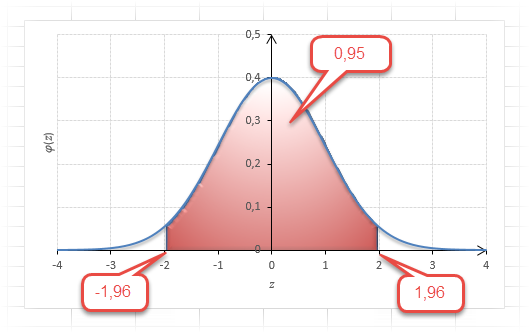
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
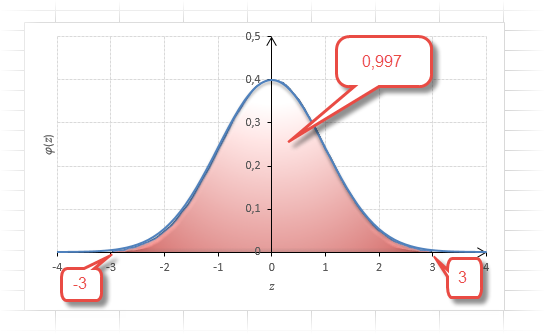
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
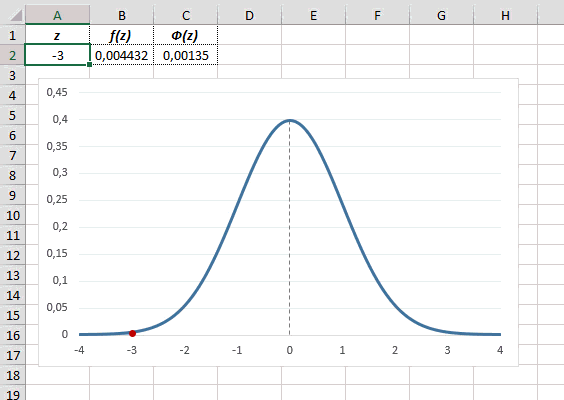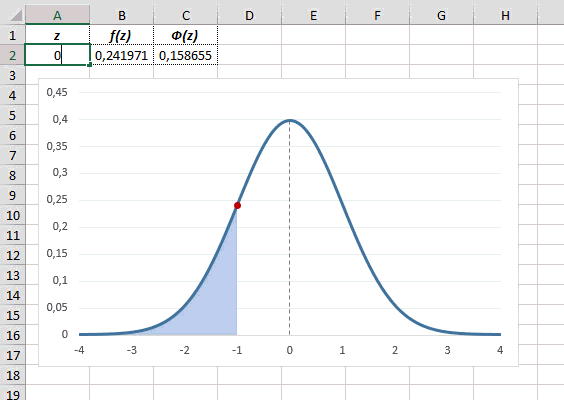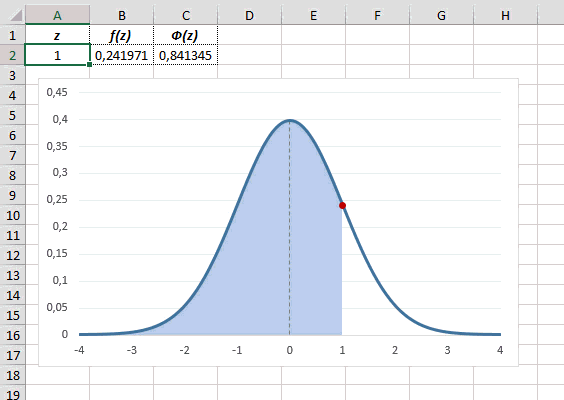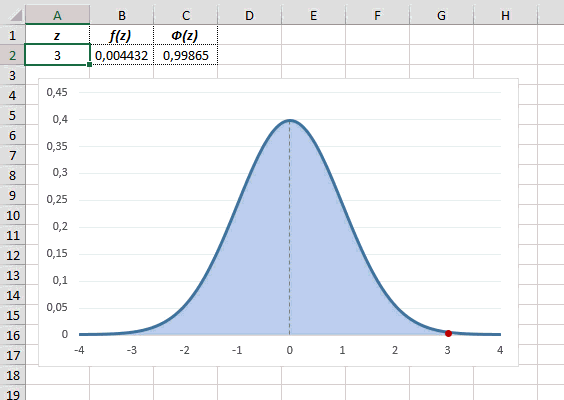
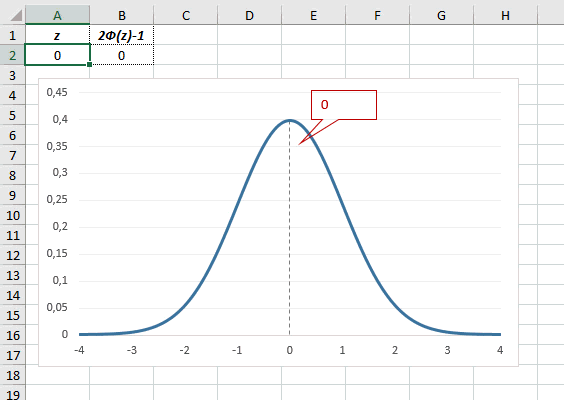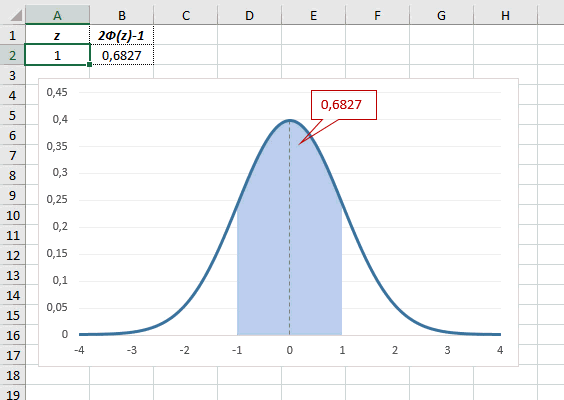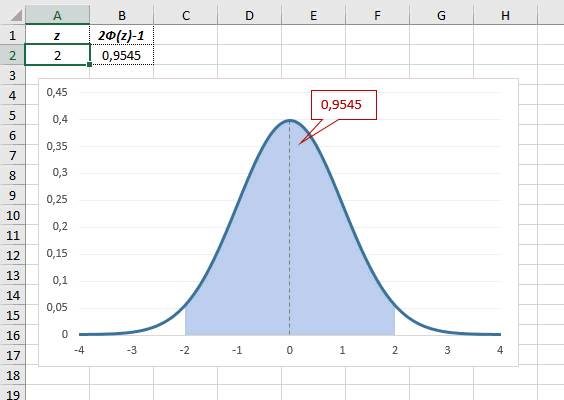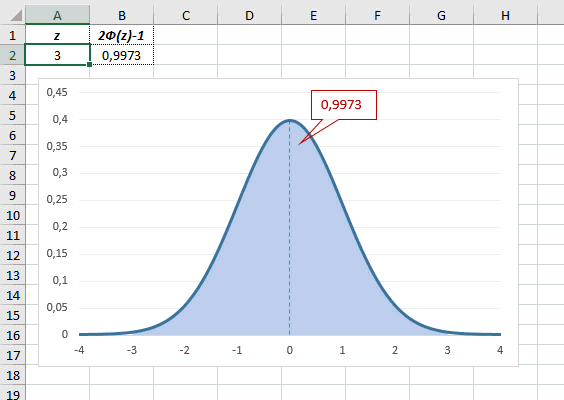
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
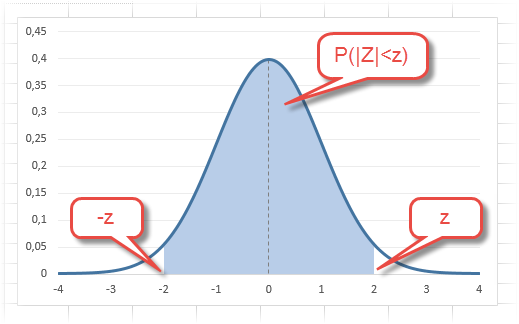
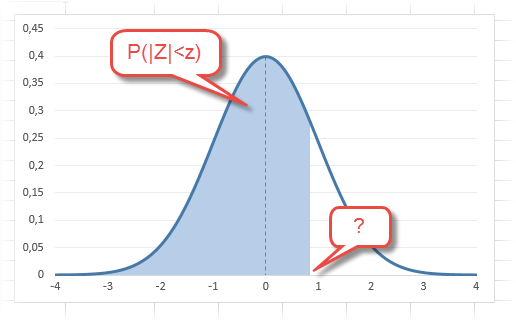
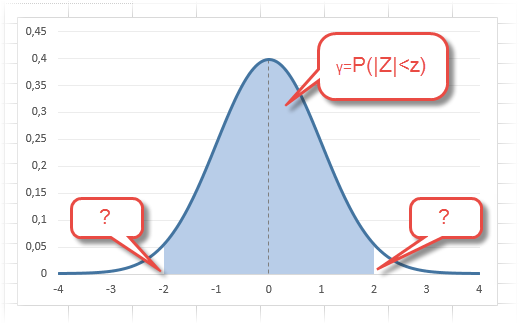
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
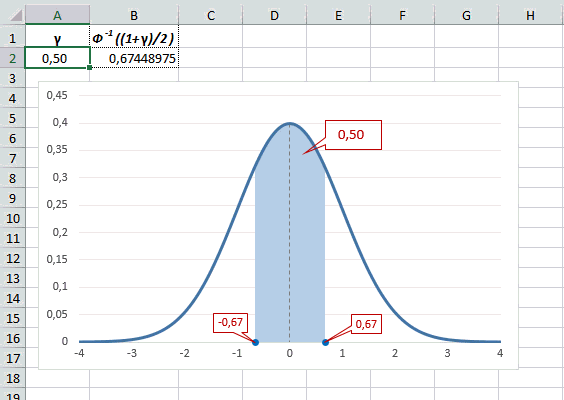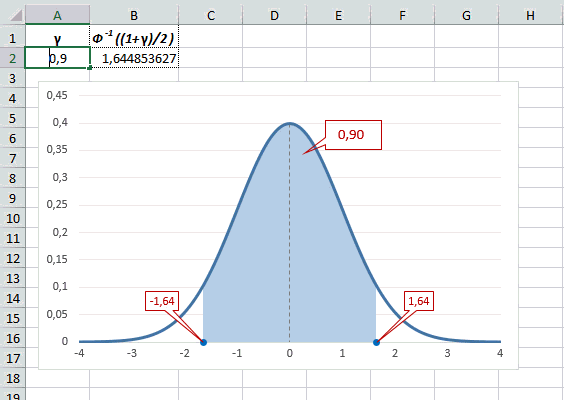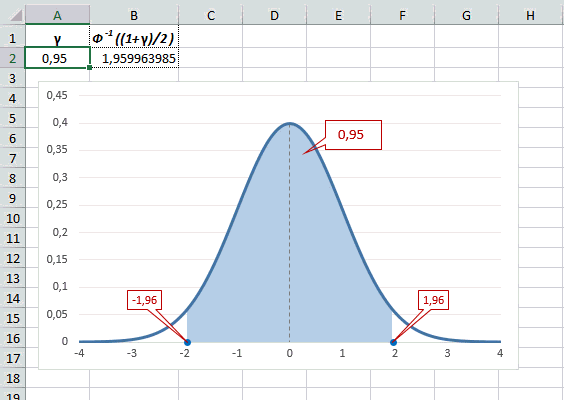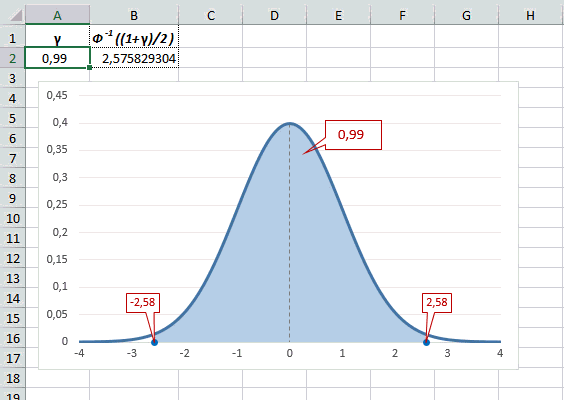
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
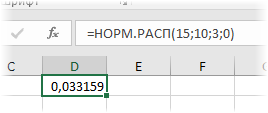
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
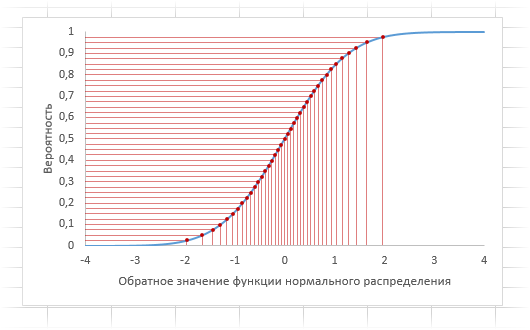
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
Содержание:
- Примеры с решением
- Нормальное распределение и его числовые характеристики
- Логарифмически-нормальное распределение
Нормальное распределение является наиболее распространенным типом распределения, предполагаемым в техническом анализе фондового рынка и в других видах статистического анализа. Стандартное нормальное распределение имеет два параметра: среднее значение и стандартное отклонение . Для нормального распределения 68% наблюдений находятся в пределах +/- одно стандартное отклонение от среднего значения, 95% находятся в пределах +/- два стандартных отклонения, а 99,7% находятся в пределах + — три стандартных отклонения.
Определение:
Общим нормальным распределением вероя тностей непрерывной случайной величины 

Нормальное распределение задается двумя параметрами: 

По определениям математического ожидания и дисперсии после выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы формулы: 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение:
Нормальное распределение с параметрами 


Поскольку функция является четной, неопределенный интеграл от нее — нечетная функция, и потому вместо функции распределения используется функция Лапласа 


Пусть случайная величина X задана плотностью нормального распределения ; тогда вероятность того, что 





Возможно вам будут полезны данные страницы:
Модель нормального распределения мотивирована центральной предельной теоремой.
Теория утверждает, что средние значения, рассчитанные из независимых идентично распределенных случайных величин, имеют приблизительно нормальные распределения, независимо от типа распределения, из которого выбираются переменные (при условии, что они имеют конечную дисперсию). Нормальное распределение иногда путают с симметричным распределением. Симметричное распределение — это то, где разделительная линия создает два зеркальных изображения, но фактические данные могут быть двумя горбами или серией холмов в дополнение к кривой колокола, которая указывает на нормальное распределение.
Примеры с решением
Пример 1.
Случайная величина распределена по нормальному закону с математическим ожиданием и средним квадратическим отклонением, соответственно равными 10 и 5. Найти вероятность того, что 
Решение:
Воспользуемся формулой . По условию 



Пример 2.
Магазин продает мужские костюмы. По данным статистики, распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, соответственно равным 48 и 2. Определить процент спроса на костюмы 50-го размера при условии разброса значений этого размера в интервале (49, 51).
Решение:
По условию задачи 

Следовательно, спрос на костюмы 50-го размера составит около 24%, и магазину нужно предусмотреть это в общем объеме закупки.
Нормальное распределение и его числовые характеристики
ДСВ — дискретная случайная величина
НСВ — непрерывная случайная величина.
В этом подразделе мы создадим функцию распределения для каждого типа НСВ и создадим график, выясним числовые свойства этого типа НСВ и узнаем тип НСВ в реальных ситуациях из содержания задачи. вы будете учиться. Наиболее распространенным в природе, экономике, социологии и других науках является нормальное распределение непрерывных случайных величин.
Используя нормальное распределение, вы можете описать плотность вероятности НСВ, когда появляются отклонения от среднего случайного значения из-за различных явлений, действующих независимо друг от друга, но в одинаковой степени.
Чем больше случайных случайных величин добавлено, тем точнее результат. Все эти явления не зависят друг от друга, но, воздействуя на процесс изготовления примерно с одинаковой силой, обусловливают то, что закон, по которому изменяется НСВ (например, размер конкретной детали), описывается нормальным распределением.
Самое точное изготовление детали с заданными размерами — «эталон» — будет соответствовать математическому ожиданию т, разброс фактических значений случайной величины размера детали — понятию дисперсии (точнее — среднеквадратическому отклонению 








Рис. 2.9

Подстановкой 

Поэтому для удобства вводится нечетная функция 


Математическое ожидание 




Случайную величину






Величины параметров нормального распределения СВ 





Величина математического ожидания 









Логарифмически-нормальное распределение
Определение. Непрерывная случайная величина 




Дифференцируя по 


(рис. 4.14).
Можно доказать, что числовые характеристики случайной величины 





Если в нормальном законе параметр а выступает в качестве среднего значения случайной величины, то в логнормальном — в качестве медианы. Логнормальное распределение используется для описания распределения доходов, банковских вкладов, цен активов, месячной заработной платы, посевных площадей под разные культуры, долговечности изделий в режиме износа и старения и др.
Нормальное распределение, также известное как распределение Гаусса, является распределением вероятностей , симметричным относительно среднего значения, показывающим, что данные около среднего значения встречаются чаще, чем данные, далекие от среднего значения.
Пример 3.
Проведенное исследование показало, что вклады населения в данном банке могут быть описаны случайной величиной 


Решение:
а) Найдем средний размер вклада, т.е. 
б) Доля вкладчиков, размер вклада которых составляет не менее 1000 ден. ед., есть 
При определении 



Теперь 
(рис. 4.15).
в) Вычислим моду случайной величины 




Лекции:
- Площадь поверхности цилиндра
- Найти определитель матрицы
- Как привести к общему знаменателю
- Геометрическое распределение
- Замечательные пределы примеры решения
- Формула Муавра
- Интерполяция кусочно-полиномиальными функциями
- Дисперсия случайной величины
- Уравнение прямой
- Найдите координаты точки пересечения прямых
Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
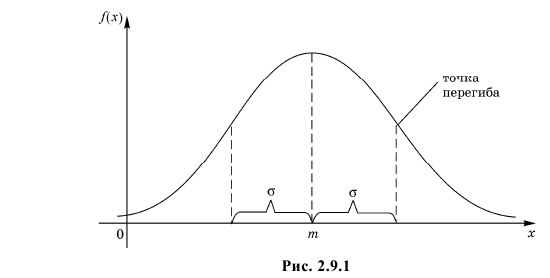
График функции плотности вероятности (2.9.1) имеет максимум в точке 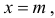

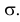
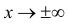
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
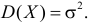
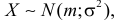

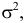
где 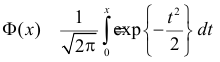
Значения функции 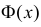
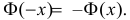
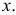
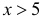
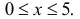
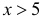
Если 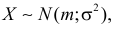
Пример:
Случайная величина X имеет нормальный закон распределения 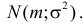
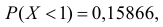
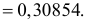
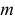
Решение. Воспользуемся формулой (2.9.2):
Так как 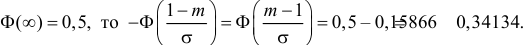
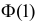
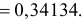
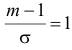
Аналогично 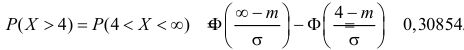
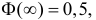
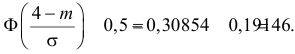
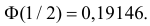
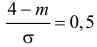
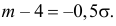
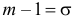
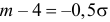
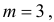
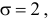
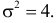
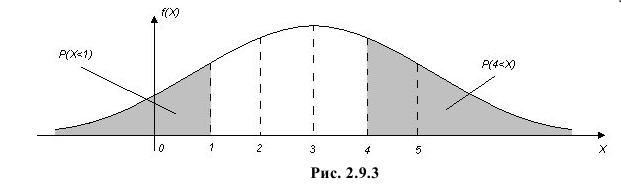
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
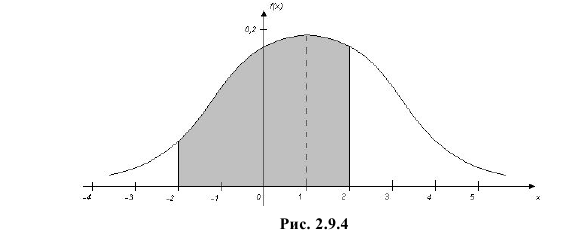
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 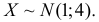
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 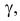
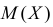
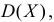
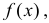
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 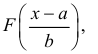
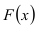
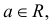
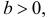
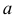
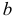
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 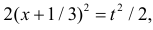
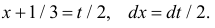
Умножим и разделим левую часть равенства на 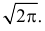
Так как 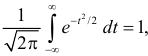
Поэтому
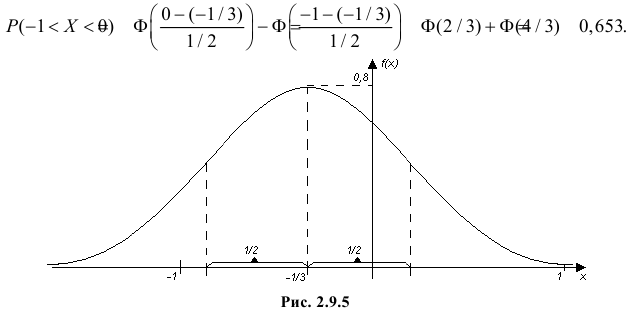
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 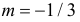
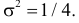
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 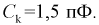
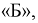
Решение.
Статистическими исследованиями в цеху установлено, что 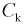
Чтобы вычислить количество транзисторов, попадающих в группу 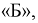
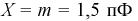
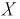
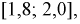
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 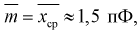
Обозначая 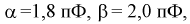
Тогда количество транзисторов 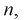
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно».
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, «оплывет» вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади «ломтика» кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста — достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона — чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько «популярен» выбранный нами рост. Напомним, что мода — самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 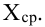
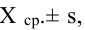
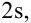
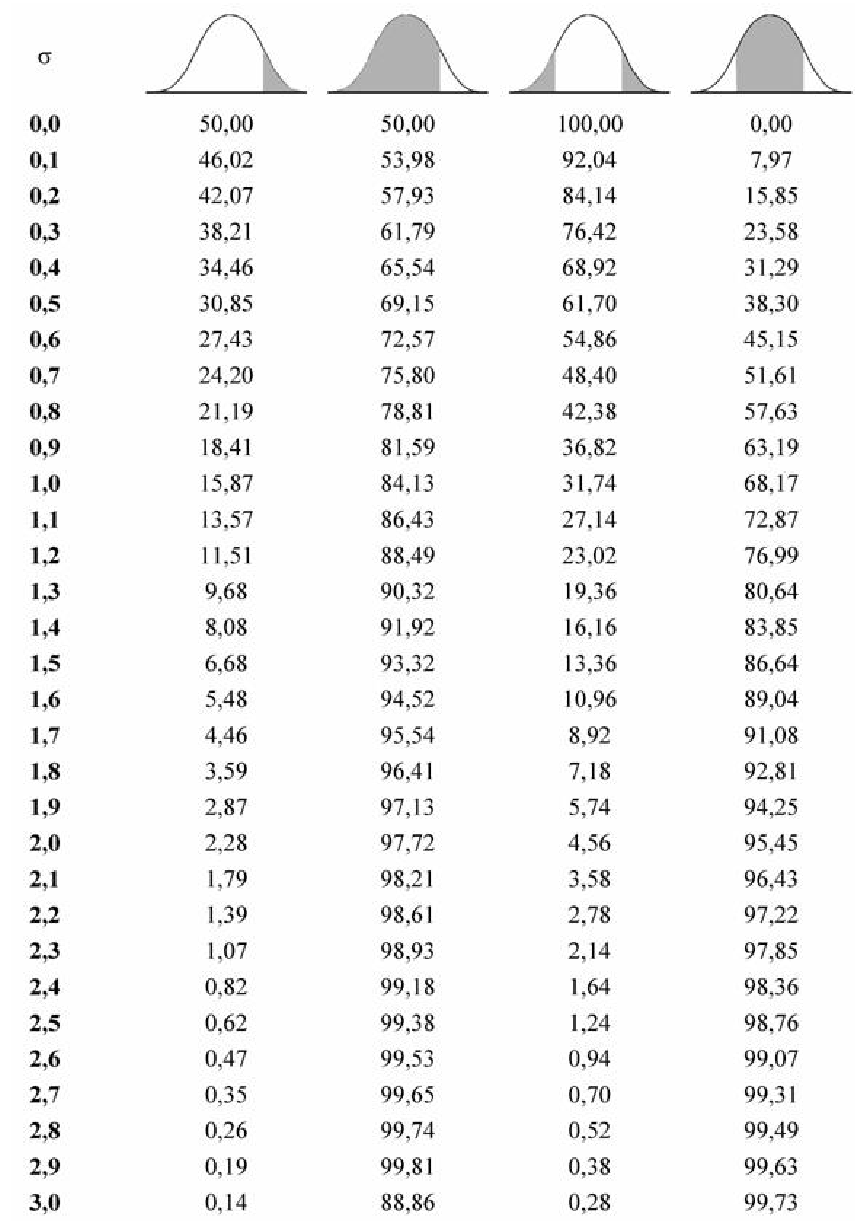
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой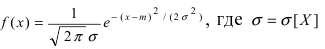
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 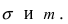
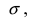
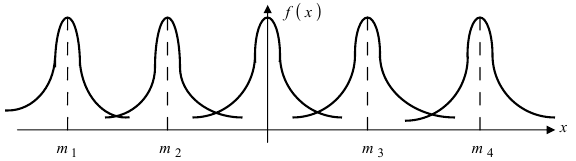
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 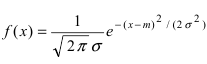
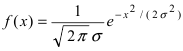
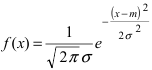
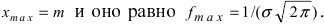
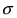
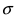
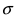
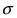
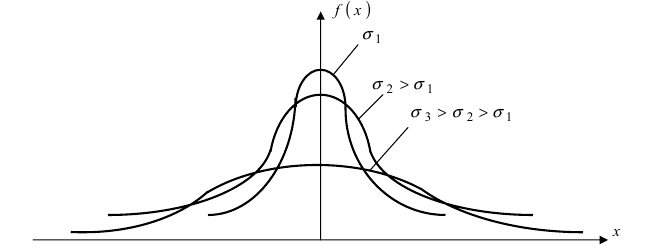
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
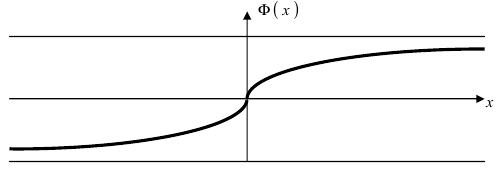
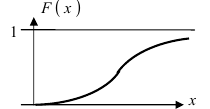
Интегральная функция нормального распределения имеет вид:
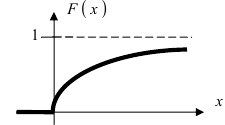
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 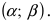
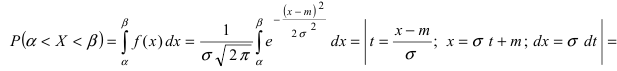
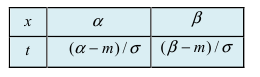
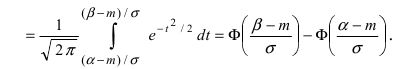
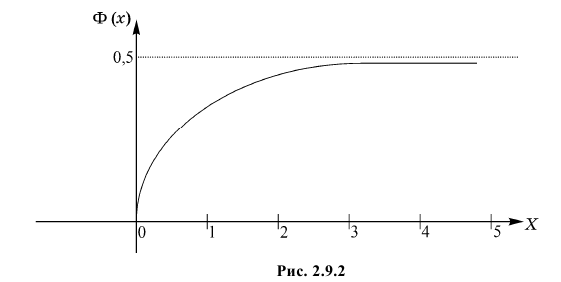
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 — график функции Лапласа проходит через начало координат.
- Ф (-х) = — Ф(х) — функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
— график функции Лапласа имеет горизонтальные асимптоты
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 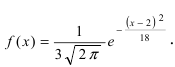
Решение:
Согласно условиям задачи 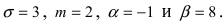
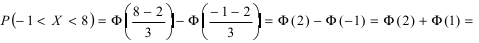
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 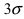
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 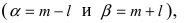
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 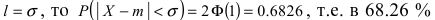
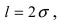
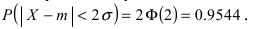
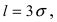
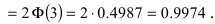
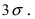
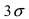
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
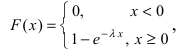
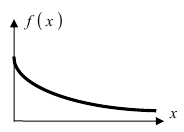
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
Дифференциальная функция распределения (плотность вероятности) имеет вид: 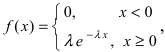
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 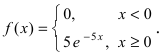
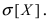
Решение:
Интегральная функция распределения 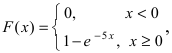
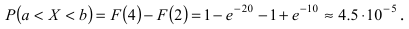
отклонение 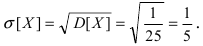
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Нормальный закон распределения и его параметры:
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.
Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.
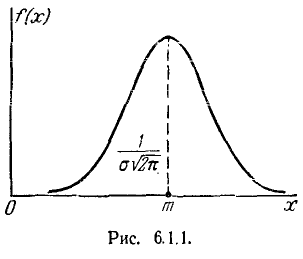
Нормальный закон распределения характеризуется плотностью вероятности вида:
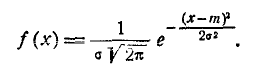
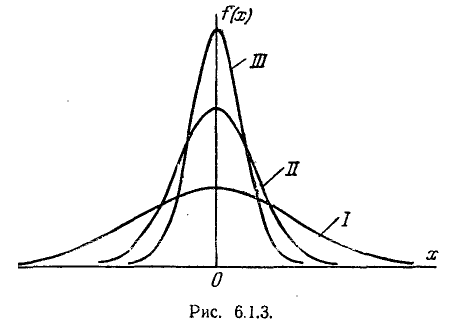
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная 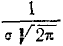
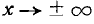
Выясним смысл численных параметров т и о, входящих в выражение нормального закона (5.1.1); докажем, что величина m есть не что иное, как математическое ожидание, а величина 
Применяя замену переменной
имеем:
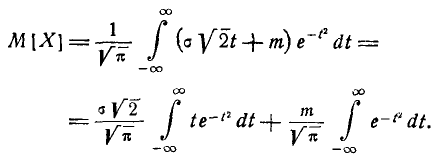
Нетрудно убедиться, что первый из двух интервалов в формуле (5.1.2) равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:
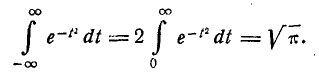
Следовательно, М[Х] = m
т. е. параметр m представляет собой математическое ожидание вели- величины X. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно — ц. р.). Вычислим дисперсию величины X:
Применив снова замену переменной
имеем:
Интегрируя по частям, получим:
Первое слагаемое в фигурных скобках равно нулю (так как 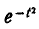
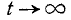
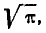
Следовательно, параметр о в формуле 5.1.1) есть не что иное, как среднее квадратическое отклонение величины X.
Выясним смысл параметров m и 
Размерность центра рассеивания—та же, что размерность случайной величины X.
Параметр о характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна 

кривой распределения всегда должна оставаться равной единице, то при увеличении о кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении 
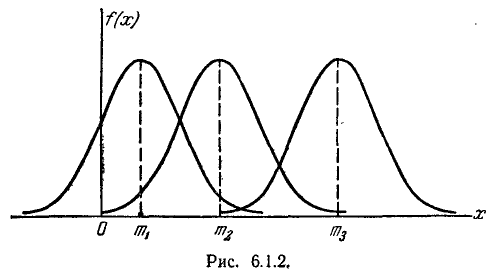
самому большому, а кривая /// — самому малому значению 

Размерность параметра 
В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению 
Размерность меры точности обратна размерности случайной величины.
Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности h, можно записать нормальный закон в виде:
Моменты нормального распределения
Выше мы доказали, что математическое ожидание случайной вели- величины, подчиненной нормальному закону 6.1.1), равно m, а среднее квадратическое отклонение равно 
Выведем общие формулы для центральных моментов любого порядка.
По определению:
Делая замену переменной
получим:
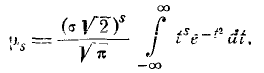
Применим к выражению (6.2.1) формулу интегрирования по частям: 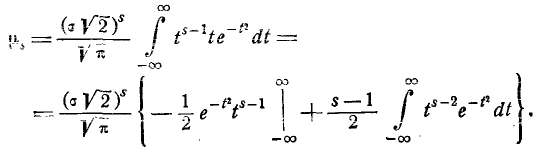
Имея в виду, что первый член внутри скобок равен нулю, получим: 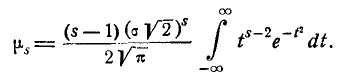
Из формулы (6.2.1) имеем следующее выражение для 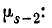
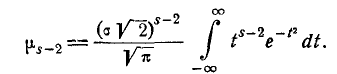
Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем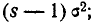
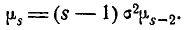
Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 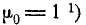


Для четных s из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:
и т. д. Общая формула для момента s-гo порядка при любом четном s имеет вид:
где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s— 1. Так как для нормального закона 
Из выражения четвертого момента
имеем:
‘) Нулевой момент любой случайной величины равен единице как математическое ожидание нулевой степени этой величины.
т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса — характеризовать сравнительную крутость данного закона по сравнению с нормальным.
Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m, 
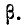
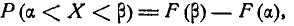
где F (х)— функция распределения величины X.
Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, 
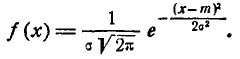
Отсюда находим функцию распределения
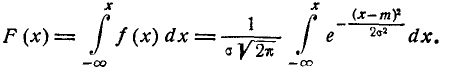
Сделаем в интеграле (6.3.3) замену переменной
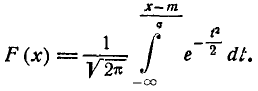
и приведем его к виду:
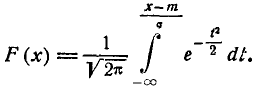
Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 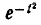
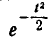
и т. д. Какой из этих функций пользоваться — вопрос вкуса. Мы выберем в качестве такой функции
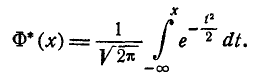
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами от m = 0, 
Условимся называть функцию Ф*(х) нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции Ф*(х)
Выразим функцию распределения (6.3.3) величины X с пара- параметрами m и 
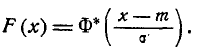
Теперь найдем вероятность попадания случайной величины X на участок от а до 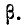
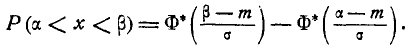
Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф* (х), соответствующую простейшему нормальному . закону с параметрами 0,1. Заметим, что аргументы функции Ф* в фор- формуле (6.3.7) имеют очень простой смысл: 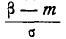
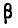
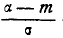
Как и всякая функция распределения,, функция Ф*(х) обладает свойствами:
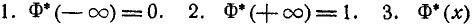
Кроме того, из симметричности нормального распределения с параметрами m = 0, 
ф* (— х)=1— Ф* (х). (6.3.8)
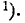
Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения Ф(х) как для положительных, так и для отрицательных аргументов.
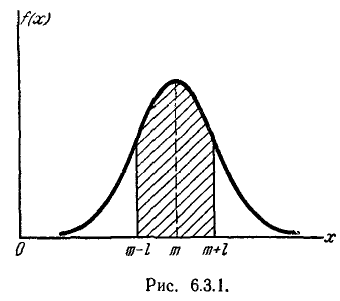
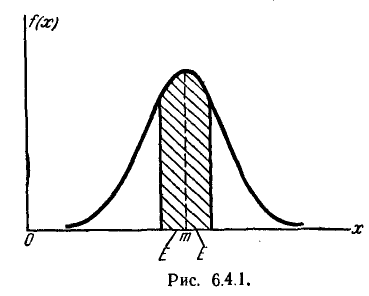
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m. Рассмотрим такой участок длины 2l (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7):
Учитывая свойство (6.3.8) функции Ф*(х) и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:
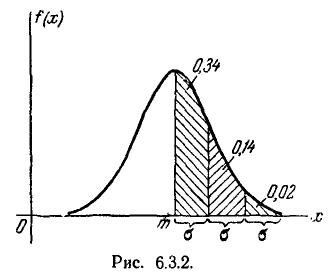
Решим следующую задачу. Отложим от центра рассеивания m последовательные отрезки длиной 
По формуле (6.3.7) находим:
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.
Округляя вероятности попадания в отрезки до 0,01 (до 1%). получим три числа, которые легко запомнить: 0,34; 0,14; 0,02.
Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке m± З
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма«. Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения 
Пример:
Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м) среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).
Решение:
Ошибка измерения есть случайная величина X, подчинен- подчиненная нормальному закону с параметрами m= 1,2 и 
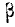
Пользуясь таблицами функции Ф* (х) (приложение, табл. 1), найдем:
Ф* (0,5) = 0,6915; Ф* (—3,5) = 0,0002,
откуда Р (—1,6 < X < 1,6) = 0,6915 — 0,0002 = 0,6913 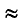
Пример:
Найти ту же вероятность, что в предыдущем примере, но при условии, что систематической ошибки нет.
Решение:
По формуле (6.3.10), полагая l=1.6, найдем:
Пример:
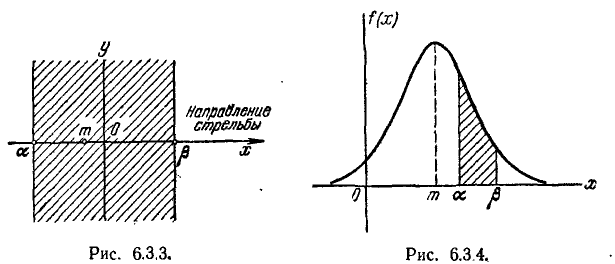
По цели, имеющей вид полосы (автострада), ширина которой равна 20 м, ведется стрельба в направлении, перпендикулярном автостраде, прицеливание ведется по средней линии автострады. Среднее квадратическое отклонение в направлении стрельбы равно 
Решение:
Выберем начало координат в любой точке на средней линии автострады (рис. 6.3.3) и направим ось абсцисс перпендикулярно автостраде. Попадание или непопадание снаряда в автостраду определяется значением только одной координаты точки падения X (другая координата Y нам безразлична). Случайная величина X распределена по нормальному закону
с параметрами m = —3, 
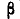
Пример:
Имеется случайная величина Х, нормально распределенная, с центром рассеивания m (рис. 6.3.4) и некоторый участок 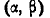
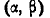
Решение:
Имеем:
Продифференцируем эту функцию величины 
Применяя правило дифференцирования интеграла по переменной, входящей в его предел, получим:
Аналогично
Для нахождения экстремума положим:
При 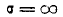
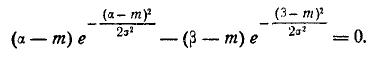
Уравнение (6.3.13) можно решить численно или графически.
6.4. Вероятное (срединное) отклонение
В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой Е (иногда В).
Вероятным (срединным) отклонением случайной величины X, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.
Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение Е — это половина длины участка оси абсцисс, симметричного относительно точки m, на кото- который опирается половина площади кривой распределения.
Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».
Рассмотрим случайную величину X, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания m меньше чем на Е, по определению вероятного отклонения Е, равна
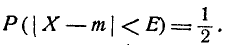
Вероятность того, что она отклонится от m больше чем на Е, тоже равна 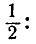
Таким образом, при большом числе опытов в среднем половина значений случайной величины X отклонится от m больше чем на Е, а половина — меньше. Отсюда и термины «срединная ошибка», «срединное отклонение».
Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего rвадратического отклонения 
Отсюда
По таблицам функции Ф* (х) можно найти такое значение аргумента х, при котором она равна 0,75. Это значение аргумента приближенно равно 0,674; отсюда
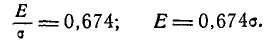
Таким образом, зная значение 
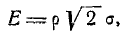
где р — такое значение аргумента, при котором одна из форм интеграла вероятностей — так называемая функция Лапласа
— равна половине. Численное значение величины р приближенно равно 0,477.
В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой 
Если в качестве характеристики рассеивания принято вероятное отклонение Е, то плотность нормального распределения записывается в виде:
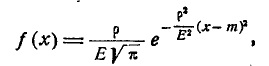
а вероятность попадания на участок от а до 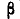
где
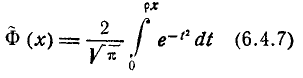
Сделаем подсчет, аналогичный выполненному в предыдущем п° для среднего квадратического отклонения 
Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке
Пример:
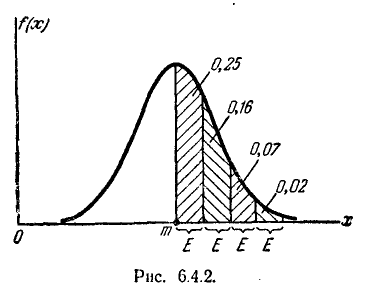
Самолет-штурмовик производит обстрел колонны войск противника, ширина которой’ равна 8 м. Полет — вдоль колонны, прицеливание— по средней линии колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо но направлению полета. Главные вероятные отклонения: по направлению полета 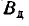
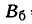
25%, 16%, 7%, 2%,
оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.
Решение:
Для решения задачи достаточно рассмотреть одну координату точки попадания — абсциссу X в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания m = 2 и вероятным отклонением 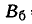
0,4-25% =0,1.
Влево от центра рассеивания цель занимает участок б м. Это — целое вероятное отклонение E м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна:
Таким образом, вероятность попадания в колонну приближенно равна:
0,1+0,25 + 0,03 = 0,38.
Вероятность хотя бы одного попадания при трех выстрелах равна:
Закон нормального распределения случайных величин
Смотрите также:
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность








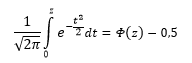
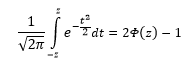
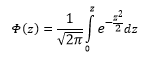






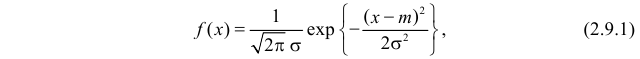
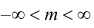
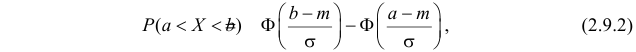
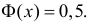
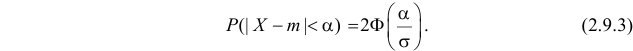
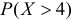
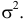
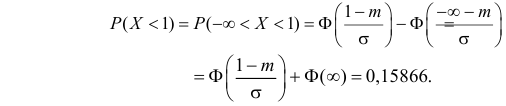
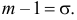
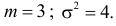
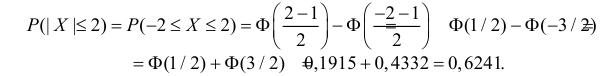
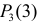
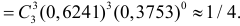
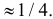
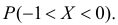
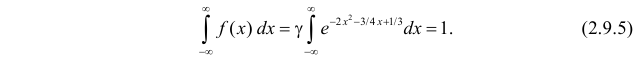
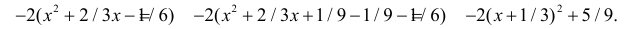
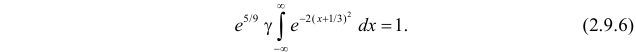

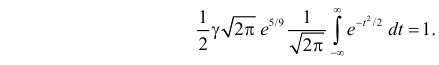

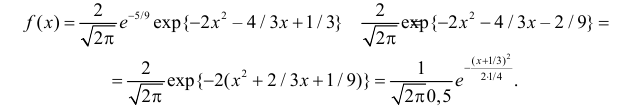
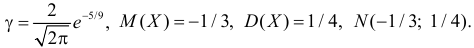
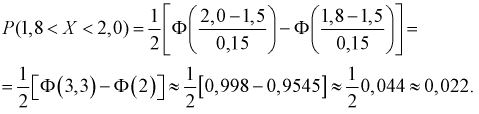
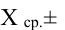
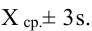
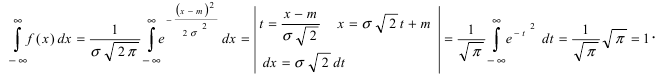
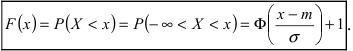
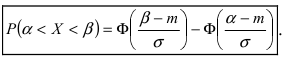
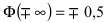 — график функции Лапласа имеет горизонтальные асимптоты
— график функции Лапласа имеет горизонтальные асимптоты