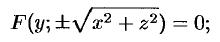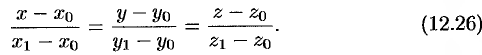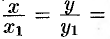poverkhnosti (решение типового расчета по аналитической геометрии вариант 1 на поверхности второго порядка мт факультет условие см ниже)
2021-01-192021-01-19СтудИзба
Описание файла
Документ из архива «решение типового расчета по аналитической геометрии вариант 1 на поверхности второго порядка мт факультет условие см ниже»,
который расположен в категории «».
Всё это находится в предмете «линейная алгебра и аналитическая геометрия» из 1 семестр, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана.
Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. .
Онлайн просмотр документа «poverkhnosti»
Текст из документа «poverkhnosti»
Домашнее задание «Поверхности второго порядка»
Студент:
Факультет: МТ
Группа: МТ5-
Вариант №1
Задача 1.Составить уравнение поверхности,полученной вращением данной кривой вокруг данной оси.Построить эту поверхность методом сечений.
Ось вращения: OZ
,
– однополостный гиперболоид
При z=0,
При y=o, – гипербола
П
— гипербола
Задача 2. Привести уравнение поверхности к каноническому виду. Определить тип поверхности.
Построить эту поверхность методом сечений.
Задача 2А.
-Однополостный гиперболоид
Ось вращения – OY
При x=0,
При у=0,
При z=0,
Задача 2Б
– эллиптический конус
При x=0,
При y=0,
При z=0,
Задача 2В
xy-2x—y+3=0
x(у-2)-(y-2)+1=0
(x-1)(y-2)=-1 – гиперболический цилиндр
=
При x=0, y=3
При y=0,x
При z=0,
Задача 2Г
–гиперболический параболоид
При x=0, — парабола
При y=0, — парабола
П
=-1 – сопряженная гипербола
Задача 3.Определить типы данных поверхностей . Построить обе поверхности методом сечений в одной системе координат . Составить уравнение проекции линии пересечения на данную координатную плоскость. Построить их линию пересечения
1)
При x=0,
При z=0,
При y=h ,
— окружность
2)y-2z=1 — плоскость
3)На OXZ
4
1- эллипс- уравнение линии пересечения 1 поверхности со 2
1
Свежие статьи
Популярно сейчас
Зачем заказывать выполнение своего задания, если оно уже было выполнено много много раз? Его можно просто купить или даже скачать бесплатно на СтудИзбе. Найдите нужный учебный материал у нас!
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
574
Средний доход
с одного платного файла
Обучение Подробнее
Как составить уравнение поверхности полученной вращением данной кривой вокруг данной оси
Глава VI. Простейшие криволинейные поверхности и тела вращения.
§ 75*. Поверхности вращения
1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.
Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение
y = f(x), х [а; b]. (1)
Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).
Очевидно, точка M с координатами (х; у; z), где х [а; b], принадлежит искомой поверхности вращения тогда и только тогда, когда
Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).
Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид
y 2 + z 2 = (f(x)) 2 , х [а; b]. (2)
Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,
В частности, если кривая L задана уравнением
то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид
т. е. просто y 2 заменяем на y 2 + z 2 .
2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.
Пусть в плоскости хОу эллипс задан уравнением
(5)
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим
(6)
Это уравнение обычно записывают так:
При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).
Пусть в плоскости хОу гипербола задана уравнением
(7)
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим
(8)
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим
(9)
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.
Составим уравнение гиперболы:
Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).
Пусть на плоскости хОу парабола задана уравнением
Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим
Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.
Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).
Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.
Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.
Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение
Эта цилиндрическая поверхность изображена на рис. 223.
Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.
В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.
Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид
Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).
Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.
Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.
Как составить уравнение поверхности полученной вращением данной кривой вокруг данной оси
Так как точка N (0, yN, z) лежит на кривой L, то получаем: . Это уравнение задаёт рассматриваемую поверхность вращения.
Пример 5. Составить уравнение поверхности, образованной при вращении кривой y = x 3 вокруг оси OY.
Решение. Не изменяя переменную y (так как вокруг оси OY совершается вращение), заменим в уравнении кривой переменную x на .
После возведения в квадрат:
8.5. Задачи с решениями
1. Составить уравнение окружности с центром в точке C(а, b) и радиусом R.
Решение. Если M(x, y) — произвольная точка окружности, то расстояние |MC| = R. В координатной форме получаем уравнение:
или проще: (x — a) 2 + (y — b) 2 = R 2
2. Составить уравнение окружности, если точки A(8, —4) и B(6, 0) являются концами одного из диаметров.
Решение. Центр окружности C делит отрезок AB пополам. Поэтому координаты центра: .
Так как радиус окружности r = |AB| = |BC|, то .
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Поверхности. Касательная плоскость и нормаль
Краткие теоретические сведения
Способы задания поверхностей
Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.
Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$
Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.
Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.
Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.
Решение задач
Задача 1 (Феденко №544)
Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.
Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.
Задача 2 (Феденко № 546)
Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end
Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac<(x-x_0)^2>+frac<(y-y_0)^2>+frac<(z-z_0)^2>=1. end
Задача 3 (Феденко №528)
В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.
Решение задачи 3
Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end
Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end
Касательная плоскость. Нормаль
Краткие теоретические сведения
Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.
Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$
Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac>
Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.
Уравнение касательной плоскости:
1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end
Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.
Уравнение нормали:
1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac<varPhi_x>=displaystylefrac<varPhi_y>=displaystylefrac<varPhi_z>. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac<-1>. end
Решение задач
Задача 1 (Феденко №574)
Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefrac<pi><4>right)$ поверхности.
Задача 2
Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.
Ответ. $z=0, -2X-2Y+Z+2=0$.
Задача 3
Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec<2,1,-1>$.
Задача 4
Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.
Ответ. $X-Z=0$, $3X-4Y+5Z=0$.
Задача 5 (Феденко №594)
Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.
Решение задачи 5
Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left<2x_0,-2y_0,0right>. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end
http://www.chem-astu.ru/chair/study/algebra-geometry/?p=233
http://vmath.ru/vf5/diffgeom/seminar5
Поверхности вращения. Конические поверхности
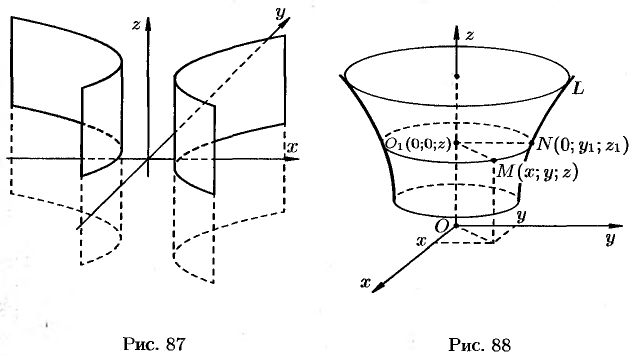
Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая 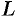
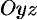
Найдем уравнение поверхности, образованной вращением кривой 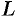
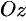
Возьмем на поверхности произвольную точку 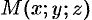
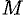
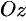
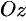
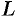
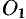
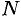
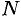
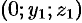
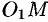
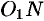
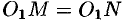
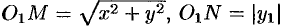
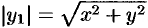
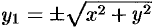
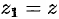
Так как точка 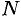
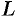
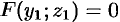
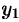
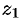
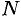
Уравнение (12.23) — искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точки 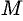
Как видно, уравнение (12.23) получается из (12.22) простой заменой 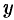
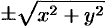
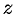
Понятно, что если кривая (12.22) вращается вокруг оси 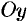
если кривая лежит в плоскости 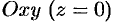
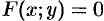
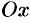
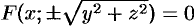
Так, например, вращая прямую 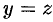
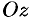
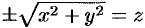
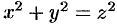
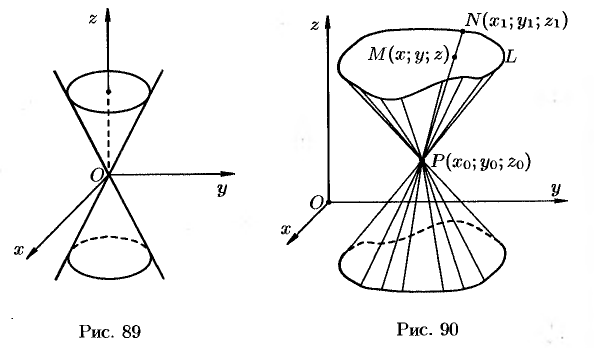
Поверхность, образованная прямыми линиями, проходящими через данную точку 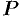
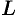
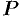
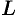
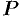
Пусть направляющая 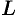
а точка 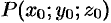
Возьмем на поверхности конуса произвольную точку 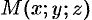
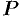
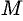
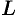
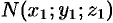
Канонические уравнения образующих, проходящих через точки 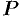
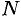
Исключая 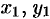
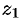
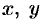
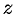
Пример №12.3.
Составить уравнение конуса с вершиной в точке 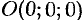
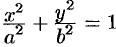
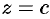
Решение:
Пусть 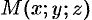
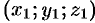
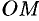
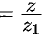
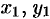
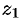
(точка 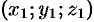

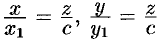
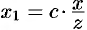
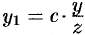
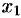
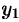
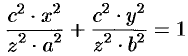
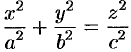
Это и есть искомое уравнение конуса.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Наиболее
просто получают поверхность вращением
плоской
кривой относительно некоторой неподвижной
оси.
☺☺
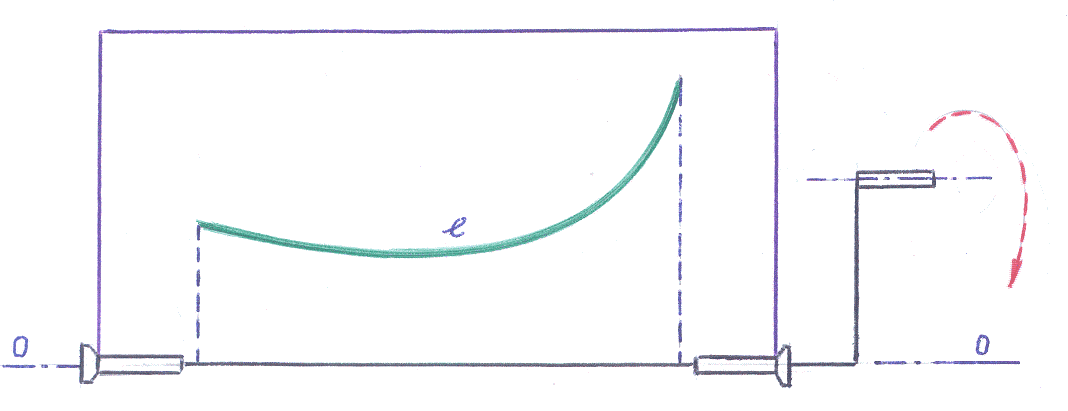
Пример 6–03:
Точнее было бы назвать это не примером,
а экспериментом. На прозрачной тонкой
прямоугольной пластине нарисуем
произвольную линию
.
Закрепим пластину на неподвижной оси
вращения
.
Станем достаточно быстро вращать
пластину при помощи рукоятки вокруг
оси вращения (боковые упоры не позволяют
пластине смещаться вдоль оси
).
Учитывая свойство инерции нервной
системы глаза, ожидаем увидеть
равномерно окрашенную поверхность,
описываемую произвольной линией
.
Замечание:
изготовить предложенный механизм
достаточно просто; если пользоваться
набором пластин с разными линиями,
то это позволит сформировать устойчивый
образ процесса получения поверхностей
вращения!
Поверхностью
второго порядка называют совокупность
точек
пространства, координаты которых
удовлетворяют уравнению:
. (1)
Уравнение
(1) называют общим
уравнением
поверхности 2-го порядка. Присваивая
коэффициентам уравнения (1):
,
;
произвольные значения, можно получить
(мы в этом убедимся!) всё многообразие
поверхностей 2-го порядка.
Применяя
преобразование координат вращением
относительно общей точки (подробно
показано при рассмотрении темы
«Преобразование координат»), получают
более простое уравнение для поверхностей
2-го порядка:

Прежде,
чем приступить к рассмотрению возможных
случаев дальнейшего упрощения уравнения
(2), рассмотрим получение простейших
поверхностей второго порядка.
П
вращения:
поверхности, образованные вращением
плоской линии около некоторой оси.
Пусть
линия l
задана в пространстве (x,y,z)
уравнениями: (3)
Для
нахождения уравнения поверхности,
получаемой вращением линии
,
вокруг оси
,
берём на поверхности произвольную точку
и проводим через неё плоскость,
перпендикулярную оси
.
Так как плоскость пересекает поверхность
вращения, то линия пересечения плоскости
с поверхностью – окружность с центром
,
расположенным на оси
.
Уравнение этой окружности:
=
=
,
где
=
,
если уравнение плоскости:
=
.
Из вышесказанного
следует достаточно простой приём
получения уравнения поверхности
вращения:
▫ Пусть
задана плоская линия
:
.
Приводим её уравнение одному из видов
записи:

▫ Составим
одно из уравнений: =
,
=
, (5)
=
.
▫ Учитывая
уравнения (5), получены поверхности
вращения относительно осей
,
,
,
соответственно.
П
вращения 2-го порядка образуются вращением
линий 2-го порядка относительно ихосей
симметрии.
Рассмотрим применение выражений (4) и
(5) для всех известных нам кривых 2-го
порядка.
10.
Пусть имеем эллипс
:
Совершим вращение этого эллипса вокруг
оси
:
и сложим уравнения этой системы:
.
Последнее
уравнение легко приводится к виду:
– эллипсоид
вращения,
с осью вращения
.
☺☺
Пример 6–04:
Используя общие выражения и алгоритм
построения поверхностей вращения,
построить уравнение эллипсоида вращения
с осью вращения
.
Р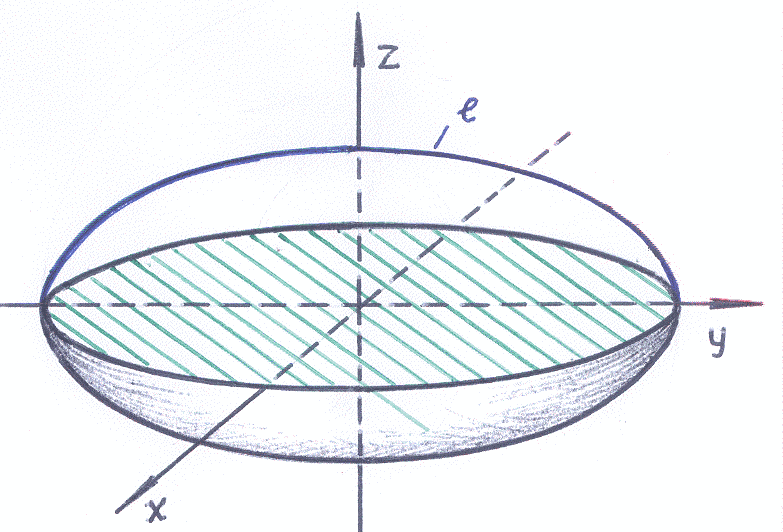
20.
Пусть имеем эллипс
:
Совершим вращение этого эллипса вокруг
оси
:
и сложим уравнения этой системы:
.
Последнее
уравнение легко приводится к виду:
– эллипсоид
вращения,
с осью вращения
.
Ответ:
– эллипсоид
вращения,
с осью вращения
..
☻
Замечание:
нетрудно заметить, что вращение эллипса
вокруг осиприводит к уравнению эллипсоида вращения,
в котором равными являются оси по
переменным;
при вращении эллипса вокруг осиравными являются оси по переменным
;
не рассматривая подробно случай вращения
эллипса вокруг оси,
можем утверждать, что теперь равными
должны быть оси по переменным!
В отличие
от эллипса, при вращении гиперболы
относительно действительной и мнимой
осей получаются принципиально различные
поверхности. И называются они по-разному:
однополостный гиперболоид и двуполостный
гиперболоид (имеется в виду количество
полостей в получающейся фигуре вращения).
Рассмотрим оба случая.
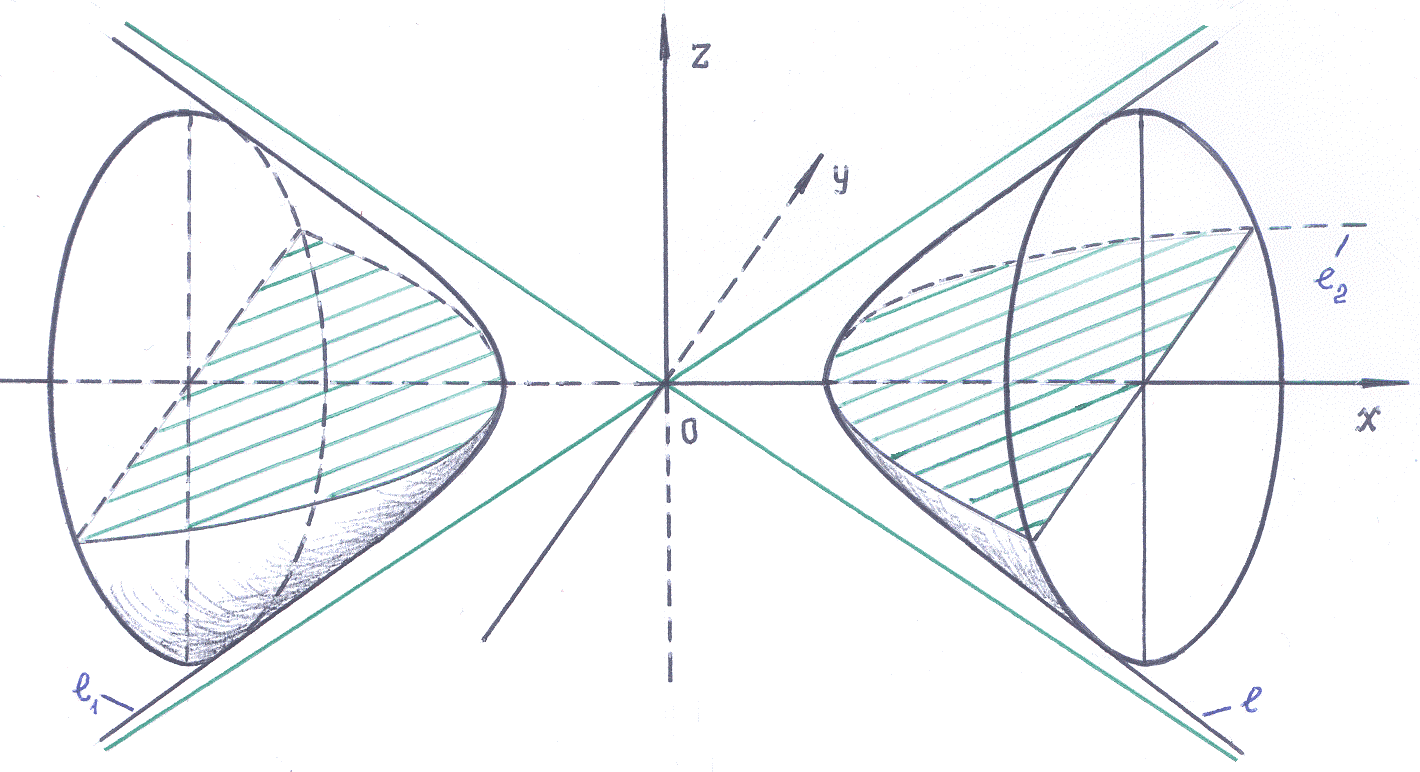
3
имеем гиперболу :
Эта гипербола на рисунке выделена
красным цветом: расположена в плоскости
.
Совершим вращение линии
вокруг оси
:

уравнения этой системы:
.
Последнее
уравнение легко приводится к виду:
– однополостный
гиперболоид вращения
с осью вращения
.
На
рисунке выделена ещё одна линия
,
которая отличается только тем, что
теперь гипербола расположена в плоскости
.
В качестве
упражнения построим ещё одну поверхность
вращения.
☺☺
Пример 6–05:
Используя общие выражения и алгоритм
построения поверхностей вращения,
построить уравнение поверхности вращения
линии
с осью вращения
.
Решение:
1). Пусть
имеем гиперболу
:
Совершим вращение линии
вокруг оси
:
и сложим уравнения этой системы:
.
2).
Последнее уравнение легко приводится
к виду:
– однополостный
гиперболоид вращения
с осью вращения
.
Ответ:
– однополостный
гиперболоид вращения
с осью вращения
.
☻
Замечание: однотипность
построения поверхностей вращения
подсказывает: не требуется специально
запоминать конечные уравнения этих
поверхностей, следует помнить только
принцип их построения!
40. Пусть
имеем гиперболу :
Эта гипербола расположена в плоскости
.
Совершим вращение линии
вокруг действительной оси
:
и сложим уравнения этой системы:
.
Последнее уравнение легко приводится
к виду:
– двуполостный
гиперболоид вращения
с осью вращения
.
На
рисунке выделена ещё одна линия
,
которая отличается только тем, что
теперь гипербола расположена в плоскости
.
В качестве
упражнения построим ещё одну поверхность
вращения
☺☺
Пример 6–06:
Используя общие выражения и алгоритм
построения поверхностей вращения,
построить уравнение поверхности вращения
линии
с осью вращения
.
Решение:
1). Пусть
имеем гиперболу
:
Совершим вращение линии
вокруг оси
:
и сложим уравнения этой системы:
.
2).
Последнее уравнение легко приводится
к виду:
– двуполостный
гиперболоид вращения
с осью вращения
.
Ответ:
– двуполостный
гиперболоид вращения
с осью вращения
.
☻
Рассмотрим
применение вращения кривой 2-го порядка
– параболы относительно осей
,
,
,
соответственно.
5
Пусть имеем параболу:
Эта парабола расположена в плоскости
.
Совершим вращение линии
вокруг оси
:
и сложим уравнения этой системы:
– это уравнение параболоида
вращения
с осью вращения
.
Если
вращать параболу:
расположенную в плоскости
вокруг той же оси
,
то получим параболоид вращения
,
ничем не отличающийся от параболоида,
рассмотренного выше.
А что
если вращать параболу
(или )
вокруг оси
(или
)?
Получится ли поверхность вращения 2-го
порядка?
Решим возникший
вопрос в качестве отдельного упражнения.
☺☺
Пример 6–07:
Пусть парабола :
вращается вокруг оси
.
Используя общие выражения и алгоритм
построения поверхностей вращения, найти
уравнение поверхности вращения для
этого случая.
Решение:
1). По
условию линия :
вращается вокруг оси
.
Отметим: ось
не является осью симметрии линии .
2). Так
как общий алгоритм построения поверхностей
вращения предполагает только вращение
плоских линий относительно осей
координат, то совершим вращение линии
:
вокруг оси
:
и сложим уравнения этой системы:
.
3).
Последнее уравнение легко приводится
к виду:
– алгебраическая
поверхность вращения:
представлена многочленом 4-й степени.
Ответ:
– алгебраическая
поверхность вращения.
☻
При
изучении кривых 2-го порядка были выделены
частные случаи:
– пара пересекающихся прямых, и
– пара параллельных прямых.
Оба
выделенных случая с прямыми линиями
можно было бы объединить: вокруг некоторой
оси вращаем произвольную
прямую линию. Требуется найти уравнение
образующейся при этом поверхности
вращения. Мы ограничимся
более простой задачей:
мы станем вращать прямую линию
только тремя способами:
▫ вокруг
оси, пересекающей прямую линию
под некоторым острым углом;
▫ вокруг
оси, параллельной линии
;
▫ вокруг
оси, перпендикулярной линии
.
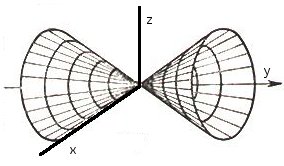
60.
Пусть задана линия, состоящая из двух
пересекающихся прямых:
Для того, чтобы детально наблюдать
процесс вращения линии представим эту
пару как:
Нетрудно заметить, что в этом случае
ось координат
является биссектрисой угла этих прямых!
Запишем отдельно эти прямые :
и :
С
вращение линии
вокруг оси
:
и сложим уравнения этой системы:
– это уравнение конуса
вращения
с осью вращения
.
Нетрудно
заметить, что вращение линии
определяется
той же системой:
Это значит, что алгоритм вращения каждый
раз использует только одну линию. В
данном случае результаты совпали, так
как возведение в квадрат безразлично
к знаку числа!
Замечание: на
рисунке представлена только верхняя
часть конической поверхности, так как
получение уравнения поверхности
вращения:сохраняет осевую симметрию (относительно
)
и симметрию относительно плоскости;
представленная половина конуса в
наглядности не проигрывает!
Ниже
приводится пример, в котором определены
более общие начальные условия: точка,
определяющая вершину конуса, смещена,
но ось конуса остаётся параллельной
одной из осей координат. В этом случае
необходимо вспомнить простейшее
преобразование координат: параллельный
перенос.
☺☺
Пример 6–08:
Составить уравнение конуса с вершиной
в точке (0,0,),
направляющая которого дана уравнениями
,
=0.
Решение:
1).
Образующая конуса есть вращающаяся
прямая, имеющая одну точку (0,0,)
неподвижной, а вторую точку принадлежащей
эллипсу, расположенному в плоскости
.
Выделим одну из образующих точкой
(,0,0).
Тогда уравнение вращающейся вокруг оси
линии можем записать в виде
:
=
.
2).
Применим преобразование координат:
,
,
.
Этим преобразованием задача преобразована
к виду, уже рассмотренному выше: вращается
линия:
построить поверхность вращения.
3). Легко
получаем уравнение:
– это уравнение конуса
вращения
с осью вращения
и вершиной в точке (0,0,).
Ответ:
– конуса
вращения
с осью вращения
и вершиной, расположенной в точке
(0,0,).
☻
П
теперь имеем прямую, параллельную оси
вращения. Необходимо найти уравнение
поверхности вращения.
70.
Пусть задана линия, состоящая из двух
параллельных прямых:
Для того, чтобы детально наблюдать
процесс вращения линии представим эту
пару как:
Нетрудно заметить, что в этом случае
вращаемые прямые располагаются
симметрично относительно оси вращения
!
Запишем отдельно эти прямые :
и :
Совершим
вращение линии
вокруг оси
:
и сложим уравнения этой системы:
– это уравнение цилиндра
вращения
с осью вращения
.
Нетрудно
заметить, что вращение линии
определяется
той же системой:
Это значит, что алгоритм вращения каждый
раз использует только одну линию. В
данном случае результаты совпали, так
как возведение в квадрат безразлично
к знаку числа!
☺☺
Пример 6–09:
Пусть задана линия, состоящая из двух
параллельных прямых :
Вращением
вокруг оси
найти уравнение поверхности вращения.
Решение:
1). По
условию линия
распадается на две параллельные прямые:
Вращение осуществляется вокруг оси
.
2).
Вращением любой из двух прямых линий
получаем:
Складывая уравнения, получаем уравнение
поверхности вращения:
– это уравнение цилиндра
вращения
с осью вращения
.
Ответ:
– уравнение цилиндра
вращения
с осью вращения
.
☻
Пусть
теперь имеем прямую, перпендикулярную
оси вращения. Необходимо найти уравнение
поверхности вращения.
8
Пусть задана линия, состоящая из двух
параллельных прямых:
Представим эту пару как:
Запишем отдельно эти прямые :
и :
В этом случае
получить поверхность вращения, применяя
алгоритм вращения, не удаётся.
Исходя
из геометрических соображений, нетрудно
записать уравнения двух параллельных
плоскостей:
и
.
Замечание: применение
общего алгоритма получения поверхности
вращения в рассматриваемом случае не
удаётся из-за того, что не может быть
установлена зависимость между переменными
и
.
Вывод: 1). Рассмотрен
класс поверхностей, уравнения которых
можно получить, применяя общий алгоритм
действий – это поверхности вращения.
2).
Получаемые вращением плоской кривой
уравнения поверхностей имеют отличительный
признак: все они имеют из трёх параметров
два равных. Такие уравнения не относят
к каноническим уравнениям.
3).
Большинство поверхностей вращения 2-го
порядка получаются вращением кривых
2-го порядка. Вращение прямой линии
относительно оси, составляющей с этой
линией некоторый острый угол (включая
ноль), тоже приводит к поверхности 2-го
порядка.
Соседние файлы в папке ЛА и АГ пособие
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лучший ответ
|
|
 |
|