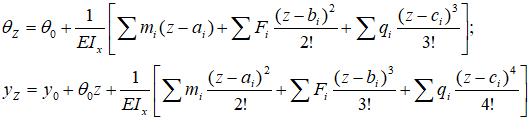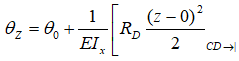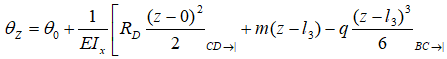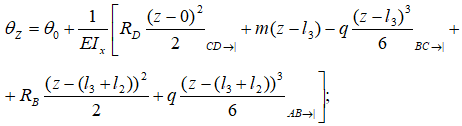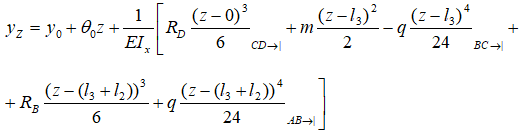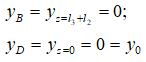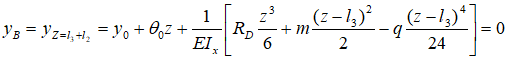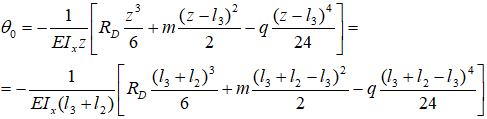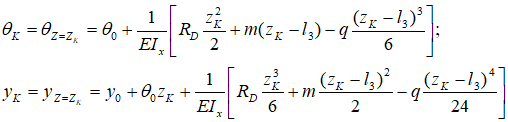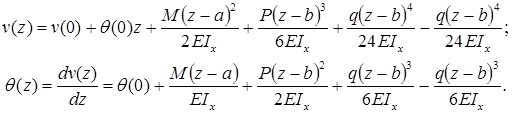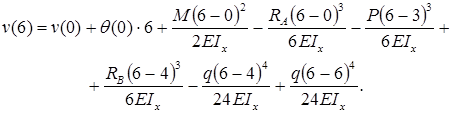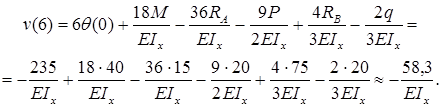Как составить уравнение прогибов

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым охватим всю теоретическую часть по максимуму.

Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки.

Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях — упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом использования метода начальных параметров (МНП).

Универсальное уравнение МНП

После введения базы, системы координат и обозначения расстояний а, б, в, г записываем универсальное уравнение МНП, с помощью которого, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки):

Теперь поговорим об этой формуле, проанализируем, так сказать:

• E – модуль упругости;
• I – момент инерции;
• V_K – прогиб сечения K;
• V_O – прогиб сечения O;
• θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу слева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_K, который дополнительно умножается на жесткость балки — EI:

В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения, которое совпадает с выбранной базой. Причем произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку, которая находится слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами скобка возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен по часовой стрелке и отрицательным, соответственно, если против часовой стрелки:

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки. Но так как, конец распределенной нагрузки совпадает с сечением, прогиб которого мы хотим вычислить, в этом случае, в уравнении учитывается только ее начало.

Причем важно, даже если бы в этом сечении была сила или момент, их бы также не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобка возводится в 4 степень и делится на 24. А правило знаков такое же, как и для сосредоточенных сил.

Граничные условия

Чтобы решить уравнение, нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, V_O и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и никаких поворотов, то есть V_O = 0 и θ_O = 0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно-подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок, помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок.

Условие задачи

Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10⁵ МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см⁴). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае рассматриваемый метод будет работать.

В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м от базы и заканчивается на 4 м. В таком случае нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно направленной нагрузкой. Тем самым в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении у нас содержится две неизвестные величины: искомый прогиб V_O и угол поворота этого сечения — θ_O:

Но чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:

Из второго уравнения найдем угол поворота:

После чего рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Метод начальных параметров (сокр. — МНП) позволяет определять прогибы и углы наклона сечений в прямых балках с постоянной жесткостью поперечного сечения EI_x.

МНП является одним из относительно простых способов расчета угловых и линейных перемещений при изгибе в балках с любым количеством силовых участков.

Пример расчета перемещений сечений балки смотрите в нашем видеоуроке:

Другие видео

Для применения метода начальных параметров есть ограничения: рассчитываемая балка должна быть выполнена из однородного материала, иметь прямую ось и постоянные форму и размеры поперечного сечения.

Универсальные уравнения МНП

Для балок с типичным набором нагрузок универсальные уравнения метода начальных параметров имеют вид:

где
θ_z, y_z – соответственно угловое и линейное перемещения рассматриваемого сечения балки;
θ₀, y₀ – угол наклона и прогиб сечения балки в выбранном начале координат (НК). Это и есть начальные параметры (являются постоянными интегрирования) по которым назван сам метод. Определяются из соответствующих опорных условий;
m, F и q – все сосредоточенные моменты (пары сил), силы (включая опорные реакции) и распределенные нагрузки (в т.ч. компенсирующие) приложенные к рассматриваемой балке;
z – расстояние от выбранного начала координат до рассматриваемого сечения балки (положение сечения);
a и b – расстояния от начала координат до соответствующих моментов и сосредоточенных сил;
c – расстояние от НК до начала действия распределенной нагрузки;
E – модуль продольной упругости материала балки;
I_x — момент инерции сечения относительно оси x.

Данные уравнения МНП являются лишь шаблонами, по которым записываются уравнения для конкретных расчетных схем (пример рассмотрен ниже).

Примечания к методу

Перед записью уравнений метода начальных параметров выбирается начало координат балки.

Начало координат выбирается в крайнем левом или правом конце балки (лучше в том, который расположен на опоре).

Слагаемые в уравнениях записываются последовательно по силовым участкам от начала координат.

Знаки отдельных слагаемых в универсальных уравнениях МНП принимаются по правилу знаков для изгибающего момента, т.е. слагаемые с нагрузками, которые на рассматриваемом участке стремятся сжать верхние слои балки, записываются положительными.

Другие видео

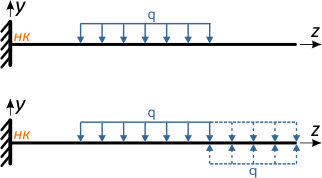
Если распределенная нагрузка q действует в пределах части длины балки (обрывается, не доходя до конца), то ее действие продлевается в сторону, противоположную от начала координат, до конца балки и добавляется компенсирующая нагрузка той же интенсивности но обратного направления.

Начальные параметры универсальных уравнений МНП определяются из условий закрепления балки в опорах.
На шарнирных опорах вертикальные линейные перемещения (прогибы) равны нулю, т.е. y_A=0 и y_B=0.

В жесткой заделке отсутствуют (равны нулю) и угловые и линейные перемещения (θ_A=0, y_A=0).

Положительное значение рассчитанного прогиба y_z соответствует перемещениям сечения вверх по отношению к продольной оси балки.

Знак угла поворота θ_z зависит от выбора начала координат: при выборе НК в крайнем левом сечении балки угол θ_z будет считаться положительным при повороте сечения против хода часовой стрелки

Соответственно, если начало координат выбрано справа – положительным считается угол при повороте по часовой стрелке.

Пример составления уравнений МНП

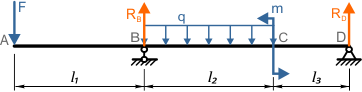
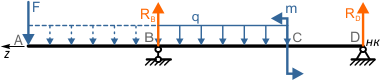
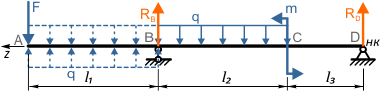
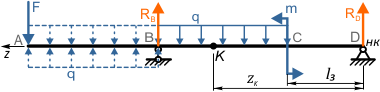
Порядок составления уравнений МНП и расчета перемещений рассмотрим на примере двухопорной балки

Выбор начала координат

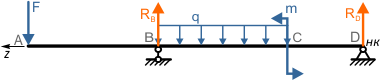
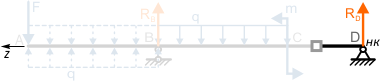
Начало координат в данной расчетной схеме выбираем в самой правой точке D балки, так как она расположена на опоре, и, следовательно, прогиб в этой точке будет отсутствовать.
Ось z направляем соответственно влево.

Теперь для данной балки правый торец будем считать ее началом, левый – соответственно концом.

Действия с распределенной нагрузкой

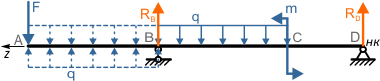
Как видно по схеме, действие распределенной нагрузки обрывается в точке B, не доходя до конца балки.

Поэтому ее действие необходимо продлить

при этом схема нагружения балки изменилась. Теперь, чтобы вернуться к начальной системе нагрузок, добавляем компенсирующую распределенную нагрузку обратного направления.

Это действие выполняется, потому что в уравнениях МНП параметр «c» учитывает только начало действия нагрузки.

Составление уравнений МНП

Универсальные уравнения МНП для заданной балки записываются последовательно по участкам со стороны начала координат.

При этом желательно отделять части уравнения для каждого из участков.

Запишем уравнение угловых перемещений θ_z метода начальных параметров.
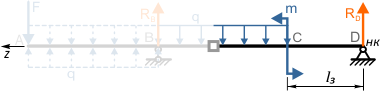
Участок CD
Мысленно закрепив балку между сечениями C и D,

в стороне начала балки видим только опорную реакцию R_D которая по правилу знаков записывается положительной, так как сжимает верхние слои балки.

Участок BC
На этом участке, как и на всех остальных, закрепив балку в произвольном месте, смотрим в сторону НК.

Видим момент m и распределенную нагрузку q.

Момент положителен т.к. сжимает верхние слои балки, нагрузка q отрицательна т.к. сжимает ее нижние слои.

Заметим, что здесь мы записали сразу всю «верхнюю» распределенную нагрузку q. В данном уравнении для других участков ее записывать больше не надо.
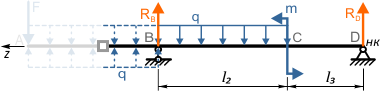
Участок AB
При рассмотрении данного участка к уравнению добавляются реакция в опоре B и «нижняя» компенсирующая нагрузка q.

Записываем их положительными, т.к. они стремятся сжать верхние слои балки.

Силы и моменты, приложенные в самом конце балки, в уравнения не входят.
На вопрос «Разве сила F не влияет на перемещение сечений?» ответ следующий: В уравнениях метода начальных параметров поперечная сила и момент, приложенные к концу балки оказывают влияние на перемещения опосредованно, через опорные реакции R.

Уравнение метода начальных параметров для прогибов составляется аналогично.

Определение начальных параметров

В правой части полученных уравнений известны все параметры кроме начальных θ₀ и y₀ (переменная z задается при решении).

Прогиб и угол наклона сечения в начале координат определим из опорных условий.

Балка закреплена на двух шарнирных опорах (точки B и D), в которых прогибы всегда равны нулю.

Граничные условия метода начальных параметров:

Так как точка D была принята за начало координат, то прогиб в этой точке и есть y₀, т.е. правильно выбрав НК, мы сразу определили один из двух начальных параметров.

Угловое перемещение в начале координат θ₀ рассчитаем из оставшегося (первого) опорного условия.

Для этого запишем уравнение прогибов для точки B, которое равно нулю

От НК до сечения B два участка, поэтому берется не все уравнение, а только его части, включающие нагрузки на соответствующих участках (CD и BC).
Из него выражаем и находим значение θ₀.

Теперь можно рассчитывать перемещения любого сечения балки.

Расчет перемещений

Для определения перемещений сечения расположенного на i-м участке от начала координат в расчете участвуют только части уравнений от НК до i-го участка включительно.

Выбирая нужное уравнение и задавая положение z сечений от начала координат определяются их угловые и линейные перемещения.

Например, для расчета угла наклона и прогиба сечения K расположенного на расстоянии z_K от НК

уравнения метода начальных параметров будут иметь вид:

Остается только подставить значения и провести расчеты.

Пример расчета перемещений сечений балки методом начальных параметров >
Примеры решения задач >
Лекции по сопромату >

Метод начальных параметров

Решение дифференциального
уравнения изогнутой оси балки заклю­чается
в составлении такой формы уравнения,
из которого можно было бы получить
непосредственную связь между прогибами
y
и абсциссой z.

Аналитический метод решения
состоит в двукратном интегрирова­нии
дифференциального уравнения, в результате
которого первое интегрирование дает
уравнение углов поворота

а второе интегрирование –
уравнение прогибов

После каждого интегрирования
получаем постоянную интегриро­вания.
Таким образом, для каждого участка балки
в результате двух­кратного интегрирования
уравнения изогнутой оси получают две
постоянные интегрирования.

Постоянные интегрирования опре­деляют
из условий закрепления балки (опорных
условий), а также из усло­вий на границах
смежных участков (граничных условий).
При этом:

а) каждая неподвижная или подвижная
опора дает одно условие – равенство
нулю прогиба в сечении балки на опоре;

б) от каждой жесткой
заделки (защемления) можно получить два
условия – равенство нулю прогиба и угла
поворота в сечении заделки;

в) от каждой границы двух смежных
участков полу­чаем два условия –
равенство между собой прогибов и углов
по­ворота общих сечений на границе
обоих участков.

Начальными параметрами
называются значения усилий и перемещений
в сечении балки, принятом за начальное
при отсчете абсцисс; другими
словами, это значения ординат эпюр при
z
= 0 (
).

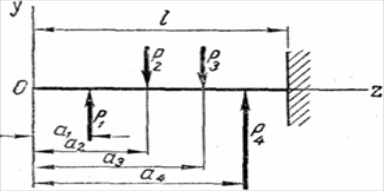
Сущность этого метода
покажем на примере балки постоянного
сучения, находящейся под действием
сосредоточенных сил P_1,
P_2,
… P_n
на расстояниях а₁,
а₂,
…, а_п
от левого конца
балки (рис.11).

Рис. 11.

Напишем дифференциальные уравнения
для участков балки.

Для 1-го участка (при а₁
≤ z
≤ a₂
)

Для 2-го участка (при а₂≤
z
≤ a₃
)

Для 3-го участка (при а₃≤
z
≤ a₄
)

…………………………………………………………………

Для n-го
участка (при а_n≤
z
≤ a_n+1
)

Проинтегрируем каждое из
составленных дифференциальных урав­нений
дважды, не раскрывая скобок. После
первого инте­грирования получим:

…………………………………………………………………

В результате второго интегрирования
получим:

…………………………………………………………………

При принятом способе
интегрирования все постоянные каждого
интегрирования получаются равными
между собой, так как на любой границе,
например при z
= а₃,
у обоих смежных
участков изогнутой оси балки касательная
и прогиб будут общими, т. е. у’₂
= у’₃
и у₂=
у₃.

Подставив в соответствующие
уравнения (второе и третье в каждой
группе) значения z
= a₃
и приравняв их
правые части, получим С₂
= С₃
и D₂
= D₃,
так как члены с множителем (z
– а₃)
обращаются в нуль.
Таким образом, граничные условия
представляются равенствами

и число постоянных интегрирования
сведется только к двум, которые всегда
могут быть определены исходя из условий
закрепления балки.

Равенства постоянных
интегрирования можно достигнуть и для
случая загружения балки равномерно
распределенной нагрузкой, даже если
такая нагрузка претерпевает разрыв в
некотором сечении, например при z
= а₂
(рис. 12). Здесь равенство
постоянных интегри­рования может
быть достигнуто при применении
искус­ственного приема, а именно:
распределенную
нагрузку продолжают до правого конца
балки. Чтобы
не изменить условия ее работы, к ней в
этой же части прикладывают нагрузку,
равную добавленной, но противоположную
по направлению.

Рис. 12.
Рис. 13.

При загружении балки
сосредоточенной парой т₀
(рис. 13) обыч­ный
способ составления выражения изгибающего
момента на втором участке не приведет
к равенству постоянных интегрирования.
В этом случае дифференциальные уравнения
будут иметь вид:

при

.

при

Как видно, член, учитывающий
во втором уравнении влияние т₀,
не содержит множителя
(z
– а). Следовательно,
после интегрирования он не обратится
в нуль на границе участков, а это
необходимо для получения равенства
постоянных интегрирования.

В этом случае применяем
искусственный прием: во второе уравнение
вместо члена т₀
(при значении z
> а) вводят
равный ему член т₀
(z
– а)⁰,
поскольку (z
– а)⁰
= 1. Благодаря этому
приему равен­ство постоянных
интегрирования будет обеспечено.

Выведем уравнение изогнутой
оси балки в общем виде для слу­чаев
простых загружении балок: сосредоточенными,
равномерно рас­пределенными нагрузками
и сосредоточенными парами сил.

При применении изложенных
выше искусственных приемов отпадает
необ­ходимость составлять и интегрировать
дифференциальные уравнения для каждого
участка балки; доста­точно ограничиться
составлением и интегрированием только
одного дифференциального уравнения
для последнего (крайнего правого) участка
и пользоваться этим урав­нением для
других участков.

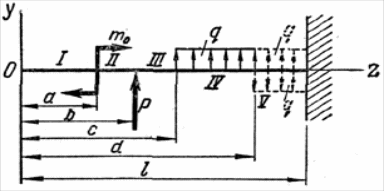
Рис. 14.

Пусть балка, изображенная
на рис. 14, подвержена действию на­грузок
т₀,
Р
и q.
Составим диффе­ренциальное
уравнение для последнего участка:

интегрируем его дважды:

Физический смысл постоянных
интегрирования С
и D
может быть выяснен
из рассмотрения упругой линии 1-го
участка.

Ввиду отсутствия нагрузки
на 1-м участке дифференциальное урав­нение
упругой линии будет EJy»
= 0.
Интегрируя его дважды, получим

Обозначив тангенс угла
наклона касательной к упругой линии и
начале координат ₀.
а прогиб в том же сечении f₀
при z
= 0,
получим

Следовательно, постоянная
С выражает тангенс угла наклона
каса­тельной в начале координат,
умноженный на жесткость сечения балки
EJ,
а постоянная D
– прогиб в начале
координат, умноженный на ту же величину
жесткости сечения балки.

Подставив значения постоянных
интегрирования С и
D
для случаев многократного
повторения рассмотренных видов нагрузок,
получим:

уравнение углов поворота

уравнение прогибов

Полученные уравнения называются общими,
или универсальными, уравнениями
упругой линии балки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

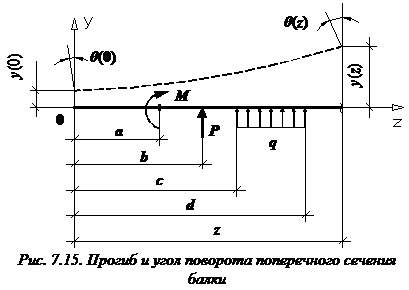
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 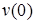и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

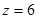
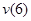
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки:

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .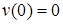

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

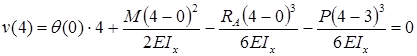
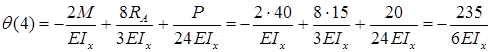
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

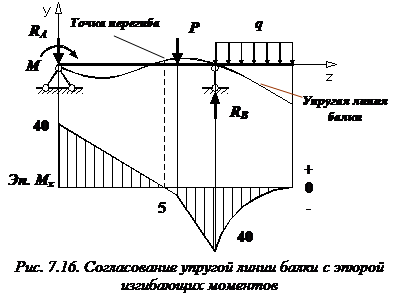
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.