Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya — координаты первой точки A,
xb и yb — координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya — координаты точки, лежащей на прямой,
{l;m} — координаты направляющего вектора прямой,
t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za — координаты первой точки A,
xb, yb и zb — координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za — координаты точки, лежащей на прямой,
{l;m;n} — координаты направляющего вектора прямой,
t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} — координаты точки, лежащей на прямой, {{l;m}} — координаты направляющего вектора прямой, t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b — x_a; y_b — y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.
Получить уравнение прямой по двум точкам бывает необходимо, когда мы решаем задачи, связанные с анализом различных фигур на плоскости. В этом случае бывает полезно знать уравнение прямой, проходящей через две точки. Например, составляя такое уравнение мы уже знаем – как проходит прямая, с какие углом наклона к осям координат и можем рассчитать расположение прямой по отношению к другим прямым или к фигурам.
Составляем уравнение прямой по двум точкам
Итак, пусть нам даны две точки и
. Наша прямая проходит через две эти точки, давайте получим уравнение этой прямой. Уравнение пучка прямых, проходящих через точку с координатами
имеет вид:
То есть если прямая проходит через две точки и
она – одна из этого пучка прямых, проходящих через точку
и эта прямая имеет определенный коэффициент
. Значит, координаты точки
должны удовлетворять уравнению (1), то есть
.
Находим из (2) :
и подставим в уравнение (1):
.
Преобразовывая уравнение (3) получим:
Это и есть уравнение прямой, проходящей через две точки
и
.
Примечание: если точки и
лежат на прямой, которая параллельна оси
или оси
, то уравнение прямой будет иметь вид
или
соответственно.
Зная координаты любых двух точек прямой, мы всегда сможем определить угловой коэффициент прямой:
Геометрический вывод уравнения прямой
Действительно, давайте нарисуем прямую в системе координат и отметим на прямой две точки
и
, координаты которых известны
и
и отметим на этой прямой произвольную точку
.
Из подобия треугольников и
находим:
Из рисунка видно, что:
,
Таким образом, получаем уравнение прямой по двум точкам:
Задача
Составим уравнение прямой, проходящей через две точки и
.
Решение: Имеем ,
,
,
. Подставим эти значения в уравнение прямой, проходящей через две заданные точки:
Умножим левую и правую части уравнения на 5, получим:
– получившееся уравнение прямой.
Давайте сделаем проверку – если мы все решили правильно, то при подстановке координат точек и
мы получим верное равенство. Итак, подставим сначала координаты точки
:
Теперь координаты точки :
Значит, уравнение прямой мы нашли верно.
Ответ:
Условие прохождения прямой через три заданные точки
Если нам в задаче нужно убедиться, что три точки с заданными координатами лежат на одной прямой, можно рассуждать так:
- Если две точки с заданными координатами образуют прямую, то их координаты удовлетворяют уравнению прямой, проходящей через две точки.
- Если третья точка также лежит на этой прямой, то и ее координаты будут удовлетворять этому уравнению.
Таким образом, если нам даны три точки ,
и
, лежащие на одной прямой, то их координаты будут удовлетворять условию:
Теперь вы легко сможете составить уравнение прямой по двум точкам, а также найти угловой коэффициент прямой и проверить – принадлежит ли третья точка этой прямой.
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.
Пример 1.
Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).
Решение:
1 способ — составим уравнение прямой с угловым коэффициентом.
Уравнение прямой с угловым коэффициентом имеет вид y=kx+b. Подставив координаты точек A и B в уравнение прямой (x= -3 и y=9 — в первом случае, x=2 и y= -1 — во втором), получаем систему уравнений, из которой находим значения k и b:
Сложив почленно 1-е и 2-е уравнения, получим: -10=5k, откуда k= -2. Подставив во второе уравнение k= -2, найдём b: -1=2·(-2)+b, b=3.
Таким образом, y= -2x+3 — искомое уравнение.
2 способ — составим общее уравнение прямой.
Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:
Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.
Умножив первое уравнение системы на -1 и сложив почленно со вторым:
получим: 5a-10b=0. Отсюда a=2b.
Подставим полученное выражение во второе уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Подставляем a=2b, c= -3b в уравнение ax+by+c=0:
2bx+by-3b=0. Осталось разделить обе части на b:
2x+y-3=0.
Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:
y= -2x+3.
3 способ — составим уравнение прямой, проходящей через 2 точки.
Уравнение прямой, проходящей через две точки, имеет вид:
Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)
(то есть x1= -3, y1=9, x2=2, y2= -1):
и упростим:
По основному свойству пропорции
откуда 2x+y-3=0.
В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.
Замечание.
Если при подстановке координат заданных точек один из знаменателей уравнения
окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.
Пример 2.
Составить уравнение прямой, проходящей через две точки C(5; -2) и D(7;-2).
Решение:
Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D:
Пример 3.
Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).
Решение:
В этой статье мы рассмотрим концепцию уравнения прямой прямой. Мы попытаемся понять общее уравнение прямой, формулу прямой, способ нахождения уравнения прямой и откроем для себя другие интересные аспекты этого. Попробуйте свои силы в решении нескольких интересных примеров и вопросов для лучшего понимания концепции.
Определение
Уравнение прямой — может быть записано в различных формах. Прямая линия -это двумерная геометрическая фигура, которая простирается на обоих своих концах до бесконечности.
Для того чтобы освоить описанные приемы, необходимо много практиковаться, чтобы они стали привычными.
После прочтения информации по этой теме вы должны уметь:
- находить уравнение прямой прямой, учитывая ее наклон и пересечение с осью y;
- находить уравнение прямой, учитывая ее наклон и одну точку, лежащую на ней;
- найти уравнение прямой, учитывая две точки, лежащие на ней;
- дать уравнение прямой в любой из форм y = mx + c или ax + by + c = 0
Уравнения прямых могут принимать различные формы в зависимости от фактов, которые мы знаем о прямых. Итак, для начала предположим, что у нас есть прямая линия содержащая точки из следующего списка.
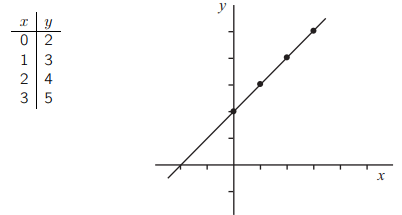
На прямой есть еще много точек, но уже достаточно, чтобы увидеть закономерность. Если мы возьмем любое значение x и прибавим 2, мы получим соответствующее значение y: 0 + 2 = 2, 1 + 2 = 3, 2 + 2 = 4, и так далее. Между координатами x и y любой точки на прямой существует фиксированная зависимость, и уравнение y = x + 2 всегда верно для точек на прямой. Мы можем обозначить прямую, используя это уравнение.
Уравнение прямой, проходящей через начало координат с заданным коэффициентом
Предположим, что у нас есть прямая с уравнением y = x. Тогда для каждой точки на прямой координата y должна быть равна координате x. Таким образом, прямая будет содержать точки из следующего списка.
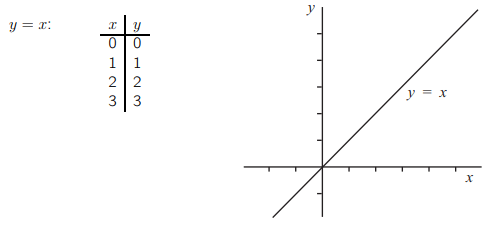
Мы можем найти коэффициент прямой, используя формулу для нахождения коэффициента:
[ m=frac{y 2-y 1}{x 2-x 1} ]
Далее следует подставить первые два набора значений из таблицы. Получаем:
[ m=frac{1-0}{1-0}=1 ]
Таким образом, коэффициент этой прямой равен 1.
А как насчет уравнения y = 2x? Оно также представляет собой прямую линию, и для всех точек на y в два раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующем списке.
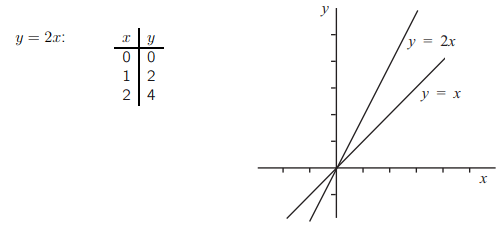
Если мы вычислим коэффициент прямой y = 2x, используя первые два набора значений в таблице, то получим:
[ m=frac{2-0}{1-0}=2 ]
Таким образом, коэффициент этой прямой равен 2.
Теперь возьмем уравнение y = 3x. Оно также представляет собой прямую линию, и для всех точек на прямой. Каждая точка y в три раза больше соответствующего значения x. Таким образом, линия будет содержать точки из следующего списка.
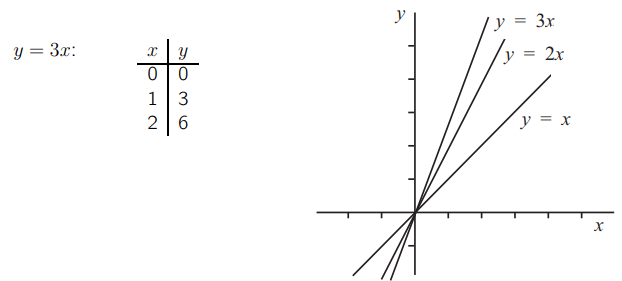
Если мы вычислим коэффициент прямой y = 3x, используя первые два набора значений в таблице, мы получим:
[ m=frac{3-0}{1-0}=3 ]
Следовательно, коэффициент этой прямой равен 3.
Мы можем начать видеть здесь закономерность. Все эти прямые имеют уравнения, где y равно некоторому числу, умноженному на x. И в каждом случае линия проходит через начало координат, а коэффициент прямой равен m.
Таким образом, если бы у нас была прямая с уравнением y = 13x, то мы бы указали, что коэффициент прямой будет равен 13. Аналогично, если бы у нас была прямая с уравнением y = -2x, то коэффициент будет равен -2. Таким образом, в общем случае уравнение y = mx представляет собой прямую линию, проходящую через начало координат с коэффициентом m.
Важно
Уравнение прямой с коэффициентом m, проходящей через начало координат, имеет вид:
[y = mx]
Пересечение прямой y
Рассмотрим прямую линию с уравнением y = 2x + 1. Это уравнение имеет несколько иную форму в отличие от тех, которые мы видели ранее. Чтобы нарисовать график прямой, мы должны вычислить некоторые значения.
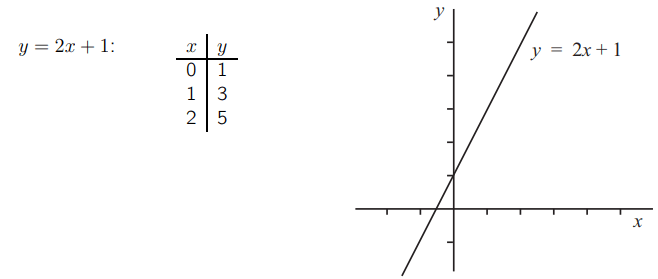
Обратите внимание, что при x = 0 значение y равно 1. Значит, эта прямая пересекает ось y в точке y = 1.
А как насчет прямой y = 2x + 4? Мы снова можем вычислить некоторые значения.
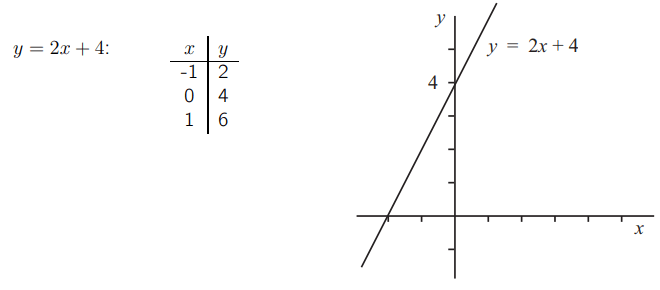
Эта линия пересекает ось y в точке y = 4.
А как насчет прямой y = 2x — 1? Мы снова можем вычислить некоторые значения.
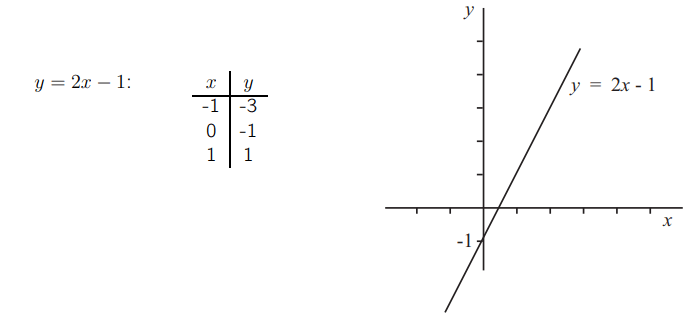
Эта линия пересекает ось y в точке y = — 1.
Общее уравнение прямой — y = mx + c, где m — коэффициент, а y = c — значение на оси у, при через которое проходим прямая.
Это число c является пересечением с осью y.
Важно
Уравнение прямой с коэффициентом m и точкой пересечения c на оси y имеет вид:
[y = mx + c]
Иногда нам задают уравнение прямой в другой форме. Предположим, у нас есть уравнение 3y — 2x = 6. Как показать, что оно представляет собой прямую линию, и найти ее коэффициент и значение точки пересечения с осью y?
Мы можем использовать алгебраическую перестановку, чтобы получить уравнение в виде y = mx + c:
3y — 2x = 6,
3y = 2x + 6,
[y=frac{2}{3} x+2]
Теперь уравнение находится в стандартной форме, и мы видим, что коэффициент равен [frac{2}{3}], а значение точки пересечения с осью y равно 2.
Мы также можем работать в обратном направлении. Предположим, мы знаем, что прямая имеет коэффициент [frac{1}{5}] и имеет вертикальное пересечение в точке y = 1. Каким будет ее уравнение?
Чтобы найти уравнение, достаточно подставить нужные значения в общую формулу y = mx + c.
Здесь m равно [frac{1}{5}], а c — 1, поэтому уравнение равно y =[frac{1}{5}]x + 1. Если мы хотим убрать дробь, мы можем также привести уравнение к виду 5y = x + 5, или 5y — x — 5 = 0.
Уравнение прямой прямой с заданным коэффициентом, проходящее через заданную точку на оси у
Предположим, что мы хотим найти уравнение прямой с коэффициентом [frac{1}{3}], которое проходит через точку (1, 2). Здесь, хотя мы знаем коэффициент, мы не знаем значение точки пересечения с осью у, оно равно c.
Начнем с общего уравнения прямой y = mx + c.
Мы знаем, что коэффициент равен [frac{1}{3}], именно поэтому мы можем сразу подставить это значение на место m. Это дает: [y=frac{1}{3} x+c]
Теперь мы используем тот факт, что прямая проходит через (1, 2). Это означает, что когда x = 1, y должно быть равна 2. Подставляя эти значения, находим:
[2=frac{1}{3}(1)+c]
так что
[c=2-frac{1}{3}=frac{5}{3}]
Таким образом, уравнение прямой имеет вид:
[y=frac{1}{3} x+frac{5}{3}]
Мы можем вывести общую формулу для задач такого типа, используя тот же метод. Мы возьмем общую прямую с коэффициентом m, проходящую через фиксированную точку [mathrm{A}left(x_{1}, y_{1}right)].
Начнем с общего уравнения прямой y = mx + c. Теперь мы используем тот факт, что прямая проходит через точку [mathrm{A}left(x_{1}, y_{1}right)]. Это означает, что при x = [x_{1}], y должно быть [y_{1}]. Подставляя эти значения, находим:
[y_{1}=m x_{1}+c]
так что
[mathrm{c}=y_{1}-mathrm{m} x_{1}]
Таким образом, уравнение прямой имеет вид y = mx + [y_{1}-mathrm{m} x_{1}].
Мы можем записать его в альтернативной форме
[mathrm{y}-y_{1}=mathrm{m}left(mathrm{x}-x_{1}right)]
Тогда это прямая с уклоном m, проходящая через точку [left(x_{1}, y_{1}right)]. Таким образом, эта общая форма полезна, если вы знаете коэффициент и одну точку на прямой.
Важно
Уравнение прямой с коэффициентом m, проходящей через точку [left(x_{1}, y_{1}right)], имеет вид:.
[y-y_{1}=mleft(x-x_{1}right)]
Например, мы знаем, что прямая имеет коэффициент -2 и проходит через точку (-3, 2).
Мы можем воспользоваться формулой [y-y_{1}=mleft(x-x_{1}right)] и сразу подставить значения:
y — 2 = -2(x — (-3))
y — 2 = -2(x + 3)
y — 2 = -2x — 6
y = -2x — 4 .
Упражнение 1
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) коэффициент 3, проходящей через (1, 4);
(2) коэффициент -2, проходящей через (2, 0);
(3) коэффициент [frac{2}{5}], проходящий через (5, -1);
(4) коэффициент 0, проходящий через (-1, 2);
(5) коэффициент -1, проходящий через (1, -1).
Нет времени решать самому?
Наши эксперты помогут!
Уравнение прямой проходящей через две заданные точки
Что нужно сделать, если мы хотим найти уравнение прямой, проходящей через две точки (-1, 2) и (2, 4)?
Здесь мы не знаем коэффициент прямой, поэтому кажется, что мы не можем использовать ни одну из формул, которые мы знаем на данный момент. Но мы знаем две точки на прямой, и поэтому можем использовать их для определения коэффициента.
Следует просто использовать формулу [mathrm{m}=frac{left(y_{2}-y_{1}right)}{left(x_{2}-x_{1}right)}].
Получаем: [m=frac{4-2}{2-(-1)}=frac{2}{3}].
Таким образом, коэффициент прямой равен [frac{2}{3}].
Нам известны две точки на прямой, поэтому мы можем использовать одну из них в формуле y — y1 = m(x — x1). Если мы возьмем точку (2, 4), то получим:
y — 4 = [frac{2}{3}](x — 2)
3y — 12 = 2x — 4
3y = 2x + 8
[y=frac{2}{3} x+frac{8}{3}]
Как и в предыдущих случаях, будет полезно найти общую формулу, которую можно использовать для примеров такого рода.
Итак, предположим, что общая прямая проходит через две точки [mathrm{A}left(x_{1}, y_{1}right) text { и } mathrm{B}left(x_{2}, y_{2}right)]. Пусть общая точка на прямой будет P(x, y).
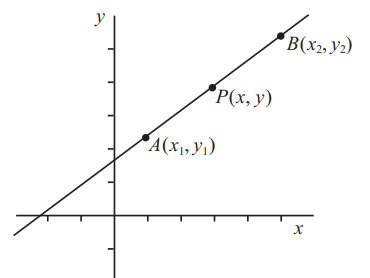
Теперь мы знаем, что коэффициент AP должен быть таким же, как коэффициент AB, так как все три точки лежат на одной прямой. Но коэффициент AP равен:
[mathrm{mAP}=frac{left(y_{2}-y_{1}right)}{left(x_{2}-x_{1}right)}]
тогда как коэффициент AB равен:
[mathrm{mAB}=frac{left(y_{2}-y_{1}right)}{left(x_{2}-x_{1}right)}]
Тогда mAP = mAB, поэтому мы имеем:
[ frac{left(y-y_{1}right)}{left(mathrm{x}-mathrm{x}_{1}right)}=frac{left(y_{2}-y_{1}right)}{left(mathrm{x}_{2}-mathrm{x}_{1}right)} ]
Эта формула довольно сложна, но ее легче запомнить, если все члены с участием y находятся на одной стороне, а все члены с участием x — на другой. Если мы будем преобразовывать эту формулу, сначала мы сможем получить:
[mathrm{y}-y_{1}=mathrm{x}-mathrm{x}_{1} frac{left(y_{2}-y_{1}right)}{left(mathrm{x}_{2}-mathrm{x}_{1}right)}]
а затем
[frac{left(y-y_{1}right)}{left(y_{2}-y_{1}right)}=frac{left(x-x_{1}right)}{left(x_{2}-x_{1}right)}]
Запомнить эту формулу вам поможет замечание, что закономерность в левой части, с участием y, такая же, как и с участием x в правой части.
Важно
Уравнение прямой, проходящей через две точки (x1, y1) и (x2, y2), имеет вид:
[frac{left(y-y_{1}right)}{left(y_{2}-y_{1}right)}=frac{left(x-x_{1}right)}{left(x_{2}-x_{1}right)}]
Теперь мы можем использовать эту формулу для решения примеров. Предположим, что мы хотим найти уравнение прямой, проходящей через две точки (1, -2) и (-3, 0).
Попробуем подставить в формулу и решить:
[frac{(y-(-2))}{(0-(-2))}=frac{(x-1)}{(-3-1)}]
[frac{y+2}{2}=frac{x-1}{-4}]
[ y+2=frac{x-1}{-2} ]
[ y+2=-frac{1}{2}(x-1) ]
-2y — 4 = x — 1
-2y = x + 3
[ y=-frac{1}{2} x-frac{1}{2} ]
Таким образом, прямая имеет коэффициент — [frac{1}{2}], а значение и точку пересечения с осью [y-frac{1}{2}].
Мы также можем преобразовать уравнение, чтобы получить 2y = -x — 3, или 2y + x + 3 = 0.
Упражнение 2
Найдите уравнение описанных ниже прямых (приведите уравнение в виде y = mx + c):
(1) проходящей через (4, 6) и (8, 26),
(2) проходящей через (1, 1) и (4, -8),
(3) проходящий через (3, 4) и (5, 4),
(4) проходящий через (0, 2) и (4, 0),
(5) проходящий через (-2, 3) и (2, -5).
Общее уравнение прямой прямой
Существует еще одна форма уравнения прямой, которая иногда бывает необходима. Это уравнение: ax + by + c = 0 .
Мы уже писали уравнения в этой форме для некоторых наших примеров. Мы можем увидеть некоторые особые случаи этого уравнения, установив либо a, либо b равными нулю.
Если a = 0, то получаются прямые с общим уравнением by + c = 0, то есть y = [-frac{c}{b}].
Эти прямые горизонтальны, то есть параллельны оси x.
Если b = 0, то получаются две прямые с общим уравнением ax + c = 0, следовательно есть x = [frac{c}{a}].
Эти прямые вертикальны, то есть параллельны оси y. Уравнение вертикальной прямой не может быть записано в виде y = mx + c. Уравнение ax + by + c = 0 является наиболее общим уравнением для прямой и может использоваться там, где другие формы уравнения не подходят.
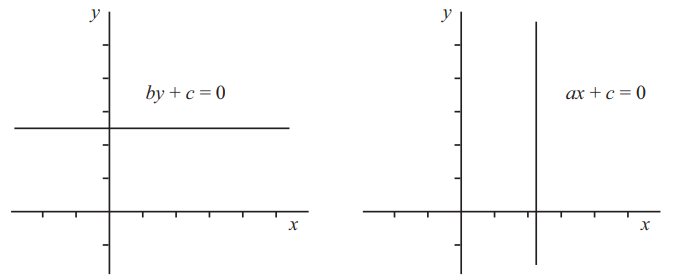
Важно
Общим уравнением прямой прямой является уравнение:ax + by + c = 0.
Если a = 0, то линия горизонтальна, а если b = 0, то линия вертикальна.
Упражнение 3
Найдите уравнение описанных ниже прямых (приведите уравнение в виде
ax + by + c = 0, где a, b и c — целые числа и a > 0):
(1) прямая из упражнения 2 (2)
(2) прямая в упражнении 2 (5)
(3) прямая в упражнении 3 (3)
(4) прямая в упражнении 4 (2)
(5) прямая в упражнении 4 (4)
(6) прямая в упражнении 4 (5)
(7)прямая , проходящая через (3, -2) и (3, 2)
(8) вертикальная прямая, проходящая через точку (0, [frac{2}{3}]).
Упражнение 1
(1) y = 3x + 1,
(2) y = -2x + 4,
(3) y =x — 3,
(4) y = 2,
(5) y = — x.
Упражнение 2
(1) y = 5x — 14,
(2) y = -3x + 4,
(3) y = 4,
(4) y = —x + 2,
(5) y = -2x — 1.
Упражнение 3
(1) 2x + y + 1 = 0,
(2) 3x + 4y — 2 = 0,
(3) 2x — 5y — 15 = 0,
(4) 3x + y — 4 = 0,
(5) x + 2y — 4 = 0,
(6) 2x + y + 1 = 0,
(7) x — 3 = 0,
(8) x = 0.


