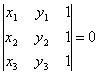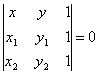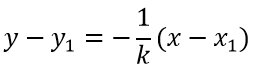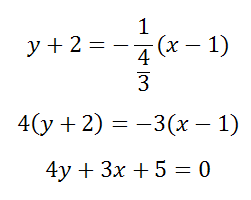Как составить уравнение прямой перпендикулярной отрезку

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k1x+b1 — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

    [y = - frac{1}{{k_1 }}x + b_2 .]

Если эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b.

Примеры.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Решение:

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

    [k_2 = - frac{1}{{k_1 }} = - frac{1}{5} = - 0,2.]

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

    [y = - 0,2x + b.]

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

    [3 = - 0,2 cdot ( - 10) + b,]

откуда b=1.

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

    [y = - 0,2x + 1.]

Ответ: y= -0,2x+1.

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Решение:

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

Ответ: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Решение:

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Ответ: x=7.

Источник

  1. Image titled Find the Equation of a Perpendicular Line Step 1

    1

    Simplify the equation of the line. If you are given the equation of a line and one common point and asked to find a line that runs perpendicular to it, it is important that you first convert the equation into the y=mx+b format. To do this, you want to get the y by itself.[3]

  2. Image titled Find the Equation of a Perpendicular Line Step 2

    2

    Calculate the opposite reciprocal of the slope. When a line is perpendicular to another line, the slope will be the negative opposite of the original line. This is called the opposite reciprocal. The lines cross each other at a right angle, so the slopes must be opposite. Two perpendicular slopes multiplied together will always equal -1.[4]

    Advertisement

  3. Image titled Find the Equation of a Perpendicular Line Step 3

    3

    Plug the point into the slope equation to find the y-intercept. Now that you have the slope of the perpendicular line, you can plug the value of the slope and the point you were given into a slope equation. This will give you the value of the y-intercept. Using the y-intercept, you can move on to complete the slope equation.[5]

  4. Image titled Find the Equation of a Perpendicular Line Step 4

    4

    Solve the equation for the y-intercept. Once you have your values entered into the slope equation, it is time to isolate b, or the y-intercept. To isolate b, you must move all other numbers from one side of the equation. After you solve for the y-intercept, you will know all of the numbers needed to write the equation of the perpendicular line.[6]

  5. Image titled Find the Equation of a Perpendicular Line Step 5

    5

    6. Advertisement

  1. Image titled Find the Equation of a Perpendicular Line Step 6

    1

    Understand the coordinates you were given. If you are given three coordinates from two perpendicular lines, they cannot all be used for the same equations. The first two coordinates will be used for one line, and the third will be used once you begin calculating the equation of the perpendicular line. The goal is finding two perpendicular y=mx+b equations.[8]

  2. Image titled Find the Equation of a Perpendicular Line Step 7

    2

  3. Image titled Find the Equation of a Perpendicular Line Step 8

    3

  4. Image titled Find the Equation of a Perpendicular Line Step 9

    4

    Simplify the equation to solve for y. Once you have your chosen point and slope plugged into the equation, it is time to simplify. This will give you the equation of one line. After you know the equation of this line, you will be able to figure out the equation of the line that runs perpendicular to it.[11]

  5. Image titled Find the Equation of a Perpendicular Line Step 10

    5

    Find the slope of the perpendicular line using the opposite reciprocal. A line perpendicular to another line will always have an opposite slope. If the slope of the original line is a positive whole number, then the slope of the perpendicular line will be a negative fraction. Two perpendicular slopes multiplied together will always equal -1.[12]

  6. Image titled Find the Equation of a Perpendicular Line Step 11

    6

    7. Advertisement

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

About This Article

Thanks to all authors for creating a page that has been read 70,426 times.

Did this article help you?

Источник

210

Определить, какие из точек M1(3; 1), M2(2; 3), M3(6; 3), M4(-3;
-3), M5(3; -1), M6(-2; 1) лежат
на прямой и какие на ней не лежат. 211 Точки P1,
P2, P3, P4, P5 расположены
на прямой ; их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 212 Точки Q1,
Q2, Q3, Q4, Q5 расположены
на прямой ; их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 213 Определить точки
пересечения прямой с координатными
осями и построить эту прямую на чертеже. 214 Найти точку
пересечения двух прямых , . 215 Стороны АВ, ВС и АС
треугольника АВС даны соответственно
уравнениями , , . Определить
координаты его вершин. 216 Даны уравнения двух
сторон параллелограмма , и уравнение одной из
его диагоналей .
Определить координаты вершин
этого параллелограмма. 217 Стороны
треугольника лежат на прямых , , . Вычислить его площадь S. 218 Площадь
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой . Определить координаты вершины С. 219 Площадь
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой .
Определить координаты третьей
вершины С. 220 Составить
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy: 220.1 k=2/3, b=3; 220.2 k=3, b=0; 220.3 k=0, b=-2; 220.4 k=-3/4, b=3; 220.5 k=-2, b=-5; 220.6 k=-1/3, b=2/3. 221 Определить угловой
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых: 221.1 ; 221.2 ; 221.3 ; 221.4 ; 221.5 . 222 Дана прямая . Определить угловой коэффициент k
прямой: 222.1 Параллельной
данной прямой; 222.2 Перпендикулярно к
данной прямой. 223 Дана прямая . Составить уравнение прямой,
проходящей через точку М0(2; 1): 223.1 Параллельно данной
прямой; 223.2 Перпендикулярно
данной прямой. 224 Даны уравнения двух
сторон прямоугольника , и одна из его вершин
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника. 225 Даны уравнения двух
сторон прямоугольника , и уравнение одной из
его диагоналей .
Найти вершины прямоугольника. 226 Найти проекцию
точке Р(-5; 13) относительно прямой . 227 Найти точку Q,
симметричную точке Р(-5; 13) относительно прямой . 228 В каждом из
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними: 228.1 , ; 228.2 , ; 228.3 , ; 228.4 , ; 228.5 , . 229 Вычислить угловой
коэффициент k прямой, проходящей через две данные
точки: 229.1 M1(2;
-5), M2(3; 2); 229.2 P(-3, 1), Q(7; 8); 229.3 A(5; -3), B(-1; 6). 230 Составить
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам. 231 Даны середины
сторон треугольника M1(2; 1), M2(5;
3), M3(3; -4). Составить
уравнение его сторон. 232 Даны две точки P(2; 3),
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку . 233 Составить
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую. 234 Даны вершины
треугольника M1(2; 1), M2(-1; -1),
M3(3; 2). Составить уравнения
его высот. 235 Стороны
треугольника даны уравнениями , , . Определить точку пересечения его
высот. 236 Даны вершины
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В. 237 Даны вершины
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А. 238 Составить
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0). 239 Через точки M1(-1; 2), M2(2; 3) проведена
прямая. Определить точки пересечения этой прямой
с осями координат. 240

Доказать,
что условие, при котором три точки M1(x1,
y1), M2(x2, y2), M3(x3,
y3) лежат на одной прямой,
может быть записано в следующем виде:

241

Доказать,
что уравнение прямой, проходящей через две
данные точки M1(x1, y1),
M2(x2, y2), может
быть записано в следующем виде:

242 Даны
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей. 243 Даны две смежные
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма. 244 Даны уравнения двух
сторон прямоугольника , и уравнение его
диагонали . Составить уравнения остальных
сторон и второй диагонали этого прямоугольника. 245 Даны вершины
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А. 246 Составить
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15). 247 Найти проекцию
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1). 248 Найти точку M1, симметричную точке М2(8;
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2). 249 На оси абсцисс
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей. 250 На оси ординат
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей. 251 На прямой найти такую точку Р, сумма
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей. 252 На прямой найти такую точку Р, разность
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей. 253 Определить угол между двумя прямыми: 253.1 , ; 253.2 , ; 253.3 , ; 253.4 , . 254 Дана прямая . Составить уравнение прямой,
проходящей через точку M0(2; 1) под углом 450 к данной прямой. 255 Точка А(-4; 5)
является вершиной квадрата, диагональ которого
лежит на прямой . Составить
уравнения сторон и второй диагонали этого
квадрата. 256 Даны две
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон. 257 Точка E(1; -1) является
центром квадрата, одна из сторон которого лежит
на прямой . Составить уравнения
прямых, на которых лежат остальные стороны этого
квадрата. 258 Из точки M0(-2; 3) под углом к оси
Ox направлен луч света. Известно, что . Дойдя
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи. 259 Луч света направлен
по прямой , луч от нее отразился.
Составить уравнение прямой, на которой лежит
отраженный луч. 260 Даны уравнения
сторон треугольника , , . Доказать, что этот треугольник
равнобедренный. Решить задачу при помощи
сравнения углов треугольника. 261 Доказатть, что
уравнение прямой, проходящей через точку M1(x1; y1) параллельно
прямой , может быть записано в виде . 262 Составить
уравнение прямой, проходящей через точку М1(2: -3) параллельно
прямой: 262.1 ; 262.2 ; 262.3 ; 262.4 ; 262.5 . 263 Доказать, что
условие перпендикулярности прямых ; может быть записано
в следующем виде: . 264 Установить, какие
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 264.1  , ; 264.2 , ; 264.3 , ; 264.4 , ; 264.5 , ; 264.6 , . 265

Доказать,
что формула для определения угла между
прямыми , может
быть записана в следующей форме:

266 Определить угол , образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 266.1 , ; 266.2  , ; 266.3  , . 267 Даны две вершины
треугольника M1(-10; 2), M2(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M3. 268 Даны две вершины A(3;
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника. 269 В треугольнике АВС
даны: уравнение стороны АВ: , уравнения
высот АМ: и BN: . Составить уравнения двух
других сторон и третьей высоты этого
треугольника. 270 Составить
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан , . 271 Составить
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот , . 272 Составить
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис , . 273 Составить
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты и
биссектрисы , проведенных из одной вершины. 274 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты и биссектрисы , проведенных из
различных вершин. 275 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты и медианы , проведенной из
одной вершины. 276 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты и медианы , проведенных из
различных вершин. 277 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы и медианы , проведенных из
одной вершины. 278 Составить
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы и медианы , проведенных из
различных вершин. 279 Составить
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми , образует
треугольник с площадью, равной 1,5. 280 Среди прямых,
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми , , делится в точке Р
пополам. 281 Через точку Р(-3; -1)
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми , , делится
в точке Р пополам. 282 Через точку Р(0; 1)
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми , , делился бы в точке Р
пополам. 283 Составить
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми , , равна . 284 Составить
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми , , равна 5.
Источник


2.5.4. Как найти прямую, перпендикулярную данной?

В отличие от предыдущих задач п. 2.5, рассмотренные ниже схемы работают лишь в декартовой системе

координат (но не в общем аффинном случае):

Задача 79

Прямая задана уравнением  в декартовой системе координат. Составить

уравнение перпендикулярной прямой , проходящей через точку .

Решение: по условию известна точка  ( – значок принадлежности), и нам неплохо бы найти направляющий вектор прямой . Так как прямые перпендикулярны, то фокус прост:  из уравнения  «снимаем» вектор нормали: , который и будет направляющим вектором прямой .

Уравнение прямой  составим по точке  и направляющему вектору :

Ответ:

Развернём геометрический этюд:
И аналитическая проверка решения:

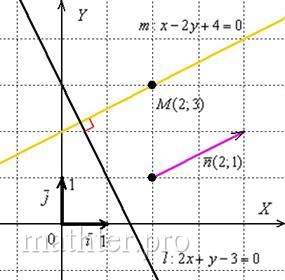
1) Из уравнений ,   вытаскиваем направляющие векторы  и с помощью скалярного произведения приходим к выводу, что прямые действительно

перпендикулярны:
.
Кстати, можно использовать векторы нормали, это даже проще.

2) Проверяем, удовлетворяет ли точка  полученному уравнению
Оба пункта легко выполнить устно!

Самостоятельно:

Задача 80

Найти точку пересечения перпендикулярных прямых , если известно уравнение  в декартовой системе координат  и точка .

В задаче несколько действий, поэтому решение удобно оформить по пунктам.

И наше увлекательное путешествие продолжается:

2.5.5. Как вычислить расстояние от точки до прямой?

2.5.3. Как найти точку пересечения прямых?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Источник

Skip to content

1.Пусть прямая, проходит через точку T1(x1;y1) и перпендикулярно прямой y=kx+b, тогда её можно представить уравнением (уравнение прямой перпендикулярной данной прямой):
Уравнение прямой, проходящей через данную точку перпендикулярно к данной прямой

Это и есть уравнение прямой, проходящей через точку перпендикулярно к прямой.
2.  Если прямая проходит через ту же точку T1(x1;y1) и перпендикулярно прямой, но только записанной в виде Ax+By+C = 0, то уравнение можно представить как:

A (y − y1) − B (x − x1 ) = 0

Пример 1
Составить уравнение прямой, проходящей через точку L(1;-2) и перпендикулярно прямой

4x-3y-1 =  0 (на рисунке прямая, обозначенная красным цветом)

Решение
Данную прямую можно представить уравнением y = 4/3x-1/3 (здесь a = 4/3). Уравнение искомой прямой есть

Пример 2
Составить уравнение прямой, проходящей через точку M(-1;-2) и перпендикулярной к прямой 3y+2=0

Решение
Здесь A=0, B=3, получаем 3(x+1)=0, т.е. x+1=0. В этом случае формула неприменима.

23237


Источник

Понравилась статья? Поделить с друзьями:
  • Наследство как найти имущество
  • Как найти координаты аналитическим способом
  • Как составить свой автопортрет пример
  • Как исправить прикус остеопат
  • Как найти сколько градусов в круге