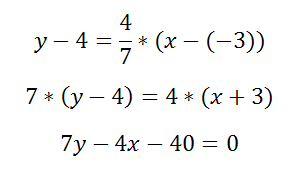Как составить уравнение прямой по одной точке параллельно прямой - Исправление недочетов и поиск решений вместе с Examum.ru

Как составить уравнение прямой параллельной данной прямой и проходящей через данную точку?

Пусть y = k₁x+b₁ — данная прямая. С учётом условия параллельности прямых уравнение прямой, параллельной данной, имеет вид y = k₁x+b₂.

Так как эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b:

y_o= k₁∙x_o+ b₂, откуда b₂= y_o— k₁∙x_o.

Примеры.

1) Составить уравнение прямой, которая проходит через точку A(4;21) и параллельна прямой y=3x-8.

Решение:

Так как угловые коэффициенты у параллельных прямых равны, то k₂=k₁=3 и уравнение прямой, параллельной прямой y=3x-8, имеет вид y=3x+b. Так как искомая прямая проходит через точку A(4;21), подставляем в уравнение прямой координаты A (x=4; y=21):

21=3·4+b, откуда находим b: b= 21-12= 9.

Итак, уравнение прямой, параллельной прямой y=3x-8, проходящей через точку A(4;21) — y=3x+9.

Ответ: y=3x+9.

2) Написать уравнение прямой, параллельной прямой x=5, проходящей через точку B(-3; 5).

Решение:

Так как прямая x=5 параллельна оси Oy, то и параллельная ей прямая также параллельна Oy, а значит, уравнение этой прямой имеет вид x=a.

Так как эта прямая проходит через точку B(-3; 5), то её абсцисса удовлетворяет уравнению прямой: a= -3.

Итак, уравнение прямой, параллельной прямой x=5 и проходящей через точку B(-3; 5) — x= -3.

Ответ: x= -3.

3) Написать уравнение прямой, параллельной прямой y= -11, проходящей через точку K(2; 4).

Решение:

Так как прямая y= -11 параллельна оси Ox, то и параллельная ей прямая также параллельна оси Ox. Поэтому уравнение прямой имеет вид y=b.

Поскольку эта прямая проходит через точку K(2; 4), то её ордината удовлетворяет уравнению прямой: b=4.

Уравнение прямой, параллельной прямой y= -11 и проходящей через точку K(2; 4) — y=4.

Ответ: y=4.

Источник

Пусть прямая, проходящая через точку K₁(x₁;y₁) и параллельная прямой y=kx+b, записывается в виде уравнения:

y-y₁=k·(x-x₁)

Это уравнение называется уравнением прямой, проходящей через данную точку K₁(x₁;y₁) параллельно данной прямой y=kx+b

Пример 1
Составить уравнение прямой, проходящей через точку M(-3;4) и параллельно прямой

4x-7y+1=0

Решение
Данную прямую можно представить уравнением y=4/7x+1/7 (здесь k=4/7). Уравнение искомой прямой есть

Решение представим на графике

Пример 2
Составить уравнение прямой, проходящей через точку (-3;4) и параллельно прямой
5x+6=0
Решение

Здесь A=5, B=0, получаем 5(x+3)=0, т.е. x+2=0. В этом случае формула неприменима.

32010

Источник

2.5.2. Как найти прямую, параллельную данной?

За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.

Задача 75

Прямая задана уравнением . Составить уравнение параллельной прямой, которая

проходит через точку .

Решение: обозначим неизвестную прямую буквой . Что о ней

сказано в условии? Прямая проходит через точку . А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для

построения прямой «дэ».

Вытаскиваем направляющий вектор из уравнения :

Уравнение искомой прямой составим по точке и направляющему вектору :

Ответ:

Геометрия задачи выглядит незатейливо:

Аналитическая же проверка состоит в следующих шагах:

1) Проверяем, что у прямых один и тот же направляющий вектор (если

уравнения не упрощены должным образом, то векторы будут коллинеарны). Да что тут векторы?! – посмотрим на коэффициенты:
– параллельность прямых понятна без всякого чертежа!

2) Проверяем, удовлетворяет ли точка полученному уравнению . И это тоже устный пункт!

Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница

всяких загадок.

Задача 76

Составить уравнение прямой, проходящей через точку , параллельную прямой , если

Существует рациональный и не очень рациональный способ решения. Самый короткий путь в конце книги.

С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому перейдём к задаче, которая

хорошо знакома вам из школьной программы:

2.5.3. Как найти точку пересечения прямых?

2.5.1. Взаимное расположение двух прямых

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Уравнение прямой, проходящей через точку параллельно прямой

Материал из Циклопедии

Перейти к навигации
Перейти к поиску

Уравнение прямой, проходящей через точку параллельно прямой, задаётся равенством нулю векторного произведения вектора-разности радиусов-векторов соответствующих точек и направляющего вектора прямой.

Обозначения[править]

Введём обозначения:

— радиус-вектор точки прямой;

${displaystyle {bar {r}}_{0}=(x_{0},y_{0},z_{0})}$ — радиус-вектор точки;

${displaystyle {bar {s}}_{1}=(l_{1},m_{1},n_{1})}$ — направляющий вектор прямой;

${displaystyle {frac {x-x_{1}}{l_{1}}}={frac {y-y_{1}}{m_{1}}}={frac {z-z_{1}}{n_{1}}}}$ — уравнение прямой.

Формулы:[править]

Векторная форма:

Координатная форма:

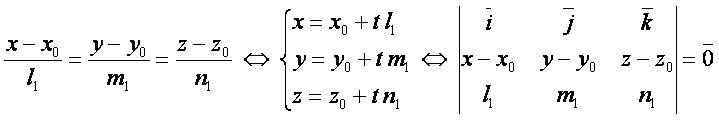
Уравнения прямой:[править]

уравнение прямой, проходящей через две точки;
уравнение прямой, равноудалённой от трёх точек;
уравнение прямой, проходящей через точку в направлении вектора;
уравнение прямой, проходящей через точку параллельно прямой;
уравнение прямой, проходящей через точку перпендикулярно плоскости;
уравнение прямой, образованной пересечением двух плоскостей;
уравнение проекции прямой на плоскость;
уравнение перпендикуляра из точки к прямой в трёхмерном пространстве;
уравнение перпендикуляра из точки к плоскости;
уравнение перпендикуляра к двум прямым.

Ссылки[править]

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.223.
Участник:Logic-samara

Источник

Отвечаю сразу на все три Ваших вопроса.

Уравнение любой, наперед заданной прямой можно преобразовать к виду y=k1*x+b. Как именно проходит прямая, определяется «угловым коэффициентом» (или тангенсом угла наклона) k1.

Общее уравнение прямой, проходящей через заданную точку с координатами (c; d) имеет вид (y-d)=k2*(x-c) или y=k2*x+(d-k2*c). Я намеренно вместо просто «k», пишу «k1» и «k2», чтобы не путать символы из двух разных уравнений.

Теперь, чтобы прямая, проходящая через заданную точку с координатами (c; d), была параллельна заданной прямой, достаточно, чтобы «k2» равнялось «k1».

Это ответ конкретно на этот вопрос. он же является ответом на следующий вопрос, но, поскольку он более общий, просто не нужно ограничивать «а» и «с», т.е. они могут быть любыми.

Чтобы прямая, проходящая через заданную точку с координатами (c; d), была перпендикулярна заданной прямой, достаточно, чтобы «k2″ равнялось -1/»k1». Это ответ на Ваш третий вопрос.

Источник