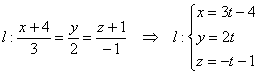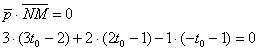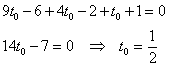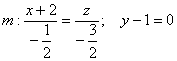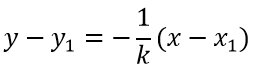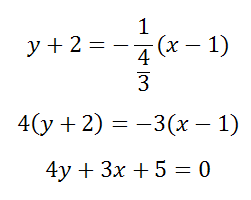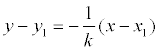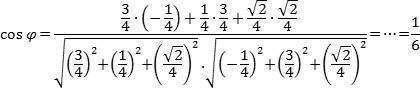Как составить уравнение прямой проходящей через точку перпендикулярно другой прямой

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

Примеры.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Решение:

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

откуда b=1.

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

Ответ: y= -0,2x+1.

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Решение:

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

Ответ: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Решение:

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Ответ: x=7.

Did this article help you?

5.5.6. Как найти прямую, перпендикулярную данной?

Обращаю внимание, что для скрещивающихся прямых таких прямых можно провести бесконечно много, а вот для

пересекающихся – задача имеет единственное решение:

Задача 157

а) Составить уравнения прямой, проходящей через точку  перпендикулярно

прямой  (прямые пересекаются).

б) Найти расстояние от точки  до прямой ,   в) симметричную точку .

а)  Решение: обозначим неизвестную прямую через :

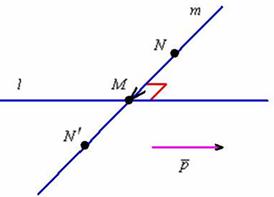
И начинаем

раскручивать задачу: что нам известно об этой прямой?

Известна её точка . Неплохо бы найти направляющий вектор. В качестве

такого вектора вполне подойдёт вектор . Но мы не знаем точку . Вот ей-то и займёмся

План есть, и мы счастливы:

1) Вытащим из уравнений прямой «эль» её направляющий вектор , а сами

уравнения перепишем в параметрической форме:

И вот уже в третий раз используем тот же самый фокус. Рассмотрим точку  с пока ещё неизвестными координатами. Поскольку точка , то её

координаты  удовлетворяют параметрическим уравнениям прямой «эль» и им

соответствует конкретное значение параметра :
, или в строчку:  

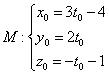
Тогда:

2) По условию прямые должны быть перпендикулярны, следовательно, их направляющие векторы  – ортогональны. А если векторы ортогональны, то их скалярное

произведение равно нулю:

Что получилось? Простейшее линейное уравнение с одной неизвестной:

3) Значение параметра известно, находим точку:
 

И направляющий вектор: .

4) Уравнения прямой  составим по точке  и вектору… избавимся-ка мы от дробей и возьмём направляющий вектор :

Ответ:

Но, разумеется, тут можно было взять и вектор :

Проверка состоит из двух этапов:

1) проверяем направляющие векторы прямых на ортогональность;

2) подставляем координаты точки  в уравнения каждой прямой, они должны «подойти» и там и там.

Об этих действиях говорилось много, поэтому я выполнил проверку на черновике.

5.5.7. Как найти расстояние от точки до прямой?

5.5.5. Пересекающиеся прямые в пространстве

| Оглавление |



Автор: Aлeксaндр Eмeлин

Skip to content

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Определение. Прямая,
проходящая через точку М₁ (х₁ ,
у₁ )
и перпендикулярная к прямой у = kx + b
представляется уравнением:

Расстояние от точки до прямой

Теорема. Если
задана точка М(х₀ ,
у₀ ),
то расстояние до прямой Ах + Ву + С =0
определяется как

.

Доказательство. Пусть
точка М ₁(х ₁,
у ₁)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М₁ :

Второе
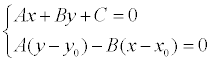
уравнение системы – это уравнение
прямой, проходящей через заданную точку
М ₀ перпендикулярно
заданной прямой. Если преобразовать
первое уравнение системы к виду:

A(x
– x ₀ )
+ B(y – y₀ )
+ Ax₀ +
By₀ +
C = 0,

то,
решая, получим:
Подставляя эти выражения в уравнение
(1), находим:

Угол между двумя прямыми.

.
Угол между двумя прямыми равен углу
между их направляющими векторами. Таким
образом, если вам удастся найти координаты
направляющих векторов a = (x₁;
y₁;
z₁)
и b = (x₂;
y₂;
z₂),
то сможете найти угол. Точнее, косинус
угла по формуле:

Посмотрим,
как эта формула работает на конкретных
примерах:

Угол между двумя прямыми

30
мая 2011

Буду
кратким. Угол между двумя прямыми равен
углу между их направляющими векторами.
Таким образом, если вам удастся найти
координаты направляющих векторов a =
(x₁;
y₁;
z₁)
и b = (x₂;
y₂;
z₂),
то сможете найти угол. Точнее, косинус
угла по формуле:

Посмотрим,
как эта формула работает на конкретных
примерах:

Задача.
В кубе ABCDA₁B₁C₁D₁ отмечены
точки E и F — середины ребер A₁B₁ и
B₁C₁ соответственно.
Найдите угол между прямыми AE и BF.

Поскольку
ребро куба не указано, положим AB = 1.
Введем стандартную систему координат:
начало в точке A, оси x, y, z направим вдоль
AB, AD и AA₁ соответственно.
Единичный отрезок равен AB = 1. Теперь
найдем координаты направляющих векторов
для наших прямых.

Найдем
координаты вектора AE. Для этого нам
потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1).
Поскольку точка E — середина отрезка
A₁B₁,
ее координаты равны среднему арифметическому
координат концов. Заметим, что начало
вектора AE совпадает с началом координат,
поэтому AE = (0,5; 0; 1).

Теперь
разберемся с вектором BF. Аналогично,
разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к.
F — середина отрезка B₁C₁.
Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак,
направляющие векторы готовы. Косинус
угла между прямыми — это косинус угла
между направляющими векторами, поэтому
имеем:

Задача.
В правильной трехгранной призме
ABCA₁B₁C₁,
все ребра которой равны 1, отмечены точки
D и E — середины ребер A₁B₁ и
B₁C₁соответственно.
Найдите угол между прямыми AD и BE.Введем
стандартную систему координат: начало
координат в точке A, ось x направим вдоль
AB, z — вдоль AA₁.
Ось y направим так, чтобы плоскость OXY
совпадала с плоскостью ABC. Единичный
отрезок равен AB = 1. Найдем координаты
направляющих векторов для искомых
прямых.

Для
начала найдем координаты вектора AD.
Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1),
т.к. D — середина отрезка A₁B₁.
Поскольку начало вектора AD совпадает
с началом координат, получаем AD = (0,5; 0;
1).

Теперь
найдем координаты вектора BE. Точка B =
(1; 0; 0) считается легко. С точкой E —
серединой отрезка C₁B₁ —
чуть сложнее. Имеем:Осталось
найти косинус угла:Задача.
В правильной шестигранной призме
ABCDEFA₁B₁C₁D₁E₁F₁,
все ребра которой равны 1, отмечены точки
K и L — середины ребер A₁B₁ и
B₁C₁ соответственно.
Найдите угол между прямыми AK и BL.Введем
стандартную для призмы систему координат:
начало координат поместим в центр
нижнего основания, ось x направим вдоль
FC, ось y — через середины отрезков AB и
DE, а ось z — вертикально вверх. Единичный
отрезок снова равен AB = 1. Выпишем
координаты интересующих нас точек:Точки
K и L — середины отрезков A₁B₁ и
B₁C₁ соответственно,
поэтому их координаты находятся через
среднее арифметическое. Зная точки,
найдем координаты направляющих векторов
AK и BL:

Теперь
найдем косинус угла:Задача.
В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, отмечены
точки E и F — середины сторон SB и SC
соответственно. Найдите угол между
прямыми AE и BF.Введем
стандартную систему координат: начало
в точке A, оси x и y направим вдоль AB и AD
соответственно, а ось z направим
вертикально вверх. Единичный отрезок
равен AB = 1.

Точки
E и F — середины отрезков SB и SC соответственно,
поэтому их координаты находятся как
среднее арифметическое концов. Выпишем
координаты интересующих нас точек:
A
= (0; 0; 0); B = (1; 0; 0)

Координаты
вектора AE совпадают с координатами
точки E, поскольку точка A — начало
координат. Осталось найти косинус угла:

Условия
параллельности и перпендикулярности
прямых

Определение
1.Уравнением
линии на плоскости Oxy называется
уравнение F(x,y)=0,
которому удовлетворяют координаты x и y каждой
точки линии и только они.

Если
из этого уравнения выразить переменную y,
то получится уравнение y=f(x).

Если
линии заданы уравнениями, то точкой
пересечения двух линий называется
любая точка, координаты x и y которой
удовлетворяют уравнениям, т.е. являются
решением системы двух уравнений.

Основные
виды уравнений прямой на плоскости:

1) у=0
— уравнение оси Ох; y=b —
уравнение прямой, параллельной оси Ох;

2) х=0
— уравнение оси Оу; х=а —
уравнение прямой, параллельной оси Оу;

3) y=kх —
уравнение прямой, проходящей через
начало координат, с угловым
коэффициентом k=tga,
где a- угол наклона прямой к оси Oх;

4) y=kх+b — уравнение
прямой с угловым коэффициентом k=tga,
где a- угол наклона прямой с положительным
направлением оси Oх.

y—y₀=k(x—x₀)
— уравнение
прямой, проходящей через точку (x₀,y₀)
и имеющей
угловой коэффициент k.

уравнение
прямой, проходящей через две данные
точки (x₁,y₁)
и (x₂,y₂)
, если x₁¹x₂ и y₁¹y₂.

Определение
1.Уравнение
с двумя переменными Ax + By + C =
0, где A и B не
равны 0 одновременно, называется общим
уравнением прямой на плоскости.

Теорема
1.Любая
прямая на плоскости может быть задана
общим уравнением.

Если
В¹0, то 

т.е. y=кх+b .
При этом:
а)
если А=0, то y=b;

б)
если А=0 и С=0, то y=0;

в)
если С=0, то y=кх .

Если
В=0 и А¹0, то ,
т.е.х=а —
если С¹0 и х=0
— если С=0.

Теорема
доказана.

Точка
пересечения двух прямых A₁x + B₁y + C₁ =
0и A₂x + B₂y + C₂ =
0есть решение системы линейных уравнений

Пусть
две прямые заданы уравнениями с угловыми
коэффициентами y=к₁х+b₁ и y=к₂х+b₂,
т.е. k₁=tga₁ и k₂=tga₂ ,
где a₁ и
a₂ —
углы наклона прямых к оси Ох.

Рассмотрим
угол j=a₂-a₁ —
угол между данными прямыми. Тогда, по
формуле тангенса разности, ,
т.е..

Если
прямые параллельны, то j = 0 , tgj = 0.

Итак, условием
параллельности двух прямых является
равенство их угловых коэффициентов,
т.е. k₁= k₂ .

Если
прямые перпендикулярны, то j = p/2 , ctgj = 0.

Итак, условием
перпендикулярности двух прямых является
равенство k₁× k₂ =-1.

Замечание.Можно
показать, что если две прямые заданы
общими уравнениями A₁x + B₁y + C₁ =
0и A₂x + B₂y + C₂ =
0, то:

условие
параллельности прямых: ;

условие
перпендикулярности прямых: A₁A₂ + B₁B₂ =
0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #