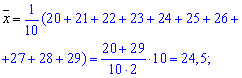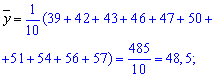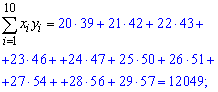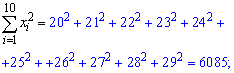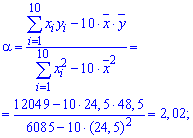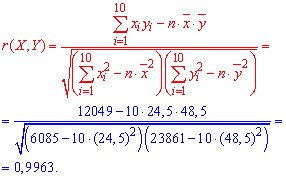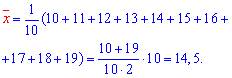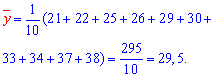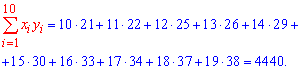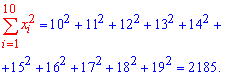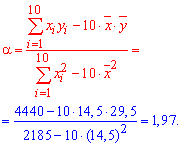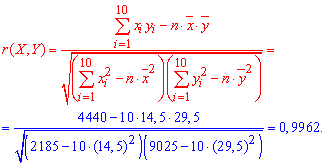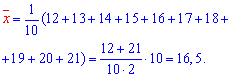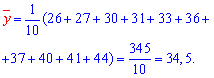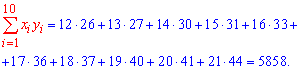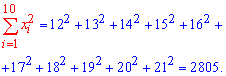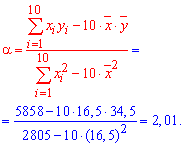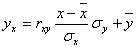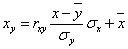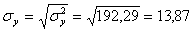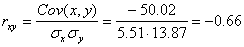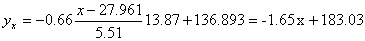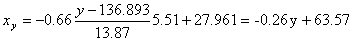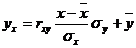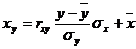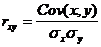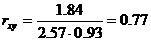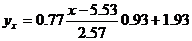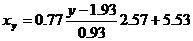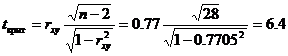Как составить уравнение прямой регрессии

Продолжаем анализировать ответы к индивидуальным заданиям по теории вероятностей. Из этой статьи Вы научитесь составлять (строить) уравнение прямой регрессии Y на X (y=alpha*x+beta ). Такие примеры распространены в теории вероятностей для студентов экономических факультета и статистики. Приведенные решения взяты из программы для экономистов ЛНУ им. И.Франка. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения, поэтому много полезного для себя должен взять каждый студент.
Индивидуальное задание 1
Вариант 11

Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем средние арифметические значения признаков Х та Y


Находим величины которые фигурируют в уравнении регрессии — alpha, beta




После вычислений выборочное уравнение регрессии Y на X записываем по формуле
y=2,02*x-0,99.
Чтобы подтвердить правильность предположения о линейности связи между признаками Х и Y находим выборочный коэффициент корреляции по формуле:

Так как выборочный коэффициент корреляции r(X,Y) является достаточно близким к единице, то предположение о линейной зависимости между X и Y — правильное. Кроме этого коэффициент корреляции положительный r>0, поэтому случайные величины X и Y увеличиваются одновременно.

Вариант 1

Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Находим величины которые необходимы для вычисления коэффициентов уравнения регрессии




Вычисляем alpha, beta


и составляем уравнение регрессии Y на X
y=19,7*x+0,935.
Xтобы убедиться что предположение о линейной свя связи между Х и Y является правильным, находим выборочный коэффициент корреляции по формуле:

Поскольку выборочный коэффициент корреляции =0,9962 достаточно близок к единице, то предположение о линейной связи между X и Y -правильное.
К тому же коэффициент корреляции положительный (r>0), поэтому и связь между X и Y является положительной, то есть эти случайные величины увеличиваются одновременно.

Вариант-12

Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем средние арифметические значения каждой из выборок, а также остальные составляющие для построения уравнения регрессии Y на X:




Находим коэффициенты alpa, beta по формулам


Подставляем коэффициенты в уравнение прямой регрессии y=2,01*x+1,335.
Находим точечную оценку для коэффициента корреляции по формуле:

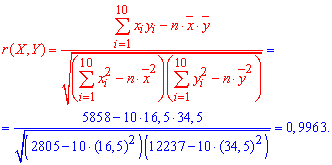
Поскольку выборочный коэффициент корреляции достаточно близок к единице то предположение о линейной зависимости между X и Y — правильное.
Также r>0, поэтому связь между X и Y положительная и эти случайные величины увеличиваются одновременно.
Теперь Вы знаете, как составить уравнение прямой регрессии Y на X .

Готовые решения по теории вероятностей

  • Предыдущая статья — Формулы числовых характеристик статистического распределения
  • Следующая статья — Как найти доверительный интервал?
Источник

Корреляционная таблица

Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .

y/x 15 20 25 30 35 40
100 2 2
120 4 3 10 3
140 2 50 7 10
160 1 4 3
180 1 1

Решение:
Уравнение линейной регрессии с y на x будем искать по формуле

а уравнение регрессии с x на y, использовав формулу:

где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
и
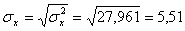
Определим коэффициент корреляции:

где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):

и уравнение x(y):

Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.

Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:

X / Y 2 4 6 8 10
1 5 4 2 0 0
2 0 6 3 3 0
3 0 0 1 2 3
5 0 0 0 0 1

Уравнение линейной регрессии с y на x имеет вид:

Уравнение линейной регрессии с x на y имеет вид:

найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:


Запишем уравнения линий регрессии y(x):

и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):

и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.

Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение

Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.

Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4

Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7

Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение

Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.

X / Y 0 2 7 12 17 22 27 32 37 42
0 3 6 0 0 0 0 0 0 0 0
1 25 108 44 8 2 0 0 0 0 0
2 30 50 60 21 5 5 0 0 0 0
3 1 11 33 32 13 2 3 1 0 0
4 0 5 5 13 13 7 2 0 0 0
5 0 0 1 2 12 6 3 2 1 0
6 0 1 0 1 0 0 2 1 0 1
7 0 0 1 1 0 0 0 1 0 0

Решение.
Скачать решение

Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:

  1. Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
  2. Определить линии регрессии и построить их графики.

Скачать

Уравнение прямой регрессии y на x и x на y

Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Решаем уравнение простой линейной регрессии

В статье рассматривается несколько способов определения математического уравнения линии простой (парной) регрессии.

Все рассматриваемые здесь способы решения уравнения основаны на методе наименьших квадратов. Обозначим способы следующим образом:

  • Аналитическое решение
  • Градиентный спуск
  • Стохастический градиентный спуск

Для каждого из способов решения уравнения прямой, в статье приведены различные функции, которые в основном делятся на те, которые написаны без использования библиотеки NumPy и те, которые для проведения расчетов применяют NumPy. Считается, что умелое использование NumPy позволит сократить затраты на вычисления.

Весь код, приведенный в статье, написан на языке python 2.7 с использованием Jupyter Notebook. Исходный код и файл с данными выборки выложен на гитхабе

Статья в большей степени ориентирована как на начинающих, так и на тех, кто уже понемногу начал осваивать изучение весьма обширного раздела в искусственном интеллекте — машинного обучения.

Для иллюстрации материала используем очень простой пример.

Условия примера

У нас есть пять значений, которые характеризуют зависимость Y от X (Таблица №1):

Таблица №1 «Условия примера»

Будем считать, что значения — это месяц года, а — выручка в этом месяце. Другими словами, выручка зависит от месяца года, а — единственный признак, от которого зависит выручка.

Пример так себе, как с точки зрения условной зависимости выручки от месяца года, так и с точки зрения количества значений — их очень мало. Однако такое упрощение позволит, что называется на пальцах, объяснить, не всегда с легкостью, усваиваемый новичками материал. А также простота чисел позволит без весомых трудозатрат, желающим, порешать пример на «бумаге».

Предположим, что приведенная в примере зависимость, может быть достаточно хорошо аппроксимирована математическим уравнением линии простой (парной) регрессии вида:

где — это месяц, в котором была получена выручка, — выручка, соответствующая месяцу, и — коэффициенты регрессии оцененной линии.

Отметим, что коэффициент часто называют угловым коэффициентом или градиентом оцененной линии; представляет собой величину, на которую изменится при изменении .

Очевидно, что наша задача в примере — подобрать в уравнении такие коэффициенты и , при которых отклонения наших расчетных значений выручки по месяцам от истинных ответов, т.е. значений, представленных в выборке, будут минимальны.

Метод наименьших квадратов

В соответствии с методом наименьших квадратов, отклонение стоит рассчитывать, возводя его в квадрат. Подобный прием позволяет избежать взаимного погашения отклонений, в том случае, если они имеют противоположные знаки. Например, если в одном случае, отклонение составляет +5 (плюс пять), а в другом -5 (минус пять), то сумма отклонений взаимно погасится и составит 0 (ноль). Можно и не возводить отклонение в квадрат, а воспользоваться свойством модуля и тогда у нас все отклонения будут положительными и будут накапливаться. Мы не будем останавливаться на этом моменте подробно, а просто обозначим, что для удобства расчетов, принято возводить отклонение в квадрат.

Вот так выглядит формула, с помощью которой мы определим наименьшую сумму квадратов отклонений (ошибки):

где — это функция аппроксимации истинных ответов (то есть посчитанная нами выручка),

— это истинные ответы (предоставленная в выборке выручка),

— это индекс выборки (номер месяца, в котором происходит определение отклонения)

Продифференцируем функцию, определим уравнения частных производных и будем готовы перейти к аналитическому решению. Но для начала проведем небольшой экскурс о том, что такое дифференцирование и вспомним геометрический смысл производной.

Дифференцирование

Дифференцированием называется операция по нахождению производной функции.

Для чего нужна производная? Производная функции характеризует скорость изменения функции и указывает нам ее направление. Если производная в заданной точке положительна, то функция возрастает, в обратном случае — функция убывает. И чем больше значение производной по модулю, тем выше скорость изменения значений функции, а также круче угол наклона графика функции.

Например, в условиях декартовой системы координат, значение производной в точке M(0,0) равное +25 означает, что в заданной точке, при смещении значения вправо на условную единицу, значение возрастает на 25 условных единиц. На графике это выглядит, как достаточно крутой угол подъема значений с заданной точки.

Другой пример. Значение производной равное -0,1 означает, что при смещении на одну условную единицу, значение убывает всего лишь на 0,1 условную единицу. При этом, на графике функции, мы можем наблюдать едва заметный наклон вниз. Проводя аналогию с горой, то мы как будто очень медленно спускаемся по пологому склону с горы, в отличие от предыдущего примера, где нам приходилось брать очень крутые вершины:)

Таким образом, проведя дифференцирование функции по коэффициентам и , определим уравнения частных производных 1-го порядка. После определения уравнений, мы получим систему из двух уравнений, решив которую мы сможем подобрать такие значения коэффициентов и , при которых значения соответствующих производных в заданных точках изменяются на очень и очень малую величину, а в случае с аналитическим решением не изменяются вовсе. Другими словами, функция ошибки при найденных коэффициентах достигнет минимума, так как значения частных производных в этих точках будут равны нулю.

Итак, по правилам дифференцирования уравнение частной производной 1-го порядка по коэффициенту примет вид:

уравнение частной производной 1-го порядка по примет вид:

В итоге мы получили систему уравнений, которая имеет достаточно простое аналитическое решение:

begin
begin
na + bsumlimits_^nx_i — sumlimits_^ny_i = 0
\
sumlimits_^nx_i(a +bsumlimits_^nx_i — sumlimits_^ny_i) = 0
end
end

Прежде чем решать уравнение, предварительно загрузим, проверим правильность загрузки и отформатируем данные.

Загрузка и форматирование данных

Необходимо отметить, что в связи с тем, что для аналитического решения, а в дальнейшем для градиентного и стохастического градиентного спуска, мы будем применять код в двух вариациях: с использованием библиотеки NumPy и без её использования, то нам потребуется соответствующее форматирование данных (см. код).

Визуализация

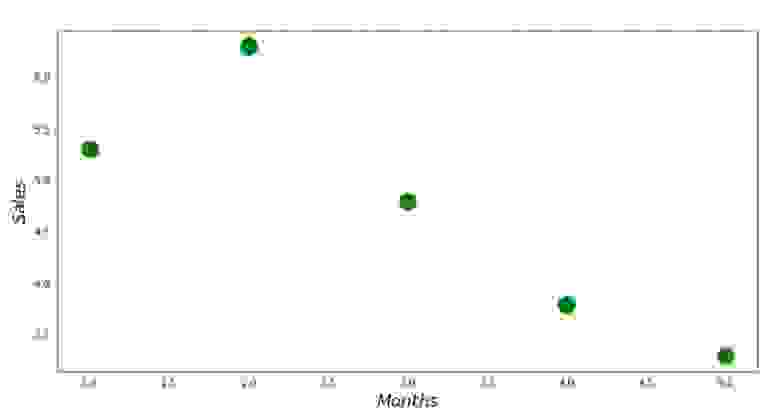
Теперь, после того, как мы, во-первых, загрузили данные, во-вторых, проверили правильность загрузки и наконец отформатировали данные, проведем первую визуализацию. Часто для этого используют метод pairplot библиотеки Seaborn. В нашем примере, ввиду ограниченности цифр нет смысла применять библиотеку Seaborn. Мы воспользуемся обычной библиотекой Matplotlib и посмотрим только на диаграмму рассеяния.

График №1 «Зависимость выручки от месяца года»

Аналитическое решение

Воспользуемся самыми обычными инструментами в python и решим систему уравнений:

begin
begin
na + bsumlimits_^nx_i — sumlimits_^ny_i = 0
\
sumlimits_^nx_i(a +bsumlimits_^nx_i — sumlimits_^ny_i) = 0
end
end

По правилу Крамера найдем общий определитель, а также определители по и по , после чего, разделив определитель по на общий определитель — найдем коэффициент , аналогично найдем коэффициент .

Вот, что у нас получилось:

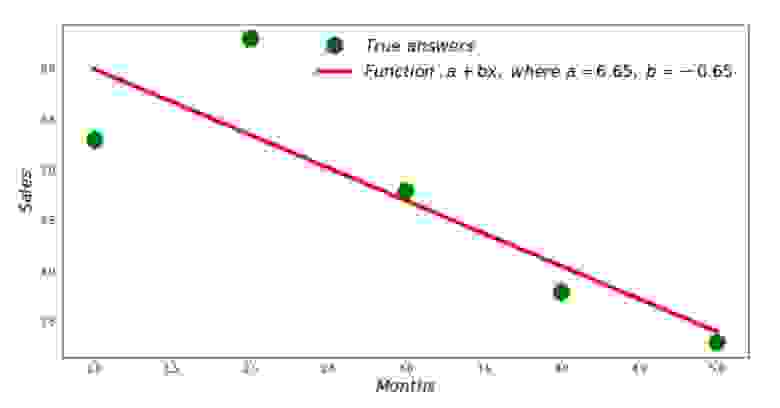
Итак, значения коэффициентов найдены, сумма квадратов отклонений установлена. Нарисуем на гистограмме рассеяния прямую линию в соответствии с найденными коэффициентами.

График №2 «Правильные и расчетные ответы»

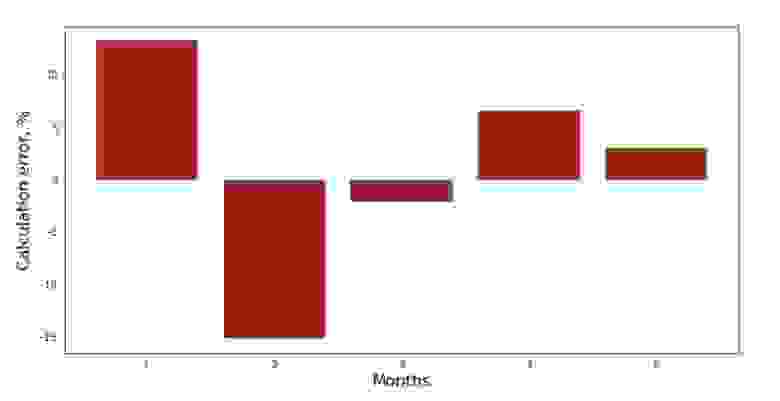
Можно посмотреть на график отклонений за каждый месяц. В нашем случае, какой-либо значимой практической ценности мы из него не вынесем, но удовлетворим любопытство в том, насколько хорошо, уравнение простой линейной регрессии характеризует зависимость выручки от месяца года.

График №3 «Отклонения, %»

Не идеально, но нашу задачу мы выполнили.

Напишем функцию, которая для определения коэффициентов и использует библиотеку NumPy, точнее — напишем две функции: одну с использованием псевдообратной матрицы (не рекомендуется на практике, так как процесс вычислительно сложный и нестабильный), другую с использованием матричного уравнения.

Сравним время, которое было затрачено на определение коэффициентов и , в соответствии с 3-мя представленными способами.

На небольшом количестве данных, вперед выходит «самописная» функция, которая находит коэффициенты методом Крамера.

Теперь можно перейти к другим способам нахождения коэффициентов и .

Градиентный спуск

Для начала определим, что такое градиент. По-простому, градиент — это отрезок, который указывает направление максимального роста функции. По аналогии с подъемом в гору, то куда смотрит градиент, там и есть самый крутой подъем к вершине горы. Развивая пример с горой, вспоминаем, что на самом деле нам нужен самый крутой спуск, чтобы как можно быстрее достичь низины, то есть минимума — места где функция не возрастает и не убывает. В этом месте производная будет равна нулю. Следовательно, нам нужен не градиент, а антиградиент. Для нахождения антиградиента нужно всего лишь умножить градиент на -1 (минус один).

Обратим внимание на то, что функция может иметь несколько минимумов, и опустившись в один из них по предложенному далее алгоритму, мы не сможем найти другой минимум, который возможно находится ниже найденного. Расслабимся, нам это не грозит! В нашем случае мы имеем дело с единственным минимумом, так как наша функция на графике представляет собой обычную параболу. А как мы все должны прекрасно знать из школьного курса математики — у параболы существует только один минимум.

После того, как мы выяснили для чего нам потребовался градиент, а также то, что градиент — это отрезок, то есть вектор с заданными координатами, которые как раз являются теми самыми коэффициентами и мы можем реализовать градиентный спуск.

Перед запуском, предлагаю прочитать буквально несколько предложений об алгоритме спуска:

  • Определяем псевдослучайным образом координаты коэффициентов и . В нашем примере, мы будем определять коэффициенты вблизи нуля. Это является распространённой практикой, однако для каждого случая может быть предусмотрена своя практика.
  • От координаты вычитаем значение частной производной 1-го порядка в точке . Так, если производная будет положительная, то функция возрастает. Следовательно, отнимая значение производной, мы будем двигаться в обратную сторону роста, то есть в сторону спуска. Если производная отрицательна, значит функция в этой точке убывает и отнимая значение производной мы двигаемся в сторону спуска.
  • Проводим аналогичную операцию с координатой : вычитаем значение частной производной в точке .
  • Для того, чтобы не перескочить минимум и не улететь в далекий космос, необходимо установить размер шага в сторону спуска. В общем и целом, можно написать целую статью о том, как правильнее установить шаг и как его менять в процессе спуска, чтобы снизить затраты на вычисления. Но сейчас перед нами несколько иная задача, и мы научным методом «тыка» или как говорят в простонародье, эмпирическим путем, установим размер шага.
  • После того, как мы из заданных координат и вычли значения производных, получаем новые координаты и . Делаем следующий шаг (вычитание), уже из рассчитанных координат. И так цикл запускается вновь и вновь, до тех пор, пока не будет достигнута требуемая сходимость.

Все! Теперь мы готовы отправиться на поиски самого глубокого ущелья Марианской впадины. Приступаем.

Мы погрузились на самое дно Марианской впадины и там обнаружили все те же значения коэффициентов и , что собственно и следовало ожидать.

Совершим еще одно погружение, только на этот раз, начинкой нашего глубоководного аппарата будут иные технологии, а именно библиотека NumPy.


Значения коэффициентов и неизменны.

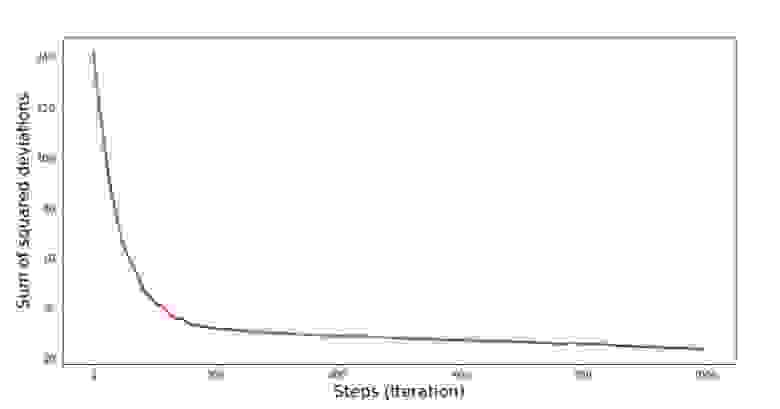
Посмотрим на то, как изменялась ошибка при градиентном спуске, то есть как изменялась сумма квадратов отклонений с каждым шагом.

График №4 «Сумма квадратов отклонений при градиентном спуске»

На графике мы видим, что с каждым шагом ошибка уменьшается, а спустя какое-то количество итераций наблюдаем практически горизонтальную линию.

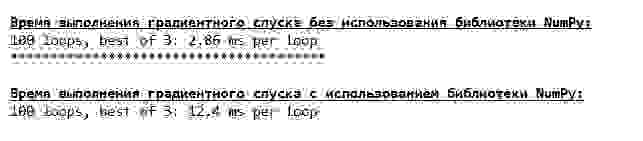
Напоследок оценим разницу во времени исполнения кода:

Возможно мы делаем что-то не то, но опять простая «самописная» функция, которая не использует библиотеку NumPy опережает по времени выполнения расчетов функцию, использующую библиотеку NumPy.

Но мы не стоим на месте, а двигаемся в сторону изучения еще одного увлекательного способа решения уравнения простой линейной регрессии. Встречайте!

Стохастический градиентный спуск

Для того, чтобы быстрее понять принцип работы стохастического градиентного спуска, лучше определить его отличия от обычного градиентного спуска. Мы, в случае с градиентным спуском, в уравнениях производных от и использовали суммы значений всех признаков и истинных ответов, имеющихся в выборке (то есть суммы всех и ). В стохастическом градиентном спуске мы не будем использовать все значения, имеющиеся в выборке, а вместо этого, псевдослучайным образом выберем так называемый индекс выборки и используем его значения.

Например, если индекс определился за номером 3 (три), то мы берем значения и , далее подставляем значения в уравнения производных и определяем новые координаты. Затем, определив координаты, мы опять псевдослучайным образом определяем индекс выборки, подставляем значения, соответствующие индексу в уравнения частных производных, по новому определяем координаты и и т.д. до позеленения сходимости. На первый взгляд, может показаться, как это вообще может работать, однако работает. Правда стоит отметить, что не с каждым шагом уменьшается ошибка, но тенденция безусловно имеется.

Каковы преимущества стохастического градиентного спуска перед обычным? В случае, если у нас размер выборки очень велик и измеряется десятками тысяч значений, то значительно проще обработать, допустим случайную тысячу из них, нежели всю выборку. Вот в этом случае и запускается стохастический градиентный спуск. В нашем случае мы конечно же большой разницы не заметим.

Смотрим внимательно на коэффициенты и ловим себя на вопросе «Как же так?». У нас получились другие значения коэффициентов и . Может быть стохастический градиентный спуск нашел более оптимальные параметры уравнения? Увы, нет. Достаточно посмотреть на сумму квадратов отклонений и увидеть, что при новых значениях коэффициентов, ошибка больше. Не спешим отчаиваться. Построим график изменения ошибки.

График №5 «Сумма квадратов отклонений при стохастическом градиентном спуске»

Посмотрев на график, все становится на свои места и сейчас мы все исправим.

Итак, что же произошло? Произошло следующее. Когда мы выбираем случайным образом месяц, то именно для выбранного месяца наш алгоритм стремится уменьшить ошибку в расчете выручки. Затем выбираем другой месяц и повторяем расчет, но ошибку уменьшаем уже для второго выбранного месяца. А теперь вспомним, что у нас первые два месяца существенно отклоняются от линии уравнения простой линейной регрессии. Это значит, что когда выбирается любой из этих двух месяцев, то уменьшая ошибку каждого из них, наш алгоритм серьезно увеличивает ошибку по всей выборке. Так что же делать? Ответ простой: надо уменьшить шаг спуска. Ведь уменьшив шаг спуска, ошибка так же перестанет «скакать» то вверх, то вниз. Вернее, ошибка «скакать» не перестанет, но будет это делать не так прытко:) Проверим.

График №6 «Сумма квадратов отклонений при стохастическом градиентном спуске (80 тыс. шагов)»

Значения коэффициентов улучшились, но все равно не идеальны. Гипотетически это можно поправить таким образом. Выбираем, например, на последних 1000 итерациях значения коэффициентов, с которыми была допущена минимальная ошибка. Правда нам для этого придется записывать еще и сами значения коэффициентов. Мы не будем этого делать, а лучше обратим внимание на график. Он выглядит гладким, и ошибка как будто уменьшается равномерно. На самом деле это не так. Посмотрим на первые 1000 итераций и сравним их с последними.

График №7 «Сумма квадратов отклонений SGD (первые 1000 шагов)»

График №8 «Сумма квадратов отклонений SGD (последние 1000 шагов)»

В самом начале спуска мы наблюдаем достаточно равномерное и крутое уменьшение ошибки. На последних итерациях мы видим, что ошибка ходит вокруг да около значения в 1,475 и в некоторые моменты даже равняется этому оптимальному значению, но потом все равно уходит ввысь… Повторюсь, можно записывать значения коэффициентов и , а потом выбрать те, при которых ошибка минимальна. Однако у нас возникла проблема посерьезнее: нам пришлось сделать 80 тыс. шагов (см. код), чтобы получить значения, близкие к оптимальным. А это, уже противоречит идее об экономии времени вычислений при стохастическом градиентном спуске относительно градиентного. Что можно поправить и улучшить? Не трудно заметить, что на первых итерациях мы уверенно идем вниз и, следовательно, нам стоит оставить большой шаг на первых итерациях и по мере продвижения вперед шаг уменьшать. Мы не будем этого делать в этой статье — она и так уже затянулась. Желающие могут и сами подумать, как это сделать, это не сложно :)

Теперь выполним стохастический градиентный спуск, используя библиотеку NumPy (и не будем спотыкаться о камни, которые мы выявили раннее)

Значения получились почти такими же, как и при спуске без использования NumPy. Впрочем, это логично.

Узнаем сколько же времени занимали у нас стохастические градиентные спуски.

Чем дальше в лес, тем темнее тучи: опять «самописная» формула показывает лучший результат. Все это наводит на мысли о том, что должны существовать еще более тонкие способы использования библиотеки NumPy, которые действительно ускоряют операции вычислений. В этой статье мы о них уже не узнаем. Будет о чем подумать на досуге:)

Резюмируем

Перед тем как резюмировать, хотелось бы ответить на вопрос, который скорее всего, возник у нашего дорогого читателя. Для чего, собственно, такие «мучения» со спусками, зачем нам ходить по горе вверх и вниз (преимущественно вниз), чтобы найти заветную низину, если в наших руках такой мощный и простой прибор, в виде аналитического решения, который мгновенно телепортирует нас в нужное место?

Ответ на этот вопрос лежит на поверхности. Сейчас мы разбирали очень простой пример, в котором истинный ответ зависит от одного признака . В жизни такое встретишь не часто, поэтому представим, что у нас признаков 2, 30, 50 или более. Добавим к этому тысячи, а то и десятки тысяч значений для каждого признака. В этом случае аналитическое решение может не выдержать испытания и дать сбой. В свою очередь градиентный спуск и его вариации будут медленно, но верно приближать нас к цели — минимуму функции. А на счет скорости не волнуйтесь — мы наверняка еще разберем способы, которые позволят нам задавать и регулировать длину шага (то есть скорость).

А теперь собственно краткое резюме.

Во-первых, надеюсь, что изложенный в статье материал, поможет начинающим «дата сайнтистам» в понимании того, как решать уравнения простой (и не только) линейной регрессии.

Во-вторых, мы рассмотрели несколько способов решения уравнения. Теперь, в зависимости от ситуации, мы можем выбрать тот, который лучше всего подходит для решения поставленной задачи.

В-третьих, мы увидели силу дополнительных настроек, а именно длины шага градиентного спуска. Этим параметром нельзя пренебрегать. Как было подмечено выше, с целью сокращения затрат на проведение вычислений, длину шага стоит изменять по ходу спуска.

В-четвертых, в нашем случае, «самописные» функции показали лучший временной результат вычислений. Вероятно, это связано с не самым профессиональным применением возможностей библиотеки NumPy. Но как бы то ни было, вывод напрашивается следующий. С одной стороны, иногда стоит подвергать сомнению устоявшиеся мнения, а с другой — не всегда стоит все усложнять — наоборот иногда эффективнее оказывается более простой способ решения задачи. А так как цель у нас была разобрать три подхода в решении уравнения простой линейной регрессии, то использование «самописных» функций нам вполне хватило.

Предыдущая работа автора — «Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения»
Следующая работа автора — «Приводим уравнение линейной регрессии в матричный вид»

источники:

http://yukhym.com/ru/sluchajnye-velichiny/postroenie-uravneniya-pryamoj-regressii-y-na-x.html

http://habr.com/ru/post/474602/

Источник

Основы линейной регрессии

Время на прочтение
13 мин

Количество просмотров 124K

Здравствуй, Хабр!

Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.

! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.

Содержание

  • Введение
  • Метод наименьших квадратов
    • Математический анализ
    • Статистика
    • Теория вероятностей
  • Мультилинейная регрессия
    • Линейная алгебра
  • Произвольный базис
  • Заключительные замечания
    • Проблема выбора размерности
    • Численные методы
  • Реклама и заключение

Введение

Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.


Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.

Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.

Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).

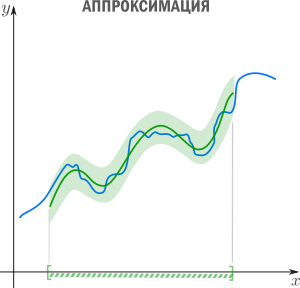
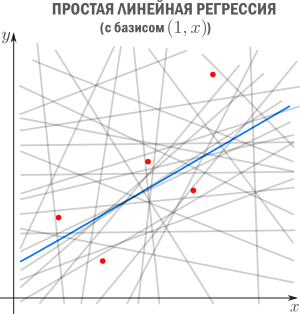
В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций

${f_i}$

$ f = sum_i w_i f_i. $

Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию

$f$ (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).

Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.

Метод наименьших квадратов

Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости

${(x_1,y_1),cdots,(x_N,y_N)}$ и мы ищем такую аффинную функцию

$ f(x) = a + b cdot x, $

чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной

$(1, x)$.

Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого

$x_i,$ поэтому измерять нужно вдоль оси

$y$.

Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц

$|f(x_i) - y_i|$. Простейший вариант — сумма модулей отклонений

$sum_i |f(x_i) - y_i|$ приводит к Least Absolute Distance (LAD) регрессии.

Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)

$ text{SSE}(a,b)=text{SS}_{res[iduals]}=sum_{i=1}^N{text{отклонение}_i}^2=sum_{i=1}^N(y_i-f(x_i))^2=sum_{i=1}^N(y_i-a-bcdot x_i)^2, $

Метод наименьших квадратов (по англ. OLS) — линейная регрессия c

$text{SSE}(a,b)$ в качестве функции потерь.

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу

$text{SSE}(a,b)$.

Математический анализ

Простейший способ найти

$text{argmin}_{a,b} , text{SSE}(a,b)$ — вычислить частные производные по

$ a $ и

$ b $, приравнять их нулю и решить систему линейных уравнений

$ begin{aligned} frac{partial}{partial a}text{SSE}(a,b)&=-2sum_{i=1}^N(y_i-a-bx_i), \ frac{partial}{partial b}text{SSE}(a,b)&=-2sum_{i=1}^N(y_i-a-bx_i)x_i. end{aligned} $

Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям

$ begin{aligned} 0 &= -2sum_{i=1}^N(y_i-hat{a}-hat{b}x_i), \ 0 &= -2sum_{i=1}^N(y_i-hat{a}-hat{b}x_i)x_i, end{aligned} $

которые легко решить

$ begin{aligned} hat{a}&=frac{sum_i y_i}{N}-hat{b}frac{sum_i x_i}{N},\ hat{b}&=frac{frac{sum_i x_i y_i}{N}-frac{sum_i x_isum_i y_i}{N^2}}{frac{sum_i x_i^2}{N}-left(frac{sum_i x_i^2}{N}right)^2}. end{aligned} $

Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.

Статистика

Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего

$langle{cdot}rangle$, вариации

$sigma_{cdot}$ (стандартного отклонения), ковариации

$sigma({cdot},{cdot})$ и корреляции

$rho({cdot},{cdot})$

$ begin{aligned} hat{a}&=langle{y}rangle-hat{b}langle{x}rangle, \ hat{b}&=frac{langle{xy}rangle-langle{x}ranglelangle{y}rangle}{langle{x^2}rangle-langle{x}rangle^2}. end{aligned} $

Перепишем

$hat{b}$ как

$ hat{b} = frac{sigma(x,y)}{sigma_x^2}, $

где

$sigma_x$ это нескорректированное (смещенное) стандартное выборочное отклонение, а

$sigma(x,y)$ — ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)

$ rho(x,y)=frac{sigma(x,y)}{sigma_x sigma_y} $

и запишем

$ hat{b}=rho(x,y)frac{sigma_y}{sigma_x}. $

Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так

$ boxed{y-langle {y} rangle = rho(x,y)frac{sigma_y}{sigma_x}(x-langle {x} rangle)}. $

Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:

Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения

$y$ отклоняется от своего среднего значения меньше чем

$x$, потому что

$|rho(x,y)|leq1$. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.

Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации

$R = rho^2$. Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.

$R^2$, равный

$1$, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что

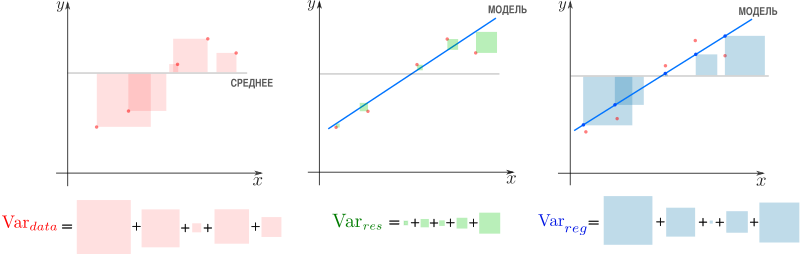
$R^2$ показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения

$ begin{aligned} text{Var}_{data} &= frac{1}{N}sum_i (y_i-langle y rangle)^2, \ text{Var}_{res} &= frac{1}{N} sum_i (y_i-text{модель}(x_i))^2, \ text{Var}_{reg} &= frac{1}{N} sum_i (text{модель}(x_i)-langle y rangle)^2. end{aligned} $

$text{Var}_{data}$ — вариация исходных данных (вариация точек

$y_i$).

$text{Var}_{res}$ — вариация остатков, то есть вариация отклонений от регрессионной модели — от

$y_i$ нужно отнять предсказание модели и найти вариацию.

$text{Var}_{reg}$ — вариация регрессии, то есть вариация предсказаний регрессионной модели в точках

$x_i$ (обратите внимание, что среднее предсказаний модели совпадает с

$langle y rangle$).

Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)

$ boxed{{color{red}{text{Var}_{data}}} ={color{green}{text{Var}_{res}}}+ {color{blue}{text{Var}_{reg}}}.} $

или

$ sigma^2_{data} =sigma^2_{res}+ sigma^2_{reg}. $

Как видим, стандартные отклонения образуют прямоугольный треугольник.

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует

$R^2$, равный единице минус доля вариации ошибок в суммарной вариации

$ R^2=frac{text{Var}_{data}-text{Var}_{res}}{text{Var}_{data}}=1-frac{color{green}{text{Var}_{res}}}{color{red}{text{Var}_{data}}} $

или доле объясненной вариации (доля вариации регрессии в полной вариации)

$ R^2=frac{color{blue}{text{Var}_{reg}}}{color{red}{text{Var}_{data}}}. $

$R$ равен косинусу угла в прямоугольном треугольнике

$(sigma_{data}, sigma_{reg}, sigma_{res})$. Кстати, иногда вводят долю необъясненной вариации

$FUV=1-R^2$ и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.

Теория вероятностей

Ранее мы пришли к функции потерь

$text{SSE}(a,b)$ из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть

$N$ независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например

$mu$ и

$sigma$). Для этого нужно вычислить вероятность получить

$N$ датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.

Вернемся к задаче простой регрессии. Допустим, что значения

$x$ нам известны точно, а в измерении

$y$ присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда

$ y = a + bx + epsilon, $

где

$epsilon$ — нормально распределенная случайная величина

$ epsilon sim mathcal{N}(0,,sigma^{2}), qquad p(epsilon) = frac{1}{sqrt{2 pi sigma^2}} e^{-frac{epsilon^2}{2sigma^2}}. $

Исходя из предположений выше, запишем функцию правдоподобия

$ begin{aligned} L(a,b|mathbf{y})&=P(mathbf{y}|a,b)=prod_i P(y_i|a,b)=prod_i p(y_i-a-bx|a,b)=\ &= prod_i frac{1}{sqrt{2 pi sigma^2}} e^{-frac{(y_i-a-bx)^2}{2sigma^2}}= frac{1}{sqrt{2 pi sigma^2}}e^{-frac{sum_i (y_i-a-bx)^2}{2 sigma^2}}=\ &= frac{1}{sqrt{2 pi sigma^2}}e^{-frac{text{SSE}(a,b)}{2 sigma^2}} end{aligned} $

и ее логарифм

$ l(a,b|mathbf{y})=log{L(a,b|mathbf{y})}=-text{SSE}(a,b)+const. $

Таким образом, максимум правдоподобия достигается при минимуме

$text{SSE}$

$ (hat{a},hat{b})=text{argmax}_{a,b} , l(a,b|mathbf{y}) = text{argmin}_{a,b} , text{SSE}(a,b), $

что дает основание принять ее в качестве функции потерь. Кстати, если

$ begin{aligned} epsilon sim text{Laplace}(0, alpha), qquad p_{L}(epsilon; mu, alpha) =frac{alpha}{2}e^{-alpha |epsilon-mu|} end{aligned} $

мы получим функцию потерь LAD регрессии

$ E_{LAD}(a,b)=sum_i |y_i-a-bx_i|, $

которую мы упоминали ранее.

Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.

Мультилинейная регрессия

До сих пор мы рассматривали задачу регрессии для одного скалярного признака

$x$, однако обычно регрессор — это

$n$-мерный вектор

$mathbf{x}$. Другими словами, для каждого измерения мы регистрируем

$n$ фич, объединяя их в вектор. В этом случае логично принять модель с

$n+1$ независимыми базисными функциями векторного аргумента —

$n$ степеней свободы соответствуют

$n$ фичам и еще одна — регрессанту

$y$. Простейший выбор — линейные базисные функции

$(1, x_1, cdots, x_n)$. При

$n = 1$ получим уже знакомый нам базис

$(1, x)$.

Итак, мы хотим найти такой вектор (набор коэффициентов)

$mathbf{w}$, что

$ sum_{j=0}^n w_j x_j^{(i)}= mathbf{w}^{top}mathbf{x}^{(i)} simeq y_i, qquad qquad qquad qquad i=1dots N. $

Знак «

$simeq$» означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок

$ hat{mathbf{w}}=text{argmin}_mathbf{w} , sum_{i=1}^N left({y_i - mathbf{w}^{top}mathbf{x}^{(i)}}right)^2 $

Последнее уравнение можно переписать более удобным образом. Для этого расположим

$mathbf{x}^{(i)}$ в строках матрицы (матрицы информации)

$ X= begin{pmatrix} - & mathbf{x}^{(1)top} & - \ cdots & cdots & cdots\ - & mathbf{x}^{(N)top} & - end{pmatrix} = begin{pmatrix} | & | & & | \ mathbf{x}_0 & mathbf{x}_1 & cdots & mathbf{x}_n \ | & | & & | end{pmatrix} = begin{pmatrix} 1 & x^{(1)}_{1} & cdots & x^{(1)}_{n} \ cdots & cdots & cdots & cdots\ 1 & x^{(N)}_{1} & cdots & x^{(N)}_{n} end{pmatrix}. $

Тогда столбцы матрицы

$mathbf{x}_{i}$ отвечают измерениям

$i$-ой фичи. Здесь важно не запутаться:

$N$ — количество измерений,

$n$ — количество признаков (фич), которые мы регистрируем. Систему можно записать как

$ X , mathbf{w} simeq mathbf{y}. $

Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь

$ text{SSE}(mathbf{w}) = {|mathbf{y}-X mathbf{w}|}^2, qquad qquad mathbf{w} in mathbb{R}^{n+1}; , mathbf{y} in mathbb{R}^{N}, $

которую мы намерены минимизировать

$ begin{aligned} hat{mathbf{w}}&=text{argmin}_mathbf{w} , text{SSE}(mathbf{w}) = text{argmin}_mathbf{w} , (mathbf{y}-X mathbf{w})^{top}(mathbf{y}-X mathbf{w})=\ &= text{argmin}_mathbf{w} ,(mathbf{y}^{top}mathbf{y}-2mathbf{w}^{top}X^{top}mathbf{y}+mathbf{w}^{top}X^{top}Xmathbf{w}). end{aligned} $

Продифференцируем финальное выражение по

$mathbf{w}$ (если забыли как это делается — загляните в Matrix cookbook)

$ frac{partial , text{SSE}(mathbf{w})}{partial mathbf{w}}=-2 X^{top}mathbf{y}+2 X^{top}Xmathbf{w}, $

приравняем производную к

$mathbf{0}$ и получим т.н. нормальные уравнения

$ X^{top}X , hat{mathbf{w}}=X^{top}mathbf{y}. $

Если столбцы матрицы информации

$X$ линейно независимы (нет идеально скоррелированных фич), то матрица

$X^{top}X$ имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать

$ boxed{hat{mathbf{w}} = (X^{top}X)^{-1}X^{top}mathbf{y}=X^{+}mathbf{y}}, $

где

$ X^{+}=(X^{top}X)^{-1}X^{top} $

псевдообратная к

$X$. Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.

Напомню, что обратить

$X^{top}X$ и найти

$X^{+}$ можно только если столбцы

$X$ линейно независимы. Впрочем, если столбцы

$X$ близки к линейной зависимости, вычисление

$(X^{top}X)^{-1}$ уже становится численно нестабильным. Степень линейной зависимости признаков в

$X$ или, как говорят, мультиколлинеарности матрицы

$X^{top}X$, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе

$X^{top}X$ к вырожденной и неустойчивее вычисление псевдообратной.

Линейная алгебра

К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению

$ X , mathbf{w} simeq mathbf{y}. $

Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор

$mathbf{w}$, образ которого

$Xmathbf{w}$ ближе остальных к

$mathbf{y}$. Напомню, что множество образов или колоночное пространство

$mathcal{C}(X)$ — это линейная комбинация вектор-столбцов матрицы

$X$

$ begin{pmatrix} | & | & & | \ mathbf{x}_0 & mathbf{x}_1 & cdots & mathbf{x}_n \ | & | & & | end{pmatrix} mathbf{w} = w_0 mathbf{x}_0 + w_1 mathbf{x}_1 + cdots w_n mathbf{x}_n . $

$mathcal{C}(X)$ —

$n+1$-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов

$X$. Итак, если

$mathbf{y}$ принадлежит

$mathcal{C}(X)$, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.

Если в дополнение к векторам

$mathcal{C}(X)$ мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из

$mathbb{R}^{N}$ разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай

$mathbf{v} in mathbb{R}^{N}$, тогда

$ X^top mathbf{v} = begin{pmatrix} - & mathbf{x}_0^{top} & - \ cdots & cdots & cdots\ - & mathbf{x}_n^{top} & - end{pmatrix} mathbf{v} = begin{pmatrix} mathbf{x}_0^{top} cdot mathbf{v} \ cdots \ mathbf{x}_n^{top} cdot mathbf{v} \ end{pmatrix} $

равен нулю в том и только в том случае, если

$mathbf{v}$ перпендикулярен всем

$mathbf{x}_i$, а значит и целому

$mathcal{C}(X)$. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все

$mathbb{R}^N$. Иногда это обозначают c помощью символа ортогональной прямой суммы

где

$text{ker}(X^{top})={mathbf{v}|X^{top}mathbf{v}=mathbf{0}}$. В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.

Теперь представим

$mathbf{y}$ в виде разложения

$ mathbf{y} = mathbf{y}_{text{proj}} + mathbf{y}_{perp}, qquad mathbf{y}_{text{proj}} in mathcal{C}(X), qquad mathbf{y}_{perp} in text{ker}(X^{top}). $

Если мы ищем решение

$hat{mathbf{w}}$, то естественно потребовать, чтобы

$|| mathbf{y} - Xmathbf{w} ||$ была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора

$ text{argmin}_mathbf{w} || mathbf{y} - Xmathbf{w} || = text{argmin}_mathbf{w} || mathbf{y}_{perp} + mathbf{y}_{text{proj}} - Xmathbf{w} || = text{argmin}_mathbf{w} sqrt{|| mathbf{y}_{perp} ||^2 + || mathbf{y}_{text{proj}} - Xmathbf{w} ||^2}, $

но поскольку, выбрав подходящий

$mathbf{w}$, я могу получить любой вектор колоночного пространства, то задача сводится к

$ Xhat{mathbf{w}} = mathbf{y}_{text{proj}}, $

а

$mathbf{y}_{perp}$ останется в качестве неустранимой ошибки. Любой другой выбор

$hat{mathbf{w}}$ сделает ошибку только больше.

Если теперь вспомнить, что

$X^{top} mathbf{y}_{perp} = mathbf{0}$, то легко видеть

$ X^top X mathbf{w} = X^{top} mathbf{y}_{text{proj}} = X^{top} mathbf{y}_{text{proj}} + X^{top} mathbf{y}_{perp} = X^{top} mathbf{y}, $

что очень удобно, так как

$mathbf{y}_{text{proj}}$ у нас нет, а вот

$mathbf{y}$ — есть. Вспомним из предыдущего параграфа, что

$X^{top} X$ имеет обратную при условии линейной независимости признаков и запишем решение

$ mathbf{w} = (X^top X)^{-1} X^top mathbf{y} = X^{+} mathbf{y}, $

где

$X^{+}$ уже знакомая нам псевдообратная матрица. Если нам интересна проекция

$mathbf{y}_{text{proj}}$, то можно записать

$ mathbf{y}_{text{proj}} = X mathbf{w} = X X^{+} mathbf{y} = text{Proj}_X mathbf{y}, $

где

$text{Proj}_X$ — оператор проекции на колоночное пространство.

Выясним геометрический смысл коэффициента детерминации.

Заметьте, что фиолетовый вектор

$bar{y} cdot boldsymbol{1}=bar{y} cdot (1,1,dots,1)^{top}$ пропорционален первому столбцу матрицы информации

$X$, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике

$ {color{red}{mathbf{y}-hat{y} cdot boldsymbol{1}}}={color{green}{mathbf{y}-bar{mathbf{y}}}}+{color{blue}{hat{mathbf{y}}-bar{y} cdot boldsymbol{1}}}. $

Так как этот треугольник прямоугольный, то по теореме Пифагора

$ {color{red}{|mathbf{y}-hat{y} cdot boldsymbol{1}|^2}}={color{green}{|mathbf{y}-bar{mathbf{y}}|^2}}+{color{blue}{|hat{mathbf{y}}-bar{y} cdot boldsymbol{1}|^2}}. $

Это геометрическая интерпретация уже известного нам факта, что

$ {color{red}{text{Var}_{data}}} = {color{green}{text{Var}_{res}}}+{color{blue}{text{Var}_{reg}}}. $

Мы знаем, что

$ R^2=frac{color{blue}{text{Var}_{reg}}}{color{red}{text{Var}_{data}}}, $

а значит

$ R=cos{theta}. $

Красиво, не правда ли?

Произвольный базис

Как мы знаем, регрессия выполняется на базисных функциях

$f_i$ и её результатом есть модель

$ f = sum_i w_i f_i, $

но до сих пор мы использовали простейшие

$f_i$, которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей

$f_0(mathbf{x}) = 1$. Как можно было заметить, на самом деле ни вид

$f_i$, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки

${(x_1,y_1),cdots,(x_N,y_N)}$ ложатся на параболу, а не на прямую, то стоит выбрать базис

$(1, x, x^2)$. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.

Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации

$ Phi = begin{pmatrix} - & boldsymbol{f}^{(1)top} & - \ cdots & cdots & cdots\ - & boldsymbol{f}^{(N)top} & - end{pmatrix} = begin{pmatrix} {f}_{0}left(mathbf{x}^{(1)}right) & {f}_{1}left(mathbf{x}^{(1)}right) & cdots & {f}_{n}left(mathbf{x}^{(1)}right) \ cdots & cdots & cdots & cdots\ {f}_{0}left(mathbf{x}^{(N)}right) & {f}_{1}left(mathbf{x}^{(N)}right) & cdots & {f}_{n}left(mathbf{x}^{(N)}right) end{pmatrix}, $

записываем функцию потерь

$ E(mathbf{w})={|{boldsymbol{epsilon}}(mathbf{w})|}^2={|mathbf{y}-Phi , mathbf{w}|}^2 $

и находим её минимум, например с помощью псевдообратной матрицы

$ hat{mathbf{w}} = text{argmin}_mathbf{w} ,E(mathbf{w}) = (Phi^{top}Phi)^{-1}Phi^{top}mathbf{y}=Phi^{+}mathbf{y} $

или другим методом.

Заключительные замечания

Проблема выбора размерности

На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).

Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что

$R^2$ монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент

$ bar{R}^2=1-(1-R^2)left[frac{N-1}{N-(n+1)}right], $

где

$N$ — размер выборки,

$n$ — количество независимых переменных. Следя за

$bar{R}^2$, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.

Вторая группа подходов — регуляризации, самые известные из которых Ridge(

$L_2$/гребневая/Тихоновская регуляризация), Lasso(

$L_1$ регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов

$mathbf{w}$ неограниченно расти и тем самым воспрепятствуют переобучению

$ begin{aligned} E_{text{Ridge}}(mathbf{w})&=text{SSE}(mathbf{w})+alpha sum_i |w_i|^2 = text{SSE}(mathbf{w})+alpha | mathbf{w}|_{L_2}^2,\ E_{text{Lasso}}(mathbf{w})&=text{SSE}(mathbf{w})+beta sum_i |w_i| =text{SSE}(mathbf{w})+beta | mathbf{w}|_{L_1},\ E_{text{EN}}(mathbf{w})&=text{SSE}(mathbf{w})+alpha | mathbf{w}|_{L_2}^2+beta | mathbf{w}|_{L_1}, \ end{aligned} $

где

$alpha$ и

$beta$ — параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента

$b$

$ y = a + bx + epsilon,qquad epsilon sim mathcal{N}(0,,sigma^{2}),qquad left{begin{aligned} &b sim mathcal{N}(0,,tau^{2})&leftarrowtext{Ridge},\ &b sim text{Laplace} (0,,alpha)&leftarrowtext{Lasso}. end{aligned}right. $

Численные методы

Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.

Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.

Реклама и заключение

Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:

  • все материалы должны быть доступны студентам с первой пары;
  • лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
  • конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
  • наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).

Если хотите посмотреть на результат — загляните на страничку курса на GitHub.

Надеюсь вам было интересно, спасибо за внимание.

Источник

  1. Уравнение прямой линии регрессии. Метод наименьших квадратов.

Теоретической
линией регрессии называется линия,
вокруг которой группируются точки
корреляционного поля и которая указывает
основное направление, основную тенденцию
связи между признаками. Для
взаимного погашения случайных причин
линия регрессии проводится так, чтобы
сумма отклонений точек поля корреляции
от соответствующих точек теоретической
линии регрессии равнялась нулю, а сумма
квадратов этих отклонений была бы
минимальной величиной (метод
наименьших квадратов).

Рассмотрим
уравнение прямой линии .

Для
нахождения параметров и уравнения
регрессии используем
метод наименьших квадратов: сумма
квадратов отклонений эмпирических
точек от теоретической линии регрессии
должна быть минимальной:

Параметр в
линейном уравнении называют коэффициентом
регрессии.

  1. Выборочный метод

Вся подлежащая
изучению совокупность объектов
называется генеральной совокупностью.
В математической статистике понятие
генеральной совокупности трактуется
как совокупность всех мыслимых
наблюдений, которые могли бы быть
произведены при данном реальном
комплексе условий.

Та часть объектов,
которая отобрана для непосредственного
изучения из генеральной совокупности,
назыв. выборочной совокупностью или
выборкой.

Сущность выборочного
метода состоит в том, чтобы по некоторой
части генеральной совокупности ( по
выборке) выносит суждение о ее свойствах
в целом.

Чтобы по данным
выборке иметь возможность судить о
генеральной совокупности, она должна
быть отобрана случайно.

Выборка назыв.
репрезентативной (представительной),
если она достаточно хорошо воспроизводит
генеральною совокупность.

Виды выборок:

  • Собственно-случайная
    выборка, образованная случайным выбором
    элементов без расчленения на части
    или группы;

  • Механическая
    выборка, в которую элементы из генеральной
    совокупности отбираются через
    определенный интервал. Например, если
    объем выборки должен составлять 10%, то
    отбирается каждый 10-й элемент и т.д.;

  • Типическая
    (стратифицированная) выборка, в которую
    случайным образом отбираются элементы
    из типических групп, на которые по
    некоторому признаку разбивается
    генеральная совокупность;

  • Серийная (гнездовая)
    выборка, в которую случайным образом
    отбираются не элементы, а целые группы
    совокупности (серии), а сами серии
    подвергаются сплошному наблюдению.

ДВА способа
образования выборки:

  • Повторный отбор
    (по схеме возвращенного шара), когда
    каждый элемент, случайно отобранный
    и обследованный, возвращается в общую
    совокупность и может быть повторно
    отобран;

  • Бесповторный
    отбор (по схеме невозвращенного шара),
    когда отобранный элемент не возвращается
    в общую совокупность.

Наименование

характеристики

Генеральная

совокупность

Выборка

Средняя

Дисперсия

Доля

—
значение признака (случайной величины
Х);

N
и n
— объемы генеральной и выборочной
совокупностей;

и
—
число элементов генеральной и выборочной
совокупностей со значением признака
;

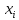
M
и m
— число элементов генеральной и выборочной
совокупностей, обладающих данным
признаком.

Средние арифметические
распределения признака в генеральной
и выборочной совокупностях называются
соответственно генеральной и выборочной
средними, а дисперсии этих распределений
– генеральной и выборочной дисперсиями.
Отношение числа элементов генеральной
и выборочной совокупностей, обладающих
некоторым признаком А, к их объемам,
называются соответственно генеральной
и выборочной долями.

Важнейшей задачей
выборочного метода является оценка
параметров генеральной совокупности
по данным выборки.

Соседние файлы в папке Экзамен

  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Как составить запрос в министерство обороны
  • Sql как найти разницу между двумя датами
  • Зависимость сопротивления от температуры как найти температуру
  • Как найти потерянный телефон если его украли
  • Как найти драгоценности в воде