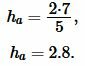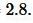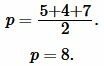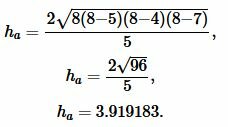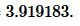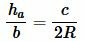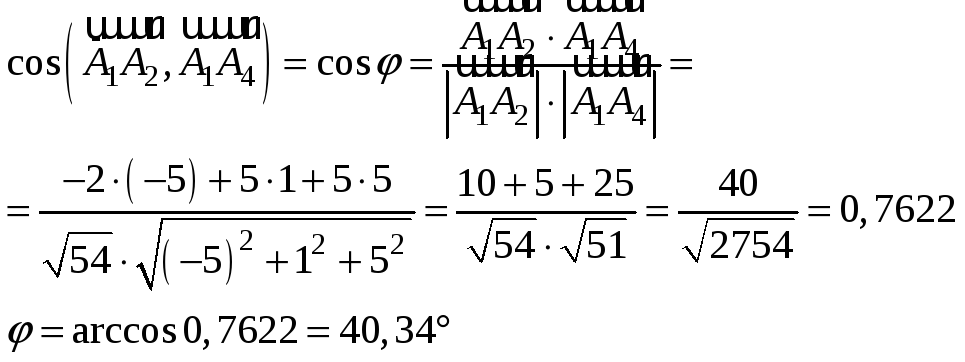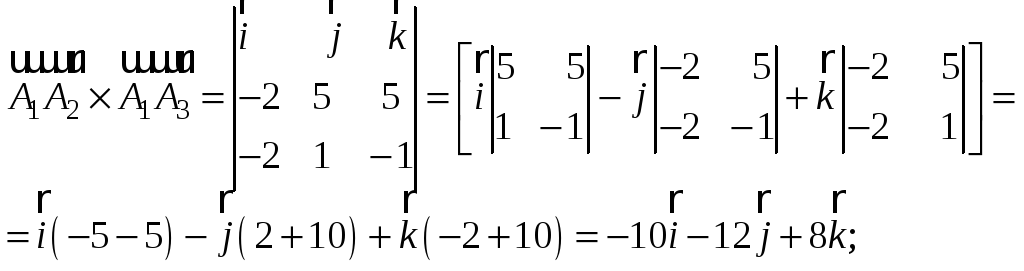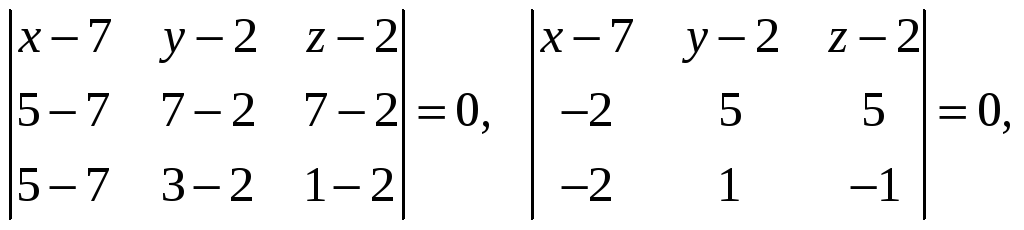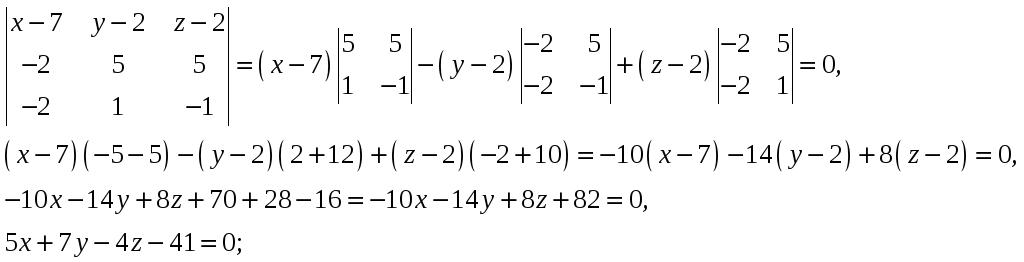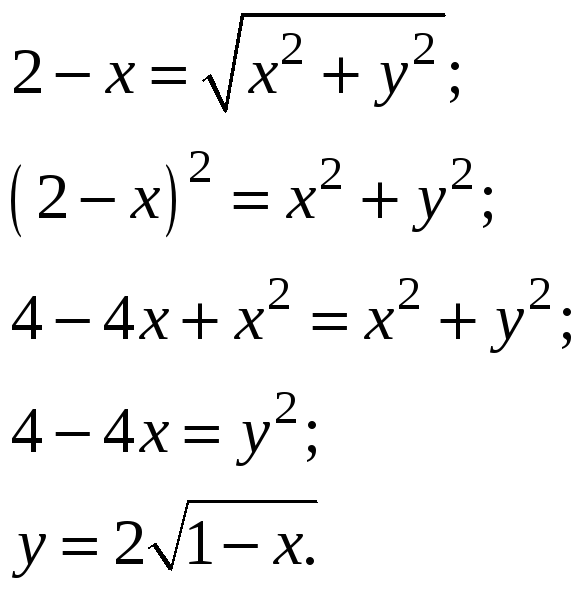Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
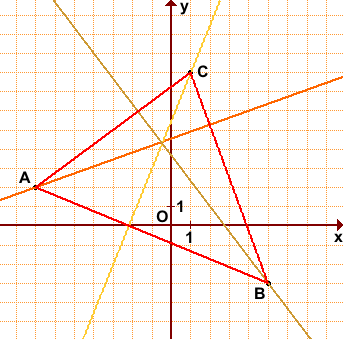
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6df326b7aa8c0c42 • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Высота треугольника онлайн
С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
Высота треугольника. Определение
Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).
Теорема о пересечении высот треугольника
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
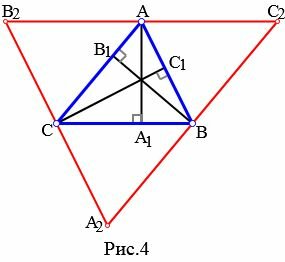
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.
Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
Высота треугольника по основанию и площади
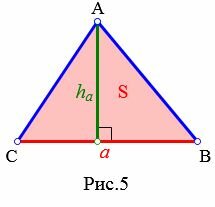
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
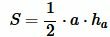
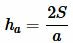 . . |
(1) |
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.
Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
Ответ:
Высота треугольника по трем сторонам
Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
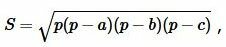 |
(2) |
где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:
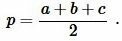 |
(3) |
Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
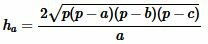 . . |
(4) |
Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):
Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:
Ответ:
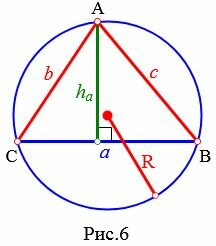
Высота треугольника по двум сторонам и радиусу описанной окружности
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
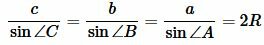 |
(5) |
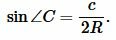 |
(6) |
Далее, из теоремы синусов имеем:
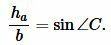 |
(7) |
Подставляя (6) в (7), получим:
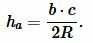 |
(8) |
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Проверим сначала условие (9):
(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )
Высота треугольника по стороне и прилежащему к ней углу
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:
( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )
| ( small h_a=c cdot sin angle B. ) | (11) |
Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:
http://matworld.ru/geometry/vysota-treugolnika.php
8
Даны вершины
треугольника.
Найти:
-
длину стороны ВС;
-
уравнение высоты ВС;
-
уравнение высоты, проведённой из вершины
А; -
длину высоты, проведённой из вершины
А; -
угол В.
Сделать чертёж.
Дано: А(-8;3), В(4;-2), С(7;2).
РЕШЕНИЕ
-
Длину стороны ВС находим по формуле
.
По условию имеем В(4;-2), С(7;2).
-
Найдём уравнение стороны ВС. Найдём
уравнение прямой, на которой лежит
сторона ВС. Используем уравнение прямой,
проходящей через две точки
,
полагая
-
Найдём уравнение высоты, проведённой
из вершины А. При составлении уравнения
прямой, на которой лежит высота
треугольника, воспользуемся формулой
и условием перпендикулярности двух
прямых
:
Определим угловой коэффициент прямой
ВС. Для этого разрешим уравнение стороны
ВС относительно у:
Следовательно, высота, проведённая из
точки А, имеет угловой коэффициент
Тогда, уравнение высоты, опущенной из
вершины А(-8;3) на сторону ВС:
-
Найдём длину высоты, проведённой из
вершины А. Она равна расстоянию от точки
А(-8;3) до прямой ВС заданной уравнением
.
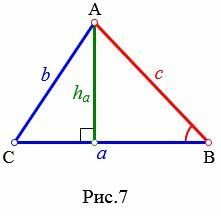
По формуле
вычисляем расстояние от точки А до
прямой ВС, полагая
-
Найдём угол В. Угол В равен углу между
прямыми ВС и АВ и может быть найден с
помощью формулы
.
Угловой коэффициент прямо ВС известен
и равен
.
Найдём угловой коэффициент прямой АВ
по формуле:
Тогда получаем,
И угол равен
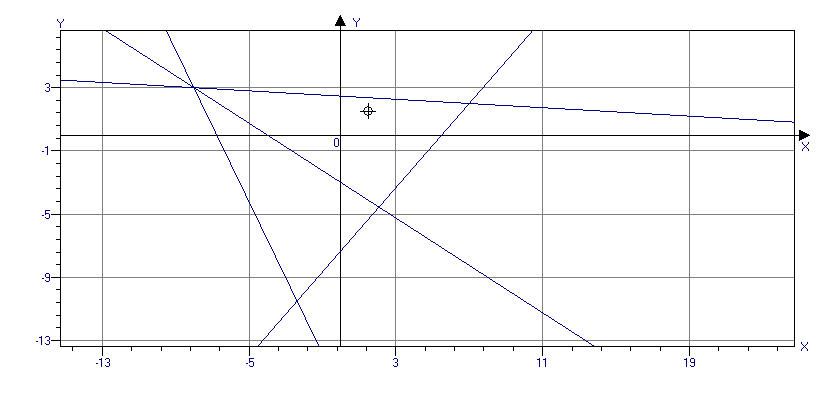
Выполним чертёж. В прямоугольной
декартовой системе координат хОу строим
исходные точки и получаем треугольник
АВС. Затем из вершины А опустим
перпендикуляр на сторону ВС, получим
АК.
18
Даны координаты вершин пирамиды А1А2А3А4.
Найти:
-
координаты вектора
и длину ребра
;
-
угол между рёбрами
и
;
-
площадь грани
;
-
объём пирамиды;
-
уравнение плоскости
;
-
уравнение прямой
;
-
угол между ребром
и гранью
;
-
уравнение высоты, опущенной из вершины
на грань
;
Сделать чертёж.
Дано: А1(7;2;2), А2(5;7;7), А3(5;3;1),
А4(2;3;7).
РЕШЕНИЕ
-
Вектор
равен
Длину ребра
можно найти как расстояние между двумя
точками
и
,
оно равно
Получаем
-
Угол между рёбрами
и
найдём как угол между векторами
и
.
Вектор
Таким образом, имеем два вектора
и
,
угол между ними найдём по формуле:
Скалярное произведение двух векторов
в числителе дроби находили как сумму
произведений одноимённых координат
(проекций).
-
Площадь грани
равна половине площади параллелограмма,
построенного на векторах, как на
сторонах. И площадь треугольника
можно вычислить через векторное
произведение
Координаты вектора
или
Векторное произведение вычислим через
определитель 3-го порядка, разложив его
по элементам первой строки:
Модуль векторного произведения
-
Объём треугольной пирамиды А1А2А3А4
можно рассматривать как одну шестую
часть объёма параллелепипеда, построенного
на векторах
,
и
как на рёбрах:
Смешанное произведение трёх векторов
равно
-
Уравнение плоскости
имеет вид
или для нашей задачи
Разложим определитель по элементам
первой строки:
-
Уравнения прямой
найдём в канонической форме, для этого
воспользуемся уравнением прямой,
проходящей через две заданные точки
и
:
,
-
Углом ψ между ребром
и гранью
будет острый угол между прямой
и её проекцией на плоскость
.
Для нахождения угла ψ воспользуемся
формулой
Канонические уравнения прямой
получим как:
Отсюда l=5; m=1;
n=-5, где l,
m, n –
координаты направляющего вектора прямой
:
;
Уравнение плоскости
было получено в пункте 5:
Отсюда А=5; В=7; С=-4, где А, В, С – координаты
нормального вектора плоскости
:
Тогда получаем
-
Уравнения высоты, опущенной из вершины
на грань
.
Канонические уравнения прямой, проходящей
через точку
,
имеют вид
,
где l, m, n
– координаты направляющего вектора
прямой.
Так как высота перпендикулярна плоскости
,
то из условия перпендикулярности прямой
и плоскости
координаты направляющего вектора
прямой, перпендикулярной плоскости
можно заменить координатами нормального
вектора плоскости l=A=5;
m=B=7; n=C=-4.
Окончательно получим
Выполним чертёж пирамиды как пересечения
плоскостей её граней:
Грань А1А2А4:
Грань А1А2А3:
Грань А1А3А4:
Грань А2А3А4:
28
Составить уравнение и построить линию,
каждая точка которой равноотстоит от
оси ординат и от окружности
РЕШЕНИЕ
В системе координат хОу строим ось
ординат х=0 и окружность
Пусть точка М(х; у) – произвольная точка
искомого геометрического места точек.
Опустим перпендикуляры на ось ординат
и на окружность.
Тогда расстояние от произвольной точки
М(х; у) до оси ординат
–
абсцисса точки М(х; у), а расстояние от
точки М(х; у) до окружности
.
Приравнивая эти расстояния и снимая
знак модуля, получаем
Получили уравнение параболы, строим
верхнюю часть окружности и параболы,
так как чертёж симметричный:
Соседние файлы в папке Приборостроителям
- #
- #
- #
- #
- #
- #
- #
- #
- #
1) Зная координаты вершин Можем узнать координаты вектора BC (2-3; -3-1) = BC(-1; -4)
Прямая проходящая через точку A должна идти коллинеарно вектору BC, то есть
(х-0) = k•(-1)
(y-4) = k•(-4)
откуда получаем -х=k и -y/4 +1 = k, приравниваем k
-x = -y/4 + 1 или
4x — y = -4
2) Медиана треугольника приходит в середину противоположной стороны. То есть в точку М — середина AС. Её координаты х = (0+2)/2 = 1; y = (4+(-3))/2 = 0,5; M(1; 0,5)
Получаем медиана идет из точки B в направлении вектора MB (3-1; 1-0,5) = MB (2; 0,5)
Получаем (x-3)/2 = (y-1)/0,5
0,5х — 1,5 = 2y — 2
x — 4y = -1
3) Высота из вершины С перпендикулярна стороне AB. То есть Вектора AB и CH ортогональны и их скалярное произведение = 0
AB (3-0; 1-4) = AB(3; -3)
CH (x-2; y-(-3))
<AB•СH> = 3•(х-2) + (-3)•(y+3) = 0
3x-6 — 3y — 9 = 0
x-y = 5 — получили уравнение прямой высоты CH
Уравнение прямой AB: (х-0)/3 = (y-4)/(-3)
x+y = 4
Точка Н — пересечение этих двух прямых:
Решая систему уравнений подстановкой, находим х=4,5; y=-0,5
CH (4,5-2; -0,5+3) = CH(2,5; 2,5)
|CH| = √(2,5² + 2,5²) = 2,5•√2
Ответ:
1) 4x — y = -4;
2) x — 4y = -1;
3) 2,5•√2
�������
���� ����� A(6;1), B(- 5; — 4), C(- 2;5). ��������� ���������
������, �� ������� ����� ������ ������������ ABC, �����ģ���� ��
������� A.
���������
��������� ������� ������������������ ���� ������ (
k1 . k2 = — 1).
�����
x + 3y — 9 = 0.
���ģ� ��������� ������ BC �� ���� ������:
=
, ��� y = 3x + 11.
����� ţ ������� ����������� k1 = 3. ���� k2 — ������� �����������
������, ���������������� ������, ��
k1 . k2 = — 1. �������
k2 = — = —
.
��������� ������� ������, ���������� ������ AH ������������ ABC, ���ģ� ��
����� A(6;1) � �������� ������������
k2 = — :
y — 1 = — (x — 6).
������� ��������� ���� ������ � ����� ����:
x + 3y — 9 = 0.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 4246 |