Как составить уравнение равновесия онлайн

Определение опорных реакций

Построение эпюр поперечных сил и моментов

Просмотр хода решения

Расчет выполняется по следующей методике:

1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.

2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.

3. Освобождаемся от опор и заменяем их действие на балку реакциями.
Реакции опор при такой нагрузке будут только вертикальными.

4. Составляем уравнения равновесия вида:
M_A = 0; M_B = 0,
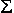
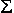
Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).

5. Выполним проверку решения. Для этого составим уравнение равновесия:
Y = 0,
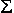
Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.

6. Строим эпюру поперечных сил Q_x. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Q_лев и Q_прав.
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:
а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Q_x.

7. Строим эпюру изгибающих моментов М_x. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно М_лев и М_прав. В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:
а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;
б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.

Пример решения балки:

Расчёт статически определимых балок

(определение реакций и построение эпюр)

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи! Создать новую модель Для расчёта необходимо полностью определить модель (с закреплением и нагрузкой) 12

В данном расчёте не задано ни одного объекта. Для создания объектов модели перейдите в раздел «Операции»

δ ?EJEJXYαhwRauto0°180°-180°0°90°180°-90°0°180°-180°

Данный онлайн калькулятор предназначен для нахождения опорных реакций в простейшей балке, находящейся под воздействием поперечных сил. Простая балка — прямолинейный брус, закрепленная на двух опорах: одной — шарнирно-неподвижной (опора А), другой — шарнирно-подвижной (опора В). Калькулятор выводит опорные реакции V_A и V_B, уравнения равновесия в символьном виде и показывает модель нагрузок. Обратите внимание, что если требуется задать нагрузку действующую левее опоры A, то расстояние от опоры нужно задать со знаком минус. Теорию и формулы расчета можно найти ниже под калькулятором.

Реакции опор

Под воздействием нагрузок в опорах балки возникают уравновешивающие силы, называемые реакциями опор. Эти силы зависят от вида нагрузки и типа самих опор.

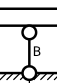
Шарнирно подвижная опора ( в нашей модели обозначена как «B») позволяет балке свободно перемещаться в горизонтальной плоскости и препятствует вертикальному перемещению, поэтому при любой нагрузке она имеет только вертикальную реакцию V_B.

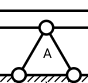
Шарнирно неподвижная опора крепится к балке, что препятствует её горизонтальному и вертикальному перемещению. При наличии сил, действующих на балку в горизонтальной плоскости, эта опора дает еще и горизонтальную реакцию. Однако в нашей модели все силы действуют поперечно балке, поэтому горизонтальная реакция опоры A всегда будет равна нулю. Вертикальную реакцию опоры A обозначим V_A.

Уравнения равновесия

Как мы знаем из статики, все силы и моменты сил в неподвижной системе, уравновешены. Поэтому суммы сил и моментов в любой точке этой системы равны нулю.
Все силы при поперечной нагрузке на простую балку действуют параллельно оси Y, поэтому можно составить только два независимых уравнения равновесия для проекции сил и моментов на ось Y. Этого вполне достаточно для нахождения двух неизвестных реакций опор V_A и V_B.
При составлении уравнений у нас есть выбор:

• составить одно уравнение равновесия проекции сил и одно уравнение равновесия моментов в некоторой точке
• составить два уравнения равновесия моментов в двух точках.

Воспользуемся вторым способом, а первый оставим для проверки полученного результата.
Удобнее всего составлять уравнения для точек А и B, в которых находятся опоры:

Напомним, что моментом силы в определенной точке называется произведение силы F на кратчайшее расстояние от этой точки до линии действия силы (плечо) l:

Исходя из этого, уравнения равновесия моментов в точках А и B для системы поперечных сил F₁…F_n, действующих на балку приобретают вид:

Где F_i — модуль приложенной силы или реакции опоры в Ньютонах. l_iA и l_iB — длина рычага в метрах (кратчайшее расстояние от точки приложения силы i до опоры A и B соответственно). s_iA и s_iB — знак момента силы i в точке A и B соответственно.
Правило выбора знаков момента сил: знак положительный (+1) для момента, закручивающего балку вокруг выбранной точки по часовой стрелке ↻ и отрицательный (-1) для противоположного направления ↺. Можно выбрать и противоположные значения. Уравнения примут немного другой вид, но результат от этого не изменится.

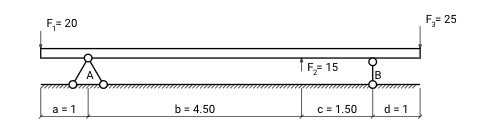
Например, для системы сил, показанной на рисунке выше, уравнения равновесия можно записать следующим образом:

Вычисляя, получаем значения реакций опор: V_A = 15.42 и V_B = 14.58. Проверим, что сумма всех сил равна нулю (для сил действующих вниз — знак положительный, для действующих вверх — отрицательный):

Составляя уравнения, мы исходили из того, что реакции обеих опор направлены вверх. При расчетах может получиться так, что реакция опоры окажется отрицательной. Это означает, что реакция такой опоры направлена вниз (сумма моментов сил, действующих на балку, пытается оторвать её от опоры).

Распределенная нагрузка

В расчетах, иногда требуется задать нагрузку, которая распределена определенным образом по участку длины a. Для вычисления реакций опор такую нагрузку можно заменить её равнодействующей силой. Точкой приложения такой силы считается центр масс распределенной нагрузки, а модуль вычисляется как интеграл от функции распределения нагрузки на заданном участке. Для простых функций модуль легко выразить через заданную интенсивность нагрузки.

В таблице ниже представлены формулы для модуля сосредоточенной равнодействующей силы и точек её приложения для всех видов распределенных нагрузок, поддерживаемых калькулятором:

В формулах q — это интенсивность нагрузки в Н/м, a — диапазон действия распределенной нагрузки, точка приложения силы отсчитывается от начала диапазона действия распределенной нагрузки. Интенсивность для линейно распределенной нагрузки задается для участка максимума нагрузки ( полагаем, что в точке минимума, интенсивность = 0).
После вычисления модуля и плеча равнодействующей распределенной нагрузки их можно подставить в уравнения моментов, точно так же, как мы это делали с сосредоточенными силами.

Сосредоточенный момент

Еще один способ задания нагрузки в калькуляторе — при помощи момента в Нм, приложенного к некоторой точке. Значение сосредоточенного момента добавляется к уравнениям равновесия со знаком, определяемым направлением момента в соответствии с правилом знаков. Точка приложения сосредоточенного момента для вычисления реакций опор в простой балке значения не имеет.

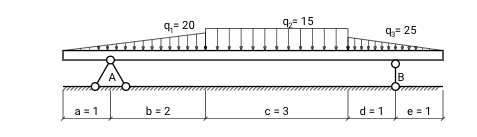
Подробный ход решения — расчет балки, построение эпюр

Заменим распределенную нагрузку равнодействующей

Q₁ = 16·2 = 32кН

Составим
уравнения равновесия для определения реакций опор

Σ M_A = + P · 2 + Q1 · 3 — M — R_E · 6= + 412 · 2 + 32 · 3 — 10 — R_E · 6=0

Σ M_E = — P · 4 — Q1 · 3 — M + R_A · 6= — 412 · 4 — 32 · 3 — 10 + R_A · 6=0

Из этих уравнений находим реакции опор

R_A = 292.3кН.

R_E = 151.7кН.

Записываем уравнения поперечных сил и изгибающих моментов на
участках балки
, используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 292.3 = 292.333 кН

M(z₁) = + R_A · z = + 292.3 · z

M(0) = 0 кНм

M(2) = 584.667 кНм

На участке BC: (2 ≤ z₂ ≤ 4 м )

Q(z₂) = + R_A — P — q₁·(z — 2) = + 292.3 — 412 — 16·(z — 2)

Q(2) = -119.667 кН

Q(4) = -151.667 кН

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2)²/2 = + 292.3 · z — 412·(z — 2) — 16·(z — 2)²/2

M(2) = 584.667 кНм

M(4) = 313.333 кНм

На участке CD: (4 ≤ z₃ ≤ 5 м )

Q(z₃) = + R_A — P — Q₁ = + 292.3 — 412 — 32 = -151.667 кН

M(z₃) = + R_A · z — P·(z — 2) — Q₁·(z — 3) = + 292.3 · z — 412·(z — 2) — 32·(z — 3)

M(4) = 313.333 кНм

M(5) = 161.667 кНм

На участке DE: (5 ≤ z₄ ≤ 6 м )

Q(z₄) = + R_A — P — Q₁ = + 292.3 — 412 — 32 = -151.667 кН

M(z₄) = + R_A · z — P·(z — 2) — Q₁·(z — 3) — M = + 292.3 · z — 412·(z — 2) — 32·(z — 3) — 10

M(5) = 151.667 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M_max = 585 кНм. По этому значению
подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Подбираем двутавровое сечение при допускаемом напряжении [σ] = 160 МПа
W_min=585000 / 160 = 3656.25 см³
Из сортамента выбираем двутавр № с моментом сопротивления W = 0 см³ и площадью A = см²
Максимальные нормальные напряжения в двутавре составляют
σ_max = M_max/Wx = 585000/0 = 0 МПа
Максимальные касательные напряжения в двутавре (на центральной оси) составляют
τ_max = Q_max×Sx/b×Ix = 292000×0×10^-6/0××10^-8 = 0×10⁶ Па = 0 МПа
Касательные напряжения на границе полки и стенки составляют
τ_max = Q_max×Sx’/b×Ix = 292000×0×10^-6/0××10^-8 = 0×10⁶ Па = 0 МПа,
где статический момент отсеченной полки составляет
Sx’=b×t×(h-t)/2=0×0×(0-0)/2=0 см³.
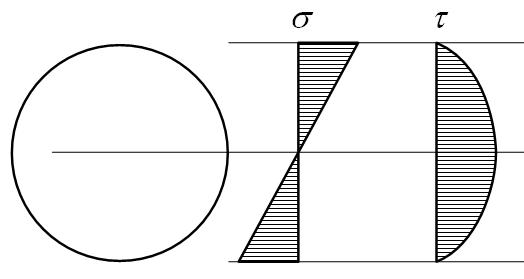
Эпюры нормальных и касательных напряжений для двутавра:

Подбираем круг.
W_min=585000/160=3656 см³
Момент сопротивления сплошного круглого сечения
W=π×d³ / 32
d³=32×W / π = 32×3656 / π = 37259
Диаметр сечения будет таким d=33.4 см
Площадь сечения
A=π×d²/4=π×33.4²/4=875.71 см²
Максимальные нормальные напряжения составляют
σ_max = 32×M_max/π×d³ = 32×585000/π×33.4³ = 160.01 МПа
Максимальные касательные напряжения для круга составляют
τ_max = 4Q_max/3A = 4×292000/3×875.71×100 = 4.446 МПа
Эпюры нормальных и касательных напряжений для круга:

Подбираем трубу с отношением диаметров α = d/D = 0.9
W_min=585000 / 160=3656 см³
Момент сопротивления трубчатого сечения
W=π×D³ ×(1-α⁴)/32
D³=32×W / π×(1-α⁴) = 32×3656 / π×(1-0.9⁴)=108341
Диаметр сечения будет таким D=47.7 см
Площадь сечения A=π×D²(1-α²)/4=π×47.7²(1-0.9²)/4=339.36 см²
Максимальные нормальные напряжения составляют
σ_max = 32×M_max/π×D³×(1-α⁴) = 32×585000/π×47.7³×(1-0.9⁴) = 159.73 МПа
Максимальные касательные напряжения для трубы определим по формуле Журавского
τ_max = Q_max×Sx/b×Ix, где b=D-d
Статический момент полусечения
Sx=2R³/3-2r³/3=(D³-d³)/12=(47.7³-(47.7×0.9)³)/12=2451 см³
Момент инерции сечения
Ix=π×D⁴×(1-α⁴)/64=π×47.7⁴×(1-0.9⁴)/64=87348.48 см⁴
τ_max = 292000×2451×10^-6/(47.7-0.9×47.7)×0.01×87348.48^-8=0.172×10⁶ Па = 0.172 МПа
Эпюры нормальных и касательных напряжений для трубы:

Подбираем квадрат.
W_min=585000 / 160=3656 см³
Момент сопротивления квадратного сечения
W=a³/6
Сторона квадрата будет такой a= 28 см
Площадь сечения A=a²=28²=784 см²

Подбираем прямоугольное сечение с отношением сторон h / b=2
W_min=585000 / 160 = 3656 см³
Момент сопротивления прямоугольного сечения
W=b×h² / 6 = b³ × 2² / 6 = b³×0.67
b³=3656 / 0.67=5457
Ширина сечения b=17.6 см, Высота сечения h=b×2=17.6×2=35.2 см
Площадь сечения A=b×h=17.6×35.2=619.52 см²
Максимальные нормальные напряжения составляют
σ_max = 6×M_max/b×h² = 6×585000/17.6×35.2² = 160.96 МПа
Максимальные касательные напряжения для прямоугольника составляют
τ_max = 3Q_max/2A = 3×292000/2×619.52×100 = 7.07 МПа
Эпюры нормальных и касательных напряжений для прямоугольного сечения:

Записываем уравнения углов поворота и прогибов по методу начальных параметров

На участке AB: (0 ≤ z₁ ≤ 2 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6

На участке BC: (2 ≤ z₂ ≤ 4 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2 — P·(z — 2)²/2 — q₁·(z — 2)³/6

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6 — P·(z — 2)³/6 — q₁·(z — 2)⁴/24

На участке CD: (4 ≤ z₃ ≤ 5 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2 — P·(z — 2)²/2 — q₁·(z — 2)³/6 + q₁·(z — 4)³/6

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6 — P·(z — 2)³/6 — q₁·(z — 2)⁴/24 + q₁·(z — 4)⁴/24

На участке DE: (5 ≤ z₄ ≤ 6 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2 — P·(z — 2)²/2 — q₁·(z — 2)³/6 + q₁·(z — 4)³/6 — M· (z — 5)

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6 — P·(z — 2)³/6 — q₁·(z — 2)⁴/24 + q₁·(z — 4)⁴/24 — M· (z — 5)²/2

Из условий закрепления по этим уравнениям вычислим начальные параметры:

— начальный угол поворота φ₀ = -994.1 кНм²

— начальный прогиб балки v₀ = 0 кНм³

Найдем углы поворота и прогибы сечений на каждом участке

На участке AB

EJ×φ(0) = -994.1 кНм²

EJ×v(0) = 0 кНм³

EJ×φ(0.5) = -957.5 кНм²

EJ×v(0.5) = -490.9 кНм³

EJ×φ(1) = -847.9 кНм²

EJ×v(1) = -945.3 кНм³

EJ×φ(1.5) = -665.2 кНм²

EJ×v(1.5) = -1327 кНм³

EJ×φ(2) = -409.4 кНм²

EJ×v(2) = -1598 кНм³

На участке BC

EJ×φ(2) = -409.4 кНм²

EJ×v(2) = -1598 кНм³

EJ×φ(2.5) = -132.3 кНм²

EJ×v(2.5) = -1732 кНм³

EJ×φ(3) = 112.8 кНм²

EJ×v(3) = -1736 кНм³

EJ×φ(3.5) = 324 кНм²

EJ×v(3.5) = -1625 кНм³

EJ×φ(4) = 499.3 кНм²

EJ×v(4) = -1418 кНм³

На участке CD

EJ×φ(4) = 499.3 кНм²

EJ×v(4) = -1418 кНм³

EJ×φ(4.25) = 572.9 кНм²

EJ×v(4.25) = -1284 кНм³

EJ×φ(4.5) = 637 кНм²

EJ×v(4.5) = -1132 кНм³

EJ×φ(4.75) = 691.6 кНм²

EJ×v(4.75) = -966.1 кНм³

EJ×φ(5) = 736.8 кНм²

EJ×v(5) = -787.3 кНм³

На участке DE

EJ×φ(5) = 736.8 кНм²

EJ×v(5) = -787.3 кНм³

EJ×φ(5.25) = 770 кНм²

EJ×v(5.25) = -598.8 кНм³

EJ×φ(5.5) = 793.7 кНм²

EJ×v(5.5) = -403.1 кНм³

EJ×φ(5.75) = 807.9 кНм²

EJ×v(5.75) = -202.8 кНм³

EJ×φ(6) = 812.6 кНм²

EJ×v(6) = 0 кНм³