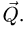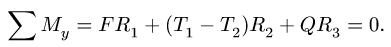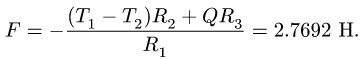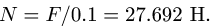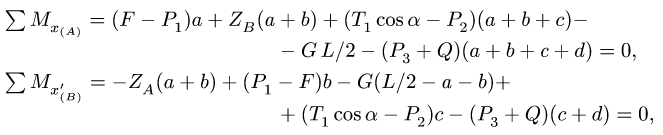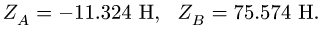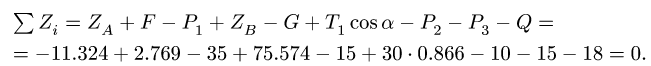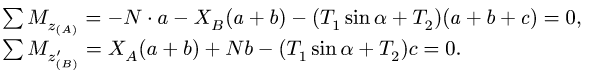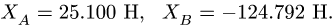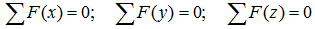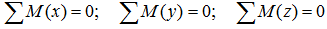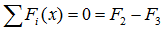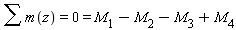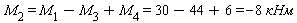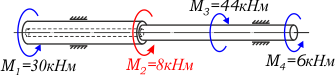Преподаватель который помогает студентам и школьникам в учёбе.
Равновесие вала в теоретической механике
Равновесие вала:
Постановка Задачи. Горизонтальный вал может вращаться в цилиндрических шарнирах. К одному шкиву вала приложено нормальное давление и касательная сила сопротивления, пропорциональная давлению. На шкивы вала действуют известные нагрузки. Найти силу давления и реакции шарниров при условии равновесия вала.
План решения:
1. Действие каждой из опор заменяем двумя взаимно перпендикулярными реакциями, лежащими в плоскости, перпендикулярной валу.
2. Для определения силы давления составляем уравнение моментов относительно оси вала. Момент силы натяжения ремня, нити и т.п. (наклонной или нет) вычисляем как произведение величины силы на соответствующий радиус со знаком, соответствующим направлению вращения вокруг вала. Уравнение содержит одну неизвестную, которую легко найти.
3. Определяем вертикальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия горизонтальных реакций шарниров. Решаем эти уравнения.
4. Проверяем найденные реакции, составляя уравнение равновесия в проекции на вертикаль.
5. Определяем горизонтальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров.
6. Проверяем горизонтальные реакции, составляя уравнение равновесия в проекции на ось вдоль линии действия горизонтальных реакций.
Задача:
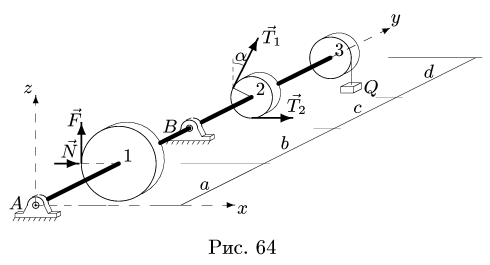
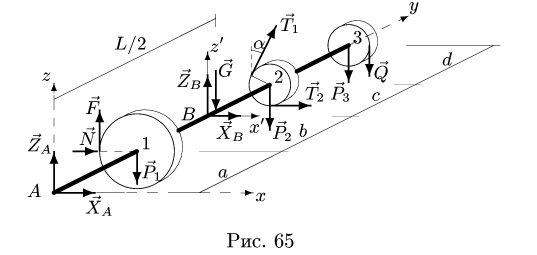
Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 64). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0.1 N.
Решение
1. Действие цилиндрических опор А и В заменим реакциями 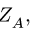
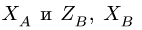
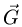
2. Для определения силы давления составляем уравнение моментов относительно оси вата:
Уравнение содержит одну неизвестную F. Линии действия остальных сил пересекают ось 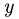
Из полученного уравнения находим
По условию
3. Определяем вертикальные реакции шарнирных опор вала. Для этого составляем два уравнения моментов относительно горизонтальных осей, проходящих через шарниры А а В. Рассматриваем для удобства проекцию всех сил на плоскость 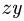
Знаки моментов сил определяем как в задачах плоской статики: момент силы, вращающей тело вокруг моментной точки против часовой стрелки считается положительным, по часовой стрелке — отрицательным. Моменты сил, перпендикулярных плоскости 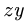
Решая уравнения
находим
4. Проверяем правильность нахождения вертикальных реакций, составляя уравнение равновесия в проекции на ось 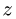
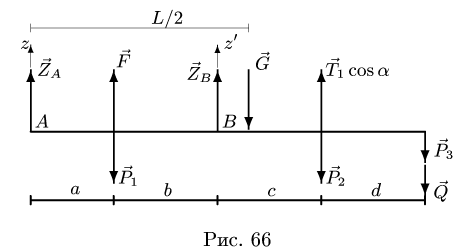
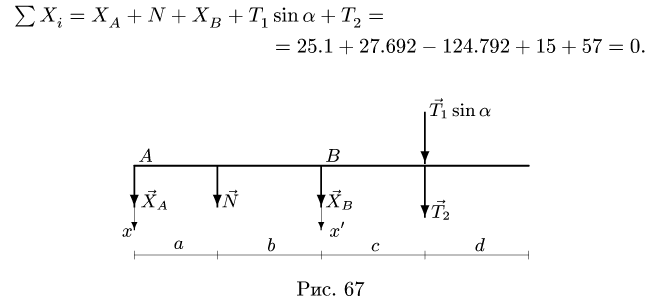
5. Определяем горизонтальные реакции опор вата. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров. Рассматриваем горизонтальную проекцию силовой схемы (рис. 67):
Решая уравнения, находим
6. Проверяем правильность нахождения горизонтальных реакций, составляя уравнение равновесия в проекции на ось х вдоль линии действия горизонтальных реакции:
Результаты расчетов в 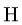
- Определение усилий в стержнях, поддерживающих плиту
- Тело на сферической и стержневых опорах
- Приведение системы сил к простейшему виду
- Плоское движение тела
- Задачи на вращательное движение тела
- Равновесие тяжелой рамы
- Расчет составной конструкции
- Момент силы относительно оси
Равновесие вала в теоретической механике
Равновесие вала:
Постановка Задачи. Горизонтальный вал может вращаться в цилиндрических шарнирах. К одному шкиву вала приложено нормальное давление и касательная сила сопротивления, пропорциональная давлению. На шкивы вала действуют известные нагрузки. Найти силу давления и реакции шарниров при условии равновесия вала.
1. Действие каждой из опор заменяем двумя взаимно перпендикулярными реакциями, лежащими в плоскости, перпендикулярной валу.
2. Для определения силы давления составляем уравнение моментов относительно оси вала. Момент силы натяжения ремня, нити и т.п. (наклонной или нет) вычисляем как произведение величины силы на соответствующий радиус со знаком, соответствующим направлению вращения вокруг вала. Уравнение содержит одну неизвестную, которую легко найти.
3. Определяем вертикальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия горизонтальных реакций шарниров. Решаем эти уравнения.
4. Проверяем найденные реакции, составляя уравнение равновесия в проекции на вертикаль.
5. Определяем горизонтальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров.
6. Проверяем горизонтальные реакции, составляя уравнение равновесия в проекции на ось вдоль линии действия горизонтальных реакций.
Задача:
Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 64). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0.1 N.
1. Действие цилиндрических опор А и В заменим реакциями 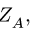
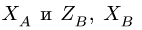
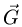
2. Для определения силы давления составляем уравнение моментов относительно оси вата:
Уравнение содержит одну неизвестную F. Линии действия остальных сил пересекают ось 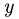
Из полученного уравнения находим
По условию
3. Определяем вертикальные реакции шарнирных опор вала. Для этого составляем два уравнения моментов относительно горизонтальных осей, проходящих через шарниры А а В. Рассматриваем для удобства проекцию всех сил на плоскость 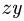
Знаки моментов сил определяем как в задачах плоской статики: момент силы, вращающей тело вокруг моментной точки против часовой стрелки считается положительным, по часовой стрелке — отрицательным. Моменты сил, перпендикулярных плоскости 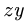
находим
4. Проверяем правильность нахождения вертикальных реакций, составляя уравнение равновесия в проекции на ось 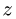
5. Определяем горизонтальные реакции опор вата. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров. Рассматриваем горизонтальную проекцию силовой схемы (рис. 67):
Решая уравнения, находим
6. Проверяем правильность нахождения горизонтальных реакций, составляя уравнение равновесия в проекции на ось х вдоль линии действия горизонтальных реакции:
Результаты расчетов в 
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определение усилий в стержнях, поддерживающих плиту
- Тело на сферической и стержневых опорах
- Приведение системы сил к простейшему виду
- Плоское движение тела
- Задачи на вращательное движение тела
- Равновесие тяжелой рамы
- Расчет составной конструкции
- Момент силы относительно оси
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
iSopromat.ru
Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
Пример составления уравнений равновесия
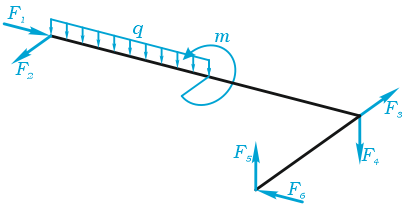
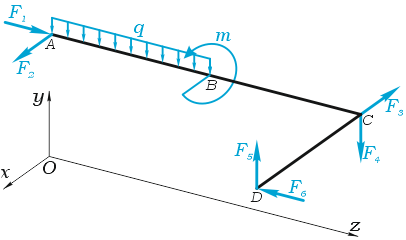
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Примеры решения задач

Решение
1. Моменты сил относительно оси Ох:
2. Моменты сил относительно оси Оу.
Пример 2. На горизонтальном валу закреплены два колеса, г1 = 0,4 м; г2 = 0,8 м. Остальные размеры — на рис. 7.7. К колесу 1 приложена сила F1, к колесу 2 — силы F2 = 12 кН, F3 = 4кН.
Определить силу F1 и реакции в шарнирах А и В в состоянии равновесия.
1. При равновесии выполняются шесть уравнений равновесия.
Уравнения моментов следует составлять относительно опор А и В.
Моменты этих сил относительно соответствующих осей равны нулю.
3. 
Решение
1. Определяем силу F, составив уравнение моментов сил относительно оси Oz:
2. Определяем реакции в опоре А. На опоре действуют две составляющие реакции (YA; XA).
Составляем уравнение моментов сил относительно оси Ох’ (в опоре В).
Поворот вокруг оси Ох’ не происходит:
Знак «минус» означает, что реакция направлена в противоположную сторону.
Поворот вокруг оси Оу’ не происходит, составляем уравнение моментов сил относительно оси Оу’ (в опоре В):
3.Определяем реакции в опоре В. На опоре действуют две составляющие реакции (XB, YB). Составляем уравнение моментов сил относительно оси Ох (опора А):
Составляем уравнение моментов относительно оси Оу (опора А):
4.Проверка. Используем уравнения проекций:
Расчёт выполнен верно.
Пример 3. Определить численное значение силы P1, при котором вал ВС (рис. 1.21, а) будет находиться в равновесии. При найденном значении силы Р1определить опорные реакции.

Решение
Опоры вала, изображенные на рис. 1.21, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей и и v (выбранная система координат показана на рис. 1.21, б).
Освобождаем вал от связей и заменяем их действие реакциями VВ, НВ,VC, НС (рис. 1.21, б). Получили пространственную систему сил, для которой составляем уравнения равновесия, пользуясь выбранной системой координат (рис. 1.21,6):
где А1*1,25D/2 — момент относительно оси и силы A1, приложенной к правому зубчатому колесу.
Моменты относительно оси и сил Т1 и А1 (приложенных к среднему зубчатому колесу), Р1 (приложенной к правому зубчатому колесу) и Р равны нулю, так как силы Р, T1, Р1 параллельны оси и, а сила А1 пересекает ось и.
Составим проверочное уравнение:
следовательно, реакции VB и VС определены верно;
где А1* 1,25D/2 — момент относительно оси v силы А1, приложенной к среднему зубчатому колесу.
Моменты относительно оси v сил Т, Р1 (приложенной к среднему зубчатому колесу), А1 и Т1 (приложенных к правому зубчатому колесу) равны нулю, так как силы Т, Р1, Т1 параллельны оси v, сила А1 пересекает ось v.
Составим проверочное уравнение:
следовательно, реакции НВ и НС определены верно.
В заключение отметим, что опорные реакции получились со знаком плюс. Это указывает на то, что выбранные направления VB, НВ, VC и НС совпадают с действительными направлениями реакций связей.

Определить натяжения ветвей ременной передачи и реакции подшипников А и В, пренебрегая массой вала.
Решение
Рассматриваем равновесие горизонтального коленчатого вала со шкивом. Прикладываем в соответствии с условием задачи заданные силы Р, S1, S2 иG. Освобождаем вал от опорных закреплений и заменяем их действие реакциями VA, НА, VB и НВ. Координатные оси выбираем так, как показано на рис. 1.22. В шарнирах А и В не возникает реакций вдоль оси w, так как натяжение ветвей ремня и все остальные силы действуют в плоскостях, перпендикулярных этой оси.
Составим уравнения равновесия:
Кроме того, по условию задачи имеем еще одно уравнение
Таким образом, здесь имеется шесть неизвестных усилий S1, S2, НА, VA, НВ иVB и шесть связывающих их уравнений.
Уравнение проекций на ось w в рассматриваемом примере обращается в тождество 0 = 0, так как все силы лежат в плоскостях, перпендикулярных оси w.
Подставляя в уравнения равновесия S1=2S2 и решая их, находим:
Значение реакции НВ получилось со знаком минус. Это значит, что в действительности ее направление противоположно принятому на рис. 1.22.
Контрольные вопросы и задания
1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил.
2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил.
3. Запишите формулу для расчета главного момента пространственной системы сил.
4. Запишите систему уравнений равновесия пространственной системы сил.
5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R1 (рис. 7.8)?
6. Определите главный момент системы сил (рис. 7.9). Точка приведения — начало координат. Координатные оси совпадают с ребрами куба, ребро куба равно 20 см;F1 — 20кН;F2 — 30кН.
7. Определите реакцию Хв (рис. 7.10). Вертикальная ось со шкивом нагружена двумя горизонтальными силами. Силы F1 и F2 параллельны осиОх. АО = 0,3 м; ОВ = 0,5 м; F1 = 2кН; F2 = 3,5 кН.
http://isopromat.ru/sopromat/otvet/uravnenia-statiki
http://mydocx.ru/12-105308.html
Б. Рпр. Расчет статически определимого вала на прочность и жесткость.
Задается:
схема нагружения вала (рис. 27), длины
участков вала:
;
;
;
;
,
величины распределенных моментов:
;
;
;
;
,
величины сосредоточенных моментов:
;
;
;
;
;
;
;
;
;
;
.
Требуется:
-
построить
эпюру крутящих моментов
;
-
из
расчета на прочность, приняв
,
определить размеры поперечных сечений
бруса; -
построить
эпюру касательных напряжений
;
-
построить
эпюру углов закручивания
;
-
произвести
проверку условия жесткости на отдельных
участках вала (при невыполнении условия
жесткости подобрать соответствующие
размеры из последнего); -
выполнить
эскиз вала в соответствии с назначенными
размерами.
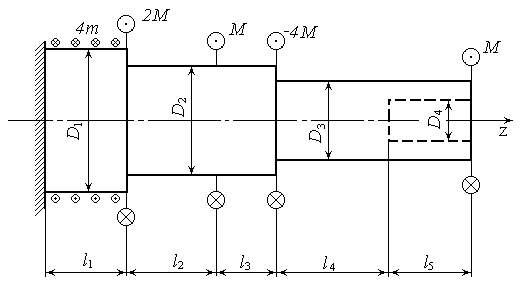
Рис. 27. Схема
нагружения вала.
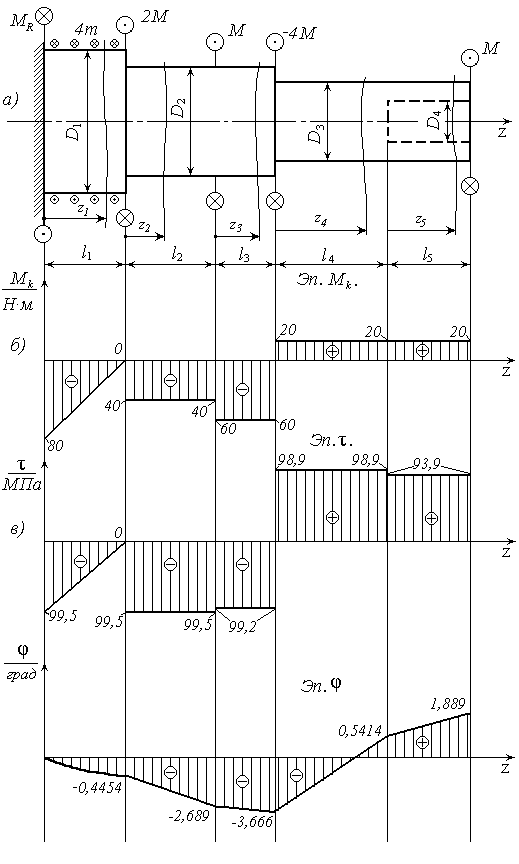
Рис. 28. Расчетная
схема вала, эпюры крутящих моментов,
касательных напряжений и углов
закручивания.
Решение
-
Определение
реактивного момента
в заделке (рис. 28,а).
Для
определения реактивного момента
составляется уравнение равновесия
вала:
.
Учитывая,
что
,
определяется реактивный момент:
.
-
Разбивка
вала на участки.
Для
построения эпюры крутящих моментов
по длине вала необходимо рассмотреть
пять участков с координатами:
,
,
,
,
(рис. 8,а).
-
Определение
законов изменения крутящего момента
по участкам вала.
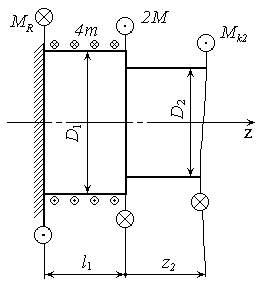
3.1.
Первый участок (рис. 29).
Рис.
29. К определению
на первом участке.
Координата
для первого участка изменяется в пределах
.
Уравнение
равновесия для отсеченной (левой) части
вала имеет вид:


Крутящий
момент на границах участка принимает
значения:
при
;
,
при
;
.
3.2.
Второй участок (рис. 30).
Рис.
30. К определению
на втором участке.
На
втором участке координата
изменяется в пределах
.
Уравнение
равновесия для отсеченной части вала
записывается в виде:
,
.
На
втором участке крутящий момент постоянен
по длине участка и равен
.
3.3.
Третий участок (рис. 31).
Рис.
31. К определению
на третьем участке.
Координата
для третьего участка изменяется в
пределах
.
Уравнение
равновесия для отсеченной части вала
и значения крутящего момента в граничных
сечениях участка соответственно равны:
.
На
третьем участке крутящий момент постоянен
по длине участка и равен
.
3.4.
Четвертый участок (рис. 32).
Рис.
32. К определению
на четвертом участке.
Координата
для третьего участка изменяется в
пределах
.
Уравнение
равновесия для отсеченной части вала
и значения крутящего момента в граничных
сечениях участка соответственно равны:
.
На
третьем участке крутящий момент постоянен
по длине участка и равен
.
3.5.
Пятый участок (рис. 33).
Рис.
33. К определению
на пятом участке.
Координата
на пятом участке изменяется в пределах
.
Уравнение
равновесия для отсеченной (левой) части
вала имеет вид:
.
На
пятом участке крутящий момент постоянен
по длине участка и равен
.
-
Из
условия прочности определяем размеры
поперечных сечений бруса (приняв
).
.
4.1. Первый участок:
;
;
.
Примем
.
4.2.
Второй участок:
;
,
.
4.3.
Третий участок:
;
,
.
Примем
.
4.4.
Четвертый участок:
;
,
.
Примем
.
4.5.
Пятый участок:
;
,
.
Примем
,
следовательно
.
-
Определение
закона изменения касательного напряжения
по участкам вала.
5.1. На
первом участке закон изменения
касательного напряжения в соответствии
с формулой (8) имеет вид:
Касательное
напряжение линейно зависит от координаты
и на границах участка принимает значения:
при
;
;
при
;
.
5.2.
На втором участке касательное напряжение
на границах участка принимает значения:
.
5.3.
На третьем участке касательное напряжение
равно:
.
5.4.
Касательное напряжение на четвертом
участке равно:
.
5.5.
На пятом участке касательное напряжение
равно:
.
По
результатам вычислений строится эпюра
касательных напряжений
(рис.28,
в).
-
Определение
закона изменения углов закручивания
на участках вала.
6.1.
На первом участке угол закручивания в
соответствии с законом Р. Гука равен:

Угол
закручивания изменяется по кривой
второго порядка и на границах участка
принимает значения:
при
;
,
при
;
.
Определим
выпуклость кривой

следовательно кривая
выпукла вниз.
Условие
экстремума кривой –
,
,
следовательно функция
имеет экстремум на границе участка при
.
Вычислим
угол закручивания при
:
6.2.
На втором участке угол закручивания
равен:

при
;
,
при
;
.
6.3.
На третьем участке угол закручивания
равен:
;
при
;
;
при
;
.
6.4.
На четвертом участке угол закручивания
равен:

при
;
;
при
;
.
6.5.
На пятом участке угол закручивания
равен:

;
;
при
;
.
-
Выполняется
проверка условия жесткости на каждом
участке вала. Условие жесткости имеет
вид:
,
где
.
;
;
;
;
.
Так
как размеры сечений бруса выбранные из
условия жесткости меньше, чем размеры
выбранные из условия прочности, то
принимаются такие размеры, которые
будут удовлетворять условию прочности.
Рис. 34. Эскиз
проектируемого вала.
Вопросы
и задания для самопроверки.
1.
При каком нагружении брус испытывает
деформацию кручения?
2.
Что называется валом?
3.
Какое правило знаков принято для крутящих
моментов?
4.
Какие напряжения возникают в поперечных
сечениях вала круглого сечения при
кручении? Закон его распределения по
высоте сечения вала?
5.
Как записывается условие прочности при
кручении?
6.
Напишите выражения полярных моментов
инерции и полярных момен-тов сопротивления
круглого (сплошного и кольцевого)
сечения.
7.
Как выбираются допускаемые напряжения
при кручении?
8.
Как записываются условия жесткости при
кручении?
9.
Что называется жесткостью сечения вала?
10.
Приведите примеры реальных конструкций,
работающих в условиях кручения,
применительно к вашей специальности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи по расчету уравновешивающего внешнего крутящего момента из условия равновесия вала.
Задача
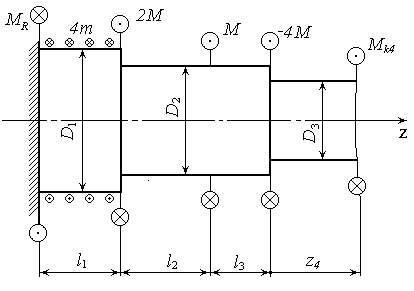
Вал нагружен скручивающими моментами. Определить величину и направление неизвестного уравновешивающего момента M2 (рис. 1), если M1=30кНм, M3=44кНм, M4=6кНм
рис. 1
Другие примеры решений >
Помощь с решением задач >
Пример решения
Величина и направление неизвестного скручивающего момента M2 определяется из условия неподвижности вала.
Конечно на самом деле вал при работе вращается, собственно для этого он и предназназначен — вращаясь передавать крутящий момент.
Но в сопротивлении материалов, при расчетах валов, часть крутящего момента необходимая для вращения вала отбрасывается, и учитываются только моменты деформирующие (скручивающие) вал.
Таким образом будем полагать что рассматриваемый вал не вращается. Для этого должно выполняться следующее условие: сумма крутящих моментов относительно продольной оси вала должна быть равна нулю
Для составления уравнения равновесия зададим произвольным образом направление искомого крутящего момента M2, например по ходу часовой стрелки (рис. 2)
рис. 2
Запишем уравнение равновесия вала относительно продольной оси z, при этом моменты вращающие вал в одну сторону запишем со знаком «+», а моменты обратного направления соответственно со знаком «-«:
отсюда следует, что
Знак «-» в результате показывает, что реальное направление крутящего момента M2 противоположно ранее выбранному, т.е. в данном случае момент M2 направлен против хода часовой стрелки и равен 8кНм.
Проверить себя можно сложив отдельно величины крутящих моментов направленных по ходу часовой стрелки и моментов обратного направления. Эти суммы должны получиться одинаковыми.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее