Как составить уравнение регрессии онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

МНК и регрессионный анализ Онлайн + графики

Данный онлайн-сервис позволяет найти с помощью метода наименьших квадратов уравнения линейной, квадратичной, гиперболической, степенной, логарифмической, показательной, экспоненциальной регрессии и др., коэффициенты и индексы корреляции и детерминации. Показываются диаграмма рассеяние и график уравнения регрессии. Также калькулятор делает оценку значимости параметров уравнения регрессии с помощью F-критерия Фишера, t-критерия Стьюдента и критерия Дарбина-Уотсона.

Можно задать уровень значимости alpha и указать, до какого знака после запятой округлять расчётные величины.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Задачу, в которой по данным, полученным в результате эксперимента или измерений, приходится решать студентам и специалистам в разных областях деятельности. Например, при решении экономических задач или задач прогнозирования. Чаще всего требуется решить задачу линейно регрессии или построить квадратичную или кубическую линию регрессии. Иногда — экспоненциальную регрессию. Тип регрессии зависит от исходного набора данных.

Итак, в задаче как правило задан набор пар данных. Требуется построить кривую, наилучшим образом описывающую эти данные. А также найти уравнение этой кривой. С помощью нашего решателя это можно сделать быстро и просто. Для этого надо ввести в решатель соответствующую команду. Приведем пример команды для линейной регрессии.

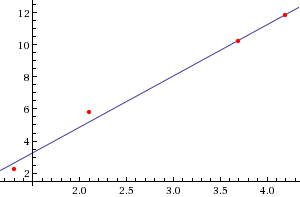
linear fit {1.3, 2.2},{2.1, 5.8},{3.7, 10.2},{4.2, 11.8}

В результате будет получен график, который вы видите на картинке вверху слева и уравнение прямой регрессии: (3.19383 x-1.52256). Красные точки на рисунке — точки построенные по исходным данным, а прямая линия — искомая линия регрессия.

Теперь приведем пример команды для квадратичной регрессии:

quadratic fit {10.1,1.2},{12.6, 2.8},{14.8,7.6},{16.0,12.8},{17.5,15.1}

Для кубической регрессии команда имеет вид, приведенный ниже. Обратите внимание на этот пример. Здесь введены только данные второй координаты. Если первая не вводится (как в этом примере), то по умолчанию в качестве первой координаты берутся порядковые номера данных из набора данных.

cubic fit 20.9,23.2,26.2,26.4,16.3,-12.2,-60.6,-128.9

И еще один пример — экспоненциальная регрессия:

exponential fit 0.783,0.552,0.383,0.245,0.165,0.097

А теперь логарифмическая регрессия:

log fit {15.2,8.9},{31.1,9.9},{38.6,10.3},{52.2,10.7},{75.4,11.4}

Чтобы попробовать решатель в работе, скопируйте любой пример (ctrl+c) и вставьте в решатель (ctrl+v), а потом нажмите кнопку «решить».

Похожие публикации

2015-11-22 • Просмотров [ 11783 ]

Источник

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной

Квадратичная аппроксимация

Аппроксимация степенной функцией

Показательная аппроксимация

Логарифмическая аппроксимация

Гиперболическая аппроксимация

Экспоненциальная аппроксимация

Точность вычисления

Знаков после запятой: 4

Коэффициент линейной парной корреляции

Средняя ошибка аппроксимации, %

Логарифмическая регрессия

Средняя ошибка аппроксимации, %

Гиперболическая регрессия

Средняя ошибка аппроксимации, %

Экспоненциальная регрессия

Средняя ошибка аппроксимации, %

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Линейная регрессия

Уравнение регрессии:

Коэффициент a:
$a&=frac{sum x_i sum y_i- nsum x_iy_i}{left(sum x_iright)^2-nsum x_i^2}$

Коэффициент b:
$b&=frac{sum x_i sum x_iy_i-sum x_i^2sum y_i}{left(sum x_iright)^2-nsum x_i^2}$

Коэффициент линейной парной корреляции:
$r_{xy}&=frac{nsum x_iy_i-sum x_isum y_i}{sqrt{left(nsum x_i^2-left(sum x_iright)^2right)!!left(nsum y_i^2-left(sum y_iright)^2 right)}}$

Коэффициент детерминации:
$R^2=r_{xy}^2$

Средняя ошибка аппроксимации:
$overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%$

Квадратичная регрессия

Уравнение регрессии:
$widehat{y}=ax^2+bx+c$

Система уравнений для нахождения коэффициентов a, b и c:
$begin{cases}asum x_i^2+bsum x_i+nc=sum y_i,,\[2pt] asum x_i^3+bsum x_i^2+csum x_i=sum x_iy_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2=sum x_i^2y_i,;end{cases}$

Коэффициент корреляции:
$R= sqrt{1-frac{sum(y_i-widehat{y}_i)^2}{sum(y_i-overline{y})^2}}$ ,
где
$overline{y}= dfrac{1}{n}sum y_i$

Коэффициент детерминации:
R^2

Средняя ошибка аппроксимации:
$overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%$

Кубическая регрессия

Уравнение регрессии:
$widehat{y}=ax^3+bx^2+cx+d$

Система уравнений для нахождения коэффициентов a, b, c и d:
$begin{cases}asum x_i^3+bsum x_i^2+csum x_i+nd=sum y_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2+dsum x_i=sum x_iy_i,,\[2pt] asum x_i^5+bsum x_i^4+csum x_i^3+dsum x_i^2=sum x_i^2y_i,,\[2pt] asum x_i^6+bsum x_i^5+csum x_i^4+dsum x_i^3=sum x_i^3y_i,;end{cases}$

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:
$widehat{y}=acdot x^b$

Коэффициент b:
$b=dfrac{nsum(ln x_icdotln y_i)-sumln x_icdotsumln y_i }{nsumln^2x_i-left(sumln x_iright)^2 }$

Коэффициент a:
$a=exp!left(dfrac{1}{n}sumln y_i-dfrac{b}{n}sumln x_iright)$

Показательная регрессия

Уравнение регрессии:
$widehat{y}=acdot b^x$

Коэффициент b:
$b=expdfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }$

Коэффициент a:
$a=exp!left(dfrac{1}{n}sumln y_i-dfrac{ln b}{n}sum x_iright)$

Гиперболическая регрессия

Уравнение регрессии:
$widehat{y}=a + frac{b}{x}$

Коэффициент b:
$b=dfrac{nsumdfrac{y_i}{x_i}-sumdfrac{1}{x_i}sum y_i }{nsumdfrac{1}{x_i^2}-left(sumdfrac{1}{x_i}right)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumdfrac{1}{x_i}$

Логарифмическая регрессия

Уравнение регрессии:

Коэффициент b:
$b=dfrac{nsum(y_iln x_i)-sumln x_icdot sum y_i }{nsumln^2x_i-left(sumln x_iright)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumln x_i$

Экспоненциальная регрессия

Уравнение регрессии:
$widehat{y}=e^{a+bx}$

Коэффициент b:
$b=dfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sumln y_i-dfrac{b}{n}sum x_i$

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:
$begin{cases} sum [y_i - F(x_i, a, b)]cdot F^prime_a(x_i, a, b)=0 \ sum [y_i - F(x_i, a, b)]cdot F^prime_b(x_i, a, b)=0 end{cases}$

Для функции вида частные производные равны:
,

Подставив производные, получим:
$begin{cases} sum (y_i - ax_i-b)cdot x_i=0 \ sum (y_i - ax_i-b)=0 end{cases}$

Далее:
$begin{cases} sum y_ix_i - a sum x_i^2-bsum x_i=0 \ sum y_i - asum x_i - nb=0 end{cases}$

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Источник

Линейная регрессия это способ описания зависимости между двумя или более исходными данными. При использовании линейная регрессии в математическом анализе можно узнать:
Зависимость одной переменной (y) от переменной(x), или нескольких других переменных.
На сколько значение (y) может изменяться в зависимости от значения (x).
На сколько значение (y) зависит от значения (x).
Появляется возможность предсказать значение (y) от значения (x).

Калькулятор расчета регрессии

Важно! В качестве разделителя для чисел используйте пробел

Значение Y (зависимая переменная от x)

Значение X (независимая переменная или предиктор)

Корреляция или R² (свидетельствует о том, что между двумя числовыми диапазонами существует сильная прямая взаимосвязь. Возможные значения от -1 до +1, если 0 то переменные не зависят друг от друга.)

Наклон (величина, на которую Y увеличивается в среднем, если мы увеличиваем X на одну единицу)

Пересечение или Intercept (это значение Y, когда X=0 )

Предсказать значение Y при помощи линейной регрессии

Введите X (для определения Y)

Значение Y (в зависимости от X будет равно)

Формулы

Уравнение регрессии Y = a + bx
Наклон b = (NΣXY — (ΣX)(ΣY)) / (NΣX² — (ΣX)²)
Перехват a = (ΣY — b(ΣX)) / N
a = Точка пересечения линии регрессии и оси y
b = Наклон линии регрессии
X и Y-переменные
N = Количество значений или элементов

Как пользоваться калькулятором линейной регрессии

Самый простой способ понять что такое линейная регрессия, это объяснить все на конкретном примере.

За исходными данными обратимся к официальному сайту федеральной службы государственной статистики. Возьмем от туда размер средней пенсии в России за последние одиннадцать лет и введем эти числа в поле Y, (15400 14900 14300 13620 13132 11783 10888 10400 9040 8202 7476 5191). Теперь в поле X внесем соответствующие им года (2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009).

После нажатия на кнопку «Вычислить», в поле «Наклон» (взято математическое название данной величины, не сарказм), вы увидите величину на которую каждый год изменяется размер средней пенсии. Поле «Корреляция» говорит нам о том, на сколько эти два числовых диапазона взаимосвязаны. Если ближе к -1, то противоположная связь. Если ближе к +1, то значение Y прямо зависит от значения X. Ели ближе к нулю, то зависимость между данными отсутствует.

Если вы хотите предсказать какое нибудь значение, тогда воспользуйтесь второй частью данного калькулятора. В поле «Введите X» поставьте год, в котором вы хотите узнать какой будет размер пенсии, затем нажмите «Вычислить». В поле «Значение Y» появится число, означающее размер пенсии в соответствующий период времени. Например если в поле «Введите X» поставим 2024 год, то узнаем какая средняя пенсия будет в этом году, она равна 19624 рублей.

Источник

Quadratic regression is a type of a multiple linear regression. It can be manually found by using the least squares method. Use our online quadratic regression calculator to find the quadratic regression equation with graph.

Find the Quadratic Regression Equation with Graph

Code to add this calci to your website

Formula:

Quadratic Regression Equation(y) = a + b x + c x^2
c = { [ Σ x² y * Σ xx ] — [Σ xy * Σ xx² ] } / { [ Σ xx * Σ x²x ²] — [Σ xx² ]² }
b = { [ Σ xy * Σ x²x² ] — [Σ x²y * Σ xx² ] } / { [ Σ xx * Σ x²x ²] — [Σ xx² ]² }
a = [ Σ y / n ] — { b * [ Σ x / n ] } — { a * [ Σ x ² / n ] }

Where ,

Σ x x = [ Σ x ² ] — [ ( Σ x )² / n ]
Σ x y = [ Σ x y ] — [ ( Σ x * Σ y ) / n ]
Σ x x² = [ Σ x ³ ] — [ ( Σ x ² * Σ x ) / n ]
Σ x² y = [ Σ x ² y] — [ ( Σ x ² * Σ y ) / n ]
Σ x² x² = [ Σ x ⁴ ] — [ ( Σ x ² )² / n ]
x and y are the Variables.
a, b, and c are the Coefficients of the Quadratic Equation
n = Number of Values or Elements
Σ x= Sum of First Scores
Σ y = Sum of Second Scores
Σ x²= Sum of square of First Scores
Σ x³= Sum of Cube of First Scores
Σ x⁴ = Sum of Power Four of First Scores
Σ xy= Sum of the Product of First and Second Scores
Σ x²y = Sum of Square of First Scores and Second Scores

Quadratic Regression is a process of finding the equation of parabola that best suits the set of data. The equation can be defined in the form as a x² + b x + c. Quadratic regression is an extension of simple linear regression. While linear regression can be performed with as few as two points, whereas quadratic regression can only be performed with more data points to be certain your data falls into the “U” shape. Just enter the set of X and Y values separated by comma in the given quadratic regression calculator to get the best fit second degree quadratic regression and graph.

All the results including graphs generated by this quadratic regression calculator are accurate. Make use of this quadratic regression equation calculator to do the statistics calculation in simple with ease.

Related Calculators:

Linear Regression Calculator
Correlation Coefficient Calculator
Autocorrelation Calculator
Regression Coefficient Confidence Interval
Spearman’s Rank Correlation Coefficient (RHO) Calculator
Golf Handicap Calculator
Central Limit Theorem Calculator (CLT)

Источник