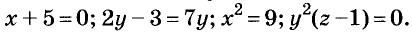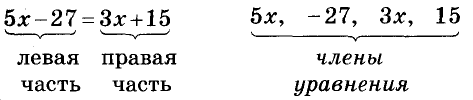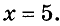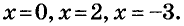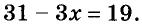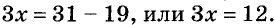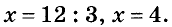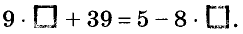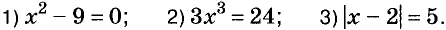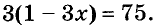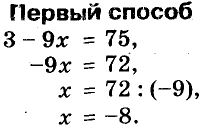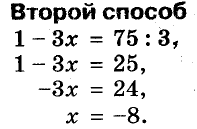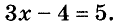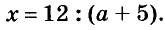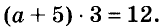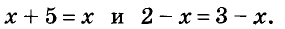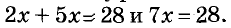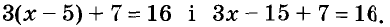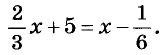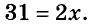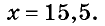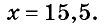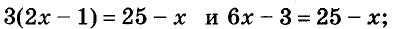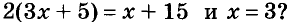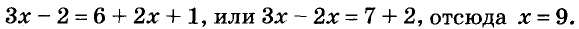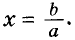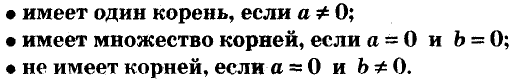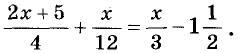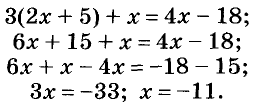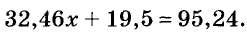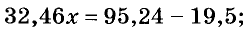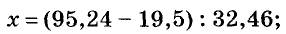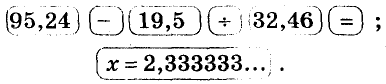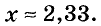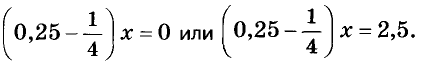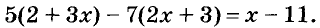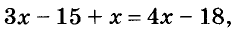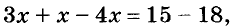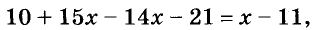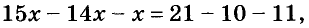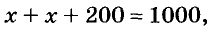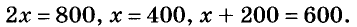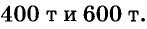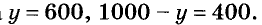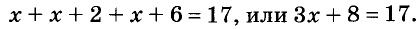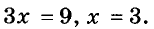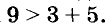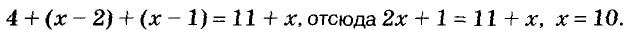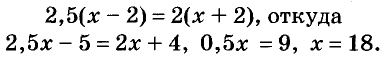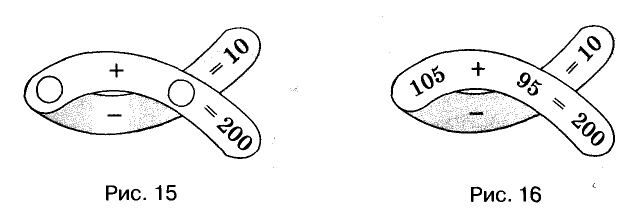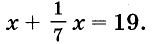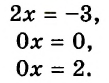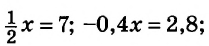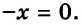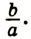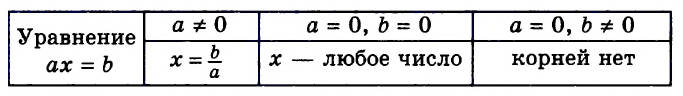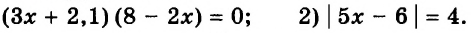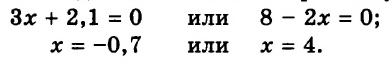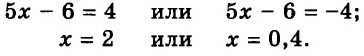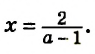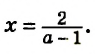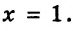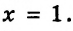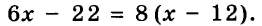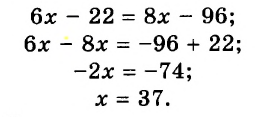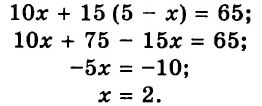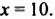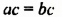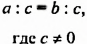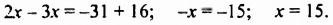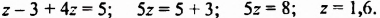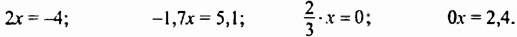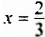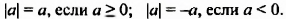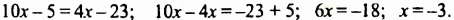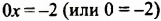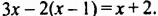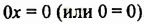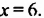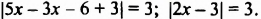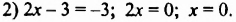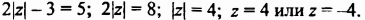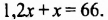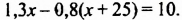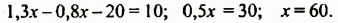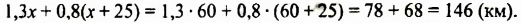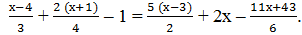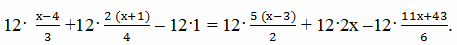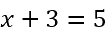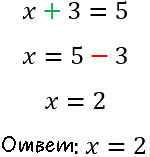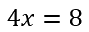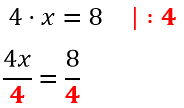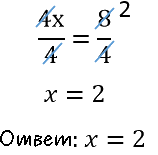Линейные уравнения: определение и решение
1 июля 2022
Сегодня мы познакомимся с линейными уравнениями. Узнаем, как их решать. Разберём и простые примеры, и довольно хитрые. Это один из важнейших уроков в курсе алгебры 7 класса.
Содержание
- Краткая вводная по уравнениям
- Что такое линейное уравнение
- Решение простых уравнений
- Более сложные задачи
- Практика: 3 дополнительных уравнения
1. Краткая вводная по уравнениям
Уравнение — это любое равенство, в котором присутствует хотя бы одна переменная.
Примеры равенств и уравнений.
- Равенство $5-3=2$ — это не уравнение. Да, оно верное, но в нём нет переменной.
- Равенство $5+3=2$ — тоже не уравнение. Оно ещё и само по себе неверное.
- А вот равенство $5-x=2$ или $5+3x=2$ — это уравнения. В них есть переменная $x$.
Мы знаем, что равенства могут быть верными, а могут быть и неверными. Чтобы проверить это, достаточно вычислить выражение, стоящее с каждой стороны от знака «равно» и сравнить полученные значения: если числа слева и справа одинаковые, то равенство верно. А если числа получились разные — равенство неверное.
С уравнениями всё сложнее. Их нельзя просто взять и вычислить, потому что мы не знаем, какое значение принимает переменная. Но если вместо переменной подставить какое-либо число, то уравнение превращается в обычное равенство — и дальше всё легко.
Пример 1. Рассмотрим уравнение: $x+5=8$.
Если подставить $x=10$, получим равенство $10+5=8$, которое, очевидно, не верно.
Но если $x=3$, то получится $3+5=8$ — это верное равенство.
Итак, есть значения переменных, при которых уравнение обращается в верное числовое равенство. А есть значения, при которых равенство получается неверным. Это позволяет ввести понятие корня уравнения.
Определение. Корень уравнения — это такое значение переменной, при подстановке которого это уравнение обращается в верное числовое равенство.
Решить уравнение — значит найти все его корни, либо доказать, что таких корней нет.
Существует бесчисленное множество разных уравнений. Одни решаются легко, другие вообще не решаются.
Умение решать такие уравнения — это сложный и очень ценный навык. И сегодня мы начнём осваивать этот навык. Для этого рассмотрим самый простой вид уравнений — линейные.
2. Что такое линейное уравнение
Определение. Линейным уравнением называется уравнение вида $ax+b=0$, где $a$ и $b$ — числа, $x$ — переменная.
Также линейными называют все уравнения, которые сводятся к виду $ax+b=0$ путём элементарных преобразований. Рассмотрим несколько примеров.
Пример 2. Линейные уравнения:
[begin{align}x+5 &=18 \ 2x &=8 \ 7-left( x-3 right) &=x-6 end{align}]
А вот эти уравнения не являются линейными:
[begin{align}{{x}^{2}} &=0 \ frac{5}{x} &=1 \ left| x right| &=64 end{align}]
Ещё раз: линейные уравнения могут выглядеть очень по-разному. Но все они сводятся к виду $ax+b=0$ с помощью элементарных преобразований. По таким преобразованиям у нас будет отдельный урок, а сейчас просто вспомним, что это такое.
2.1. Элементарные преобразования уравнений
Существует ровно три вида преобразований, которые называются элементарными:
- 1.Прибавить к обеим частям уравнения одно и то же выражение.
- 2.Умножить обе части уравнения на одно и то же выражение, отличное от нуля.
- 3.Поменять местами выражения, стоящие слева и справа от знака равенства.
Замечательное свойство всех этих преобразований состоит в том, что они не меняют корни уравнения. Но при этом зачастую позволяют получить уравнение, разрешённое относительно переменной, т.е. уравнение вида $x=a$, где $a$ — некоторое числовое выражение, которое уже не содержит переменную $x$.
Пример 3. Решите уравнение: $x+5=18$.
Вычтем из обеих частей пятёрку:
[begin{align}x+5-5 &=18-5 \ x &=13 end{align}]
Получили $x=13$ — это и есть корень.
Иногда переход от уравнения $x+5=18$ к уравнению $x=18-5$ называют «переносом слагаемого их левой части в правую». Мы тоже будем так говорить. Но помните: во «взрослой» алгебре (а именно такой мы будем заниматься с 7 по 11 класс) никаких «переносов» нет. Есть только прибавление слагаемых (пускай и противоположных к исходным).
3. Решение простых уравнений
Итак, у нас есть уравнение $ax+b=0$. Первое, что хочется сделать — это перенести слагаемое $b$ вправо, а затем разделить всё на $a$:
[begin{align}ax+b &=0 \ ax &=-b \ x &=-frac{b}{a} end{align}]
С первым шагом проблем возникнуть не должно: мы вправе прибавлять к обеим частям уравнения любое выражение, в т.ч. $-b$:
[begin{align}ax+b-b &=0-b \ ax &=-bend{align}]
А вот дальше начинаются проблемы. Если коэффициент $ane 0$, то снова никаких проблем: мы вправе поделить обе части уравнения на любое ненулевое выражение, в т.ч. на это самое $ane 0$:
[begin{align}ax &=-b \ frac{ax}{a} &=-frac{b}{a} \ x &=-frac{b}{a} end{align}]
Большинство уравнений действительно так и решаются. Взгляните на примеры:
Пример 4. Решите уравнение: $5x=10$.
Просто делим обе части уравнения на 5:
[begin{align}5x &=10 \ x &=2 end{align}]
Получили $x=2$ — это и есть искомый корень.
Пример 5. Решите уравнение: $-8x=48$.
Всё то же самое, просто делим на отрицательное число:
[begin{align}frac{-8x}{-8} &=frac{48}{-8} \ x &=-6 end{align}]
Корень уравнения: $x=-6$. То, что он отрицательный, нисколько не должно нас смущать.
Но что делать вот с такими уравнениями?
[0cdot x=10;quad 0cdot x=0]
В первом случае корней вообще нет. Потому что при любом значении $x$ мы умножаем это значение на ноль и получаем ноль, который никак не может равняться 10.
Во втором уравнении корнем наоборот будут все числа. Потому что опять же любое число при умножении на ноль даст ноль — и именно этот ноль от нас и требуется.
3.1. Основной алгоритм
Итого мы получаем три варианта развития событий. Пусть дано уравнение $ax+b=0$. Тогда:
- 1.Если $ane 0$, то уравнение имеет один корень: $x=-{b}/{a};$.
- 2.Если $a=0$, но $bne 0$, то корней нет.
- 3.Если же $a=0$ и $b=0$, то корни — все числа.
Вот так всё просто. Однако я не хочу, чтобы вы просто зазубрили эти три пункта и бездумно применяли их, когда видите линейное уравнение. Пожалуйста, помните, как и почему возникают эти правила, что такое элементарные преобразования и какие ограничения в них присутствуют (на самом деле ограничение лишь одно: нельзя умножать и делить на ноль).
Пример 6. Решите уравнение: $7x-2=6+3x$.
Вычитаем из обеих частей $3x$ и добавляем 2:
[begin{align}7x-2 &=6+3x|-3x+2 \ 4x &=8 end{align}]
Делим обе части уравнения на 4:
[begin{align}4x &=8|:4 \ x &=2 end{align}]
Получили корень уравнения $x=2$.
Пример 7. Решите уравнение: $x-11=x+5$.
Вычитаем из обеих частей $x$ и добавляем 11:
[begin{align}x-11 &=x+5|-x+11 \ 0 &=16 end{align}]
Последнее равенство уже не является уравнением. Точнее, является, но это будет уравнение вида $0cdot x=16$. Коэффициент $a=0$, коэффициент $b=16ne 0$. Следовательно, корней нет.
При решении настоящих уравнений вовсе не обязательно детально комментировать каждый шаг. Достаточно поставить вертикальную черту справа от уравнения и арифметическими знаками пояснить, что именно вы собираетесь делать.
А в будущем и этих пояснений от вас уже не потребуется.
4. Более сложные соображения
В начале урока мы обнаружили, что далеко не все уравнения сводятся к линейным с помощью элементарных преобразований. Существует множество способов преобразовать уравнение, но нам пока доступны лишь три элементарных преобразования и ещё вот такая хитрость:
Теорема. Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю.
Другими словами, если $acdot b=0$, то обязательно либо $a=0$, либо $b=0$.
А это уже интересный приём, который значительно расширяет наши возможности!
Пример 8. Решите уравнение: $left( 2x-6 right)left( x+1 right)=0$.
Произведение равно нулю, поэтому либо $2x-6=0$, либо $x+1=0$. Получили два линейных уравнения. Решим первое из них:
[begin{align}2x-6 &=0 \ 2x &=6 \ x &=3 end{align}]
Теперь решим второе. Тут вообще всё просто:
[begin{align}x+1 &=0 \ x &=-1 end{align}]
Итого уравнение имеет два различных корня: $x=3$ и $x=-1$.
Пример 9. Решите уравнение: $xleft( 5x+15 right)=0$.
Всё то же самое: произведение равно нулю, поэтому либо $x=0$, либо $5x+15=0$. Первое уравнение уже решено, а второе решается по стандартному алгоритму:
[begin{align}5x+15 &=0 \ 5x &=-15 \ x &=-3 end{align}]
Итого вновь два корня: $x=0$ и $x=-3$.
Разумеется, множителей может быть не два, а три и более. Алгоритм решения от этого никак не меняется: приравнять каждый множитель к нулю и решить каждое полученное уравнение отдельно.
5. Практика
Задача 1
Решите уравнение:
[6x+72=0]
Решение. Это линейное уравнение решается через элементарные преобразования:
[begin{align}6x+72 &=0 \ 6x &=-72 \ x &=-frac{72}{6} \ x &=-12 end{align}]
Ответ: $x=-12$. Уравнение имеет один корень.
Задача 2
Решите уравнение:
[5left( x+9 right)=5x+45]
Решение. Сначала раскроем скобки.
Это действие не является элементарным преобразованием уравнений. Оно вообще не относится к уравнениям — оно относился к выражениям с переменной (точнее, как мы позже узнаем, к многочленам):
[5x+45=5x+45]
Теперь собираем все слагаемые с переменной $x$ слева, а все числовые слагаемые — справа:
[begin{align}5x+45 &=5x+45 \ 5x-5x &=45-45 \ 0cdot x &=0 end{align}]
Ответ: все числа. Это уравнение имеет бесконечное множество корней.
Задача 3
Решите уравнение:
[left( 6-x right)+left( 12+x right)-left( 3-2x right)=15]
Решение. Вновь сначала раскроем все скобки и упростим полученное выражение:
[begin{align}left( 6-x right)+left( 12+x right)-left( 3-2x right) &=15 \ 6-x+12+x-3+2x &=15 \ 2x+15 &=15 end{align}]
Дальше остаётся лишь выполнить элементарные преобразования:
[begin{align}2x &=15-15 \ 2x &=0 \ x &=0 end{align}]
Ответ: $x=0$. Уравнение имеет единственный корень.
Важное замечание
Линейное уравнение вида $ax+b=0$ требует особого внимания при $a=0$. Потому что делить на ноль нельзя.
Однако если $ane 0$, но зато $b=0$, то ничего страшного и «нестандартного» не происходит. Получается уравнение $ax=0$, корнем которого является $x=0$.
Смотрите также:
- Иррациональное уравнение: учимся решать методом уединения корня
- Что такое дискриминант? И зачем он нужен для решения квадратных уравнений.
- Тест на тему «Значащая часть числа»
- Иррациональные неравенства. Часть 1
- Процент: налоги и зарплата. Считаем с помощью коэффициентов
- Более сложные задачи на производительность
Содержание:
Линейное уравнение с одной переменной
Уравнение — одно из важнейших понятий не только математики, но и многих прикладных наук. Это наиболее удобная математическая модель, наилучшее средство для решения сложнейших задач. Образно говоря, уравнение — это ключ, которым можно отворять тысячи дверей в неизвестное. Основные темы главы:
- общие сведения об уравнениях;
- равносильные уравнения;
- линейные уравнения;
- решение задач с помощью уравнений.
Общие сведения об уравнении
Алгебра в течение многих столетий развивалась как наука об уравнениях.
Уравнение — это равенство, содержащее не-известные числа, обозначенные буквами.
Неизвестные числа в уравнении называют переменными. Переменные чаще всего обозначают буквами х, у, z (икс, игрек, зет), хотя их можно обозначить и другими буквами.
Примеры уравнений:
Например:
Рассмотрим уравнение 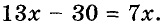
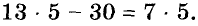
Число, удовлетворяющее уравнение, называется его корнем.
Уравнение 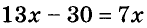
Уравнение 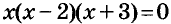
Уравнение 
Уравнение 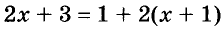
Решить уравнение — это означает, что надо найти все его корни или показать, что их не существует.
Простейшие уравнения можно решать, пользуясь известными зависимостями между слагаемыми и суммой, между множителями и произведением и т. п.
Пример:
Решите уравнение
Решение:
В данном случае неизвестно вычитаемое. Чтобы найти его, следует от уменьшаемого отнять разность:
Здесь неизвестный множитель х. Чтобы найти его, надо произведение разделить на известный множитель:
Ответ. х = 4.
Уравнение — это своеобразный кроссворд. Только в клеточки кроссворда вписывают буквы, чтобы получить нужные слова, а в уравнение вместо переменных подставляют числа, чтобы получались правильные равенства.
Например, уравнение 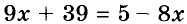
Какое число надо поставить в квадратики, чтобы получилось верное равенство?
Уравнения бывают разных видов, в частности — содержащие неизвестную переменную в квадрате, в кубе, под знаком модуля и т. п. Решим, например, уравнения:
1) Ответим на вопрос: какое число надо возвести в квадрат, чтобы получить 9? Это числа 3 и -3. Это и есть корни данного уравнения.
2) Разделим обе части уравнения 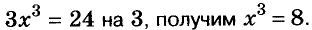
3) Если модуль числа x — 2, то это число равно 5 или -5. Имеем: x — 2 = 5, отсюда х = 7, или x — 2 = -5, отсюда х = -3. Значит, уравнение 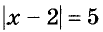
Пример:
Решите уравнение
Решение:
Пример:
Я задумал число. Если его умножить на 3, от результата отнять 4, то получим 5. Какое число я задумал?
Решение:
Обозначим искомое число буквой х. Если умножить его на 3, то получим Зх. Отняв от результата 4, получим Зх — 4. Имеем уравнение:
Решим это уравнение: 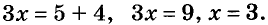
Пример:
При каком значении а уравнение 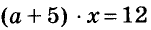
Решение:
Первый способ. Найдём неизвестный множитель х как частное от деления произведения 12 и известного множителя а + 5:
По условию x + 3, поэтому 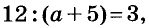
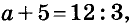
Второй способ. Подставим в уравнение 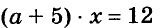
Решим полученное уравнение относительно переменной а. Имеем:
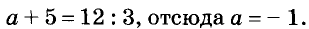
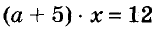
Равносильные уравнения
Рассмотрим два уравнения: 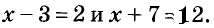
Два уравнения называют равносильными, если каждое из них имеет те же корни, что и другое. Равносильными считают и такие уравнения, которые не имеют корней.
Например:
Чтобы решать более сложные уравнения, нужно уметь заменять их более простыми и равносильными данным. Покажем, как это делается.
Из распределительного закона умножения следует, что при любом значении х числа 2x + 5x = 7x. Поэтому равносильными будут такие, например, уравнения:
Из распределительного закона следует, что при каждом значении х числа 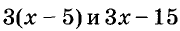
Вообще, если в любой части уравнения свести подобные слагаемые или раскрыть скобки, то получим уравнение, равносильное данному.
Прибавив к обеим частям верного числового равенства одно и то же число, получим также верное равенство. Подобно этому тела с равными массами, положенные на чаши уравновешенных весов, не нарушают равновесия (рис. 4).
Отсюда следует, что когда, например, к обеим частям уравнения 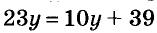
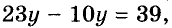
Вспомним также, что обе части числового равенства можно умножить или разделить на одно и то же число, отличное от нуля. Поэтому если обе части уравнения умножить иди разделить на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному. Например, умножив обе части уравнения 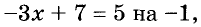
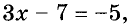
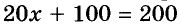
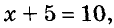
Всегда справедливы такие основные свойства уравнений.
- В любой части уравнения можно свести подобные слагаемые или раскрыть скобки, если они есть.
- Любой член уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный.
- Обе части уравнения можно умножить или разделить на одно и то число, отличное от нуля.
В результате таких преобразований всегда получаем уравнение, равносильное данному.
Сформулированные свойства часто используют для решения уравнений. Для примера решим уравнение:
Решение:
Умножим обе части уравнения на 6:
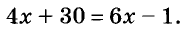
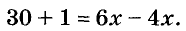
Разделим обе части уравнения на 2:
Ответ.
Откуда произошло название науки — алгебра? От названия книги об уравнениях узбекского математика IX в. Мухаммеда аль-Хо-резми (Мухаммеда из Хорезма). В те далёкие времена отрицательные числа не считались настоящими. Поэтому когда в результате перенесения отрицательного члена уравнения из одной его части в другую этот член становился положительным, считалось, что Qh восстанавливался, переходил из ненастоящего в настоящий. Такое преобразование уравнений Мухаммед аль-Хорезми назвал восстановлением (аль-джебр). Свойство об уничтожении одинаковых членов уравнения в обеих частях он назвал противопоставлением (аль-мукабала). Книга об этих преобразованиях называлась «Китаб мухтасар аль-джебр ва-л-мукабала» («Книга о восстановлении и противопоставлении»). Со временем её перевели на латинский Язык, взяв для названия только одно слово, которое стали писать Algebr. Отсюда и пошло название науки — алгебра. Преобразование «аль,-джебр» стало важным шагом в развитии алгебры, так как упростило решение уравнений.
Алгебра, арифметика, геометрия, математический анализ — основные составляющие математики (рис. 5). Арифметику — науку о числах и вычислениях — вы уже изучали на уроках математики. В 7-9 классах будете изучать алгебру и геометрию, с математическим анализом ознакомитесь в старших классах.
Пример:
Равносильны ли уравнения:
а)
б)
Решение:
а) Если раскрыть скобки в первом уравнении, то получим второе. Значит, уравнения равносильны.
б) Решим первое уравнение:
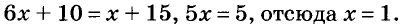
Ответ. а) Равносильны; б) не равносильны.
Пример:
Решите уравнение:
Решение:
Раскроем скобки и приведём подобные слагаемые: 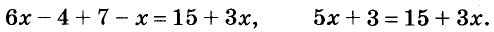
Разделим обе части уравнения на 2. Получим: х = 6. Ответ. х = 6.
Пример:
Найдите корни уравнения:
Решение:
Умножим обе части уравнения на 3. Получим:
Линейные уравнения
Уравнение вида ax = b, где a и b — данные числа, называется линейным уравнением с переменной х.
Числа a и b — коэффициенты уравнения ax = b , a— коэффициент при переменной х,b — свободный член уравнения.
Если 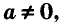
Каждое уравнение первой степени с одной переменной имеет один корень. Линейное уравнение может не иметь корней, иметь один или бесконечное множество корней.
Линейное уравнение ах = b:
Например, уравнение 0x = 5 не имеет ни одного корня, так как не существует числа, которое при умножении на 0 в произведении давало бы 5.
Уравнение 0x = 0 имеет бесконечное множество корней, так как его удовлетворяет любое значение переменной х.
Решая уравнение, его сначала стараются упростить, свести к линейному. Делают это преимущественно в такой последовательности.
- Избавляются от знаменателей (если они есть).
- Раскрывают скобки (если они есть).
- Переносят члены, содержащие переменные, в левую часть уравнения, а не содержащие — в правую.
- Приводят подобные слагаемые.
В результате такого преобразования получают уравнение, равносильное данному; его корни являются также корнями данного уравнения.
Пример 1. Решите уравнение:
Решение. Умножим обе части уравнения на 12 — наименьшее общее кратное знаменателей 2, 3, 4 и 12:
Ответ. -11.
Если коэффициенты уравнения многозначные, его удобно решать, пользуясь калькулятором. Пример 2. Решите уравнение
Ответ.
Найденное значение корня — приближённое. Точное значение пришлось бы записать в виде смешанной дроби, а именно 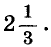
Уравнение первой степени — это отдельный вид линейных уравнений. Соотношение между этими двумя видами уравнений наглядно проиллюстрировано на рисунке 7.
Ниже приведём примеры линейных уравнений, которые не являются уравнениями первой степени.
Уравнения первой степени
Уравнения 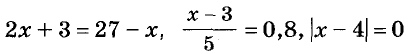
Почему уравнение вида ах = b называют линейными, станет понятно, когда вы ознакомитесь с линейными функциями.
Пример:
Решите уравнения:
а) 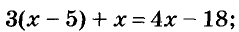
Решение:
а)
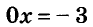
б)
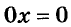
Ответ. а) Уравнение корней не имеет;
б) уравнение имеет бесконечное множество корней.
Пример:
Найдите два числа, полусумма которых вдвое больше их полуразности, которая равна 35.
Решение:
Если полуразность чисел равна 35, то разность будет вдвое больше, а именно — 70. Обозначим меньшее число буквой х, тогда большее будет равно
70 + х. По условию задачи 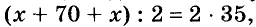
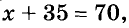
Решение задач с помощью уравнений
Чтобы решить задачу с помощью уравнения, сначала надо составить соответствующее этой задаче уравнение. Образно говоря, надо перевести задачу с обычного языка на язык алгебры, то есть составить математическую модель данной задачи. Как это можно сделать, покажем на нескольких примерах.
Пример:
На двух токах 1000т зерна. Сколько зерна на каждом току, если на первом его на 200т меньше, чем на втором?
Решение:
Пусть на первом току 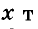
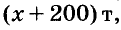
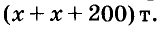
отсюда
Ответ.
Уравнение 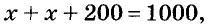
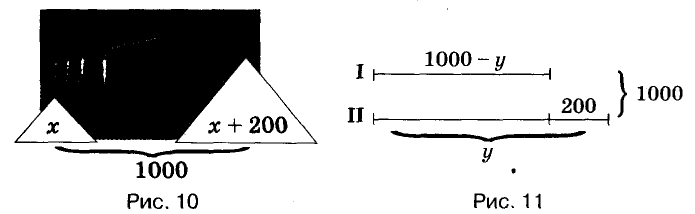
Составить уравнения часто помогает рисунок или схема (рис. 10)
Данную задачу можно решить и другими способами.
Если на втором току есть у т зерна, то на первом 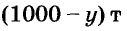
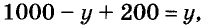
Ответ тот же.
Рисунок 10, рисунок 11., уравнение 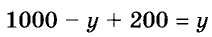
Модель всегда подобна оригиналу. В ней отображаются те или иные важные свойства исследуемого объекта. Такими являются уменьшенные модели автомобиля, самолёта, строения. Глобус — модель Земли, кукла — модель человека. Если модель создана на основе уравнений, формул или других математических понятий, её называют математической моделью.
Для решения задач на движение также используют разные модели. Надо помнить, что при равномерном движении пройденное телом расстояние равно произведению скорости на время 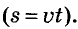
Рассмотрим задачу, составить уравнение к которой помогает таблица — ещё один вид математических моделей.
Пример:
Катер должен был пройти расстояние между городами со скоростью 15 км/ч, а на самом деле шёл со скоростью 12 км/ч и потому опоздал на 3 ч. Найдите расстояние между городами.
Ответ. Построим таблицу и заполним её в соответствии с условием задачи.
Катер шёл на 3 ч дольше, чем должен был идти. Этому условию соответствует уравнение:
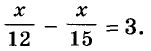
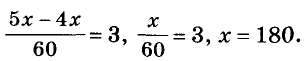
Решив задачу с помощью уравнения, нужно всегда анализировать полученное значение неизвестного. Может получиться, что найденный корень уравнения не соответствует условию задачи.
Пример:
Периметр треугольника равен 17 см. Найдите его стороны, если одна из них короче другой на 2 см, а третьей — на б см.
Решение:
Пусть длина самой короткой стороны треугольника равна х см. Тогда длины других сторон соответственно будут равны 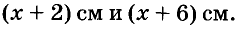
Решим его:
Если длина первой стороны 3 см, то вторая и третья соответственно будут равны 5 и 9 см.
Существует ли треугольник с такими сторонами? Нет, так как каждая сторона треугольника короче суммы двух других, а
Ответ. Задача не имеет решения.
Решение прикладных задач методом математического моделирования состоит из трёх этапов:
- создание математической модели данной задачи;
- решение соответствующей математической задачи;
- анализ ответа.
Иногда с помощью уравнения решают не всю задачу, а только её часть.
Покажем, например, как можно заполнять пустые клеточки магического квадрата — таблицы чисел с одинаковым количеством строк столбцов, с одинаковой суммой чисел во всех строках, столбцах и по диагоналям.
Пример:
Перерисуйте в тетрадь рисунок 12 и в его пустые клеточки впишите такие числа, чтобы получился магический квадрат.
Решение:
Обозначим буквой х число в правой верхней клеточке Тогда сумма всех чисел первой строки будет равна 5+6+x, или 11 + x Такими же должны быть суммы и в каждой диагонали, и в среднем столбце поэтому в нижней строке следует написать 4, x — 2 , x — 1 (рис. 13). Та как сумма чисел должна быть равна 11 + х, то составим уравнение:
Подставим вместо х его значение 10, после чего пустые клеточки рисунка 14 заполнить нетрудно. 
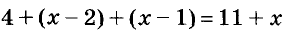
Пример:
Катер прошёл расстояние между пристанями по течению реки за 2 ч, а обратно — за 2,5 ч. Найдите собственную скорость катера, если скорость течения равна 2 км/ч.
Решение:
Пусть собственная скорость катера равна x км/ч. Тогда:
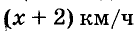
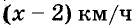
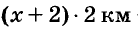
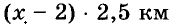
Расстояния 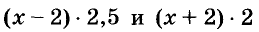
Ответ. 18 км/ч.
Пример:
Решите математический кроссворд (рис. 15).
Решение:
В кружки следует вписать два числа так, чтобы их сумма была равна 200, а разность — 10. Если второе число обозначим буквой х, то первое будет равно 200 — х. Их разность равна 10, следовательно, 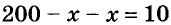
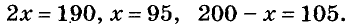
Исторические сведения:
Уравнения первой степени с одной переменной люди научились решать очень давно. Египетские учёные почти четыре тысячи лет тому назад искомое неизвестное число называли «аха» (в переводе — «куча») и обозначали специальным знаком. В папирусе, дошедшем до нас, есть такая задача: «Куча и её седьмая часть составляют 19. Найдите кучу». Теперь бы мы сформулировали её так: «Сумма неизвестного числа и его седьмой части равна 19. Найдите неизвестное число».
Задача сводится к уравнению
Подобные задачи умели решать учёные Древней Греции, древних Индии, Китая. Древнегреческий математик Диофант (III в.) решал и более сложные уравнения, в частности такие, которые в современных символах имеют вид 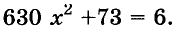
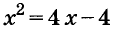
Аль-Хорезми и многие его преемники все уравнения записывали словами, не используя математических знаков.
От фамилии аль-Хорезми происходит ещё один важный для современной науки термин — алгоритм. Так называют совокупность правил, пользуясь которыми можно решить любую задачу из определённого класса задач. Например, известный вам способ умножения чисел «столбиком», способ определения наибольшего общего делителя двух или нескольких чисел — это алгоритмы. В современной науке понятие «алгоритм» играет огромную роль, существует даже специальная область математики — теория алгоритмов. Подробнее с алгоритмами вы ознакомитесь в старших классах.
Сначала алгеброй называли науку, изучающую различные способы решения уравнений. Со временем она значительно расширилась, обогатилась новыми идеями. Теперь уравнение — только одна из составляющих алгебры.
Напомню:
Уравнение — это равенство, которое содержит неизвестные числа, обозначенные буквами.
Числа, удовлетворяющие уравнение, — его корни. Решить уравнение — это значит найти все его корни или показать, что их не существует.
Два уравнения называют равносильными, если каждое из них имеет те же корни, что и другое. Уравнения, которые не имеют корней, также считают равносильными друг другу.
Основные свойства уравнений.
- В любой части уравнения можно привести подобные слагаемые или раскрыть скобки, если они есть.
- Любой член уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный.
- Обе части уравнения можно умножить или разделить на одно и то же число, отличное от нуля.
Уравнение вида ах = b, где а и b — произвольные числа, называют линейным уравнением с переменной х. Если 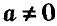
Каждое уравнение первой степени ах = b имеет один корень 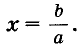
Решение прикладных задач методом математического I моделирования состоит из трёх этапов:
- создание математической модели данной задачи;
- решение соответствующей математической задачи;
- анализ ответа.
Линейное уравнение с одной переменной
Рассмотрим три уравнения:
Очевидно, что число -1,5 является единственным корнем первого уравнения.
Поскольку произведение любого числа на нуль равно нулю, то корнем второго уравнения является любое число.
Понятно, что третье уравнение корней не имеет.
Несмотря на существенное различие полученных ответов, приведенные уравнения внешне похожи: все они имеют вид 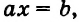
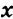
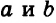
Уравнение вида 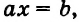
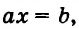
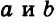
Вот еще примеры линейных уравнений:
Текст, выделенный жирным шрифтом, разъясняет смысл термина «линейное уравнение». В математике предложение, раскрывающее суть нового термина (слова, понятия, объекта), называют определением.
Итак, мы сформулировали (или говорят: «дали») определение линейного уравнения.
Заметим, что, например, уравнения 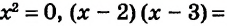
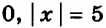
Если 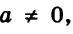
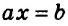
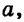
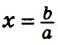
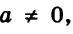
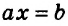
Если же 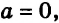
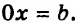
В первом случае получаем уравнение 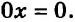
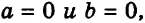
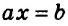
Во втором случае, когда 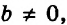
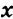
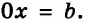
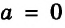
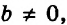
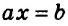
Следующая таблица подытоживает приведенные рассуждения.
Пример:
Решите уравнение:
1)
Решение:
1) Так как произведение нескольких множителей равно нулю, когда хотя бы один из множителей равен нулю, получаем:
Ответ: -0,7; 4.
2) Учитывая, что модуль только чисел 4 и -4 равен числу 4, имеем:
Ответ: 2; 0,4.
Обратим ваше внимание на то, что рассмотренные уравнения не являются линейными, однако решение каждого из них сводится к решению линейных уравнений.
Пример:
Решите уравнение:
Решение:
1) При 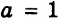
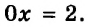
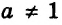
Ответ: если 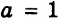
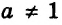
2) При 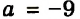
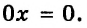
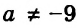
Ответ: если 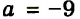
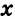
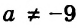
Решение задач с помощью уравнений
Вам много раз приходилось решать задачи с помощью составления уравнений (текстовые задачи). И разнообразие решенных задач является лучшим подтверждением эффективности и универсальности этого метода. В чем же заключается секрет его силы?
Дело в том, что условия непохожих друг на друга задач удается записать математическим языком. Полученное уравнение — это результат перевода условия задачи с русского языка на математический.
Часто условие задачи представляет собой описание какой-то реальной ситуации. Составленное по этому условию уравнение называют математической моделью этой ситуации.
Конечно, чтобы получить ответ, уравнение надо еще решить. Для этого в алгебре разработаны различные методы и приемы. С некоторыми из них вы уже знакомы, многие другие вам еще предстоит изучить.
Найденный корень — это еще не ответ задачи. Следует выяснить, не противоречит ли полученный результат реальной ситуации, описанной в условии.
Рассмотрим, например, такие задачи:
- За 4 ч собрали 6 кг ягод. Сколько ягод собирали за каждый час?
- Несколько мальчиков собрали 6 кг ягод. Каждый из них собрал по 4 кг. Сколько мальчиков собирали ягоды?
Обе задачи приводят к одному и тому же уравнению 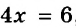
При решении задач на составление уравнений удобно пользоваться следующей схемой:
- по условию задачи составить уравнение (сконструировать математическую модель задачи);
- решить уравнение, полученное на первом шаге;
- выяснить, соответствует ли найденный корень смыслу задачи, и дать ответ.
Эту последовательность действий, состоящую из трех шагов, можно назвать алгоритмом решения текстовых задач.
Пример:
Рабочий должен был выполнить заказ за 8 дней. Однако, изготавливая ежедневно 12 деталей сверх нормы, он уже за 6 дней работы не только выполнил заказ, но и изготовил дополнительно 22 детали. Сколько деталей ежедневно изготавливал рабочий?
Решение:
Пусть рабочий изготавливал ежедневно 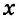
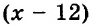
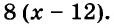
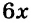
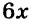
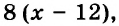
Тогда
Ответ: 37 деталей.
Пример:
Велосипедист проехал 65 км за 5 ч. Часть пути он проехал со скоростью 10 км/ч, а оставшийся путь — со скоростью 15 км/ч. Сколько времени он ехал со скоростью 10 км/ч и сколько — со скоростью 15 км/ч?
Решение:
Пусть велосипедист ехал 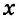
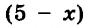
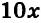
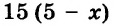
Следовательно, со скоростью 10 км/ч велосипедист ехал 2 ч, а со скоростью 15 км/ч — 3 ч.
Ответ: 2 ч, 3 ч.
——
Что такое уравнение, линейное уравнение, что значит решить уравнение
Алгебра длительное время была частью арифметики — одной из древнейших математических дисциплин. Слово «арифметика» в переводе с греческого означает «искусство чисел». Алгебру же после выделения ее в отдельную науку рассматривали как искусство решать уравнения.
В данном разделе мы выясним, что такое уравнение, линейное уравнение, что значит решить уравнение, как решать задачи с помощью уравнений.
Что такое уравнение
Рассмотрим задачу:
Масса 4 больших и 15 малых деталей равна 270 г. Масса большой детали в три раза больше массы малой. Какова масса малой детали?
Пусть масса малой детали равна 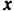
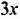
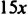
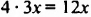
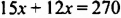
Мы пришли к равенству, которое содержит неизвестное число, обозначенное буквой 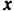
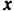
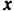
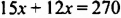
Равенство с неизвестным значением переменной называют уравнением с одной переменной (или уравнением с одним неизвестным).
Корень уравнения
Рассмотрим уравнение 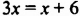
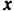
Значение переменной, при котором уравнение превращается в верное числовое равенство, называют корнем, или решением уравнения.
Итак, число 3 является корнем уравнения 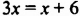
Количество корней уравнения
Уравнения могут иметь разное количество корней. Например:
уравнению 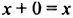
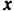
Уравнение может и не иметь корней. Рассмотрим, например, уравнение 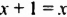
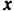
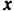
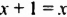
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Решим уравнение, составленное выше по условию задачи о больших и малых деталях:
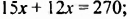
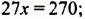
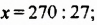
Таким образом, масса малой детали равна 10 г.
Примеры решения уравнений:
Пример №86
Является ли число 2,5 корнем уравнения 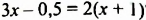
Решение:
Если 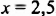
значение левой части уравнения равно: 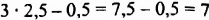
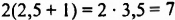
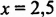
- Заказать решение задач по высшей математике
Пример №87
Решить уравнение:
а) 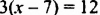
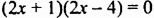
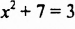
а) 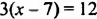
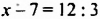
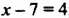
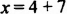
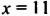
б) Произведение равно нулю только тогда, когда хотя бы один из множителей равен нулю. Следовательно, 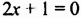
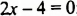
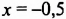
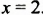
в) 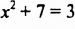
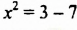
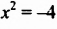
Решение уравнений. Свойства уравнений
Решение любого уравнения сводится к выполнению определенных преобразований, в результате которых данное уравнение заменяют более простым.
Решим, например, уравнение:
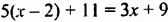
1. Раскроем скобки:
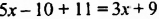
2. Приведем подобные слагаемые в левой части уравнения:
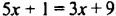
3. Перенесем слагаемые с переменной 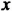
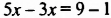
4. Приведем подобные слагаемые в каждой части уравнения:
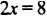
5. Разделим обе части уравнения на 2:
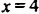
Таким образом, уравнение (1) имеет единственный корень — число 4.
При решении уравнения (1) мы выполняли некоторые преобразования: раскрывали скобки, приводили подобные слагаемые, переносили слагаемые из одной части уравнения в другую, делили обе части уравнения на число. С этими преобразованиями связаны следующие основные свойства уравнений:
Свойство 1. В любой части уравнения можно раскрыть скобки или привести подобные слагаемые.
Свойство 2. Любое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.
Свойство 3. Обе части уравнения можно умножить или разделить на одно и то же число, отличное от нуля.
Если в некотором уравнении выполнить одно из преобразований, указанных в свойствах 1, 2 или 3, то получим уравнение, имеющее те же корни, что и начальное уравнение.
Решая уравнение (1), мы последовательно получали уравнения (2), (3), (4), (5). Все они вместе с уравнением (1) имеют один и тот же корень — число 4.
Для тех, кто хочет знать больше
Свойства уравнений можно обосновать, используя следующие свойства числовых равенств:
Если а — b — верное числовое равенство и с — некоторое число, то:
Если к обеим частям верного числового равенства прибавить одно и то же число, то получим верное числовое равенство.
Если обе части верного числового равенства умножить на одно и то же число, то получим верное числовое равенство.
Если обе части верного числового равенства разделить на одно и то же число. отличное от нуля то получим верное числовое равенство.
Из первого свойства числовых равенств можно получить такое следствие: если из одной части верного числового равенства перенести в другую часть слагаемое, изменив его знак на противоположный, то получим верное числовое равенство.
Используя свойства числовых равенств, докажем, например, что уравнение
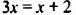
имеет тс же корни, что и уравнение
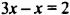
(Это свойство 2 для уравнения 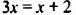
• Пусть 
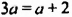
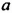
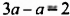

Наоборот, пусть 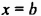
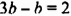
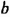
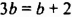
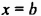
Примеры решения уравнений:
Пример №88
Решить уравнение 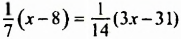
Решение:
Умножив обе части уравнения на 14, получим:
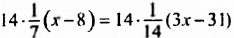
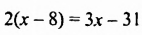
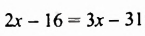
Ответ. 15.
Пример №89
Решить уравнение 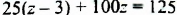
Решение:
Разделив обе части уравнения на 25, получим:
Ответ. 1,6.
Линейные уравнения с одной переменной
Линейные уравнения с одной переменной
Рассмотрим уравнения:
Левая часть каждого из этих уравнений является произведением некоторого числа и переменной, а права часть — некоторым числом. Такие уравнения называют линейными уравнениями с одной переменной.
Определение:
Уравнение вида 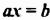
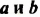
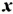
Числа а и b называют коэффициентами линейного уравнения.
Когда при решении уравнения выполняют некоторые преобразования, приводя данное уравнение к более простому, то во многих случаях этим «простым» уравнением является именно линейное уравнение.
Выясним, сколько корней может иметь линейное уравнение. Для этого рассмотрим сначала три следующих уравнения:
1) 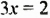
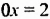
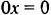
- Чтобы решить уравнение
, достаточно обе его части разделить на 3. Получим один корень:
- В уравнении
значение левой части равно 0 для любого числа
. Правая же часть уравнения не равна нулю. Следовательно, данное уравнение корней не имеет.
- Равенство
является верным для любого числа
. Поэтому корнем уравнения
является любое число (уравнение имеет бесконечно много корней).
В общем случае для линейного уравнения 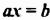
Итог: количество корней линейного уравнения
|
уравнение |
Коэффициенты | Корни |
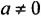 |
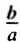 — единственный корень — единственный корень |
|
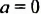 и и 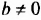 |
корней нет | |
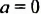 и и 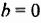 |
корнем является любое число (уравнение имеет бесконечно много корней) |
Уравнения с модулями
Напомним, что модулем положительного числа и числа 0 является это же число, модулем отрицательного числа является противоположное ему число:
Так, 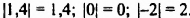
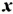
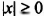
Уравнения 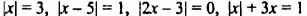
Уравнение вида 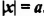
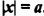
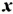
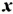
Рассмотрим уравнение 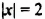
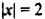
Рис. 1
Уравнение 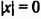
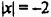
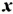
В общем случае уравнение 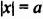
Решение уравнений с модулями, исходя из определения модуля числа
Решим уравнение
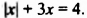
Это уравнение нельзя привести к виду 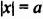
1. Если 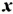
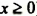
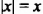
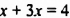
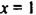
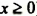
2. Если 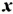
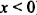

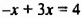
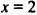
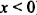
Таким образом, уравнение 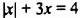
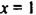
Примеры выполнения заданий:
Пример №90
Решить уравнение 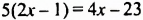
Решение:
Ответ. -3.
Пример №91
Решить уравнение 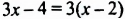
Решение:
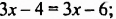
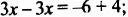
Ответ. Уравнение корней не имеет.
Пример №92
Решить уравнение
Решение:
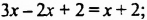
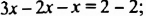
Ответ. Корнем уравнения является любое число.
Пример №93
Решить уравнение 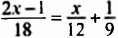
Решение:
Умножив обе части уравнения на 36 (36 — наименьшее общее кратное знаменателей дробей), получим:
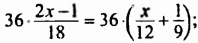
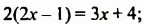
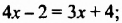
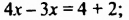
Ответ. 6.
Итог. При решении уравнения нужно придерживаться следующей схемы:
- Если в уравнении есть выражения с дробными коэффициентами, то умножить обе его части на наименьший общий знаменатель дробей.
- Раскрыть скобки.
- Перенести все слагаемые, содержащие переменную, в одну часть уравнения (как правило, в левую), а слагаемые, не содержащие переменной, — в другую часть (в правую).
- Привести подобные слагаемые.
- Разделить обе части уравнения на коэффициент при переменной, если он не равен нулю. Если же он равен 0, то уравнение или не имеет корней, или его корнем является любое число.
Пример №94
Решить уравнение 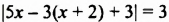
Решение:
Если модуль числа равен 3, то этим числом является 3 или -3. Поэтому возможны два случая:
1) 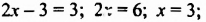
Ответ. 3; 0.
Пример №95
Решить уравнение 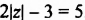
Решение:
Ответ. -4; 4.
Решение задач с помощью уравнений
При решении задач с помощью уравнений в большинстве случаев придерживаются следующей схемы:
- выбирают неизвестное и обозначают его буквой
(или какой-нибудь другой буквой);
- используя условие задачи, составляют уравнение;
- решают уравнение и отвечают на вопросы, поставленные в задаче.
Рассмотрим примеры.
Пример №96
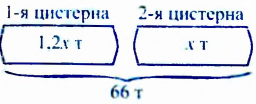
В двух цистернах находится 66 т бензина, причем в первой бензина в 1,2 раза больше, чем во второй. Сколько бензина в каждой цистерне?
Решение:
Пусть во второй цистерне 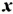
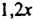
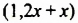
Решим это уравнение: 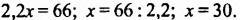
Таким образом, во второй цистерне 30 т бензина, а в первой — 1,2 • 30 = 36 (т).
Ответ. 36 т, 30 т.
Примечание. Чтобы решить задачу 1, можно рассуждать и так. Пусть во второй цистерне 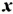
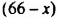
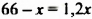
Пример №97
Из. города А в город В выехал грузовой автомобиль. Через 30 мин навстречу ему из города В выехал легковой автомобиль, скорость которого на 25 км/ч больше скорости грузового. Автомобили встретились через 1,3 ч после выезда грузового автомобиля из города А. Найти расстояние между городами, если за все время движения грузовой автомобиль проехал на 10 км больше, чем легковой.
Решение:
Пусть скорость грузового автомобиля 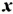
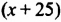
До момента встречи грузовой автомобиль был в пути 1,3 ч, а легковой на 30 мин = 0,5 ч меньше: 1,3 ч — 0,5 ч = 0,8 ч. За 1,3 ч грузо&ой автомобиль проехал 1,3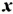
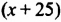
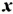
| Скорость, км/ч | Время, ч | Путь, км | |
| Грузовой автомобиль | 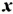 |
1,3 | 1,3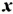 |
| Легковой автомобиль | 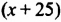 |
0,8 | 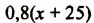 |
Получили уравнение:
Решим это уравнение:
Итак, скорость грузового автомобиля равна 60 км/ч.
Расстояние между городами равно сумме расстояний, которые проехали оба автомобиля, то есть 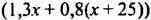
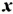
Ответ. 146 км. •
Примечание. Опираясь на решение задач 1 и 2, проанализируем первые два шага приведенной выше схемы решения задач с помощью уравнений.
1) Выбор неизвестного, которое мы обозначали буквой, в решениях этих задач был разным. В задаче 1 мы обозначили через 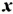
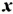
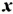
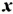
Таким образом, обозначать через 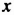
2) Чтобы составить уравнение, сначала выражаем через 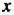
Математическая модель:
Вам, наверное, уже приходилось видеть модели корабля, самолета, автомобиля, изготавливать модели куба, прямоугольного параллелепипеда. Каждая модель, в зависимости от ее предназначения, отображает некоторые свойства оригинала.
Математическая модель — это описание некоторого реального объекта или процесса на языке математики.
Опишем на языке математики задачу 2. Определяя скорость грузового автомобиля в этой задаче, мы обозначили ее через 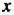
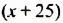
На языке математики расстояние, пройденное грузовым автомобилем, записывают: 1,3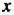
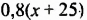
По условию задачи грузовой автомобиль проехал на 10 км больше, чем легковой, что на языке математики можно выразить так: разность расстояний, пройденных грузовым и легковым автомобилями, равна 10 км, и записать: 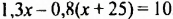
Полученное уравнение и является математической моделью задачи на движение автомобилей. Построив математическую модель, мы свели задачу на движение к математической задаче — решить уравнение.
Кроме уравнений, есть и другие виды математических моделей, с которыми ми познакомимся в процессе изучения алгебры.
Интересно знать. История науки знает немало примеров, когда в рамках удачно построенной математической модели с помощью вычислений, как говорят, «на кончике пера», удавалось предвидеть существование новых физических объектов и явлений. Так, опираясь на математические модели, астрономы Дж. Адамс (Англия) в 1845 году и У. Леверье (Франция) в 1846 году независимо друг от друга пришли к выводу о существовании неизвестной тогда еще планеты и указали ее расположение на небе. По расчетам Леверье астроном Г. Галле (Германия) нашел эту планету. Ее назвали Нептуном.
Интересно знать
На протяжении многих столетий алгебра была наукой об уравнениях и способах их решения. Линейные уравнения умели решать еще древние египтяне и вавилоняне (1 тысячелетие до н. э.).
О состоянии математики в Древнем Египте свидетельствуют математические тексты, написанные на особой бумаге — папирусе, изготовленном из стеблей растения, которое имеет такое же название. Написание некоторых папирусов относят к XVIII в. до н. э., хотя описанные в них математические факты были известны древним египтянам задолго до их изложения.
Один из таких папирусов был найден в 1872 году в одной из египетских пирамид. Его приобрел английский коллекционер древностей Райнд, и сейчас >тот папирус — папирус Райнда — хранится в Лондоне.
В папирусе Райнда особое место занимают задачи на «аха» («хау»).
Это задачи, которые решаются с помощью линейных уравнений с одним нечестным. «Аха» («хау») означает «совокупность», «куча» (неизвестная величина). Пример такой задачи: «Куча. Ее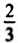
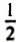
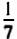
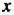
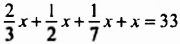
Более заметные успехи в создании начал алгебры были достигнуты в Древнем Вавилоне. До нашего времени сохранились вавилонские глиняные плитки с комбинациями клиновидных черточек — клинописью. Такие плитки имели в Вавилоне то же значение, что и папирусы в Египте. На плитках встречаются и и клинописные математические тексты, которые свидетельствуют, что уже более 4000 лет гому назад в Вавилоне могли решать уравнения, содержащие квадрат неизвестного.
Начиная с VII в. до н. э., древние греки после знакомства с достижениями египтян и вавилонян в сфере математики продолжили их науку. При этом достаточно мало греческих ученых при решении задач использовали уравнения. Одним из тех, кто использовал уравнения, был древнегреческий математик Диофант.
О Диофанте известно мало, даже точно не установлены годы его жизни. Кое-что о жизни Диофанта и о том, сколько он прожил лет, можно узнать из надписи на его могильной плите.
| Надпись на плите | Языком алгебры |
| Путник! Здесь погребен Диофант. И числа поведать могут, о чудо, сколь долог был век его жизни. | 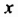 |
| Часть шестую его представляло прекрасное детство. | 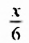 |
| Двенадцатая часть протекла его жизни — покрылся пухом тогда подбородок. | 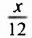 |
| Седьмую в бездетном браке провел Диофант. | 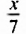 |
| Прошло пятилетие; он был осчастливлен рождением прекрасного первенца-сына, | 5 |
| коему рок дал половину лишь жизни прекрасной и светлой на земле по сравнению с отцом. | 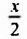 |
| И в печали глубокой старец земного удела конец воспринял, переживши года четыре с тех пор, как сына лишился. | 4 |
| Скажи, сколько лет жизни достигнув, смерть воспринял Диофант? | 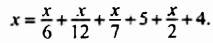 |
Греческую науку в Средневековье заимствовали ученые Востока — индийцы и арабы. Именно на Востоке в IX в. алгебра становится самостоятельной математической наукой.
Происхождение слова «алгебра» также связано с Востоком.
Город Багдад в VII-IX в. был столицей могущественного Арабского халифата. Багдадские халифы оказывали содействие развитию природоведения и математических наук. За годы правления халифа Гаруна аль-Рашида в Багдаде была оборудована большая библиотека, а халиф аль-Мамун организовал своеобразную академию — «Дом мудрости» и построил хорошо оборудованную обсерваторию.
При дворе аль-Мамуна жил и работал ученый Мухаммед бен Муса аль-Хорезми (около 780 — около 850). Он собрал и систематизировал способы решения уравнений и описал их в работе «Китаб аль-джебр аль-мукабала», что дословно означает «Книга о восстановлении и противопоставлении». В то время отрицательные числа считались «ненастоящими», и, когда в процессе решения уравнения в какой-то его части появлялось отрицательное число, его нужно было перенести в другую часть. Эту операцию называли восстановлением (аль-джебр), то есть переведением «ненастоящих» (отрицательных) чисел в «настоящие» (положительные). С помощью противопоставления (аль-мукабала) отбрасывали одинаковые слагаемые в обеих частях уравнения.
В XII в. сочинение аль-Хорезми перевели на латинский язык, сохранив в его названии только слово «аль-джебр», которое вскоре стали произносить как алгебра.
Постепенно сформировалась современная алгебра, которая охватывает не только теорию решения уравнений, а и способы проведения операций (действий) с разнообразными объектами (в частности, с числами).
- Целые выражения
- Одночлены
- Многочлены
- Формулы сокращенного умножения
- Отношения и пропорции
- Рациональные числа и действия над ними
- Делимость натуральных чисел
- Выражения и уравнения
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид
aх + b = 0, где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.
Например, все уравнения:
2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.
Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения.
Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.
А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.
Решение любых линейных уравнений сводится к решению уравнений вида
aх + b = 0.
Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим
aх = ‒ b.
Если a ≠ 0, то х = ‒ b/a .
Пример 1. Решите уравнение 3х + 2 =11.
Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.
Выполним вычитание, тогда
3х = 9.
Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9 : 3.
Значит, значение х = 3 является решением или корнем уравнения.
Ответ: х = 3.
Если а = 0 и b = 0, то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.
Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.
Приведем подобные члены:
0х = 0.
Ответ: х — любое число.
Если а = 0 и b ≠ 0, то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .
Пример 3. Решите уравнение х + 8 = х + 5.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.
Приведем подобные члены:
0х = ‒ 3.
Ответ: нет решений.
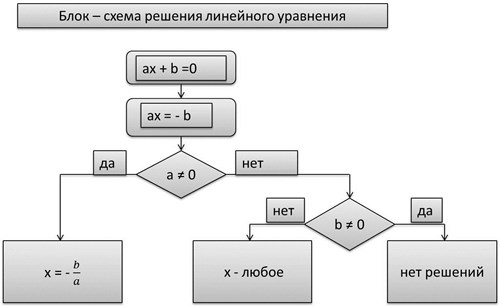
На рисунке 1 изображена схема решения линейного уравнения
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.
Пример 4. Пусть надо решить уравнение
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)
3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим
х = 7.
Как видим, корень уравнения равен семи.
Вообще такие уравнения можно решать по следующей схеме:
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;
г) привести подобные члены;
д) решить уравнение вида aх = b,которое получили после приведения подобных членов.
Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2), третьего (Пример. 1, 3) и даже с пятого этапа, как в примере 5.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 5. Решите уравнение 2х = 1/4.
Находим неизвестное х = 1/4 : 2,
х = 1/8 .
Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.
Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.
Решение
2х + 6 = 5 – 6х
2х + 6х = 5 – 6
8х = ‒1
х = ‒1 : 8
х = ‒ 0, 125
Ответ: ‒ 0, 125
Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.
Решение
– 30 + 18х = 8х – 7
18х – 8х = – 7 +30
10х = 23
х = 23 : 10
х = 2,3
Ответ: 2,3
Пример 8. Решите уравнение
Решение:
3(3х – 4) = 4 · 7х + 24
9х – 12 = 28х + 24
9х – 28х = 24 + 12
-19х = 36
х = 36 : (-19)
х = — 36/19
Ответ: — 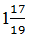
Пример 9. Найдите f(6), если f (x + 2) = 37-х
Решение
Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.
Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.
Если х = 4, тогда
f(6) = 37-4 = 33 = 27
Ответ: 27.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ. Буду рада Вам помочь!
Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
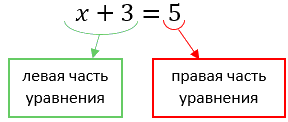
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
Раскроем скобки.
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$
$х=-{17}/{5}$
$х = — 3,4$
Ответ: $- 3,4$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
$x = 0; ax + b = 0$
2. Решаем получившиеся уравнения каждое отдельно.
Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$
$4х^2 — 5х = 0$
Вынесем х как общий множитель за скобки:
$х (4х — 5) = 0$
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
$ax^2 + c = 0$
$ax^2 = — c$
$x_2 = {-c}/{a}$
При решении последнего уравнения возможны два случая:
если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$
если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.
$x^2 — 16 = 0$
$x^2 = 16$
$x = ±4$
Ответ: $х_1 = 4, х_2 = — 4$
Решение полного квадратного уравнения
Решение с помощью дискриминанта
Дискриминантом квадратного уравнения D называется выражение
$b^2 — 4ac$.
При решении уравнения с помощью дискриминанта возможны три случая:
1. $D > 0$. Тогда корни уравнения равны:
$x_{1,2}={-b±√D}/{2a}$
2. $D = 0$. В данном случае решение даёт два двукратных корня:
$x_{1}=x_{2}={-b}/{2a}$
3. $D < 0$. В этом случае уравнение не имеет корней.
$3х^2 — 11 = -8х$
Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней
$3х^2 + 8х — 11 = 0$
$a = 3 ,b = 8, c = — 11$
$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$
$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$
$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$
Ответ: $x_1=1, x_2=-3{2}/{3}$
Устные способы
Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$
$4х^2+ 3х — 7 = 0$
$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$
Ответ: $х_1= 1, х_2 = -{7}/{4}$
Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$
$5х^2+ 7х + 2 = 0$
$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$
Ответ: $х_1= -1, х_2 = -{2}/{5}$
Кубические уравнения
Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.
$(x — 3)^3 = 27$
Представим обе части как основания в третьей степени
$(x — 3)^3 = $33
Извлечем кубический корень из обеих частей
$х — 3 = 3$
Соберем известные слагаемые в правой части
$x = 6$
Ответ: $х = 6$
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
$4x + 1 — {3}/{x} = 0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x + 1 — {3}/{x}= 0¦· x$
$4x · x + 1 · x — {3·x}/{x} = 0$
3. решаем полученное уравнение
$4x^2 + x — 3 = 0$
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = {3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = {3}/{4}$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$
${3х-5}/{-2}={1}/{х}$
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х (3х — 5) = -2$
Раскроем скобки и соберем все слагаемые в левой части уравнения
$3х^2- 5х + 2 = 0$
Решим данное квадратное уравнение первым устным способом, т.к.
$a + b + c = 0$
$x_1 = 1, x_2 = {2}/{3}$
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1 = 1, x_2 = {2}/{3}$
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
Например,
${2}/{x}+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-{3}/{x}=0$
Решение:
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x ≠ 0$
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x+1-{3}/{x}=0|·x$
$4x·x+1·x-{3·x}/{x}=0$
3. решаем полученное уравнение
$4x^2+x-3=0$
Решим вторым устным способом, т.к. $а+с=b$
Тогда, $x_1=-1, x_2=-{3}/{4}$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=-1, x_2=-{3}/{4}$
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$
Решить уравнение ${3x-5}/{-2}={1}/{x}$
Решение:
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
$x≠0$
Воспользуемся основным свойством пропорции
$х(3х-5)=-2$
Раскроем скобки и соберем все слагаемые в левой стороне
$3х^2-5х+2=0$
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
$x_1=1, x_2={2}/{3}$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $x_1=1, x_2={2}/{3}$
Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.
Чтобы решить иррациональное уравнение, необходимо:
- Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
- Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
- Решить полученное рациональное уравнение.
- Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.
Решение:
Обе части уравнение возведем в квадрат:
$√{4х-3}^2=х^2$
Получаем квадратное уравнение:
$4х-3=х^2$
Перенесем все слагаемые в левую часть уравнения:
${-х}^2+4х-3=0$
Решим данное квадратное уравнение устным способом, так как
$a+b+c=0$
$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$√{4·1-3}=1$
$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.
$√{4·(3)-3}=3$
$√9=3$
$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит
$х_1=1$ наименьший корень.
Ответ: $1$
Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$
Решить уравнение: $х-6=√{8-х}$
Возведем обе части уравнения в квадрат
$(х-6)^2=8-х$
В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение
$х^2-2·6·х+6^2=8-х$
$х^2-12х+36=8-х$
Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.
$х^2-12х+36-8+х=0$
Приводим подобные слагаемые:
$х^2-11х+28=0$
Найдем корни уравнения через дискриминант:
$D=b^2-4ac=121-4·28=121-112=9=3^2$
$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$
$x_1=7; x_2=4$
Проведем проверку корней, подставив их вместо икса в исходное уравнение
$x_1=7$
$7-6=√{8-7}$
$1=1$, получили верное равенство, следовательно, корень нам подходит.
$x_2=4$
$4-6=√{8-4}$
$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.
Ответ: $7$
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n⋅a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.
Решить уравнение $25·5^х=1$
Решение:
В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$
$5^2·5^х=5^0$
При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются
$5^{2+х}=5^0$
Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели
$2+х=0$
$х=-2$
Ответ: $-2$
Решить уравнение $2^{3х+2}-2^{3х-2}=30$
Решение:
Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель
$2^{3x+2}-2^{3x-2}=30$
$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$
$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$
$2^{3x-2}(2^4-1)=30$
$2^{3x-2}·15=30$
Разделим обе части уравнения на $15$
$2^{3х-2}=2$
$2^{3х-2}=2^1$
$3х-2=1$
$3х=3$
$х=1$
Ответ: $1$
Для решения линейных уравнений используют два основных правила (свойства).
Свойство № 1
или
правило переноса
Запомните!
При переносе из одной части уравнения в другую
член уравнения меняет свой знак на противоположный.
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую.
Так как
в левой части уравнения у числа «3»
был знак «+», значит в правую часть уравнения
«3» перенесется со знаком «−».
Полученное числовое значение «x = 2» называют корнем уравнения.
Важно!
Не забывайте после решения любого уравнения записывать ответ.
Рассмотрим другое уравнение.
5x = 4x + 9
По правилу переноса перенесем «4x» из правой
части уравнения в левую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака,
мы понимаем, что перед «4x» стоит знак «+».
5x = 4x + 9
5x = +4x + 9
5x − 4x = 9
Теперь приведем подобные и решим уравнение до конца.
5x − 4x = 9
x = 9
Ответ: x = 9
Свойство № 2
или
правило деления
Запомните!
В любом уравнении можно разделить левую и правую часть на одно и то же число.
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
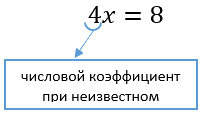
Число «4», которое стоит при «x»,
называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.
Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент
«1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы
получить
«1»?».
Ответ очевиден, нужно разделить на «4».
Используем правило деления и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.
Используем сокращение дробей и решим линейное уравнение до конца.
Как решить уравнение, если «x» отрицательное
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже.
−2x = 10
Чтобы решить такое уравнение, снова зададим себе вопрос:
«На что нужно разделить «−2»,
чтобы получить «1»?». Нужно разделить на «−2».
−2x = 10 |:(−2)
=
x = −5
Ответ: x = −5
Примеры решения линейных уравнений
Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно
применять оба свойства (правило переноса и правило деления).
Также требуется вспомнить правило раскрытия скобок и
правило приведения подобных.
-
25x − 1 = 9
25x = 9 + 1
25x = 10 |: 25=
x =
Ответ: x =
-
11(y − 4) + 10(5 − 3y) − 3(4 − 3y) = −611y − 44 +
50 −
30y − 12
+ 9y = −611y − 30y +
9y −
44 + 50 − 12 = −620y − 30y + 6 − 12 = −6
−10y − 6 = −6
−10y = −6 + 6
−10y = 0 |:(−10)
=
y = 0
Ответ: y = 0
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
4 июня 2021 в 18:53
Одинахон Иномова
Профиль
Благодарили: 0
Сообщений: 1
Одинахон Иномова
Профиль
Благодарили: 0
Сообщений: 1
Найдите корень уравнения:√39-2х=5
0
Спасибо
Ответить
2 февраля 2022 в 23:15
Ответ для Одинахон Иномова
Лопух-Бурьянович Травкин
Профиль
Благодарили: 0
Сообщений: 1
Лопух-Бурьянович Травкин
Профиль
Благодарили: 0
Сообщений: 1
√39-2x = 5
√39-5 = 2x
x = ((√39)-5):2
x = (6.2449979984 — 5):2
x = 1.2449979984: 2
x = 0.62249899919
или по формуле Герона √(a2 + b) = a +
√39-2x = 5
√39-5 = 2x
x = ((√39)-5)/2
x = (√(36+3) — 5)/2
x = (√(62+3) — 5)/2
x = ((6 +
) — 5)/2
x = (6 — 5)/2
x = 1 / 2
x =
x =
0
Спасибо
Ответить
20 апреля 2020 в 19:08
Егор Семенов
Профиль
Благодарили: 0
Сообщений: 1
Егор Семенов
Профиль
Благодарили: 0
Сообщений: 1
Найти наименьшее значение выражения: (4х²+6x+9)/3x, при x>0,
0
Спасибо
Ответить
18 августа 2020 в 1:23
Ответ для Егор Семенов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(x) = + + 2 ≥ f(1,5) = 6.
0
Спасибо
Ответить
26 марта 2020 в 16:35
Антон Манукян
Профиль
Благодарили: 0
Сообщений: 1
Антон Манукян
Профиль
Благодарили: 0
Сообщений: 1
Найдите сумму коэффициентов линейного уравнения с двумя неизвестными 3x-2y-4=0.
0
Спасибо
Ответить
20 мая 2020 в 9:40
Ответ для Антон Манукян
Сергей Глазов
Профиль
Благодарили: 0
Сообщений: 1
Сергей Глазов
Профиль
Благодарили: 0
Сообщений: 1
3-2-4=-3
0
Спасибо
Ответить
21 декабря 2016 в 14:00
Даня Буйновский
Профиль
Благодарили: 0
Сообщений: 1
Даня Буйновский
Профиль
Благодарили: 0
Сообщений: 1
0,6x+0.42=0 решите пж уравнение
0
Спасибо
Ответить
11 февраля 2017 в 16:25
Ответ для Даня Буйновский
Алексей Карапов
Профиль
Благодарили: 0
Сообщений: 9
Алексей Карапов
Профиль
Благодарили: 0
Сообщений: 9
0.6 · ?0.7 +0.42 =0
Так как 0.6 · ?0.7 = ?0.42, а ?0.42 +0.42 =0
0
Спасибо
Ответить
11 сентября 2016 в 23:15
Антон Ершов
Профиль
Благодарили: 0
Сообщений: 2
Антон Ершов
Профиль
Благодарили: 0
Сообщений: 2
?ЗАДАНИЕ: Найдите корень уравнения?
(P.S) Мне нужно полностью всё решение. Заранее — спасибо.
1) 0,9x ? 0,6 (x ? 3) = 2 (0,2x ? 1,3)
2) ? 0,4 (3x ? 1) + 8 (0,8x ? 0,3) = 5 ? (3,8x + 4)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Спасибо! Решено!
0
Спасибо
Ответить
19 сентября 2016 в 14:52
Ответ для Антон Ершов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1)0,9x ? 0,6x + 1,8 = 0,4x ? 2,6
0,1x=4,4
x=44
2) ?1,2 +0,4 +6,4x ?2,4 =5 ?3,8x ?4
9x =3
x=
0
Спасибо
Ответить
16 сентября 2015 в 11:06
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
?2x ? 3y=1
?3x + y=7
Помогите Пожалуйста!)
0
Спасибо
Ответить
5 сентября 2016 в 15:32
Ответ для Макс Простов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
2 уравнения, 2 неизвестных. Выразим y через x и подставим в первое выражение. Найдя ответ, подставим в полученное значение x.
3x +y=7
y=7 ? 3x
2x ?3(7 ?3x)=1
2x ?21 +9x=1
11x=22
x=2
y=7 ?3 · 2 = 1
Проверка:
2 · 2 ?3 · 1=1
3 · 2 +1=7
Верно
Ответ: x=2, y=1.
0
Спасибо
Ответить
16 сентября 2015 в 10:32
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
1. 2x? ?7x +3
2. 3x? +5x ?2
0
Спасибо
Ответить
5 сентября 2016 в 15:28
Ответ для Макс Простов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1) D=49 ? 4 · 3 · 2 = 25
x1= = = 3
x2===0,5
Проверка:
2 · 0,52 ? 7 · 0,5 + 3 = 0
0=0
2 · 32 ? 7 · 3 + 3 = 0
0=0
2) D=25 ?4 · 3 · (-2) = 25 + 24 = 49
x1=
x2=-2
проверка аналогично.
0
Спасибо
Ответить
13 сентября 2015 в 12:33
Киара Артуровна
Профиль
Благодарили: 0
Сообщений: 1
Киара Артуровна
Профиль
Благодарили: 0
Сообщений: 1
2х-1
2х+1=2х+1
2х-1 + 8
1-4х2
0
Спасибо
Ответить
5 сентября 2016 в 13:39
Ответ для Киара Артуровна
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
4x2 + 2x ? 1 ? 2x + 1 ? 2x ? 1 + 2x + 1 ? 8 + 1 = 0
4x2? 7 = 0
4x2=7
x2=
x=±?()
0
Спасибо
Ответить
28 апреля 2015 в 13:19
Дарья Баширова
Профиль
Благодарили: 0
Сообщений: 1
Дарья Баширова
Профиль
Благодарили: 0
Сообщений: 1
Как решить?
х+3х=9.7*3х
0
Спасибо
Ответить
16 апреля 2016 в 8:42
Ответ для Дарья Баширова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
X+3X=9,7 · 3X
4X=29,1X
33,1Х=0
Х=0
Проверка:
0+3 · 0 = 9,7 · 3 · 0
0=0
Ответ: Х=0
0
Спасибо
Ответить