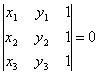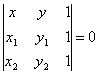Как составить уравнение сторон треугольника через уравнения медианы

Уравнения сторон треугольника

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

Таким образом, уравнение стороны AB

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

Отсюда уравнение стороны BC —

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

Задача 41259 Найти уравнение сторон треугольника.

Условие

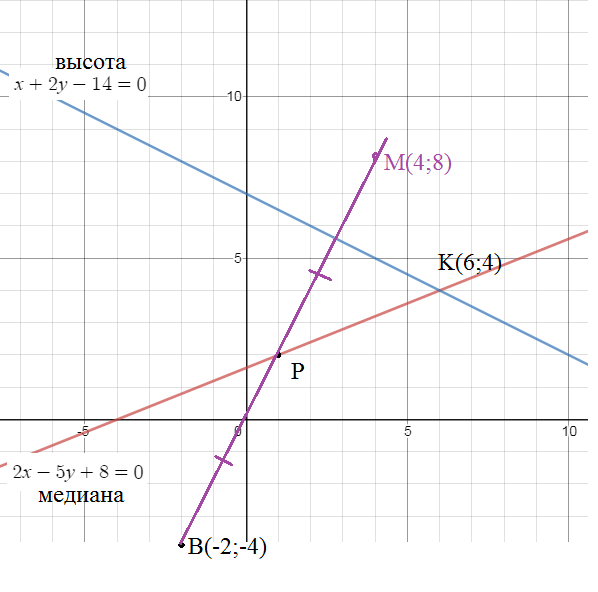
Найти уравнение сторон треугольника, если известны одна из вершин В(-2;-4) и уравнение медианы 2х-5у+8=0 и высоты х+2у-14=0 проведеденных из этой вершины

Все решения

Найдем координаты точки пересечения медианы и высоты:
<2x-5y+8=0

Назовем ее точка К

Скорее всего дана точка В и два уравнения медианы и высоты,
проведенных из других вершин треугольника

Составим уравнение прямой ВК, как прямой проходящей через две точки:

х+2=y+4
[b]x-y-2=0 [/b]- уравнение ВК

высота x+2y-14=0 и ВК не перпендикулярны,так как произведение угловых коэффициентов взаимно перпендикулярных прямых должно быть равно (-1).

Значит высота перпендикулярна стороне ВМ.

Координату точки М требуется найти

Уравнение стороны ВМ, как прямой, перпендикулярной x+2y-14=0
и проходящей через точку В легко написать.

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
Значит, угловой коэффициент стороны ВМ
k_(BM)=2

Общий вид такой прямой
y=2x+b

Так как ВМ проходит через точку В, подставим ее координаты в уравнение
y=2x+b
и найдем b

уравнение BM: [b]y=2x[/b]

Найдем координаты точки пересечения ВМ и медианы.
Решаем систему уравнений:
<2х–5у+8=0

Пусть это точка Р(1;2)

Уравнение КМ, как уравнение прямой проходящей через две точки:
[m]frac>-x_>=frac>-y_>[/m]

[b]2х+у-8=0[/b] — уравнение МК

О т в е т. x-y-2=0; y=2x; 2х+у-8=0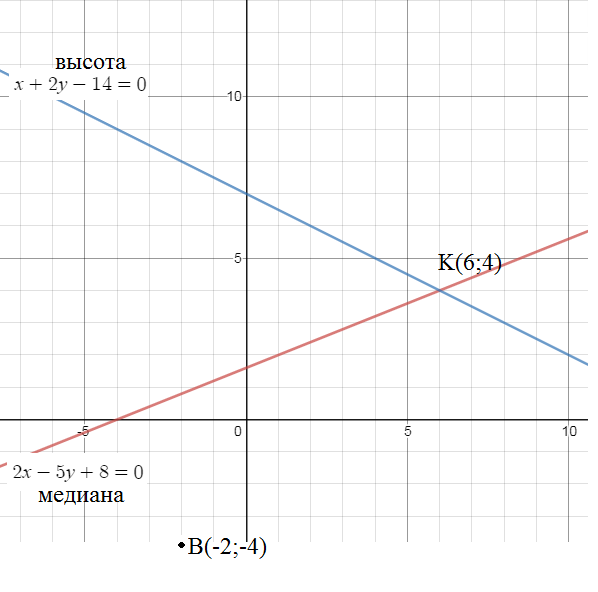

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Автор	Сообщение
	Заголовок сообщения: Как составить уравнения сторон трегольника Добавлено: 07 янв 2012, 09:09
Начинающий Зарегистрирован: 22 дек 2011, 18:07 Сообщений: 9 Cпасибо сказано: 0 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Помогите решить задачку.две медианы треугольника лежат на прямых x+y=3 и 2x+3y+1,а точка A(1;1)является вершиной треугольника.Составить уравнения сторон треугольника. Я думаю, что, составив систему из уравнений прямых и найдя икс и игрик, мы найдем точку пересечения прямых, то есть это будет точка пересеченя медиан треугольника. Далее я думаю нужно как-то найти координаты вершин треугольника, потому, зная их, легко уже составить уравнения сторон.
Вернуться к началу

vvvv	Заголовок сообщения: Re: как составить уравнения сторон трегольника Добавлено: 07 янв 2012, 12:58
	datgen писал(а): помогите решить задачку.две медианы треугольника лежат на прямых x+y=3 и 2x+3y+1,а точка A(1;1)является вершиной треугольника.Составить уравнения сторон треугольника. Я думаю что составив систему из уравнений прямых и найдя икс и игрик мы найдем точку пересечения прямых то есть это будет точка пересеченя медиан треугольника.Далее я думаюнужно как то найти координаты вершин треугольника потомузная их легко уже составить уравнея сторон. В этой задаче нужно найти две недостающие вершины треугольника, тогда уравнения сторон записать легко. Я решал по такому плану: 1.Нашел точку пересечения двух заданных медиан (т.О) 2.Записал уравнение прямой, содержащую третью медиану (через т.А и т.О) 3.Нашел точку пересечения третьей медианы со стороной треугольника (воспользовавшись свойством медианы) т.D 4.Записал систему из четырех уравнений относительно неизвестных координат двух неизвестных вершин треугольника. Решил систему — получил координаты двух недостающих вершин треугольника. Конечно,самым интересным является п.№4 — какие уравнения записать ??? Условия для составления уравнения таковы: — две неизвестные вершины треугольника лежат на двух известных медианах — расстояния неизвестных вершин до т.D равны — координаты неизвестных вершин треугольника и т.D пропорциональны т.к.лежат на одной прямой. Записать уравнения прямых, проходящих через две точки — это тривиально. Картинка получилась такая
Вернуться к началу

datgen	Заголовок сообщения: Re: как составить уравнения сторон трегольника Добавлено: 07 янв 2012, 14:59
	vvvv Извините а как найти точку пересечения D.
Вернуться к началу

210

Определить, какие из точек M₁(3; 1), M₂(2; 3), M₃(6; 3), M₄(-3;
-3), M₅(3; -1), M₆(-2; 1) лежат
на прямой и какие на ней не лежат. 211 Точки P₁,
P₂, P₃, P₄, P₅ расположены
на прямой ; их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 212 Точки Q₁,
Q₂, Q₃, Q₄, Q₅ расположены
на прямой ; их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 213 Определить точки
пересечения прямой с координатными
осями и построить эту прямую на чертеже. 214 Найти точку
пересечения двух прямых , . 215 Стороны АВ, ВС и АС
треугольника АВС даны соответственно
уравнениями , , . Определить
координаты его вершин. 216 Даны уравнения двух
сторон параллелограмма , и уравнение одной из
его диагоналей .
Определить координаты вершин
этого параллелограмма. 217 Стороны
треугольника лежат на прямых , , . Вычислить его площадь S. 218 Площадь
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой . Определить координаты вершины С. 219 Площадь
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой .
Определить координаты третьей
вершины С. 220 Составить
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy: 220.1 k=2/3, b=3; 220.2 k=3, b=0; 220.3 k=0, b=-2; 220.4 k=-3/4, b=3; 220.5 k=-2, b=-5; 220.6 k=-1/3, b=2/3. 221 Определить угловой
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых: 221.1 ; 221.2 ; 221.3 ; 221.4 ; 221.5 . 222 Дана прямая . Определить угловой коэффициент k
прямой: 222.1 Параллельной
данной прямой; 222.2 Перпендикулярно к
данной прямой. 223 Дана прямая . Составить уравнение прямой,
проходящей через точку М₀(2; 1): 223.1 Параллельно данной
прямой; 223.2 Перпендикулярно
данной прямой. 224 Даны уравнения двух
сторон прямоугольника , и одна из его вершин
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника. 225 Даны уравнения двух
сторон прямоугольника , и уравнение одной из
его диагоналей .
Найти вершины прямоугольника. 226 Найти проекцию
точке Р(-5; 13) относительно прямой . 227 Найти точку Q,
симметричную точке Р(-5; 13) относительно прямой . 228 В каждом из
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними: 228.1 , ; 228.2 , ; 228.3 , ; 228.4 , ; 228.5 , . 229 Вычислить угловой
коэффициент k прямой, проходящей через две данные
точки: 229.1 M₁(2;
-5), M₂(3; 2); 229.2 P(-3, 1), Q(7; 8); 229.3 A(5; -3), B(-1; 6). 230 Составить
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам. 231 Даны середины
сторон треугольника M₁(2; 1), M₂(5;
3), M₃(3; -4). Составить
уравнение его сторон. 232 Даны две точки P(2; 3),
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку . 233 Составить
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую. 234 Даны вершины
треугольника M₁(2; 1), M₂(-1; -1),
M₃(3; 2). Составить уравнения
его высот. 235 Стороны
треугольника даны уравнениями , , . Определить точку пересечения его
высот. 236 Даны вершины
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В. 237 Даны вершины
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А. 238 Составить
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0). 239 Через точки M₁(-1; 2), M₂(2; 3) проведена
прямая. Определить точки пересечения этой прямой
с осями координат. 240

Доказать,
что условие, при котором три точки M₁(x₁,
y₁), M₂(x₂, y₂), M₃(x₃,
y₃) лежат на одной прямой,
может быть записано в следующем виде:

241

Доказать,
что уравнение прямой, проходящей через две
данные точки M₁(x₁, y₁),
M₂(x₂, y₂), может
быть записано в следующем виде:

242 Даны
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей. 243 Даны две смежные
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма. 244 Даны уравнения двух
сторон прямоугольника , и уравнение его
диагонали . Составить уравнения остальных
сторон и второй диагонали этого прямоугольника. 245 Даны вершины
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А. 246 Составить
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15). 247 Найти проекцию
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1). 248 Найти точку M₁, симметричную точке М₂(8;
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2). 249 На оси абсцисс
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей. 250 На оси ординат
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей. 251 На прямой найти такую точку Р, сумма
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей. 252 На прямой найти такую точку Р, разность
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей. 253 Определить угол между двумя прямыми: 253.1 , ; 253.2 , ; 253.3 , ; 253.4 , . 254 Дана прямая . Составить уравнение прямой,
проходящей через точку M₀(2; 1) под углом 45⁰ к данной прямой. 255 Точка А(-4; 5)
является вершиной квадрата, диагональ которого
лежит на прямой . Составить
уравнения сторон и второй диагонали этого
квадрата. 256 Даны две
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон. 257 Точка E(1; -1) является
центром квадрата, одна из сторон которого лежит
на прямой . Составить уравнения
прямых, на которых лежат остальные стороны этого
квадрата. 258 Из точки M₀(-2; 3) под углом к оси
Ox направлен луч света. Известно, что . Дойдя
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи. 259 Луч света направлен
по прямой , луч от нее отразился.
Составить уравнение прямой, на которой лежит
отраженный луч. 260 Даны уравнения
сторон треугольника , , . Доказать, что этот треугольник
равнобедренный. Решить задачу при помощи
сравнения углов треугольника. 261 Доказатть, что
уравнение прямой, проходящей через точку M₁(x₁; y₁) параллельно
прямой , может быть записано в виде . 262 Составить
уравнение прямой, проходящей через точку М₁(2: -3) параллельно
прямой: 262.1 ; 262.2 ; 262.3 ; 262.4 ; 262.5 . 263 Доказать, что
условие перпендикулярности прямых ; может быть записано
в следующем виде: . 264 Установить, какие
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 264.1  , ; 264.2 , ; 264.3 , ; 264.4 , ; 264.5 , ; 264.6 , . 265

Доказать,
что формула для определения угла между
прямыми , может
быть записана в следующей форме:

266 Определить угол , образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых. 266.1 , ; 266.2  , ; 266.3  , . 267 Даны две вершины
треугольника M₁(-10; 2), M₂(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M₃. 268 Даны две вершины A(3;
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника. 269 В треугольнике АВС
даны: уравнение стороны АВ: , уравнения
высот АМ: и BN: . Составить уравнения двух
других сторон и третьей высоты этого
треугольника. 270 Составить
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан , . 271 Составить
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот , . 272 Составить
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис , . 273 Составить
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты и
биссектрисы , проведенных из одной вершины. 274 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты и биссектрисы , проведенных из
различных вершин. 275 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты и медианы , проведенной из
одной вершины. 276 Составить
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты и медианы , проведенных из
различных вершин. 277 Составить
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы и медианы , проведенных из
одной вершины. 278 Составить
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы и медианы , проведенных из
различных вершин. 279 Составить
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми , образует
треугольник с площадью, равной 1,5. 280 Среди прямых,
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми , , делится в точке Р
пополам. 281 Через точку Р(-3; -1)
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми , , делится
в точке Р пополам. 282 Через точку Р(0; 1)
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми , , делился бы в точке Р
пополам. 283 Составить
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми , , равна . 284 Составить
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми , , равна 5.

составьте уравнения сторон треугольника зная одну из его вершин A(-1,2) и уравнения двух медиан x-y-3=0 и 5x+4y-9=0 решение

математика ВУЗ
857

Найдем точку пересечения медиан
{x–y–3=0 ⇒ х=у+3
{5x+4y–9=0 ⇒ 5*(y+3)+4y-9=0 ⇒ 9y=-6 ⇒ y=-2/3; x=(-2/3)+3=7/3

M(7/3; -2/3)

Составим уравнение третьей медианы АМ как прямой, проходящей через две точки

A (x_(A);y_(A)) и M (x_(M);y_(M)) и имеет вид:

[m]frac{x-x_{A}}{x_{M}-x_{A}}=frac{y-y_{A}}{y_{M}-y_{A}}[/m]

[m]frac{x-(-1)}{frac{7}{3}-(-1)}=frac{y-2}{-frac{2}{3}-2}[/m] ⇒[m]frac{x+1}{frac{10}{3}}=frac{y-2}{-frac{8}{3}}[/m]

пропорция
[m]-frac{8}{3}(x-1)=frac{10}{3}(y-2)[/m]

[m]-8x+8=10y-20[/m]

[m]8x+10y-28=0[/m]

[m]4x+5y-14=0[/m]

Медиана АМ проходит через точку F- середину отрезка BC
[m]4x_{F}+5y_{F}-14=0[/m]

[m]x_{F}=frac{x_{B}+x_{C}}{2}[/m]

[m]y_{F}=frac{y_{B}+y_{C}}{2}[/m]

Пусть точка C принадлежит первой медиане х=у+3 , точка B принадлежит второй медиане 5x+4y–9=0

[m]х_{C}=у_{C}+3[/m]
[m]5x_{B}+4y_{B}–9=0[/m]

Решаем систему уравнений:

[m]left{begin {matrix}4x_{F}+5y_{F}-14=0\x_{F}=frac{x_{B}+x_{C}}{2}\y_{F}=frac{y_{B}+y_{C}}{2}\х_{C}=у_{C}+3\5x_{B}+4y_{B}–9=0end {matrix}right.[/m]

[m]left{begin {matrix}x_{F}frac{14-5y_{F}}{4}\frac{14-5y_{F}}{4}=frac{x_{B}+x_{C}}{2}\y_{F}=frac{y_{B}+y_{C}}{2}\х_{C}=у_{C}+3\5x_{B}+4y_{B}–9=0end {matrix}right.[/m]

Находим координаты точек B и С

Составляем уравнения сторон

Пример 1:

Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:

1) уравнения сторон треугольника АВС;

2) координаты точки пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины А;

4) площадь треугольника.

Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А

Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:

Пример 3:

По координатам вершин треугольника ABC найти:

• периметр треугольника;
• уравнения сторон AB и BC;
• уравнение высоты AD; угол ABC;
• площадь треугольника.

Сделать чертеж.

А(1; 2); В (–1; 2); С(3; 0).

Решение от преподавателя:

Пример 4:

Даны координаты вершин треугольникаА, В, С.

Требуется найти:

1) уравнение и длину стороны ВС;

2) уравнение и длину высоты, проведённой из вершиныА;

3) уравнение медианы, проведённой из вершиныА;

4) площадь треугольника.

Сделать чертёж.

А(4;-3), B(-2;-1), C(3;-2).

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

1)

2)

3) Находим координаты точки М – середины стороны ВС:

       

Определяем длину медианы АМ:

4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору , то составляем уравнение высоты по формуле , где (a,b) – координаты вектора перпендикулярного искомой прямой,  – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:

и подставляем в формулу, ,

6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:

1. Уравнение прямой 
   Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 
   
   Уравнение прямой AB 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-3/₇x + ¹⁶/₇ или 7y + 3x — 16 = 0 
2. Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 
   
   
   M(3;1) 
   Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому: 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-1/₁₁x + ¹⁴/₁₁ или 11y + x — 14 = 0 
3. Уравнение высоты через вершину C 
   Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
   
   Найдем уравнение высоты через вершину C 
   
   y = ⁷/₃x + ⁶²/₃ или 3y -7x — 62 = 0
4. уравнение параллельной прямой AB, проходящей через точку (-8,2)
   Уравнение прямой AB: y = ^-3/₇x + ¹⁶/₇
   Уравнение KN параллельно AB находится по формуле:
   y — y₀ = k(x — x₀)
   Подставляя x₀ = -8, k = ^-3/₇, y₀ = 2 получим:
   y-2 = ^-3/₇(x-(-8))
   или
   y = ^-3/₇x — ¹⁰/₇ или 7y + 3x +10 = 0

Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5). 

Решение от преподавателя:

4) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-1/₄x + ¹⁵/₂ или 4y +x -30 = 0 
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k₁ прямой AB. 
Уравнение AB: y = 4x -3, т.е. k₁ = 4 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k₁*k = -1. 
Подставляя вместо k₁ угловой коэффициент данной прямой, получим: 
4k = -1, откуда k = ^-1/₄ 
Так как перпендикуляр проходит через точку C(10,5) и имеет k = ^-1/₄,то будем искать его уравнение в виде: y-y₀ = k(x-x₀). 
Подставляя x₀ = 10, k = ^-1/₄, y₀ = 5 получим: 
y-5 = ^-1/₄(x-10) 
или 
y = ^-1/₄x + ¹⁵/₂ или 4y + x — 30 = 0 
Найдем точку пересечения с прямой AB: 
Имеем систему из двух уравнений: 
y -4x +3 = 0 
4y + x — 30 = 0 
Из первого уравнения выражаем y и подставим во второе уравнение. 
Получаем: 
x = ⁴²/₁₇ 
y = ¹¹⁷/₁₇ 
D(⁴²/₁₇;¹¹⁷/₁₇) 
Длина высоты треугольника, проведенной из вершины C 
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины: 

Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника 
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 


Е(7;9) 
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁴/₃x ^-1/₃ или 3y -4x +1 = 0 
Найдем длину медианы. 
Расстояние между двумя точками выражается через координаты формулой: 

6) CD—диаметр окружности. Центр окружности точка О лежит в середине отрезка CD

Уравнение окружности  (x-x₀)²+(y-y₀)²=r²

(x-106/17)²+(y-101/17)²=256/17 

Уравнение прямой, параллельной CD, проходящей через точку A 

Пример 8:

Решение от преподавателя:

Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)

Пример 9:

Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4),  С (-1,6).

Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;

2) периметр (сумму длин) треугольника;

3) уравнение высоты СН;

4) расстояние d от точки С до прямой АВ;

5) сделайте чертеж.

Решение от преподавателя:

Решение.

1) уравнения сторон треугольника АВ, ВС и АС

Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника

Расстояние между двумя точками

3) уравнение высоты СН

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ

Расстояние от точки до прямой

Пример 10:

Даны вершины A (x₁; y₁), B (x₂; y₂), C (x₃; y₃)    треугольника.

Найти: 1) уравнение стороны AB;

2) уравнение медианы, проведенной из вершины C;

3) уравнение высоты, проведенной из вершины C ;

4) уравнение прямой, проходящей через вершину C параллельно стороне AB .

A (6; 0), B (2; − 6), C (−3; −9).

Решение от преподавателя:

Пример 11:

Решение от преподавателя:

Пример 12:

Дан треугольник  с координатами вершин найти:

а) длину стороны AB;

б) косинус угла ABC;

в) площадь треугольника ABC (через векторное произведение);

Решение от преподавателя:

Пример 13:

Решение от преподавателя:

Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9). 
1) Уравнение прямой 
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 

Уравнение прямой AB 
Каноническое уравнение прямой: 

или 

или 
y = ³/₂x -9 или 2y -3x +18 = 0 

2) Уравнение медианы треугольника 
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(4;-3) 
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁶/₇x ^-45/₇ или 7y -6x +45 = 0 
3) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-2/₃x -11 или 3y +2x + 33 = 0 
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9) 
Уравнение прямой AB: 2y -3x +18 = 0 
Уравнение СN параллельно AB находится по формуле: 

Или     2y -3x +9 = 0 

Пример 14:

Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.

Решение от преподавателя:

Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(-1;0) 
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 

или 

или 
y = ¹/₉x + ¹/₉ или 9y -x — 1 = 0 
3) Уравнение высоты через вершину B

Пример 15:

Дан треугольник АВС. Найти:

а) величину угла А;

б) уравнение стороны АС;

в) уравнение высоты и медианы, опущенных из вершины В.

Сделать чертеж.

А(-1,2); В(1,3); С(3,-4).

Решение от преподавателя:

Пример 16:

Треугольник задан вершинами А(-6; -2);  В(4; 8); С(2; -8). Найти:

а) уравнение прямой BN, параллельной  стороне АС;

б) уравнение медианы CD;

в) уравнение высоты АЕ;

Решение от преподавателя:

а) уравнение прямой BN, параллельной  стороне АС;

Уравнение прямой AC:

Каноническое уравнение прямой:

или

или
y = ^-3/₄x ^-13/₂ или 4y + 3x +26 = 0

Уравнение BN параллельно AC находится по формуле:
y — y₀ = k(x — x₀)
Подставляя x₀ = 4, k = ^-3/₄, y₀ = 8 получим:
y-8 = ^-3/₄(x-4)
или
y = ^-3/₄x + 11 или 4y + 3x — 44 = 0

б) уравнение медианы CD;

Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.


M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:

или

или
y = ^-11/₃x ^-2/₃ или 3y + 11x +2 = 0

в) уравнение высоты АЕ;

Прямая, проходящая через точку Е₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем уравнение высоты через вершину A

y = ^-1/₈x — ¹¹/₄ или 8y +x + 22 = 0

Пример 17:

A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:

Пример 18:

В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).

Составить уравнения стороны (AB), высоты (ВК)  и медианы (CМ).

Решение от преподавателя:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:

или

или
y = ^-1/₄x + 3 или 4y + x — 12 = 0

Найдем уравнение высоты через вершину B

y = 4x + 13 или y -4x — 13 = 0

Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;¹/₂), поэтому:
Каноническое уравнение прямой:

или

или
y = ¹/₂₄x + ²/₃ или 24y -x — 16 = 0

Пример 19:

Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).

Решение от преподавателя: