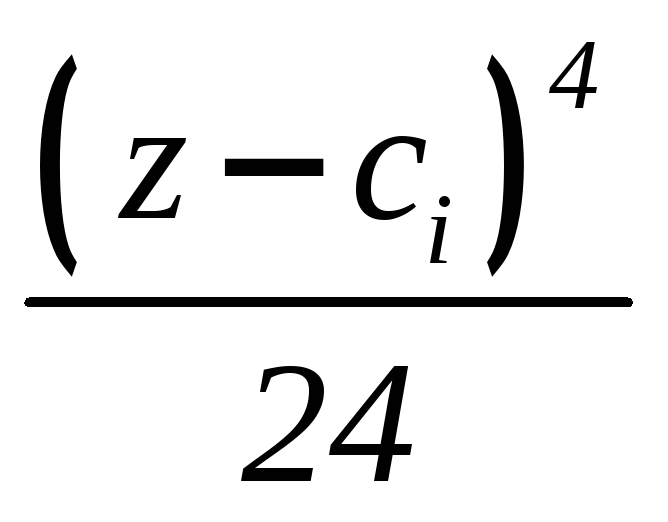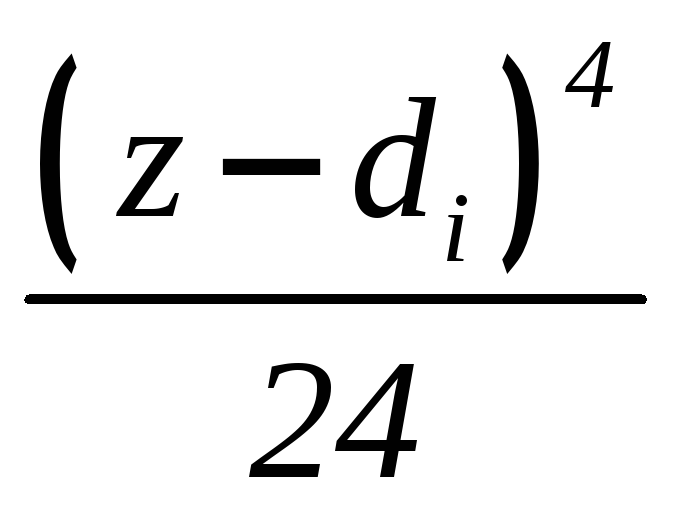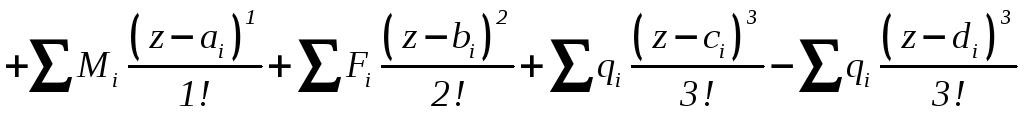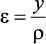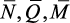Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений
Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
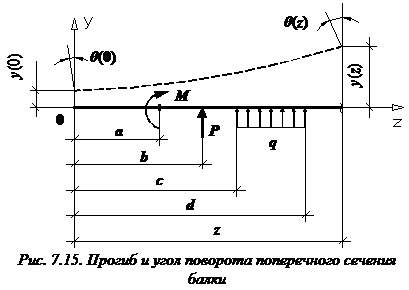
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 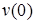
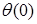
Уравнение упругой линии балки на примере
Определим прогиб балки на консоли при 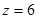
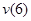
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 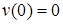
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
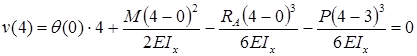
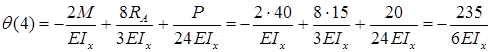
Прогиб консоли при z=6м:
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Дифференциальное уравнение упругой линии балки и его интегрирование
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .
Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):
.
В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,
.
Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем
.
Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки
.
Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений
,
а после второго интегрирования – прогибы балки
.
Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
Универсальное уравнение упругой линии балки
Дифференциальные соотношения
Рассмотрим рисунок 5.1. Балка постоянного сечения под воздействием внешней нагрузки Р деформируется так, что ее концевая точка C перемещается в положение С1. Нейтральная ось балки, называемая в дальнейшем упругой линией, в точке с координатой z имеет кривизну 1/r, прогиб y, угол наклона q =y¢, вторую производную y².
Перечисленные параметры связаны между собой соотношением, доказываемым в дифференциальной геометрии: (5.1)
Для малых перемещений величиной y’ 2 по сравнению с 1 можно пренебречь, тогда: (5.2)
Учитывая (5.2) и (3.7.b) получим:
(5.3)
С учетом соотношений (4.1) и (4.2) можно получить цепочки дифференциальных соотношений для случая бруса переменного сечения:
(5.4)
а также для бруса с постоянным сечением:
(5.5)
В частности, при нагружении бруса постоянного сечения равномерно распределенной нагрузкой q:
(5.6)
Следовательно, эпюры в соответствии с дифференциальными соотношениями (5.5), в зависимости от рассматриваемого параметра, будут иметь следующие формы (рис.5.2): q — горизонтальная прямая, Q — наклонная прямая, М — квадратичная парабола, q — кубическая парабола, у – кривая четвертого порядка. Если q=0, но имеется сосредоточенная сила Р, то ось будет изогнута по кривой третьего порядка. Если балка нагружена только изкибающим моментом М, то ось выразится кривой второго порядка.
Наибольшие удлинения и напряжения в брусе вычисляются по формулам, вытекающим из (4.6) и (4.7):
(5.7)
(5.8)
Пример 5.1
Определим прогибы балки, изображенной на рис.5.1. Изгибающий момент в сечении z равен: M = P (l — z)
После двукратного интегрирования выражения
Постоянную интегрирования С1 найдем из граничного условия: при z = 0имеем: y¢ = 0. Отсюда С1 = 0, но для общности решения пока оставим этот член в формуле:
. (5.9)
Постоянную интегрирования С2 определяем из граничного условия: при z = 0 y = 0. Следовательно, С2= 0, тогда для произвольной точки:
. (5.10)
Максимальные угол наклона и прогиб имеют место в точке приложения силы Р.
Таким образом,при z=l имеем:
(5.11)
Универсальное уравнение упругой линии балки
Из примера 5.1 видно, что для каждого участка балки после интегрирования уравнения появляются две произвольные постоянные (С1,С2 в 5.9). Если балка имеет n участков, то для определения 2n постоянных интегрирования необходимо совместно решить 2n уравнений. Для бруса постоянной жесткости EJx этого можно избежать, если при составлении уравнения упругой линии придерживаться определенных правил.
Рассмотрим брус (рис.5.3), нагруженный наиболее часто встречающимися силовыми факторами: сосредоточенным моментом Ма, сосредоточенной силой Р и распределенной нагрузкой интенсивности q. Из этих типов силовых факторов могут быть скомбинированы почти все встречающиеся на практике виды нагрузок. За положительные направления сил при движении от левого конца примем те, которые указаны на рисунке, то есть для Р и q — вверх, а для момента Ма — по часовой стрелке. Система указанных силовых факторов должна удовлетворять условиям равновесия.
Выявим особенности, вносимые в уравнение упругой линии различными типами внешних силовых факторов. Для этого составим выражения изгибающих моментов для каждого из пяти отмеченных на рисунке участков:
(5.12)
Видно, что изгибающий момент для каждого последующего участка целиком включает в себя выражение изгибающего момента предыдущего участка и отличается от него добавкой нового слагаемого. При переходе от четвертого участка к пятому указанная закономерность сохранена специально. При этом равномерно распределенная нагрузка четвертого участка продолжена, как это показано пунктиром, на пятый участок, и одновременно на пятом участке приложена отрицательная (компенсирующая) нагрузка интенсивности q.
Проинтегрируем полученные выражения один раз, не раскрывая скобок. Для того чтобы сохранить однотипность полученных выражений, интеграл от Ма напишем в виде Ма(z-a), что скажется только на величине произвольной постоянной Сi. В итоге, с учетом выражения y² = M / EJx получим следующие выражения для угла наклона упругой линии у’ :
(5.13)
Произвольные постоянные Сi, должны быть подобраны так, чтобы при переходе от одного участка к другому величина у’ не претерпевала разрыв. Следовательно, при z=а у’1=у’2, при z=b у’2=у’3,и так далее.
Так как брус имеет постоянную жесткость, очевидно, что
Угол наклона q0 упругой линии в начале координат определяется из выражения для первого участка:
Интегрируя полученные выражения второй раз найдем:
(5.14)
Произвольные постоянные Di, должны быть подобраны из условия непрерывности функции у на границах участков. Следовательно, при z=а у1=у2, при z=b у2=у3 и т.д. Так как брус имеет постоянную жесткость, очевидно, что
,
где у0 – ордината упругой линии в начале координат. Уравнения (5.14) удобно записать в виде одного общего, так называемого универсального уравнения упругой линии балки: (5.15)
Для определения координат точек упругой линии первого участка следует пользоваться членами уравнения, расположенными слева от вертикальной черты с индексом I. Для второго участка надо брать слагаемые до черты с индексом II, и т.д. Для определения ординат на пятом участке следует производить вычисления, пользуясь полным уравнением 5.15. Преимущество универсального уравнения заключается в том, что оно позволяет составлять уравнение упругой линии, минуя громоздкое определение произвольных постоянных. Независимо от числа участков, необходимо определить только две постоянные: у0 и q0.
Пример 5.2
Написать уравнение упругой линии для консоли с жестко защемленным левым концом и загруженной на среднем участке распределенной нагрузкой q (рис.5.4). Определяем реакцию и момент в заделке:
Теперь можно вместо левой заделки рисовать на схеме эквивалентные ей реакции опор. Таким образом, схема сведена к виду, для которого выписано универсальное уравнение. Начало координат помещаем на левом конце балки. Здесь q0 = 0 и y0 = 0.
Далее, из уравнения (5.15) «набираем» члены уравнения, соответствующие рассматриваемой балке.
В первый участок входят слагаемые силы и момента в заделке. На втором участке к ним добавляется слагаемое распределенной нагрузки. На третьем участке перемещения определяются всеми слагаемыми уравнения. Если раскрыть скобки, то для последнего участка получим:
.
Здесь упругая линия представляет собой прямую, поскольку изгибающий момент равен нулю.
http://mysopromat.ru/uchebnye_kursy/sopromat/izgib/peremescheniya_pri_izgibe/differentsialnoe_uravnenie_uprugoi_linii_balki/
http://allrefrs.ru/3-44905.html
Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений
Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 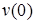
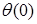
Уравнение упругой линии балки на примере
Определим прогиб балки на консоли при 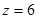
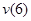
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 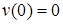
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
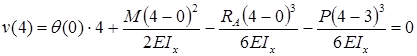
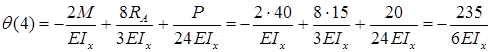
Прогиб консоли при z=6м:
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
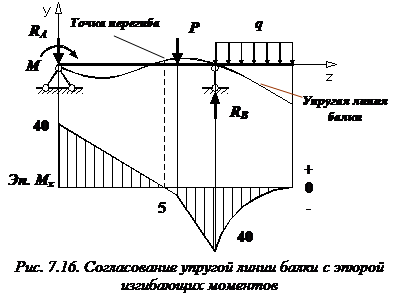
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Использование
изложенной техники определения
перемещений для балок, имеющих несколько
участков, оказывается достаточно
трудоемким, так как для n участков число
произвольных констант (C
и D)
возрастает до 2n.
Для уменьшения вычислительной работы
в подобных случаях был разработан ряд
методов, в том числе и метод начальных
параметров, позволяющий при любом числе
участков свести решение к отысканию
всего двух констант – прогиба и угла
поворота в начале координат.
Д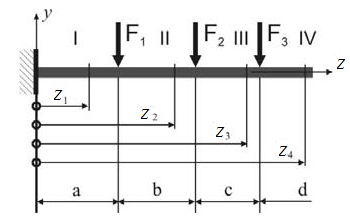
реализации метода начальных параметров
необходимо при составлении уравнения
моментов по участкам и интегрировании
этого уравнения придерживаться следующих
правил:
1) начало координат
необходимо выбирать общим для всех
участков в крайней левой точке балки;
2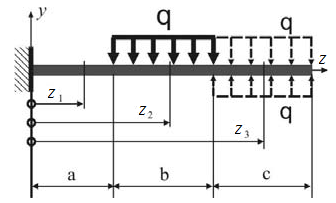
все составляющие уравнения моментов
на предыдущем участке должны сохраняться
неизменными в уравнении моментов
последующих участков;
3) в случае обрыва
распределенной нагрузки ее продлевают
до конца балки, а для восстановления
действительных условий нагружения
вводят «компенсирующую» нагрузку
обратного направления
4) интегрировать
уравнения на всех участках следует, не
раскрывая скобок.
Р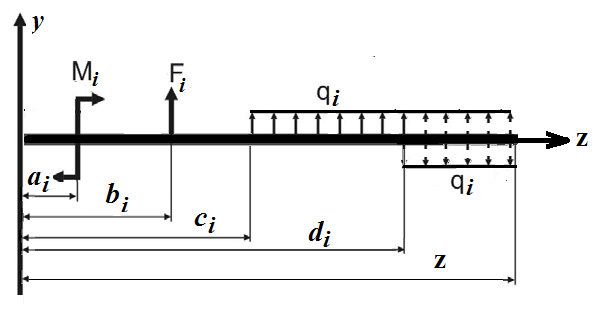
некоторый отрезок балки, нагруженной
произвольной системой сил и моментов
(реакции опор также представляем как
внешние силы), и составим для нее уравнение
моментов в произвольном сечении с
соблюдением указанных правил:
|
I |
M |
0 |
|
|
II |
M |
ai |
|
|
III |
M |
bi |
(6.4) |
|
IV |
M |
ci |
|
|
V |
M |
z |
Подставляя формулу
(6.4) в выражения (6.2), можно записать
|
I |
EI |
0 |
|
|
II |
EI |
ai |
|
|
III |
EI |
bi |
|
|
IV |
EI + |
ci |
(6.5) |
|
V |
EI + |
z |
Постоянные Ci
(i
= 1, 2, 3, 4, 5) нужно подобрать так, чтобы
функция угла поворота
при переходе от участка к участку была
непрерывной, т.е.:
(ai
-0) =
(ai
+0),
(bi
-0) =
(bi
+0),
(ci
-0) =
(ci
+0),
(di
-0) =
(di
+0.
Отсюда следует,
что С1
= С2
=С3
= С4=
С5 =
С. Есл
обозначить угол поворота сечения балки
в начале координат
(0) =0,
то
EI0
= C.
Интегрируя
выражения (6.5)
получим
|
I |
EIy |
0 |
|
|
II |
EIy |
ai |
|
|
III |
EIy |
bi |
|
|
IV |
EIy = +qi |
ci |
(6.6) |
|
V |
EIy = +qi |
z |
Постоянные Di
(i
= 1, 2, 3, 4, 5) нужно подобрать так, чтобы
функция прогиба сечения балки y
при переходе от участка к участку была
непрерывной. Откуда следует условие:
D1
= D2
=D3
= D4=
D5
= D
= EIy0
Применяя принцип
суперпозиции, запишем универсальное
уравнение изогнутой оси балки в самом
общем виде:
(6.7)
Дифференцируя
уравнение (6.7) получим уравнения для
определения углов поворота:
(6.8)
Метод определения
прогибов и углов поворота балки,
основанный на формулах (6.7-6.8) называют
методом начальных параметров.
Отметим, что при
решении задач удобно записать универсальные
уравнения сначала для наиболее удаленного
от начала координат участка, тогда
уравнения для предыдущих участков легко
получить, вычеркивая из полученного
уравнения члены, учитывающие нагрузку
на последующих участках.
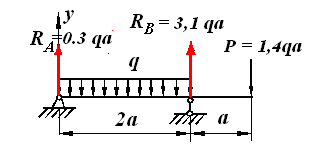
Пример 6.1
Однопролётная балка с консолью
находится под действием распределённой
нагрузки q
(рис. 6.3). Найти дифференциальное уравнение
изгиба и найти прогибы и углы поворота
в середине пролета балки и на конце ее
консольной части методом начальных
параметров.
Рис. 6.3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 9. НАПРЯЖЕНИЯ И ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Гипотезы при изгибе. Нейтральный слой, радиус кривизны, кривизна,
распределение деформаций и нормальных напряжении по высоте поперечного
сечения стержня. Касательные напряжения при плоском поперечном изгибе
стержней. Расчет балок на прочность при изгибе. Перемещения при изгибе.
Нормальные напряжения при чистом прямом изгибе. Так как нормальные
напряжения зависят только от изгибающих моментов, то вывод формулы для
вычисления можно производить применительно к чистому изгибу. Отметим,
что методами теории упругости можно получить точную зависимость для
нормальных напряжений при чистом изгибе, если же решать эту задачу
методами сопротивления материалов, необходимо ввести некоторые
допущения.
Таких гипотез при изгибе три:
1) гипотеза плоских сечений (гипотеза Бернулли) – сечения плоские
до деформации остаются плоскими и после деформации, а лишь
поворачиваются относительно некоторой линии, которая называется
нейтральной осью сечения балки. При этом волокна балки, лежащие с одной
стороны от нейтральной оси будут растягиваться, а с другой – сжиматься;
волокна, лежащие на нейтральной оси своей длины не изменяют;
2) гипотеза о постоянстве нормальных напряжений – напряжения,
действующие на одинаковом расстоянии у от нейтральной оси, постоянны по
ширине бруса;
3) гипотеза об отсутствии боковых давлений – соседние продольные волокна не давят друг на друга.

Рис. 28. Гипотеза Бернулли
Статическая задача о плоском изгибе. Изгибающий момент в сечении
представляет собой сумму моментов всех элементарных внутренних
нормальных сил σ•dA, возникающих на элементарных площадках поперечного
сечения балки (рис. 29), относительно нейтральной оси: 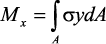
Данное выражение представляет собой статическую сторону задачи
о плоском изгибе. Но его нельзя использовать для определения нормальных
напряжений, так как неизвестен закон распределения напряжений по
сечению.
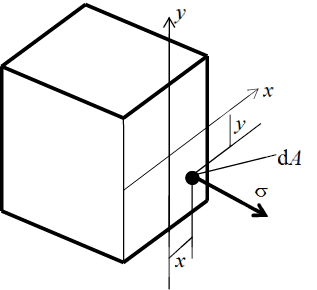
Рис. 29. Статическая сторона задачи
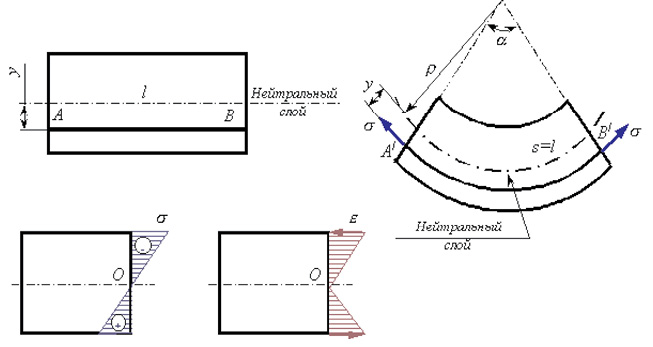
Геометрическая сторона задачи о плоском изгибе. Выделим двумя
поперечными сечениями элемент балки длиной dz. Под нагрузкой нейтральная
ось искривляется (радиус кривизны ρ), а сечения поворачиваются
относительно своих нейтральных линий на угол dθ. Длина отрезка волокон
нейтрального слоя при этом остается неизменной (рис. 30, б):
dz = ρ•dθ.
а б
в г
Рис. 30. Геометрическая сторона задачи:
а – элемент балки; б – искривление нейтральной оси; в – эпюра σ•dA; г – эпюра ε
Определим длину отрезка волокон, отстоящего от нейтрального слоя на расстоянии y
dz1 = (ρ + y)dθ .
Относительное удлинение в этом случае будет
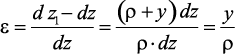
Зависимость
отражает геометрическую сторону задачи о плоском изгибе, из которой
видно, что деформации продольных волокон изменяются по высоте сечения по
линейному закону.
Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем.
Линия, по которой поперечное сечение балки пересекается с нейтральным слоем балки, называется нейтральной линией сечения.
Физическая сторона задачи о плоском изгибе. Используя закон Гука при осевом растяжении, получаем
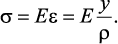
Подставив в выражение, отражающее статическую сторону задачи о плоском изгибе, значение σ, получаем
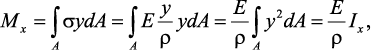
откуда
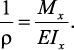
Подставив значение 
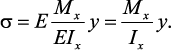
Данное выражение отражает физическую сторону задачи о плоском
изгибе, которое дает возможность рассчитать нормальные напряжения по
высоте сечения.
Хотя это выражение получено для случая чистого изгиба, но как
показывают теоретические и экспериментальные исследования, оно может
быть использовано и для плоского поперечного изгиба.
Нейтральная линия. Положение нейтральной линии определим из
условия равенства нулю нормальной силы в сечениях балки при чистом
изгибе
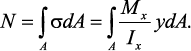
Так как Mx ≠ 0 и Ix ≠ 0, то необходимо, чтобы нулю был равен интеграл 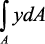
Данный интеграл представляет собой статический момент сечения
относительно нейтральной оси. Так как статический момент сечения равен
нулю только относительно центральной оси, следовательно, нейтральная
линия при плоском изгибе совпадает с главной центральной осью инерции
сечения.
Касательные напряжения. Касательные напряжения, которые возникают
в сечениях балки при плоском поперечном изгибе, определяются по
зависимости:
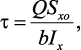
где Q – поперечная сила в рассматриваемом сечении балки; Sxo –
статический момент площади отсеченной части сечения относительно
нейтральной оси балки; b – ширина сечения в рассматриваемом слое;
Ix –момент инерции сечения относительно нейтральной оси.
Касательные напряжения равны нулю в крайних волокнах сечения и максимальны в волокнах нейтрального слоя.
Расчет балок на прочность при изгибе. Прочность балки будет обеспечена, если будут выполняться условия:
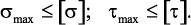
Максимальные нормальные напряжения при изгибе возникают
в сечениях, где действует максимальный изгибающий момент, в точках
сечения наиболее удаленных от нейтральной оси
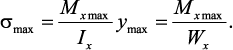
Максимальные касательные напряжения возникают в сечениях балки, где действует максимальная поперечная сила
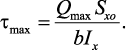
Касательные напряжения τmax обычно малы по сравнению с σmax
и в расчетах, как правило, не учитываются. Проверка по касательным
напряжениям производится только для коротких балок.
Перемещения при изгибе. Под расчетом на жесткость понимают оценку
упругой податливости балки под действием приложенных нагрузок и подбор
таких размеров поперечного сечения, при которых перемещения не будут
превышать установленных нормами пределов.
Условие жесткости при изгибе
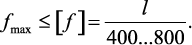
Перемещение центра тяжести сечения по направлению
перпендикулярному к оси балки, называется прогибом. Прогиб обозначается
буквой W.
Наибольший прогиб в пролете или на консоли балки, называется стрелой прогиба и обозначается буквой ƒ.
Угол q, на который каждое сечение поворачивается по отношению к своему первоначальному положению и есть угол поворота.
Угол поворота считается положительным, при повороте сечения против хода часовой стрелки
Угол поворота сечения равен значению производной от прогиба по координате Z в этом же сечении, то есть:
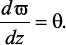
Уравнение упругой линии балки
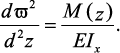
Существуют три метода решения дифференциального уравнения упругой
линии балки. Это метод непосредственного интегрирования, метод Клебша
и метод начальных параметров.
Метод непосредственного интегрирования. Проинтегрировав уравнение
упругой линии балки первый раз, получают выражение для определения углов
поворота:
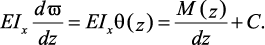
Интегрируя второй раз, находят выражения для определения прогибов:
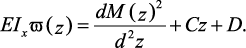
Значения постоянных интегрирования С и D определяют из начальных условий на опорах балки
Метод Клебша. Для составления уравнений необходимовыполнить следующие основные условия:
- начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
- интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
- при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z – a), где а – координата сечения, в котором приложен момент;
- в случае обрыва распределенной нагрузки ее продлевают до конца
балки, а для восстановления действительных условий нагружения вводят
«компенсирующую» нагрузку обратного направления
Метод начальных параметров
Для углов поворота
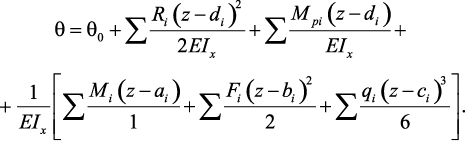
Для прогибов:
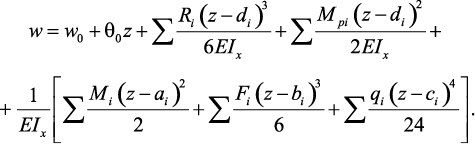
где θ – угол поворота сечения; w – прогиб; θo – угол поворота
в начале координат; w0 – прогиб в начале координат; dі – расстояние от
начало координат до i-й опоры балки; ai – расстояние от начало координат
до точки приложения сосредоточенного момента Mi; bi – расстояние от
начало координат до точки приложения сосредоточенной силы Fi; сi –
расстояние от начало координат до начала участка распределенной нагрузки
qi; Ri и Мрi – реакция и реактивный момент в опорах балки.
Определение стрелы прогибов для простых случаев
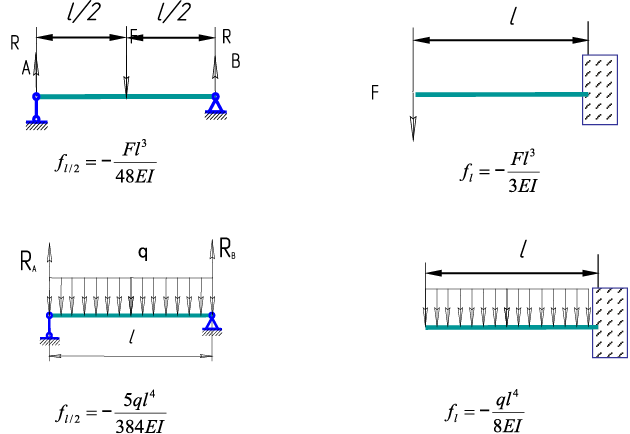
Рис. 31. Примеры нагрузок балок
Вычисление перемещений методом Мора
Если не требуется знание уравнения изогнутой линии бруса,
а необходимо определить только линейные или угловые перемещения
отдельного сечения, удобнее всего воспользоваться методом Мора.Для балок
и плоских рам интеграл Мора имеет вид:
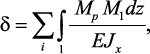
где δ – искомое перемещение (линейное или угловое); Мp, Мi –
аналитические выражения изгибающих моментов соответственно от заданной
и единичной cилы; EJx – жесткость сечения балки в плоскости изгиба. При
определении перемещений нужно рассматривать два состояния системы: 1 –
действительное состояние, с приложенной внешней нагрузкой; 2 –
вспомогательное состояние, в котором балка освобождается от внешней
нагрузки, а к сечению, перемещение которого определяется, прикладывается
единичная сила, если определяется линейное перемещение, или единичный
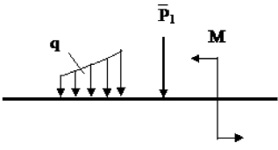
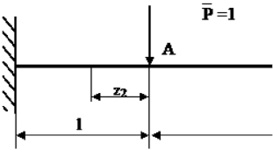
момент, если определяется угловое перемещение (рис. 32).
а б
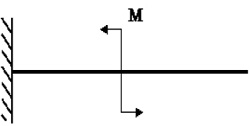
в
Рис. 32. Определение перемещений:
а – действительное состояние; б, в – вспомогательные состояния
Формулу Мора можно получить, например. используя принцип возможных перемещений.
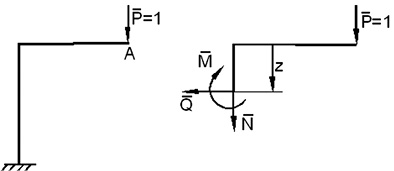
а б
Рис. 33. Схема рамы:
а – под воздействием силы; б – внутренние усилия
Рассмотрим схему (рис. 33а), когда в точке А в направлении искомого перемещения ΔA приложена единичная сила 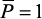
(рис. 33, б). В соответствии с принципом возможных перемещений работа
этих внутренних силовых факторов на любых возможных перемещениях должна
равняться работе единичной силы 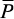
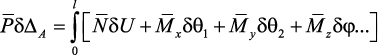
Выбираем возможные перемещения пропорциональными действительным:
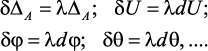
И после подстановки получим:
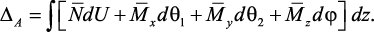
При учете, что
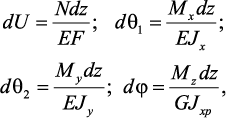
приходим к формуле Мора
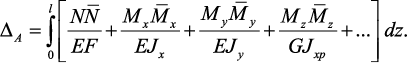
которая служит для определения любых обобщённых перемещений в стержневых системах.
В случае, когда брус работает только на изгиб (Mx ≠ 0, Nz = Mz = My = Qx = Qy = 0), выражение (1) принимает вид:
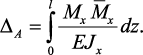
Правило Верещагина позволяет заменить непосредственное
интегрирование в формулах Мора так называемым перемножением эпюр. Способ
вычисления интеграла Мора путем замены непосредственного интегрирования
перемножением соответствующих эпюр называется способом (или правилом)
Верещагина, заключающемся в следующем: чтобы перемножить две эпюры, из
которых хотя бы одна является прямолинейной, нужно площадь одной эпюры
умножить на ординату другой эпюры, расположенную под центром тяжести
первой (ординаты используются только с прямолинейных эпюр). Эпюры
сложного очертания могут быть разбиты на ряд простейших: прямоугольник,
треугольник, квадратичную параболу и т.п. (рис. 34).
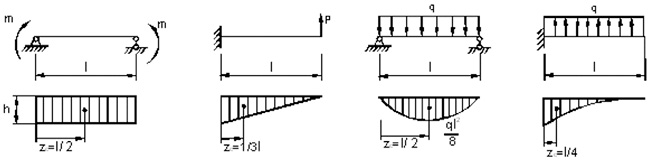
Рис. 34. Простейшие эпюры
Справедливость правила Верещагина.
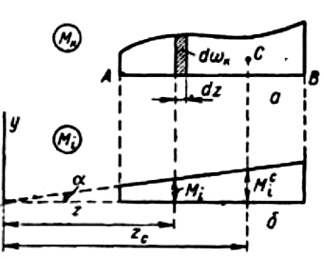
Рис. 35. Схема перемножения эпюр:
а – произвольная эпюра; б – прямолинейная
Приведены две эпюры изгибающих моментов, из которых одна Мk имеет
произвольное очертание, а другая Мi прямолинейна (рис. 35). Сечение
стержня считаем постоянным. В этом случае
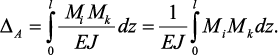
Величина Mkdz представляет собой элементарную площадь dω эпюры Мk (заштрихована). Получаем
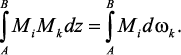
Но Mi = ztg α, поэтому,
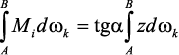
Выражение 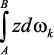
собой статический момент площади эпюры Мk относительно оси у,
проходящей через точку О, равный ωkΖc, где ωk – площадь эпюры моментов;
Ζс – расстояние от оси у до центра тяжести эпюры Мk. Из рисунка
очевидно:
Ζc = Мi/tg α,
где Мi – ордината эпюры Mi, расположенная под центром тяжести эпюры Мk (под точкой С).
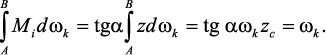
Формула (21) представляет правило вычисления интеграла Мора:
интеграл равен произведению площади криволинейной эпюры на ординату,
взятую с прямолинейной эпюры и расположенную под центром тяжести
криволинейной эпюры.
Встречающиеся на практике криволинейные эпюры могут быть разбиты
на ряд простейших: прямоугольник, треугольник, симметричную квадратичную
параболу и т.п.
При помощи разбивания эпюр на части можно добиться того, что при перемножении все эпюры были бы простой структуры.
Пример вычисления перемещений. Требуется определить прогиб
в середине пролета и угол поворота левого опорного сечения балки,
нагруженной равномерно распределенной нагрузкой (рис. 36, а), способом
Мора-Верещагина.
Рассмотрим 3 состояния балки: грузовое состояние ( при действии
распределенной нагрузки q;) ему соответствует эпюра Mq (рис. 36, б),
и два единичных: при действии силы 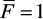
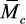
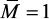
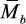
Прогиб балки в середине пролета:
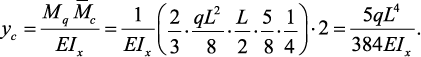
Обратим внимание, что перемножение эпюр выполняется для половины
балки, а затем из-за симметрии) полученный результат удваивается. При
вычислении угла поворота сечения в точке В площадь эпюры Mq умножается
на расположенную под ее центром тяжести ординату эпюры 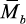
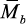
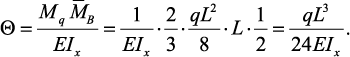
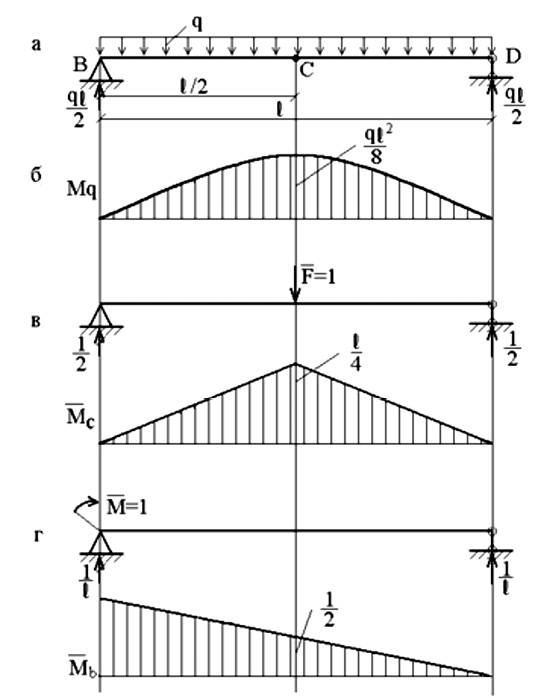
Рис. 36. Пример расчета:
а – заданная схема балки; б – грузовая эпюра моментов;
в – единичная эпюра от единичной силы; г – от единичного момента


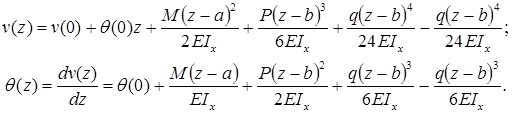

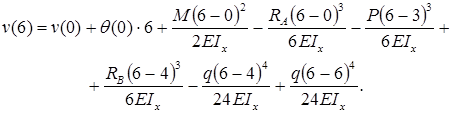
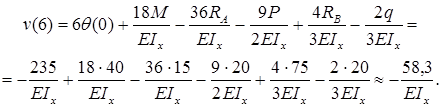
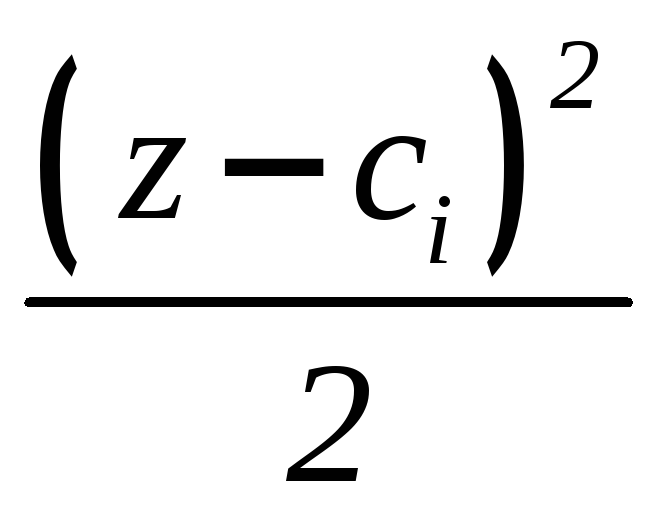
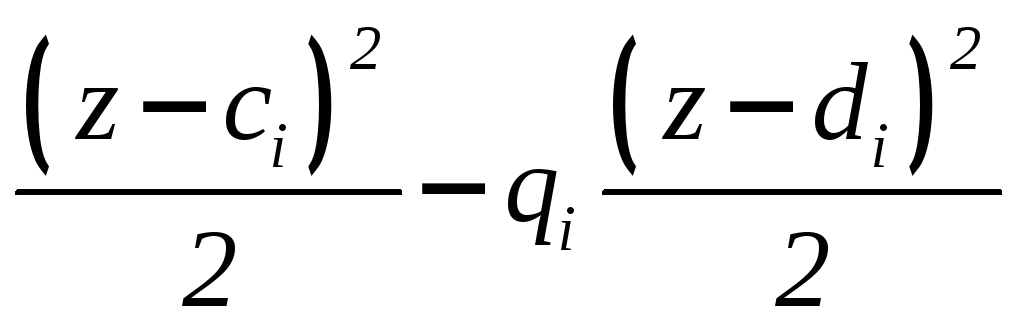
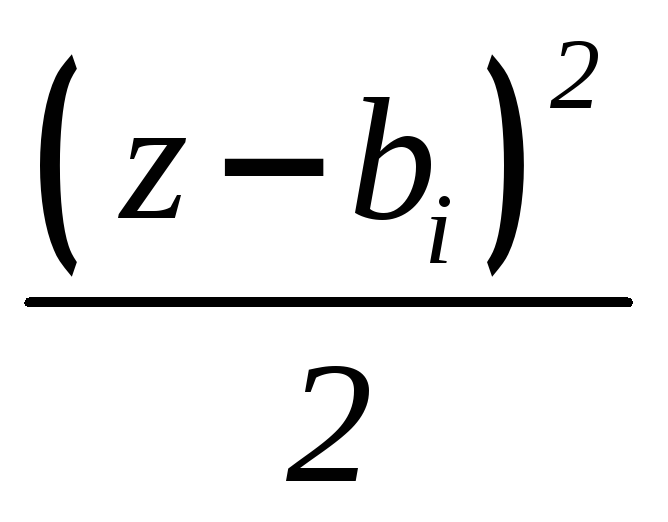
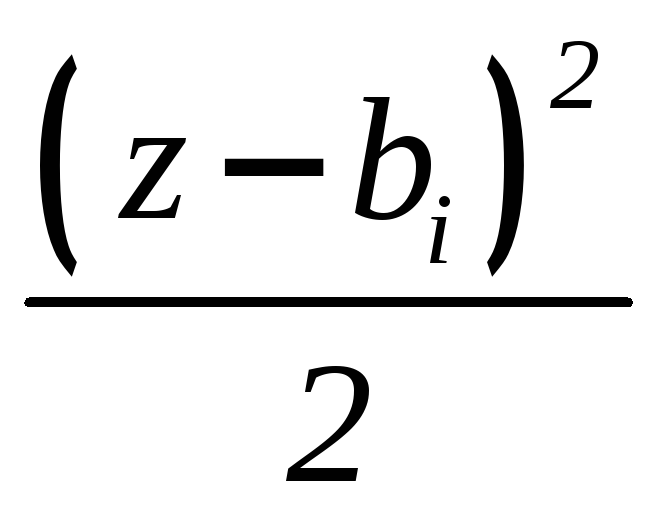 +
+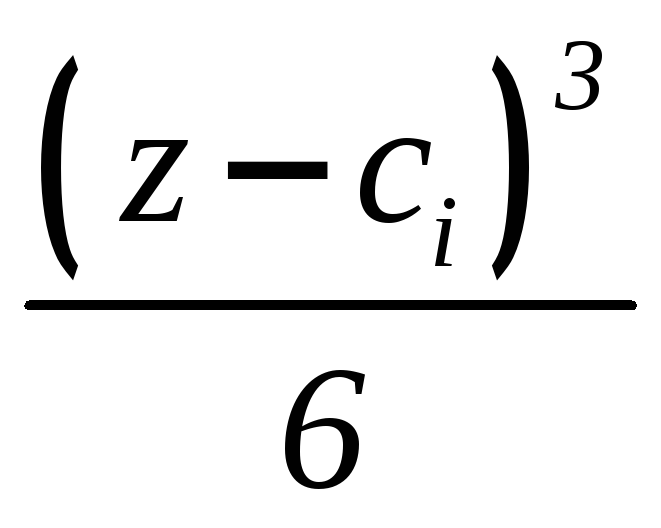
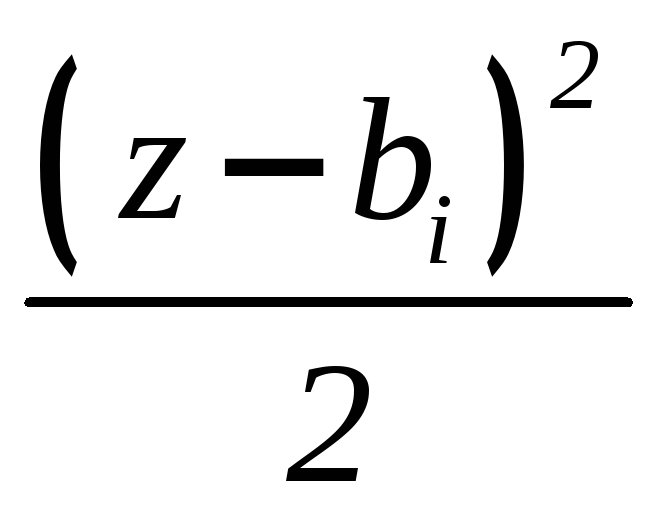 +
+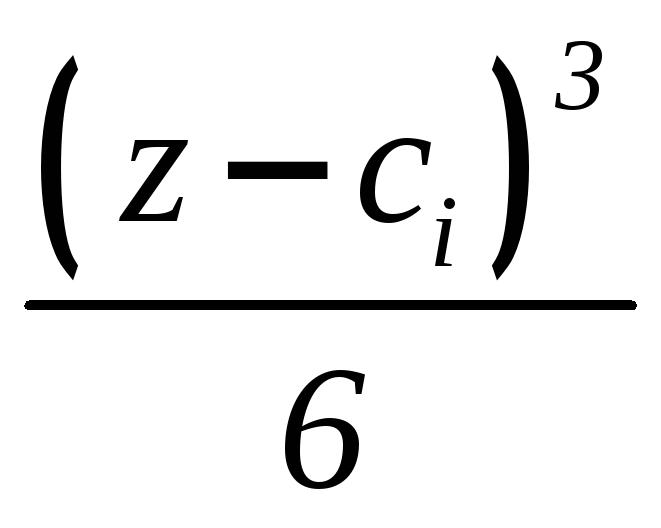
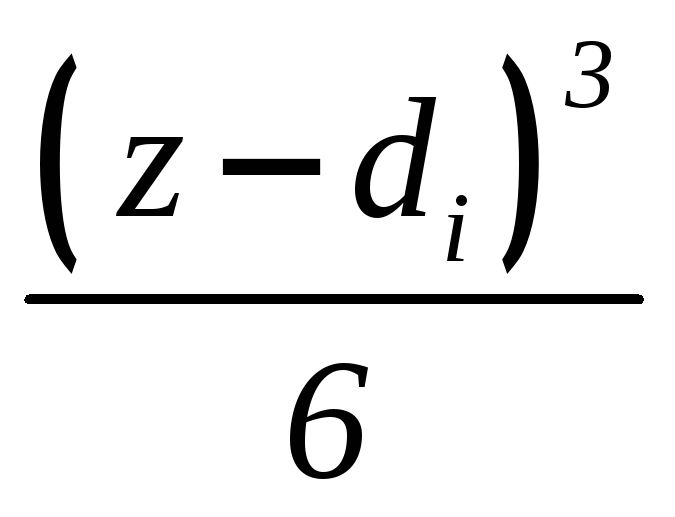
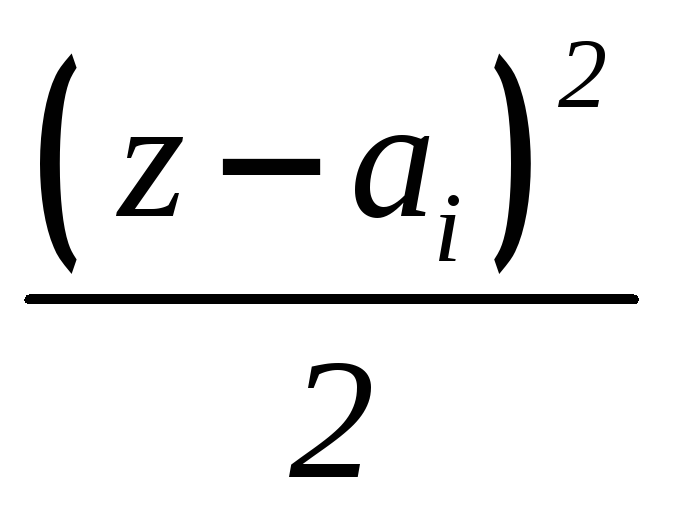
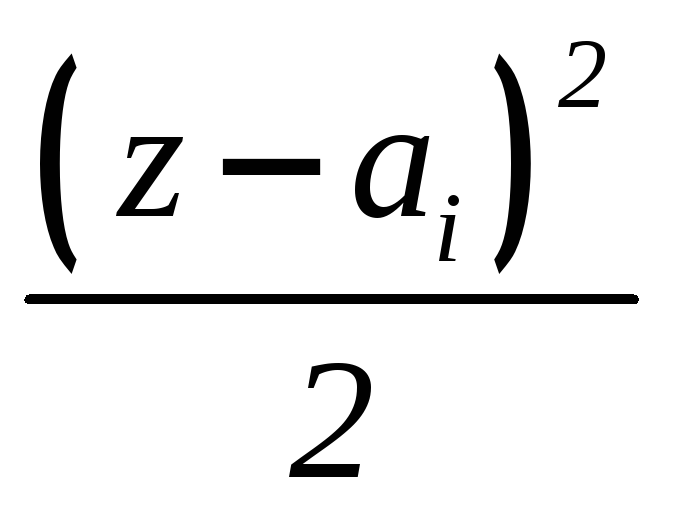
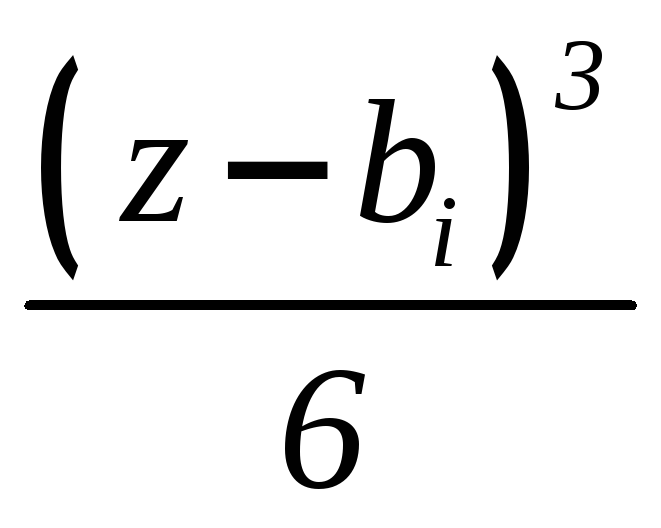
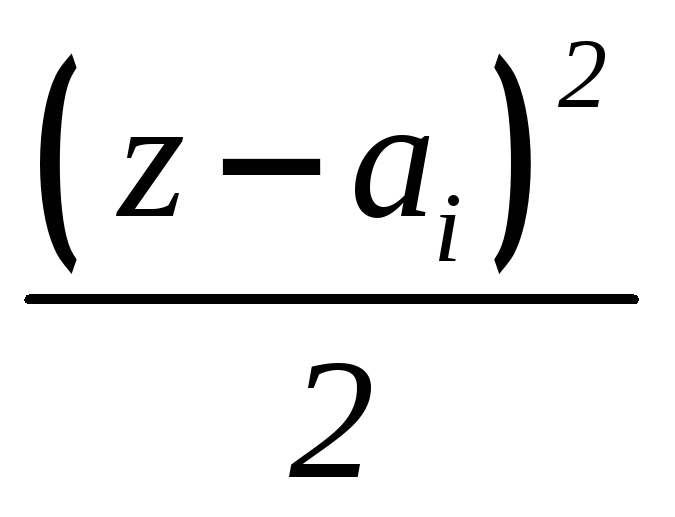
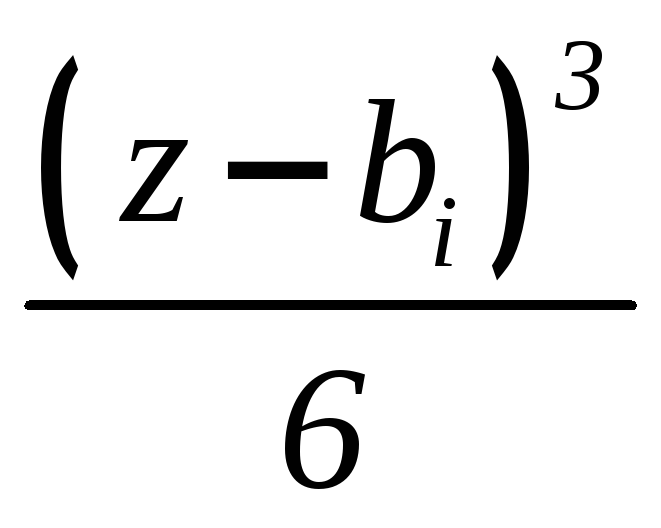 +
+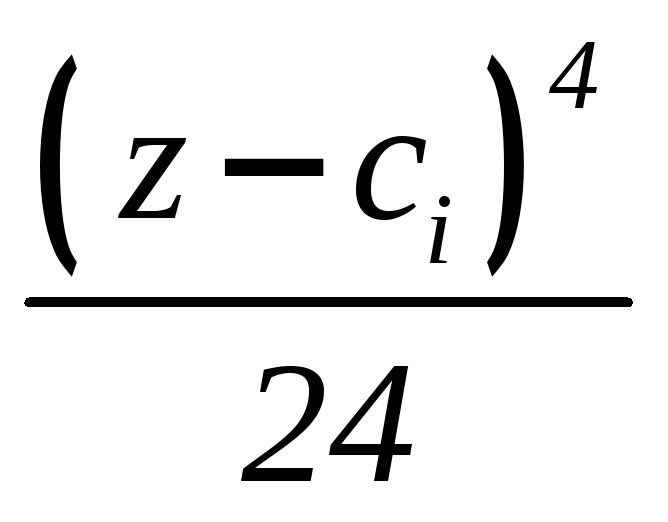
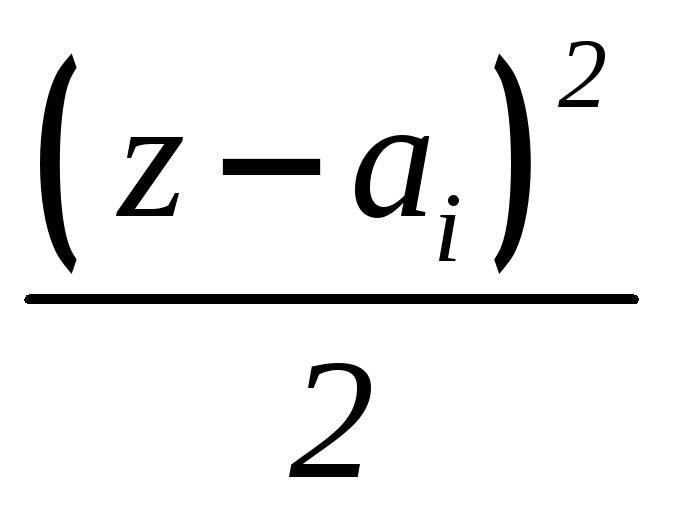
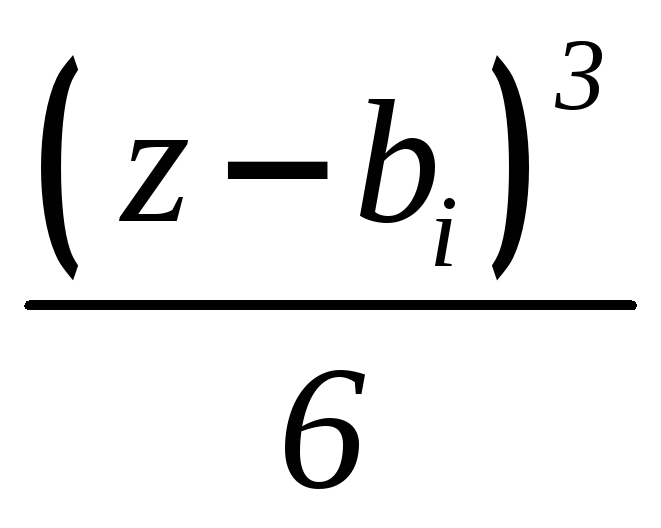 +
+