Как составить уравнение в динамике

Содержание:

  1. Общее уравнение динамики
  2. Порядок решения задач на применение общего уравнения динамики
  3. Примеры решения задач на тему: Общее уравнение динамики

Общее уравнение механики представляет собой математическую формулировку принципа Д’Аламбера — Лагранжа, дающего общий метод решения задач динамики и статики и являющегося одним из основных принципов теоретической механики.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Общее уравнение динамики

Законы Ньютона установлены для свободной материальной точки и свободной материальной системы. Однако, чаще встречаются несвободные системы. Это обстоятельство существенно усложняет использование законов Ньютона для решения задач динамики несвободных механических систем, а зачастую и вовсе не позволяет решать такие задачи.

Необходимость решения задач динамики несвободных механических систем в связи с их важным практическим значением обусловила разработку ряда методов решения таких задач.

В этом первостепенное значение принадлежит общим принципам и общим уравнениям механики.

Из принципов ранее были рассмотрены следующие.

Принцип Даламбера. Он заключается в том, что

в каждый момент времени уравновешиваются между собой действующие на Общее уравнение динамики — ту точку несвободной материальной системы активные силы Общее уравнение динамики, реакции связей Общее уравнение динамики и силы инерции Общее уравнение динамики, которые приложены к этим точкам. Этот принцип записывается формулой 12.6:

Общее уравнение динамики

Принцип возможных перемещений. Он в наиболее общей форме устанавливает условия равновесия несвободных материальных систем и состоит в том, что

для равновесия материальной системы, подчиняющейся идеальным стационарным связям, необходимо и достаточно, чтобы сумма элементарных работ, осуществляемых активными силами Общее уравнение динамики на возможных перемещениях Общее уравнение динамики точек механической системы, равнялась нулю:

Общее уравнение динамики

Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики для решения задач динамики. Итак, применяя эти два принципа одновременно, можно получить общий метод решения задач динамики, который имеет название общего уравнения динамики:

при движении системы с идеальными связями в каждый данный момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю

Общее уравнение динамики

где Общее уравнение динамики — сумма элементарных работ активных сил на возможных перемещениях точек приложения этих сил;

Общее уравнение динамики — сумма элементарных работ сил инерции точек системы на их возможных перемещениях.

Уравнение (14.3) в развернутой форме можно записать в виде:

Общее уравнение динамики

Порядок решения задач на применение общего уравнения динамики

Установить, движение какой несвободной системы рассматривается.

Определить характер связей, которые наложенные на систему, учитывая свойство идеальных связей.

Обозначить активные силы, которые действуют на точки системы.

Определить возможные перемещения системы.

Условно приложить к точкам системы силы инерции и подсчитать их величину.

Составить сумму работ активных сил и сил инерции на установленных перемещениях системы.

Из полученного соотношения найти искомые величины.

Применить общее уравнение динамики к решению задач необходимо в том случае, когда по условию задачи с известными активными силами необходимо определить ускорение системы (линейное или угловое), а также силы, действующие на точки системы.

Примеры решения задач на тему: Общее уравнение динамики

Задача №1

Груз Общее уравнение динамики весом Общее уравнение динамики, опускаясь по гладкой наклонной плоскости, которая составляет с горизонтом угол Общее уравнение динамики, приводит к вращению барабана Общее уравнение динамики весом Общее уравнение динамики с радиусом Общее уравнение динамики с помощью невесомой нити, что не растягивается, рис.14.1).

Определить угловое ускорение барабана, если считать барабан однородным круглым цилиндром. Массой неподвижного блока Общее уравнение динамики пренебречь.

Решение. Данная несвободная система состоит из груза Общее уравнение динамики и барабана Общее уравнение динамики, силы тяжести (активные силы) которых Общее уравнение динамики и Общее уравнение динамики — заданные. Связью между грузом и барабаном является невесомая нить, которая не растягивается. Внешними связями по отношению к системе являются наклонная поверхность, а также подшипники Общее уравнение динамики и Общее уравнение динамики.

Общее уравнение динамики

Определим возможные перемещения системы. Для барабана возможным перемещением будет угол поворота Общее уравнение динамики, для поступательного движения груза Общее уравнение динамики возможное перемещение Общее уравнение динамики. Установим зависимость между величинами Общее уравнение динамики и Общее уравнение динамики.

При перемещении груза вниз на величину Общее уравнение динамики, нить сматывается с барабана на ту же самую величину Общее уравнение динамики, а барабан повернется на угол Общее уравнение динамики. То есть

Общее уравнение динамики

Приложим к несвободной механической системе силы инерции. Если Общее уравнение динамики груз опускается с ускорением Общее уравнение динамики, направленным вниз по наклонной поверхности, то сила инерции груза Общее уравнение динамики направлена в противоположную сторону. Момент сил инерции Общее уравнение динамики барабана направлен так, как показано на рисунке 14.1, в сторону, противоположную угловому ускорению Общее уравнение динамики.

Составим общее уравнение динамики системы в форме (14.3)

Общее уравнение динамики

где 

Общее уравнение динамики

Тогда:

Общее уравнение динамики

Реакции Общее уравнение динамики и Общее уравнение динамики работы на элементарном перемещении не выполняют.

Уравнение (1) с учетом направлений сил и возможных перемещений запишем в виде:

Общее уравнение динамики

или

Общее уравнение динамики

Определим величины Общее уравнение динамики и Общее уравнение динамики, выражая при этом линейное ускорение груза через угловое ускорение барабана:

Общее уравнение динамики

где Общее уравнение динамики — момент инерции барабана относительно оси Общее уравнение динамики;

Общее уравнение динамики— угловое ускорение барабана.

Подставляя эти данные в уравнение (2), получим:

Общее уравнение динамики

Поскольку Общее уравнение динамики, то будем иметь:

Общее уравнение динамики

Откуда определяем угловое ускорение барабана:

Общее уравнение динамики

Ответ: Общее уравнение динамики

Задача № 2

Два зубчатых колеса 1 и 2 с радиусами Общее уравнение динамики и Общее уравнение динамики находятся во внешнем зацеплении. Моменты инерции колес относительно их осей вращения равны соответственно Общее уравнение динамики и Общее уравнение динамики.

Определить угловое ускорение колеса 1, если к нему приложен вращательный момент Общее уравнение динамики. Силами сопротивления пренебречь (рис.14.2).

Общее уравнение динамики

Решение. Данная механическая система состоит из двух зубчатых колес 1 и 2, которые вращаются вокруг осей Общее уравнение динамики и Общее уравнение динамики. Пара зубчатых колес является системой с одной степенью свободы, поскольку угол поворота одного из колес определяет положение второго колеса. Активными силами являются силы тяжести Общее уравнение динамики и Общее уравнение динамики , вращательный момент Общее уравнение динамики

Предоставим возможное угловое перемещение Общее уравнение динамики колесу 1, тогда колесо 2 осуществит возможно перемещение Общее уравнение динамики.

Зависимость между Общее уравнение динамики и Общее уравнение динамики может быть получена с помощью возможного перемещения Общее уравнение динамики точки Общее уравнение динамики касания колес. Поскольку точка Общее уравнение динамики принадлежит обоим зубчатым колесам, то

Общее уравнение динамики

откуда

Общее уравнение динамики

Знак минус показывает, что возможные перемещения Общее уравнение динамики и Общее уравнение динамики направлены в разные стороны.

Определим силы инерции частей механической системы. При вращении колес вокруг неподвижных осей их силы инерции приводятся к парам сил, моменты которых противоположны по знаку угловым ускорением и равны по модулю произведениям моментов инерции относительно осей вращения на модули соответствующих угловых ускорений.

Угловые ускорения связаны соотношением, которое вытекает из равенства тангенциальных ускорений в месте соприкасания колес 1 и 2:

Общее уравнение динамики или Общее уравнение динамики

(минус введен потому, что колеса вращаются в разные стороны).

Момент пары сил инерции колеса 1 равен:

Общее уравнение динамики

Момент пары сил инерции колеса 2:

Общее уравнение динамики

С учетом зависимости (2) получим Общее уравнение динамики

Для составления общего уравнения динамики необходимо подсчитать сумму работ активных сил и сил инерции на возможных перемещениях точек системы и приравнять эту сумму к нулю:

Общее уравнение динамики

Работа сил тяжести Общее уравнение динамики и Общее уравнение динамики равна нулю, поскольку точки приложения этих сил неподвижны.

Воспользовавшись формулами (1), (3) и (4), после сокращения на Общее уравнение динамики, получим:

Общее уравнение динамики

Отсюда определим искомое угловое ускорение зубчатого колеса 1:

Общее уравнение динамики

Ответ: Общее уравнение динамики

Задача № 3

На треугольной призме, боковые грани которой создают с горизонтом углы Общее уравнение динамики и Общее уравнение динамики, размещены два груза Общее уравнение динамики и Общее уравнение динамики , которые весят Общее уравнение динамики и Общее уравнение динамики, соответственно. Они связаны между собой невесомой нитью, которая не растягивается и перекинута через блок Общее уравнение динамики (рис.14.3). Коэффициент трения скольжения равен Общее уравнение динамики.

Определить ускорение грузов и натяжение нити. Массой блока пренебречь.

Решение. Данная механическая система состоит из двух грузов, которые движутся поступательно. Нить, масса которой не учитывается, является связью. Система имеет одну степень свободы.

Допустим, что Общее уравнение динамики груз движется вниз с ускорением Общее уравнение динамики, а груз Общее уравнение динамики вверх, причем ускорение груза Общее уравнение динамики равно ускорению груза Общее уравнение динамики, поскольку нить не растягивается. Покажем заданные силы – силы тяжести Общее уравнение динамики и Общее уравнение динамики, нормальные реакции боковых граней призмы Общее уравнение динамики и Общее уравнение динамики и силы трения Общее уравнение динамики и Общее уравнение динамики (рис.14.3).

Модули сил трения равны:

Общее уравнение динамики

Общее уравнение динамики

где

Общее уравнение динамики

Поэтому

Общее уравнение динамики

Силы трения направлены в стороны, противоположные направлениям движения грузов.

Поскольку грузы движутся поступательно, то равнодействующие сил инерции приложены в центрах масс тел, а их модули равны:

Общее уравнение динамики

Приложим к грузам условно силы инерции Общее уравнение динамики и Общее уравнение динамики, направив их противоположно ускорению Общее уравнение динамики.

Предоставим мысленно системе возможное поступательное перемещение Общее уравнение динамики, например, в сторону движения грузов. Составим общее уравнение динамики, в которое не войдут нормальные реакции граней призмы Общее уравнение динамики и Общее уравнение динамики, направления которых перпендикулярны возможным перемещениям грузов:

Общее уравнение динамики

где

Общее уравнение динамики

Тогда уравнение (1) примет вид:

Общее уравнение динамики

После сокращения на Общее уравнение динамики получим:

Общее уравнение динамики

Из последнего уравнения находим ускорение Общее уравнение динамики:

Общее уравнение динамики

Если

Общее уравнение динамики

то грузы движутся в принятом направлении.

Для определения натяжения Общее уравнение динамики нити, разрежем ее возле груза Общее уравнение динамики, тогда сила Общее уравнение динамики станет внешней. Далее применим принцип Даламбера в проекции на ось Общее уравнение динамики (рис.14.4):

Общее уравнение динамики

откуда

Общее уравнение динамики

Общее уравнение динамики

Подставив в уравнение (4) значение Общее уравнение динамики из уравнения (2), после преобразований получим:

Общее уравнение динамики

Окончательно,

Общее уравнение динамики

Ответ: Общее уравнение динамики

Задача № 4

Механическая система (рис.14.5) состоит из обмотанных нерастяжимой и невесомой нитью блока 1 с радиусом Общее уравнение динамики и ступенчатого шкива 2 (радиусы ступеней Общее уравнение динамики Общее уравнение динамики радиус инерции относительно оси вращения Общее уравнение динамики вес шкива Общее уравнение динамики), а также из грузов 3 (весом Общее уравнение динамики) и 4 (весом Общее уравнение динамики), которые прикреплены к этой нити.

Общее уравнение динамики

Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом Общее уравнение динамики приложенным к блоку 1, вес которого принимается равным нулю.

Определить ускорение Общее уравнение динамики груза 3, пренебрегая трением.

Решение. Рассматривается движение механической системы с одной степенью свободы . Связи, наложенные на систему — идеальны.

Для определения ускорения Общее уравнение динамики тела 3, применим общее уравнение динамики (14.3):

Общее уравнение динамики

где Общее уравнение динамики — сумма элементарных работ активных сил,

Общее уравнение динамики —  сумма элементарных работ сил инерции.

Изобразим на рисунке 14.5 активные силы Общее уравнение динамики — силы тяжести, и пару сил с моментом Общее уравнение динамики, которые действуют на тела механической системы. Задаемся направлением ускорения Общее уравнение динамики тела 3, определяем направление ускорения Общее уравнение динамики ступенчатого шкива 2 и ускорение Общее уравнение динамики груза 4.

Направление сил инерции Общее уравнение динамики, и пары сил инерции с моментом Общее уравнение динамики изображены на рис.14.5.

Определяем величины Общее уравнение динамики и Общее уравнение динамики:

Общее уравнение динамики

где Общее уравнение динамики — момент инерции шкива 2.

Предоставим шкиву 2 возможное перемещение Общее уравнение динамики, с которым связаны возможные перемещения других тел системы и составим уравнение (1):

Общее уравнение динамики

Выразим все возможные перемещения через Общее уравнение динамики:

Общее уравнение динамики

Подставим значения (2) и (4) в уравнение (3)

Общее уравнение динамики

Величины Общее уравнение динамики и Общее уравнение динамики, которые входят в последнее уравнение, выразим через искомую величину Общее уравнение динамики:

Общее уравнение динамики

Тогда:

Общее уравнение динамики

Поскольку Общее уравнение динамики,то

Общее уравнение динамики

Решаем последнее уравнение относительно Общее уравнение динамики:

Общее уравнение динамики

С учетом числовых значений получим:

Общее уравнение динамики

Знак „минус” показывает на то, что ускорение груза 3 и ускорение других тел направлены противоположно показанным на рис.14.5.

Ответ: Общее уравнение динамики

Задача № 5

Механическая система, состоящая из двух грузов Общее уравнение динамики и Общее уравнение динамики весом Общее уравнение динамики и Общее уравнение динамики, связанных нерастяжимой абсолютно гибкой нитью, а также однородного диска Общее уравнение динамики весом Общее уравнение динамики и радиусом Общее уравнение динамики (рис. 14.6), находится в движении (груз Общее уравнение динамики движется вниз).

Общее уравнение динамики

Определить величину приложенного к диску тормозящего момента Общее уравнение динамики, необходимого для того, чтобы остановить систему в течение заданного времени Общее уравнение динамики, если в момент начала торможения (при Общее уравнение динамики) скорость груза Общее уравнение динамики была Общее уравнение динамики.

При решении задачи учесть силу трения Общее уравнение динамики между грузом Общее уравнение динамики и столом, если коэффициент трения равен Общее уравнение динамики.

Решение. Наложенная на груз Общее уравнение динамики связь не идеальна, но общим уравнением динамики воспользоваться можно, если активных сил. Грузы Общее уравнение динамики, Общее уравнение динамики и диск Общее уравнение динамики осуществляют равномерно замедленное движение с заданными ускорениями

Общее уравнение динамики

Изображаем действующие на систему активные силы Общее уравнение динамики, Общее уравнение динамики  и Общее уравнение динамики, а также силы инерции Общее уравнение динамики и Общее уравнение динамики грузов Общее уравнение динамики и Общее уравнение динамики, и момент сил инерции Общее уравнение динамики диска Общее уравнение динамики. В рассматриваемом случае имеем:

Общее уравнение динамики

где

Общее уравнение динамики

Данная система сил имеет одну степень свободы, обусловленную углом поворота Общее уравнение динамики диска Общее уравнение динамики. Тогда возможные перемещения системы будут

Общее уравнение динамики и Общее уравнение динамики

где Общее уравнение динамики и Общее уравнение динамики отсчитываются вдоль траектории грузов Общее уравнение динамики и Общее уравнение динамики.

Составляя общее уравнение динамики (14.4), получим:

Общее уравнение динамики

Подставим в это уравнение значения Общее уравнение динамики

Общее уравнение динамики

Поскольку Общее уравнение динамики, то нулю равно выражение в квадратных скобках.

Тогда

Общее уравнение динамики

Ответ: Общее уравнение динамики

Услуги по теоретической механике:

  1. Заказать теоретическую механику
  2. Помощь по теоретической механике
  3. Заказать контрольную работу по теоретической механике

Учебные лекции:

  1. Статика
  2. Система сходящихся сил
  3. Момент силы
  4. Пара сил
  5. Произвольная система сил
  6. Плоская произвольная система сил
  7. Трение
  8. Расчет ферм
  9. Расчет усилий в стержнях фермы
  10. Пространственная система сил
  11. Произвольная пространственная система сил
  12. Плоская система сходящихся сил
  13. Пространственная система сходящихся сил
  14. Равновесие тела под действием пространственной системы сил
  15. Естественный способ задания движения точки
  16. Центр параллельных сил
  17. Параллельные силы
  18. Система произвольно расположенных сил
  19. Сосредоточенные силы и распределенные нагрузки
  20. Кинематика
  21. Кинематика твердого тела
  22. Движения твердого тела
  23. Динамика материальной точки
  24. Динамика механической системы
  25. Динамика плоского движения твердого тела
  26. Динамика относительного движения материальной точки
  27. Динамика твердого тела
  28. Кинематика простейших движений твердого тела
  29. Работа и мощность силы
  30. Обратная задача динамики
  31. Поступательное и вращательное движение твердого тела
  32. Плоскопараллельное (плоское) движение твёрдого тела
  33. Сферическое движение твёрдого тела
  34. Движение свободного твердого тела
  35. Сложное движение твердого тела
  36. Сложное движение точки
  37. Плоское движение тела
  38. Статика твердого тела
  39. Равновесие составной конструкции
  40. Равновесие с учетом сил трения
  41. Центр масс
  42. Колебания материальной точки
  43. Относительное движение материальной точки
  44. Статические инварианты
  45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
  46. Динамика системы материальных точек
  47. Общие теоремы динамики
  48. Теорема об изменении кинетической энергии
  49. Теорема о конечном перемещении плоской фигуры
  50. Потенциальное силовое поле
  51. Метод кинетостатики
  52. Вращения твердого тела вокруг неподвижной точки
Источник

Цель занятия:

— отработка
практических навыков решения задач на
общее уравнение динамики материальных
систем.

Вопросы для
подготовки:

  1. Принципы механики,
    используемые при выводе общего уравнения
    механики.

  2. Принцип Даламбера
    – Лагранжа.

  3. Общее уравнение
    динамики.

Методические
рекомендации к решению задач по теме
«Общее уравнение динамики ».

1)
изобразить на чертеже все активные силы
и силы трения, если они действуют;

2)
к активным силам добавить силы инерции
и моменты сил инерции, направив их
противоположно линейным или угловым
ускорениям;

3).
сообщить системе столько независимых
между собой возможных перемещений,
сколько степеней свободы имеет система;

4) выразить все
линейные и угловые ускорения через
ускорение того тела, движение которому
мы задаем;

5)
выразить все линейные и угловые возможные
перемещения через возможные перемещения
того тела, движение которому мы задаем;

6)
записать общее уравнение динамики и
определить искомые величины.

Пример
выполнения задания Д 19.

Тема: Применение общего уравнения
динамики к исследованию движения
механической системы».

Механическая
система под действием силы тяжести
приходит в движение из состояния покоя,
необходимо определить ускорения всех
тел, входящих в систему. Массами нитей
пренебречь. Трение качения и силы
сопротивления в подшипниках не учитывать.
Каток 3 – однородный цилиндр. Схема
механической системы показана на рисунке
9.

Дано:

;
;
;;;f=0,1.

Рис.9

Решение:

Покажем
на механической системе веса тел
,,;
ускорения груза 1и центра цилиндра 3;
углы поворотов тел, совершающих
вращательное движение,;
угловые ускорения,;
силу трения груза 1;
силы инерции,;
моменты сил инерции,,
как указано на рисунке 9.

Используем общее уравнение динамики:

Если
механическая система, на которую наложены
голономные, стационарные, идеальные
связи, движется с ускорением, то, добавляя
к действующей на неё активным силам и
моментам этих сил, фиктивные силы инерции
и моменты сил инерции, получим формально
уравновешенную систему сил, к которой
можно применить принцип возможных
перемещений.

; (1)

, (2)

где
— внешние силы, действующие на систему;

—
силы инерции, действующие на систему;

—
возможное перемещение.

Запишем все
уравнения связей для механической
системы:

; (3)

где:

ε2,
— угловое ускорение катка 3;

a1,
ac3
— линейные
ускорения груза 1 и центра однородного
катка 3.

Так
как система приходит в движение из
состояния покоя, направления ускорения
тел соответствуют направлениям движения
тел.

Покажем все заданные
силы и приложим силы и моменты инерции.
Сила инерции груза 1, движущегося
поступательно равна:

. (4)

Сила
инерции центра однородного цилиндра,
центр которого движется поступательно,
равна:

; (5)

Используя
уравнение связи , определим момент сил
инерции блока 2, совершающего вращательное
движение:

. (6)

Используя
(3) и (6), определим момент сил инерции
однородного цилиндра 3, совершающего
вращательное движение:

. (7)

Сообщив
механической системе возможное
перемещение
и возможный угол поворота,
составим общее уравнение динамики.

Так как

; (8)

, (9)

то общее уравнение
динамики примет вид:

(11)

Учитывая
уравнения (3) и исходные данные, полученные
из условия задачи, получим:

;(12)

Разделим
каждое составляющее выражения на
,и выразим ускорение груза 1:

.

Для
нахождения ускорений остальных тел
воспользуемся уравнениями связи:

;

;

.

Результаты
расчётов по данному методу представим
в виде таблицы.

,

,

,

,

ВОПРОСЫ ДЛЯ
САМОКОНТРОЛЯ

  1. Что такое число
    степеней свободы?

  2. Какие принципы
    используются при получении общего
    уравнения динамики?

  3. Как
    записывается общее уравнение динамики
    для системы, подчиненной голономным,
    стационарным, удерживающим и идеальным
    связям?

  4. Как
    определить работу, совершаемую силами
    инерции при различных видах движения
    твердого тела?

САМОСТОЯТЕЛЬНАЯ
РАБОТА

Практические
занятия и самостоятельная работа
включает в себя решение задач: [9]

№№ 47.1; 47.3; 47.4;47.5;
47.6; 47.9; 47.11; 47.12; 47.15 47.21; 47.24.

Выдача расчетно-графической работы Д19
на тему «Применение общего уравнения
динамики к механической системе с одной
степенью свободы».[4]

Практическое
занятие 8

Тема:
Уравнения
Лагранжа II
рода

Цель занятия:

—
отработка практических навыков
составления дифференциальных уравнений
движения механической системы в
обобщенных координатах с помощью
уравнений Лагранжа второго рода.

Вопросы для
подготовки:

  1. Обобщенные
    координаты.

  2. Методы определения
    обобщенных сил.

  3. Уравнения
    Лагранжа II
    рода.

  4. Функция Лагранжа.

  5. Достоинства
    уравнений Лагранжа II
    рода.

Методические
рекомендации к решению задач по теме
«Уравнения Лагранжа второго рода ».

Уравнения
Лагранжа второго рода представляют
собой дифференциальные уравнения
движения механической системы в
обобщенных координатах. Для составления
уравнений необходимо:

1)
проанализировать состав рассматриваемой
механической системы, в которую могут
входить материальные точки и тела;

2)
определить силы, приложенные к точкам
и телам механической системы; выявить
среди них консервативные силы;

3) определить число
степеней свободы механической системы;

4)
выбрать обобщенные координаты, зная
координаты материальных точек и точек
приложения сил к телам, входящих в
систему;

5)
выразить координаты точек приложения
сил к телам и координаты материальных
точек системы через координаты
обобщенные;

6) определить
обобщенные скорости;

7)
определить кинетическую энергию
механической системы с учетом выбранных
обобщенных координат и скоростей;

8)
определить частные производные от
кинетической энергии по обобщенным
координатам;

9)
определить частные производные от
кинетической энергии по обобщенным
скоростям;

10)
определить производные по времени от
частных производных от кинетической
энергии по обобщенным скоростям;

11)
определить обобщенные силы как
коэффициенты перед вариациями обобщенных
координат в выражении для виртуальной
работы;

12)
составить уравнения Лагранжа второго
рода и определить искомые величины.

Пример
решения задач по теме:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

iSopromat.ru

Рассмотрим общее уравнение динамики механической системы, которое также называется принципом Даламбера-Лагранжа:

Объединяя этот принцип с принципом возможных перемещений для систем с идеальными связями получаем уравнение:

которое называют общим уравнением динамики (или принципом Даламбера-Лагранжа).

При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нолю.

Поскольку в уравнении присутствуют силы инерции, а следовательно и ускорения, то эти уравнения представляют собой дифференциальные уравнения движения механической системы с идеальными связями.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Общее уравнение динамики. Пример решения задачи

Условие задачи

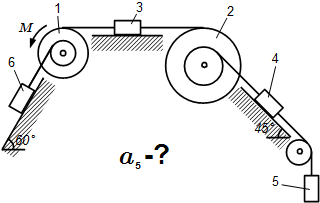
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R 1 = 0,2 м , r 1 = 0,1 м , а шкива 2 – R 2 = 0,3 м , r 2 = 0,15 м ; их радиусы инерции относительно осей вращения равны соответственно ρ 1 = 0,1 м и ρ 2 = 0,2 м .

Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P 1 = 40 Н , P 2 = 0 , P 3 = 0 , P 4 = 20 Н , P 5 = 30 Н , P 6 = 10 Н . Грузы, веса которых равны нулю, на чертеже не изображать.

Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).

Решение задачи

Дано: R 1 = 0,2 м , r 1 = 0,1 м , R 2 = 0,3 м , r 2 = 0,15 м , ρ 1 = 0,1 м , ρ 2 = 0,2 м . P 1 = 40 Н , P 2 = 0 , P 3 = 0 , P 4 = 20 Н , P 5 = 30 Н , P 6 = 10 Н , M = 10 Н·м .

Установление кинематических соотношений

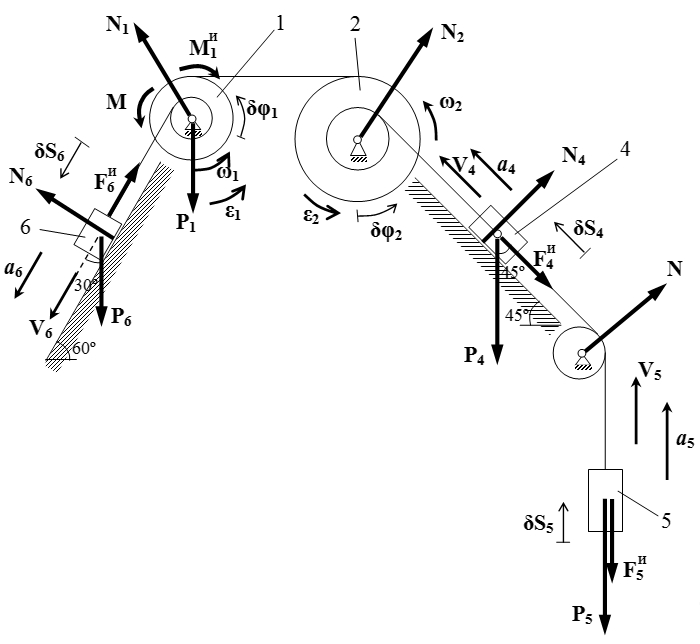
Установим кинематические соотношения. Пусть V 4 , V 5 , V 6 , a 4 , a 5 , a 6 , δS 4 , δS 5 , δS 6 – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω 1 , ω 2 , ε 1 , ε 2 , δφ 1 , δφ 2 – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.

Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.

Итак, мы нашли связь между скоростями тел.
;
;
.

Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.

Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.

Активные внешние силы

Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P 1 = 40 Н , P 4 = 20 Н , P 5 = 30 Н и P 6 = 10 Н , направленные вниз;
заданная пара сил с моментом M = 10 Н·м ;
силы давления осей N 1 , N 2 и N шкивов 1, 2 и невесомого блока;
силы реакции N 4 и N 6 , действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.

Силы инерции

Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера — Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.

Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε 1 и ε 2 , соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a 4 , a 5 и a 6 , соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a 5 . Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).

Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a 5 .
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.

Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.

Применение общего уравнения динамики

Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS 5 . Тогда угол поворота δφ 1 шкива 1 и перемещения δS 4 и δS 6 грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.

Определение суммы работ внешних активных сил и сил инерции

Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними.

Работа, произведенная моментом сил , вычисляется аналогично:
.

Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P 1 , N 1 , N 2 и N не совершают работу. Поскольку силы N 4 и N 6 перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.

Находим сумму работ остальных активных сил и сил инерции.

.
Подставляем выражения для сил инерции и применяем кинематические соотношения.

.
Сокращаем на δS 5 и преобразовываем.

.
Подставляем численные значения.

;
;
м/с 2 .

Автор: Олег Одинцов . Опубликовано: 02-08-2015

Общее уравнение динамики

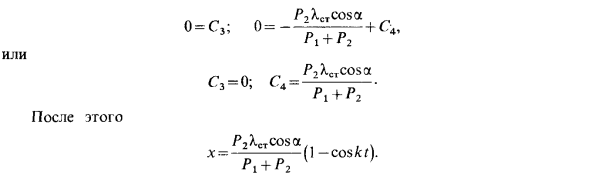
Общее уравнение динамики

  • Соответствует балансу сил в каждой точке системы в соответствии с принципом Дарренва: механическая система, активная сила, объединенная сила реакции и сила инерции. Fk + Lk + Fk = 0, k = 1, 2, …, N, (23) Где Гк — активная сила. Rk — сила реакции связи; Фк — сила инерции точки. Умножение каждого из этих соотношений на возможное смещение точки 8rk на скаляр и суммирование всех точек в системе дает: ДFk ^ k + ДFk-8rk + ДФк • 8гк = 0. (24) Это общее уравнение динамики связанных систем. Обычно используется для систем с полной связью. * 5? * = 0- В этом случае (24) принимает одну из следующих форм (W) • «.» 0; (Ft-mta *) • 8rt = 0; D (^ — Людмила Фирмаль

В случае равновесия системы, если все силы инерции системы указывают на ноль, мы переходим к принципу статического возможного смещения без доказательства достаточности равновесия системы. Уравнениям общей динамики могут быть даны другие эквивалентные формы. Выявление скалярного произведения векторов можно выразить как: £ + ® „) Sy + (A, + Φ,.) 6 -.] — 0. Где xk, yk, zk — координаты k-й точки в системе. Учтите, что проекция сил инерции на оси координат за счет проекции ускорения на эти оси выражается следующей зависимостью: F * x =

тках = -тхх; Fku = -tkaku = -tkuk, F4; = -tkakg = -mkzk, общее уравнение для динамики дано в виде £ [(Ffc, -mjkxJk) 8xlk + (fi, -Wl | kA) 8 No. + (Fte-m) tfJk) 8zjk] = 0. (25 ‘).

В таком виде оно называется общим уравнением динамики в аналитическом виде. Общие уравнения для динамики систем, подверженных голономным и идеальным неразрывным связям, дают полную информацию о поведении таких систем. Это похоже на это. Вы можете получить полную систему дифференциальных уравнений о том, как равновесное состояние системы получается из принципа возможного смещения. Вывод этих уравнений требует использования обобщенных координат и обобщенных концепций сил. Предположим, у вас есть система, которая зависит от голономного, идеального, неизданного соединения.

Предположим, что положение в пространстве определяется обобщенными координатами qt, q2, …. q „, поскольку степень свободы равна n. Радиус-вектор каждой точки системы в общем случае нестационарных соотношений равен Обобщенные координаты и время, т. Е. ^ = M * (? 1, qz, nn, 0. (26) Потому что время считается неизменным. После подстановки (26) в общее динамическое уравнение (25) и изменения порядка сумм k и i получается следующее. к. (27) Используйте активную силу O, обобщенную силу O и силу инерции 21F ‘. (28) 4 = 1 * ‘? * = 1 001 Из (27) получите общее динамическое уравнение в следующем формате: Z (e (+ e> φ,) 8 ?. = ° — (29) Обобщенные координаты системы независимы. Эти изменения координат не только независимы, но и необязательны.

Предполагая, что только одна из обобщенных вариаций координат не равна нулю, а все остальные равны нулю, (29) дает следующую условную систему: 0 (+0! Φ) = 0, r = 1, 2, … и т. Д. (30) Условие (30) называется принципом Даламбера системы и выражается обобщенной силой. Условие уравнения для системы b следует (30), = 0, α = 1, 2, …, n, если сила инерции точки системы и, следовательно, обобщенная сила инерции, равна нулю. При использовании общих динамических уравнений необходимо уметь рассчитывать основную работу сил инерции системы при возможных смещениях. Для этого используется формула, соответствующая полученной работе начальной школы Для нормальной мощности.

  • Рассмотрим приложение к силе инерции твердого тела для определенного движения. Поступательное движение. В этом случае тело имеет три степени свободы и принудительно соединено, поэтому может выполняться только поступательное движение. Движение тела, которое обеспечивает связь, также является поступательным движением. Инерционная сила при переносе уменьшается до результирующего Ф * = -Мас = -Ма. Для суммы основной работы силы инерции на возможность поступательного движения тела, ггйгй = = Φ * 8 8s = * * -8r = -L / d-8g, Где 8gs = 8g — возможное смещение центра тяжести и любой точки тела, потому что переводимое смещение одинаково во всех точках тела. Ускорение такое же, то есть как есть. Когда тело вращается вокруг фиксированной оси. Тело в этом случае имеет одну степень свободы.

Он может вращаться вокруг неподвижной оси Oz. Возможные перемещения, которые возможны благодаря наложенному соединению, такие же, как и вращение тела на базовый угол 8 (когда центр тяжести выбран в качестве центра торможения). Сумма основных сил инерции возможных инерционных перемещений на плоскости является основной работой главного вектора сил инерции = -массовая работа возможного движения центра масс и основной относительно оси Cz через центр масс Основной момент инерции общего вращательного движения сводится к работе элемента.

Следовательно, в этом случае ось ротора будет оставаться направленной на одну и ту же звезду и для наблюдателя, находящегося на Земле, она будет следовать за звездой в ее суточном движении. Людмила Фирмаль

В этом случае ненулевую базовую работу можно выполнить, только проецируя главный момент инерции на ось Cz, т.е. L $, = -JCze. Так что в рассматриваемом случае, ZФ * ’8г * = Ф-5гс + 1, . 8 , При повороте на базовый угол 8 ; z2 = 2Zcos «p. Изменяя эти зависимости, есть: 8.V] = Zcos ; Sz2 = -Zsin ; 8z2 = -2Zsin , оно становится следующим. — (Z1 + Zsinq>) «e2Z cosip-Z’sinip -cZsinipcosip -gsin 3-PTg -Qtg = официальный 1 приложение Система, предполагая, что координата FL-z постоянна, нам нужно вычислить инерцию смещения точки_ при изменении координаты x.

Поскольку мы дали 6x возможных движений в направлении увеличения координаты x, уравнение (b) 0! = O, сила тяжести Pt, P2 перпендикулярна возможному движению, сила упругости (одна добавляется к нагрузке, другая изначально равна, но направление противоположно), к призме точки крепления пружины ) В сумме приведем базовую работу, равную нулю с константой s. Для каждой обобщенной силы инерции -F18l-Ф2.8й. P, x + P2 (от cosa + x) Q * ‘= — = — (Ф 、 + Ф2 、) = —————!

= 8 раз Призма инерции Доска У нас есть @ P2sina83 — F6s Суммированная река Сена По возрастающей координате z всегда вычисляется по формуле.

Если s рассчитывается из положения статического равновесия нагрузки B, поскольку сила упругости F = cX = c (XCI + 3), HS — статическое растяжение пружины под действием силы тяжести. Равновесие. В положении Статика удовлетворяет условию Равновесие. Обобщенные Инерция у нас есть интеграция (A) Получите следующее Константа С, Synaf + cj, условия Со второй интеграцией x = -L ^^ lcoskt + Cjt + Cf — (S-h-xcosa), г Где Ф2 — проекция инерции нагрузки B на ось.

Подставьте полученное значение обобщенной системы нагнетания для дифференциального уравнения. Исключите следующее выражение для s из второго выражения: P2 [P | + P2 (1-интеграция (r), получить s

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

источники:

http://1cov-edu.ru/mehanika/dinamika-tel/obschee-uravnenie-dinamiki-primer-resheniya-zadachi/

http://lfirmal.com/obshchee-uravnenie-dinamiki/

Источник

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Первая часть: «Введение в теорию автоматического управления. Основные понятия теории управления техническим системами»

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

Рис. 2.1.1 – Схематическое представление САУ (звена)

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

$left[ begin{gathered} y(t) =y_0 + Delta y(t)\ u(t) = u_0 + Delta u(t)\ end{gathered} right.$

где:

$y_0,u_0$ — стационарные значения входного и выходного воздействий;

$Delta y, Delta u$ — отклонения от станционара, соотвесвенно.

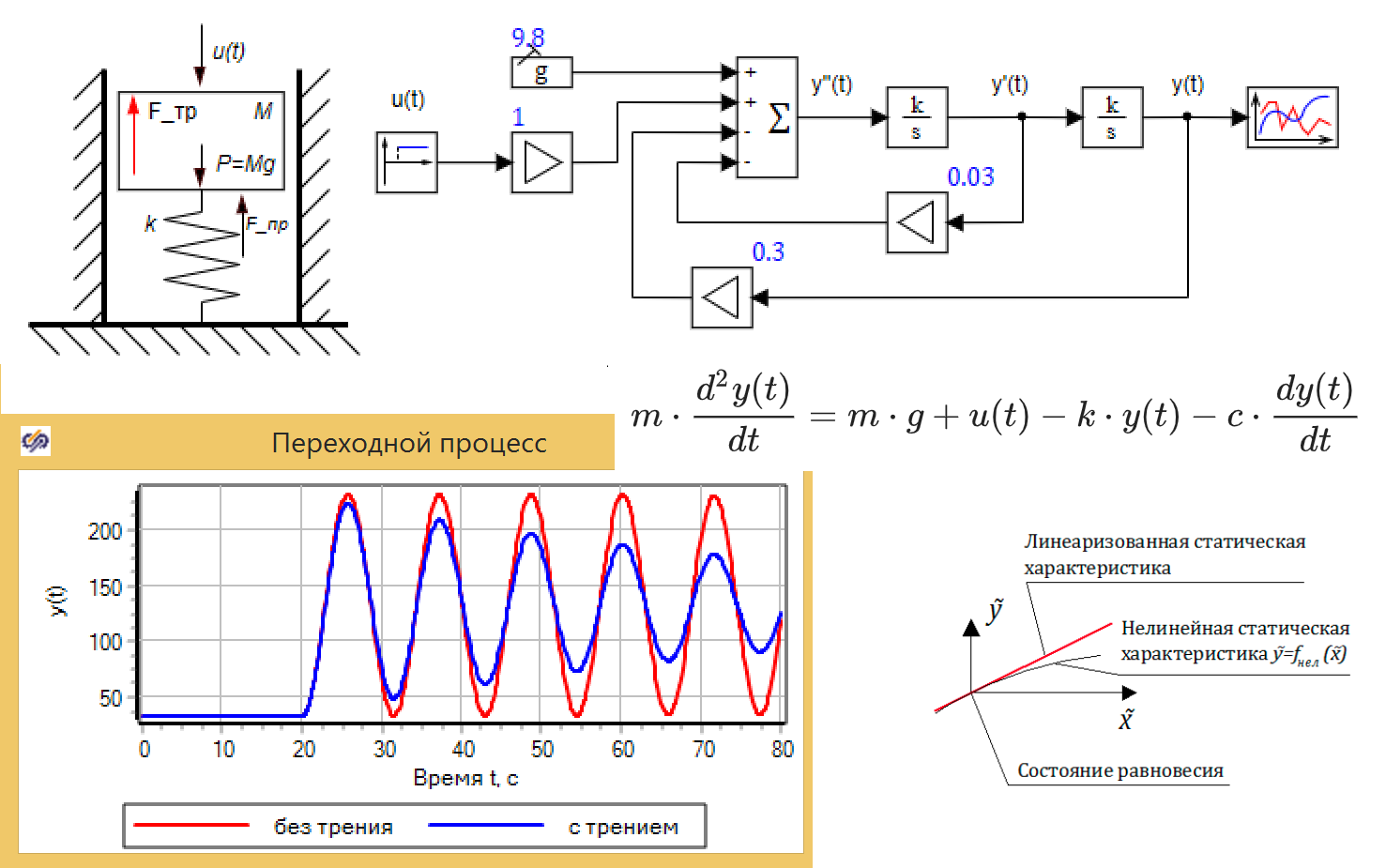
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Рис. 2.1.2 – Механический демпфер

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

$m cdot frac{d^2 y(t)}{dt} = sum F_j mathbf{(2.1.1)}$

где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

$m cdot frac{d^2y(t)}{dt} = mcdot g+ u(t) - k cdot y(t) - c cdot frac{dy(t)}{dt} mathbf{(2.1.2)}$

где $mcdot g$ — сила тяжести; $k cdot y(t)$ — сила сопротивления пружины, $c cdot frac{dy(t)}{dt}$ — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

$m cdot g Rightarrow [frac{кг cdot м}{ с^2}]; c Rightarrow [frac{кг}{с}]; k Rightarrow [frac{кг}{с^2}]$

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

$left { begin{eqnarray} t &le 0 \ u(t) &= u_0\ y(t) &= y_0\ end{eqnarray} right.$

перейдем к отклонениям от стационарного состояния:
Пусть при t>0

$left[ begin{gathered} y(t) =y_0 + Delta y(t); u(t) = u_0 + Delta u(t);\ y'(t) = [Delta y(t)]'; y''(t) =[Delta y(t)]''\ end{gathered} right.$. Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

$m cdot frac{d^2Delta y(t)}{dt^2} = m cdot g - k cdot y_0- k cdot Delta y(t) - cfrac{dDelta y(t)}{dt} mathbf{(2.1.3)}$

если

$t le 0$, то уравнение принимает вид:

$0 = m cdot g+u_0 - k cdot y_0 mathbf{(2.1.4)}$

или

$y_0 = frac{1}{k} cdot[u_0+m cdot g] mathbf{(2.1.5)}$

Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Рис. 2.1.3 – Статическая характеристика механического демпфера

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

$mcdot frac{d^2 Delta y(t)}{dt^2} = Delta u(t) - k cdot Delta y(t) - c cdot frac{d Delta y(y)}{dt}, $

тогда, разделив на k, имеем:

$T_2^2 cdot frac{d^2 Delta y(t)}{dt^2}+ T_1 cdot frac{d Delta y(t)}{dt} + Delta y(t) = k_1 cdot Delta u(t) mathbf{(2.1.6)}$

где:

$T_2^2= frac{m}{k}; T_1= frac{c}{k}; k_1=frac{1}{k}.$

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

$T_1 = frac{c}{k} Rightarrow [frac{кг cdot c^2}{c cdot кг}] = [c]$

$T_2^2 = frac{m}{k} Rightarrow [frac{кг cdot c^2}{kg}] =[c^2]$

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [$c^2$];
— коэффициент в правой части ($k_1$): [$frac{c^2}{кг}$].
Тогда уравнение (2.1.6) можно записать в операторной форме:

$(T_2^2 cdot p^2 + T_1 cdot p+1)Delta y(t) = k_1 Delta u(t)$, что эквивалентно

$L(p)Delta y(t) = N(p) Delta u(t) mathbf{(2.1.6.а)}$

где:

$p= frac{d}{dt}$ — оператор диффренцирования;

$L(p) = T_2^2 cdot p^2 + T cdot p + 1$ -линейный дифференциальный оператор;

$L(p)$

$N(p)$ — линейный дифференциальный оператор, вырожденный в константу, равную

$k_1$.

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

$left[ begin{gathered} widetilde y(t) = frac {y(t)-y_0}{y_0} = frac {Delta y(t)}{y_0}\ widetilde u(t) = frac {u(t)-u_0}{u_0} =frac {Delta u(t)}{u_0}\ end{gathered} right. Rightarrow left[ begin{gathered} y(t) =y_0 cdot [1+ widetilde y(t)]\ u(t) = u_0 cdot [1+ widetilde u(t)]\ end{gathered} right. Rightarrow left[ begin{gathered} y'(t) =y_0 cdot widetilde y(t)'\ y''(t) = y_0 cdot widetilde y(t)''\ end{gathered} right. $

Подставляя эти соотношения в уравнение (2.1.2), имеем:

$m cdot y_0 cdot frac{d^2 widetilde y(t)}{dt^2} = m cdot g +u_0 cdot[1+widetilde u(t)] -k cdot y_0 cdot[1+widetilde y(t)] - c cdot y_0 cdot frac{d widetilde y(t)}{dt}; или$

$m cdot y_0 cdot frac{d^2 widetilde y(t)}{dt^2} = underline {m cdot g} + underline {u_0} +u_0 cdot widetilde u(t) - underline {k cdot y_0} - k cdot y_0 cdot widetilde y(t) - c cdot y_0 cdot frac{d widetilde y(t)}{dt}.$

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие

$widetilde y(t)$, и, разделив на

$k cdot y_0$, получаем:

$frac{m cdot y_0}{k cdot y_0} cdot frac{d^2 widetilde y(t)}{dt^2} + frac {c cdot y_0}{k cdot y_0} cdot frac{d widetilde y(t)}{dt} +widetilde y(t)= frac{u_0}{k cdot y_0} cdot widetilde u(t) Rightarrow $

$(T_2^2 cdot p^2 + T cdot p + 1) cdot widetilde y(t) = k_x cdot widetilde u(t) mathbf{(2.1.7)}$

где:

$T_2^2= frac{m}{k}; T_1= frac{c}{k}; k_x=frac{u_0}{k cdot y_0} $ — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента $k_x$

$left[frac{кг cdot м}{с^2} cdot frac{c^2}{кг} cdot frac{1}{м}right] =[1].$

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Рис. 2.1.4 – Статические характеристики механического демпфера

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

$L(p) cdot widetilde y(t) = N(p) cdot widetilde u(t) mathbf{(2.1.8)}$

где

$L(p), N(p) - $ дифференциальные операторы.

Если дифференциальные операторы $L(p), N(p) - $ — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если $L(p), N(p) - $ – нелинейные дифференциальные операторы, или $widetilde y_{stat} neq k cdot widetilde u_{stat}$, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

  1. Нелинейностью статической характеристики.
  2. Нелинейностью динамических членов в уравнениях динамики.
  3. Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 << 1, и поэтому уравнения динамики ядерного реактора, в принципе, могут быть линеаризованы.

Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Рис. 2.2.2 – Звено САР

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

$L(p) cdot y(t) = N(p) cdot u(t) mathbf{(2.2.1)}$

Перенесем $N(p) u(t)$ в левую часть уравнения и запишем уравнение в виде%

$F(y,y',y'',...y^{n}, u, u',u'', ...u^m,t)=0 mathbf{(2.2.2)}$

где $F$ -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

$y'=y''=...y^n=u'=u''=...u^m=0 Rightarrow F(y_0,u_0)=0 mathbf{(2.2.3)}$

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния $(y_0, u_0)$.

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если $y = f(x)$, то «простое» разложение функции в ряд Тейлора в окрестности точки $x = x_0$ будет выглядеть так:

$ begin{eqnarray} y(x) = f(x) = f(x_0)+ frac{1}{1!} cdot left( frac{df}{dx}right)_{x=x_0} cdot (x-x_0)+ frac{1}{2!} cdot left( frac{d^2f}{dx^2} right)_{x=x_0} cdot (x-x_0)^2 +\ ...+frac{1}{n!} cdot left( frac{d^nf}{dx^n} right)_{x=x_0} cdot (x-x_0)^n end{eqnarray}$

C учетом вышеприведенного разложение принимает вид:

$begin{eqnarray} F(y,y',y'',...y^{n}, u, u', ...u^m,t) = F(y_0,u_0)+frac{1}{1!}cdot left( frac{partial F}{partial y}right)_{ y=y_0;u =u_0 } cdot (y-y_0)+\ + frac{1}{2!} cdot left( frac{partial^2F}{partial y^2}right)_{y=y_0;u =u_0}cdot (y-y_0)^2+frac{1}{3!} cdot left( frac{partial^3F}{partial y^3}right)_{y=y_0;u =u_0}cdot (y-y_0)^3 +..\+frac{1}{k!} cdot left( frac{partial^kF}{partial y^k}right)_{y=y_0;u =u_0}cdot (y-y_0)^k+ frac{1}{1!}cdot left( frac{partial F}{partial y'}right)_{ 0 } cdot (y') +frac{1}{2!}cdot left( frac{partial^2F}{partial(y')^2}right)_{ 0 } cdot (y')^2+\ ..+frac{1}{1!}cdot left( frac{ partial F}{partial y^{(n)}}right)_{ 0 } cdot (y^{(n)})+ frac{1}{2!}cdot left( frac{partial ^2F}{partial(y^{n})^2}right)_{ 0 } cdot (y^{(n)})^2+..\ ..+frac{1}{1!}cdot left( frac{partial F}{partial u}right)_{ 0 } cdot (u-u_0)+frac{1}{2!} cdot left( frac{partial^2F}{partial u^2}right)_{0}cdot (u-u_0)^2+..\ ..+frac{1}{k!}cdot left( frac{partial^kF}{partial(u^{m})^k}right)_{ 0 } cdot (u^{(m)})^k+.. end{eqnarray}$

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:$frac{Delta y(t)}{y_0} <<1; frac{Delta u(t)}{u_0} <<1;$), оставим в разложении только члены первого порядка малости (линейные). Поскольку $[y(t)-y_0] equiv Delta y(t); y'(t) = [y_0+Delta y(t)]' = (Delta y(t))'$, получаем:

$ F(y,y',y''..y^{(n)},u,u',u''..u^{m},t)simeq left( frac{partial F}{partial y} right)_0cdot Delta y+left(frac{partial F}{partial y'}right)_0 cdot (Delta y)' +left(frac{partial F}{partial y''}right)_0 cdot (Delta y)''+..\ ..+left(frac{partial F}{partial u}right)_0 cdot Delta u+ left(frac{partial F}{partial u'}right)_0 cdot (Delta u)' + left(frac{partial F}{partial u''}right)_0 cdot (Delta u)''+..+ left(frac{partial F}{partial u^{m}}right)_0 cdot (Delta u)^{(m)} mathbf{(2.2.4)}$

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

$a_n^0 cdot frac{d^{(n)}}{dt^n} Delta y +a_{n-1}^0 cdot frac{d^{(n-1)}}{dt^{n-1}} Delta y +..+a_{1}^0 cdot frac{d}{dt} Delta y +a_{0}^0cdotDelta y = \ =b_m^0 cdot frac{d^{(m)}}{dt^m} Delta u +b_{m-1}^0 cdot frac{d^{(m-1)}}{dt^{m-1}} Delta u +..+b_{1}^0 cdot frac{d}{dt} Delta u +b_{0}^0cdotDelta u mathbf{(2.2.5)}$

где:

$a_0^0= left( frac{partial F}{partial y} right)_{y =y_0;u =u_0};a_1^0= left( frac{partial F}{partial y'} right)_{y =y_0;u =u_0}; ...a_n^0= left( frac{partial F}{partial y^{(n)}} right)_{y =y_0;u =u_0} ; \ b_0^0= left( frac{partial F}{partial u} right)_{y =y_0;u =u_0};b_1^0= left( frac{partial F}{partial u'} right)_{y =y_0;u =u_0}; ...b_m^0= left( frac{partial F}{partial u^{(m)}} right)_{y =y_0;u =u_0}.$

Коэффициенты $a_i^0, b_j^0$ — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

$L(p)cdotDelta y(t) = N(p) cdot Delta u(t) mathbf{(2.2.6)}$

где

$p = frac{partial }{partial t}$ – оператор дифференцирования;

$L(p)$ — линейный дифференциальный оператор степени n;

$N(p)$ — линейный дифференциальный оператор степени m, причем обычно порядок оператора

$L(p)$ выше порядка оператора

$N(p)$:

$ n ≥ m.$

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов $a_i^0, b_j^0$ может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) $(y_0, u_0)$ и выполнив некоторые преобразования, получаем:

$a_n^* cdot tilde{y}^{(n)} +a_{(n-1)}^* cdot tilde{y}^{(n-1)} +..+a_1^* cdot tilde{y}'+a_0^* cdot tilde{y} = \ =b_m^* cdot tilde{u}^{(m)} +b_{(m-1)}^* cdot tilde{u}^{(m-1)} +..+b_1^* cdot tilde{u}'+b_0^* cdot tilde{u} mathbf{(2.2.7)}$

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

$[a_0^*] = [1] ; [a_1^*]= [c]; [a_2^*]= [c^2]; [a_3^*]= [c^3];...[a_n^*]= [c^n]\ [b_0^*] = [1] ; [b_1^*]= [c]; [b_2^*]= [c^2]; [b_3^*]= [b^3];...[b_m^*]= [c^m]$

Если вынести в правой части (2.2.7) коэффициент $b_0^*$ за общую скобку и разделить все уравнение на $a_0^*$, то уравнение принимает вид:

$a_n cdot tilde{y}^{(n)} +a_{(n-1)}cdot tilde{y}^{(n-1)} +..+a_1cdot tilde{y}'+tilde{y} = \ =k cdot [b_m cdot tilde{u}^{(m)} +b_{(m-1)} cdot tilde{u}^{(m-1)} +..+b_1 cdot tilde{u}'+ tilde{u}] mathbf{(2.2.8)}$

где:

$a_n = frac{a_n^*}{a_0^*}; a_{n-1} = frac{a_{n-1}^*}{a_0^*}; ...a_{1} = frac{a_{1}^*}{a_0^*}; k = frac{b_0^*}{a_0^*} \ b_n = frac{b_n^*}{b_0^*}; b_{n-1} = frac{b_{n-1}^*}{b_0^*}; ...b_{1} = frac{b_{1}^*}{b_0^*}; $

или в операторном виде:

$(a_n cdot p^{(n)} +a_{(n-1)}cdot p^{(n-1)} +..+a_1cdot p'+1) cdot tilde{y} = \ =k cdot (b_m cdot p^{(m)} +b_{(m-1)} cdot p^{(m-1)} +..+b_1 cdot tilde{u}'+ 1)cdot tilde{u}\ L(p)cdot tilde{y} =k cdot N(p) cdot tilde{u} mathbf{(2.2.9)}$

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

$Если t ≤ 0 Rightarrow left[ begin{gathered} tilde {y}(t) = tilde {y}(0) =0;\ tilde u(t) = tilde u(0) = 0.\ end{gathered} right.$

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:

$a_3^0 cdot y'''(t) +a_2^0 cdot y''(t)+a_1^0 cdot y'(t) cdot[y(t)-d]+ a_2^0 cdot y^2(t)=b_1^0 cdot x'(t) +b_0^0 cdot x(t); $

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

$a_0^0 cdot y^2(0) = b_0^0 cdot x(0); Rightarrow y_0 = sqrt{frac{b_0^0}{a_0^0} cdot x_0} = sqrt {k_0 cdot x_0}$

Рис. 2.2.3 – Линеаризации статической характеристики

• во-вторых, слагаемое в левой части $a_1^0 cdot y'(t) cdot[y(t)-d]$ — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

  1. Перейдем к безразмерным переменным (нормализованным);
  2. Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

$tilde{y}(t) = frac{y(t) - y_0}{y_0}; Rightarrow y(t) = y_0 cdot [1+ tilde{y}(t)]; \ tilde{x}(t) = frac{x(t) - x_0}{x_0}; Rightarrow x(t) = x_0 cdot [1+ tilde{x}(t)].$

Заметим, что:
$x(t) = x_0+ Delta x(t) = x_0+ x_0 cdot tilde{x}(t) и y(t) = y_0+ Delta y(t) = y_0+ y_0 cdot tilde{y}(t)$.

Подставляя значения x(t) и y(t) в исходное уравнение:

$ a_3^0 cdot y_0 cdot tilde y'''(t) +a_2^0 cdot y_0 cdot tilde y''(t)+a_1^0 cdot y_0 cdot tilde y'(t) cdot[y_0+y_0 cdot tilde y(t) -d]+a_0^0 cdot y_0^2 cdot[1+ tilde y(t)]^2 = \ = b_1^0 cdot x_0 cdot tilde x'(t) + b_0^0 cdot х_0 cdot[1+tilde x(t)]; Rightarrow раскрыв скобки Rightarrow \ a_3^0 cdot y_0 cdot tilde y'''(t)+a_2^0 cdot y_0 cdot tilde y''(t)+a_1^0 cdot y_0^2 cdot tilde y'(t) + a_1^0 cdot y_0^2 cdot tilde y'(t) cdot tilde y(t)-a_1^0 cdot y_0 cdot tilde y'(t) cdot d + \ +a_0^0 cdot y_0^2 +2 cdot a_0^0 cdot y_0^2 cdottilde y(t) +a_0^0 cdot y_0^2 cdottilde y(t)^2 = b_1^0 cdot x_0 cdot tilde x'(t) + b_0^0 cdot х_0+ b_0^0 cdot х_0 cdot tilde x(t)];$

Удаляем полученного уравнения уравнения стационара: $a_0^0 cdot y_0^2= b_0^0 cdot х_0$, а так же пренебрегая слагаемыми второго прядка малости: $ a_1^0 cdot y_0^2 cdot tilde y'(t) cdot tilde y(t)$, получаем следующее уравнение:

$ a_3^0 cdot y_0 cdot tilde y'''(t)+a_2^0 cdot y_0 cdot tilde y''(t)+(a_1^0 cdot y_0^2 -a_1^0 cdot y_0 cdot d) cdot tilde y'(t)+2 cdot a_0^0 cdot y_0^2 cdottilde y(t) =\ = b_1^0 cdot x_0 cdot tilde x'(t) + b_0^0 cdot х_0 cdot tilde x(t);$

Вводим новые обозначения:

$a_3^* = a_3^0 cdot y_0 ; a_2^* = a_2^0 cdot y_0; a_1^* = a_1^0 cdot y_0^2 -a_1^0 cdot y_0 cdot d; a_0^* =2 cdot a_0^0 cdot y_0^2; \ b_1^* = b_1^0 cdot x_0; b_0^*=b_0^0 cdot х_0 $

Получаем уравнения в «почти» классическом виде:

$a_3^* cdot tilde y'''(t)+a_2^* cdot tilde y''(t)+a_1^* cdot tilde y'(t)+ a_0^* cdottilde y(t) = b_1^* cdot tilde x'(t) + b_0^* cdot tilde x(t);$

Если в правой части вынести за общую скобку $b_0^*$ и разделить все уравнение на $a_0^*$, то уравнение (линеаризованное) принимает вид:

$a_3 cdot tilde y'''(t)+a_2 cdot tilde y''(t)+a_1 cdot tilde y'(t)+ tilde y(t) = k cdot[ b_1 cdot tilde x'(t) + tilde x(t)]$

где:

$a_3 = frac{a_3^*}{a_0^*}; a_2 = frac{a_2^*}{a_0^*}; a_1 = frac{a_2^*}{a_0^*}; k = frac{b_o^*}{a_0^*}; b_1 = frac{b_1^*}{b_0^*}; $

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

$L(p) cdot y(t) = N(p)*x(t), mathbf{(2.3.1)}\ где: L(p) = a_ncdot p^n + ..+a_1 cdot p + a_0 \ N(p) = b_m cdot p^m+..+b_1 cdot p+b_0 $

Переходя к полной символике, имеем: $Rightarrow$

$a_n cdot y^{(n)}+a_{n-1} cdot y^{(n-1)}+..+a_1 cdot y'+a_{0} = b_m cdot x^{(m)}+b_{n-1} cdot x^{(n-1)}+..+b_1 cdot y'+b_{0} mathbf{(2.3.2)};$

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

Известно, что

$y(t) = y_{общ.}(t)+y_{част.}(t), mathbf{(2.3.3)}$

где: $y_{общ.}(t)$ — решение однородного дифференциального уравнения $L(p) y(t) = 0; $y_{част.}(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения $y_{общ.} = y_{собств.}$, собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть $y_{част.} = y_{вын.}$, вынужденным, так как эта часть решения определяется внешним воздействием $x(t)$, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

$y(t) = y_{собств.}(t)+y_{вын.}(t), mathbf{(2.3.4)}$

Напомним этапы решения:

1) Если имеется уравнение вида $L(p) cdot y(t) = N(p)*x(t)$, то сначала решаем однородное дифференциальное уравнение:

$a_n cdot y^{(n)}+a_{n-1} cdot y^{(n-1)}+..+a_1 cdot y'+a_{0} =0 $

2) Записываем характеристическое уравнение:

$L(lambda) =0; Rightarrow a_n cdot lambda^{n}+a_{n-1} cdot lambda^{n-1}+..+a_1 cdot lambda+a_{0} =0 mathbf{(2.3.5)}$

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения $lambda_i$
4) Тогда собственное решение записывается в виде:

$y_{собств.}(t)=sum_{j=1}^n C_j cdot e^{lambda_j cdot t}, mathbf{(2.3.6)}$

если среди $lambda_i$ нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

$y_{собств.}(t)=sum_{j=1}^{n-2} C_j cdot e^{lambda_{j} cdot t} +C_{n-1} cdot e^{lambda_{n-1} cdot t}cdot [1+C_ncdot t]. mathbf{(2.3.7)}$

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

$y_{собств.}(t)=sum_{j=1}^{n-k} C_j cdot e^{lambda_{j} cdot t} +C_{n+1-k} cdot e^{lambda_{n+1-k} cdot t}cdot [1+C_{n+2-k}cdot t+C_{n+3-k}cdot t^2+.. \ ..+C_{n}cdot t^{k-1}]. mathbf{(2.3.8)}$

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. $y_{вын.}(t) = f_{вын}(t)$.

6) Суммируя полученные составляющие (собственную и вынужденную), имеем: $Rightarrow$

$y_{полн.}(t)=sum_{j=1}^n C_j cdot e^{lambda_j cdot t} + f_{вын}(t).$

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования $C_j$. $Rightarrow$ Обычно получается система алгебраических уравнений. $Rightarrow$ Решая систему, находим значения постоянных интегрирования $C_j$

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

$left{ begin{gathered} 2 cdot y''(t)+5 cdot y'(t)+2 cdot y(t) =1- e^{-t}\ Начальные условия t = 0; Rightarrow y(0) = 0; y'(0) =0. end{gathered} right.$

Решение. $Rightarrow$ Запишем однородное ОДУ: $2 cdot y''(t)+5 cdot y'(t)+2 cdot y(t) =0$
Характеристическое уравнение имеет вид: $2 cdot lambda ^2+5 cdot lambda+2 = 0$; Решая, имеем: $lambda_1 = -2; lambda = 0.5,$ тогда:

$y_{соб} = С_1 cdot e^{-2 cdot t}+С_2 cdot e^{-0.5 cdot t},$

где

$С_1, С_2$ — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем $y_{вын}(t)$ как:

$у_{вын}(t) =A+B cdot e^{-t} Rightarrow у_{вын}'(t) = -Bcdot e^{-t} Rightarrow у_{вын}''(t) = Bcdot e^{-t} $

Подставляя в исходное уравнение, имеем:

$2cdot B cdot e^{-t} - 5 cdot B cdot e^{-t}+2cdot A +2 cdot B cdot e^{-t} =1 - e^{-t} Rightarrow left{ begin{gathered} 2 cdot A =1\ -B = -1 end{gathered} right. Rightarrow\ Rightarrow left{ begin{gathered} A = frac{1}{2}\ B = 1 end{gathered} right. Rightarrow y_{вын.}(t) = frac{1}{2} -e^{-t};$

Суммируя $y_{соб}, y_{вын}$, имеем: $y(е) = С_1 cdot e^{-2 cdot t}+С_2 cdot e^{-0.5 cdot t}+frac{1}{2}+ e^{-t}.$

Используя 1-е начальное условие (при t = 0), получаем: $0 =C_1+C_2+0.5+1$, а из 2-го начального условия имеем: $0 = -2 cdot C_1 - 0.5 cdot C_2 -1.$

Решая систему уравнений относительно $С_1$ и $С_2$, имеем: $С_1 = -1/6; C_2 = -4/3. $
Тогда окончательно:

$y(t) = - frac{1}{6} e^{-2t}- frac{4}{3} e^{-0.5t}+frac{1}{2}+e^{-t};$

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

$2 cdot y''(t)+5 cdot y'(t)+2 cdot y(t) =1- e^{-t} Rightarrow \ Rightarrow y''(t) = 0.5 - 0.5cdot e^{-t} - 2.5 cdot y'(t)- y(t)$

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).


Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

Рис. 2.3.2 – Решение уравнения динамики

Ссылки по теме:

  1. Википедия про ряд Тейлора
  2. Дифференциальные уравнения на Match24.ru
  3. Пример создания модели груза на пружине.
  4. Начало лекций здесь: Введение в теорию автоматического управления. Основные понятия теории управления техническим системами.
  5. Следующая часть здесь: Математическое описание систем автоматического управления. ч. 2.2 — 2.8

Продолжениее: Математическое описание систем автоматического управления. 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (РЕГУЛИРОВАНИЯ).
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ.
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.
3.3. Апериодическое звено 1–го порядка (инерционное звено). На примере входной камеры ядерного реактора.
3.4. Апериодическое звено 2-го порядка.
3.5. Колебательное звено.
3.6. Инерционно-дифференцирующее звено.
3.7. Форсирующее звено.
3.8. Инерционно-интегрирующее (звено интегрирующее звено с замедлением).
3.9 Изодромное звено (изодром).

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти скрытую карту тинькофф
  • Как составить деловую речь
  • Как я могу исправить свои слабые стороны
  • Как найти хорошего психиатра в москве форум
  • Как найти хорошую дружбу