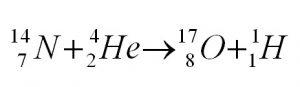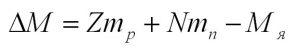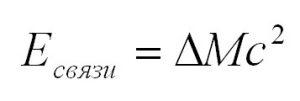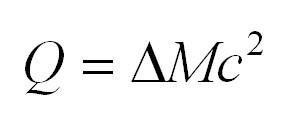Как составить уравнение ядерной реакции - Исправление недочетов и поиск решений вместе с Examum.ru

Примеры ядерных реакций: особенности, решение и формулы

На протяжении долгого времени человека не оставляли мечты о взаимопревращении элементов – точнее, о превращении различных металлов в один. После осознания бесплодности этих попыток утвердилась точка зрения о незыблемости химических элементов. И только открытие структуры ядра в начале XX века показало, что превращение элементов один в другой возможно – но не химическими методами, то есть воздействием на внешние электронные оболочки атомов, а путем вмешательства в структуру атомного ядра. Такого рода явления (и некоторые другие) относятся к ядерным реакциям, примеры которых будут рассмотрены ниже. Но прежде необходимо вспомнить о некоторых основных понятиях, которые потребуются в ходе этого рассмотрения.

Общее понятие о ядерных реакциях

Вам будет интересно: Ацетон: состав и свойства

Существуют явления, в которых ядро атома того или иного элемента вступает во взаимодействие с другим ядром или какой-либо элементарной частицей, то есть обменивается с ними энергией и импульсом. Подобные процессы и называются ядерными реакциями. Результатом их может стать изменение состава ядра или образование новых ядер с испусканием определенных частиц. При этом возможны такие варианты, как:

превращение одного химического элемента в другой;
деление ядра;
синтез, то есть слияние ядер, при котором образуется ядро более тяжелого элемента.

Вам будет интересно: Что такое главные члены предложения и второстепенные члены предложений?

Начальная фаза реакции, определяемая типом и состоянием вступающих в нее частиц, называется входным каналом. Выходные каналы – это возможные пути, по которым реакция будет протекать.

Правила записи ядерных реакций

В примерах, приведенных ниже, демонстрируются способы, с помощью которых принято описывать реакции с участием ядер и элементарных частиц.

Первый способ – тот же, что применяется в химии: в левой части ставятся исходные частицы, в правой – продукты реакции. Например, взаимодействие ядра бериллия-9 с налетающей альфа-частицей (так называемая реакция открытия нейтрона) записывается следующим образом:

94Be + 42He → 126C + 10n.

Верхние индексы обозначают количество нуклонов, то есть массовые числа ядер, нижние – количество протонов, то есть атомные номера. Суммы тех и других в левой и правой части должны совпадать.

Вам будет интересно: Что такое дисциплина: описание, задачи, методы

Сокращенный способ написания уравнений ядерных реакций, часто применяющийся в физике, выглядит так:

Общий вид такой записи: A (a, b1b2…) B. Здесь A – ядро-мишень; a – налетающая частица или ядро; b1, b2 и так далее – легкие продукты реакции; B – конечное ядро.

Энергетика ядерных реакций

В ядерных превращениях выполняется закон сохранения энергии (наряду с другими законами сохранения). При этом кинетическая энергия частиц во входном и выходном канале реакции могут различаться за счет изменения энергии покоя. Так как последняя эквивалентна массе частиц, до и после реакции массы также будут неодинаковы. Но полная энергия системы всегда сохраняется.

Разность энергии покоя вступающих в реакцию и выходящих из нее частиц называется энергетическим выходом и выражается в изменении их кинетической энергии.

В процессах с участием ядер задействуются три вида фундаментальных взаимодействий – электромагнитное, слабое и сильное. Благодаря последнему ядро обладает такой важнейшей особенностью, как высокая энергия связи между составляющими его частицами. Она существенно выше, чем, например, между ядром и атомными электронами или между атомами в молекулах. Об этом свидетельствует заметный дефект массы – разница между суммой масс нуклонов и массой ядра, которая всегда меньше на величину, пропорциональную энергии связи: Δm = Eсв/c2. Расчет дефекта массы производится по простой формуле Δm = Zmp + Amn – Мя, где Z – заряд ядра, A – массовое число, mp – масса протона (1,00728 а.е.м.), mn – масса нейтрона (1,00866 а.е.м.), Mя – масса ядра.

При описании ядерных реакций используется понятие удельной энергии связи (то есть в расчете на один нуклон: Δmc2/A).

Энергия связи и стабильность ядер

Наибольшей устойчивостью, то есть наивысшей удельной энергией связи, отличаются ядра с массовым числом от 50 до 90, например, железо. Такой «пик стабильности» обусловлен нецентральным характером ядерных сил. Поскольку каждый нуклон взаимодействует только с соседями, на поверхности ядра он связан слабее, нежели внутри. Чем меньше в ядре взаимодействующих нуклонов, тем меньше и энергия связи, поэтому легкие ядра менее стабильны. В свою очередь, с ростом количества частиц в ядре возрастают кулоновские силы отталкивания между протонами, так что энергия связи тяжелых ядер тоже уменьшается.

Таким образом, для легких ядер наиболее вероятными, то есть энергетически выгодными, являются реакции слияния с формированием устойчивого ядра средней массы, для тяжелых же – напротив, процессы распада и деления (нередко многоступенчатые), в результате которых также образуются более стабильные продукты. Этим реакциям свойственен положительный и часто очень высокий энергетический выход, сопровождающий увеличение энергии связи.

Вам будет интересно: Пополняем словарный запас: дискредитация — это.

Ниже мы рассмотрим некоторые примеры ядерных реакций.

Реакции распада

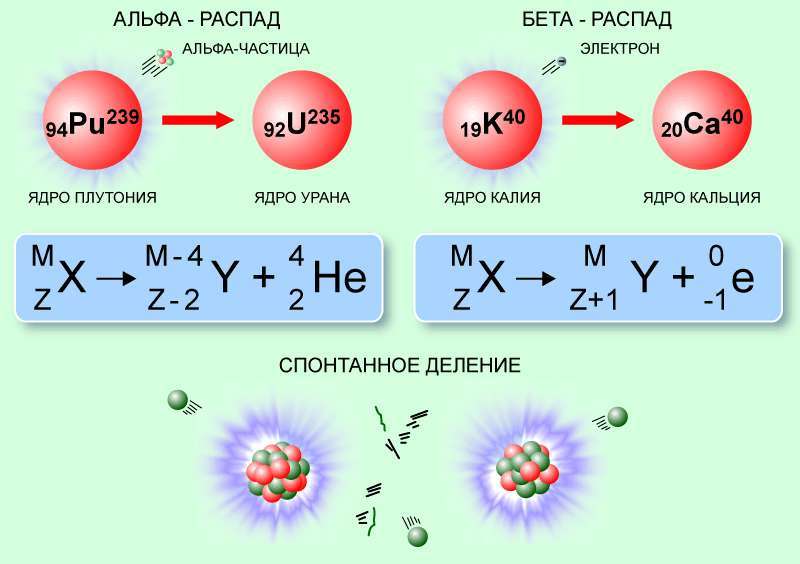
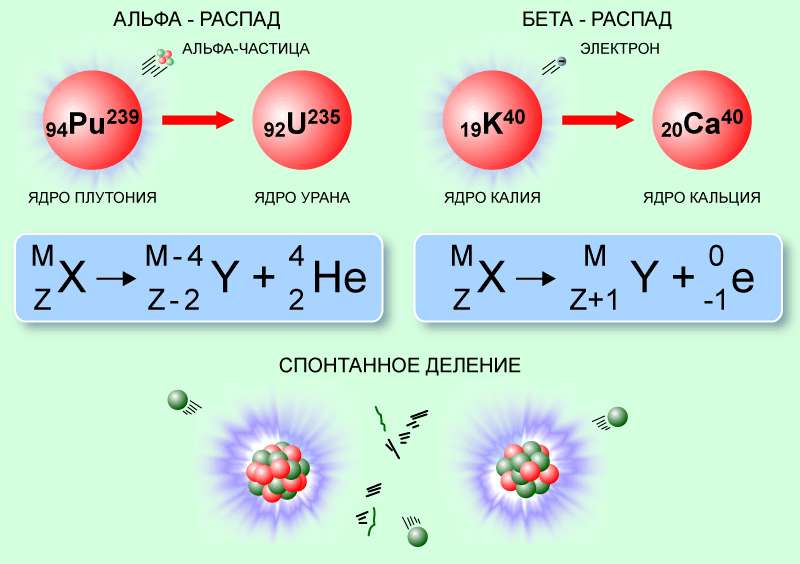
Ядра могут претерпевать спонтанное изменение состава и структуры, при которых происходит испускание каких-либо элементарных частиц или фрагментов ядра, таких как альфа-частицы или более тяжелые кластеры.

Так, при альфа-распаде, возможном благодаря квантовому туннелированию, альфа-частица преодолевает потенциальный барьер ядерных сил и покидает материнское ядро, которое, соответственно, уменьшает атомный номер на 2, а массовое число – на 4. Например, ядро радия-226, испуская альфа-частицу, превращается в радон-222:

22688Ra → 22286Rn + α (42He).

Энергия распада ядра радия-226 составляет около 4,87 МэВ.

Бета-распад, обусловленный слабым взаимодействием, происходит без изменения количества нуклонов (массового числа), но с увеличением или уменьшением заряда ядра на 1, при испускании антинейтрино или нейтрино, а также электрона или позитрона. Примером ядерной реакции данного типа является бета-плюс-распад фтора-18. Здесь один из протонов ядра превращается в нейтрон, излучаются позитрон и нейтрино, а фтор превращается в кислород-18:

189K → 188Ar + e+ + νe.

Энергия бета-распада фтора-18 – около 0,63 МэВ.

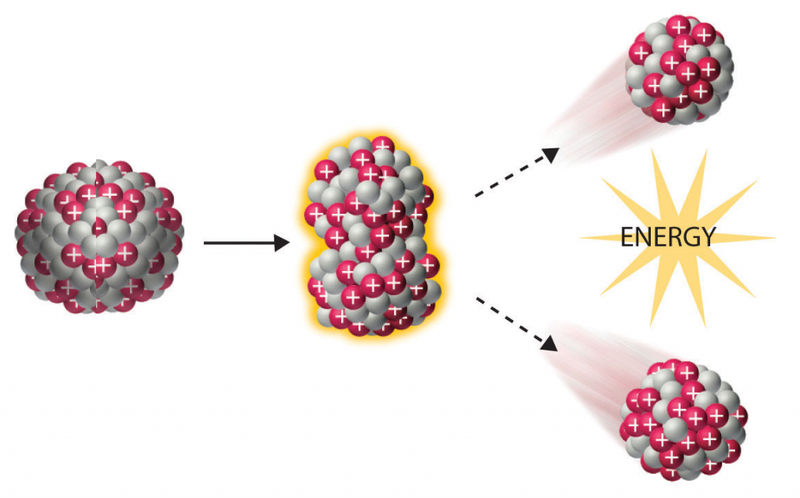
Деление ядер

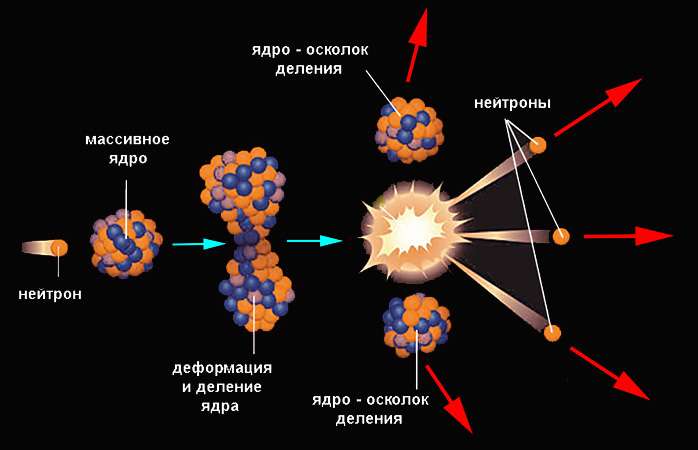
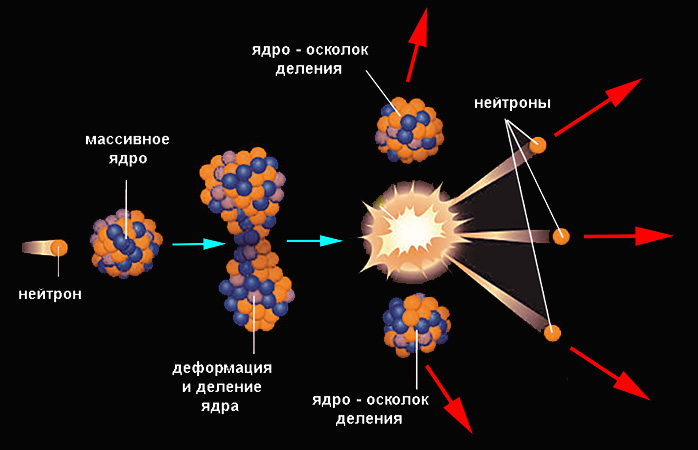
Гораздо больший энергетический выход имеют реакции деления. Так называется процесс, при котором ядро самопроизвольно или вынужденно распадается на близкие по массе осколки (как правило, два, редко – три) и некоторые более легкие продукты. Ядро делится, если его потенциальная энергия превысит исходное значение на некоторую величину, называемую барьером деления. Однако вероятность спонтанного процесса даже для тяжелых ядер невелика.

Она существенно возрастает при получении ядром соответствующей энергии извне (при попадании в него частицы). Наиболее легко проникает в ядро нейтрон, поскольку он не подвержен силам электростатического отталкивания. Попадание нейтрона приводит к повышению внутренней энергии ядра, оно деформируется с образованием перетяжки и делится. Осколки разлетаются под действием кулоновских сил. Пример ядерной реакции деления демонстрирует уран-235, поглотивший нейтрон:

23592U + 10n → 14456Ba + 8936Kr + 3 10n.

Расщепление на барий-144 и криптон-89 – лишь один из возможных вариантов деления урана-235. Эту реакцию можно записать в виде 23592U + 10n → 23692U* → 14456Ba + 8936Kr + 3 10n, где 23692U* – сильно возбужденное составное ядро с высокой потенциальной энергией. Избыток ее наряду с разностью энергий связи материнского и дочерних ядер выделяется главным образом (около 80%) в форме кинетической энергии продуктов реакции, а также частично в форме потенциальной энергии осколков деления. Общая энергия деления массивного ядра – примерно 200 МэВ. В пересчете на 1 грамм урана-235 (при условии, что прореагировали все ядра) это составляет 8,2 ∙ 104 мегаджоулей.

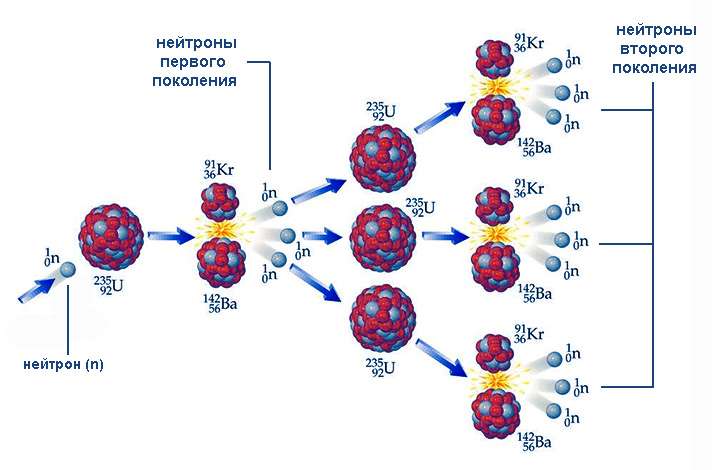
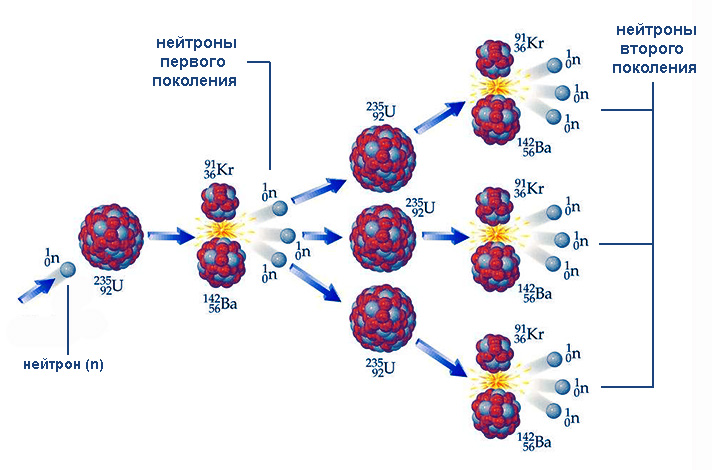
Цепные реакции

Деление урана-235, а также таких ядер, как уран-233 и плутоний-239, характеризуется одной важной особенностью – наличием среди продуктов реакции свободных нейтронов. Эти частицы, проникая в другие ядра, в свою очередь, способны инициировать их деление опять-таки с вылетом новых нейтронов и так далее. Подобный процесс именуется цепной ядерной реакцией.

Течение цепной реакции зависит от того, как соотносится число вылетающих нейтронов очередного поколения с количеством их в предыдущем поколении. Это отношение k = Ni/Ni–1 (здесь N – количество частиц, i – порядковый номер поколения) носит название коэффициента размножения нейтронов. При k 1 число нейтронов, а значит, и делящихся ядер, возрастает лавинообразно. Пример цепной ядерной реакции такого типа – взрыв атомной бомбы. При k = 1 процесс протекает стационарно, примером чему служит реакция, управляемая при помощи поглощающих нейтроны стержней, в ядерных реакторах.

Ядерный синтез

Наибольшее энерговыделение (в расчете на один нуклон) происходит при слиянии легких ядер – так называемых реакциях синтеза. Чтобы вступить в реакцию, положительно заряженные ядра должны преодолеть кулоновский барьер и сблизиться на расстояние сильного взаимодействия, не превышающее размеров самого ядра. Поэтому они должны обладать чрезвычайно большой кинетической энергией, что означает высокие температуры (десятки миллионов градусов и выше). По этой причине реакции синтеза еще называют термоядерными.

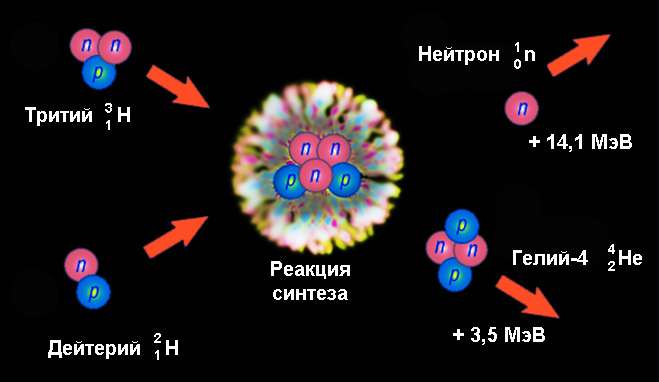
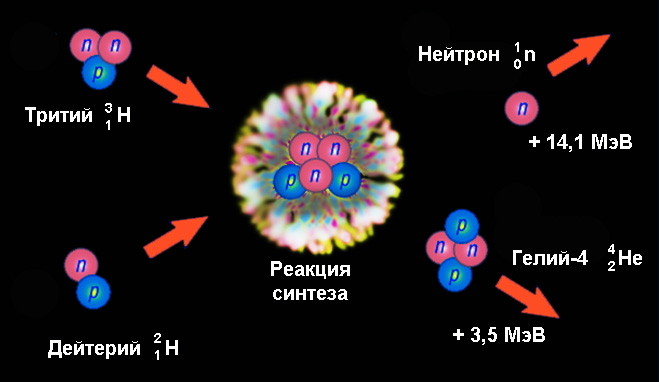
Пример ядерной реакции синтеза – образование гелия-4 с вылетом нейтрона при слиянии ядер дейтерия и трития:

21H + 31H → 42He + 10n.

Здесь высвобождается энергия 17,6 МэВ, что в расчете на один нуклон более чем в 3 раза превышает энергию деления урана. Из них 14,1 МэВ приходится на кинетическую энергию нейтрона и 3,5 МэВ – ядра гелия-4. Такая существенная величина создается за счет огромной разницы в энергиях связи ядер дейтерия (2,2246 МэВ) и трития (8,4819 МэВ) с одной стороны, и гелия-4 (28,2956 МэВ) – с другой.

В реакциях деления ядра высвобождается энергия электрического отталкивания, в то время как при синтезе энерговыделение происходит за счет сильного взаимодействия – самого мощного в природе. Это и определяет столь значительный энергетический выход данного типа ядерных реакций.

Примеры решения задач

Рассмотрим реакцию деления 23592U + 10n → 14054Xe + 9438Sr + 2 10n. Каков ее энергетический выход? В общем виде формула для его расчета, отражающая разность энергий покоя частиц до и после реакции, выглядит следующим образом:

Q = Δmc2 = (mA + mB – mX – mY + …) ∙ c2.

Вместо умножения на квадрат скорости света можно умножить разность масс на коэффициент 931,5 и получить значение энергии в мегаэлектронвольтах. Подставив в формулу соответствующие значения атомных масс, получим:

Q = (235,04393 + 1,00866 – 139,92164 – 93,91536 — 2∙1,00866) ∙ 931,5 ≈ 184,7 МэВ.

Еще один пример – на реакцию синтеза. Это один из этапов протон-протонного цикла – главного источника солнечной энергии.

32He + 32He → 42He + 2 11H + γ.

Применим ту же формулу:

Q = (2 ∙ 3,01603 – 4,00260 — 2 ∙ 1,00728) ∙ 931,5 ≈ 13,9 МэВ.

Основная доля этой энергии – 12,8 МэВ – приходится в данном случае на гамма-фотон.

Мы рассмотрели только простейшие примеры ядерных реакций. Физика этих процессов чрезвычайно сложна, они отличаются огромным разнообразием. Исследование и применение ядерных реакций имеет большое значение как в практической области (энергетика), так и в фундаментальной науке.

Ядерные реакции (примеры объяснения фото)

Ядерные реакции это реакции где взаимодействует атомное ядро с другими элементарными частицами или же другим ядром, в результате чего в зависимости от условий образуется новое вещество.

В первые ядерную реакцию произвел Резерфорд.

Что такое простейшие ядерные реакции

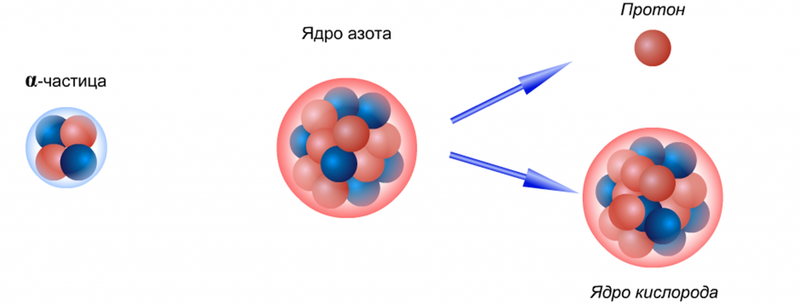
В 1919 г. Резерфорд впервые осуществил искусственное превращение ядра атома одного элемента — азота в ядро атома другого элемента — кислорода.

Реакция происходила при воздействии (ударе) альфа-частицами, полученными при распаде радия, о ядра атомов азота, которым была предварительно заполнена камера Вильсона.

В результате реакции в камере были обнаружены атомы изотопа кислорода с массовым числом 17 и частицы, имеющие единичный положительный заряд и единичную массу, т. е. протоны.

Реакцию записывают так:

Схема реакции показана на рис. , а. На рис. 2 приведена фотография камеры Вильсона, в которой происходит эта реакция.

На рисунке видны следы альфа-частиц от радиоактивного препарата, помещенного сбоку камеры.

На одном из следов имеется несимметричная развилка — след происшедшей реакции: более толстый и короткий след принадлежит тяжелой частице — ядру кислорода, более тонкий и длинный след — легкой частице — протону.

В качестве другого примера приведем реакцию (Дж. Чедвик, 1932 г.), при которой впервые был выделен из ядра атома нейтрон. Реакция заключается в действии на ядра бериллия альфа-частицами. В результате реакции получаются ядра углерода и нейтроны:

Реакция схематически показана на рис. , б, Нейтрон не существует долго в свободном состоянии или он в процессе теплового движения соударяется с ядром атома какого-либо вещества и вызывает соответствующую ядерную реакцию, или претерпевает радио-активный распад: излучает бета-частицу (электрон) и превращается в протон.

Период полураспада нейтронов составляет 12,8 мин.

Механизм ядерных реакций

Механизм ядерных реакций заключается в том, что, ударяясь о ядро атома с большой силой, альфа-частица сближается с ним на расстояние действия ядерных сил.

Между нуклонами альфа-частицы и ядра возникают ядерные силы. На мгновение ядро поглощает ударившую в него частицу, и в нем происходит перегруппировка нуклонов с образованием нового комплекса частиц.

Если для устойчивости комплекса какая-либо частица оказывается лишней, то она при этом выбрасывается (см. схему на рис. , в).

Основным условием осуществления ядерной реакции является высокая кинетическая энергия частицы, доста точная, чтобы вызвать неупругий удар и перестройку связей в ядре между нуклонами.

Основным правилом составления уравнений ядерных реакций является сохранение равенства обеих частях его суммы индексов: верхних (массовых чисел) и нижних (атомных номеров) ядер.

Эти равенства являются выражением законов сохранения массы и заряда частиц, участвующих в реакции.

Часто применяют сокращенный способ записи ядерных реакций в виде формулы, состоящей из четырех символов: исходное ядро, действующая частица, выбрасываемая частица, конечное ядро.

Символы частиц заключают в скобки, а порядковый номер элемента часто опускают. Например, реакция Резерфорда:

реакция получения нейтрона:

Ве 9 (α; п) С 12; и т. д.

Условия при которых происходит ядерные реакции

Рассмотрим условия, при которых происходят ядерные реакции. В лабораторных условиях для этого пользуются потоком частиц с высокой кинетической энергией, который направляется на небольшое количество соответствующего вещества, нанесенного на экран, называемое мишенью.

В веществе ядра атомов расположены на расстояниях, в десятки тысяч раз превышающих диаметры самих ядер. Падая на вещество, поток частиц пронизывает главным образом электронные оболочки атомов, в которых производит ионизацию, и только единичные частицы сталкиваются с ядрами атомов (весьма условно это показано на рис. 3 ).

При этом, чтобы вызвать ядерную реакцию, частица при столкновении должна обладать достаточной кинетической энергией. Проходя сквозь электронные оболочки, заряженные частицы взаимодействуют с полем атомов, тормозятся и теряют энергию.

Поэтому вероятность столкновения с ядром частиц, имеющих достаточно высокую энергию, необходимую для осуществления ядерной реакции, становится еще меньше.

Соударение частиц с ядром атома в зависимости от энергии частиц может быть упругим и неупругим. В первом случае происходит только упругое рассеяние частиц, сопровождающееся перераспределением кинетической энергии между частицей и ядром.

При неупругом соударении происходит или неупругое рассеяние, когда часть кинетической энергии частицы затрачивается на возбуждение ядра (возбужденное ядро излучает гамма-фотон и возвращается в основное состояние), или ядерная реакция, когда кинетическая энергия частицы затрачивается на внутреннюю перестройку ядра.

Вероятность ядерной реакции

Вероятность ядерной реакции характеризуют ее эффективным поперечным сечением σ, под которым понимают отношение числа п актов осуществленной реакции за 1 сек к количеству N частиц, падающих за 1 сек на 1 см 2 площади вещества, перпендикулярной потоку частиц:

Величина а зависит от природы вещества, характера реакции и от энергии частиц, ее вызывающих. Порядок величины эффективного сечения для различных ядерных реакций от 10 -18 до 10 -24 см 2 , т. е. из N частиц, которые действуют на вещество, только (10 -18 ÷ 10 -24 ) N частиц в действительности вызывают реакцию.

Большая вероятность ядерных реакций имеет место при действии на вещество нейтронов. Не обладая электрическим зарядом, нейтроны проходят через электронные оболочки без потери энергий, поэтому, сталкиваясь с ядрами, они чаще вызывают ядерные реакции.

Закон пропорциональности массы и энергии

Согласно теории относительности масса тел увеличивается с повышением скорости в следующем соотношении:

где т — масса тела при скорости υ , т₀ — масса тела при относительном покое, с — скорость света.

В ядерной физике, которая оперирует со скоростями движения частиц, соизмеримыми со скоростью света, изменение массы частиц в зависимости от скорости становится существенным.

В связи с этим различают полную массу движущейся частицы и массу покоя, т. е. массу частицы при относительном покое или незначительной скорости характера теплового движения.

Полная масса т равняется массе покоя т₀ плюс приращение массы m_v при данной скорости движения:

Из предыдущей формулы путем несложных преобразований можно получить зависимость между приращением m_υ массы тела при движении со скоростью v и соответствующей кинетической энергией Е_к тела.

Кинетическая энергия тела численно равняется приращению его массы при движении, умноженной на квадрат скорости света.

Соотношение Эйнштейна

Это соотношение, называемое соотношением Эйнштейна, согласно теории относительности является общим законом, обусловливающим связь между массой т и энергией Е тела: полная энергия тела пропорциональна его массе:

где Е — выражено в эргах, т — в граммах и с — в сантиметрах в секунду Закон пропорциональности массы и энергии находится в полном соответствии с одним из основных положений диалектического материализма во взаимосвязи материи и движения.

Из закона пропорциональности массы и энергии следует, что массе покоя частиц должна соответствовать внутренняя энергия, по величине удовлетворяющая этому соотношению.

Эта величина, однако, превышает величину всех известных в те времена форм внутренней энергии тел (химической, электрической и т. п.) почти в миллион раз.

Как оказалось в даль нейшем, этой энергией является внутренняя потенциальная энергия ядер атомов, связанная с действующими между нуклонами ядерными силами.

Соотношение Эйнштейна является универсальным, однако практическое применение оно находит главным образом в области энергетических расчетов при ядерных реакциях.

При ядерных реакциях происходит перегруппировка нуклонов, соответственно изменяется и внутренняя потенциальная энергия ядра. Если при реакции эта энергия уменьшилась, это значит, что часть ее перешла в другие виды энергии, например в кинетическую энергию частиц — продуктов реакции. В этом случае имеется возможность ее полезного использования.

Энергетическим баланс ядерной реакции

Энергетическим балансом ядерной реакции называют соотношение между кинетической энергией частиц, вступивших в реакцию, и кинетической энергией частиц, образовавшихся в результате реакции.

Если общая кинетическая энергия частиц в результате реакции увеличилась (что произошло за счет уменьшения потенциальной энергии вновь образовавшегося ядра), то баланс реакции считается положительным.

В обратном случае (когда, наоборот, часть кинетической энергии частиц, входящих в реакцию, переходит в потенциальную энергию ядра) — отрицательным.

Для составления баланса можно воспользоваться законом сохранения энергии, согласно которому полная энергия Е’ частиц, вступивших в реакцию, равняется полной энергии Е» частиц, образовавшихся в результате нее:

или, развертывая выражение для полной энергии:

где Е₀ энергия, соответствующая массе покоя частиц,

а E_к — их кинетическая энергия. Для удобства расчета энергия, соответствующая массе покоя частиц в обеих частях уравнения, может быть выражена, пользуясь соотношением Эйнштейна, через массу покоя соответствующих частиц. Получаем:

Обозначая разность между массами покоя частиц до и после реакции как ∆m₀, получаем:

т. е. изменение кинетической энергии частиц в результате ядерной реакции численно равняется изменению массы покоя частиц, участвующих в реакции, умноженному на квадрат скорости света

Если в результате реакции масса покоя частиц уменьшилась, то энергетический баланс ее положителен, если, наоборот, масса покоя увеличилась, то — отрицателен.

Расщепление протоном ядра лития

Рассмотрим осуществленную в 30-х годах реакцию расщепления протоном ядра лития на две альфа-частицы:

Как показывает расчет, масса покоя двух альфа-частиц на ∆m₀ — = 0,0185 а. е. м. меньше массы частиц, вступающих в реакцию.

Этому соответствует энергия (переводя массу в граммы и энергию в электронвольты Е = ∆m₀с 2 = 0,0185•1,66•10 -24 . (3•10 10 ) 2 •6,24•10 5 = 17 Мэв.

Кинетическая энергия альфа-частиц, определенная по пробегу в воздухе, составляет 2•8,8 = 17,6 Мэв. Совпадение с расчетом вполне удовлетворительное.

Если учесть, что протон должен быть предварительно ускорен до энергии 0,5 Мэв, получается положительный баланс реакции в 17,0 — 0,5 = — 16,5 Мэв на одно ядро лития.

Эта реакция дала полное подтверждение соотношения Эйнштейна и, кроме того, впервые показала принципиальную возможность выделения внутриядерной энергии.

Количество ядерной энергии, освобождающейся на грамм-атом (т.е. 7 г) лития при этой реакции, равняется Е_к = 0,17•10 20 эрг или в тепловых единицах 4•10 8 ккал.

Если сравнить это с количеством теплоты, выделяющейся при сгорании лучшего угля (калорийность 8000 ккал/кг), то получится 50 000 кг или 50 т угля.

Таков порядок энергии, которая может освобождаться при ядерных реакциях. Однако в данном случае это не является экономически оправданным.

Вероятность ядерной реакции, как указывалось, составляет примерно 1 : 10 20 . Следовательно, для реакции, которую вызовет одна частица, необходимо затратить энергию на ускорение 10 20 протонов.

Использование ядерной энергии получило практическое значение только после открытия реакции деления ядер урана под действием нейтронов.

Примером отрицательного баланса может быть баланс реакции Резерфорда: кинетическая энергия альфа-частицы, вызывающей реакцию, должна быть не менее 7,7 Мэв энергия ядра азота ничтожно мала, энергия ядра кислорода после реакции 0,5 Мэв и энергия протона 6 Мэв.

Отрицательный баланс реакции 1,2 Мэв на одно ядерное превращение.

Аннигиляция реакция образования и аннигиляции пары

Позитрон и электрон, будучи античастицами, взаимодействуют и превращаются в два гамма-фотона (рис. 4, а):

Реакция была названа реакцией аннигиляции (уничтожения) пары.

Название это не отражает сущности явления, которое имеет существенное значение для правильного понимания единой природы материи.

В данном случае происходит превращение одной из форм материи — частиц вещества в другую форму — частицы поля (фотоны).

Это значение реакции аннигиляции подчеркивается тем, что существует обратная ей реакция образования пары, при которой гамма-фотон достаточно высокой энергии, пролетая сквозь вещество, под действием поля атома превращается в пару электрон-позитрон (рис. 4, б):

При обеих реакциях должно выполняться соотношение Эйнштейна. Массе покоя т_е электрона или позитрона соответствует энергия Е_е = 0,51 Мэв или 8,2•10 -7 эрг. В первом случае эта энергия сообщается каждому из фотонов, в соответствии с чем они должны иметь частоту:

Это подтверждается опытом.

Во втором случае hv ≥ т_ес 2 , т. е. энергия фотона должна быть не меньше суммы энергий электрона и позитрона, т. е. hv = 2•0,51 = 1,02 Мэв.

Это также подтверждается опытом. При соблюдении этого условия интенсивность образования пар зависит от природы вещества, в котором явление происходит. Она тем больше, чем выше атомный номер вещества.

Статья на тему Ядерные реакции

Ядерные реакции

В курсе ядерной физики в школе изучается явление взаимного превращения одного вещества в другое. Данные превращения могут быть как спонтанные (радиоактивный распад), так и индуцированные (несколько ядер сталкивают друг с другом). В результате такой реакции получается новые вещества. Для описания таких превращений используют введённую нами форму записи для элементов и организуют их в подобие уравнения:

где
- , — ядра до взаимодействия,
- , — ядра после взаимодействия,
- — — количество нуклонов (протонов+нейтронов) в соответствующих атомах,
- — — количество протонов в соответствующих атомах.

Единственное, чем мы можем пользоваться в таких уравнениях, это простая логика — количество нуклонов и протонов в ходе реакции измениться не должно, таким образом, мы можем получить два уравнения:

Такие задачи обычно нацелены на поиск неизвестного элемента, и соотношений (2) — (3) для этого хватает. Находим количество протонов и нейтронов и, используя таблицу Менделеева, определяем нужный элемент.

Пример: пусть ядро азота и ядро гелия, сталкиваясь образуют ядро кислорода и неизвестный элемент. Найти данный элемент. По задаче сформируем уравнение:

Воспользуемся законом сохранения нуклонов (2) и (3):

Тогда искомый элемент — водород ( ).

Среди элементов, которые текстово могут встретиться в таких задачах, присутствуют:

нейтрон — ,
протон — , аналогом протона является ядро водорода ( ),
дейтерий — — ядро водорода (изотоп), которое приобрело дополнительный нейтрон,
тритий — — ядро водорода (изотоп), которое приобрело два дополнительных нейтрона,
— частица (альфа-частица) — ядро гелия — ,
— частица (бетта-частица) — по сути электрон — ,
— частица (гамма-частица) — фактический фотон — .

Бетта-частица является обычным электроном, однако в ядре электронов нет, тогда электроны из ядра получается в результате ядерной реакции: .

Вывод: задачи на данную тематику практически всегда касаются поиска конкретного элемента в реакции. Поиск осуществляется законом сохранения нуклонов (уравнения (1) и (2)).

источники:

http://znaesh-kak.com/e/d/%D1%8F%D0%B4%D0%B5%D1%80%D0%BD%D1%8B%D0%B5-%D1%80%D0%B5%D0%B0%D0%BA%D1%86%D0%B8%D0%B8

http://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/elementy-yadernoj-fiziki/yadernye-reakcii/

Источник

Общее понятие о ядерных реакциях

превращение одного химического элемента в другой;
деление ядра;
синтез, то есть слияние ядер, при котором образуется ядро более тяжелого элемента.

Правила записи ядерных реакций

⁹₄Be + ⁴₂He → ¹²₆C + ¹₀n.

Сокращенный способ написания уравнений ядерных реакций, часто применяющийся в физике, выглядит так:

⁹₄Be (α, n) ¹²₆C.

Общий вид такой записи: A (a, b₁b₂…) B. Здесь A – ядро-мишень; a – налетающая частица или ядро; b₁, b₂ и так далее – легкие продукты реакции; B – конечное ядро.

Энергетика ядерных реакций

В процессах с участием ядер задействуются три вида фундаментальных взаимодействий – электромагнитное, слабое и сильное. Благодаря последнему ядро обладает такой важнейшей особенностью, как высокая энергия связи между составляющими его частицами. Она существенно выше, чем, например, между ядром и атомными электронами или между атомами в молекулах. Об этом свидетельствует заметный дефект массы – разница между суммой масс нуклонов и массой ядра, которая всегда меньше на величину, пропорциональную энергии связи: Δm = E_св/c². Расчет дефекта массы производится по простой формуле Δm = Zm_p + Am_n – М_я, где Z – заряд ядра, A – массовое число, m_p – масса протона (1,00728 а.е.м.), m_n – масса нейтрона (1,00866 а.е.м.), M_я– масса ядра.

При описании ядерных реакций используется понятие удельной энергии связи (то есть в расчете на один нуклон: Δmc²/A).

Энергия связи и стабильность ядер

Ниже мы рассмотрим некоторые примеры ядерных реакций.

Реакции распада

²²⁶₈₈Ra → ²²²₈₆Rn + α (⁴₂He).

Энергия распада ядра радия-226 составляет около 4,87 МэВ.

¹⁸₉K → ¹⁸₈Ar + e⁺ + ν_e.

Энергия бета-распада фтора-18 – около 0,63 МэВ.

Деление ядер

²³⁵₉₂U + ¹₀n → ¹⁴⁴₅₆Ba + ⁸⁹₃₆Kr + 3 ¹₀n.

Расщепление на барий-144 и криптон-89 – лишь один из возможных вариантов деления урана-235. Эту реакцию можно записать в виде ²³⁵₉₂U + ¹₀n → ²³⁶₉₂U* → ¹⁴⁴₅₆Ba + ⁸⁹₃₆Kr + 3 ¹₀n, где ²³⁶₉₂U* – сильно возбужденное составное ядро с высокой потенциальной энергией. Избыток ее наряду с разностью энергий связи материнского и дочерних ядер выделяется главным образом (около 80%) в форме кинетической энергии продуктов реакции, а также частично в форме потенциальной энергии осколков деления. Общая энергия деления массивного ядра – примерно 200 МэВ. В пересчете на 1 грамм урана-235 (при условии, что прореагировали все ядра) это составляет 8,2 ∙ 10⁴ мегаджоулей.

Цепные реакции

Течение цепной реакции зависит от того, как соотносится число вылетающих нейтронов очередного поколения с количеством их в предыдущем поколении. Это отношение k = N_i/N_i_–1 (здесь N – количество частиц, i – порядковый номер поколения) носит название коэффициента размножения нейтронов. При k < 1 цепная реакция не идет. При k > 1 число нейтронов, а значит, и делящихся ядер, возрастает лавинообразно. Пример цепной ядерной реакции такого типа – взрыв атомной бомбы. При k = 1 процесс протекает стационарно, примером чему служит реакция, управляемая при помощи поглощающих нейтроны стержней, в ядерных реакторах.

Ядерный синтез

Пример ядерной реакции синтеза – образование гелия-4 с вылетом нейтрона при слиянии ядер дейтерия и трития:

²₁H + ³₁H → ⁴₂He + ¹₀n.

Примеры решения задач

Рассмотрим реакцию деления ²³⁵₉₂U + ¹₀n → ¹⁴⁰₅₄Xe + ⁹⁴₃₈Sr + 2 ¹₀n. Каков ее энергетический выход? В общем виде формула для его расчета, отражающая разность энергий покоя частиц до и после реакции, выглядит следующим образом:

Q = Δmc²= (m_A + m_B – m_X – m_Y + …) ∙ c².

Q = (235,04393 + 1,00866 – 139,92164 – 93,91536 — 2∙1,00866) ∙ 931,5 ≈ 184,7 МэВ.

³₂He + ³₂He → ⁴₂He + 2 ¹₁H + γ.

Применим ту же формулу:

Q = (2 ∙ 3,01603 – 4,00260 — 2 ∙ 1,00728) ∙ 931,5 ≈ 13,9 МэВ.

Основная доля этой энергии – 12,8 МэВ – приходится в данном случае на гамма-фотон.

Источник

−

следует рассматривать как превращение одного из нейтронов ядра в

протон, электрон и антинейтрино: n → p + e + ν.

При этом порядковый номер ядра увеличивается на единицу, а массовое

число остается постоянным, т.к. me << mp. Например,

19 K40 →20 Ca40 +β− +ν) +1,3 МэВ.

Аналогично позитронный β+ − распад

Z XA →Z−1YA +β+ +ν

следует рассматривать как превращение протона ядра в нейтрон, позитрон и нейтрино:

p → n +β+ + ν .

Такое превращение может происходить только в ядре, т.к. в свободном состоянии протон – стабильная частица.

При таком распаде массовое число не изменяется, а заряд ядра уменьшается на единицу. Например,

6 C11→5B11 +β+ +ν+0,931МэВ.

В третьем типе β-распада – электронном захвате – материнское ядро с избытком протонов захватывает орбитальный электрон из атомных оболочек. По-

сле захвата, как и в позитронном распаде, один протон превращается в нейтрон: p +e → n +ν.

Электронный захват обозначают, как и оболочку: К – захват, L – захват и т.д. Уравнение электронного захвата

Z XA n→Z−1YA ,

где n – обозначение оболочки, например,

4 Be7 K→3 L7 .

Энергия К – захвата ЕР = 0,864 МэВ.

7.3.1.Уравнение ядерной реакции

Ядерными реакциями называются превращения атомных ядер, происходящие в результате их взаимодействия с элементарными частицами или друг с другом. Обычно ядерная реакция вызывается бомбардировкой ядер мишени

ZXA потоком ускоренных частиц: α-частиц, протонов, электронов, нейтронов и т.д. В результате интенсивного взаимодействия исходного ядра и налетающей частицы а образуется новое ядро Z1YA1 и некоторая частица b, разлетающиеся в разных направлениях. Ядерную реакцию, как и химическую, обычно записывают в виде уравнения

Z	XA + a →	Z1	YA1	+ b или	Z	XA (a,b)	YA1 .
				Z1

−

Впервые ядерную реакцию осуществил Э.Резерфорд в 1919 г., бомбардируя ядра азота α-частицами. α-частицы с энергией 7,7 МэВ проникали в ядра азота и вызывали ядерные реакции, в результате возникали ядра кислорода 8О17 и протоны. Это было первым подтверждением, что протоны входят в состав ядра. Уравнение реакции:

7 N14 + α →8 O17 + P, или 7 N14 (α, P) 8O17 .

7.3.2. Законы сохранения в ядерных реакциях

В ядерных реакциях выполняются те же законы сохранения, что и при радиоактивном распаде: законы сохранения энергии, импульса, электрического заряда, количества нуклонов, спина.

Запишем закон сохранения энергии в реакции Z XA (a, b)Z1 Y A1 , учитывая,

что полная энергия ядер и частиц равна энергии покоя и кинетической энергии:

МЯ(Z,A)c2 + mac2 + K + Ka = MЯ(Z1,A1 )c2 + mbc2 + K1 + Kb .

Изменение кинетической энергии в реакции называют энергией реакции

или тепловым эффектом: Q = (K1 + kb)−(K + Ka). Как видно

Q = [M

(Z, A)+ m

− M

(Z , A

)− m

]c2 =

M c2 .

(7.3.1)

Если массы ядер и частиц выражать в а.е.м.,

то

Q = 931 [MЯ(Z, A)+ ma − M (Z1, A1 )− mb ], МэВ.

(7.3.2)

В эндотермической реакции

Q > 0 происходит преобразование части

энергии покоя ядра мишени и бомбардирующей частицы в кинетическую энергию продуктов реакции. Примером такой реакции является 5 В10 (n, α)3 Li7 ,

для которой Q ≈ 2,8 МэВ.

Реакции, которые могут осуществляться только с поглощением энергии Q < 0, называются эндотермическими. Такая реакция становится возможной лишь при некоторой минимальной энергии налетающей частицы, которая называется пороговой энергией данной эндотермической реакции:

ЕПОР =	A + A0	Q	.	(7.3.3)

A

Например, для эндотермической реакции
4 Be9 (P,n) 5B9 ,			EПОР ≈ 2,07 МэВ.

7.3.3. Составное ядро

В 1936 г. Бор дал теоретическое объяснение ядерной реакции на основе составного (промежуточного) ядра. Эта теория хорошо объясняет ядерные превращения до энергий частиц 50 МэВ. По этой теории ядерная реакция проте-

кает в два этапа. На первом этапе ядро ZAA захватывает частицу а. В результате образуется составное ядро С в возбужденном состоянии Z XA + a → C * .

Энергия возбуждения быстро равномерно распределяется между нуклонами. Многочисленные столкновения между нуклонами могут затем привести к пере-

			−
даче энергии возбуждения частице b,	находящейся в поверхностном слое со-
ставного ядра. После этого наступает распад составного ядра:
С* →Z1 YA1 + b .
Время,	за которое частица а	пролетает расстояние, равное диаметру ядра,
называют	ядерным временем	τЯ,	которое	по порядку	величины	равно
~10-21 с. Среднее время жизни составного ядра	τ ~ 10-14 с,	т.е. τ	Я	<< τ	. Та-
				С			С

кое длительное существование составного ядра делает процесс его распада независимым от первого этапа реакции – захвата частицы а. Поэтому составное ядро может распадаться различными путями. С учетом составного ядра уравнение ядерной реакции будет

Z XA + a → C* →Z1 Y A1 + b .

Так, первая реакция	7 N14 (α, P) 8O17 записывается так:
7	N14	+ α → (	9	F18 )* → P +	8	O17 .

7.3.4. Типы ядерных реакций

Реакции под действием α-частиц. При изучении реакции (α, b) были получены первые сведения о строении ядра. С помощью естественных α— излучателей (например, 88Ra226) были установлены некоторые закономерности протекания ядерных реакций. Кроме первой реакции 7 N14 (α, P) 8O17 были открыты и другие, важные для ядерной физики реакции. Так, в 1932 г. Д.Чедвику с помощью реакции 4 Be9 (α, n) 8C12 удалось открыть нейтрон. Реакция

типа (α, n) до настоящего времени используется в качестве лабораторных источников нейтронов, например, полоний-бериллиевые источники (Ро – Ве). В 1934 г. Ирен и Фредерик Жолио-Кюри с помощью реакции (α, n) открыли явление искусственной радиоактивности. При облучении α-частицами 13Al27 образуется радиоактивный фосфор с периодом полураспада 2,5 мин. Реакция эта идет по схеме

13	Al27	+ α →	15	P30	+ n;	15	P30	→	14	Si30	+β+ + ν.

Реакции под действием протонов.	Протоны могут вызвать реакции типа

(Р, γ), (Р, n), (Р, α). Для осуществления этих реакций используют ускорители заряженных частиц. В реакциях (Р, γ) ядро мишень захватывает протон, образуется составное ядро в возбужденном состоянии, которое переходит в нормальное с испусканием γ-кванта. Этот тип реакций называют радиационным

захватом протона. Примеры таких реакций	6 C12 (P, γ) 7 N14 ; 13 Al27 (P, γ)14Si28
и др.
В реакциях	(P, n) протон захватывается ядром и выбрасывается нейтрон,
т.е. протон	и нейтрон меняются	местами. Примеры реакций:

3 Li7 (P,n) 4Be7; 5B11(P, n) 6C11 и др.

Реакция с ядрами 3Li7 является исторически первой реакцией, осуществленной в 1932 г. Д.Кокрофтом и Э.Уолтоном с искусственно ускоренными

−

протонами. Ядро 3Li7 под действием протонов расщеплялось на две α— частицы. Это экзотермическая реакция с энергией Q = 17,3 МэВ. На этой реакции было проверено соотношение Эйнштейна: E = mc2.

Реакция под действием дейтронов. Дейтрон состоит из протона и нейтрона. Слабая связь между ними (ЕСb = 2,225 МэВ) обуславливает особенности протекания реакций (d, b). Ядерная реакция может идти как через составное ядро, так и без образования составного ядра. При небольших энергиях нейтрон отрывается от протона и проникает в ядро – мишень. В результате идет прямая реакция (d, Р), при которой происходит захват нейтрона и освобождение протона:

Z XA + d →Z YA+1 + P.

Пример таких реакций:

Cu63 (d,P)Cu64 ; P31(d,P)P32 .

Реакции под действием нейтронов. Нейтрон является нейтральной частицей и может свободно проходить внутрь любого ядра от легкого до тяжелого. Каждый нейтрон при этом приносит в ядро энергию 7÷8 МэВ. Возникающее при этом составное ядро оказывается возбужденным и испытывает распад различными способами, в зависимости от степени возбуждения. Реакции, вызываемые нейтронами, подразделяются на следующие: упругое рассеяние (n, n); неупругое рассеяние (n, r); радиационный захват (n, γ); расщепление с вылетом заряженных частиц (n, P); (n, d), например, последняя реакция используется для

регистрации нейтронов − 5 B10 (n,α) 3Li7 реакции типа (n, 2n), реакции деления.

Ядерный фотоэффект. Поглощение ядром γ-кванта может вызвать реакции (γ, n) и (γ, P). Эти реакции называют ядерным фотоэффектом. Примеры таких реакций: 8 O16 (γ,n) 8O15; 12Mg24 (γ, n)12Mg23; 12Mg26 (γ,P) и др.

7.3.5. Трансурановые элементы

Природные элементы заполняют периодическую таблицу Менделеева до урана (Z = 92). Химические элементы, расположенные за ураном, называют трансурановыми. Все они радиоактивны и получены искусственным путем с помощью ядерных реакций. Первый изотоп с порядковым номером Z = 93

	был получен в 1940 г. в результате реакции	92 U238 (n, γ) 92U239 и дальнейше-
	го распада 92U239:	~
	92 U239 →93 Np239
	+β− + ν.

Полученный изотоп был назван нептунием. В настоящее время известно 107 трансурановых элементов, полученных с помощью ядерных реакций.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.201596.28 Кб13Laboratornaya_rabota_3.doc
#
#
#
#
#
#
#
#
#
#

Источник

Ядерная реакция – процесс взаимодействия ядра с элементарной частицей или другим ядром, в процессе которого происходит изменение строения и свойств ядра. Например, испускание ядром элементарных частиц, его деление, испускание фотонов с высокой энергией (гамма-квантов). Одним из результатов ядерных реакций является образование изотопов, не существующих в естественных условиях на Земле.

Протекать ядерные реакции могут при бомбардировке атомов быстрыми частицами (протоны, нейтроны, ионы, альфа-частицы).

Больше полезной информации по разным темам – у нас в телеграм.

Ядерные реакции

Одна из первых проведенных людьми ядерных реакций была осуществлена Резерфордом в 1919 году с целью обнаружения протона. Тогда еще не было известно, что ядро состоит их нуклонов (протоны и нейтроны). При расщеплении многих элементов была обнаружена частица, являющаяся ядром атома водорода. На основе опытов Резерфорд сделал предположение, что данная частица входит в состав всех ядер.

Эта реакция как раз и описывает один из экспериментов ученого. В опыте выше газ (азот) бомбардируется альфа-частицами (ядра гелия), которые, выбивая из ядер азота протон, превращают его в изотоп кислорода. Запись этой реакции выглядит следующим образом:

При решении задач на ядерные реакции следует помнить, что при их протекании выполняются классические законы сохранения: заряда, момента импульса, импульса и энергии.

Также существует закон сохранения барионного заряда. Это значит, что число нуклонов, участвующих в реакции, остается неизменным. Если мы посмотрим на реакцию, то увидим, что суммы массовых чисел (цифра сверху) и атомных чисел (снизу) в правой и левой частях уравнения совпадают.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Удельная энергия связи ядер

Как известно, внутри ядра на расстояниях порядка его размера действует одно из фундаментальных физических взаимодействий – сильное взаимодействие. Чтобы его преодолеть и «развалить» ядро, необходимо большое количество энергии.

Энергия связи ядра – минимальная энергия, необходимая, чтобы расщепить ядро атома на составляющие его элементарные частицы.

Масса любого атомного ядра меньше, чем масса составляющих его частиц. Разность масс ядра и его составляющих нуклонов называется дефектом масс:

Числа Z и N легко определяются при помощи таблицы Менделеева, а почитать о том, как это делается, можно тут. Энергия связи высчитывается по формуле:

Энергия ядерных реакций

Ядерные реакции сопровождаются энергетическими превращениями. Существует величина, называемая энергетическим выходом реакции и определяемая формулой

Дельта M – дефект масс, но в данном случае это разница масс между начальными и конечными продуктами ядерной реакции.

Реакции могут протекать как с выделением энергии, так и с ее поглощением. Такие реакции называются соответственно экзотермическими и эндотермическими.
Чтобы протекала экзотермическая реакция, необходимо выполнение следующего условия: кинетическая энергия начальных продуктов должна быть больше кинетической энергии продуктов, образовавшихся в ходе реакции.

Эндотермическая реакция возможна в случае, когда удельная энергия связи нуклонов в исходных продуктах меньше удельной энергии связи ядер конечных продуктов.

Примеры решения задач по ядерной реакции

А теперь пара практических примеров с решением:

Даже если Вам попалась задачка со звездочкой, стоит помнить – нерешаемых задач не существует. Студенческий сервис поможет выполнить любое задание.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

$displaystyle {}_{{{p}_{1}}}^{z1}{{A}_{1}}+{}_{p2}^{z2}{{A}_{2}}to {}_{p3}^{z3}{{A}_{3}}+{}_{p4}^{z4}{{A}_{4}}$ (1)

где

displaystyle z1+z2=z3+z4 (2)

displaystyle p1+p2=p3+p4 (3)

$displaystyle {}_{7}^{14}N+{}_{2}^{4}Heto {}_{p}^{z}X+{}_{8}^{17}O$ (4)

Воспользуемся законом сохранения нуклонов (2) и (3):

Тогда искомый элемент — водород ( $displaystyle {}_{1}^{1}H$ ).

Среди элементов, которые текстово могут встретиться в таких задачах, присутствуют:

Бетта-частица является обычным электроном, однако в ядре электронов нет, тогда электроны из ядра получается в результате ядерной реакции: $displaystyle {}_{0}^{1}nto {}_{1}^{1}p+{}_{-1}^{0}beta$ .

Источник

Примеры ядерных реакций: особенности, решение и формулы

Общее понятие о ядерных реакциях

Правила записи ядерных реакций

Энергетика ядерных реакций

Энергия связи и стабильность ядер

Реакции распада

Деление ядер

Цепные реакции

Ядерный синтез

Примеры решения задач

Ядерные реакции (примеры объяснения фото)

Что такое простейшие ядерные реакции

Механизм ядерных реакций

Условия при которых происходит ядерные реакции

Вероятность ядерной реакции

Закон пропорциональности массы и энергии

Соотношение Эйнштейна

Энергетическим баланс ядерной реакции

Расщепление протоном ядра лития

Аннигиляция реакция образования и аннигиляции пары

Похожие страницы:

Leave a Comment

Ядерные реакции

Общее понятие о ядерных реакциях

Правила записи ядерных реакций

Энергетика ядерных реакций

Энергия связи и стабильность ядер

Реакции распада

Деление ядер

Цепные реакции

Ядерный синтез

Примеры решения задач

7.3.1.Уравнение ядерной реакции

7.3.2. Законы сохранения в ядерных реакциях

7.3.3. Составное ядро

7.3.4. Типы ядерных реакций

7.3.5. Трансурановые элементы

Ядерные реакции

Удельная энергия связи ядер

Энергия ядерных реакций

Примеры решения задач по ядерной реакции