Практическая работа
Построение простой компьютерной модели.
Цель работы: построение простой компьютерной модели, проведение исследования на основе построенной компьютерной модели.
2. Оборудование, приборы, аппаратура, материалы: персональный компьютер с выходом в Интернет.
3. Краткие теоретические сведения.
Моделирование – это модель познания, состоящая в создании и исследовании моделей.
Модель. Каждый объект имеет большое количество различных свойств. В процессе построения модели выделяют главные наиболее существенные для проводимого исследования (с точки зрения цели моделирования) свойства. В процессе исследования аэродинамических качеств модели имела геометрическое подобие оригиналу, но не важен, например, её цвет. При построении электрических схем – необходимо учитывать порядок подключения элементов цепи друг к другу, но не важно их геометрическое расположение друг относительно друга и т.д.
Разные науки исследуют объекты и процессы под разными углами зрения и строят различные типы моделей. В физике изучаются процессы взаимодействия и изменения объектов, в химии – их химический состав, в биологии- строение и поведение живых организмов и т.д.
Возьмём в качестве примера человека, в разных науках он исследуется в рамках различных моделей. В рамках механики его можно рассматривать как материальную точку, в химии – как объект, состоящий из различных химических веществ, в биологии – как систему, стремящуюся к самосохранению и т.д.
Модель – это такой новый объект, который отражает существенные с точки зрения цели проводимого исследования (цели моделирования) свойства изучаемого объекта, явления или процесса.
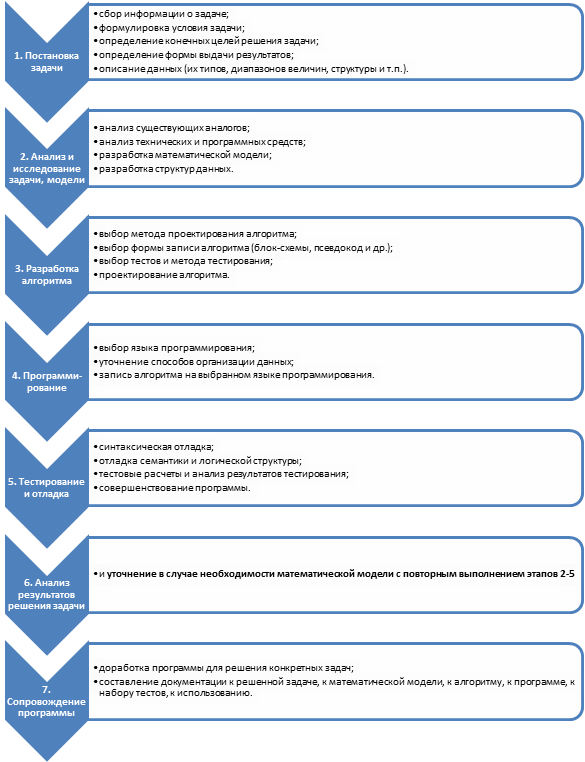
Основные этапы разработки и исследования моделей на компьютере
Использование компьютера для исследования информационных моделей различных объектов и процессов позволяет изучить их изменения в зависимости от значения тех или иных параметров. Процесс разработки моделей и их исследования на компьютере можно разделить на несколько основных этапов.
На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные, с точки зрения целей проводимого исследования (целей моделирования), свойства объекта, а несущественными свойствами пренебрегает.
На втором этапе создаётся формализованная модель, т.е. описательная информационная модель записывается с помощью какого- либо формального языка. В таком модели с помощью формул, уравнений, неравенств и т.д. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.
Однако далеко не всегда удаётся найти формулы, явно выражающие искомые величины через исходные данные. В таких случаях используются приближённые математические методы, позволяющие получать результаты с заданной точностью.
На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, т.н. выразить её на понятном для компьютера языке. Компьютерные модели разрабатывают преимущественно программисты, а пользователи могут проводить компьютерные эксперименты.
В настоящее время широкое распространение получили компьютерные интерактивные визуальные модели. В таких моделях исследователь может менять начальные условия и параметры протекания процессов и наблюдать изменения в поведении модели.
Задание 1. Описать иерархическую систему.
Цель: обучение построению информационных моделей иерархических систем в виде графовых схем – деревьев
Используемые программные средства: MS Word.
Задание.
Постройте родословное древо потомков Владимира Мономаха.
Потомки Владимира Мономаха.
Владимир Мономах умер в 1125г. Он оставил 4 сыновей: Мстислава (год смерти – 1132), Ярополка (1139), Вячеслава Туровского (1154) и Юрия Долгорукого (1157). После Мстислава осталось 3 сына: Изяслав Волынский (1154), Всеволод Новгородский (1138) и Ростислав Смоленский (1168). У Изяслава Волынского был сын Роман (1205), у Романа – Даниил Галицкий (1264). Ростислав Смоленский имел 4 сыновей: Романа (1180), Рюрика (1215), Давида (1197) и Мстислава Храброго (1180). После Романа Ростиславовича остался один сын Мстислав Киевский (1224), после Мстислава Храброго – сын Мстислав Удалой(1228), Юрий Долгорукий имел 3 сыновей: Андрея Боголюбского (1175), Михаила (1177) и Всеволода (1212). Сыновьями Всеволода были Константин (1217), Юрий (1238) и Ярослав (1246). У Ярослава Всеволодовича было 3 сына: Александр Невский (1263), Андрей Суздальский (1264) и Ярослав Тверской (1272). Сыновья Александра Невского: Димитрий Переяславский (1294), Андрей Городецкий (1304) и Даниил Московский (1303). У Андрея Суздальского был сын Василий (годы его жизни неизвестны), у Ярослава Тверского – сын Михаил (1318).
Глядя на полученное древо, ответьте на вопрос: сколько поколений князей оно отражает?
Задание 2. Построить табличную информационную модель
Цель: обучение построению табличных информационных моделей систем;
Используемые программные средства: MS Word.
1. Используйте средства работы с таблицами MS Word, постройте таблицу типа << объект – свойство >> по следующим данным:
Полярная звезда находится в создании Малой Медведицы. Бетельгайзе находится в созвездии Ориона. Расстояние до Спики – 260 сетевых лет. Денеб находится в созвездии Лебедя. Акрукс ярче Солнца в 2200 раз. Расстояние до Капеллы – 46 сетевых лет. Спика находится в созвездии Девы. Антрас находится в созвездии Скорпиона. Расстояние до Арктура – 36 световых лет. Альдебаран ярче Солнца в 165 раз. Бетельгайзе ярче Солнца в 22000 раз. Расстояние до Акрукса – 260 световых лет. Денеб ярче Солнца в 72500 раз. Расстояние до Антареса – 425 световых лет. Альдебаран находится в созвездии Тельца. Антарес ярче Солнца в 6600 раз. Расстояние до Канопуса – 181 световой год. Арктур находится в созвездии Волопаса. Капелла ярче Солнца в 150 раз. Расстояние до Полярной звезды – 780 световых лет. Ригель находится в созвездии Ориона. Спика ярче Солнца в 2200 раз. Акрукс находится в созвездии Южного Креста. Расстояние до Альдебарана – 70 световых лет. Арктур ярче Солнца в 105 раз. Расстояние до Денеба -1600 световых лет. Канопус ярче Солнца в 6600 раз. Капелла находится в созвездии Возничего. Полярная звезда ярче Солнца в 6000 раз. Расстояние до Ригеля – 820 световых лет.
1. Ответьте на вопросы (по таблице):
· какая звезда самая удаленная?
· какая звезда самая близкая?
· какая звезда самая яркая?
· какие звёзды по яркости находятся между звёздами Антарес и Альдебаран?
Подсказка : для ответа на вопросы воспользуйтесь возможностью сортировки таблиц, имеющийся в MS Word (информацию получите в справочном разделе редактора).
2. Используя средства работы с таблицами Ms Word, постройте таблицу типа «объект-объект» по следующим данным:
Время в пути на метро от станции Отрадное до станции Кутузовская занимает 37 мин. Время в пути от станции Театральная до станции Юго-Западная занимает 24 мин. Время в пути от станции Октябрьская до станции Отрадное занимает 32 мин. Время в Пути от станции Курская до станции Кутузовская занимает 23 мин. Время в пути от станции Октябрьская до станции Кутузовская занимает 16 мин. Время в пути от станции Юго-Западная до станции Отрадное занимает 46 мин. Время в пути от станции Театральная до станции Отрадное занимает 27 мин. Время в пути от станции Октябрьская до станции Театральная занимает 13 мин. Время в пути от станции Курская до станции Отрадное занимает 28 мин. Время в пути от станции Театральная до станции Кутузовская занимает 19 мин. Время в пути от станции Октябрьская до станции Юго-Западная занимает 23 мин. Время в пути от станции Юго-Западная до станции Кутузовская занимает 33 мин. Время в пути от станции Курская до станции Театральная занимает 10 мин.
Время в пути от станции Октябрьская до станции Курская занимает 10 мин. Время в пути от станции Курская до станции Юго-Западная занимает 32 мин.
1. Каким свойством таблицы вы пользовались, чтобы заполнить все клетки?
2. Ответьте на вопросы:
какие станции наиболее удаленные друг от друга?
какие станции наиболее близки друг к другу?
в каком порядке располагаются станции метро по мере увеличения их расстояния от ст. Отрадное?
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Модель – это…
2. Формализация – это…
3. Компьютерная модель – это…
4. Классификация моделей?
5. Основные этапы разработки и исследования моделей на компьютере?
6. Приведите пример создания моделей в процессе обучения.
7. В каких случаях могут быть опущены отдельные этапы построения и исследования модели?
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§14. Математическое моделирование.
Постановка задачи
Ключевые слова:
• математическая модель • хорошо поставленные задачи • существенные данные • тестирование модели • компьютерная модель • эксперимент • анализ результатов моделирования
Для того чтобы исследовать модель с помощью компьютера, нужно записать её на каком-то формальном языке. Условия многих задач точнее всего записываются с помощью языка математики — в виде формул. Такие модели называются математическими.
Когда формулы написаны, для исследования модели с помощью компьютера нужно написать программу — составить компьютерную модель. В этом параграфе мы на примерах рассмотрим основные этапы разработки и исследования математических моделей.
Этап постановки задачи — самый важный при моделировании. Если здесь допущена ошибка, то фактически решается совсем не та задача, которую нужно решить, и после завершения моделирования всё придётся начать заново.
Для того чтобы задачу можно было решить, она должна быть хорошо поставлена (корректна). Это значит, что:
• заданы все связи между исходными данными и результатом;
• известны все исходные данные;
• решение существует;
• решение единственно.
К сожалению, в реальных задачах бывает сложно строго доказать существование и единственность решения; более того, задача может иметь множество решений. В таких случаях формулировку задачи можно уточнить, например, так:
• найти любое решение, если оно существует;
• найти все решения в некоторой области (например, все решения уравнения на отрезке [0,1]);
• найти всё множество решений (например, для уравнения sin х = 1).
Приведём примеры плохо поставленных (некорректных) задач.
Задача 1. Уроки в школе начинаются в 8-30. В 10-00 к школе подъехал красный автомобиль. Определите, когда Шурик выйдет играть в футбол.
Задача 2. Мальчик Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Через какое время мяч впервые ударится о земную поверхность?
Задача 3. Решите уравнение sinx = 4.
Задача 4. Найдите функцию, график которой проходит через точки (0, 0) и (1, 1).
Для каждой из этих задач определите, почему их нельзя считать хорошо поставленными.
Что делать, если полученная задача плохо поставлена? Решить её нельзя, поэтому остаётся уточнять условия и исходные данные. Если и это невозможно, нужно вводить допущения — упрощающие предположения, которые позволят сделать задачу хорошо поставленной.
Все дальнейшие рассуждения мы будем проводить для задачи 2.
Она плохо поставлена, потому что неизвестно, из какой точки и под каким углом брошен мяч. Дополним условие, чтобы сделать задачу корректной, например, так: Вася бросает мяч вертикально вверх. В момент броска мяч находится на высоте 1,5 м.
Всегда ли существует решение задачи 2? Да, всегда. По закону всемирного тяготения мяч притягивается к земной поверхности и когда-нибудь упадёт на поверхность.
Единственно ли решение? Да, в этой задаче решение единственно.
Разработка математической модели
На этапе разработки математической модели нужно:
1) выделить исходные данные, существенные для решения данной задачи;
2) построить математическую модель, отражающую только существенные свойства оригинала.
Какие данные в формулировке задачи 2, на ваш взгляд, существенные, а какие — нет?
Введём некоторые допущения:
• мяч — материальная точка (его размеры малы в сравнении с высотой полета);
• сопротивление воздуха не учитывается.
При решении задачи могут использоваться несколько моделей разных типов. Например, для лучшею понимания полезно построить графическую модель задачи (рис. 3.1).

Рис. 3.1За начало координат удобно принять точку, отсуда вылетает мяч. Обозначим через и v0 начальную скорость мяча, через h0 — начальную высоту мяча h0 = 1,5 м) — это исходные данные. Нужный результат — это время полёта мяча tn (рис. 3.2).

Рис. 3.2
Графическая модель не даёт ответа на поставленный вопрос, а только позволяет лучше понять задачу. Поэтому для численных расчётов нужно построить математическую модель — связать с помощью законов физики известные данные и результат.
Координата y при движении тела, брошенного вертикально вверх, вычисляется по формуле:

где g ? 9,81 м/с2 — ускорение свободного падения. Эта формула и представляет собой математическую модель задачи. В ней нет упоминания о Васе, мяче, и т. п., есть только условные обозначения. Мы выполнили формализацию — построили формальную модель на языке математических формул.
По условию задачи нужно найти время tn, при котором мяч упадёт на земную поверхность. Запишите условие «мяч упадёт на землю» в виде формулы и затем запишите уравнение, которое нужно решить.
Тестирование модели
После построения модели её обязательно нужно протестировать (проверить).
Тестирование — это проверка модели на наборе исходных данных с известным результатом.
Например, при моделировании накопления денег в банке сумма не должна меняться при нулевой ставке. Тестирование модели движения судна тоже начинается с простых задач: если штурвал поворачивают влево, судно должно уходить влево, и наоборот.
Удачное тестирование модели не гарантирует, что она правильна; тестирование может только установить ошибочность модели. Чтобы доказать её правильность, нужно проверить модель при всех допустимых исходных данных (в том числе и для тех, для которых правильный ответ неизвестен), а это практически невозможно.
Выполним тестирование математической модели, построенной для нашей задачи:

Используя эту модель, определите:
а) чему равна координата у мяча при t = О?
б) станет ли в какой-то момент координата у равной нулю? Почему?
в) что произойдёт при нулевой начальной скорости?
Все результаты не противоречат теории, поэтому можно считать, что тестирование успешно.
Можно ли считать, что мы доказали правильность модели? Почему?
Руслан построил свою модель движения мяча, брошенного вертикально вверх:

Выполните тестирование модели по тем же критериям, сделайте выводы.
У Марии для той же задачи получилась ещё одна модель:

Выполните тестирование модели по тем же критериям, сделайте выводы.
Построение компьютерной модели
Мы только что получили модель задачи, которая свелась к уравнению:

Это квадратное уравнение можно решить аналитически, получить точный ответ в виде формул. Эти формулы нужно заложить в программу. Приведём программы на алгоритмическом языке и на языке Паскаль, которые находят решение по формулам, известным вам из курса математики:

Изучите программу и ответьте на вопросы.
— Что обозначают переменные а, b, с, D, t1 и t2?
— Какое из двух решений квадратного уравнения нужно выбрать?
— Какой результат возвращает стандартная функция sqrt?
— Может ли случиться так, что уравнение не будет иметь вещественных корней?
— Как изменить начальную высоту шарика и начальную скорость?
В более сложных случаях точное решение найти не удаётся, и приходится строить компьютерную имитационную модель. Для этого можно применить табличный процессор (OpenOffice Calc, Microsoft Excel и т.п.), написать собственную программу на одном из языков программирования или использовать готовую среду для моделирования (например, Simulink или VisSim). К сожалению, такие модели чаще всего дают только приближённое (неточное) решение задачи.
Попробуем написать свою программу для имитационного моделирования. Как вы знаете, компьютер — это дискретное устройство, он работает с дискретными данными. Поэтому нужно выполнить дискретизацию задачи. Мы будем вычислять скорость и высоту шарика только в отдельные моменты времени
— это небольшой интервал времени, который называют интервалом дискретизации. Таким образом, рассматриваются только значения времени
, где
Пусть в начале отрезка [ti, ti+1] (при t = tt) мы знаем координату (высоту) шарика y1 и значение его скорости vt. Для простоты будем считать, что в течение времени tt ? t < ti+1 скорость не изменяется, а в конце отрезка изменяется скачком. Тогда координату и скорость в конце отрезка (в момент ti+1) можно вычислить по формулам:

Здесь g — это ускорение свободного падения, благодаря которому изменяется скорость.
Запишите значения координаты и скорости в конце первого и второго отрезков времени (в моменты t1 и t2), выразив их через известные величины:
Так как в каждый конкретный момент нас интересуют только текущие значения координаты и скорости, в программе будем использовать всего одну переменную у для хранения текущей координаты (т. е. координаты в данный момент времени) и одну переменную v для хранения текущей скорости. Получается такая программа:

Изучите программу и ответьте на вопросы.
— Что обозначают переменные y, v и t?
— Какие начальные значения присваиваются переменным y, v, и t? Почему именно такие?
— Когда работа цикла завершится?
— Может ли случиться так, что цикл будет работать бесконечно?
— Что произойдёт, если в условии работы цикла использовать строгое неравенство y > 0?
— Значение какой переменной выводится в качестве результата? Почему?
— Как изменятся при уменьшении интервала дискретизации
длина текста программы и количество операций, выполняемых компьютером?
Для тестирования этой программы нужно провести контрольные расчёты для простых случаев с известным результатом, например для тех, которые мы ранее использовали при тестировании математической модели. Если проверка прошла удачно (противоречий не обнаружено), можно переходить к компьютерному эксперименту.
Эксперимент с моделью
Эксперимент — это испытание модели в тех условиях, которые нас интересуют (результатов мы заранее не знаем). Например, для модели накопления денег в банке задаётся ненулевая ставка (процент ежегодного увеличения); движение судна моделируется с учётом случайных помех — морского волнения и ветра и т. п.
Объём данных, получаемых при математическом моделировании сложных физических процессов, часто настолько велик (мегабайты и даже гигабайты!), что эти данные сначала сохраняют в виде файлов, а потом обрабатывают специальными программами.
Можно ли слепо верить результатам моделирования? Конечно же нет, ведь мы не проверяли (и не могли проверить!) работу модели в этих условиях. Поэтому необходим анализ результатов.
Анализ результатов
Во-первых, нужно убедиться, что результаты моделирования не противоречат известным из теории фактам, например не нарушаются законы сохранения вещества и энергии.
Например, если оказалось, что при наличии трения объект движется быстрее, чем без трения, то модель, скорее всего, ошибочна.
Во-вторых, необходимо проверить результаты моделирования на реальном объекте — провести эксперимент с оригиналом. Если нам удалось решить поставленную задачу (поведение оригинала соответствует 1) поведению модели), можно считать модель адекватной и работу законченной.
Часто считается, что допустимо расхождение результатов эксперимента и моделирования не более, чем на 10%.
Если же результаты нас не устраивают (поведение объекта и оригинала значительно различаются), требуется вернуться к одному из предыдущих этапов и повторить моделирование, например:
• изменить алгоритм или условия моделирования;
• изменить модель: учесть дополнительные свойства, которые ранее считались несущественными (например, учесть сопротивление воздуха);
• изменить постановку задачи (если выяснилось, что решили не ту задачу, которую нужно было решать).
Возможно, что несоответствие вызвано принятыми допущениями. Так, в задаче с полётом мяча полезно ответить на следующие вопросы, которые помогут выяснить причину неудачи:
— Что изменится, если начальная скорость будет отличаться от заданной?
— Что изменится, если мяч не считать материальной точкой?
— Насколько сильно сопротивление воздуха влияет на результат? И т. д. …
Выводы
• Математическая модель — это модель, записанная в виде математических формул.
• Основные этапы математического моделирования — это постановка задачи, разработка модели, тестирование модели, разработка компьютерной модели, эксперимент с моделью и анализ результатов.
• Задача называется хорошо поставленной, если:
— заданы все связи между исходными данными и результатом;
— известны все исходные данные;
— решение существует;
— решение единственно.
• При построении модели нужно выделить существенные данные, влияющие на результат.
• Тестирование — это проверка модели на простых исходных данных с известным результатом.
• Для проведения компьютерных экспериментов нужно построить компьютерную модель на основе математической модели. Для этого можно написать свою программу, использовать табличный процессор или специальную среду моделирования.
• Компьютерный эксперимент — это испытание модели в тех условиях, для которых мы не знаем результата.
• После выполнения компьютерного эксперимента выполняется анализ результатов.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Что делать, если задача плохо поставлена?
2. Как выделить существенные свойства, которые нужно учесть в модели?
3. В чём различие между математической моделью и словесным описанием?
4. Как вы думаете, перечень этапов моделирования при использовании моделей других типов (не математических) будет таким же или другим?
5. Задача сформулирована так:
Электрик Семён в зелёном комбинезоне едет на красном автомобиле «Лада Калина» из Москвы в Воронеж. Его средняя скорость равна 90 км/ч, причём каждые 2 часа Семён отдыхает по 15 минут. Когда он приедет в Воронеж?
Какие данные здесь существенны, а какие — нет? Каких данных не хватает?
6. Можно ли доказать правильность (или ошибочность) модели с помощью тестирования?
7. Чем эксперимент с моделью отличается от тестирования?
8. Что делать, если после анализа результатов моделирования обнаружилось, что поведение оригинала существенно отличается от поведения модели?
9. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Математическое моделирование»
б) «Программные средства для моделирования»
Оглавление
§13. Модели и моделирование.
§14. Математическое моделирование.
§15. Табличные модели. Диаграммы.
Анастасия Николаевна Королева
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Этапы решения задачи на компьютере
Решение задач при помощи компьютера делится на следующие основные этапы, которые частично осуществляются без участия компьютера.
Математическая модель
Математическая модель строится с использованием математических соотношений (уравнений, неравенств, формул, отношений и т.д.), которые отражают существенные свойства объекта или явления.
Любое природное явление является бесконечно сложным. Для его описания нужно определить его наиболее существенные свойства, закономерности, внутренние связи, роль отдельных характеристик явления. При выделении наиболее важных факторов можно пренебречь менее существенными.
Наиболее эффективно математическая модель реализуется на компьютере в виде вычислительного эксперимента. Если в модели не учесть важные стороны действительности, то можно получить результаты вычислительного эксперимента, которые не будут соответствовать действительности.
При создании математической модели для решения задач необходимо:
- построить предположения, на которых будет основываться математическая модель;
- определить исходные данные и результаты;
- записать математические соотношения, которые связывают результаты с исходными данными.
При создании математических моделей не всегда возможно использование формул, которые явно выражают искомые величины через данные. В таком случае используют математические методы, которые позволяют дать ответы с той или иной степенью точности.
Замечание 1
Помимо создания математической модели явления используют визуально-натурное моделирование, которое обеспечивает отображение исследуемых явлений с помощью средств машинной графики. Визуально-натурная модель представлена в виде своеобразного «компьютерного мультфильма», который снимается в реальном масштабе времени и характеризуется очень высокой наглядностью.
«Этапы решения задач с помощью компьютера. Математическая модель» 👇
Пример построения математической модели
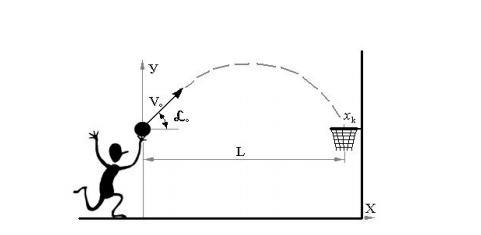
Разработаем математическую модель, которая позволяет выполнить описание полета баскетбольного мяча. Мяч брошен игроком в баскетбольную корзину.
С помощью модели нужно получить возможность:
- находить положение мяча в заданный момент времени;
- вычислять после броска точность попадания мяча в корзину при задании разных начальных параметров.
В качестве исходных данных возьмем:
- массу мяча;
- радиус мяча;
- начальные координаты мяча;
- начальную скорость мяча;
- угол броска мяча;
- координаты центра корзины;
- радиус корзины.
Модель должна не просто описывать движение, но и прогнозировать его результат.
Движение баскетбольного мяча можно описать по законам классической механики Ньютона.
Принимаем следующие гипотезы:
- объект моделирования – баскетбольный мяч с радиусом R;
- мяч – материальная точка, которая имеет массу m и ее положение совпадает с центром масс мяча;
- на движение мяча влияет поле сил тяжести и постоянное ускорение свободного падения g;
- мяч движется в плоскости, которая располагается перпендикулярно поверхности Земли и проходит через точку броска и центр корзины;
- пренебрегается сопротивление воздуха и последствия собственного вращения мяча вокруг центра масс.
Параметры движения мяча:
- координаты x и y;
- проекции скорости vx и vy центра масс мяча.
Получаем, что для определения положения мяча в заданный момент времени нужно записать закон движения центра масс мяча. Таким образом, нужно найти зависимость от времени координат x и y и проекций вектора скорости vx и vy центра мяча.
После математических расчетов получаем следующие зависимости движения мяча:
$V_x (t)=V_0 cosα$, $x(t)=x_0+V_0 cosα t$;
$V_y (t)=V_0 sinα-gt$, $y(t)=y_0+V_0 sinα t- frac{gt^2}{2}$.
Соотношения для t_k принимают вид:
$V_0 sinα-gt_k
Отсюда:
$t_k > frac{V_0 sinα}{g}$, $V_0 sinα t_k- frac{gt_k^2}{2}-(y_k-y_0 )=0$
Получили квадратное уравнение для определения t_k, один из корней которого выбирается по дополнительному условию.
Точность в этом случае будет вычисляться с помощью формулы:
$∆=x_0+V_0 cosα t_k-x_k$.
Рассчитаем штрафной бросок, принимая начальное положение мяча на уровне кольца:
$x_0=y_0=y_k=0, x_k=4.225, V_0=6.44, α=45°, g=9.8$.
Закон движения:
$V_x=4.55, x=4.55t$;
$V_y=4.55-9.80t, y=4.55t-4.9t^2$.
Из соотношений для t_k:
$t_k>0.46, 4.55t_k-4.9t_k^2=0$
получаем $t_k=0.93$.
При этом рассчитаем точность броска:
$∆=x(t_k )-x_k=4.55cdot 0.93-4.225=0.006$.
Получили отличную четкость, т.к. диаметр баскетбольного кольца – 29 см, а мяча – 23–24 см.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Цель урока: изучить моделирование в экономических задачах для оптимального планирования производства.
Задача оптимального планирования производства
Задача 1. Кондитерский цех выпускает два вида тортов: «Лакомка» и «Медовый». На изготовление торта «Лакомка» затрачивается в среднем 0,3 ч, а на изготовление торта «Медовый» — 0,4 ч. Рабочий день длится 8 ч. Для хранения готовой продукции в цехе имеется холодильник на 25 тортов. Торт «Лакомка» продается по цене 12 руб., а торт «Медовый» — по цене 15 руб. Каким должен быть дневной план производства тортов, чтобы объем производства в денежном выражении был максимальным?
При установке программы Excel ее надстройки автоматически не устанавливаются.
Для установки надстройки Поиск решения следует выбрать пункт Параметры Excel. Открывается диалоговое окно Параметры.
В левом вертикальном меню этого диалогового окна выбирают пункт Надстройки. Открывается вкладка Надстройки.
На вкладке Надстройки в ее последнем разделе Управление: размещено поле, в котором должна находиться надпись Надстройки Excel.

Правее надписи в текстовом поле щелкают по кнопке Перейти … . Появляется еще одно диалоговое окно Надстройки.
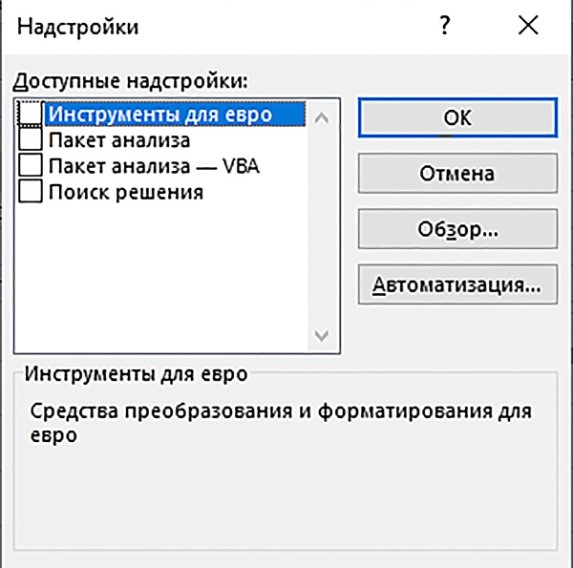
В окне Надстройки отмечают пункт Поиск решения и щелкают по кнопке ОK. Надстройка Поиск решения устанавливается.
Построение компьютерной расчетной модели
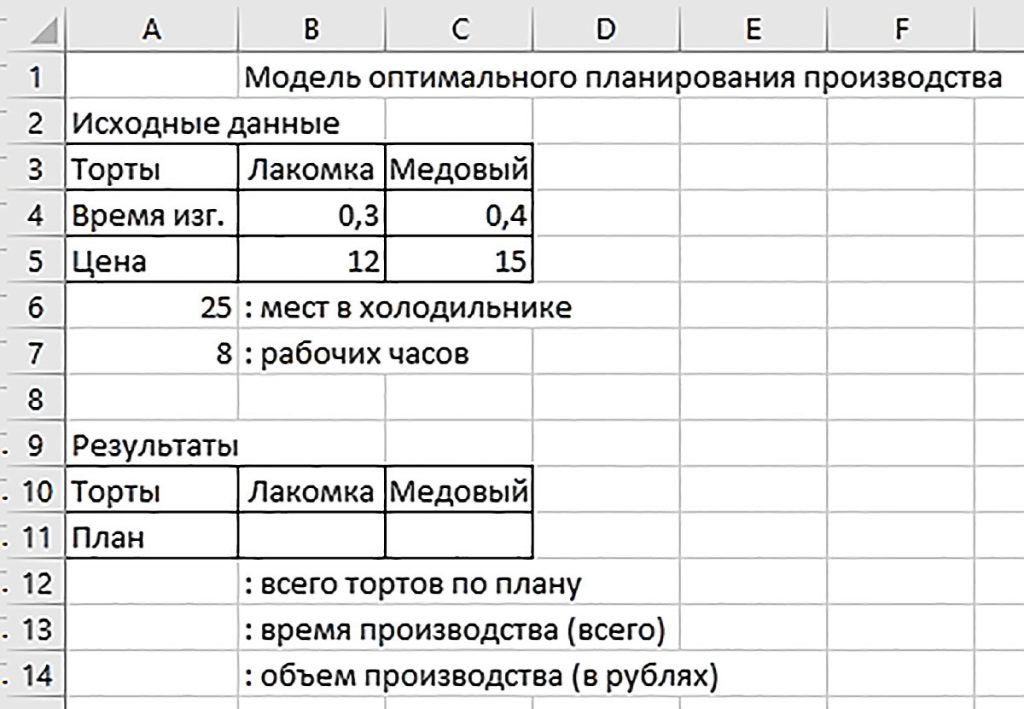
Вводим формулы
A12: =B11+C11
A13: =B4*B11+C4*C11
A14: =B5*B11+C5*C11
Работа с надстройкой «Поиск решения»
Надстройка Поиск решения вызывается на вкладке Данные в группе Анализ инструментом Поиск решения. Появляется диалоговое окно Параметры поиска решения
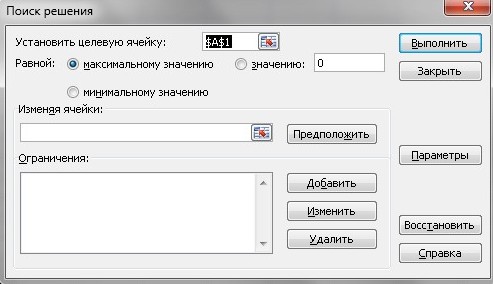
В поле первой строки следует ввести ссылку на ячейку со значением целевой функции. Если там есть данные, то их удаляем и щелкаем по ячейке A14. В строке Равной: должен быть выбран критерий Максимум.
В поле ввода Изменяя ячейки: вводим диапазон B11:C11, выделяя его в таблице протяжкой мыши.
Далее нужно ввести ограничения задачи в большое поле В соответствии с ограничениями:
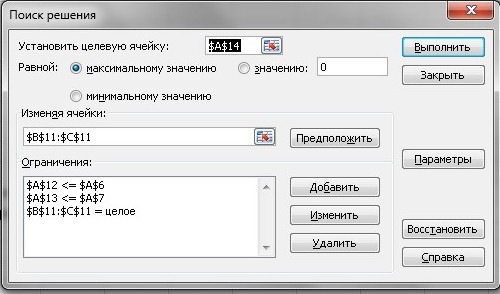
Выбираем Параметры Неотрицательные значения.
Когда параметры поиска введены, нужно щелкнуть по кнопке Выполнить. Расчет проводится практически мгновенно. В разделе Результаты модели появляются искомые значения плановых показателей. Также появляется окно Результаты поиска решения, в котором предлагаются способы сохранения данных на листе книги Excel.
Задача оптимального планирования времени производства
Задача 2. Кондитерский цех выпускает два вида тортов: «Лакомка» и «Медовый». На изготовление торта «Лакомка» затрачивается в среднем 0,3 ч, а на изготовление торта «Медовый» — 0,4 ч. Для хранения готовой продукции в цехе имеется холодильник на 25 тортов. Торт «Лакомка» продается по цене 12 руб., а торт «Медовый» — по цене 15 руб. Каким должен быть план производства, чтобы заказ стоимостью не менее 150 руб. был выполнен за минимальное время?
На новый лист рабочей книги электронных таблиц вставим копию компьютерной расчетной модели, построенной для решения задачи 1.
Для этого открываем лист с компьютерной моделью задачи 1 оптимального планирования производства. Щелкнув по кнопке над заголовком первой строки таблицы, выделяем весь лист и копируем его в буфер обмена любым способом. Затем открываем новый лист рабочей книги, также выделяем его весь и вставляем скопированный лист каким угодно способом.
Меняем часть заголовка модели.
В ячейку B8 вводим текст: объем заказа (в рублях), а в ячейку A8 — число 150.
В диалоговом окне Параметры поиска решения в поле Оптимизировать целевую функцию: необходимо внести ссылку на ячейку A13, выбрать критерий — Минимум, ввести диапазон изменяемых ячеек — B11:C11.
Далее следует ввести ограничения:
A12 ≤ A6,
A14 ≥ A8,
B11:C11 = целое.
Выбрать параметры Неотрицательные значения.
Щелчок по кнопке Выполнить запускает процесс решения задачи.

Задания по теме урока
1. Повторите на компьютере построение компьютерной расчетной модели для задач 1 и 2.
2. Решите следующую задачу. Цех мебельной фабрики выпускает детские мебельные наборы «Буслик» и «Гном». Для каждого набора «Буслик» требуется 0,2 ч машинного времени и 3,5 м2 мебельного щита, а для каждого набора «Гном» требуется 0,5 ч машинного времени и 4 м2 мебельного щита. В неделю можно использовать не более 150 ч машинного времени и не более 1600 м2 мебельных щитов. Набор «Буслик» продается по цене 130 руб., а набор «Гном» — по цене 200 руб. Сколько наборов каждого вида следует выпускать в неделю для достижения максимального объема производства в денежном выражении?
3. Решите следующую задачу. Цех мебельной фабрики выпускает детские мебельные наборы «Буслик» и «Гном». Для каждого набора «Буслик» требуется 0,2 ч машинного времени и 3,5 м2 мебельного щита, а для каждого набора «Гном» требуется 0,5 ч машинного времени и 4 м2 мебельного щита. В неделю можно использовать не более 1600 м2 мебельных щитов. Набор «Буслик» продается по цене 130 руб., а набор «Гном» — по цене 200 руб. Сколько наборов каждого вида следует выпускать в неделю, чтобы объем производства в денежном выражении был не ниже 60 000 руб., а использование машинного времени было минимальным?

Домашнее задание
§ 14.1 электронного пособия и § 15.1 электронного пособия, ответить на вопросы
Форма отправки
Форма видна только зарегистрированным пользователям.
Моделирование в электронных таблицах
- Шевякова Екатерина Вячеславовна, заместитель директора по учебно-воспитательной работе
Разделы: Информатика
Урок № 1. Задача о попадании точки в заданную фигуру. 2 часа.
Цель урока: построить в Excel компьютерную модель заданной на плоскости фигуры, исследовать ее, вводя координаты различных точек.
Учащиеся должны уметь: строить чертеж в Word, строить математическую модель фигуры, строить компьютерную модель в Excel.
Решение задачи о попадании точки в фигуру на примерах с использованием логических функций Excel. 40 мин.
Спонсор поста: Clash of Clans
Практическая работа: решить задачу для заданной фигуры в Excel, построить чертеж фигуры в Word, построить математическую модель, построить компьютерную модель, вставить решение из Excel в Word как объект с целью дальнейшего тестирования и проверки задачи. 40 мин.
Домашнее задание: построить математическую и компьютерную модель (программа на Паскале) для заданной фигуры.
Математическая модель: рис. 2
Компьютерная модель:
формула в Excel:
=ЕСЛИ(И(СТЕПЕНЬ(A2;2)+СТЕПЕНЬ(B2;2)>=4;СТЕПЕНЬ(A2;2)+СТЕПЕНЬ(B2;2)=16);»попадает»;»не попадает»)
Рассмотрим еще один пример: рис 3. Разделим фигуру на две части.
Математическая модель: 1 часть: рис. 4 2 часть: рис. 5
Компьютерная модель:
формула в Excel:
=ЕСЛИ(ИЛИ(И(A2>=-2; А2<=0;B2>=0;B2<=3);И(СТЕПЕНЬ(А2;2)+СТЕПЕНЬ(В2;2)<=9;
A2>=0;B2>=0));»попадает»;»не попадает«)
Значения координат точки можно задать случайными числами. Для этого использовать встроенную функцию СЛЧИС(), которая выдает случайное число на отрезке[0;1] .
Для вставки объекта Excel в документ Word необходимо:
сохранить решение задачи в Excel;
в документе Word установить курсор на место вставки;
Вставка — Объект — создать из файла — Обзор — Найти файл с решением задачи — Вставить.
Учащимся выдаются заранее подготовленные карточки с различными фигурами.
Цель урока: построить имитационную модель игры.
Учащиеся должны знать: понятие модели, случайного процесса, формализации, информационной модели, компьютерной модели, основные приемы работы в Excel, логические функции Excel, функцию случайных чисел.
Учащиеся должны уметь: работать с электронной таблицей, проводить формализацию задачи, строить информационную и компьютерную модель задачи.
Разбор задачи «Кубики» и задачи о проверке знания таблицы умножения — объяснение у доски (40 мин).
Самостоятельная работа: задача «Домино» — работа за компьютером (40 мин).
Задача «Кубики».
Смоделируйте игру «Кубики»: двое игроков бросают игральный кубик. Определить результат игры.
Информационная модель:
Выходные параметры: результат — кто победил.
Связь: если х>у, то победил первый игрок, иначе если х=у, то — ничья, иначе — победил второй игрок. Можно связь представить в виде блок-схемы.
Компьютерная модель:
Очки, выпавшие у первого и второго игрока, выводятся только после введения имен игроков. Очистка таблицы производится клавишей F9.
В ячейке первого игрока формула:
=ЕСЛИ(ЕПУСТО(B4);»»;ОКРУГЛ(СЛЧИС()*6;0))
В ячейке второго игрока формула:
=ЕСЛИ(ЕПУСТО(B2);»»;ОКРУГЛ(СЛЧИС()*6;0))
В ячейке результата формула:
=ЕСЛИ(ИЛИ(ЕПУСТО(B2);ЕПУСТО(B4));»»;ЕСЛИ(B3>B5;»выиграл первый»;ЕСЛИ(B3<B5;»выиграл второй»;»ничья»)))
Постановка задачи.
Смоделируйте работу программы проверки знания таблицы умножения.
Информационная модель:
Входные параметры: х,у — сомножители, р — ответ, вводимый учеником.
Связь: если р=х*у, то результат — сообщение: ответ правильный, иначе — результат: сообщение об ошибке. Связь также можно представить в виде блок-схемы.
Для вычисления сомножителей применяются формулы:
=ОКРУГЛ(СЛЧИС()*9;0)
Для проверки результата используется формула:
=ЕСЛИ(ИЛИ(ЕПУСТО(B2);ЕПУСТО(D2);ЕПУСТО(B3));»»;ЕСЛИ(B2*D2=B3;»правильно»;»ошибка«))
Постановка задачи:
Смоделируйте выбор наугад двух костей домино из полного набора костей этой игры (0-0, 0-1, …, 6-6). Определить, можно ли приставить эти кости одна к другой в соответствии с правилами домино.
Информационная модель:
Выходные параметры: ответ: можно приставить кости одну к другой или нет.
Связь: если х1=х2 или х1=у2 или у1=х2 или у1=у2, то ответ: можно, иначе — ответ: нельзя. Связь можно представить в виде блок-схемы.
Компьютерная модель:
Для получения значений «костей» домино используются формулы:
=ОКРУГЛ(СЛЧИС()*6;0)
Для определения результата используется формула:
=ЕСЛИ(ИЛИ(B2=B3;B2=D3;D2=B3;D2=D3);»можно»;»нельзя»)
Урок № 3. Моделирование биоритмов. 2 часа.
Цель урока: составить модель биоритмов для каждого учащегося от указанной текущей даты на месяц вперед для дальнейшего анализа модели, построить суммарные биоритмы для определения совместимости двух человек.
Учащиеся должны знать: понятие модели, биоритмов.
План урока.
Постановка задачи. 5 мин.
Математическая модель. 5 мин.
Построение компьютерной модели в среде Excel. 20 мин.
Анализ результатов моделирования. 10 мин.
Построение суммарных биоритмов. 20 мин.
Оформление работы. 20 мин.
Домашнее задание: построить биоритмы на текущий месяц членам своей семьи.
Постановка задачи.
За точку отсчета всех биоритмов берется день рождения человека. В этот момент все три биоритма пересекают ось абсцисс, т.к. процесс появления на свет очень труден для человека, ведь происходит смена водной среды на воздушную. Происходит глобальная перестройка всего организма.
Физический биоритм характеризует жизненные силы человека. Периодичность ритма составляет 23 дня.
Эмоциональный биоритм характеризует внутренний настрой человека, его возбудимость, способность эмоционального восприятия окружающего. Продолжительность периода эмоционального цикла равна 28 дням.
Третий биоритм характеризует мыслительные способности, интеллектуальное состояние человека. Его цикличность — 33 дня.
Физический цикл F(x)=sin
Эмоциональный цикл F(x)=sin
Интеллектуальный цикл F(x)=sin, где х — возраст человека в днях.
Компьютерная модель.
заполнить вниз
Формулы для расчета кривых:
В ячейке А3 находится дата рождения, в ячейке В3 — первое число расчетного периода.
Физическое состояние Эмоциональное состояние Интеллект. состояние
заполнить вниз
Проанализировав диаграмму, выбрать неблагоприятные дни для сдачи зачета по физкультуре.
Выбрать день для похода в цирк.
Выбрать дни, когда ответы на уроках будут наиболее (наименее) удачными.
Как вы думаете, что будет показывать график, если сложить все три биоритма? Можно ли будет по нему что-либо определить?
Построить модель физической, эмоциональной и интеллектуальной совместимости двух друзей.
Выделить рассчитанные три столбца своих биоритмов, скопировать и вставить в другие столбцы только значения. Ввести дату рождения друга. Провести расчет суммарных биоритмов. По суммарным столбцам построить диаграмму совместимости. Максимальные значения по оси Y на диаграмме указывают на степень совместимости: если они превышают 1,5 , то вы с другом в хорошем контакте.
Что показывают суммарные графики одноименных биоритмов? Что можно по ним определить?
Какая из трех кривых показывает наилучшую (наихудшую) совместимость с другом?
Выбрать наиболее благоприятные дни для совместного участия с другом в командной игре, например в футбольном матче. Можно ли вообще вам с другом выступать в соревнованиях единой командой? Ответ обоснуйте.
Определите дни, когда вам не следует общаться. Что можно ожидать в эти дни?
Спрогнозировать результат совместного с другом разгадывания кроссворда в указанные дни месяца, например, 10-го, 15-го и 21-го.
В какой области совместной деятельности вы с другом могли бы преуспеть?
Не закрывая Excel, открыть документ Word. Скопировать в него обе диаграммы (собственных и суммарных биоритмов). Ответы на вопросы оформить в виде списка с ответами по собственным и суммарным биоритмам. Сохранить текстовый файл на учительском компьютере (файл — сохранить как — мое сетевое окружение — соседние компьютеры — Teacher — Мои документы).
Литература: