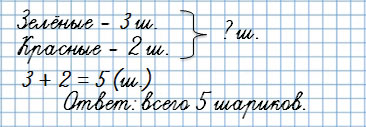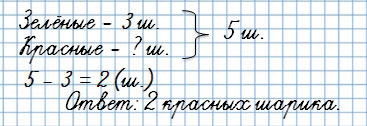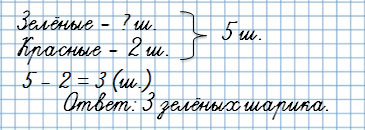Как составить задачу обратную данной 2 класс примеры задач по математике - Исправление недочетов и поиск решений вместе с Examum.ru

Математика, 2 класс

Урок № 10. Задачи, обратные данной

Перечень вопросов, рассматриваемых в теме:

Что такое задачи, обратные данной?
Как составлять и решать обратные задачи?

Глоссарий по теме:

Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27

2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17

3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31

Теоретический материал для самостоятельного изучения

Решим три задачи.

Составим по рисунку первую задачу.

В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?

Составим схематический рисунок.

Решим задачу:

10 + 8 = 18 (д.)

Ответ: 18 детей в классе.

Составим вторую задачу.

В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?

Решим задачу:

18 – 10 = 8 (м.)

Ответ: 8 мальчиков в классе.

Составим третью задачу.

В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?

Решим задачу:

18 – 8 = 10 (д.)

Ответ: 10 девочек в классе.

Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.

Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.

Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.

Тренировочные задания.

1. Решите задачу. Выберите задачи, обратные данной.

Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?

Варианты ответов:

1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?

2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?

3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?

Правильные варианты:

1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?

2 . Восстановите пропуски в задачах.

1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?

2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?

3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?

Варианты ответов:

30, 20, ясных, пасмурных, июне

Правильный вариант:

1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?

2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?

3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?

Источник

Что значит «обратная задача» в математике (1, 2, 3, 4 класс)?

Как записать и решить обратную задачу, пример?

В математике обратная задача составляется на основании какой-либо имеющейся задачи.

В обратных задачах искомые данные уже известны.

Требуется найти одну из величин, которые были даны в условии исходной задачи.

Пример 1

Исходная задача.

В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм.

Требуется узнать, на сколько груши дороже яблок.

Для решения этой задачи нужно найти разницу между 2 числами — стоимостью груш и стоимостью яблок.

150 — 120 = 30 (руб.)

Таким образом, груши дороже яблок на 30 рублей.

Обратная задача.

Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей.

Будем находить либо стоимость яблок, либо стоимость груш — то есть можно составить 2 разных обратных задачи.

1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши?

Решение:

120 + 30 = 150 (руб.)

2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки?

Решение:

150 — 30 = 120 (руб.)

Пример 2

Исходная задача.

Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм.

Сколько он должен заплатить?

Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами.

1 килограмм = 1000 грамм.

500 грамм — это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2.

Таким образом, покупатель заплатит не 200 рублей, а только половину:

200 / 2 = 100 (руб.)

Обратная задача.

Здесь нам будет известна цена покупки, то есть 100 рублей.

Можно найти, например, стоимость за 1 килограмм.

Вот формулировка подобной задачи:

Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины?

Решение:

1) 1 килограмм — это 1000 грамм.

1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм.

2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.)

модератор выбрал этот ответ лучшим

Математический термин «обратная задача» включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная.

Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию.

Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи.

Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи.

Это мое определение термину «обратная задача», простого определения для начальной школы я не нашла.

Проще пояснить на примерах.

Исходная задача:

Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама?

Решение

5+7=12 (шт.) выпечки купила мама.

Обратная ей задача:

Обратных задач можно в этом случае составить две:

1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама?

Решение

12-5=7 (к.) купила мама.

2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама?

Решение

12-7=5 (п.) купила мама.

Марина Вологда
[295K]

3 года назад

Обратная задача — это такая задача, в которой все искомые величины уже известны.

Из этих известных величин и составляем обратную задачу.

Например, нам дана задача:

В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин.

Составляем обратную задачу:

1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5.

Решение: 8-5 = 3 машины красного цвета.

2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета?

Решение: 8-3 = 5 машин белого цвета.

Алиса в Стране
[364K]

3 года назад

Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время.

Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время):

Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость):

Не знаю, кто их назвал «обратными» потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным.

Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое — вместо сложения — вычитание, вместо деления — умножение (как и наоборот)

Вот пример.

У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ — пять.

Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ — три.

Zummy out off
[226K]

3 года назад

Обратная задача в математике — это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи.

Составление обратных задач тренирует «мозги» для решения задач в математике.

Пример составления обратной задачи.

Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши?

Решение: 20-12=8. Ответ: 8 рублей осталось у Маши.

Обратная задача.

В условие задачи надо включить сумму сдачи 8 руб.

Составляем задачу:

Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради?

Решение: 12+8=20. Ответ: 20 рублей было у Маши.

Бархатные лапки
[382K]

3 года назад

Обратная задача составляется на основе уже имеющейся решенной задачи.

В обратной задаче требуется узнать то, что было известно в нашей задаче.

Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15

Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок.

Решение: 15 — 5 = 10 яблок у Иры.

Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок.

Решение: 15 — 10 = 5, у Маши 5 яблок.

KritikSPb
[93.7K]

4 года назад

Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной.

Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте?

Решение: 10 / 5 = 2 часа.

А теперь обратная задача:

За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час.

Решение: 2 * 5 = 10 км.

Для составления обратной задачи необходимо решить исходную.

Бекки Шарп
[71.2K]

3 года назад

Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно.

Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок)

Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши — 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок)

Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи — 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок)

Val111111
[506]

4 года назад

Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти.

Пример, есть три яблока. Два забрали. Сколько осталось?

Обратная задачка: Забрали два яблока, осталось одно, сколько было?

TheSun
[2.3K]

3 года назад

В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат.

Рассмотрим на примере.

У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей?

4+3=7 (шт.) мячей у Маши.

Теперь обратная задача.

У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей?

7-4=3 (шт.) зелёных мяча у Маши.

Знаете ответ?

Источник

Главная
Справочники
Справочник по математике для начальной школы
Задачи
Обратные задачи

В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.

Прямая задача:

У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?

Первая обратная задача:

У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?

Ты видишь, что известная величина — красные шарики — стала неизвестной.

А неизвестная величина — общее количество шариков — стало известной.

Вторая обратная задача:

У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?

Ты видишь, что известная величина — зелёные шарики — стала неизвестной.

А неизвестная величина — общее количество шариков — стало известной.

ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.

Советуем посмотреть:

Образцы оформления задачи

Цена. Количество. Стоимость

Скорость, время, расстояние

Задачи

Правило встречается в следующих упражнениях:

1 класс

Страница 48. Урок 25,
Петерсон, Учебник, часть 2

Страница 50. Урок 26,
Петерсон, Учебник, часть 2

Страница 53. Урок 27,
Петерсон, Учебник, часть 2

Страница 60. Урок 31,
Петерсон, Учебник, часть 2

Страница 63. Урок 32,
Петерсон, Учебник, часть 2

Страница 8. Урок 5,
Петерсон, Учебник, часть 3

Страница 25. Урок 13,
Петерсон, Учебник, часть 3

Страница 33. Урок 17,
Петерсон, Учебник, часть 3

Страница 65. Урок 33,
Петерсон, Учебник, часть 3

Страница 91. Повторение,
Петерсон, Учебник, часть 3

2 класс

Страница 39,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 12. Урок 4,
Петерсон, Учебник, часть 3

3 класс

Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 35. Урок 13,
Петерсон, Учебник, часть 1

Страница 74. Повторение,
Петерсон, Учебник, часть 3

4 класс

Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 87,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 49,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2

Источник

Примеры решения прямых и обратных задач по математике

Запомни:

Решение обратной задачи представляет проверку решения прямой задачи.
Каждому действию прямой задачи соответствует действие той же ступени в обратной задаче.
Количество комбинаций при составлении обратной задачи ограниченно: оно равно количеству данных в задаче.
Количество действий при решении прямой и обратной задач совпадает (это правило нарушается крайне редко).

Пример 1.

Прямая задача
Решение: 16 · 7 = 112 руб. Ответ: 112 рублей.
Вася Перепёлкин купил 7 банок сока по 16 рублей. Сколько заплатил он за свою покупку?
Цена 1 банки с соком	Количество	Стоимость?
16 руб.	7 банок	? руб.

Обратная задача
Решение: 112 : 16 = 7 (банок) Ответ: 7 банок
Вася Перепёлкин купил сок по 16 рублей заплатив 112 рублей. Сколько банок с соком он купил?
Цена 1 банки с соком	Количество	Стоимость?
16 руб.	? банок.	112 руб.

Обратная задача
Решение: 112 : 7 = 16 руб. Ответ: 16 рублей
Вася Перепёлкин купил 7 банок сока заплатив 112 рублей. Сколько стоила банка с соком?
Цена 1 банки с соком	Количество	Стоимость?
? руб.	7 банок.	112 руб.

Пример 2.

Прямая задача
Решение: 420 : 6 = 70 руб. Ответ: 70 рублей.
В магазине за шесть чашек мама заплатила 420 рублей. Сколько стоит одна чашка?
Цена 1 чашки	Количество	Стоимость?
? руб.	6 чашек	420 руб.

Обратная задача
Решение: 70 · 6 = 420 руб. Ответ: 420 рублей.
В магазине мама купила 6 чашек по 70 рублей. Сколько стоила вся покупка?
Цена 1 чашки	Количество	Стоимость?
70 руб.	6 банок.	? руб.

Обратная задача
Решение: 420 : 70 = 6 (чашек) Ответ: 6 чашек
В магазине мама купила чашки по 70 рублей заплатив продавцу 420 рублей. Сколько чашек она купила?
Цена 1 чашки	Количество	Стоимость?
70 руб.	? руб.	420 руб.

Коротко:

Известные и великие математики

ученые древности, средневековья и современности, и их вклад в мировую науку

Карл Фридрих Гаусс

математик, механик

Дата рождения: 30 апреля 1777 г

Место рождения: Брауншвейг, Брауншвейг-Вольфенбюттель

Дата смерти: 23 февраля 1855 г. (77 лет)

Биография

Родился в немецком герцогстве Брауншвейг. Дед Гаусса был бедным крестьянином; отец, Гебхард Дитрих Гаусс, — садовником, каменщиком, смотрителем каналов; мать, Доротея Бенц, — дочерью каменщика. Будучи неграмотной, мать не записала дату рождения сына, запомнив только, что он родился в среду, за восемь дней до праздника Вознесения, который отмечается спустя 40 дней после Пасхи. В 1799 г. Гаусс вычислил точную дату своего рождения, разработав метод определения даты Пасхи на любой год.

Уже в двухлетнем возрасте мальчик показал себя вундеркиндом. В три года он умел читать и писать, даже исправлял арифметические ошибки отца. Известна история, в которой юный Гаусс выполнил некое арифметическое вычисление гораздо быстрее всех одноклассников; обычно при изложении этого эпизода упоминается вычисление суммы чисел от 1 до 100, но первоисточник этого неизвестен. До самой старости он привык большую часть вычислений производить в уме.

Гаусс некоторое время колебался в выборе между филологией и математикой, но предпочёл последнюю. Он очень любил латинский язык и значительную часть своих трудов написал на латыни; любил английскую и французскую литературу, которые читал в подлиннике. В возрасте 62 лет Гаусс начал изучать русский язык, чтобы ознакомиться с трудами Лобачевского, и вполне преуспел в этом деле.

В колледже Гаусс изучил труды Ньютона, Эйлера, Лагранжа. Уже там он сделал несколько открытий в теории чисел, в том числе доказал закон взаимности квадратичных вычетов.

С 1795 по 1798 год Гаусс учился в Гёттингенском университете, где его учителем был А. Г. Кестнер. Это — наиболее плодотворный период в жизни Гаусса.

1796 год: Гаусс доказал возможность построения с помощью циркуля и линейки правильного семнадцатиугольника. Более того, он разрешил проблему построения правильных многоугольников до конца и нашёл критерий возможности построения правильного n-угольника с помощью циркуля и линейки.

В 1798 году Гаусс вернулся в Брауншвейг и жил там до 1807 года. С 1799 года Гаусс — приват-доцент Брауншвейгского университета. 1801 год: избирается членом-корреспондентом Петербургской Академии наук.

Несколько стран наперебой приглашают Гаусса на службу. По рекомендации Александра фон Гумбольдта Гаусса назначают профессором в Гёттингене и директором Гёттингенской обсерватории. Эту должность он занимал до самой смерти.

Чем знаменит:

Алгоритм Гаусса вычисления даты Пасхи
Метод Гаусса для решения систем линейных уравнений
Интерполяционная формула Гаусса
Гауссова кривизна
Гауссовы целые числа
Квадратурная формула Гаусса — Лагерра
Гипергеометрическая функция Гаусса
Метод Гаусса — Жордана
Отображение Гаусса
Проекция Гаусса — Крюгера
Пушка Гаусса
Признак Гаусса
Методы Гаусса — Зейделя
Прямая Гаусса
Ряд Гаусса
Система единиц Гаусса для измерения электромагнитных величин
Формула Гаусса — Бонне о гауссовой кривизне
Теорема Гаусса — Лукаса о корнях комплексного многочлена
Теорема Гаусса — Остроградского в векторном анализе
Теорема Гаусса — Ванцеля о построении правильных многоугольников и числах Ферма

В честь Гаусса названы:

Кратер на Луне
Астероид № 1001 (Gaussia)
Гаусс — единица измерения магнитной индукции в системе СГС
Одна из фундаментальных астрономических постоянных — постоянная Гаусса
Вулкан Гауссберг в Антарктиде
Изобретённый им измерительный инструмент «гелиотроп»

Источник

Прочитай задачи, найди задачи, обратные данной. Раскрась их жёлтым цветом. Реши их ( запиши краткое условие, начерти схему, решение и ответ)

Мама помыла 5 чашек и 6 тарелок. Сколько всего предметов посуды помыла мама?	В коробке лежало несколько карандашей. Когда 4 карандаша забрали из коробки, то там осталось ещё 8. Сколько карандашей было в коробке сначала?	У Нади было 19 кнопок, а у Сары – на 10 кнопок меньше. Сколько кнопок у Сары?
У Леры было 11 открыток, а у Коли -8 открыток. На сколько больше открыток у Леры, чем у Коли?	Мама помыла 11 чашек и тарелок. Из них помыла 5 чашек. Сколько тарелок помыла мама?	Мама помыла 11 чашек и тарелок. Из них помыла 6 тарелок. Сколько чашек помыла мама?

Мама помыла 5 чашек и 6 тарелок. Сколько всего предметов посуды помыла мама?	В коробке лежало несколько карандашей. Когда 4 карандаша забрали из коробки, то там осталось ещё 8. Сколько карандашей было в коробке сначала?	У Нади было 19 кнопок, а у Сары – на 10 кнопок меньше. Сколько кнопок у Сары?
У Леры было 11 открыток, а у Коли -8 открыток. На сколько больше открыток у Леры, чем у Коли?	Мама помыла 11 чашек и тарелок. Из них помыла 5 чашек. Сколько тарелок помыла мама?	Мама помыла 11 чашек и тарелок. Из них помыла 6 тарелок. Сколько чашек помыла мама?

Мама помыла 5 чашек и 6 тарелок. Сколько всего предметов посуды помыла мама?	В коробке лежало несколько карандашей. Когда 4 карандаша забрали из коробки, то там осталось ещё 8. Сколько карандашей было в коробке сначала?	У Нади было 19 кнопок, а у Сары – на 10 кнопок меньше. Сколько кнопок у Сары?
У Леры было 11 открыток, а у Коли -8 открыток. На сколько больше открыток у Леры, чем у Коли?	Мама помыла 11 чашек и тарелок. Из них помыла 5 чашек. Сколько тарелок помыла мама?	Мама помыла 11 чашек и тарелок. Из них помыла 6 тарелок. Сколько чашек помыла мама?

Источник