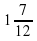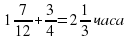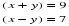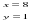Как составить задачу по графику по математике - Исправление недочетов и поиск решений вместе с Examum.ru

7 класс. Графики. Решение текстовых задач с помощью графика.

Рассмотрим следующий пример.

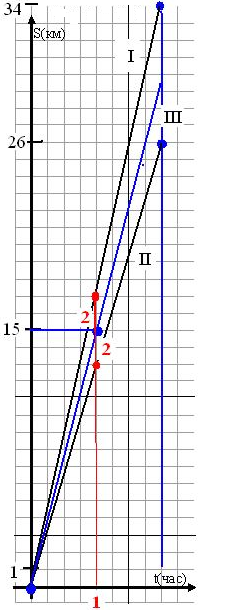
1. Ученики 7-«О» класса отправились пешком из города к озеру в 9 часов утра. Имеется траектория движения учащихся. Можно ли по графику движения определить:

а) сколько времени ученики были в пути?

б) с какой скоростью они двигались в 13 часов дня?

в) когда скорость ребят была большей

в 10 часов или в 12 часов?

Рис. 1.

С помощью графика можно ответить на все эти вопросы. По оси ОХ отмечаем время, а по оси ОУ – расстояние.

а) ученики были в пути с 9-12 ч и с 14-18 ч; итого: (12-9)+(18-14)=3+4=7.

б) ученики в 13 ч шли со скоростью 0, т.е. они находились у озера и их маршрут не менялся. На графике этот маршрут ВС, этот отрезок параллелен оси ОУ.

в) определим в какой момент времени скорость ребят была наибольшей., где v— скорость в км/ч, S- расстояние в км, а t- время в часах. = 5 км/ч т.к. t =10-9=1ч, S=5 км; в 12 ч: = 5 км/ч т.к. t=12-9=3ч, S=15 км и ; или в 11ч S=10 км, а в 12 ч S=15 км, найдем их разности и вычислим скорость, с которой шли ребята. Следовательно скорость, с которой шли ученики и в 10ч и в 12ч, была одинаковой.

Используя траектории, можно решать много задач на движение.

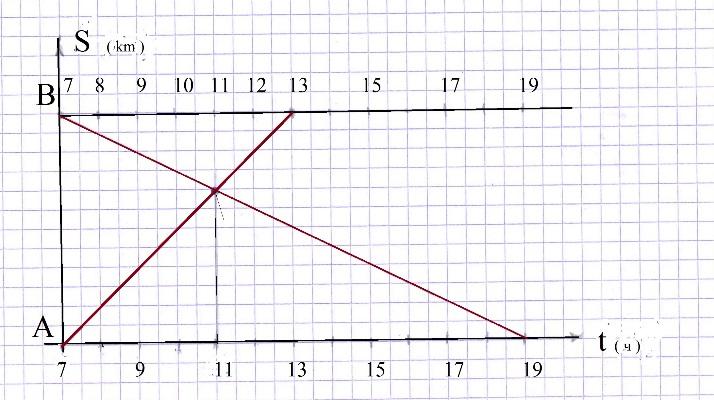
Задача 2. Из пунктов А и В навстречу друг другу с постоянными скоростями вышли 2 путника. Первый вышел из А в 7 часов и пришёл в В в 13 часов. Второй путник вышел из В в 7часов и пришёл в А в 19 часов. В какое время путники встретились?

Решение. 1) Построим траектории движения путников. Расстояние от А до В неизвестно, поэтому на оси расстояний отложим любой отрезок, например, 6 см (рис.2). По оси времени возьмём масштаб: 1 см — 1час. 2) Соединив отрезком прямой точки начала и конца пути каждого путника, получим траектории их движения. Точка пересечения этих траекторий соответствует моменту встречи. 3) Время встречи – 11 часов.

Рис.2

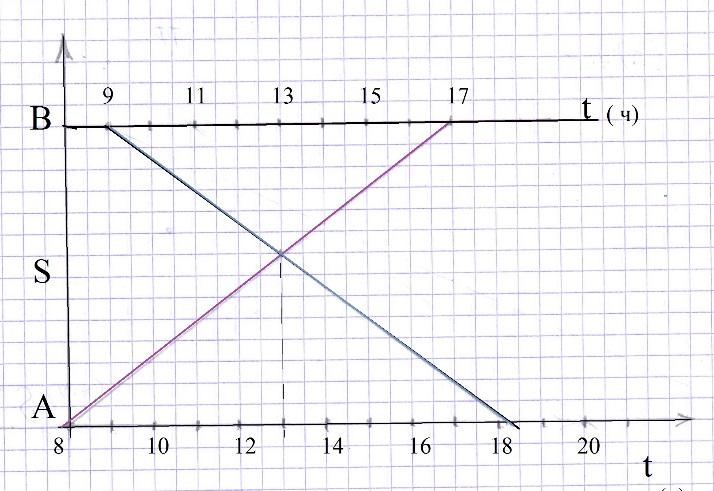
Задача 3. Алдар Косе приехал в 8 часов утра на поезде в Астану и пошел с вокзала в аул к своему другу, живущему недалеко от города, планируя прийти туда в 17 часов. В 9 часов из этого аула вышел Айдар в город Астану. Успеет ли Айдар на поезд, отходящий из Астаны в 20 часов, если встреча Алдара Косе и Айдара произошла в 13 часов?

Встреча произошла в 13 ч, Айдар прибывает в город после 18 часов, следовательно он успевает на поезд.

Рис. 3

Задачи для самостоятельного решения. Решите задачи с помощью построения графиков.

№ 1. Из аула в сторону озера вышел Алдар Косе. Первые 2 часа он шёл со скоростью 4 км/ч, затем один час со скоростью 2 км/ч и оставшиеся 3 часа – со скоростью 6 км/ч. Найти расстояние между аулом и озером. На каком расстоянии от аула был Айдар Косе через 6 часов?

№ 2. Малыш выехал из города Астаны на автомашине, а навстречу ему летит Карлсон из Караганды. Расстояние между городами 300 км. На каком расстоянии от Астаны и через какое время произойдет их встреча, если скорость автомашины 60 км/ч, а Карлсона 15 км/ч.

№ 3. Из аула в направлении гор вышла Жалмауз Кемпир со скоростью 5 км/ч. Спустя 3 часа вслед за ней выехал джигит на коне со скоростью 10 км/ч. Через какое время джигит догонит старуху?

№ 4. Из пункта А в пункт В выехал велосипедист со скоростью 10 км/ч. Одновременно с ним из пункта В в пункт А вышел пешеход со скоростью 5 км/ч. Через какое время произойдет их встреча, если расстояние от А до В составляет 75 км/ч?

№ 5. Бригада каменщиков может справиться с определенной работой за 8 недель. Через 3 недели после начала работы ей стала помогать другая бригада, которая может справиться с этой работой за 12 недель. За какое время бригады закончат работу?

№ 6. Из пунктов А и В навстречу друг другу вышли 2 путника. Первый вышел из пункта А в 8 часов и пришел в пункт В в 17 часов. Второй вышел из пункта В в 9 часов и пришел в А в 20 часов. Успели ли путники встретится до 13 часов?

№ 7. Из Астаны в Кокчетав навстречу друг другу выехали 2 поезда. Первый поезд выехал из Астаны в 7 часов и прибыл в Кокчетав в 15 часов. Второй выехал из Кокчетава в 9 часов и прибыл в Астану в 16 часов. Успеют ли машинисты поездов при встрече поприветствовать друг друга гудками до полудня?

№ 8. Два туриста из 7-го класса «О», Адай и Гани вышли из А в В навстречу друг другу. Адай вышел из В в 8 часов и пришел в А в 19 часов.Гани вышел из А в 10 часов. Успеет ли Гани до полуночи прийти в пункт В, если они встретились в 15 часов?

№ 9. Путешественник, находившийся в 100 м от домика лесника, продолжил движение со скоростью 4м/с вдоль дороги. На каком расстоянии он окажется через 15 с от домика?

№ 10. Из пункта А в пункт В выехал мотоциклист со скоростью 30 км/ч. Через 2 часа из пункта В навстречу мотоциклисту выехал автобус со скоростью 60 км/ч. На каком расстоянии от пункта А и через какое время после выезда автобуса произойдет встреча, если расстояние между А и В равно 150 км?

№ 11. Кот Леопольд выехал на велосипеде из пункта А в 8 часов и двигался со скоростью 10 км/ч в направлении пункта В. Нарисовать траекторию его движения до 18 часов.

№ 12. Расстояние между пунктами А и В равно 100 км. В 8 ч. утра выехал велосипедист, двигаясь с постоянной скоростью, в 12 часов он находился на расстоянии 40 км от А. Постройте график движения велосипедиста.

№ 13. Из пунктов А и В навстречу друг другу с постоянными скоростями вышли 2 путника. Первый вышел из А в 7 часов и пришел в В 13 часов. Второй путник вышел из В в 7 ч и пришел в А 19 ч. В какое время путники встретились?

Выполнила работу учитель математики:

Сергазиева Кулара Пернебаевна

НИШ ХБН г. Шымкент

Источник

Решение текстовых задач с помощью графиков линейной функции

Авторы
Руководители
Файлы работы
Наградные документы

Данилкин П.С. 1

1МАОУ Новоселезневская СОШ

Черноскутова Н.П. 1

1МАОУ Новоселезневская СОШ

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Математика является одним из основных предметов школьного образования, ее мы изучаем с 1-го класса. Уже в начальных классах мы нередко решаем текстовые задачи. Вообще решению текстовых задач в школе уделяется достаточно много внимания, так как современный человек, независимо от рода деятельности и уровня образования, должен уметь решать задачи. В этом я убедился, работая над проектом «Нужна ли математика?» в 5 классе. До 5 класса мы решали задачи по действиям, начиная с 5 класса, некоторые задачи мы решаем с помощью уравнения.

В этом учебном году на уроках алгебры мы изучили тему «Линейная функция, ее свойства и график», а на уроках физики при изучении темы «Механическое движение» чертили графики зависимости пути от времени движения, это были графики линейной функции. У меня сложилось мнение, что графики служат обычно для иллюстрации и лучшего запоминания свойств изучаемых функций, а построение чертежей дает возможность «увидеть» задачу. Мне стало интересно узнать, применяются ли свойства и графики линейной функции при решении задач на движение, а также других текстовых задач.

В связи с этим возникла тема моего исследования «Применение графиков линейной функции при решении текстовых задач». Работа посвящена текстовым задачам, при решении которых применяются графики линейной функции.

Актуальность моей работы заключается в том, что знание нескольких методов решения задачи увеличивает возможность её правильного решения и позволяет выбрать наиболее рациональный в данной ситуации.

Цель работы: изучить применения графиков линейной функции при решении текстовых задач.

Цель исследования обусловила следующие задачи:

1. Изучить литературу по данной теме.

2. Рассмотреть способы решения текстовых задач с помощью графиков линейной функции.

3. Провести сравнительный анализ различных методов решения текстовых задач.

4. Привести примеры решения задач из типовых экзаменационных вариантов.

Гипотеза: графический метод упрощает решение текстовых задач.

Объект исследования – текстовые задачи.

Предмет исследования – способ решения задач с помощью графиков линейной функции.

СПОСОБЫ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ

Для умения решать текстовые задачи важна всесторонняя работа над одной задачей, в частности решение её различными способами. Следует отметить, что решение задач различными способами позволяет убедиться в правильности решения задачи, даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче.

В качестве основных способов в математике различают арифметический и алгебраический.

Решить задачу арифметическим способом значит выполнить арифметические действия над числовыми данными из условия задачи, составив числовое выражение, а конечный результат вычислений – ответ на вопрос задачи.

Решить задачу алгебраическим способом — это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств).

Если использовать чертёж при решении, то можно легко дать ответ на вопрос задачи. Такой способ решения называется графическим. Графический способ даёт возможность более тесно установить связь между алгебраическим и геометрическим материалом. Следует отметить, что благодаря применению графического способа можно сократить время решения задач. В то же время умение графически решать задачу – это важное политехническое умение. Графический способ иногда даёт возможность ответить на вопрос такой задачи, которую сложно решить алгебраическим способом.

Графический способ решения любых задач и проблем очень удобен своей наглядностью, так как вырисовывается вся картина целиком, и не нужно удерживать в памяти разрозненные куски.

РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ С ПОМОЩЬЮ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ

Графический метод решения задач появился во времена Евклида (III век до нашей эры) и использовался не только в геометрии, но и в алгебре. Особенность его применения в алгебре состояла тогда в том, что он предполагал решение задач только с помощью построений и законов геометрии.

Решить задачу графическим способом — значит решить задачу с помощью графиков в прямоугольной системе координат. Решение задач графическим методом требует творческого подхода и глубокого понимания процессов, описанных в задаче. Изображая графики процессов, можно находить зависимости между величинами, применяя геометрические знания, а можно решать задачу привычным способом. Построенная модель зависимости между величинами помогает увидеть отношения между этими величинами. На этих двух подходах основано использовании графиков при решении текстовых задач.

В школьных задачах, как правило, описываются процессы с постоянной скоростью его протекания. Поэтому, независимо от вида процесса, его характеристики связаны одной и той же линейной зависимостью: результат процесса равен произведению скорости и времени его протекания.

Действие движения характеризуется тремя компонентами: пройденный путь s, скорость v и время t Известно соотношение между ними s= vt. Работу характеризуют также три компонента действия: время работы t, объем работы V и производительность N (количество произведенной работы в единицу времени). Существует следующее соотношение между этими компонентами: V = N t. В задачах на смеси и сплавы обычно присутствуют тоже три величины: концентрация (доля чистого вещества в смеси (или сплаве)), количество чистого вещества в смеси (или сплаве), масса смеси (сплава). Соотношение между этими величинами: масса смеси концентрация = количество чистого вещества.

Решение текстовой задачи графическим способом осуществляется в три этапа:

Построение графической модели задачи.

Решение получившейся графической задачи.

Перевод полученного ответа с графического языка на естественный.

Рассмотрим подробно реализацию этих этапов в процессе решения текстовых задач.

РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ

Большое значение в математике имеют задачи на движение. Задачи на движение подразделяются на следующие типы: по количеству движущихся объектов, по направлению движущихся объектов, по времени начала движения.

Методы решения текстовых задач на движение, использующие графики, обладают большой простотой и изяществом. При решении задач на движение вводится система координат, причем на оси абсцисс откладывается время, а на оси ординат – пройденное расстояние, отсчитываемое от некоторой фиксированной точки. Движущийся объект в любой момент времени занимает определённое положение, т.е. находится на определённом расстоянии от этой фиксированной точки, а значит, изображается некоторой точкой в данной системе координат. В процессе движения объект изменяет своё положение, и изображающая его точка вычерчивает некоторую линию – график движения. Приведу примеры нескольких задача, в них будем считать движение равномерным и графики движения прямолинейными.

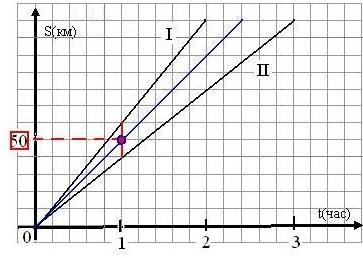
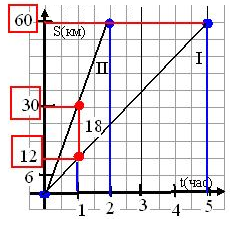
Задача 1. Из пункта A вышла грузовая машина со скоростью 60 км/ч. Через 2 ч вслед за ней из А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?

Р ешение 1. За начальный отсчет времени берется момент выхода грузовой машины (рис. 1), тогда момент выхода легковой машины будет через два часа. Зная скорости движения объектов, построим графики движения. По чертежу видно, что точка пересечения графиков показывает встречу машин, она состоялась на расстоянии 360 км.

(рис. 1) Ответ: 360 км.

Решение 2. Пусть х ч. – время движения легковой машины, тогда (х+2) ч. – время движения грузовой машины. Составляем уравнение 60(х+2)=90х. Решив уравнение, получим, что легковая машина двигалась 4 часа, отсюда расстояние равно 360 км.

Задача 2. С противоположных концов катка длиной 120 м бегут навстречу друг другу два мальчика. Через сколько секунд они встретятся, если второй начнет бег через 5 секунд после первого и если первый пробегает 6 м/с, а второй – 9 м/с? Решение 1. Отрезок ОМ – график движения . (рис.2) первого мальчика. Так как мальчики движутся навстречу друг другу, то возникает необходимость ввести вторую систему координат, где оси Оt сонаправлены, и масштабы на них одинаковые. Вертикальные оси противоположно направлены. График движения второго мальчика – отрезок O₁K. Абсцисса точки С пересечения графиков показывает время, через которое мальчики встретятся. Ответ: 11с.

Решение 2. Пусть х с.– время (рис. 2) движения второго мальчика, тогда время первого – (х+5) с. Составим уравнение, учитывая, что сумма расстояний равна 120м: решив которое, получим, что х = 6 с. Тогда время, через которое они встретятся – 11 с.

Задача 3. Из городов, расстояние между которыми равно 40 км, вышли одновременно навстречу друг другу два лыжника. Скорость одного из них была на 2 км/ч больше скорости другого. Через 2 часа лыжники оказались на расстоянии 8 км друг от друга. С какой скоростью шёл каждый лыжник?

Р ешение 1. Пусть лыжники двигались с одинаковыми скоростями. Учитывая, что они двигались навстречу друг другу и, что между ними расстояние – 8 км, построим графики движения. По графику видно, что их скорость равна 8 км/ч. Но т.к. разница в скоростях составляет 2 км/ч, получаем, что скорость первого лыжника 7 км/ч, а второго 9 км/ч. Но может быть ещё случай, когда 8 км было оооооо (рис. 3) между лыжниками после встречи. Тогда одинаковая скорость – 12км/ч, значит скорость первого лыжника 11км/ч, а второго–13км/ч.

Решение 2. Пусть х км/ч скорость первого лыжника, тогда скорость второго – (х+2) км/ч. Составим уравнение по условию задачи: 40 – (2х +2(х+2)) = 8. Решив уравнение, получим, что скорость первого лыжника 7 км/ч, а второго 9 км/ч. Во втором случае уравнение составим так: (2х +2(х+2)- 40 =8. Получим, что скорость первого лыжника 11 км/ч, а второго – 13 км/ч.

Если сравнивать способы решения, то графический метод позволяет быстрее и нагляднее решить задачу, особенно для тех учащихся, кто ошибается при составлении уравнения по условию задачи или при его решении.

РЕШЕНИЕ ЗАДАЧ НА СМЕСИ И СПЛАВЫ

Графический метод можно применить при решении задач, не связанных с движением каких-либо объектов. Сложными считаются задачи на смеси и сплавы. Рассмотрим решение таких задач двумя способами.

Задача 1. Один сплав содержит металлы в отношении 1: 5, другой сплав содержит эти же металлы в отношении 5: 7. В какой пропорции нужно взять первый и второй сплавы, чтобы получить сплав, содержащий те же металлы в отношении 1: 3?

Р ешение 1. По вертикальной оси отложим вес сплава в условных единицах (рис.1). По горизонтальной оси — вес первого металла в тех же условных единицах. Первый металл в первом сплаве составляет 1/6 часть. Взяв по горизонтали 1 у.е., а по вертикали 6 у.е., получим точку С. Прямая ОС будет характеризовать первый сплав. Взяв произвольную точку на этой прямой и спроецировав ее на оси, мы определим, сколько условных единиц весит весь сплав и сколько условных единиц составляет в . (рис.1) нем вес первого металла. Взяв по горизонтали точку 5 и по вертикали точку 12, получим точку D. Соединив ее прямой линией с началом координат, получим график, характеризующий второй сплав. Аналогично получим характеристику третьего сплава. Из любой точки вертикальной оси, например, на уровне точки D, проведем горизонтальную

прямую, пересекающую характеристики в точках М, N и D. Отношение длины отрезка ND к длине отрезка MN даст пропорцию, в которой нужно взять сплавы I и II соответственно, так как в данном случае отрезок ND в 2 раза больше отрезка MN, то необходимо взять 2 части первого сплава и 1 часть второго сплава. Можно просто измерить отрезки линейкой. Ответ: сплавы необходимо брать в пропорции 2: 1.

Решение 2. Пусть х кг – первого сплава, у кг – второго сплава. Тогда, вес первого металла в новом сплаве

, вес второго металла в новом сплаве . Новый сплав содержит металлы 1:3, тогда . Преобразовав данное выражение, получим 8у = 4х, отсюда . Ответ: 2: 1.

Задача 2. Сплавили два слитка. Первый весил 100 г и содержал 40% меди, второй весил 400 г и содержал 60 % меди. Какой процент меди содержится в получившемся сплаве? [1]

Решение 1. По вертикальной оси отложим количество чистого вещества, на горизонтальной – массу сплава (рис.2).

Построим графики, характеризующие первый и второй сплавы. Учитывая, что в 500 г получившегося сплава содержится 280 г чистого вещества, построим прямую, х арактеризующую новый сплав. По графику видно, что в 100 г нового сплава содержится 56 г чистого вещества. Следовательно, в оооо (рис. 2) получившемся сплаве содержится 56% меди.

Решение 2. Пусть х % – меди в новом сплаве, вес нового сплава 500 г. Используя условие задачи, получаем уравнение: + = . Решив уравнение, получим ответ: х = 56%.

В данном случае графики также позволяют наглядно увидеть ответ задачи, причем временные затраты меньше, чем решение задачи с помощью уравнения.

РЕШЕНИЕ ЗАДАЧ НА СОВМЕСТНУЮ РАБОТУ

При решении задач на совместную работу, на вертикальной оси откладывается отрезок, соответствующий количеству работы, а на горизонтальной время работы объектов, данных в задаче. Рассмотрим примеры решений задач двумя способами.

З адача 1. Чтобы выкачать воду из котлована, поставили два насоса. Оба насоса могли бы выкачать всю воду за 10 часов. Однако после 3 часов совместной работы один насос сломался, и другому насосу пришлось работать ещё 14 часов, чтобы выкачать оставшуюся воду. За сколько часов, действуя отдельно, каждый насос мог бы выкачать всю воду из котлована? Решение 1. По вертикали отложим отрезок, условно соответствующий количеству воды в котловане. По горизонтали – время работы насосов (пусть они начнут работу в 6 ч. утра). (рис.1). По графику видно, что если второй насос один начал (рис 1.) бы выкачивать воду в 3 часа, то окончил бы работу в 23 часа. Значит, второму насосу потребуется для выкачивания всей воды 20 часов. Т.к. оба насоса вместе выкачивают воду за 10 часов, то первому насосу потребуется также 20 часов для работы.

Решение 2. Пусть за х ч. выкачает весь котлован первый насос, за у ч.- второй насос.

Производительность в час обоих насосов , тогда за 3 часа совместной работы насосы выкачали котлована, значит осталось выкачать котлована.

Так как 14 часов работал один второй насос, то составляем уравнение: 14 . Решив это уравнение, получим х = 20. Значит, второй насос всю работы выполнит за 20 часов. Чтобы найти время работы первого насоса, решим уравнение: . Отсюда у = 20. Ответ: каждому нужно по 20 часов.

Задача 2. Игорь и Паша могут покрасить забор за 30 часов, Паша и Володя могут покрасить этот же забор за 36 часов, а Володя и Игорь – за 45 часов. За сколько часов мальчики покрасят забор, работая втроём?

Р ешение 1. На вертикальной оси отметим отрезок условно соответствующий всей работе (рис 2). На горизонтальной оси – время. Удобный масштаб: 3 часа– 1 клетка. Прямая ОD – производительность Володи и Игоря, прямая ОК – производительность Паши и Володи, прямая ОМ – Игоря и Паши. Проведя (рис.2) через любую точку горизонтальной оси, например, отметку 3 часа, вертикальную линию и отметив на ней точки пересечения ее с прямыми ОМ, ОК и OD, построим на ней сумму отрезков, соответствующих производительности каждой пары ребят. Получим точку F. Спроецировав точку F на вертикальную ось, мы можем узнать, какую часть забора покрасят 2 первых, 2 вторых и 2 третьих мальчика при совместной работе в течение одного часа. Проведя прямую ОF до пересечения с верхней горизонтальной осью, мы попадем в точку А, соответствующую времени 12 часов. Это половина необходимого времени, так как каждый мальчик участвует дважды в работе. Значит, для того, чтобы покрасить забор трем мальчикам потребуется 24 часа. Ответ: 24 часа

Решение 2. Пусть х – производительность Паши, у – производительность Володи, z – Игоря. Тогда: х+у = , у+z = , х+z = . Проссумируем : (х+у)+ (у+z) + (х+z)= + + .Из этого следует : х + у+ z = = . Значит, на всю работу потребуется 24 часа.

Трудность в данной задаче была в том, что масштаб был выбран не сразу. Мы видим, что такие задачи удобнее решать графическим методом, если задано небольшое количество часов, тогда на горизонтальной оси 1 час будет крупнее, и тогда удобнее отмечать точку F.Ответ будет читаться нагляднее.

ЗАКЛЮЧЕНИЕ

Целью данной работы было изучение применения графиков линейной функции в решении текстовых задач. В процессе работы над данной темой, выяснилось, что при решении текстовых задач наряду с традиционными методами, можно использовать и графический метод, который предполагает построение графиков линейных функций.

Были изучены материалы учебно-методической литературы, материалы из интернета. Решено множество задач из экзаменационных материалов разными способами, проведен сравнительный анализ.Гипотеза подтвердилась частично. Конечно, алгебраический способ – универсальный, но знание различных способов часто упрощает решение задачи. И, если есть сомнения, что получен правильный ответ, то можно решить задачу другим способом.

По результатам исследования можно сделать следующие выводы:

Одно из преимуществ графического метода перед алгебраическим состоит в наглядности решения, что позволяет лучше понять задачу.

Использование этого метода упрощает решение задач: нет громоздких вычислений.

Графическим методом решаются задачи не только на движение, но и на совместную работу, на смеси и сплавы.

Графический способ даёт возможность более тесно установить связь между алгебраическим и геометрическим материалами, развить функциональное мышление.

График дает возможность определить, есть ли у данной задачи решение и единственно ли оно.

Есть и «минусы»: иногда получаются приближённые значения в случаях неудачного масштаба.

Настоящее исследование значительно расширило представление о линейной функции, способствовало глубокому пониманию взаимосвязи этой функции с реальными ситуациями, возникающими в нашей жизни. Есть планы продолжить исследование в этом направлении: при решении некоторых задач применяется графико-геометрический метод, который основан на подобии треугольников.

Следует отметить, что решение задач различными способами позволяет убедиться в правильности решения задачи, даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче. Результаты работы можно использовать на уроках и дополнительных занятиях по математике при подготовке обучающихся к экзаменам. Этот материал позволит повысить образовательный уровень обучающихся.

СПИСОК ЛИТЕРАТУРЫ

Кочагин В.В. ОГЭ 2018. Математика: тематические тренировочные задания: 9 класс. – Москва: Эксмо, 2017. – 192 с.

Лунина Л.С. Обучение решению алгебраических задач геометрическим методом //Математика в школе: М.: Изд. «Школа-Пресс»,1996.-№4.- с.34-39.

Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач. Учебное пособие по математике для учителей и учащихся. Издание Томского института повышения квалификации работников образования, 1995 г.

Ященко И.В., Волчкевич М.А. и др. ЕГЭ 2018. Математика. Профильный уровень. 50 вариантов. Типовые тестовые задания от разработчиков ЕГЭ. – М.: Издательство «Экзамен», 2018. – 263 с.

https://infourok.ru/

Просмотров работы: 1490

Источник

МКОУ «Богучарская средняя общеобразовательная школа №1»

Научно-исследовательская работа по математике.

Тема: «Применение графика линейной функции к решению задач»

Автор: Ляпунова Мария

7 «В» класс
Руководитель: Фоменко Ольга Михайловна

город Богучар

2017 год

Содержание.

1.Введение………………………………………………………………… 2

2.Основная часть……………………………………………………………3-11

2.1 Методика решения текстовых задач с помощью графиков линейной функции

2.2 Решение текстовых задач на движение с помощью графиков

3.Заключение…………………………………………………………………11

4.Литература………………………………………………………………….12

ВВЕДЕНИЕ.

На уроках алгебры в 7 классе я познакомилась с темой «Линейная функция. Взаимное расположение графиков линейных функций». Я научилась строить графики линейной функции, узнала её свойства, научилась по заданным формулам определять взаимное расположение графиков. Я обратила внимание, что в учебнике Ю.Н.Макарычева

« Алгебра .7 класс» рассматриваются задачи, в которых по заданному графику необходимо ответить на ряд вопросов.

Например:

№332 Дачник отправился из дома на автомобиле в поселок. Сначала он ехал по шоссе,а затем по проселочной дороге, сбавив при этом скорость. График движения дачника изображен на рисунке. Ответьте на вопросы:

а)сколько времени ехал дачник по шоссе и сколько километров он проехал; какая скорость автомобиля была на этом участке пути;

б)сколько времени ехал дачник по проселочной дороге и сколько километров он проехал; какова была скорость автомобиля на этом участке;

в) за какое время дачник проехал весь путь от дома до поселка?

И у меня возник вопрос, можно ли решать задачи на движение не по действиям или при помощи уравнений, а применить для этого графики линейной функции?

В ходе поиска материала по этой теме в литературе и Интернете я для себя открыла, что в мире в линейной зависимости находятся многие физические, и даже общественные и экономические явления и процессы, но я остановилась на движении, как наиболее нам знакомом и популярном среди всех. В проекте я описала текстовые задачи и способы их решения с помощью графиков линейной функции.

Гипотеза: с помощью графиков можно не только получить наглядные представления о свойствах функции, познакомиться со свойствами линейной функции и её частного вида, прямой пропорциональности, но и решать текстовые задачи.

Целью моего исследования стало изучение применения графиков линейной функции в решении текстовых задач на движение. В связи с осуществлением этих целей были выдвинуты следующие задачи:

Изучить методику решения текстовых задач на движение с помощью графиков линейной функции;
Научиться решать задачи на движение данным методом;
Сделать сравнительные выводы о достоинствах и недостатках решения задач с помощью графиков линейной функции.

Объект исследования: график линейной функции.

Метод исследования:

Теоретический (изучение и анализ),системно-поисковый, практический.

Основная часть.

В своем исследовании я решила попробовать дать графическое толкование задач на движение, представленных в нашем учебнике, затем по графику ответить на поставленный вопрос задачи. Для такого приёма решения взяла задачи с прямолинейным равномерным движением на одном участке пути. Оказалось, что многие задачи таким способом решаются проще, нежели обычным способом с помощью уравнения. Единственный недостаток этого приёма: для точного получения ответа на вопрос задачи, надо суметь правильно выбрать масштаб единиц измерения на осях координат. Большую роль в правильном выборе такого масштаба играет опыт нарешивания. Поэтому, чтобы овладеть искусством решения задач с помощью графиков, мне пришлось рассмотреть их в большом количестве.

Методика решения текстовых задач с помощью графиков линейной функции.

Для того, чтобы решить текстовую задачу с помощью графиков линейной функции, надо:

задать систему координат sOt с осью абсцисс Ot и осью ординат Os. Для этого по условию задачи надо выбрать начало отсчета: начало движения объекта или из нескольких объектов избирается тот, который начал двигаться раньше или прошел большее расстояние. По оси абсцисс отметить интервалы времени в его единицах измерения, а по оси ординат отметить расстояние в выбранном масштабе его единиц измерения.
Провести линии движения каждого из объектов, указанных в условии задачи, через координаты хотя бы двух точек прямых. Обычно скорость объекта даёт информацию о прохождении расстояния за одну единицу времени от начала его движения. Если объект начинает двигаться позже, то точка начала его движения смещена на заданное число единиц вправо от начала отсчета вдоль оси абсцисс. Если объект начинает двигаться с места, удаленного от начала отсчета на определённое расстояние, то точка начала его движения смещена вверх вдоль оси ординат.
Место встречи нескольких объектов на координатной плоскости обозначено точкой пересечения прямых, изображающих их движение, значит, координаты этой точки дают информацию о времени встречи и удаленности места встречи от начала отсчета.
Разность скоростей движения двух объектов определяется длиной отрезка, состоящего из всех точек с абсциссой 1, расположенных между линиями движения этих объектов.
Точки на координатной плоскости должны быть отмечены в соответствии с масштабом по условию задачи, и линии должны быть построены аккуратно. От этого зависит точность решения задачи. Поэтому очень важно удачно выбрать масштаб делений на осях координат: его надо подобрать таким образом, чтобы координаты точек определялись более точно и, по возможности, располагались в узловых точках, т.е. в пересечениях делений осей координат. Иногда полезно за единичный отрезок на оси абсцисс брать количество клеток, кратное условиям задачи относительно времени, а на оси ординат – количество клеток, кратное условиям задачи относительно расстояния. Например, 12мин по времени требуют выбора числа клеток кратное 5, т.к. 12 мин составляет пятую часть часа.

Решение текстовых задач на движение с помощью графиков

Задача 1.(№ 673 в учебнике Ю.Н.Макарычева «Алгебра 7».)

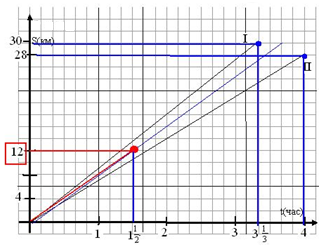
Велосипедист проехал путь АВ со скоростью 12 км/ч. Возвращаясь, он развил скорость 18 км/ч и затратил на обратный путь на 15 мин меньше, чем на путь из А в В. Сколько километров из А в В.

Решение с помощью графика линейной функции:

1. Зададим координатную плоскость sOtc осью абсцисс Оt, на которой отметим интервалы времени движения, и осью ординат Os, на которой отметим расстояние .

2. Нанесём деления в масштабе: по оси ординат – в одной клетке 3 км; по оси абсцисс – один час в 4 клетках (в 1 клетке – 15 мин).

3. Построим линию движения туда: начало движения отметим точкой (0;0). Велосипедист ехал со скоростью 12км/ч, значит, прямая должна пройти через точку (1;12).

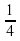
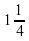
4. Построим линию движения обратно: конец линии отметим точкой (; 0), т.к. велосипедист затратил на обратный путь на 15 минут меньше . Он ехал со скоростью 18км/ч, значит, следующая точка прямой имеет координату (;18).

5. Отметим (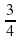; 9) — точку пересечения прямых: её ордината покажет расстояние : s = 9

Ответ: 9 км.

Решение с помощью уравнения:

Пусть х км – расстояние от А до В.

х/12ч. – время от А до В

х/18ч. – время обратно

Так как на обратный путь он затратил на 15 минут меньше , то составим уравнение

х/12-х/18=1/4

3х – 2х= 9

x=9

Ответ:9 км

Задача 2.(№ 156 в учебнике Ю.Н.Макарычева «Алгебра 7».)

По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10км/ч, а вторая уменьшит на 10км/ч, то первая за 2 часа пройдёт столько же, сколько вторая за 3 часа. С какой скоростью идут автомашины?

Решение с помощью уравнения:

Пусть х км/ч скорость машин;

(х+10) и (х-10) соответственно скорости после увеличения и уменьшения;

2(х+10)=3(х-10)

2х+20=3х-30

х=50

Ответ: 50км/ч

Решение с помощью графика линейной функции:

1. Зададим координатную плоскость sOt c осью абсцисс Оt, на которой отметим интервалы времени движения, и осью ординат Os, на которой отметим расстояние, пройденное автомашинами

2. Нанесём деления в масштабе по оси абсцисс – один час в 5 клетках (в 1 клетке – 12 мин); по оси ординат наносим деления, но не указываем масштаб.

3. Построим линию движения первой машиныI: начало движения в точке с

координатой (0;0). Далее отметим произвольную точку (2;s₁) на плоскости, т.к. машина с новой скоростью была в пути 2 часа.

4. Построим линию движения второй машиныII: начало движения в точке с координатой (0;0). Далее отметим произвольную точку (3;s₁) на плоскости, т.к. машина с новой скоростью была в пути 3 часа.

4. Определим скорость машин v до её изменения. Обозначим разность ординат точек, лежащих на прямых с абсциссой 1, значком ∆s. По условию этому отрезку соответствует длина (10+10) км, т.к. у одной из них скорость уменьшилась, а у другой скорость увеличилась на 10км/ч. Значит, линия движения машин до изменения скорости должна быть равноудалена от линийI и II и расположена на координатной плоскости между ними.. По графику Δs=2кл. соответствует 20км, v=5 кл., значит, решим пропорцию 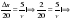v = 50км/ч.

Ответ: 50км/ч.

Задача 3 (№ 757 в учебнике Ю.Н.Макарычева« Алгебра 7»)

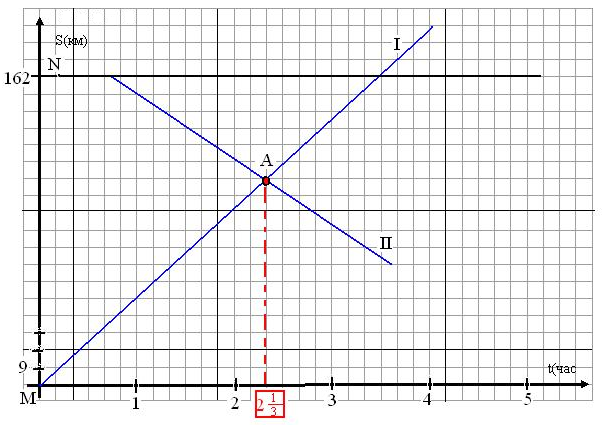
Расстояние между пристанями M и N равно 162км. От пристани M отошел теплоход со скоростью 45км/ч. Через 45 мин от пристани N навстречу ему отошел другой теплоход, скорость которого 36км/ч. Через сколько часов после отправления первого теплохода они встретятся?

Решение с помощью графика линейной функции:

1. Зададим координатную плоскость sOt с осью абсцисс Ot, на которой отметим интервалы времени движения, и ось ординат Os, на которой

отметим расстояние от пристани M до пристани N, равное 162км. Началом

отсчёта является пристань М

2. Нанесём деления в масштабе: по оси ординат – в двух клетках 18км; по оси абсцисс–один час в 6 клетках (в 1 клетке–10мин.), т.к. в условии задачи указано время в минутах.

отметим точку N(0; 162).

3. Построим линию движения первого теплохода I: начало его движения будет в точке с координатами (0;0). Первый теплоход плыл со скоростью 45км/ч, значит, прямая должна пройти через точку с координатами (1;45).

4. Построим линию движения второго теплоходаII: начало движения будет в точке с

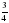
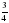
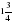
координатами (; 162), так как он вышел из пункта N, удалённого от М на 162км, на 45мин. позже первого, а 45мин. = ч. Второй теплоход плыл со скоростью 36км/ч, значит, прямая должна пройти через точку (; 126), так как второй теплоход вышел в направлении пункта М: 162 – 36 = 126(км).

5. Точкой пересечения прямыхI и II является точка А (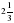;108). Абсцисса точки показывает время, через которое после отправления первого теплохода они встретились: t =, |=ч = 2ч20мин. – время встречи двух теплоходов после выхода первого теплохода.

Ответ: 2ч 20мин.

Решение с помощью уравнения:

Пусть через x часов произойдет встреча

162 -45(x+0,75)-36x=0

162-45x – 33,75 -36x=0

81x=128,25

Ответ: 2ч 20мин.

Задача 4.

Из пункта A выехал велосипедист. Одновременно вслед за ним из пункта B, отстоящего от A на расстоянии 20км, выехал мотоциклист 16км/ч. Велосипедист ехал со скоростью 12км/ч. На каком расстоянии от пункта A мотоциклист догонит велосипедиста?

Решение с помощью графика линейной функции:

1.Зададим координатную плоскость sOt с осью абсцисс Ot, на которой отметим интервалы времени движения, и ось ординат Os, на которой будем отмечать расстояние, пройденное мотоциклистом и велосипедистом

2. Нанесём деления в масштабе: по оси ординат – в 2 клетках 8 км; по оси абсцисс–в 2клетках –1ч.

3. Построим линию движения мотоциклиста II: начало его движения отметим в начале координат В(0;0). Мотоциклист ехал со скоростью 16км/ч, значит, прямаяII должна пройти через точку с координатами (1;16).

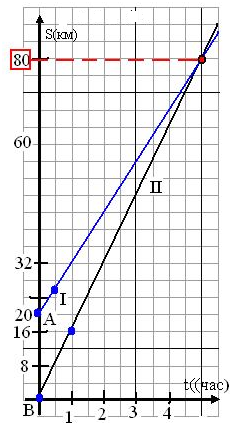
4.Построим линию движения велосипедистаI: её начало будет в точке А(0;20), т.к. пункт B расположен от пункта A на расстоянии 20км, и он выехал одновременно с мотоциклистом. Велосипедист ехал со скоростью 12км/ч, значит, прямая I должна пройти через точку с координатами (1;32).

5. Найдем Р (5; 80) – точку пересечения прямых I и II, отражающих движение мотоциклиста и велосипедиста: ее ордината покажет расстояние от пункта В, на котором мотоциклист догонит велосипедиста.

Р(5; 80) |=s = 80, |=80 – 20 = 60(км) – расстояние от пункта А, на котором мотоциклист догонит велосипедиста..

Ответ: 60км.

Решение с помощью уравнения:

Пусть x км расстояние от пункта А до места встречи

x/12 время велосипедиста

(x+20)/16 время мотоциклиста

x/12=(x+20)/16

16x=12x+240

4x=240

x=60

Ответ: 60 км

Задача 5.

Расстояние между городами мотоциклист проехал за 2ч, а велосипедист за 5 ч. Скорость велосипедиста на 18км/ч меньше скорости мотоциклиста. Найдите скорости велосипедиста и мотоциклиста и расстояние между городами.

Решение с помощью графика линейной функции:

1. Зададим координатную плоскость sOt с осью абсцисс Ot, на которой отметим интервалы времени движения, и ось ординат Os, на которой отметим расстояние.

2. Нанесем деление по оси абсцисс в 2х клетках 1 ч. По оси ординат расстояние оставим без делений.

3. Проведем линию движения I велосипедиста за 5 часов и линию движения мотоциклиста II за 2 часа. Конец обеих линий должен иметь одну ординату.

_{4. Проведём отрезок с абсциссой 1 между линиями}I и II. Длина этого отрезка отражает расстояние равное 18км. Из чертежа получаем, что 3 клетки равны 18 км, значит, в 1 клетке 6км.

5. Тогда, по графику определяем скорость велосипедиста равна12 км/ч, скорость мотоциклиста равна 30 км/ч, расстояние между городами-60 км.

Ответ: 12 км/ч; 30 км/ч; 60 км

Решение с помощью уравнения:

Пусть x км/ч скорость велосипедиста, тогда( x+18) км/ч скорость мотоциклиста

2(x+18)=5x

2x+36=5x

x=12

2) 12+18=30(км/ч) скорость мотоциклиста

3) (км) расстояние между городами

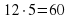
Ответ: 12 км/ч; 30 км/ч; 60 км

Ответ: 60км.

Задача 6.

По течению реки лодка за 3ч 20мин проходит расстояние 30км, а против течения за 4ч – расстояние 28км. Какое расстояние по озеру пройдет лодка за 1,5ч?

Решение с помощью графика линейной функции:

1.Зададим координатную плоскость sOt с осью абсцисс Ot, на которой отметим интервалы времени движения, и ось ординат Os, на которой отметим расстояние, пройденное лодкой

2. Нанесём деления в масштабе: по оси ординат – в двух клетках 4км; по оси абсцисс– в 6 клетках – 1ч (в 1 клетке – 10 мин.), т.к. по условию задачи дано время с минутами.

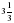
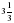
3. Построим линию движения лодки по течению рекиI: начало линии будет в точке с координатой (0;0). Лодка плывает 30км за 3ч 20мин, значит, линия должна пройти через точку с координатой (;30), т.к. 3ч 20мин. = ч.

4. Построим линию движения лодки против течения рекиII: начало движения возьмём в точке с координатой (0;0). Лодка плывет 28км за 4ч, значит, прямая движения должна пройти через точку с координатой (4;28).

5. Построим линию движения лодки по озеру: начало движения возьмём в точке с координатой (0; 0). Линия собственного движения лодки должна будет располагаться равноудалённо и между линиями движения лодки по реке. Значит, мы должны отрезок, состоящий из всех точек с абсциссой 1 между линиями движения по реке, поделить пополам и отметить его середину. От (0; 0) через эту отмеченную точку проведём луч, который и будет линией движения по озеру.

6. По условию задачи надо найти расстояние, пройденное лодкой по озеру за 1,5ч, значит, мы должны определить на этой линии ординату точки с абсциссой t = 1,5, |=s = 12, |= 12км пройдёт лодка по озеру за 1,5 часа.

Ответ: 12км.

Решение с помощью системы уравнений :

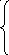
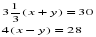
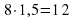
Пусть x км/ч скорость по озеру, а у км/ч скорость реки

км

Ответ: 12км.

Задача 7.

Катер проходит по течению реки 34 км за то же время, что и 26 км против течения. Собственная скорость катера равна 15км/ч. Найдите скорость течения реки.

Решение с помощью графика линейной функции:

1.Зададим координатную плоскость sOt с осью абсцисс Ot, на которой отметим интервалы времени движения, и ось ординат Os, на которой отметим расстояние, пройденное лодкой.

2. Нанесём деления в масштабе: по оси ординат – в 1 клетке 1км; по оси абсцисс время оставим без делений.

_{3. Построим линию}I движения лодки по течению реки из 0км до точки в 34 км: начало линии будет в точке с координатой (0;0).Вторая координата будет (x; 34).

_{4. Построим линию}II движения лодки против течения реки из 0км до точки в 26 км: начало линии будет в точке с координатой (0;0).Вторая координата будет (x; 26).

5. Проведем луч III из начала координат (0; 0) через середину произвольного отрезка, состоящего из всех точек с одинаковой абсциссой между двумя линиями движения I и II. Этот луч будет отражать собственное движение лодки, т.к. собственная скорость катера есть среднее арифметическое 2х скоростей по течению и против течения реки. На полученном луче найдём точку с ординатой 15, т.к. собственная скорость лодки 15км/ч. Абсцисса найденной точки будет соответствовать делению в 1 час.

6. Чтобы найти скорость течения реки, достаточно найти длину отрезка с абсциссой 1 от линии III до линии II. Скорость течения реки — 2км/ч.

Ответ: 2км/ч.

Решение с помощью уравнения:

Скорость течения реки x км/ч

34/(15+х)=26/(15-х) Решая пропорцию, получим:

60 х=120

х=2

Ответ: 2км/ч.

Заключение.

В конце исследования я смогла выявить достоинства и недостатки решения задач графическим способом.

Достоинства:

Можно кратко записать задачи;
Вполне легко работать с маленькими числами.

Недостатки:

Если неправильно рассчитать масштаб, то получится приближённое значение;
Сложно работать с большими числами.

ЛИТЕРАТУРА.

1. Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б., Алгебра: Учебник для 7 класса общеобразовательных учреждений, «Просвещение», М., 2000.

2.Булынин В., Применение графических методов при решении текстовых задач, учебно-методическая газета «Математика», № 14, 2005.

3. Звавич Л.И.Дидактические материалы по алгебре для 7 класса.

Источник

Решение
задач с помощью чертежей – диаграмм

Диаграмма
— это чертеж или рисунок, на котором условно изображены в виде отдельных фигур
различные значения одной и той же величины или несколько сравнимых величин.

Графико-вычислительные
приемы помогают решать разнообразные арифметические и геометрические задачи.
Построение этих чертежей дает возможность «увидеть» задачу, установить и
исследовать связи, существующие между величинами, входящими в задачу, выбрать
кратчайший путь решения.

Применяя
диаграммы к решению задач, будем изображать отрезками численные значения
величин, входящих в условие задачи. Действия над числами заменяют соответствующими
построениями на диаграмме.

Самостоятельное
решение задач таким путем требует определенного навыка, изобретательности. В
некоторых случаях этот путь может заменить чисто вычислительные приемы, в
других – облегчить наилучший выбор неизвестного для составления уравнения, или
подсказать ход рассуждений для отыскания арифметического решения.

Очень важное
достоинство такого пути – в наглядности: на рисунке сразу видна связь между
величинами, входящими в условие задачи; чертеж помогает расширить задачу –
поставить и решить более общие вопросы, глубже проникнуть в существо задачи,
оценить реальность результата и промежуточных действий. Особенно целесообразно
применять этот путь в тех случаях, когда требуется ответить не на один, а на
несколько вопросов.

Задача.
В одном бидоне вдвое больше молока, чем в другом. Когда из обоих бидонов отлили
по 20 литров молока, то в первом бидоне оказалось втрое больше молока, чем во
втором. Сколько литров молока было первоначально в каждом бидоне?

Решение.

Начертим
два вертикальных отрезка «бидоны», один по высоте в два раза больше, чем
другой, т.к. одном бидоне вдвое больше молока, чем в другом.

Допустим:
8 и 4 клетки.

Сколько
взять клеток, чтобы показать, что отлили по 20 литров молока, учтем условие: в
первом бидоне оказалось втрое больше молока, чем во втором. На рисунке должна
остаться одна часть во втором «бидоне» и три части в первом.

Тогда
20 л молока – это две клетки. Останется во втором «бидоне» две клетки, в первом
– шесть клеток.

Выходит, что 20
литров – это часть, таких частей в первом бидоне 4, тогда 4∙20=80 л, во втором
бидоне – две части 2∙20= 40 л.

Эту задачу легко
решить, используя алгебраический метод.

	I бидон	II бидон
Было	2x	x
стало	2x-20	x-20

Составить
уравнение помогает фраза «в первом бидоне оказалось втрое больше молока, чем во
втором».

2х
– 20= 3(х-20), х=40, 40∙20=80

Ответ:
в первом бидоне 80 л, во втором -40 л молока.

Ученик 7класса
справится с такой задачей, используя введение переменной, и решит уравнение.
Но интересен другой факт: ученик 5, 6 классов тоже способен решить такую
задачу, используя рисунок и логически рассуждая.

Задача.
Коля уплатил в кассу кафе за три блюда, Саша – за два блюда (все пять блюд
одинаковой стоимости). Когда они сели за стол, к ним присоединился Юра, и они
втроем съели все пять блюд поровну. При расчете приятелей между собой
выяснилось, что Юра должен уплатить за съеденный им обед 500 рублей. Сколько из
этих денег следует отдать Коле и сколько Саше?

Решение.

Пусть отрезок в 15
клеток – это вся стоимость обеда (Юра должен отдать 500 рублей), ведь они
втроем съели поровну блюда, то поровну и заплатили за обед. Из рисунка
очевидно, что 1 клетка – 100 рублей. И Коля за три блюда заплатил 900 рублей,
Саша – 600 рублей. Полный обед из пяти блюд стоил 1500 рублей. Следовательно,
Коле нужно отдать 900-500=400 рублей, Саше 600-500=100 рублей.

Ответ:
Коле нужно отдать 400 рублей, Саше 100 рублей.

Задача.
На трех деревьях уселось 36 галок. Когда с первого дерева перелетели на второе
6 галок, а со второго перелетели на третье 4 галки, то на всех трех деревьях
галок стало поровну. Сколько галок сидело первоначально на деревьях?

Решение.

Рисунок
подсказывает, что на втором дереве после перелетов добавились две птицы, и их
стало 12, следовательно, первоначально их было 12-2=10. Конечно, если на
рисунок вынести общее число галок, то решение будет еще более очевидным.

Ответ:
1 дерево -18 галок, 2-10 галок, 3 – 8 галок.

Задача.
Рабочие отремонтировали дорогу длиной 820 метров за три дня. Во вторник они
отремонтировали этой дороги, в среду остальной части дороги.
Сколько метров дороги отремонтировали рабочие в четверг?

Решение.
Возьмем отрезок длиной в 15 клеток – это длина всей отремонтированной дороги
(НОК (5;3)=15). Ведь нам нужно показать сначала две части из пяти, а потом две
части из трех.

Из рисунка
становится очевидным, что вся дорога разделена на пять частей, и, чтобы узнать,
какая часть осталась на четверг (это одна часть), нужно 820:5=164 метра.

Обычный путь
решения:

1)
820 ∙ =328 м была
отремонтирована во вторник,

2)
820-328=492 м осталось отремонтировать в среду и четверг,

3)
492∙=328 м отремонтировали в
среду,

4)
(820-328) -328=164 м отремонтировали в четверг.

Рисунок
позволяет решить задачу без громоздких вычислений.

Ответ.
164 метра дороги отремонтировали в четверг.

Графики
можно использовать для геометрической иллюстрации движения (перемещения).
Например, расписание движения поездов раньше разрабатывались при помощи
графиков, которые назывались «графики движения поездов». Наиболее просто
графиком изображается равномерное движение.

На
графике обычно, но не всегда, по направлению оси ОХ отсчитывают время, а по
направлению оси OY – расстояние. В
таком случае абсцисса всякой точки графика движения любого тела указывает
момент времени, а ордината – положение этого тела. Следовательно, график дает
возможность ответить на вопрос: «Где в данный момент находится тело? Когда оно
находилось или будет находиться в данном месте?»

Если
на одном чертеже построить два графика движения пешеходов, и если эти два
графика пересекаются в некоторой точке, то координаты этой точки показывают
место и время встречи пешеходов. Вот две задачи на движение, которые можно
решить с помощью графика равномерного движения. Геометрия придет на помощь
алгебре.

Задача.
Два туриста выезжают одновременно навстречу друг другу из двух пунктов А и В.
При встрече оказалось, что первый проехал на 30 км больше второго и что через
четыре дня он будет в В. Второй попадет в А через 9 дней после встречи. Найти
расстояние АВ.

Решение.
Берем произвольный отрезок АВ, изображающий расстояние между пунктами Аи В.
Отрезки АВꞌ и ВАꞌ — это графики движения первого и второго туриста (№1, №2).
Место и момент встречи определяются точкой О пересечения графиков.

Через точку О
проведем KL ‖ AB.
По условию KAꞌ =9 дней и LBꞌ =4 дня. Обозначим число дней от момента выхода туристов до их встречи
через х, тогда x=AK=BL.

Имеем
две пары подобных треугольников:

▲AOK
∞ ▲Bꞌ OL,
откуда x:4=OK:
OL

▲Aꞌ
OK ∞ ▲BOL, откуда 9:х= OK:
OL.

Отсюда
получаем x:4=9:х,

решая,
получим х=6 дней.

Обозначим
расстояние BC через y.

Тогда
LO=BC=y,
AC=KO=y+30.

Из
подобия треугольников AOK , BꞌOL
следует OK:OL=AK:
Bꞌ L или (y+30):y=6:4.

Упрощая
эту пропорцию, получим 30:y=2:4,
y=60
км.

Таким
образом, AB=2y+30=150
км.

Ответ:
расстояние между пунктами 150 км

Кроме
того, мы можем определить скорость каждого туриста.

Скорость
первого: v₁=OL:LBꞌ
=60:4=15 км в день.

Скорость
второго v₂=OL:LB=60:6=10
км в день.

Задача.
Два пешехода идут навстречу друг другу, один из пункта А, другой из пункта В.
Первый выходит из А на 6 часов позже, чем второй из В. При встрече оказывается,
что он прошел на 12 км меньше второго. Продолжая после встречи дальней путь с
той же скоростью, первый приходит в В через 8 часов, второй в А – через 9
часов. Найти скорость каждого пешехода.

Решение.
Изобразим расстояние между пунктами А и В произвольным отрезком АВ. Ось времени
теперь направим вертикально. На перпендикуляре АЕ отмечаем точку С, принимая,
что АС=6 часам. Пусть прямая СD является
графиком движения первого пешехода, а прямая ВЕ – графиком движения второго. F
– точка пересечения графиков – это место встречи пешеходов, G
– проекция на АВ точки F.

Через
точку F проведем HJ ‖ AB.

По
условию, HE=9 часов, JD=
8 часов, JB – AG=12
км.

Пусть
CH=y,
тогда BJ=AH=(y+6)
часов.

▲BGF∞▲FHE
и ▲FJD∞▲
FHC
(▲FGB=▲FBJ)

Отсюда
получаем (y+6) : 9=FJ : FH=8 : y,

Следовательно,
(y+6)
∙y=8
∙ 9

или
y²+6y
– 72=0 , y=6 часов.

Далее,
, , , FH=36
км,
FJ=48
км.

FH
– это путь, который прошел первый пешеход за время, равное y=6
часов; FJ – путь, который прошел
второй пешеход за y+6=12 часов.

Следовательно,
первый пешеход шел со скоростью 36:6=6 км/час,

а
второй – со скоростью 48:12=4 км/час.

Ответ:
6 км/час — скорость первого пешехода, 4 км/час – скорость второго пешехода.

Вот второй вариант
решения данной задачи – алгебраический, привычный для ученика и учителя. Пусть
х – путь, пройденный первым пешеходом до встречи.

		S, км	V, км/ч	t, час
До встречи	1-й пешеход	x
2-й пешеход	x+12
После встречи	1-й пешеход	x+12		8
2-й пешеход	x		9

Составить
уравнение поможет фраза «первый выходит из А на 6 часов позже, чем второй из
В», следовательно, разница во времени между ними 6 часов:

После
преобразований получим: 5х² — 12∙12х — 12∙12∙9=0, решив квадратное
уравнение, получаем х=36.

Следовательно,
второй пешеход прошел после встречи 36 км, а до встречи 36+12=48 км. Эти же 48
км прошел первый пешеход после встречи.

Первый пешеход шел
со скоростью 48:8=6 км/ч, второй – 36:9=4 км/ч.

Невозможно пройти
мимо интереснейшей задачи из рассказа Чехова «Репетитор». Чтобы освежить в
памяти, о чем идет речь, вот небольшой отрывок из этого рассказа.

«Теперь
по арифметике… Берите доску. Какая следующая задача?

Петя
плюет на доску и стирает рукавом. Учитель берет задачник и диктует:

—
«Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько
аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3
руб.?» Повторите задачу.

Петя
повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.

—
Для чего же это вы делите? Постойте! Впрочем, так… продолжайте. Остаток
получается? Здесь не может быть остатка. Дайте-ка я разделю!

Зиберов
делит, получает 3 с остатком и быстро стирает.

«Странно…
— думает он, ероша волосы и краснея. — Как же она решается? Гм!.. Это задача на
неопределенные уравнения, а вовсе не арифметическая»…

Учитель
глядит в ответы и видит 75 и 63.

«Гм!..
странно… Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».

—
Решайте же! — говорит он Пете.

—
Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты
дурак, братец! Решите уж вы ему, Егор Алексеич.

Егор
Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет,
бледнеет.

—
Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и
игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил…
понимаете? Теперь, вот, надо вычесть… понимаете? Или, вот что… Решите мне
эту задачу сами к завтраму… Подумайте…

Петя
ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство
учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из
угла в угол.

—
И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и
вздыхая. — Вот, извольте видеть…

Он
щелкает на счетах, и у него получается 75 и 63, что и нужно было.

—
Вот-с… по-нашему, по-неученому.

Учителю становится
нестерпимо жутко. С замиранием сердца поглядывает он на часы и видит, что до
конца урока остается еще час с четвертью — целая вечность!»

Задачу из рассказа
А. П. Чехова можно решать по-разному.

Для учеников,
осваивающих тему «Решение задач с помощью системы уравнений», можно предложить
такой способ.

Пусть
х – количество аршин синего сукна,

y
— количество аршин черного сукна,

тогда
5х – стоимость синего сукна,

3y
– стоимость черного сукна.

Учитывая
условие задачи, составим систему уравнений

Выразим
х через y,
получим x=138-y,
5∙(138-y)+3y=540,
y=75,
138-75=63.

Ответ:
купец
купил 75 аршин черного сукна и 63 аршина синего сукна.

Еще вариант
размышлений: если бы купец приобрел только 138 аршин синего сукна, то ему
пришлось бы заплатить 138 ∙ 5 = 690 рублей. А он заплатил 540 рублей, на 150
рублей меньше. Заменяя один аршин синего сукна на аршин черного, можно
уменьшить стоимость сукна на 2 рубля. А чтобы уменьшить стоимость 138 аршин
сукна на 150 рублей, надо заменить 150 : 2 = 75 аршин синего сукна на такое же
количество черного. Выходит, что купец купил 75 аршин черного сукна и 138-75 =
63 аршина синего.

Есть ли
какой-то смысл в действиях чеховских героев? Петя разделил 540 на 138. У него
получилось 3 и 126 в остатке. Если купить 138 аршин черного сукна, то 138∙3=414
– стоимость черного сукна, и при делении его стоимости на 138, получается 3 без
остатка. Замена 1 аршина черного сукна на аршин синего увеличивает общую
стоимость сукна 2 рубля, и остаток от деления общей стоимости на 138
увеличивается на 2. Для того, чтобы остаток стал равен 126, надо 126 : 2 = 63
аршина черного сукна заменить таким же количеством синего. Следовательно, было
куплено 63 аршина синего сукна и 138 — 63 = 75 аршин черного.

Учитель-гимназист
хотел сложить пять и три, а потом 540:3. Посмотрим, что из этого получается.
540: (5 + 3) = 67 и 1/2 аршина черного и синего сукна, Как купить на те же
деньги 138 аршин? Для того, чтобы купить еще 3 аршина черного сукна, нужно 3 ∙
3 = 9 рублей. Эти 9 рублей можно выиграть от замены 9: 2 = 4 и 1/2 аршина
синего сукна на такое же количество черного. При этом синего сукна останется 63
аршина, а черного 75 аршин.

Вот еще одно
решение с применением ломаных графиков.

Один
аршин синего сукна стоит 5 рублей, следовательно, 100 аршин стоят 500 рублей.
Отмечаем точку М и строим луч ОМ – это график стоимости синего сукна.

Один
аршин черного сукна стоит 3 рубля, следовательно, 100 аршин стоят 300 рублей.
Отмечаем точку N и строим
луч ON — это график стоимости
черного сукна.

Т.к.
точка С (138 аршин, 540 рублей) оказывается между лучами OM и ON, то,
следовательно, купили и черное, и синее сукно.

Проведем
CA‖
NO до пересечения с OM,
получим точку А. Ломаная OAС – график
нарастающей стоимости сукон – синего (OA)
и черного (AC).

Проекции
точки А на оси OX и OY
указывают, что синего сукна купили 63 аршина на 315 рублей. Задача решена.
Найти количество и стоимость черного сукна уже легко.

Можно поступить и
немного иначе: провести CB ‖ MO;
тогда ломаная OBC -график нарастающей
стоимости сукон – черного (OB)
и синего (BC). Проекции точки В на
оси OX,
OY показывают, что черного сукна купили 75 аршин на 225 рублей. Проверка:
63+75=138 аршин и 315+225=540 рублей.

Приведенные
выше пути решения задач на первый взгляд могут показаться неожиданными и
непривычными. И возникает закономерный вопрос: «Зачем нужно использовать
нестандартные приемы задач, если для усвоения стандартного пути решения очень
мало времени и не все учащиеся отрабатывают каждый прием до конца?»

Показывать
нестандартные приемы решений задач можно на факультативных занятиях, кружковых,
а самые простые рисунки и схемы для понимания смысла задачи обязательно
включать в урочную деятельность.

Если
включить в уроки, кружки, факультативы подобные пути решения заданий, то
появляется вероятность привлечь учащихся в реальную для них творческую
деятельность. И это будет важным условием формирования разных творческих
качеств мышления школьников. Это один из путей развития креативности.

Источник

Комитет по образованию администрации г. Улан-Удэ

МАОУ «Средняя общеобразовательная школа №37

XXVII городская научно-практическая конференция

«Шаг в будущее»

Секция: «математика»

Решение текстовых задач c помощью графиков линейной функции

Выполнила: Унагаева Арина

Александровна,

Ученица 9 класса «г»

МАОУ СОШ №37

Научный руководитель:

Днепровская Татьяна Николаевна,

Учитель математики

МАОУ СОШ №37

Улан-Удэ

2020

Оглавление

Паспорт проектной работы

I. Введение

II. Основная часть:

1. Решение текстовых задач с помощью графиков линейной функции

2. Решение задач на движение

3. Решение задач на совместную работу

4. Решение задач на смеси и сплавы

III. Заключение

Список использованной литературы и интернет-ресурсов

Приложения

Паспорт проектной работы

1. Название проекта: «Графики линейной функции и решения текстовых задач»

2. Руководитель проекта: Днепровская Т.Н.

3. Учебные предметы, в рамках которых проводится работа по проекту:

математика

4. Учебные дисциплины, близкие к теме проекта: алгебра

5. Возраст учащихся, на которых рассчитан проект: 9 класс (15 лет)

6. Тип проекта: индивидуальный, исследовательский

7. Заказчик проекта: учитель

8. Цель проекта:

— Научиться решать задачи с помощью графиков функций

9. Задачи проекта:

Научиться:

— Решать текстовые задачи с помощью графиков линейной функции

— Решать задачи на движение

— Решать задачи на смеси и сплавы

— Решать задачи на совместную работу

10.Этапы работы над проектом:

1. Подготовка: Определение темы и целей проекта.

2. Планирование: Определение источников информации; определение способов ее сбора и анализа. Определение способа представления результатов (формы отчета). Установление процедур и критериев оценки результата и процесса разработки проекта.

3. Исследование: Сбор информации. Решение промежуточных задач.

4. Анализ и обобщение: Анализ информации, оформление результатов сначала в виде презентации, формулировка выводов.

5. Представление проекта: Выступление перед одноклассниками и руководителем проекта, в рамках промежуточной аттестации.

6. Оценка результата и процесса: Анализ выполнения проекта; причины успехов и неудач.

11. Аннотация.

Данный проект является индивидуальной работой. В процессе работы над проектом я должна не только разобраться с решение задач, но и сделать выводы о работе с графиками. В результате работы над проектом я приобрела навыки работы с текстом, взаимодействия со взрослыми (родителями, учителем, библиотекарем). Защита проекта способствовала формированию коммуникативной компетенции. Формирование информационной компетенции происходило на всех этапах работы над проектом: во время поиска и обработки информации, подготовки и защиты презентации.

I. Введение

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека.

Решению текстовых задач в школе уделяется достаточно много внимания, так как современный человек, независимо от рода деятельности и уровня образования, должен уметь решать задачи.

Традиционными способами решения текстовых задач являются арифметический и алгебраический. При решении алгебраических задач можно также использовать графический метод. Этот метод требует точного построения графиков функций, ответ задачи читается по чертежу. Начерченный график – это краткое и наглядное описание какого – либо процесса.

Несмотря на практическое значение графиков, в школьной математике графики служат обычно для иллюстрации и лучшего запоминания свойств изучаемых функций.

Построение чертежей дает возможность «увидеть» задачу, т. е. установить и исследовать связи, существующие между величинами, входящими в задачу, выбрать кратчайший путь решения.

Работа посвящена текстовым задачам, при решении которых применяются графики линейной функции.

Актуальность работы в том, что знание нескольких методов решения задачи увеличивает возможность её правильного решения.

Методы, используемые при работе над темой: теоретический анализ учебно-методической литературы, материалов из интернета, экспериментальная работа, анализ собственного опыта.

II. Основная часть

1. Решение текстовых задач с помощью графиков линейной функции

Действие движения характеризуется тремя компонентами: пройденный путь, скорость и время. Известно соотношение между ними S= v t. Работу характеризуют также три компонента действия: время работы, объем работы и производительность (количество произведенной работы в единицу времени). Существует следующее соотношение между этими компонентами: V=N t. В задачах на смеси и сплавы обычно присутствуют тоже три величины: концентрация (доля чистого вещества в смеси (или сплаве)), количество чистого вещества в смеси (или сплаве), масса смеси (сплава). Соотношение между этими величинами: масса смеси концентрация = количество чистого вещества.

Решение текстовой задачи графическим способом осуществляется в три этапа:

Построение графической модели задачи.

Решение получившейся графической задачи.

Перевод полученного ответа с графического языка на естественный.

Рассмотрим подробно реализацию этих этапов процессе решения текстовых задач.

2. Решение задач на движение

Немаловажное значение в математике имеют задачи на движение. Задачи на движение подразделяются на следующие типы: по количеству движущихся объектов, по направлению движущихся объектов, по времени начала движения.

Методы решения текстовых задач на движение, использующие графики, обладают большой простотой и изяществом. При решении задач на движение вводится система координат, причем на оси абсцисс откладывается время, а на оси ординат – пройденное расстояние, отсчитываемое от некоторой фиксированной точки. Движущийся объект в любой момент времени занимает определённое положение, т.е. находится на определённом расстоянии от этой фиксированной точки, а значит, изображается некоторой точкой в данной системе координат. В процессе движения объекта изменяет своё положение и изображающая его точка, вычерчивая некоторую линию – график движения. В разбираемых задачах будем считать движение равномерным и графики движения прямолинейными.

Задача. Из пункта A вышла грузовая машина со скоростью 60 км/ч. Через 2 ч вслед за ней из А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?

Решение. За начальный отсчет времени берется момент выхода грузовой машины (приложение 1), тогда момент выхода легковой машины будет через два часа. Зная скорости движения объектов, построим графики движения. По чертежу видно, что точка пересечения графиков показывает встречу машин, она состоялась на расстоянии 360 км. Ответ: 360 км.

3. Решение задач на совместную работу

Задача. Чтобы выкачать воду из котлована, поставили два насоса. Оба насоса могли бы выкачать всю воду за 10 часов. Однако после 3 часов совместной работы один насос сломался, и другому насосу пришлось работать ещё 14 часов, чтобы выкачать оставшуюся воду. За сколько часов, действуя отдельно, каждый насос мог бы выкачать всю воду из котлована?

Решение. По вертикали отложим отрезок, условно соответствующий количеству воды в котловане. По горизонтали – время работы насосов (пусть они начнут работу в 6 ч. утра) (приложение 2). По графику видно, что если второй насос один начал бы выкачивать воду в 3 часа, то окончил бы работу в 23 часа. Значит, второму насосу потребуется для выкачивания всей воды 20 часов. Т.к. оба насоса вместе выкачивают воду за 10 часов, то первому насосу потребуется также 20 часов для работы.

3. Решение задач на смеси и сплавы

Задача. Один сплав содержит металлы в отношении 1: 5, другой сплав содержит эти же металлы в отношении 5: 7. В какой пропорции нужно взять первый и второй сплавы, чтобы получить сплав, содержащий те же металлы в отношении 1: 3?

Решение. По вертикальной оси отложим вес сплава в условных единицах (приложение 3). По горизонтальной оси — вес первого металла в тех же условных единицах. Первый металл в первом сплаве составляет 1/6 часть. Взяв по горизонтали 1 у.е., а по вертикали 6 у.е., получим точку С. Прямая ОС будет характеризовать первый сплав. Взяв произвольную точку на этой прямой и спроецировав ее на оси, мы определим, сколько условных единиц весит весь сплав и сколько условных единиц составляет в нем вес первого металла. Взяв по горизонтали точку 5 и по вертикали точку 12,получим точку D. Соединив ее прямой линией с началом координат, получим график, характеризующий второй сплав. Аналогично получим характеристику третьего сплава. Из любой точки вертикальной оси, например, на уровне точки D, проведем горизонтальную прямую, пересекающую характеристики в точках М, N и D. Отношение длины отрезка ND к длине отрезка MN даст пропорцию, в которой нужно взять сплавы I и II соответственно, так как в данном случае отрезок ND в 2 раза больше отрезка MN, то необходимо взять 2 части первого сплава и 1 часть второго сплава. Можно просто измерить отрезки линейкой. Ответ: сплавы необходимо брать в пропорции 2: 1.

IV. Заключение

Были изучены материалы учебно-методической литературы, материалы из интернета. Решено множество задач из экзаменационных материалов разными способами, проведен сравнительный анализ. Гипотеза подтвердилась частично. Конечно, алгебраический способ – универсальный, но знание различных способов часто упрощает решение задачи. И, если есть сомнения, что получен правильный ответ, то можно решить задачу другим способом.

По результатам исследования можно сделать следующие выводы:

Использование этого метода упрощает решение задач: нет громоздких вычислений.

Графическим методом решаются задачи не только на движение, но и на совместную работу, на смеси и сплавы.

График дает возможность определить, есть ли у данной задачи решение и единственно ли оно.

Есть и «минусы»: иногда получаются приближённые значения в случаях неудачного масштаба.

Список использованной литературы:

Кочагин В.В. ОГЭ 2018. Математика: тематические тренировочные задания: 9 класс. – Москва: Эксмо, 2017. – 192 с.
Лунина Л.С. Обучение решению алгебраических задач геометрическим методом //Математика в школе: М.: Изд. «Школа-Пресс»,1996.-№4.- с.34-39.
Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач. Учебное пособие по математике для учителей и учащихся. Издание Томского института повышения квалификации работников образования, 1995 г.
Ященко И.В., Волчкевич М.А. и др. ЕГЭ 2018. Математика. Профильный уровень. 50 вариантов. Типовые тестовые задания от разработчиков ОГЭ. – М.: Издательство «Экзамен», 2020. – 263 с.
Ресурсы Интернета.

Приложения

(1)

(2)

(3)

Источник