Как составить задачу по теорема пифагора

План урока:

Теорема Пифагора

Задачи на применение теоремы Пифагора

Пифагоровы тройки

Обратная теорема Пифагора

Формула Герона

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х². Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с²– это площадь большого (на рисунке – синего)квадрата, а х² – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

10:2 = 5

Другой катет находим с помощью теоремы Пифагора:

Задачи на применение теоремы Пифагора

Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.

Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.

Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.

Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.

Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.

Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Пифагоровы тройки

Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.

Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.

Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.

Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.

Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.

Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.

Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а², b² и с² – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а² + b² четное. Таким образом, получается, что равенство

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.

Обратная теорема Пифагора

По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:

Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.

Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство

Так как ∆А₁В₁С₁ прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:

а именно это мы и доказываем.

Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:

1) некоторое условие, которое описывает какое-то геометрическое построение;

2) вывод (или заключение), который делается для условия.

В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.

В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.

Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.

Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:

Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.

Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.

Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:

Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда

Формула Герона

Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.

Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:

По рисунку можно записать три уравнения:

Левая часть одинакова в обоих уравнениях, значит, равны и правые:

С учетом этого выразим h²:

Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть

Площадь треуг-ка вычисляется по формуле:

Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.

Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?

Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:

Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.

Задачи на применение теоремы Пифагора

Понедельник, 14 марта, 2016

Когда вы только начинали изучать квадратные корни и способы решения иррациональных уравнений (равенств, содержащих неизвестную под знаком корня), вы, вероятно, получили первое представление об их практическом использовании. Умение извлекать квадратный корень из чисел также необходимо для решения задач на применение теоремы Пифагора. Эта теорема связывает длины сторон любого прямоугольного треугольника.

Пусть длины катетов прямоугольного треугольника (тех двух сторон, которые сходятся под прямым углом) будут обозначены буквами  и , а длина гипотенузы (самой длинной стороны треугольника, расположенной напротив прямого угла) будет обозначена буквой . Тогда соответствующие длины связаны следующим соотношением:

(сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы).

Данное уравнение позволяет найти длину стороны прямоугольного треугольника в том случае, когда известна длина двух других его сторон. Кроме того, оно позволяет определить, является ли рассматриваемый треугольник прямоугольным, при условии, что длины всех трёх сторон заранее известны.

Решение задач с использованием теоремы Пифагора

Для закрепления материала решим следующие задачи на применение теоремы Пифагора.

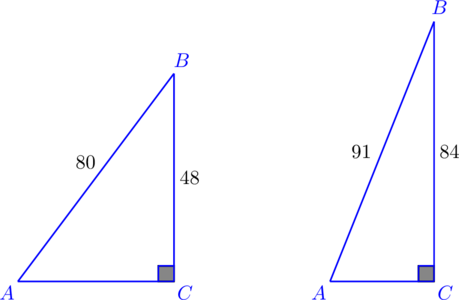
Задача 1. Используя приведённые ниже данные о длинах сторон прямоугольных треугольников, вычислите длины других сторон.

Итак, дано:

1. Длина одного из катетов равняется 48, гипотенузы – 80.
2. Длина катета равняется 84, гипотенузы – 91.

Приступим к решению:

a) Подстановка данных в приведённое выше уравнение даёт следующие результаты:

48²+ b² = 80²

2304 + b² = 6400

b² = 4096

b = 64 или b = -64

Поскольку длина стороны треугольника не может быть выражена отрицательным числом, второй вариант автоматически отбрасывается.

Ответ к первому рисунку: b = 64.

b) Длина катета второго треугольника находится тем же способом:

84²+ b² = 91²

7056 + b² = 8281

b² = 1225

b = 35 или b = -35

Как и в предыдущем случае, отрицательное решение отбрасывается.

Ответ ко второму рисунку: b = 35

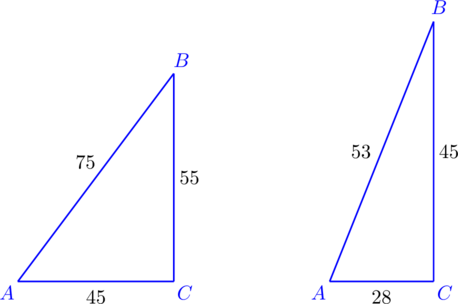
Задача 2. Используя приведённые ниже данные о длинах сторон треугольников, определите, являются ли они прямоугольными.

Нам дано:

1. Длины меньших сторон треугольника равны 45 и 55 соответственно, большей – 75.
2. Длины меньших сторон треугольника равны 28 и 45 соответственно, большей – 53.

Решаем задачу:

a) Необходимо проверить, равна ли сумма квадратов длин меньших сторон данного треугольника квадрату длины большей:

75²= 5625

45²+ 55² = 2025 + 3025 = 5050

5625 ≠ 5050

Следовательно, первый треугольник не является прямоугольным.

b) Выполняется та же самая операция:

53²= 2809

28²+ 45² = 784 + 2025 = 2809

2809 = 2809

Следовательно, второй треугольник является прямоугольным.

Задача 3. Даны точки (-2, -3), (2, 1), (5, -2) в прямоугольной системе координат на плоскости. Выясните, являются ли они вершинами прямоугольного треугольника.

Сперва найдем длину наибольшего отрезка, образованного точками с координатами (-2, -3) и (5, -2). Для этого используем известную формулу для нахождения расстояния между точками в прямоугольной системе координат:

   

Аналогично находим длину отрезка, заключенного между точками с координатами (-2, -3) и (2, 1):

   

Наконец, определяем длину отрезка между точками с координатами (2, 1) и (5, -2):

   

Поскольку имеет место равенство:

   

то соответствующий треугольник является прямоугольным.

Таким образом, можно сформулировать ответ к задаче: поскольку сумма квадратов сторон с наименьшей длиной равняется квадрату стороны с наибольшей длиной, точки являются вершинами прямоугольного треугольника.

Задача 4. Мальчик Ваня строит ворота. В высоту они должны достигать двух метров, в ширину – трёх. Если допустить, что углы, образованные косяками, окажутся прямыми, то какова будет длина троса, протянутой по диагонали от одного угла к другому?

Основание (расположенное строго горизонтально), косяк (расположенный строго вертикально) и трос (протянутый по диагонали) формируют прямоугольный треугольник, соответственно, для нахождения длины троса может использоваться теорема Пифагора:

   

Таким образом, длина троса будет составлять приблизительно 3,6 метра.

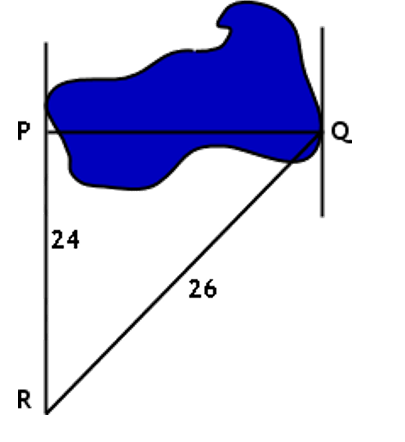
Задача 5. Мальчику Вите требуется измерить ширину пруда. Он нашёл расстояния от пункта R до пунктов P и Q, расположенных по разным сторонам пруда, как показано на рисунке ниже, и уверился в том, что угол P – прямой. Если допустить, что расчёты верны, какова протяжённость пруда с запада на восток?

Дано: расстояние от точки R до точки P (катет треугольника) равняется 24, от точки R до точки Q (гипотенуза) – 26.

Итак, помогаем Вите решить задачу. Поскольку стороны треугольника, изображённого на рисунке, предположительно образуют прямоугольный треугольник, для нахождения длины третьей стороны можно использовать теорему Пифагора:

   

Итак, ширина пруда составляет 10 метров.

Репетитор по математике на Юго-Западной, Сергей Валерьевич

Теорема Пифагора по праву считается
самой важной в курсе геометрии и заслуживает
пристального внимания. Она является основой
решения множества задач. Поэтому для
формирования понимания значимости теоремы
Пифагора при изучении как геометрии, так и других
дисциплин, умений применять теорему Пифагора к
решению задач я предлагаю восьмиклассникам
индивидуальные разноуровневые задачи, требующие
творческого подхода в решении и оформлении.
Решение таких занимательных задач помогает
также воспитывать у учащихся интерес к предмету:
математика уже не кажется им сухой и скучной
наукой, дети видят, что и здесь нужны выдумка,
полет фантазии, творческие способности.

Задача №1. Древнеиндийская задача.

Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”

Какова глубина в современных
единицах длины (1 фут приближенно равен 0,3 м) ?

Решение.

 

Выполним чертёж к задаче и обозначим
глубину озера АС =Х, тогда AD = AB = Х + 0,5 .

Из треугольника ACB по теореме Пифагора
имеем AB² – AC² = BC²,

(Х + 0,5 )² – Х² = 2² ,

Х² + Х + 0,25 – Х² = 4,

Х = 3,75.

Таким образом, глубина озера
составляет 3,75 фута.

3, 75 • 0,3 = 1,125 (м)

Ответ: 3,75 фута или 1, 125 м.

Задача №2. Задача индийского
математика XII в. Бхаскары.

На берегу реки рос тополь
одинокий. Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой с теченьем реки
его ствол составлял. Запомни теперь, что в том
месте река в четыре лишь фута была широка.
Верхушка склонилась у края реки, осталось три
фута всего от ствола. Прошу тебя, скоро теперь мне
скажи: у тополя как велика высота?

Решение.

Пусть АВ – высота ствола. По теореме Пифагора имеем СD= . АВ = АС + АD, АВ = 3 + 5 =8.

Ответ: 8 футов.

Задача №3. Задача арабского
математика XI в.

На обоих берегах реки растет по
пальме, одна против другой. Высота одной 30 локтей,
другой – 20 локтей. Расстояние между их
основаниями – 50 локтей. На верхушке каждой
пальмы сидит птица. Внезапно обе птицы заметили
рыбу, выплывшую к поверхности воды между
пальмами. Они кинулись к ней разом и достигли ее
одновременно. На каком расстоянии от основания
более высокой пальмы появилась рыба?

Решение.

Итак, в треугольнике АDВ: АВ2 =ВD2 +А D2 =302 +Х2=900+Х2; в треугольнике АЕС: АС2= СЕ2+АЕ2 =202+(50 – Х)2 =400+2500 – 100Х+Х2=2900 – 100Х+Х2. Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время. Поэтому АВ2 =АС2 , 900+Х2 =2900 – 100Х+Х2, 100Х=2000, Х=20, АD=20. Значит, рыба была на расстоянии 20 локтей от большой пальмы.

Ответ: 20 локтей.

Задача №4. Египетская задача.

На глубине 12 футов растет лотос
с 13-футовым стеблем. Определите, на какое
расстояние цветок может отклониться от
вертикали, проходящей через точку крепления
стебля ко дну.

Решение.

Пусть АВ = АС – длина стебля. Из АDС по теореме Пифагора СD =

Ответ: 5 футов.

Задача №5.

Бамбуковый ствол в 9 футов
высотой переломлен бурей так, что если верхнюю
часть его пригнуть к земле, то верхушка коснется
земли на расстоянии 3 футов от основания ствола.
На какой высоте переломлен ствол?

Решение.

Пусть АВ=9 – высота ствола, искомая высота АС=Х, тогда СК = 9 – Х. Из САК по теореме Пифагора СК2 = АС2 + АК2; (9 – Х)2 = Х2 + 32, 81 – 18Х + Х2 = Х2 + 9, 18Х = 72, Х = 4. Значит, ствол переломлен на высоте 4 футов.

Ответ: 4 фута.

Задача №6.

В центре квадратного пруда,
имеющего 10 футов в длину и ширину, растет
тростник, возвышающийся на один фут над
поверхностью воды. Если его пригнуть к берегу, к
середине стороны пруда, то он своей верхушкой
достигнет берега. Какова глубина пруда в
современных единицах длины (1 фут приближенно
равен 0,3 м)?

Решение.

Обозначим глубину озера В D = х, тогда АВ = ВС = х + 1
– длина тростника. Из ?В DС по теореме Пифагора СD²
= СВ² – ВD²,

5² = (х + 1)² – х²,

25 = х² + 2х + 1 – х²,

2х = 24,

х = 12.

Значит, глубина пруда 12 футов. 12 • 0,3 = 3,6
(м).

Ответ: 3,6 м.

Задача №7.

Эскалатор метрополитена имеет 17
ступенек от пола наземного вестибюля до пола
подземной станции. Ширина ступенек 40 см, высота 20
см. Определите а) длину лестницы, б) глубину
станции по вертикали.

Решение.

а) Пусть АВ – длина лестницы из 17 ступенек. Из АКD по теореме Пифагора АD = (см), АВ = 45 • 17 = 765 (см) = 7, 65 (м). б) ВС = 40 • 17 = 680 (см). Из АСВ по теореме Пифагора АС = (см) = 3,5 (м).

Ответ: длина лестницы 7, 65 м,
глубина станции 3,5 м.

Задача №8.

Параллельно прямой дороге на
расстоянии 500м от неё расположена цепь стрелков.
Расстояние между крайними стрелками равно 120 м,
дальность полёта пули 2800 м. Какой участок дороги
находится под обстрелом?

Решение.

Из АН D по теореме Пифагора АН = (км), АВ = 2 • АН + НК, АВ = 2 • 2,755 + 0,12 = 5,63 (км).

Ответ: 5,63 км.

Задача №9.

Пловец поплыл от берега реки,
всё время гребя в направлении по перпендикуляру
к берегу (берега реки считаем параллельными).
Плыл он, приближаясь к противоположному берегу
со скоростью 3 км/ч. Через 5 мин. он был на
противоположном берегу. Узнайте, на каком
расстоянии от мести начала заплыва он вышел на
противоположном берегу, считая скорость течения
всюду равной 6 км/ч.

Решение.

	Пловец приближался к противоположному берегу со скоростью , значит ширина реки АВ = 50 • 5 = 250 (м). Скорость течения реки , следовательно, течение снесло его за 5 мин. на 500м (ВС=500м). По теореме Пифагора находим расстояние от точки первоначального заплыва до точки выхода на противоположный берег АС = ? 250 • 2,24=560 (м)

Ответ: 560 м.

Задача №10.

Вы плывёте на лодке по озеру и
хотите узнать его глубину. Нельзя ли
воспользоваться для этого торчащим из воды
камышом, не вырывая его?

Решение.

Слегка отклонив камыш и держа его в натянутом состоянии, замерим расстояние а между точками А и В, в которых камыш пересекает поверхность воды соответственно в вертикальном и наклоненном положении. Возвратим камыш в исходное положение и определим высоту в над водой, на которую поднимется при этом точка В наклонённого камыша, заняв исходное положение С. Тогда обозначив через D основание камыша, а через х – искомую глубину АD, из прямоугольного АВD по теореме Пифагора находим х2 +а2 = (х+в)2, х2+а2= х2+2хв+в2 2хв=а2 – в2 , х=

Задача №11.

Как далеко видно с маяка данной
высоты над уровнем моря?

Решение.

Если обозначить через Н высоту маяка, а через R радиус Земли ( R приближенно равен 6400 км), то искомое расстояние будет равно S = . При Н=125 м S = 40 км.

Ответ: с высоты маяка в 125 м
обозревается расстояние в 40 км.

Задача №12.

Вертолет поднимается
вертикально вверх со скоростью 4 м/с. Определите
скорость вертолета, если скорость ветра, дующего
горизонтально, равна 3 м/с.

Решение.

 

v² = 3² + 4² = 25

v = 5.

Ответ: 5 м/с.

Литература:

• Семенов Е.Е. Изучаем геометрию: Книга для
  учащихся 6-8 классов средней школы. – М.:
  Просвещение, 1987.
• Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени
  математику. – М.: Наука, 1990.
• Перельман Я.И. Занимательная алгебра. – М.:
  Наука, 1978.
• Газета «Математика»: еженедельное
  учебно-методическое приложение к газете «Первое
  сентября», № 24, 2001 г. «Изучаем теорему Пифагора».
• Ульянова Е.А. Урок геометрии в 8-м классе по теме:
  «Теорема Пифагора» (интегрированный урок). –
  Фестиваль «Открытый урок 2005– 2006».
• Борисова Н.А. Урок-конференция по геометрии в 8-м
  классе по теме: «Пифагор и его теорема». –
  Фестиваль «Открытый урок 2005– 2006».

Оглавление

Введение        3

Основная часть        4

1.Теорема Пифагора в прикладных задачах        4

1.1. История возникновения теоремы Пифагора        4

1.2.Прикладное применение теоремы Пифагора        6

1.3.Теорема Пифагора в прикладных задачах школьного курса        15

1.4.Анализ результатов анкетирования учащихся  9 классов по теме «Теорема Пифагора в прикладных задачах»        15

1.5.Подбор прикладных задач на применение теоремы Пифагора,        16

составленных автором работы        16

Заключение        23

Список используемых источников и литературы        24

Введение

Актуальность исследования.

Различают две основные области математики — чистую математику, в которой акцент делается на дедуктивные рассуждения, и прикладную математику. Термин «прикладная математика» иногда относят к тем ветвям математики, которые созданы специально для того, чтобы удовлетворить запросы и требования науки, а иногда — к тем разделам различных наук (физики, экономики и т.п.), которые используют математику как средство решения своих задач. Многие распространенные заблуждения в отношении математики возникают в результате смешения этих двух толкований «прикладной математики». Арифметика может служить примером прикладной математики в первом смысле, а бухгалтерский учет — во втором.

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

В современных учебниках по математике для основной школы, на мой взгляд, недостаточно отражена прикладная направленность изучаемого материала, фактически отсутствует разнообразие примеров применения теоретических знаний на практике. Моё стремление к какой-то мере восполнить выявленный пробел в практической направленности математической подготовки.

Объектом исследования являлась практическая направленность школьного курса математики. Предмет исследования  — применение теоремы к решению задач прикладного характера

Цель исследования — изучение истории и технологии решения прикладных задач с применением теоремы Пифагора.

Для достижения цели исследования были выдвинуты задачи:

1. Рассмотреть историю возникновения теоремы Пифагора
2. Выявить в каких областях применяется теорема Пифагора
3. Изучить технологию решения прикладных задач с применением теоремы Пифагора
4. Составить самостоятельно задачи прикладного характера на применение теоремы Пифагора

Основная часть

1.Теорема Пифагора в прикладных задачах

1.1. История возникновения теоремы Пифагора

Геометрия владеет двумя сокровищами:

одно из них — это теорема Пифагора…

Иоганн Кеплер.

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора это её простота, красота, значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о её широком применении.

Кто такой Пифагор?

Пифагор Самосский (570—490 гг. до н. э.) — древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев.

Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание, известное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет.

Однако одни полагают, что он первым дал её полноценное доказательство, другие же отказывают ему и в этой заслуге.

О теореме Пифагора в своих работах писали многие учёные: греческий писатель-моралист Плутарх, математик 5 века Прокл и другие. Возможно, кто-то из вас читал сонет немецкого писателя — романиста Шамиссо

Пребудет вечной истина, как скоро

Её узнает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далёкий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За света луч, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, её почуя, вслед.

Они не в силах свету помешать,

А могут лишь, закрыв глаза, дрожать

От страха, что вселил в них Пифагор.

Этот рассказ о жертвоприношении, сообщаемый Диогеном, Лаэртом и Плутархом, конечно вымышлен. А поэтому, увы, лишено основания и то насмешливое замечание о переселении душ, которое встречается у Генриха Гейне: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принёс в жертву бессмертным богам».

Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось «ослиным мостом» или «бегством убогих», а сама теорема — «ветряной мельницей» или «теоремой невест». Учащиеся даже рисовали карикатуры и составляли стишки вроде этого:

Пифагоровы штаны

Во все стороны равны.

Шаржи  из учебника XVI  века к теореме Пифагора.

        

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим

И таким простым путем

К результату мы придем

Формулировки теоремы тоже различны. Общепринятой считается следующая формулировка: «В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов»

Геометрическая формулировка.

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин кат

1.2.Прикладное применение теоремы Пифагора

Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы — это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой.

Авиация

Задача 1. С аэродрома вылетели одновременно два самолёта: один — на запад, другой — на юг. Через два часа расстояние между ними было 2000 км. Найдите скорости самолётов, если скорость одного составляла 75% скорости другого.

Решение:

 По теореме Пифагора:

4x2+(0,75x*2)2=20002

6,25x2=20002

2,5x=2000

x=800

0,75x=0,75*800=600.

Ответ: 800 км/ч.; 600 км/ч

Физика

Задача 2. Найдите равнодействующую трёх сил по 200 Н каждая, если угол между первой и второй силами и между второй и третьей силами равен 60°.

Решение:

Модуль суммы первой пары сил равен:

F1+22=F12+F22+2*F1*F2 cos α 

где α — угол между векторами F1 и F2, т.е. F1+2=200√ 3 Н. Как ясно из соображений симметрии вектор F1+2 направлен по биссектрисе угла α, поэтому угол между ним и третьей силой равен:

β=60°+60°/2=90°.

Теперь найдём равнодействующую трёх сил:

R2=(F3+F1+2 )

R=400 Н.

Ответ: R=400 Н.

Строительство

Окно

Задача 3. В зданиях романского и готического стиля верхние части окон расчленяются каменными рёбрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его весьма прост: из рисунка легко найти центры шести дуг окружностей, радиусы которых равны 1)ширине окна b для наружных дуг и 2) половине ширины, т.е. b/2 -для внутренних. Остаётся ещё полная окружность, касающаяся четырёх дуг. Так как она заключена между двумя концентрическими окружностями, то её диаметр равен расстоянию между этими окружностями, т.е. b/2 и, следовательно, радиус равен b/4. Тогда становится ясным и положение её центров.

В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; рассмотрим, как применяется в таких задачах теорема Пифагора.

В романской архитектуре часто встречается мотив, представленный на этом рисунке.

Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R=b/2 и r =b/4. Радиус ρ внутренней окружности можно вычислить из прямоугольного треугольника, изображённого на рисунке пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+ρ, один катет равен b/4, а другой b/2-ρ. По теореме Пифагора имеем:

(b/4+ρ)2=(b/4)2+(b/2-ρ)2 

или

b2/16+bρ /2+ρ2=b2/16+b2/4-bρ+ρ2,

откуда

b*ρ/2=b2/4 — bρ.

Разделив на b приводя подобные члены, получим:

3*ρ/2=b/4, ρ=b/6. 

Крыша

Задача 4. При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.

Решение:

Треугольник ADC — равнобедренный AB = BC = 4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда: из треугольника DBC: DB = 2,5 м, DC =4,7 м ,  из треугольника  из треугольника ABF: AF= 5,7 м

                                        F

                                                D

A        B                        C

Задача 5. Как следовало бы поступить, чтобы надёжным образом получить прямой угол?

Решение:

Можно воспользоваться теоремой Пифагора и построить треугольник, придав его сторонам такую длину, чтобы треугольник получился прямоугольный. Проще всего взять для этого планки длиной в 3, 4 и 5 каких-либо произвольно выбранных равных отрезков.

Молниеотвод

Задача 6. Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

Решение:

По теореме Пифагора h2 ≥ a2+b2, значит h ≥ (a2+b2)½.

Ответ: h ≥ (a2+b2)½

Астрономия

Задача 7. На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч — прямой. Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равна половина пути, который проходит луч? Если обозначить отрезок AB символом l, половину времени как t, а также обозначив скорость движения света буквой c, то наше уравнение примет вид

c * t = l

Очевидно? Это ведь произведение затраченного времени на скорость!

Теперь попробуем взглянуть на то же самое явление из другой системы отсчета, с другой точки зрения, например, из космического корабля, пролетающего мимо бегающего луча со скоростью v. Раньше мы поняли, что при таком наблюдении скорости всех тел изменятся, причем неподвижные тела станут двигаться со скоростью v в противоположную сторону. Предположим, что корабль движется влево. Тогда две точки, между которыми бегает зайчик, станут двигаться вправо с той же скоростью. Причем, в то время, пока зайчик пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.

Вопрос: на сколько успеет сместится точка (чтобы превратиться в точку C), пока путешествует световой луч? Точнее, опять спросим о половине данного смещения! Если обозначить половину времени путешествия луча буквой t’, а половину расстояния AC буквой d, то получим наше уравнение в виде:

v * t’ = d

Буквой v обозначена скорость движения космического корабля. Опять очевидно, не правда ли?

Другой вопрос: какой путь при этом пройдет луч света? (Точнее, чему равна половина этого пути? Чему равно расстояние до неизвестного объекта?)

Если обозначить половину длины пути света буквой s, то получим уравнение:

c * t’ = s

Здесь c — это скорость света, а t’ — это тоже самое время, которые мы рассматривали на формулы выше.

Теперь рассмотрим треугольник ABC. Это равнобедренный треугольник, высота которого равна l. Да-да, тому самому l, которое мы ввели при рассмотрении процесса с неподвижной точки зрения. Поскольку движение происходит перпендикулярно l, то оно не могло повлиять не нее.

Треугольник ABC составлен из двух половинок — одинаковы прямоугольных треугольников, гипотенузы которых AB и BC должны быть связаны с катетами по теореме Пифагора. Один из катетов — это d, которое мы рассчитали только что, а второй катет — это s, через который проходит свет, и который мы тоже рассчитали. Получаем уравнение:

s2 = l2 + d2

Это ведь просто теорема Пифагора, верно?

                                В

                                         

        А        С

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы, которые долгое время считались искусственными) и др. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора.

Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Мобильная связь

Задача 8. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.) 

Решение:         

Пусть AB= x, BC=R=200 км, OC= r =6380 км.

OB=OA+AB

OB=r + x. 

Используя теорему Пифагора, получим 2,3 км

Ответ: 2,3 км

Телевидение

Задача 9. Какую наибольшую высоту должна иметь телевизионная вышка, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

Решение:

Пусть AB= x, BC=R=500 км, OC= r =6380 км.

OB=OA+AB
OB=r + x. 

Используя теорему Пифагора, получим

Ответ: 2,3 км.

Древние задачи

Задача 10. Из учебника Леонтия Магницкого. Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать .

 

 

Решение:

x2+1172=1252

x2=442

x=44

Ответ: 44 стопы

Задача 11. У древних индусов был обычай предлагать задачи в стихах:

Над озером тихим,

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнес его в сторону. Нет

Боле цветка над водой.

Нашел же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

Как озера вода глубока?

Решение.                                                                    0,5 м

                                                                                              Х  м        Х+0,5  м

По  теореме Пифагора имеем:

 (x+0,5)2— x2= 22,                                                                                      2 м

x2+ x + 0,25- x2= 4,

x = 3,75.

Ответ: 3,75.

Задача 12. Две задачи из «Математики в девяти книгах» (Древний Китай, II в. до н.э.).

Задача 12.1. из девятой книги. «Имеется водоем со стороной в 1 чжан (=10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?»

Решение. В ABC ABC = 90. Пусть BC = x чи, тогда AC = x + 1 (чи); AB = 5 чи. По теореме Пифагора

1) (x + 1)2 = 52 + x2;

x2 + 2x + 1 = x2 + 25;

2x = 24;

x = 12.

2) 12 + 1 = 13 (чи).

Ответ. глубина воды 12 чи, длина камыша 13 чи.

Задача 13.2. из девятой книги. «Имеется бамбук высотой 1 чжан (= 10 чи). Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня. Спрашивается: какова высота после сгибания?» (рис. 4).

Рис. 4.

Решение. BD – высота бамбука. При сгибании бамбука вершина D перешла в A. СB – высота бамбука после сгибания. Пусть CB = x чи, тогда CD = AC = 10 – x (чи), AB = 3 чи,

AC2 = AB2 + BC2,

(10 – x)2 = 9 + x2,

100 – 20x + x2 = 9 + x2,

– 20x = – 91,

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Земледелие

Задача 14. Размеры трех участков, имеющих формы прямоугольных треугольников, различны, но площади у всех одинаковы и составляют 3360 м². Катеты одного треугольника 140 м и 48 м, гипотенуза 148 м. Катеты второго треугольника 80 м и 84 м, гипотенуза 116 м. Найдите размеры третьего участка, если они также выражены целыми числами.

1.3.Теорема Пифагора в прикладных задачах школьного курса

Учебник	Прикладные задачи
Погорелов А.В. Геометрия: Учеб.для 7-11 кл. общеобразоват. учреждений. — М.: Просвещение, 2000	Задача1. Можно ли из круглого листа железа диаметром 1, 4 м вырезать квадрат со стороной 1 м? Задача 2. Могут ли увидеть друг друга космонавты, летящие над поверхностью земли на высоте 230 км, если расстояние между ними по прямой равно 2200 км? Радиус Земли 6370 км. Задача 3. Между двумя фабричными зданиями устроен покатый жёлоб для передачи материалов. Расстояние между зданиями равно 10 м, а концы жёлоба расположены на высоте 8 м 4 м над землёй. Найдите длину жёлоба.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия: Учеб.для 7-11 кл. общеобразоват. учреждений. — М.:.Просвещение, 2007	—

1.4.Анализ результатов анкетирования учащихся  9 классов по теме «Теорема Пифагора в прикладных задачах»

1. Знаете ли вы теорему Пифагора?

2) Хотели ли вы решать прикладные задачи на уроках на применение теоремы Пифагора?

1. Где применяется теорема Пифагора?

1.5.Подбор прикладных задач на применение теоремы Пифагора,

составленных автором работы

1. Парк в селе Петровка имеет форму прямоугольника. Какова длина главной аллеи, идущей по диагонали парка, если его площадь равна 7200 , длина одной из сторон 200 м?

Решение: Найдём ширину 

b = 36 м

По теореме Пифагора из прямоугольного треугольника АВС найдём АС

+

 203 (м)

Ответ:  203 м

1. Пусть каждая спичка имеет длину 1 дюйм. Сложите из 12 таких спичек одну фигуру площади 6 кв. дюйма.

3        5

4

Решение:

          S = 6 (кв. дюймов)

1. Пожарная лестница длиной 20 м стоит на машине, на высоте 2 м от земли и на расстоянии 5 м от здания. До какого этажа можно на ней добраться, если высота этажа 3 м?

В

        20 м

С        А

      2 м

Д        5 м        М        

        5 м

По теореме Пифагора из треугольника АВС найдём ВС:

= +

 

 м

Найдём BD:

 м

Найдём количество этажей:

 : 3  7

Ответ: 7

1. Между двумя зданиями устроен покатый жёлоб для передачи материалов. Расстояние между зданиями равно 10 м, а концы жёлоба расположены на высоте 12 м и 15 м над землёй. Найдите длину жёлоба.

  В

        ?

   С                А

15 м

                           12 м

        Д                                

                10                 М

Решение:

По теореме Пифагора  из треугольника АВС найдём АВ:

Ответ: 10,4 м

1. Высота водонапорной башни 20 м. Вокруг башни ров шириной 5 м. Подойдёт ли  для ремонта башни лестница длиной 21 м?

        А

        ?

             20 м

        С        5 м        B

Решение:

По теореме Пифагора  из треугольника АВС найдём АВ:

+

 20,6 (м)

Ответ: да

1. От пятнадцатиметрового столба нужно протянуть провод к зданию дома на высоте 5 метров. Столб находится на расстоянии 6 м от дома. Хватит ли провода длиной 10 м?

        В

                             15 м         C        A

        5 м

   Д                М

                                                6 м

Решение:

По теореме Пифагора  из треугольника АВС найдём АВ

 

Ответ: нет

1. Земельный участок имеет форму квадрата со  стороной 100 м. Сколько  нужно плиток размером 1 м ×1 м для тропинки шириной 1 м, идущей по диагонали участка?

                                    100 м

        В        С

      100 м

        А        Д

Решение:

По теореме Пифагора  из треугольника АВС найдём АС

+

 141,4 (м)

Ответ: 142 плитки

1. С восьмиметровой башни брошен камень. Башня находится на расстоянии 4 м от места падения камня. Какое расстояние пролетел камень?

                   А

8 м

                В        4 м                        С

Решение:

По теореме Пифагора  из треугольника АВС найдём АВ

+

  8,9 (м)

Ответ: 8,9 м

9. Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты.  Хватит ли 50 м троса для крепления мачты?

Решение:

Найдём длину одного троса АВ по теореме Пифагора из треугольника АВС:

АВ – гипотенуза, АС и ВС – катеты  треугольника АВС

Тогда длина четырёх тросов 4*13 = 52 м, а у нас всего 50 м

Ответ: не хватит двух метров.

Заключение

В своё время Ж Адама отметил, что приложения математических знаний к практике полезны и фактически необходимы для теории, потому что они ставят перед теорией новые вопросы, Он сравнивал теоретические знания и их практическое применение с деревом и листом: «Дерево держит лист, но лист питает дерево». Постепенное превращение науки в непосредственную производительную силу современного общества определило знание по предметам естественно-математического цикла как базовое для овладения специальными знаниями, как квалифицированные требования к специалистам многих современных профессий. Поэтому изучая теоретические основы того или иного предмета, учащийся должен чётко представлять в какой области практики могут быть применены полученные им знания.

Выполнив работу, получили выводы:

1. Появление задач прикладного характера обусловлено практической деятельностью человека
2. Теорема Пифагора применяется в различных областях (строительство, астрономия, авиации, физика, мобильная связь и т.д.)
3. Первые прикладные задачи с использованием теоремы Пифагора были решены в глубокой древности
4. В школьном курсе математики недостаточное количество прикладных задач
5. Задачи прикладного характера интересны ученикам школы
6. Результаты исследования могут быть полезны на уроках математики и на внеклассных занятиях

Сборник задач по теме «Теорема Пифагора»

Автор: Клейменова Ирина Николаевна

Организация: МКОУ-Усть-Луковская СОШ

Населенный пункт: Новосибирская область, Ордынский район, с. Усть-Луковка

Теорема Пифагора в геометрии важна не меньше, чем таблица умножения в арифметике. Решение многих геометрических задач (как в планиметрии, так и в стереометрии), сводится к рассмотрению прямоугольных треугольников и применению этой замечательной теоремы. Так же большинство задач по нахождению сторон прямоугольных треугольников сводится к использованию этой теоремы. Предлагаю небольшой сборник задач по теме «Теорема Пифагора». Данный дидактический материал содержит разноуровнивые задачи. Я решила, что этот материал будет интересен учащимся 8-9 классов, при изучении темы. Почему для меня актуальна этота тема? В учебнике геометрия 7-9 класс Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, очень мало задач по данной теме и этого материала не хватает для успешного усвоения данной темы. На экзамене в 9 классе, как минимум, 3 задания на данную тему и у учеников они вызывают трудности. Я надеюсь, что мой небольшой сборник поможет справиться с этими трудностями.

Приложения:

1. file0.docx.. 240,1 КБ

2. file1.docx.. 12,4 КБ

Опубликовано: 14.11.2020