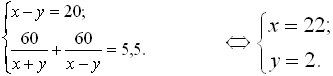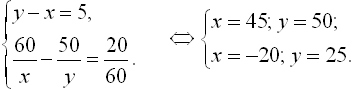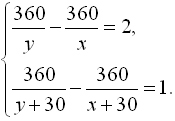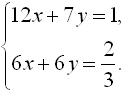Математика
Тема 7: Системы линейных уравнений с двумя переменными
Урок 3: Решение задач с помощью систем уравнений
- Видео
- Тренажер
- Теория
Заметили ошибку?
94. Решение задач с помощью систем уравнений.
Некоторые задачи проще решать с помощью системы уравнений. Обычно это те задачи, в которых нужно найти две величины. Существует алгоритм, выполняя который легко решать задачи с помощью системы уравнений.
Чтобы решить задачу с двумя неизвестными, нужно:
- Обозначить неизвестные величины буквами (обычно это те величины, значения которых и нужно найти в задаче).
- Используя условие задачи, составить систему линейных уравнений.
- Решить систему.
- Истолковать полученный ответ в соответствии с условием задачи.
Пример 1. Основание равнобедренного треугольника на 8 дм больше боковой стороны. Найдите боковую сторону треугольника, если его периметр равен 44 дм.
Решение: у треугольника три стороны. Длины этих сторон нам неизвестны. Но нам известно, что треугольник равнобедренный – это значит, что его боковые стороны равны. То есть у нас есть две неизвестные величины: длина боковой стороны и длина основания.
Пусть х (см) – длина боковой стороны равнобедренного треугольника,
у (см) – длина основания равнобедренного треугольника.
Так как нам известно, что основание треугольника больше его боковой стороны на 7 дм, мы можем составить первое уравнение
у-х = 8
Периметр треугольника – это сумма длин всех его сторон. Выразим ее через переменные х и у.
х+х+у = 2х+у (дм)
Нам известно, что периметр треугольника равен 44 дм. Используя это, составим второе уравнение
2х+у = 45
Запишем систему уравнений
y-x=82x+y=44
Умножим первое уравнение на 2
2y-2x=162x+y=44
Применим способ сложения
3y=602x+y=44
y=202x+20=44
y=192x=24
y=20x=12
Мы получили два числа. Вспомним, что за х мы обозначали боковую сторону треугольника, значит, боковая сторона треугольника равна 12 см. А за у обозначали основание треугольника. То есть основание треугольника равно 20 см. В задаче требуется найти только боковую сторону треугольника. Значит ответ будет выглядеть так: боковая сторона треугольника равна 12 см.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.
Решая задачи при помощи уравнений, мы искали, как правило, одно неизвестное. Но встречаются и задачи, где есть несколько неизвестных. Такие задачи принято решать посредством составления систем уравнений.

Навстречу друг другу из одного города в другой, расстояние между которыми составляет 30 км, едут два велосипедиста. Предположим, что если велосипедист 1 выедет на 2 ч раньше своего товарища, то они встретятся через 2,5 часа после отъезда велосипедиста 2; если же велосипедист 2 выедет 2мя часами ранее велосипедсита 1, то встреча произойдет через 3 часа после отъезда первого. С какой скоростью движется каждый велосипедист?
Решение.
1. Определим скорость велосипедиста 1 как х км/ч, а скорость велосипедиста 2 как у км/ч.
2. Если первый велосипедист выедет на 2 ч раньше второго, то, согласно условию, он будет ехать до встречи 4,5 ч, тогда как второй 2,5 часа. За 4,5 ч первый проедет путь 4,5х км, а за 2,5 ч второй проедет путь 2,5у км.
3. Встреча двух велосипедистов означает, что суммарно они проехали путь 30 км, т.е. 4,5х + 2,5 у = 30. Это и есть наше первое уравнение.
4. Если второй выедет на 2 ч раньше первого, то, согласно условию, он будет ехать до встречи 5 ч, тогда как первый – 3 ч. Используя рассуждения, аналогичные изложенным выше рассуждениям, приходим к уравнению:
3х + 5у = 30.
5. Итак, мы получили систему уравнений
{4,5х + 2,5 у = 30,
{3х + 5у = 30.
6. Решив полученную систему уравнений, мы найдем корни: х = 5, у = 3.
Т.о., первый велосипедист едет со скоростью 5 км/ч, а второй – 3 км/ч.
Ответ: 5 км/ч, 3 км/ч.
Задача 2.
Вкладчику на его сбережения через год было начислено 6 $ процентных денег. Добавив 44 $, вкладчик оставил деньги еще на год. По истечении года вновь было произведено начисление процентов, и теперь вклад вместе с процентами составил 257,5 $. Какая сумма составляла вклад первоначально и сколько процентов начисляет банк?
Решение.
1. Пусть х ($) – первоначальный вклад, а у (%) – это проценты, которые начисляются ежегодно.
2. Тогда к концу года к первоначальному вкладу добавится (у/100) ∙ х $.
Из условия получаем уравнение (ух/100) = 6.
3. По условию известно, что в конце года вкладчик внес еще 44 $, так что вклад в начале второго года составил х + 6 + 44, т.е. (х + 50) $. Таким образом, сумма, полученная к концу второго года с учетом начисления, равнялась (х + 50 + (у/100)(х + 50)) $. По условию эта сумма равна 275,5 $. Это позволило нам составить второе уравнение:
х + 50 + (у/100)(х + 50) = 257,5
4. Итак, мы получили систему уравнений:
{(ух/100) = 6,
{х + 50 + (у/100)(х + 50) = 257,5
После преобразования системы уравнений мы получим:
{ху = 600,
{100х + 50у + ху = 20750.
Решив систему уравнений, мы нашли два корня: 200 и 1,5. Только первое значение удовлетворяет нашему условию.
Подставим значение х в уравнение и найдем значение у:
если х = 200, то у = 3.
Таким образом, первоначальный вклад составлял 200 $, а банк в год производит начисление а размере 3 %.
Ответ: 200 $; 3 %.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
Шаг 1
«От смысла к буквам»:
Пусть x и y — задуманные числа.
Шаг 2
Уравнения по условию задачи::
${left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.}$
Шаг 3
Решение системы уравнений:
$(-) {left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.} Rightarrow {left{ begin{array}{c} -3y = -81 \ x = y+10 end{array} right.} Rightarrow$
$ Rightarrow {left{ begin{array}{c} x = 37 \ y = 27 end{array} right.} $
Шаг 4
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b — длина и ширина прямоугольника.
По условию:
$$ {left{ begin{array}{c} P = 2(a+b) = 48 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 3b+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 4b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a = 18 \ b = 6 end{array} right.} $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.
По условию:
$$ {left{ begin{array}{c} 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end{array} right.} (-) Rightarrow {left{ begin{array}{c} 7x+10y = 10050 \ x-y=185 | times 10 end{array} right.}$$
$$ Rightarrow (+) {left{ begin{array}{c} 7x+10y = 10050 \ 10x-10y = 1850 end{array} right.} Rightarrow {left{ begin{array}{c} 17x = 11900 \ y = x-185 end{array} right.} Rightarrow {left{ begin{array}{c} x = 700 \ y = 515 end{array} right.} $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.
По условию:
$$ {left{ begin{array}{c} 2x+3y = 1540 \ 2y-x = 210 | times 2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 2x+3y = 1540 \ -2x+4y = 420 end{array} right.} Rightarrow {left{ begin{array}{c} 7y = 1960 \ x = 2y-210 end{array} right.} Rightarrow {left{ begin{array}{c} x = 350 \ y = 280 end{array} right.} $$
Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).
По условию:
$$ {left{ begin{array}{c} 3(v-u)+2(v+u) = 73 \ 4(v+u)-3(v-u) = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 3v-3u+2v+2u = 73 \ 4v+4u-3v+3u = 29 end{array} right.}$$
$$ Rightarrow {left{ begin{array}{c} 5v-u = 73 \ v+7u = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 5(29-7u)-u = 73 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} 145-35u-u = 73 \ v = 29-7u end{array} right.} Rightarrow$$
$$ Rightarrow {left{ begin{array}{c} -36u = -72 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} v = 15 \ u = 2 end{array} right.} $$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y — тетрадки.
По условию:
$$ {left{ begin{array}{c} 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end{array} right.} Rightarrow {left{ begin{array}{c} 5x+3y = 170 |times frac{2,4}{5} \ 2,4x+6,5y = 284 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end{array} right.} $$
$$ Rightarrow {left{ begin{array}{c} (6,5-1,44)y = 284-81,6 \ x = frac{170-3y}{5} end{array} right.}Rightarrow {left{ begin{array}{c} y = 202,4:5,06 = 40 \ x = frac{170-120}{5} = 10 end{array} right.} $$
Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
$$ s_{AB} = vt = (v+3)(t-1) = (v-2)(t+1) $$
Получаем систему:
$$ {left{ begin{array}{c} vt = (v+3)(t-1) \ vt = (v-2)(t+1) end{array} right.} Rightarrow (-) {left{ begin{array}{c} vt = vt-v+3t-3 \ vt = vt+v-2t-2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} v-3t = -3 \ -v+2t = -2 end{array} right.} Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} -t = -5 \ v = 2t+2 end{array} right.} Rightarrow {left{ begin{array}{c} t = 5 \ v = 12 end{array} right.} $$
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x — объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
$$ (+) {left{ begin{array}{c} 12+a = x \ 32-a = frac{1}{2} y end{array} right.} Rightarrow x+ frac{1}{2} y = 44 $$
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ (+) {left{ begin{array}{c} 32+b = y \ 12-b = frac{1}{6} x end{array} right.} Rightarrow frac{1}{6}x+y = 44 $$
Получаем систему:
$$ {left{ begin{array}{c} x+ frac{1}{2} y = 44 | times 2 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2x+y = 88 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 1frac{5}{6} x = 44 \ y = 88-2x end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} x = 44: frac{11}{6} = 44cdot frac{6}{11} = 24 \ y = 88-2cdot24 = 40 end{array} right.} $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
$$ {left{ begin{array}{c} 1,5 = frac{s}{v} + frac{s}{u} \ 0,5 = frac{2s}{v} \ t = frac{2s}{u} end{array} right.} $$
Из второго уравнения $ frac{s}{v} = frac{0,5}{2} = 0,25 $. Подставляем в первое уравнение:
$$ frac{s}{u} = 1,5-frac{s}{v} = 1,5-0,25 = 1,25 $$
И тогда искомое время:
$$ t = frac{2s}{v} = 2cdot1,25 = 2,5 (ч) $$
Ответ: 2,5 ч
Цели урока:
- Совершенствование навыков решения текстовых задач.
- Продолжить формирование знаний учащихся по решению систем уравнений с
двумя неизвестными. - Развитие математической грамотности.
Ход урока
Приложение
1. Актуализация знаний учащихся (5 минут).
Устный счет:
1. Найдите решение системы уравнений:
Ответы: 1) (1;3); 2) (0;3); 3) (1;2); 4) (2;1).
2. Выразите из уравнения 3х + 2у = 5 переменную х через
переменную у.
Ответы:
1)
2)
3) х = 3(5 – 2у);
4) х = 3(5 + 2у).
2. Объяснение нового материала (8 минут).
Алгоритм решения задач на движение и на производительность:
- Ввести неизвестные величины.
- Составить краткую запись задачи в таблице (скорость, путь, время) или
(производительность, работа, время). - Исходя из условия задачи, составить систему двух уравнений с двумя
неизвестными. - Решить систему уравнений, исключив те корни, которые не подходят по
условию задачи. - Записать ответ по вопросу задачи.
Задача №475.
Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по
течению и против течения за 5,5 часов. Найдите скорость теплохода в стоячей воде
и скорость течения, если одна из них больше другой на 20 км/ч.
Краткая запись: пусть скорость теплохода х км/ч, а скорость течения
реки у км/ч, тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| По течению | х + у | 60 | 60/(х + у) |
| Против течения | х – у | 60 | 60/(х – у) |
Зная, что теплоход проходит это расстояние по течению и против течения реки
за 5,5 часов и скорость катера больше скорости течения реки, составим систему
двух уравнений с двумя неизвестными:
Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.
3. Решение задач (30 минут).
Задача №478.
Фермер отправился на машине в город, находящийся на расстоянии 110 км от
фермы. Через 20 минут из города на ферму выехал его сын, который проезжал в час
на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал
фермер?
Краткая запись: пусть скорость фермера х км/ч, а скорость сына у,
тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| Фермер | х | 110 – 50 = 60 | 60/х |
| Сын | у | 50 | 50/у |
Зная, что встреча произошла в 50 км от города, и сын выехал на 20 минут
позже, составим систему уравнений с двумя неизвестными:
Второе решение не подходит по условию задачи.
Ответ: 45 км/ч скорость фермера.
Задача №494.
Расстояние в 360 км легковой автомобиль прошел на 2 часа быстрее, чем
грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой
затратит на весь путь на 1 час больше, чем легковой. Найдите скорость каждого
автомобиля.
Краткая запись: пусть скорость легкового автомобиля х км/ч, а скорость
грузового у км/ч, тогда:
1 случай
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х | 360 | 360/х |
| Грузовой | у | 360 | 360/у |
2 случай
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х + 30 | 360 | 360/(х + 30) |
| Грузовой | у + 30 | 360 | 360/(у + 30) |
Зная, что в первом случае легковой автомобиль приезжает на 2 часа раньше, а
во втором на 1 час раньше, составим систему уравнений с двумя переменными:
Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового
автомобиля.
Задача №489.
Бассейн наполнится. Если первую трубу открыть на 12 минут, а вторую – на 7
минут. Если же обе трубы открыть на 6 минут. То наполнится 2/3 бассейна. За
сколько минут наполнится бассейн, если открыть только вторую трубу?
Краткая запись: пусть весь объем воды в бассейне равен 1, производительность
1 трубы х , а второй – у, тогда:
1 случай
| Производительность | Работа | Время, мин | |
| 1 труба | х | 12х | 12 |
| 2 труба | у | 7у |
2 случай
| Производительность | Работа | Время, мин | |
| 1 труба | х | 6х | 6 |
| 2 труба | у | 6у | 6 |
Зная, что в первом случае бассейн наполнится полностью, а во втором только
2/3, составим систему двух уравнений с двумя неизвестными.
Ответ: за 15 минут вторая труба заполнит весь бассейн.
Задача №492.
Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них
сделает половину всей работы, а потом остальное сделает другой, то им
потребуется 25 дней. За сколько дней каждый рабочий, работая один, может
выполнить задание?
Краткая запись: пусть производительность 1 рабочего х, а второго у,
тогда:
| Производительность | Работа | Время | |
| 1 рабочий | х | 1/2 | 1/2х |
| 2 рабочий | у | 1/2 | 1/2у |
Зная, что вместе они сделают работу за 12 дней, а работая по очереди и
выполнив по половине работы, им потребуется 25 дней, составим систему уравнений
с двумя неизвестными:
Ответ: один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.
4. Подведение итогов урока (2 минуты).
Домашнее задание: п. 22, №476, 479, 491.
Используемая литература:
- Учебник «Алгебра 9», автор Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.,
Феоктистов И.Е.
Рассмотрим уравнение с двумя неизвестными:
x + y = 10
У этого уравнения может быть много решений: x=1, y=9; x=2, y=8; x=3, y=7 и т.д.
Какое из решений выбрать — непонятно. Ситуация становится более определённой, если мы знаем, что между x и y существует ещё какая-то другая взаимосвязь. Например, мы знаем про те же самые x и y, что y-x = 2.
Итак, мы можем записать:
То, что мы записали, называется системой уравнений. Уравнения, входящие в систему, объединяются большой фигурной скобкой. Чтобы система уравнений имела решение, число уравнений должно быть равно числу неизвестных.
Так как это связанные между собой уравнения, то мы можем выразить, например, y через x в первом уравнений, и подставить получившееся выражение вместо y во второе уравнение — тем самым во втором уравнении останется только одно неизвестное (x) и мы сможем решить уравнение.
Запишем это в виде формул.
x + y = 10
y = 10 — x
Подставляем полученное выражение 10 — x вместо y во второе уравнение:
y — x = 2
10 — x — x = 2
10 — 2 = x + x
8 = 2x
x = 4
Мы нашли x. Теперь найдём y, зная, что y = 10 — x
y = 10 — 4 = 6
Мы нашли x и y. x = 4, y = 6
Проверим наше решение, подставим x и y в оба уравнения системы:
x + y = 10
y — x = 2
4 + 6 = 10
6 — 4 = 2
10 = 10
2 = 2
В обеих уравнениях левые и правые части равны, то есть x и y мы нашли правильно.
Почему мы смогли воспользоваться этим приёмом — выразить y через x в первом уравнении и подставить получившееся выражение вместо y во второе? Потому что у нас система уравнений и в этих двух уравнениях эти x и y — это одни и те же неизвестные, поэтому мы можем в одном уравнении заменять на выражения, полученные в другом
Не имеет значения — будем ли мы y выражать через x в первом уравнении и подставлять во второе, или во втором и подставлять в первое. Точно также не имеет значение, что именно мы будем подставлять — y, выраженный через x, или x, выраженные через y. Мы выражаем и подставляем то, что нам удобнее в дальнейших расчётах.
Существует и другой метод решения уравнений
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вычитание одного уравнения из другого
Рассмотрим систему уравнений:
{
5x + 6y = 80
2x + 3y = 35
Глядя на эту систему уравнений мы понимаем, что мы не можем выразить x или y через целые числа — 80 делится на цело на 5, но не делится нацело на 6, а 35 не делится нацело ни на 2, ни на 3. Если мы не умеем работать с дробными числами, то уравнение мы можем решить по другому.
Для решения этого уравнения надо из левой части первого уравнения вычесть левую часть второго уравнения, а из правой части первого вычесть правую часть второго. При этом не принципиально вычитать именно из первого уравнения второе — можно и из второго первое. Но если мы в данной системе уравнений вычтем из правой части второго уравнения правую часть
первого уравнения, то у нас получится 35 — 80 = -45, отрицательное число. Если с отрицательными числами мы работать ещё не умеем, то у нас остаётся только один вариант — из первого уравнения вычитать второе.
Почему мы можем вычесть из из левой части одного уравнения левую часть другого, а из правой части одного правую часть другого и при этом быть уверенными, что равенство сохранится? Потому что это свойство систем уравнений. При вычитании соответствующих частей уравнений друг из друга, равенство сохраняется.
Итак, запишем соответствующую операцию вычитания частей уравнений в виде формулы:
5x + 6y — (2x + 3y) = 80 — 35
5x + 6y — 2x — 3y = 45
3x + 3y = 45
x + y = 15
Итак, мы получили простое уравнение x + y = 15, где отсутствуют множители у x и y.
Теперь мы можем выразить x через y (или y через x — это без разницы) и подставить получившееся выражение в одно из уравнений системы.
x = 15 — y
Подставим это выражение вместо x во второе уравнение
2x + 3y = 35
2(15 — y) + 3y = 35
30 — 2y + 3y = 35
y = 35 — 30
y = 5
Мы нашли y, осталось найти x
x = 15 — y
x = 15 — 5 = 10
Наш ответ: x = 10, y = 5
Проверим наше решение, подставив найденные x и y в систему уравнений:
{
5x + 6y = 80
2x + 3y = 35
5∙10 + 6∙5 = 80
2∙10 + 3∙5 = 35
50 + 30 = 80
20 + 15 = 35
80 = 80
35 = 35
Обе части в обеих уравнениях равны друг другу, значит наше решение верное.
Ответ: x = 10, y = 5
Сложение одного уравнения с другим
Уравнения можно не только вычитать друг из друга, но и складывать.
Например:
{
5x + 3y = 71
2x + 4y = 48
Если мы просуммируем оба уравнения, то у нас в правой части у неизвестных x и y будут одинаковые коэффициенты 7 — нам будет удобно на эту 7 поделить, чтобы оставить x и y без коэффициентов.
Сложим два уравнения:
5x + 3y + 2x + 4y = 48 + 71
7x + 7y = 119
x + y = 17
x = 17 — y
Подставим x во второе уравнение:
2x + 4y = 48
Сначала разделим обе части уравнения на 2
x + 2y = 24
Подставим x:
17 — y + 2y = 24
y = 24 — 17
y = 7
x = 17 — y
x = 17 — 7 = 10
Ответ: x = 10, y = 7
Пример 1
{
2n + 3m = 19
3n – m = 12
Выразим m через n во втором уравнении:
3n – m = 12
3n – 12 = m
m = 3n – 12
Подставим 3n – 12 вместо m в первое уравнение
2n + 3m = 19
2n + 3(3n – 12) = 19
2n + 9n – 36 = 19
11n = 55
n = 5
Мы нашли n, теперь найдём m
m = 3n – 12
m = 3∙5 – 12
m = 3
Проверка решения:
2∙5 + 3∙3 = 19
3∙5 – 3 = 12
Ответ: m=3, n = 5
Пример 2
{
2x – 4y = 12
13x + 6y = 142
2x – 4y = 12
x – 2y = 6
x = 6 + 2y
13x + 6y = 142
13(6 + 2y) + 6y = 142
78 + 26y + 6y = 142
32y = 64
y = 2
x = 6 + 2y
x = 6 + 2∙2 = 10
Проверка:
2∙10 – 4∙2 = 12
13∙10 + 6∙2 = 142
Ответ: x = 10, y = 2
Пример 3
{
2x + 3y = 117
8x – 2y = 34
8x – 2y = 34
Разделим левую и правую части уравнения на 2:
4x – y = 17
4x – 17 = y
Теперь в первое уравнение вместо y подставим 4x-17:
2x + 3y = 117
2x + 3(4x – 17) = 117
2x + 12x – 51 = 117
14x = 117+51
14x = 168
x = 12
y = 4x – 17
y = 4∙12 – 17
y = 31
Ответ: x = 12, y = 31
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
{
2x + 3y – 2z = 19
3x – 2y + 3z = 69
4z + y – x = 97
Мы имеем дело с системой уравнений, где три уравнения и три неизвестных.
Нас это не должно пугать. Для начала выразим одну неизвестную через две других, например, x через z и y. Так как в третьем уравнении у нас возле x нет никакого множителя, то именно через третье уравнение мы и будем выражать x.
4z + y – x = 97
4z + y – 97 = x
x = 4z + y – 97
Теперь подставим полученное выражение для x во второе уравнение.
3x – 2y + 3z = 69
3(4z + y – 97) – 2y + 3z = 69
12z + 3y – 291 – 2y + 3z = 69
15z + y = 360
y = 360 — 15z
Ранее мы выразили x через z и y:
x = 4z + y – 97
Теперь полученное выражение для y (y = 360 — 15z) подставим в это выражение для x
x = 4z + 360 – 15z – 97
x + 15z – 4z = 263
x + 11z = 263
x = 263 – 11z
Итак, теперь у нас есть x, выраженный через z, и y, выраженный через z.
Запишем эти выражение ещё раз:
x = 263 – 11z
y = 360 – 15z
Теперь мы можем эти выражения подставить в первое уравнение системы, и у нас получится уравнение с одним неизвестным — z
2x + 3y – 2z = 19
2(263 – 11z) + 3(360 – 15z) — 2z = 19
526 – 22z + 1080 – 45z – 2z = 19
526 + 1080 – 19 = 2z + 45z + 22z
1587 = 69z
z = 23
Теперь подставим z в выражения для x и y:
x = 263 – 11z = 263 – 11∙23 = 10
y = 360 – 15z = 360 – 15∙23 = 15
x = 10
y = 15
z = 23
Проверка:
2∙10 + 3∙15 – 2∙23 = 19
3∙10 – 2∙15 + 3∙23 = 69
4∙23 + 15 – 10 = 97
Ответ: x = 10, y = 15, z = 23
Пример 5
{
5x — z = 17
3x – 2y + 3z = 11
2x + 8y – 6z = 30
Эта система уравнений отличается от предыдущих тем, что в первом уравнении тут не три
неизвестных, а два. Но нас это не должно пугать — наоборот, нам это только упрощает задачу.
Выразим z через x в первом уравнении:
5x – z = 17
5x – 17 = z
z = 5x – 17
Подставим полученное выражение для z во второе уравнение.
3x – 2y + 3z = 11
3x – 2y + 3(5x – 17) = 11
3x – 2y + 15x – 51 = 11
18x – 2y = 62
9x – y = 31
9x – 31 = y
y = 9x – 31
Итак, теперь у нас есть z и y, выраженные через x. Запишем их ещё раз:
z = 5x – 17
y = 9x – 31
Теперь подставим эти выражения в третье уравнение
2x + 8y – 6z = 30
2x + 8(9x – 31) – 6(5x – 17) = 30
2x + 72x – 248 – 30x + 102 = 30
44x = 30 + 248 – 102
44x = 176
x = 4
Мы нашли x, теперь найдём z и y
z = 5x — 17
z = 5∙4 – 17 = 3
y = 9x – 31
y = 9∙4 – 31 = 5
x = 4
y = 5
z = 3
Проверка:
2∙4 + 8∙5 – 6∙3 = 30
3∙4 – 2∙5 + 3∙3 = 11
5∙4 – 3 = 17
Ответ: x = 4, y = 5, z = 3
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 6
{
4x + 3y = 61
4x + 5y = 75
Тут мы не можем выразить ни x, ни y, т.к. левая и правая части уравнений не делятся на цело и на 3, и на 4, ни на 5.
Поэтому воспользуемся описанным ранее способом — вычитанием частей уравнений друг из друга. Вычтем из второго уравнения первое:
4x + 5y – (4x + 3y) = 75 – 61
4x + 5y – 4x – 3y = 14
2y = 14
y = 7
Найденный y подставим в первое уравнение:
4x + 3∙7 = 61
4x + 21 = 61
4x = 40
x = 10
x = 10
y = 7
Проверка:
4∙10 + 3∙7 = 61
4∙10 + 5∙7 = 75
40 + 21 = 61
40 + 35 = 75
Ответ: x = 10, y = 7
Пример 7
{
2x + 5y = 50
3x + 7y = 71
Эту систему уравнений можно решить двумя способами.
Первый способ
Вычтем из второго уравнение первое.
3x + 7y – (2x + 5y) = 71 – 50
3x + 7y – 2x – 5y = 21
x + 2y = 21
x = 21 – 2y
Подставим выражение для x в первое уравнение.
2(21 – 2y) + 5y = 50
42 – 4y + 5y = 50
y = 8
Подставим найденный y в выражение для x
x = 21 – 2y
x = 21 – 2∙8 = 21 – 16 = 5
Проверка:
2∙5 + 5∙8 = 50
3∙5 + 7∙8 = 71
10 + 40 = 50
15 + 56 = 71
Второй способ
{
2x + 5y = 50
3x + 7y = 71
Умножим обе части первого уравнения на 3, а обе части второго уравнения на 2.
Тем самым мы в обеих уравнениях получим множитель 6 у x, после чего при вычитании одного
уравнения из другого x у нас уйдёт (6x — 6x = 0), и останется только y.
3(2x + 5y) = 3∙50
2(3x + 7y) = 2∙71
6x + 15y = 150
6x + 14y = 142
Вычтем из первого уравнения второе.
6x + 15y – (6x + 14y) = 150 – 142
6x + 15y – 6x – 14y = 8
y = 8
Подставим найденный y в первое уравнение системы:
2x + 5y = 50
2x + 5∙8 = 50
2x + 40 = 50
2x = 50 – 40
2x = 10
x = 5
В этой системе уравнений мы применили такой приём, как умножение обеих уравнений на разные числа так, чтобы у одного из неизвестных (в нашем случае у x) в обеих уравнениях оказался один и тот же множитель. После этого мы вычли одно уравнение из другого, x у нас исчез, и мы легко смогли найти y.
Ответ: x = 5, y = 8