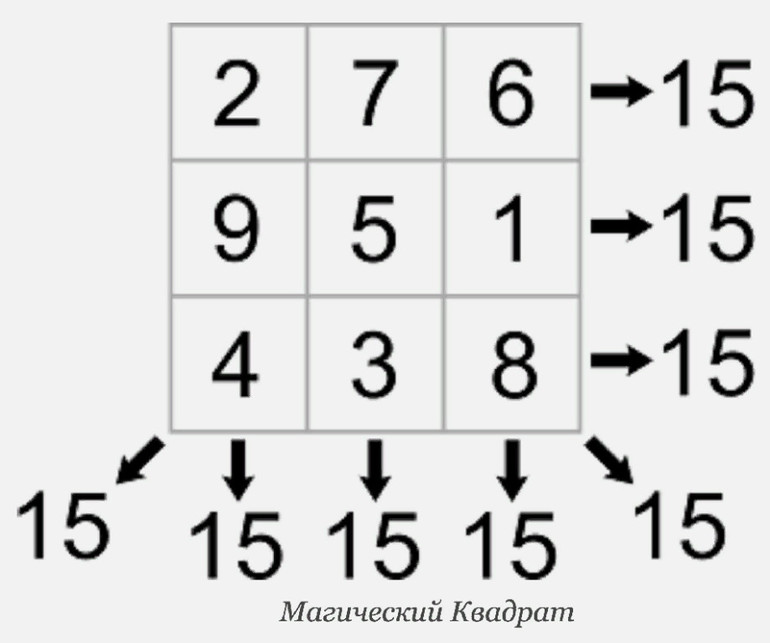
Магическая константа M — сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 — это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
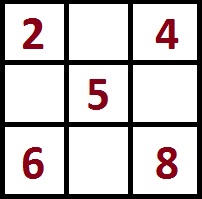
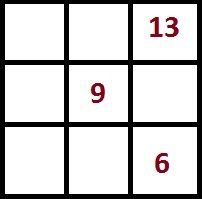
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
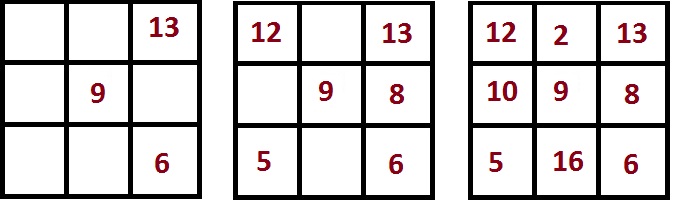
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто — надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
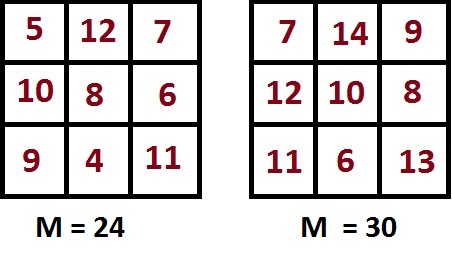
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
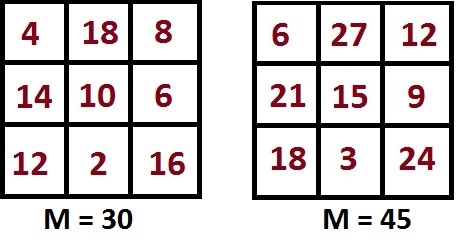
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 — та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные — а вот число в центральном квадрате одно и то же — это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке — нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Напомним этот квадрат:
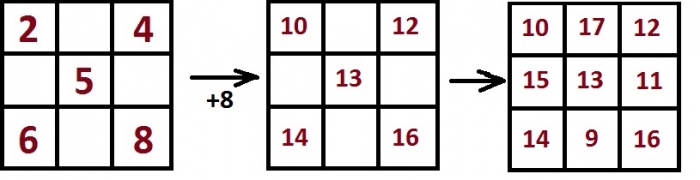
В центре этого квадрата — число 5. В центре того квадрата, который мы должны построить — число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата — 5, а по углам — чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 — они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
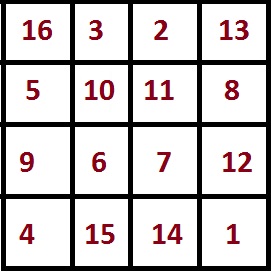
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34
16
Существует несколько различных классификаций магических квадратов
пятого порядка, призванных хоть как-то их систематизировать. В книге
Мартина Гарднера [ГМ90, сс. 244-345] описан один из таких способов –
по числу в центральном квадрате. Способ любопытный, но не более того.
Сколько существует квадратов шестого порядка, до сих пор неизвестно, но их примерно 1.77 х 1019. Число огромное, поэтому нет никаких надежд пересчитать их с помощью полного перебора, а вот формулы для подсчёта магических квадратов никто придумать не смог.
Как составить магический квадрат?
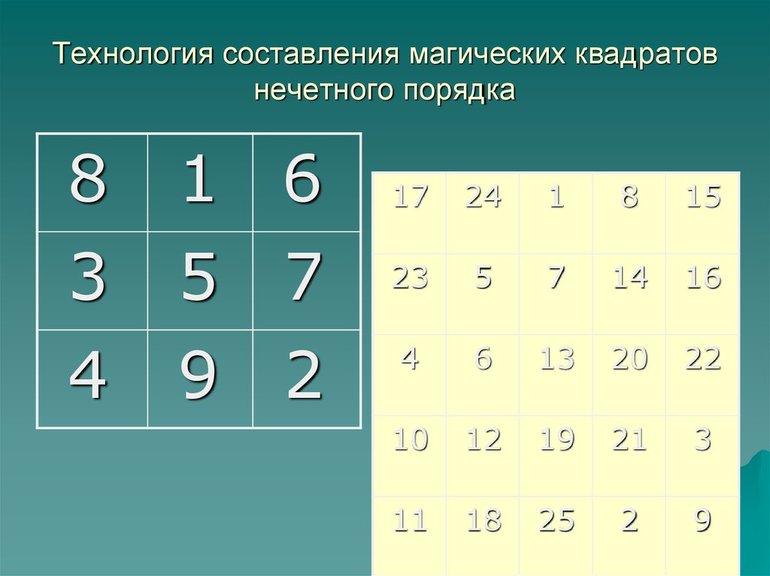
Придумано очень много способов построения магических квадратов. Проще всего составлять магические квадраты нечётного порядка. Мы воспользуемся методом, который предложил французский учёный XVII века А. де ла Лубер (De La Loubère). Он основан на пяти правилах, действие которых мы рассмотрим на самом простом магическом квадрате 3 х 3 клетки.
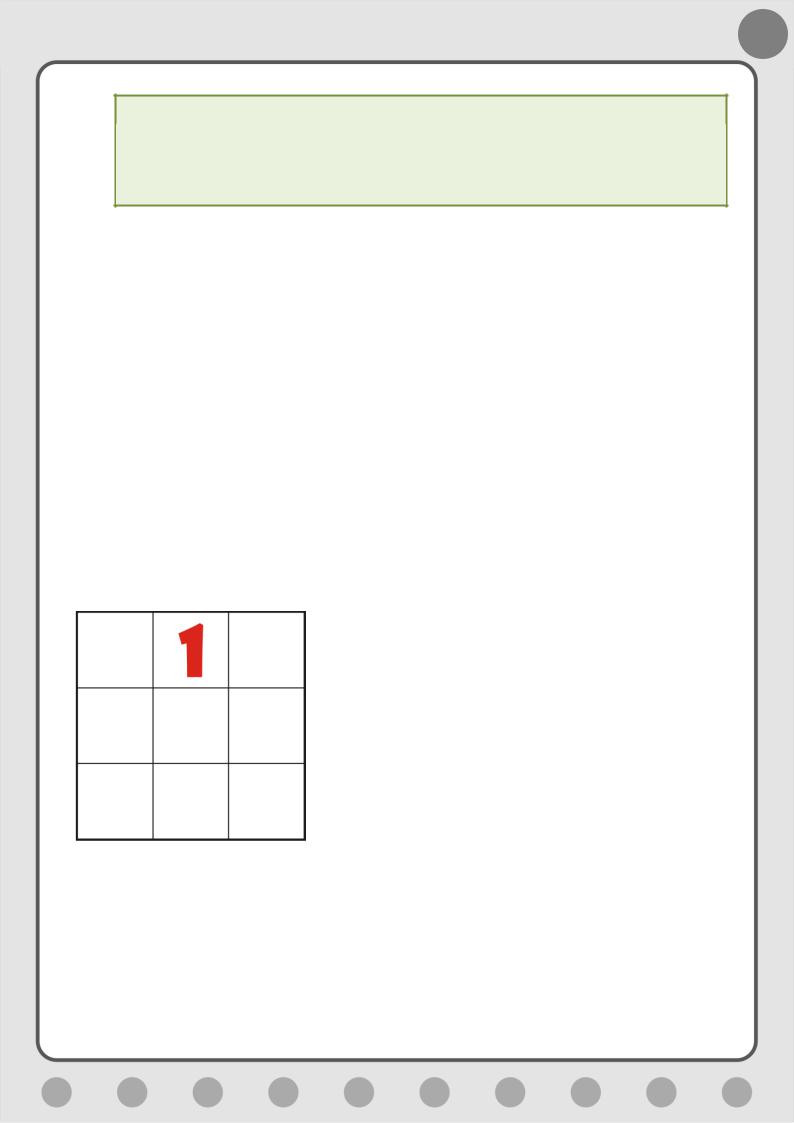
Правило 1. Поставьте 1 в среднюю колонку первой строки (Рис. 5.7).
Рис. 5.7. Первое число
Правило 2. Следующее число поставьте, если возможно в клетку, соседнюю с текущей по диагонали правее и выше (Рис. 5.8).
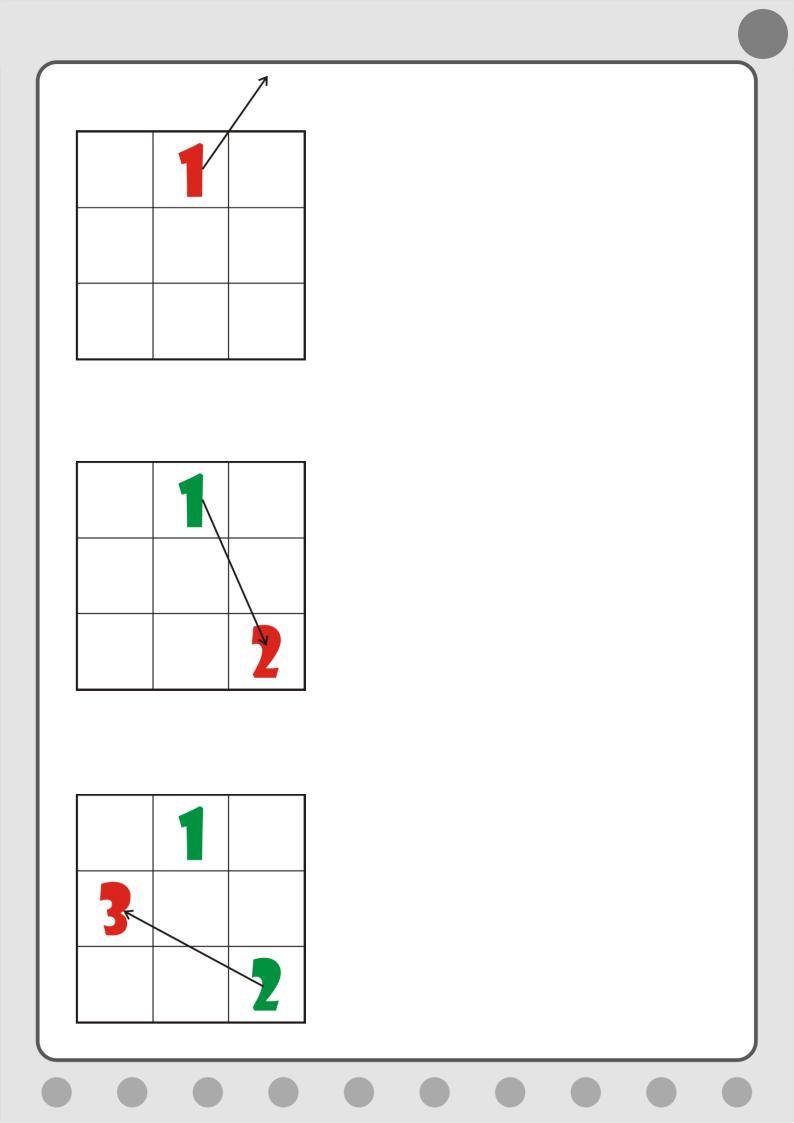
17
Рис. 5.8. Пытаемся поставить второе число
Правило 3. Если новая клетка выходит за пределы квадрата сверху, то запишите число в самую нижнюю строку и в следующую колонку (Рис. 5.9).
Рис. 5.9. Ставим второе число
Правило 4. Если клетка выходит за пределы квадрата справа, то запишите число в самую первую колонку и в предыдущую строку (Рис. 5.10).
Рис. 5.10. Ставим третье число
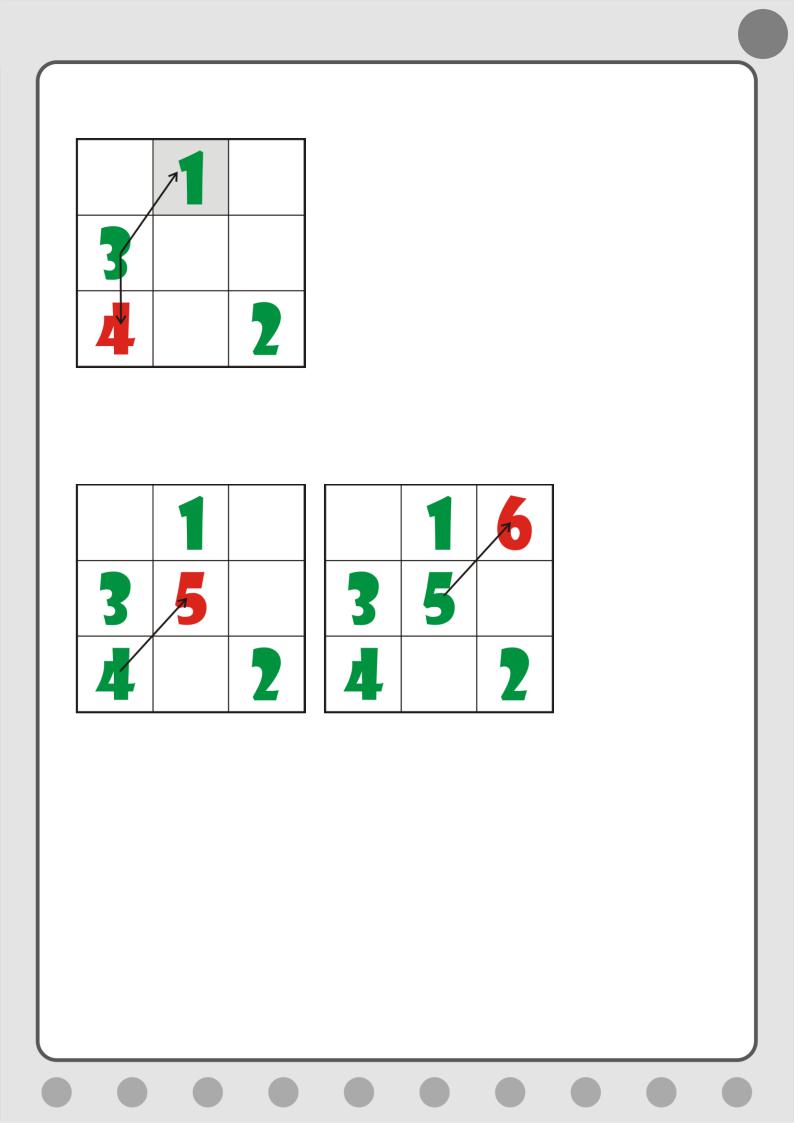
18
Правило 5. Если в клетке уже занята, то очередное число запишите под текущей клеткой (Рис. 5.11).
Рис. 5.11. Ставим четвёртое число
Далее переходите к Правилу 2 (Рис. 5.12).
Рис. 5.12. Ставим пятое и шестое число
Снова выполняйте Правила 3, 4, 5, пока не составите весь квадрат (Рис.
5.13).
Не правда ли, правила очень простые и понятные, но всё равно довольно утомительно расставлять даже 9 чисел. Однако, зная алгоритм построения магических квадратов, мы сможем легко перепоручить компьютеру всю рутинную работу, оставив себе только творческую, то есть написание программы.
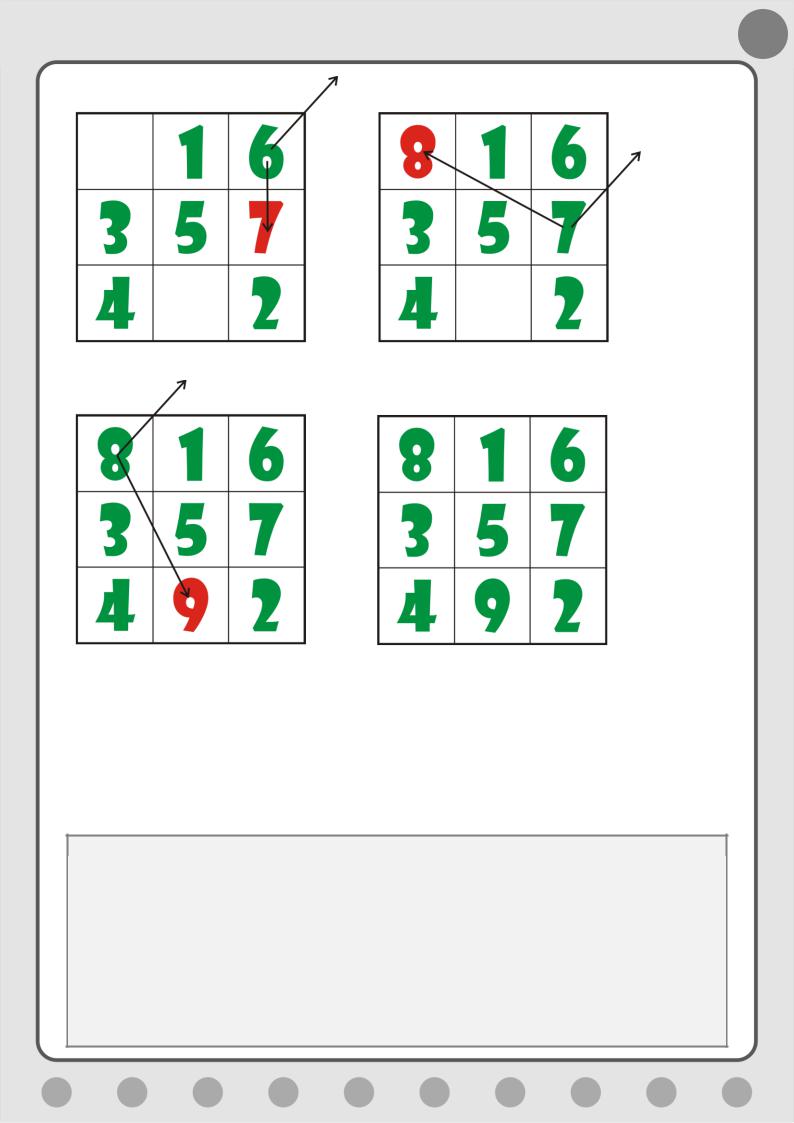
19
Рис. 5.13. Заполняем квадрат следующими числами
Проект Магические квадраты (Magic)
Набор полей для программы Магические квадраты совершенно очевиден:
//ПРОГРАММА ДЛЯ ГЕНЕРИРОВАНИЯ
//НЕЧЕТНЫХ МАГИЧЕСКИХ КВАДРАТОВ
//ПО МЕТОДУ ДЕ ЛА ЛУБЕРА
public partial class Form1 : Form
{
//макс. размеры квадрата: const int MAX_SIZE = 27; //var
int n=0; // порядок квадрата int [,] mq; // магический квадрат
int number=0;// текущее число для записи в квадрат

20
int col=0; // текущая колонка int row=0; // текущая строка
Метод де ла Лубера годится для составления нечётных квадратов любого размера, поэтому мы можем предоставить пользователю возможность самостоятельно выбирать порядок квадрата, разумно ограничив при этом свободу выбора 27-ью клетками.
После того как пользователь нажмёт заветную кнопку btnGen Генерировать!, метод btnGen_Click создаёт массив для хранения чисел и переходит в метод generate:
//НАЖИМАЕМ КНОПКУ «ГЕНЕРИРОВАТЬ»
private void btnGen_Click(object sender, EventArgs e)
{
//порядок квадрата:
n = (int)udNum.Value;
//создаем массив:
mq = new int[n+1, n+1];
//генерируем магический квадрат: generate();
lstRes.TopIndex = lstRes.Items.Count-27;
}
Здесь мы начинаем действовать по правилам де ла Лубера и записываем первое число – единицу – в среднюю клетку первой строки квадрата (или массива, если угодно):
//Генерируем магический квадрат void generate(){
//первое число: number=1;
rule1:
//колонка для первого числа — средняя: col = n / 2 + 1;
//строка для первого числа — первая: row=1;
//заносим его в квадрат: mq[row,col]= number;
Теперь мы последовательно пристраиваем по клеткам остальные числа – от двойки до n * n:
//переходим к следующему числу:
21
nextNumber:
number++;
Запоминаем на всякий случай координаты актуальной клетки
int tc=col; int tr = row;
и переходим в следующую клетку по диагонали:
col++; row—;
Проверяем выполнение третьего правила:
rule3:
if (row < 1) row= n;
А затем четвёртого:
rule4:
if (col > n) { col=1;
goto rule3;
}
И пятого:
rule5:
if (mq[row,col] != 0) { col=tc;
row=tr+1; goto rule3;
}
Как мы узнаем, что в клетке квадрата уже находится число? – Очень просто: мы предусмотрительно записали во все клетки нули, а числа в готовом квадрате больше нуля. Значит, по значению элемента массива мы сразу же определим, пустая клетка или уже с числом! Обратите внимание, что здесь нам понадобятся те координаты клетки, которые мы запомнили перед поиском клетки для следующего числа.
Рано или поздно мы найдём подходящую клетку для числа и запишем его в соответствующую ячейку массива:

22
//заносим его в квадрат: mq[row, col] = number;
Попробуйте иначе организовать проверку допустимости перехода в но-
вую клетку!
Если это число было последним, то программа свои обязанности выполнила, иначе она добровольно переходит к обеспечению клеткой следующего числа:
//если выставлены не все числа, то if (number < n*n)
//переходим к следующему числу: goto nextNumber;
И вот квадрат готов! Вычисляем его магическую сумму и распечатываем на экране:
//построение квадрата закончено: writeMQ();
} //generate()
Напечатать элементы массива очень просто, но важно учесть выравнивание чисел разной «длины», ведь в квадрате могут быть одно-, дву- и трёхзначные числа:
//Печатаем магический квадрат void writeMQ()
{
lstRes.ForeColor = Color.Black;
string s = «Магическая сумма = » + (n*n*n +n)/2; lstRes.Items.Add(s);
lstRes.Items.Add(«»);
// печатаем магический квадрат: for (int i= 1; i<= n; ++i){
s=«»;
for (int j= 1; j <= n; ++j){
if (n*n > 10 && mq[i,j] < 10) s += » «; if (n*n > 100 && mq[i,j] < 100) s += » «; s= s + mq[i,j] + » «;
}
lstRes.Items.Add(s);
}
lstRes.Items.Add(«»); }//writeMQ()
23
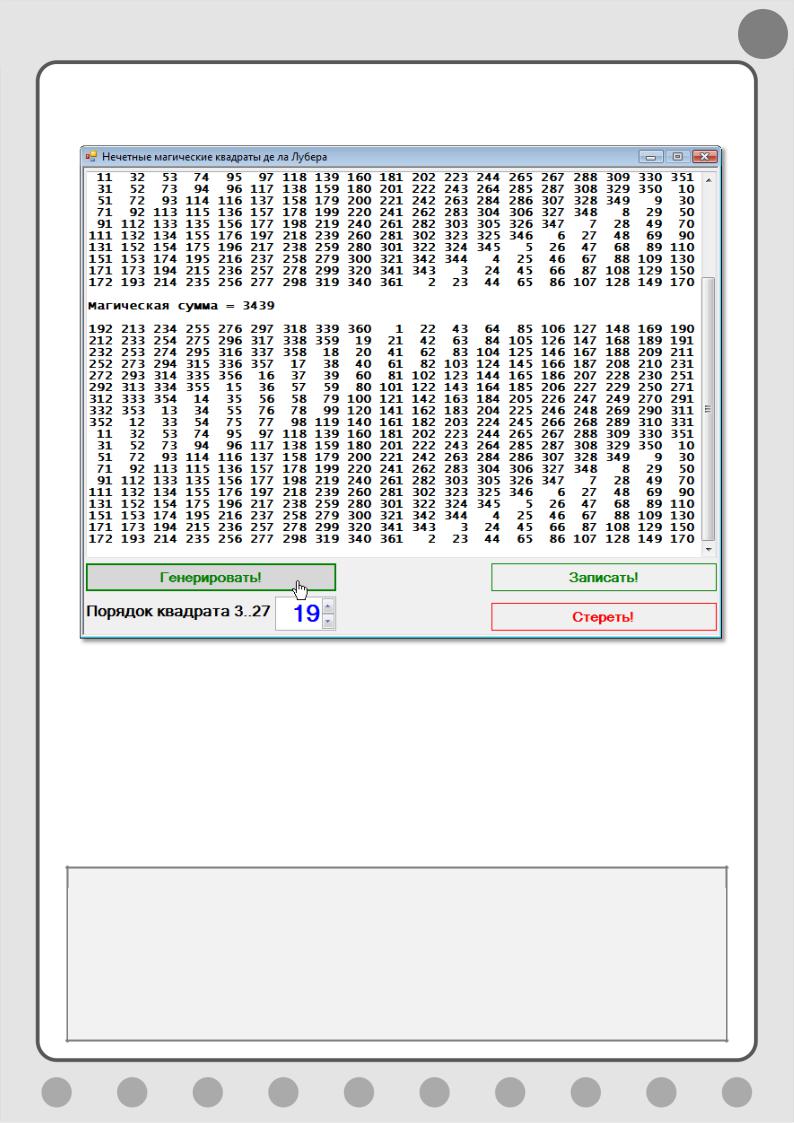
Запускаем программу – квадраты получаются быстро и на загляденье (Рис.
5.14).
Рис. 5.14. Изрядный квадратище!
В книге С.Гудман, С.Хидетниеми Введение в разработку и анализ алгорит-
мов, на страницах 297-299 мы отыщем тот же самый алгоритм, но в «сокращённом» изложении. Он не столь «прозрачен», как наша версия, но работает верно.
Добавим кнопку btnGen2 Генерировать 2! и запишем алгоритм на языке
Си-шарп в метод btnGen2_Click:
//Algorithm ODDMS
private void btnGen2_Click(object sender, EventArgs e)
{
//порядок квадрата: n = (int)udNum.Value;
//создаем массив:
mq = new int[n + 1, n + 1];
//генерируем магический квадрат: int row = 1;
24
int col = (n+1)/2;
for (int i = 1; i <= n * n; ++i)
{
mq[row, col] = i; if (i % n == 0)
{
++row;
}
else
{
if (row == 1) row = n;
else
—row;
if (col == n) col = 1;
else
++col;
}
}
//построение квадрата закончено: writeMQ();
lstRes.TopIndex = lstRes.Items.Count — 27;
}
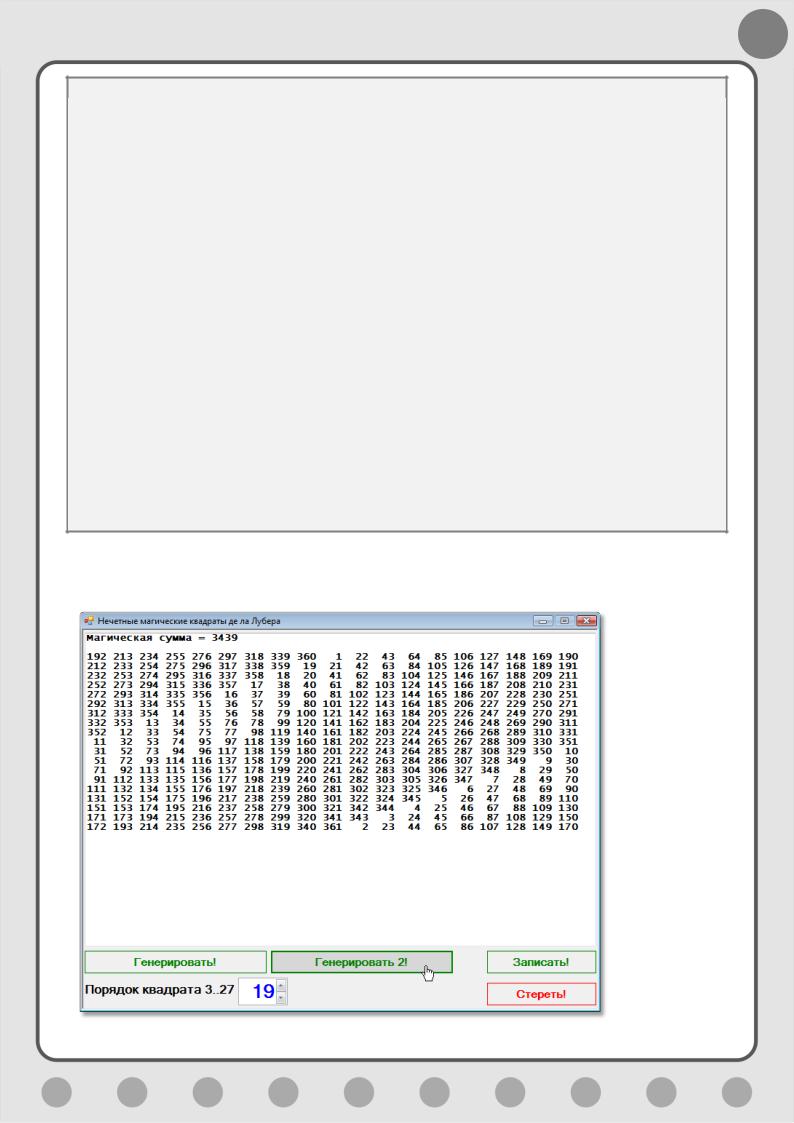
Кликаем кнопку и убеждаемся, что генерируются «наши» квадраты (Рис.
5.15).
Рис. 5.15. Старый алгоритм в новом обличии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
История и современное применение
Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.
В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.
В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.
С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.
Квадрат нечётного порядка
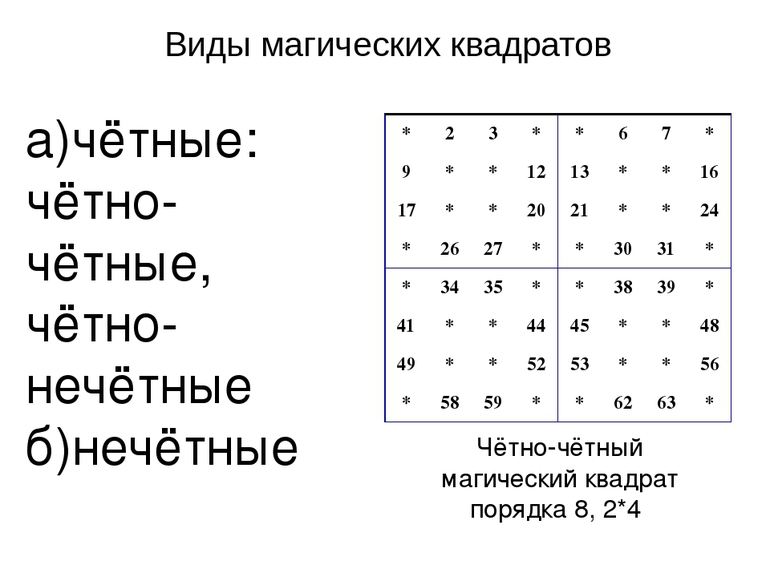
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:
- Подсчитывается сумма, которая должна получиться в каждой строке. Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.
- Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.
- В средней клетке верхней строки вписывается 1.
- Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.
- По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.
- Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.
- Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.
- Поскольку место цифры 7 уже занято, она вписывается ниже 6.
- Восьмёрка занимает место в левом нижнем углу.
- Оставшуюся клетку занимает девятка.
Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.
Одинарная чётность
Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.
Вычисление магической константы
Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.
Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.
Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.
Дальнейшие действия
Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.
Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:
- Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.
- Каждая часть заполняется как новый математический объект. Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.
В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.
Алгоритм действий:
- Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.
- Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.
- Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.
- В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1. Полученную фигуру можно обозначить А2.
- Таким же способом строят промежуточный квадрат А3.
- Эти 3 промежуточных фигуры формируют выделенную область А.
- Далее переходят в квадрант D и формируют обособленную область D.
Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.
Двойной порядок
Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.
Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.
В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:
- Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.
- В таблице 8х8 эти области включают 4 элемента (2х2).
- В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.
Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.
Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:
- В первой сверху строке и первом слева столбце пишется 1. В верхней клетке четвертого столбика — 4.
- В центр второй горизонтальной строчки ставятся цифры 6 и 7.
- В четвёртой строке слева пишется 13, а справа — 16.
По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.
Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

Содержание
- История и современное применение
- Квадрат нечётного порядка
- Одинарная чётность
- Вычисление магической константы
- Дальнейшие действия
- Двойной порядок
История и современное применение
Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.
В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.
С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.
Квадрат нечётного порядка
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:


Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.
Одинарная чётность
Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.
Вычисление магической константы
Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.
Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.
Дальнейшие действия
Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.
Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.
Алгоритм действий:

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.
Двойной порядок
Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.
Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:
Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.
Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:
По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.
Предыдущая
МатематикаАлгоритм Евклида — формулы, правила и примеры решения задач
Следующая
МатематикаМинор матрицы — способы, порядок и примеры вычисления
Магическая константа M – сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 – это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто – надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 – та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные – а вот число в центральном квадрате одно и то же – это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке – нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Напомним этот квадрат:
В центре этого квадрата – число 5. В центре того квадрата, который мы должны построить – число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата – 5, а по углам – чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 – они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34
Урок математики в 4-м классе “Формирование вычислительных навыков”
Формирование вычислительного навыка требует выполнения большого количества
однообразных упражнений. В то же время ученики младших классов в силу
недостаточно развитого произвольного внимания не могут долго выполнять
вычислительную работу. И здесь мы встречаемся с противоречием: чтобы правильно
считать, нужно много считать – много считать нельзя, в связи с возрастными
особенностями учащихся.
Опыт использования магических квадратов на уроках и во внеклассной работе
показывает, что в первую очередь решение магических квадратов вызывает интерес у
учащихся, дети с удовольствием принимаются их выполнять, что делает процесс
формирования вычислительных навыков внутренне мотивированными. Кроме того,
использование магических квадратов способствует не только формированию
вычислительных навыков, но и развитию мышления, умения планировать и
контролировать свою деятельность. Использование магических квадратов
способствует так же математическому развитию.
Задачи:
- Формировать вычислительные навыки.
- Развивать логическое мышление, умение планировать и контролировать свою
деятельность. - Создание благоприятного психологического климата для возможности
раскрытия потенциала каждого ребенка; формировать качества взаимовыручки,
ответственности, любознательности; развивать познавательную активность
учащихся; воспитывать усидчивость, уверенность в своих возможностях.
Ход урока
1. Организационный момент.
– Ребята! Готовы вы к уроку? (Да!)
– На вас надеюсь я, друзья.
– Мы хороший, дружный класс.
– Все получится у нас!
Я очень хочу, что бы урок получился интересным, познавательным, что бы мы
вместе повторили и закрепили то, что мы уже знаем и постарались открыть новые
секреты чисел и вычислений.
2. Актуализация знаний.
Мы привыкли пользоваться благами цивилизации – автомобилем, телефоном,
телевизором и прочей техникой, делающей нашу жизнь легче и интереснее. Тысячи
изобретений потребовались для этого, но самым важным из них были первыми –
колесо и число. Без них не было бы всего нашего технического великолепия. У этих
двух изобретений есть общая черта – ни колеса, ни числа в природе нет, и то, и
другое – плод деятельности человеческого разума. Арабы принесли к нам способ
записи чисел, которым мы сейчас пользуемся из Индии. Кто-то придумал знак нуля в
Древнем Вавилоне. Кто-то из индейцев Майя – в Америке. Кто-то в Китае.
Числа настолько вошли в жизнь человека, что им стали приписывать всякие
магические свойства. Так, многие не любят числа 13, число 666 называют звериным
числом, приносящим несчастье.
В Древнем Китае четные числа называют женственными, а нечетные мужественные.
Это какие?
Игра “Ай, да я!”. Дети цепочкой называют числа, хлопают в ладоши, если число
четное, то вместо числа говорят: “Ай, да я!”.
При археологических раскопках в Китае и Индии были найдены квадратные
амулеты. Квадрат разделен на девять квадратиков, в каждом из которых написано по
одному числу от 1 до 9. Замечательно, что суммы чисел в каждой строке, в каждом
столбце и по каждой из двух диагоналей были равны одному и тому же числу 15. Эту
задачу решали тысячи лет назад китайские математики.
В средние века магические квадраты были очень популярны, они приносили
счастье.
3. Постановка проблемы.
А вы хотите научиться решать магические квадраты? Эта задача – одна из самых
древних задач в математике.
Какой квадрат можно назвать магическим?
Магический квадрат – это квадрат разделенный на клетки (количество клеток по
вертикали и горизонтали одинаково), где в каждую клетку вписан последовательный
ряд чисел. Числа записаны так, что их сумма по любым направлениям (диагоналям,
горизонталям, вертикалям) постоянна. Каждое число магического квадрата участвует
в нескольких разных суммах, и все эти суммы равны между собой! Этот любопытный,
с точки зрения математики, факт вызывает большой интерес. Магия чисел
завораживает.
Рис. 1
4. Физминутка для глаз:
- Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до
5. Повторять 4–5 раз. - Крепко зажмурить глаза (считать до 3), открыть глаза, посмотреть вдаль
(считать до 5). Повторять 4–5 раз. -
Вытянуть правую руку вперед. Следить глазами, не поворачивая головы,
замедленными движениями указательного пальца вытянутой руки влево и вправо,
вверх и вниз. Повторять 4–5 раз. - Посмотреть на указательный палец вытянутой руки на счет 1–4, потом
перенести взгляд на счет 1–6, повторять 4–5 раз. - В среднем темпе проделать 3–4 круговых движения глазами в правую
сторону, столько же в левую сторону. Расслабив глазные мышцы, посмотреть
вдаль на счет 1–6. повторять 1–2 раза. - “Метелки”. Выполнить частое моргание без напряжения глаз до 10– 15 раз.
Упражнение можно сопровождать проговариванием текста: Вы метелки, усталость
сметите, - Глазки нам хорошо освежите.
Упражнение повторять 4–5 раз.
Хотите узнать историю создания магических квадратов и способы их решения?
Пусть квадрат разделен на девять клеток (малых квадратов). Требуется
разложить в них числа от 1 до 9 так, что бы сумма чисел в каждой строке, в
каждом столбце, в каждой диагонали составляла 15.
Удобно запомнить следующее решение (рис. 2).
- 1. Сначала напишем во всех 9 клетках по 5.
Понятно, что в этом случае сумма трех чисел в каждой строке составляет 15. - Оставим в трех клетках по 5 (в средней клетке стоит 5).
- В двух рядом стоящих клетках добавим к пятеркам 1 и 2.
Дальше не трудно закончить составление таблицы. Проверь: получается ли по
всем направлениям постоянная сумма 15?
Другой способ составления такого квадрата – использование симметрии (рис.
3).
- Начерти квадрат из 5 х 5 = 25 клеток.
- Внутри этого квадрата лесенкой напиши подряд числа от 1 до 9 (рис. 3).
Рис. 2
- “Перебрось” цифры 1 и 9 через цифру 5 и напиши их рядом с цифрой 5. То
же самое проделай с цифрами 3 и 7.
Остальные клетки заполнить не трудно.
5. Расслабляющая гимнастика (на фоне релаксирующей музыки):
Пусть дети присядут на край стула как им хочется, в свободной позе. Не громко
не торопливо произнесите:
Все умеют танцевать, бегать, прыгать, рисовать,
Но не все пока умеют расслабляться. Отдыхать.
Есть у нас игра такая – очень легкая, простая:
Замедляются движенья. Исчезает напряжение,
И становится понятно: расслабление приятно.
6. “Открытие” детьми нового знания.
А вы сами хотите создать магические квадраты?
В учебниках математики часто встречаются магические квадраты из девяти клеток
(3 столбца и 3 строки). Их легко составить по простому правилу: запиши такой ряд
из 9 чисел, в котором каждое следующее число на одно и то же число больше
предыдущего.
Например: 14, 16, 18, 20, 22, 24, 26, 28, 30.
Возьми вторую тройку из этих чисел и запиши их по диагонали квадрата. Рядом с
самым большим числом из этой тройки запиши самое маленькое число из ряда.
Продолжи составление этого квадрата.
Рис. 3
7. Первичное закрепление.
Проверь, что новые магические квадраты можно получить из данного, увеличивая
или уменьшая каждое из записанных в нем чисел на одно и то же число (например,
на 6) или в одно и то же число раз (например, в 2 раза).
Работа в парах.
Используя данный способ составьте свои магические квадраты и решите их.
Сумма чисел каждого ряда, столбца и каждой диагонали квадрата одинакова.
Рис. 4
Произведение каждого ряда, столбца и диагонали квадрата одинаково.
Рис. 5
Оцените свою работу в группе пословицей, поговоркой или изречением. Обведите
пословицу или поговорку:
- Терпение дает умение.
- Это успех.
- Не будь тороплив, а будь терпелив.
- Нерадивый дважды дело делает.
- Перо пишет, а ум водит.
- Захотел – сделал.
8. Физкультминутка.
Летел по небу шарик,
По небу шар летел.
Но знаем, что до неба
Наш шар не долетел.
При очередном прочтении закрывается по одному слову, заменяя его жестом (2
раза).
9. Самостоятельная работа с самопроверкой в классе.
Групповая работа (5 групп).
Задание для первой группы (средний уровень):
Докажите, что данный квадрат не является магическим:
Рис. 6
Достаточно указать, что значение сумм чисел по диагоналям не равны: 12 + 15 +
18 ≠ 9 + 15 + 24.
Оцените свою работу в группе пословицей.
Задание для второй группы (высокий уровень):
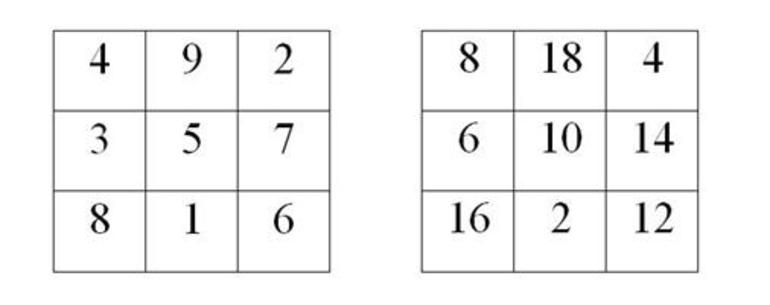
В магическом квадрате суммы чисел по любым вертикалям, по любым горизонталям
раны одному и тому же числу. Найдите это число. Укажите рациональный способ
вычислений.
Рис. 7
(Достаточно указать, найти значение одной, причем любой, из указанных в
определении сумм. Более того ученик осознает необходимость в проведении
рационального вычисления, т.к. простота вычислений в каждом случае будет разная.
Например, найти сумму чисел 8 + 18 + 16).
Оцените свою работу в группе пословицей.
Задание для третьей группы (высокий уровень):
Дан магический квадрат. Какое число должно стоять в пустой клеточке?
Рис. 8
(Можно рассуждать так: 1) найду постоянную сумму квадрата, для этого найду
сумму левого столбика: 18 + 10 + 2 = 30; 2) найду сумму известных чисел в том
столбике, где находится пустая клетка: 4 + 12 = 16; 3) найду число, которое
должно стоять в пустой клетке: 30 – 16 = 14; 4) проверю, будет ли квадрат
магическим, для этого найду сумму чисел в средней строке и сравню ее с
постоянной с постоянной суммой квадрата: 14 + 6 + 10 = 30, 30 = 30, данный
квадрат магический).
Оцените свою работу в группе пословицей.
Задание для четвертой группы (высокий уровень):
Дан магический квадрат. Докажите, что в клеточке со звездочкой (*) не может
стоять число 32.
Рис. 9
(Первый способ: можно с помощью вычислений установить, что в данной клеточке
должно стоять число 14, поэтому не может стоять 32. Второй способ: найдем
постоянную сумму: 8 + 6 + 16 = 30. Так как сумма должна быть не меньше каждого
слагаемого, то все числа в клетках должны быть не больше 30. Но 32 > 30, значит
32 не может стоять вместо *).
Оцените свою работу в группе пословицей
Задание для пятой группы (низкий уровень):
В магическом квадрате суммы чисел по любым вертикалям, по любым горизонталям,
по любым диагоналям равны одному и тому же числу. Проверьте будет ли данный
квадрат магическим:
Рис. 10
(Ученик должен сам составить в соответствии с условием все необходимые суммы,
найти их значение и сделать вывод. Три суммы дают столбики, три суммы дают
строчки, две суммы дают диагонали).
Оцените свою работу в группе пословицей.
10. Итог урока.
– Что нового узнали на уроке?
– Что было особенно интересным?
– Что вызвало затруднения, над чем еще нужно поработать?
– Оцените свою работу на уроке.
Спасибо за урок. Молодцы!
4 класс. Моро. Учебник №2. Ответы к стр. 58
Числа от 1 до 1000
Деление на двузначное и трёхзначное число
Письменное деление на двузначное число
Ответы к стр. 58
При делении с остатком на двузначное число рассуждают также, как и при делении без остатка. Объясни, как выполнено деление с остатком.
_ 324 |62 _ 526 |74 _ 793 |83
310 |5 518 |7 474 |9
14 8 46
Надо 324 разделить на 62.
Разделю 324 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 32 на 6, получу 5. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 5.
Умножу 62 на 5, получится 310. Вычту: 324 — 310 = 14, 14 меньше 62, значит, цифра 5 подходит, а 14 — остаток. Теперь её можно записать в частном.
Надо 526 разделить на 74.
Разделю 526 не на 74, а на 70, чтобы легче было найти цифру частного. Для этого разделю 52 на 7, получу 7. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 7.
Умножу 74 на 7, получится 518. Вычту: 526 — 518 = 8, 8 меньше 74, значит, цифра 7 подходит, а 8 — остаток. Теперь её можно записать в частном.
Надо 793 разделить на 83.
Разделю 793 не на 83, а на 80, чтобы легче было найти цифру частного. Для этого разделю 79 на 8, получу 9. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 9.
Умножу 83 на 9, получится 747. Вычту: 793 — 747 = 46, 46 меньше 83, значит, цифра 9 подходит, а 46 — остаток. Теперь её можно записать в частном.
211. Найди частное и остаток, проверь решение.
156 : 48 278 : 62 346 : 56 445 : 73
— 156 |48 Проверка:
144 |3 × 48
12 3
144
144 + 12 = 156
— 278 |62 Проверка:
248 |4 × 62
30 4
248
248 + 30 = 278
— 346 |56 Проверка:
336 |6 × 56
10 6
336
336 + 10 = 346
— 445 |73 Проверка:
438 |6 × 73
7 6
438
438 + 7 = 445
212. Космонавты были в полёте 290 ч. Сколько это суток и часов?
1 сутки = 24 часа
— 290 |24
24 |12 — суток
_50
48
2 — часа
О т в е т: 12 суток и 2 часа.
213. Площадь первого участка 120 м2, второго 160 м2. При одинаковой норме высева на 1 м2 на первом участке высеяли семян ржи на 1 кг меньше, чем на втором. Объясни, что означают выражения.
160 — 120 1000 : (160 — 120) 1000 : (160 — 120) • 160
160 — 120 — разница между площадями участков
1000 : (160 — 120) — столько грамм семян высеяли на 1 м2
1000 : (160 – 120) • 160 – столько грамм семян высеяли на втором участке
214. В международном автопробеге участвовало 350 машин. Экипаж каждой машины состоял из трёх спортсменов. До финиша не дошли 105 машин. Сколько машин и сколько спортсменов прибыли к финишу?
1) 350 – 105 = 245 (м.) — дошли до финиша
2) 245 • 3 = 735 (с.) — прибыли к финишу
О т в е т: 245 машин и 735 спортсменов.
215. Составь по задачам уравнения и реши их.
1) Какое число надо уменьшить на 28, чтобы получить число, равное сумме чисел 58 и 37?
2) Какое число надо увеличить в 8 раз, чтобы получить число, равное произведению чисел 80 и 12?
3) Какое число надо уменьшить в 28 раз, чтобы получить число, равное разности чисел 300 и 203?
1) x — 28 = 58 + 37
x — 28 = 95
x = 95 + 28
x = 123
2) x • 8 = 80 • 12
x • 8 = 960
x = 960 : 8
x = 120
3) x : 28 = 300 — 203
x : 28 = 97
x = 97 • 28
x = 2716
216. 384 : 96 192 : 48 648 : 72 352 • 46 — 5840 : 80
— 384 |96 — 192 |48
384 |4 192 |4
0 0
— 648 |72
648 |9
0
352 • 46 — 5840 : 80 = 16192 — 73 = 16119
× 352 — 5840|80
46 560 |73
+ 2112 —240
1408 240
16192 0
_16192
73
16119
217. Найди значения выражений 360 : с и 360 • с, если с = 1; c = 3; c = 4; c = 6; c = 10.
Наблюдай, как при этом изменяется частное, как изменяется произведение.
360 : 1 = 360 360 • 1 = 360
360 : 3 = 120 360 • 3 = 1080
360 : 4 = 90 360 • 4 = 1440
360 : 6 = 60 360 • 6 = 2160
360 : 10 = 36 360 • 10 = 3600
Значение частного уменьшается, а значение произведения увеличивается.
218. Выложи из палочек такую фигуру. Какие углы в этой фигуре? Переложи 4 палочки так, чтобы получилось два остроугольных треугольника. Будут ли эти треугольники равнобедренными? равносторонними?
В этой фигуре все углы тупые.
Эти треугольники будут и равнобедренными и равносторонними. Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине. Условие равенства двух сторон является необходимым и достаточным, чтобы считать треугольник равнобедренным. Это условие в равностороннем треугольнике выполняется всегда. Следовательно равносторонний треугольник всегда является равнобедренным.
399 : 57 236 : 59 475 : 95 609 • 27 — 4320 : 60
— 399 |57 — 236 |59
399 |7 236 |4
0 0
— 475 |95
475 |5
0
609 • 27 — 4320 : 60 = 16443 — 72 = 16371
× 609 — 4320|60
27 420 |72
+ 4263 —120
1218 120
16443 0
_16443
72
16371
ЗАДАНИЕ НА ПОЛЯХ
МАГИЧЕСКИЙ КВАДРАТ
Ответы по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4.6
/
5
(
16
голосов
)
4 класс. Моро. Учебник №2. Ответы к стр. 32
Числа от 1 до 1000
Деления на числа, оканчивающиеся нулями
Письменное деление на числа, оканчивающиеся нулями
Ответы к стр. 32
1) Объясни решение.
_ 425400 |600 _ 28500 |30 _ 43600 |40
4200 |709 270 |950 40 |1090
_ 540 _150 _36
0 150 0
_ 5400 _ 0 _ 360
5400 0 360
0 0 _0
0
0
2) Объясни, как более кратко записаны те же вычисления.
_ 425400 |600 _ 28500 |30 _ 43600 |40
4200 |709 270 |950 40 |1090
_ 5400 _150 _360
5400 150 360
0 0 0
1) Если неполное делимое меньше делителя, то делим его на нуль с записью нуля в частное. Затем приписываем к нему нуль справа и делим далее.
2) Если неполное делимое меньше делителя, то дописываем к нему нуль спарва, с записью нуля в частное, и сразу продолжаем деление.
120. Реши, записывая вычисления подробно или кратко.
35210 : 70 168000 : 400 456000 : 400
40150 : 50 258000 : 300 260100 : 900
— 35210|70 — 40150|50
350 |503 400 |803
—210 —150
210 150
0 0
— 168000|400 — 258000|300
1600 |420 2400 |860
—800 —1800
800 1800
0 0
— 456000|400 — 260100|900
400 |1140 1800 |289
—560 —8010
400 7200
_1600 _8100
1600 8100
0 0
121. Выполни деление с остатком.
83056 : 40 48179 : 80 80630 : 200 216349 : 700
— 83056|40 — 48179|80
80 |2076 480 |602
—305 —179
280 160
_256 19 – ост.
240
16 – ост.
— 80630|200 — 216349|700
800 |403 2100 |309
—630 —6349
600 6300
30 – ост. 49 – ост.
122. Два пловца спрыгнули одновременно с лодки и поплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывет второй пловец, когда первый проплывет 270 м?
Сделай схематический чертеж и реши задачу.
Составь и реши задачи, обратные данной.
1) 270 : 90 = 3 (мин) − время, которое плыли пловцы
2) 40 • 3 = 120 (м)
О т в е т: 120 м проплывает второй пловец, когда первый проплывет 270 м.
1-я задача
Два пловца спрыгнули одновременно с лодки и поплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывет первый пловец, когда второй проплывет 120 м?
1) 120 : 40 = 3 (мин) − время, которое плыли пловцы
2) 90 • 3 = 270 (м)
О т в е т: 270 м проплывет первый пловец, когда второй проплывет 120 м.
2-я задача
Два пловца спрыгнули одновременно с лодки и поплыли по реке в противоположных направлениях: первый проплыл 270 м со скоростью 90 м/мин, а второй за то же время проплыл 120 м. С какой скоростью плыл второй пловец?
1) 270 : 90 = 3 (мин) − время, которое плыли пловцы
2) 120 : 3 = 40 (м/мин)
О т в е т: скорость второго пловца 40 м/мин.
123. Реши уравнения.
x : 5 = 1400 – 900 x − 30 = 1000 – 200
x : 5 = 1400 – 900 x − 30 = 1000 − 200
x : 5 = 500 x − 30 = 800
x = 500 • 5 x = 800 + 30
x = 2500 x = 830
124. Расставь знаки действий и скобки так, чтобы получились верные равенства.
728 Ο 72 O 8 = 152 728 O 72 O 8 = 100
728 O 72 O 8 = 719 728 O 72 O 8 = 737
728 − 72 • 8 = 728 − 576 = 152
728 − 72 : 8 = 728 − 9 = 719
(728 + 72) : 8 = 800 : 8 = 100
728 + 72 : 8 = 728 + 9 = 737
Выполни деление с остатком. 438500 : 700
— 438500|700
4200 |626
—1850
1400
_4500
4200
300 – ост.
ЗАДАНИЕ НА ПОЛЯХ
МАГИЧЕСКИЙ КВАДРАТ
ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №2. Ответы к стр. 32
4.2 (83.42%) от 111 голосующих
Учебный проект по математике “Магический квадрат” (4 класс)
История появления магических квадратов.
В давние времена, научившись считать и выполнять арифметические действия, люди с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и таинственную.
Китайский император Ню, живший 4 тысячи лет назад, однажды гулял по берегу реки. И вдруг увидел черепаху. На её панцире был изображён рисунок из белых и чёрных кружков.
« Да, она священна!», – воскликнул он.
Если заменить каждую фигуру числом, показывающим, сколько в ней кружков, получится такая таблица.
9
2
3
5
7
8
1
6
(Сумма чисел строк равна сумме чисел столбцов, равна сумме чисел диагоналей и равна 15.)
Сейчас любую квадратную таблицу, составленную из чисел и обладающую таким свойством, называют магическим квадратом.
Определение магического квадрата.
Магический квадрат – квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Наверное, эту легенду китайцы придумали, когда нашли расположение чисел от 1 до 9 со столь замечательным свойством. Рисунок они назвали «ло-шу» и стали считать его магическим символом. Первое специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до 10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман.
Полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов 2*2 не существует. Существует единственный магический квадрат 3*3, так как остальные магические квадраты 3*3 получаются из него либо перестановкой строк (рис. 4а) или столбцов (рис. 4б) либо путем поворота исходного квадрата на 900 (рис. 4в) или на 1800 (рис 4г).
2
7
6
9
5
1
4
3
8
8
1
6
3
5
7
4
9
2
2
9
4
7
5
3
6
1
8
6
1
8
7
5
3
2
9
4
а б в г
В IX веке интерес к магическим квадратам вспыхнул с новой силой. Получение магических квадратов считалось популярным развлечением среди математиков. Ими создавались огромные квадраты, например, 45*45, содержащий числа от 1 до 2025, Были придуманы способы построения магических квадратов любого размера.
В XIII веке математик Ян Хэй занялся проблемой методов построения магических квадратов. Его исследования были, потом продолжены другими китайскими математиками. Из Китая магические квадраты распространились сначала в Индию, а затем и в другие страны.
Редкостью является использование магического квадрата в изобразительном искусстве, а не в научном или литературном произведении. Впервые это сделал немецкий художник Альбрехт Дюрер (1471 – 1528), выпустивший в гравюру «Меланхолия», на которой есть изображение магического квадрата четвёртого порядка. Причем два числа в середине нижней строки указывают на год создания гравюры – 1514.Этот факт говорит об умении в то время составлять магические квадраты с определённым заданным расположением некоторых чисел. Говорят, что гравюра А.Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Нострадамуса (1503-1566).
Применение магических квадратов .
Традиционной сферой применения магических квадратов являются талисманы. К примеру, талисман Луны обладает определенными свойствами: предохраняет от кораблекрушения и болезней, делает человека любезным, способствует предотвращению дурного намерения, а так же укрепляет здоровье. Его гравируют на серебре в день и час Луны, когда Солнце или Луна находится в первых десяти градусах Рака. Магический квадрат 9-ого порядка вписывается в девятиугольник (9 – число Луны, см. ниже) и окружается специальными символами.
В наши дни магические квадраты можно встретить на палубах больших пассажирских судов как площадку для игры. Известная головоломка – пазл с числами – судоку, появившаяся примерно 30 лет назад и популярная во многих странах мира, тоже содержит магические квадраты.
За последнее столетие значительно возросло число книг по занимательной математике, в которых содержатся головоломки и задачки, связанные с необычными квадратами. В наше время магические квадраты продолжают привлекать к себе внимание не только специалистов, но и любителей математических игр и развлечений.
|
Страница 66 (учебник Моро 1 часть 4 класс) ответы по математике
306. Масса тыквы, арбуза и дыни вместе 16 кг, масса тыквы и арбуза 13 кг, масса арбуза и дыни 8 кг. Найди массу дыни, арбуза и тыквы в отдельности.
1) 16 — 8 = 8 кг масса тыквы.
2) 16 — 13 = 3 кг масса дыни.
3) 8 — 3 = 5 кг масса арбуза.Ответ: 3 кг, 5 кг, 8 кг.
307. В трёх школах 1945 учеников. В первой и второй школах вместе 1225 учеников, а во второй и третьей — 1300 учеников. Сколько учеников в каждой школе? Реши и проверь решение.
1) 1945 — 1225 = 720 учеников в третьей школе.
2) 1945 — 1300 = 645 учеников в первой школе.
3) 1300 — 720 = 580 учеников во второй школе.Ответ: 645, 580 и 720 учеников.
Проверка:
720 + 645 + 580 = 1945.
308. Расставь скобки, чтобы равенства стали верными.
(640 — 480) : 4 + 360 = 120 : 4 + 360 = 40 + 360 = 400
120 + 120 : (4 + 6) = 120 + 120 : 10 = 120 + 12 = 132
160 : (4 * 2) + 10 = 160 : 8 + 10 = 20 + 10 = 30(60 — 54 : 6) : 3 = (60 — 9) : 3 = 20 — 3 = 17
309. Реши задачи, составив уравнения.
1) Разность неизвестного числа и числа 80 равна сумме чисел 360 и 140. Найди неизвестное число.
2) Из числа 430 вычли задуманное число и получили частное чисел 640 и 8. Какое число задумали?
1)
x — 80 = 360 + 140
x — 80 = 500
x = 500 + 80 = 580
2)
430 — x = 640 : 8
430 — x = 80
x = 430 — 80 = 350
310. Расстояние между двумя посёлками 96 км. Мотоциклист отправился из первого посёлка и проехал до остановки четвёртую часть пути. Сколько километров ему осталось проехать?
1) 96 : 4 = 24 км проехал мотоциклист
2) 96 — 24 = 72 км — осталось проехать мотоциклисту.Ответ: 72 км.
311.
2000 см2 = 20 дм2
3 ч 10 мин = 190 мин
45 ц = 4500 кг
23 т = 23000 кг
23 км = 23000 м
600 c = 10 мин
312.
32546 + 7008 + 82309 = 39554 + 82309 = 121863
1200 − 172 * 3 + 308 = 1200 — 516 + 308 = 684 + 308 = 992
Задание под знаком вопроса.
20782 + 5203 + 63870 = 25985 + 63870 = 89855
4508 + 498 : 6 − 892 = 4508 + 83 — 892 = 4591 — 892 = 3699
Задание на полях.
Магический квадрат.
Задание на полях.
Сравни площади фигур.
Площадь первой фигуры — 11 квадратиков, а площадь второй — 14 квадратиков.
Магический квадрат – наука или магия?
Магический квадрат – наука или магия?
Мамлин С.А. 1
1Муниципальное бюджетное общеобразовательное учреждение Нерастанновская средняя общеобразовательная школа
Садовникова О.М. 1
1Муниципальное бюджетное общеобразовательное учреждение Нерастанновская средняя общеобразовательная школа
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
ВВЕДЕНИЕ
«Я не знаю ничего более прекрасного в арифметике, чем эти числа, называемые некоторыми планетными, а другими – магическими».
Пьер де Ферма
Квадраты, всем знакомое слово, а «МАГИЧЕСКИЕ» КВАДРАТЫ.… От этого словосочетания сразу веет волшебством. На занятиях по внеурочной деятельности мы часто выполняем задания необычного характера. Одним из таких заданий, это заполнение «магических» квадратов. Само название «магические» квадраты очень привлекает. Заполняя такие квадраты, думаешь, что действительно, присутствует какая-то магия. А однажды учитель предложил нам самим составить подобное задание для ребят младших классов. Но эта работа оказалась не такой простой, как нам показалось на первый взгляд. Нас заинтересовала предложенная задача. Метод перебора нам не понравился: он отнимает очень много времени, хотя и позволяет тренировать свои вычислительные навыки. Это вызвало у нас желание заняться исследовательской работой, чтобы раскрыть секреты и найти способы составления магических квадратов.
Объект проекта: «магический» квадрат.
Цель проекта: раскрыть «секреты» «магического» квадрата.
Задачи исследования:
1) познакомиться с историей появления «магических» квадратов;
2) выяснить виды «магических» квадратов и способы их заполнения;
3) выявить области применения магических квадратов;
4) провести анкетирование и выполнить его анализ;
4) составить самостоятельно «магические» квадраты разных порядков;
5) создать брошюру «магических» квадратов.
Гипотеза: для заполнения магического квадрата существуют специальные приемы, позволяющие это сделать быстро и разнообразно.
Для решения задач проекта мы использовали следующие методы:
– анализ литературы и Интернет-ресурсов по проблеме; анкетирование.
Глава I. «МАГИЧЕСКИЙ» КВАДРАТ.
Что такое «магический» квадрат.
Магическим квадратом n-го порядка называется квадратная таблица размером n х n, заполненная натуральными числами от 1 до n2, суммы которых по всем строкам, столбцам и обеим диагоналям одинаковы. Различают магические квадраты четного и нечетного порядка (в зависимости oт четности n), Поля таблицы, в которые записывают числа, называются клетками магического квадрата, а сумма чисел, стоящих в любой строке, столбце или на диагонали, – его постоянной.
Магический квадрат – квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
1.2 ИСТОРИЯ ПОЯВЛЕНИЯ «МАГИЧЕСКИХ» КВАДРАТОВ.
Священные, волшебные, загадочные, таинственные, совершенные… Привлекающие естественной красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множество тайн… Знакомьтесь: магические квадраты – удивительные представители воображаемого мира чисел.
Понятием «магия» принято считать различные человеческие действия, которые имеют целью влиять сверхъестественным образом на тот или иной материальный предмет или явление.
Числовую фигуру обычно называют магической, если составляющие ее числа не повторяются и при определенных взаимных сочетаниях дают заранее задуманный составителем результат.
Наверное, одной из первых известных человечеству магических фигур является магический квадрат. Он встречаются в культуре, истории, верованиях и в различных мистических учениях многих народов.
Страна, в которой был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже тысячелетие нельзя установить точно. Вероятно, самым «старым» из дошедших до нас магических квадратов является таблица Ло Шу (ок. 2200 г. до н. э.). Она имеет размер 3×3 и заполнена натуральными числами от 1 до 9. В этом квадрате сумма чисел в каждой строке, столбце и диагонали равна 15 (рис. 1). Согласно одной из легенд, прообразом Ло Шу стал узор из связанных черных и белых точек, украшавший панцирь огромной черепахи, которую встретил однажды на берегу реки Ло-Шуй мифический прародитель китайской цивилизации Фуси.
Жители Поднебесной считали таблицу Ло Шу священной, у них даже не возникало мысли о составлении аналогичных квадратов большего размера, поэтому последние стали появляться только три тысячелетия спустя.
Рис.1 Таблица Ло Шу
В XI в. Из Китая магические квадраты распространились сначала в Индию, затем в Японию. Из Индии увлечение магическими квадратами перешло к арабам. Именно от арабов квадраты получили название «магические».
На востоке их считали волшебными, полными тайного смысла символами, и использовали при заклинаниях. Магические квадраты находят при раскопках поселений Золотой Орды (рис. 2), в Китае, Индии и Тибете, в Израиле, Турции и во всех странах Европы.
Рис.2
Первым квадратом, придуманным европейцем, считается квадрат А. Дюрера, изображенный на его знаменитой гравюре «Меланхолия» (рис. 3).
Рис.3
Дата создания гравюры – 1514 год – указана числами, стоящими в двух центральных клетках нижней строки.
В западной Европе в средние века магические квадраты были достоянием представителей алхимии и астрологии. Магическим квадратам приписывали различные мистические свойства. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы (рис. 4)
Рис.4
Получение магических квадратов было популярным развлечением среди математиков, создавались огромные квадраты, например, 43*43, содержащий числа от 1 до 1849, причем обладающие помимо указанных свойств магических квадратов, еще многими дополнительными свойствами. Были придуманы способы построения магических квадратов любого размера, однако до сих пор не найдена формула, по которой можно было бы найти количество магических квадратов данного размера.
В IX и XX вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры.
Глава II. СПОСОБЫ СОСТАВЛЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ.
2.1 Индийский способ
Общий метод построения квадратов неизвестен, хотя широко применяются различные частные алгоритмы. Некоторые из них я представляю ниже.
Один из существующих способов сравнительно несложен весьма древний прием, придуманный в Индии еще до начала нашего летосчисления. Его можно изложить кратко в шести правилах. Пример магического квадрата из 49 клеток. (рис.5)
1. В середине верхней строки пишут 1, а в самом низу соседнего справа столбца – 2.
2. Следующие числа пишутся по порядку в диагональном направлении вправо вверх.
3. Дойдя до правого края квадрата, переходя к крайней левой клетке ближайшей вышележащей строки.
4. Дойдя до верхнего края квадрата, переходят к самой нижней клетке соседнего справа столбца.
Примечание. Дойдя до правой верхней угловой клетки, переходят к левой нижней.
5. Дойдя до уже занятой клетки, переходят к клетке, лежащей непосредственно под последней заполненной клеткой.
6. Если последняя заполненная клетка находится в нижнем ряду квадрата, переходят к самой верхней клетке в том же столбце.
Руководясь этими правилами, можно быстро составлять магические квадраты с любым нечетным числом клеток.
Если число клеток не делится на 3, можно начинать составление магического квадрата не по правилу 1, а по другому правилу.
Единицу можно написать в любой клетке диагонального ряда, идущего от средней клетки крайнего левого столбца к средней клетке самой верхней строки квадрата. Все последующие числа вписываются согласно правилам 2 – 5.
Это дает возможность составить по индийскому способу не один, а несколько квадратов.
|
30 |
39 |
48 |
1 |
10 |
19 |
28 |
|
38 |
47 |
7 |
9 |
18 |
27 |
29 |
|
46 |
6 |
8 |
17 |
26 |
35 |
37 |
|
5 |
14 |
16 |
25 |
34 |
36 |
45 |
|
13 |
15 |
24 |
33 |
42 |
44 |
4 |
|
21 |
23 |
32 |
41 |
43 |
3 |
12 |
|
22 |
31 |
40 |
49 |
2 |
11 |
20 |
Рис.5
2.2 СПОСОБ БАШЕ
Индийский способ, это не единственный для составления квадратов с нечётным количеством клеток. Существует ещё способ Баше, или, как его иначе называют, «способ террас». Старинный прием составления нечетных магических квадратов, то есть квадратов из любого нечетного числа клеток: 3х3, 5х5, 7х7 и т.п. Прием этот предложен в XVII веке французским математиком Баше. Так как способ Баше пригоден и для 9- клеточного квадрата, то удобнее всего начать исследование способа именно с этого примера. Итак, приступим к составлению 9- клеточного магического квадрата по способу Баше.
– начертив квадрат, разграфленный на девять клеток, пишем по порядку числа от 1 до 9, располагая их косыми рядами по три в ряд;
– числа, стоящие вне квадрата, вписываем внутрь его так, чтобы они примкнули к противолежащим сторонам квадрата (оставаясь в тех же столбцах или строках, что и раньше). В результате получаем квадрат;
– применим правило Баше к составлению квадрата из 5х5 клеток. Квадрат состоит из 25 клеток. Сумма всех 25 чисел равна 325. Теперь 325 разделить на количество строк (325:5=65), получим 65, т.е. сумма чисел по любому направлению квадрата должна равняться 65. Начинаем с расположения чисел. Остается только числа, оказавшиеся за рамками квадрата, ввести внутрь его. Для этого нужно фигуры, образованные числами, стоящими вне квадрата («террасы»), мысленно вдвинуть в квадрат так, чтобы эти фигуры примкнули к противолежащим сторонам квадрата. Получится магический 25- клеточный квадрат (рис. 6).
|
4 |
10 |
|||||||
|
3 |
9 |
15 |
||||||
|
2 |
8 |
14 |
20 |
|||||
|
1 |
7 |
13 |
19 |
25 |
||||
|
6 |
12 |
18 |
24 |
|||||
|
11 |
17 |
23 |
||||||
|
16 |
22 |
|||||||
|
21 |
|
3 |
16 |
9 |
22 |
15 |
|
20 |
8 |
21 |
14 |
2 |
|
7 |
25 |
13 |
1 |
19 |
|
24 |
12 |
5 |
18 |
6 |
|
11 |
4 |
17 |
10 |
23 |
Рис.6
2.3 «МАГИЧЕСКИЙ» КВАДРАТ ПИФАГОРА
Пифагор – математик, заложивший основы нумерологии. Учёный верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения, не что иное, как число.
Магический квадрат Пифагора – фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на три уровня: материальный, души и разума.
Цифры даты рождения вписываются в определённом порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.
ГЛАВА III. ПРИМЕНЕНИЕ «МАГИЧЕСКИХ» КВАДРАТОВ.
Магические квадраты могут быть применимы в криптографии. Они позволяют создать алгоритм перевода зашифрованного текста в изображение и наоборот. Буквы сообщения расставляются в порядке, заданном магическим квадратом. Затем каждой букве сообщения ставится в соответствие цвет, тем самым в итоге получается изображение. Для того чтобы расшифровать такое сообщение, необходимо проделать обратную процедуру: вначале каждому цвету поставить в соответствие букву алфавита, а затем осуществить обратную перестановку, заданную исходным магическим квадратом. Весь описанный алгоритм реализовывает большой объем информации, а «магические» квадраты дают надежную защиту исходного открытого текста от взлома. Одним из перспективных направлений изучения применения «магических» квадратов является создание телевизоров, изображение для которых формируется по принципу «магического квадрата». Магические квадраты применяются в технологиях создания телевизоров, что позволяет обеспечить плавные цветовые переходы, полностью устраняя видимые границы на больших однотонных полях изображения.
Конечно, одно из самых доступных применений «магических» квадратов, это на уроках и внеурочной деятельности по математике. Тема математических квадратов – один из традиционных разделов занимательной математики, представляющий любознательному читателю как красивые конструкции, так и серьёзные нерешенные проблемы. Решение и составление таких квадратов развивает и расширяет познавательный кругозор и логическое мышление
Глава IV. ПРАКТИЧЕСКАЯ ЧАСТЬ.
4.1 МЕСТО «МАГИЧЕСКИХ» КВАДРАТОВ В ЖИЗНИ МОИХ СВЕРСТНИКОВ
Для того, чтобы выяснить, знают ли современные школьники что такое «магические» квадраты, мы провели опрос среди обучающихся 6-7 классов (31 человек) (приложение 2) и получили следующие данные.
Вывод: опрос показал, что многие ребята слышали о магических квадратах и решали их. Обучающиеся даже были уверены, что квадраты, действительно обладают магическими свойствами. Изучив ответы ребят, мы поняли, что мало кто пробовал составлять самостоятельно «магические» квадраты, именно поэтому и возникли ответы, что заполнение квадрата – это магия. Проведённый опрос убедил нас в актуальности выбранной темы, аименнов привлечении обучающихся к решению занимательных задач по математике, повышении их интереса к новым и загадочным головоломкам и одной из которых считаются магические квадраты.
Анализ анкет показал, что ребята довольно мало интересуется решением занимательных задач и редко обращается к материалу, находящемуся за пределами школьной программы.
Мои «магические» квадраты: 3х3, 5х5, 7х7.
Образец 1.»Магический» квадрат 3х3
Квадрат для заполнения.
|
144 |
||
|
1 |
||
|
287 |
1002 |
Заполненный квадрат
|
144 |
859 |
716 |
|
1145 |
573 |
1 |
|
430 |
287 |
1002 |
Образец № 2. «Магический» квадрат 5х5
Квадрат для заполнения.
|
13 |
91 |
49 |
127 |
85 |
|
115 |
||||
|
1 |
||||
|
67 |
||||
|
61 |
97 |
133 |
Заполненный квадрат.
|
13 |
91 |
49 |
127 |
85 |
|
115 |
43 |
121 |
79 |
7 |
|
37 |
145 |
73 |
1 |
109 |
|
139 |
67 |
25 |
103 |
31 |
|
61 |
19 |
97 |
55 |
133 |
Образец № 3. «Магический» квадрат 7х7
Квадрат для заполнения.
|
7 |
55 |
|||||
|
37 |
5 |
|||||
|
83 |
3 |
|||||
|
1 |
||||||
|
95 |
13 |
|||||
|
11 |
29 |
|||||
|
9 |
75 |
Заполненный квадрат.
|
7 |
57 |
23 |
73 |
39 |
89 |
55 |
|
69 |
21 |
71 |
37 |
87 |
53 |
5 |
|
19 |
83 |
35 |
85 |
51 |
3 |
67 |
|
81 |
33 |
97 |
49 |
1 |
65 |
17 |
|
31 |
95 |
47 |
13 |
63 |
15 |
79 |
|
93 |
45 |
11 |
61 |
27 |
77 |
29 |
|
43 |
9 |
59 |
25 |
75 |
41 |
91 |
ЗАКЛЮЧЕНИЕ
Прочитав специальную литературу, исследовав только незначительную часть методов составления магических квадратов, можно прийти к выводу: заполнение магических квадратов представляет собой замечательную гимнастику для ума. Для меня магические квадраты – это увлекательная и занимательная математика, поэтому на данной теме я не буду останавливаться. Имеется еще не мало различных типов магических квадратов, которые я хотел бы исследовать. Работая над проблемой заполнения квадратов, я пришел к заключению, что общего способа построения квадратов нет, но очень широко применяются разные частные алгоритмы.
Если использовать один из этих методов можно заполнить квадрат любого порядка. Мне удалось хорошо познакомиться с методом построения квадратов нечетного порядка. Я полагаю, что мою работу можно использовать при подготовке к олимпиадам, на внеурочных занятиях по математике для развития логики и расширения познавательного кругозора.
«Магический квадрат» – древнекитайского происхождения.
Универсального способа заполнения магических квадратов нет.
МГ является популярной головоломкой, часто встречается в олимпиадных заданиях.
С помощью МГ можно кодировать информацию.
Существует много видом МГ.
Для каждого МГ определенного порядка существуют различные способы заполнения.
Тем самым мы подтвердили нашу Гипотезу: для заполнения магического квадрата существуют специальные приемы, позволяющие это сделать быстро и разнообразно.
Заполнение и построение «магических» квадратов это целая наука, которая в очередной раз доказывает красоту чисел и необычность их свойств, что и соответствует названию «магические» квадраты.
Список литературы и Интернет-ресурсов:
http://xreferat.ru/54/540-1-magicheskie-kvadraty.html
Энциклопедический словарь юного математика. М., Педагогика, 1999г.
http://www.informio.ru/publications/id192
http://www.coolreferat.com/Магические_квадраты_часть=3
В.В.Трошин «Магия чисел и фигур» ООО «Глобус» 2014
6. Г.И. Глейзер «История математики в школе» Москва «Просвещение» 2017
7. Е.И. Игнатьев «В царстве смекалки» Москва 2019
8. Интернет. http://ru.wikipedia.org/
Просмотров работы: 374
Magic Square (4×4)
Magic Square (4×4)
Можно ли дополнить магический квадрат 4 на 4
числами от 1 до 16 для записей?
Мои решения
.
Сначала мне нужно определить мою целевую сумму.
Сумма всех значений от 1 до 16 равна 136. Деление этого результата
дает 34, что является моей целевой суммой для каждой строки, столбца и диагонали.
Затем я составляю массив чисел 1
через 16:
Просматривая суммы, нахожу, что только
суммы диагоналей равны 34:
Я пытаюсь сбалансировать результаты инвертированием
второй и четвертый ряды:
Это действие изменило суммы диагоналей,
но это дает сумму 34 для всех столбцов:
Мне нужно сбалансировать ряды.Я замечаю это
суммы строк постепенно увеличиваются от первой до
четвертый. Все нижние значения находятся в первых двух строках,
поэтому я пытаюсь сбалансировать, инвертируя второй и третий столбцы:
В результате все, кроме
диагонали в сумме дают 34:
Так что мне нужно сосредоточиться на диагоналях:
Сумма первой диагонали 38 (больше
на 4), а сумма второго равна 30 (меньше на 4).Я смотрю на
значения, которые я могу подставить в обе диагонали, но это будет
не влияет на результаты строк и столбцов.
Во втором ряду у меня 11 и 8 –
разница в 3 – и сейчас по первой диагонали 8.
Если я могу переключить 8 и 11, я могу уменьшить сумму
первая диагональ от 38 до 35.
В третьем ряду у меня 9 и 6 – разница
из 3 – и 6 сейчас находится на второй диагонали. Если я могу переключиться
6 и 9, я могу увеличить сумму второй диагонали
с 30 до 33.
Сумма 11 и 6 (которые входят в
первый столбец) равен 17, а сумма 8 и 9 (которые оба являются
в третьем столбце) тоже 17. Я могу заменить 11 и
6 в третий столбец и 8 и 9 в первый столбец
без влияния суммы этих столбцов:
Итак, теперь у меня:
Итак, мне нужно уменьшить сумму первого
диагональ на 1 и увеличьте сумму второй на 1.
Изучив массив, я вижу, что
можно поменять 10 и 7 из второго столбца на 11 и
6 в первой:
И в результате получается магический квадрат 4×4:
Магический квадрат
Что такое Магический квадрат 3×3?
| ………….. 8 …. 1 …. 6 ……………………. ………….. 3 …. 5 …. 7 …………………… . ………….. 4 …. 9 …. 2 …………………… |
Вы можете собрать числа от 1 до 9 в квадрат так, чтобы сумма строк, столбцов и диагоналей равна 15. Если взять числа от 1 до 9, получится стандартный квадрат. |
| …………. 8 + c …. 1 + c …. 6 + c ………….. …………. 3 + c …. 5 + c …. 7 + c ………….. …………. 4 + c …. 9 + c …. 2 + c ………….. |
Магический квадрат остается магическим, если поменять каждое число на константу c. Вы добавляете c слева. Еще можно вычесть, умножить или разделить. |
Вы определяете квадраты 4х4, 5х5 -… соответственно.
Волшебный квадрат 3×3
наверху
У вас есть 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. В магическом квадрате ты
приходится снова и снова складывать 3 числа.Следовательно, средняя сумма трех
числа 45: 3 = 15. Число 15 называется магическим числом
квадрат 3×3.
Также можно получить 15, если добавить среднее число
5 трижды.
Можно восемь раз уменьшить 15 в сумме трех слагаемых:
|
15 = 1 + 5 + 9 15 = 1 + 6 + 8 |
15 = 2 + 4 + 9 15 = 2 + 5 + 8 |
15 = 2 + 6 + 7 15 = 3 + 4 + 8 |
15 = 3 + 5 + 7 15 = 4 + 5 + 6 |
Нечетные числа 1,3,7 и 9 встречаются дважды в редукциях,
четные числа 2,4,6,8 три раза и цифра 5 один раз.
Следовательно, вы должны поместить цифру 5 в середину
волшебный квадрат 3×3. Остальные нечетные числа должны быть в середине.
стороны и четные числа по углам.
В этих условиях есть восемь возможностей
построение квадрата:
Все восемь квадратов переходят друг в друга, если вы отразите
их по осям симметрии. Вы считаете симметричные квадраты только один раз. Следовательно
есть только один магический квадрат 3×3.
Волшебный квадрат 4×4 наверх
Магическое число (1 + 2 +… + 15 + 16): 4
= 34 .
Компьютер обнаружил 86 сокращений от 34 до суммы четырех
слагаемые с номерами от 1 до 16.
| 34 = 01 + 02 + 15 + 16 34 = 01 + 03 + 14 + 16 34 = 01 + 04 + 13 + 16 34 = 01 + 04 + 14 + 15 34 = 01 + 05 + 12 + 16 34 = 01 + 05 + 13 + 15 34 = 01 + 06 + 11 + 16 34 = 01 + 06 + 12 + 15 34 = 01 + 06 + 13 + 14 34 = 01 + 07 + 10 + 16 34 = 01 + 07 + 11 + 15 34 = 01 + 07 + 12 + 14 34 = 01 + 08 + 09 + 16 34 = 01 + 08 + 10 + 15 34 = 01 + 08 + 11 + 14 34 = 01 + 08 + 12 + 13 34 = 01 + 09 + 10 + 14 34 = 01 + 09 + 11 + 13 |
34 = 01 + 10 + 11 + 12 34 = 02 + 03 + 13 + 16 34 = 02 + 03 + 14 + 15 34 = 02 + 04 + 12 + 16 34 = 02 + 04 + 13 + 15 34 = 02 + 05 + 11 + 16 34 = 02 + 05 + 12 + 15 34 = 02 + 05 + 13 + 14 34 = 02 + 06 + 10 + 16 34 = 02 + 06 + 11 + 15 34 = 02 + 06 + 12 + 14 34 = 02 + 07 + 09 + 16 34 = 02 + 07 + 10 + 15 34 = 02 + 07 + 11 + 14 34 = 02 + 07 + 12 + 13 34 = 02 + 08 + 09 + 15 34 = 02 + 08 + 10 + 14 34 = 02 + 08 + 11 + 13 |
34 = 02 + 09 + 10 + 13 34 = 02 + 09 + 11 + 12 34 = 03 + 04 + 11 + 16 34 = 03 + 04 + 12 + 15 34 = 03 + 04 + 13 + 14 34 = 03 + 05 + 10 + 16 34 = 03 + 05 + 11 + 15 34 = 03 + 05 + 12 + 14 34 = 03 + 06 + 09 + 16 34 = 03 + 06 + 10 + 15 34 = 03 + 06 + 11 + 14 34 = 03 + 06 + 12 + 13 34 = 03 + 07 + 08 + 16 34 = 03 + 07 + 09 + 15 34 = 03 + 07 + 10 + 14 34 = 03 + 07 + 11 + 13 34 = 03 + 08 + 09 + 14 34 = 03 + 08 + 10 + 13 |
34 = 03 + 08 + 11 + 12 34 = 03 + 09 + 10 + 12 34 = 04 + 05 + 09 + 16 34 = 04 + 05 + 10 + 15 34 = 04 + 05 + 11 + 14 34 = 04 + 05 + 12 + 13 34 = 04 + 06 + 08 + 16 34 = 04 + 06 + 09 + 15 34 = 04 + 06 + 10 + 14 34 = 04 + 06 + 11 + 13 34 = 04 + 07 + 08 + 15 34 = 04 + 07 + 09 + 14 34 = 04 + 07 + 10 + 13 34 = 04 + 07 + 11 + 12 34 = 04 + 08 + 09 + 13 34 = 04 + 08 + 10 + 12 34 = 04 + 09 + 10 + 11 34 = 05 + 06 + 07 + 16 |
34 = 05 + 06 + 08 + 15 34 = 05 + 06 + 09 + 14 34 = 05 + 06 + 10 + 13 34 = 05 + 06 + 11 + 12 34 = 05 + 07 + 08 + 14 34 = 05 + 07 + 09 + 13 34 = 05 + 07 + 10 + 12 34 = 05 + 08 + 09 + 12 34 = 05 + 08 + 10 + 11 34 = 06 + 07 + 08 + 13 34 = 06 + 07 + 09 + 12 34 = 06 + 07 + 10 + 11 34 = 06 + 08 + 09 + 11 34 = 07 + 08 + 09 + 10 . . . . |
Слагаемые с 1 по 16 регулярно распределяются в редукциях:
| Запрос: Номер: |
01 19 |
02 20 |
03 21 |
04 22 |
05 22 |
06 23 |
07 23 |
08 22 |
09 22 |
10 23 |
11 23 |
12 22 |
13 22 |
14 21 |
15 20 |
16 19 |
В отличие от квадрата 3×3 здесь не один вывод для
распределение чисел от 1 до 16 в квадрате 4х4.
Факт: существует 880 магических квадратов,
считая симметричные только один раз.
Это один из 880 возможных квадратов:
| ………… 12 …. 06 …. 15 ….. 01 ………… ………… 13 …. 03 …. 10 ….. 08 ………… ………… 02 …. 16 …. 05 ….. 11 ………… ………… 07 …. 09 …. 04 ….. 14 ………… |
Эта площадь особенная. Число 34 – это не только сумма чисел в строках, столбцах и обеих диагоналях, но также в каждом 2х2 кв. |
Волшебный квадрат 5×5
наверху
Магическое число (1 + 2 + … + 24 + 25): 5 = 65 .
Уменьшение магического числа 65.
| 65 = 01 + 02 + 13 + 24 + 25 65 = 01 + 02 + 14 + 23 + 25 65 = … 65 = … |
65 = … 65 = … 65 = 10 + 12 + 13 + 14 + 16 65 = 11 + 12 + 13 + 14 + 15 |
Компьютер обнаружил 1394 сокращения числа 65. |
Слагаемые и их количество в суммах
Вы заметили, что среднее число 13 = 65: 5 появляется чаще всего.
часто. Номера слагаемых в меньшие и большие слагаемые
падение симметрично в обе стороны.
Факт: существует 275 305 224 магических квадрата 5×5.
(Scientific American 1/1976)
Изготовление волшебного квадрата 5х5:
Вы просматриваете числа от 1 до 25.Есть два правила
для построения магического квадрата «вверху справа» и «если место занято,
один вниз “.
| ………………………………….. | Номер 1 помещается в центр первого ряда. Номер 2 следует справа вверху. Но тогда вы покидаете квадрат 5х5. Поэтому вы должны представить себе квадрат как цилиндр. В Цилиндр имеет вертикальные квадратные стороны квадрата как окружность. Горизонтальные стороны касаются друг друга и закрывают изогнутую поверхность цилиндр.Итак, справа вверху есть поле для числа 2. Если вы развернете цилиндр номер 2 перешел в последний ряд на одну позицию вправо. |
Номер 3 следует справа вверху.
| …… | Номер 4 будет лежать снаружи квадрат 5х5. Итак, вы снова представляете, что квадрат станет цилиндром, на этот раз с вертикальной осью. Вы можете найти место для номера 4. Если вы разверните цилиндр, вы найдете число в третьем ряду слева. |
Номер 5 находится вверху справа.
Вы используете второе правило для числа 6.
Если верхнее правое поле занято, вы помещаете первую строку в
тот же столбец.
Вы идете дальше с 7,
8,
и так далее. – Вы используете то же правило для числа 16
что касается числа 6.
Этим способом можно передать
формирование ко всем магическим квадратам с нечетными числами сторон ;-).
Также существуют правила для магических квадратов с четной стороной.
длина.Однако они более сложные.
The Magic nxn Squaree наверху
Существование магических квадратов nxn доказано для всех
числа n> 2. Но общего правила нет.
Магическое число (1 + 2 + 3 + … + n²): n = 0,5
* (n² + 1) * n.
Магические числа стандарта
квадраты:
Магические квадраты: 3×3
4х4 5х5 6х6
7×7 8×8 9×9
10×10
Магические числа: 15
34 65 111
175 260 369
505
Диковинки наверх
| … | Еще раз: квадрат магический , если числа имеют одинаковую сумму в строках, столбцах и диагоналях. |
| …… | Квадрат – это полумагический , если числа имеют одинаковая сумма только в строках и столбцах. |
| …… | Квадрат – это пандиагональ , если он магический и если не только номера главных диагоналей, но и ломаные диагонали иметь такую же сумму. |
| … | Этот магический квадрат пандиагонален. |
| …… | Вы найдете дополнительный квадрат , если вы замените каждое число n по 17-n. |
Квадрат самокомплеметарный , т.к. новый
симметричен старому. См. Красную ось.
| …… | Квадрат ассоциативный , если он магический и если пары чисел, лежащие симметрично центру, имеют одинаковую сумму.В сумма равна 26 = 5² + 1 = n² + 1. |
| … | Магический квадрат 3×3 Ло Шу ассоциативен. |
Вы можете зафиксировать вид чисел.
| … | Магический квадрат с простыми числами |
| … | “Полумагический квадрат квадратных чисел”. Все суммы, проходящие через центр, имеют одинаковое значение. Источник: http://www.mathpages.com/home/kmath517.htm |
Последовательность этой особой магии
квадраты не закончены. Отсутствуют магические квадраты, например.
> панмагические квадраты
> магические квадраты, образованные меньшими магическими квадратами
> магические квадраты с краями (Книга 2).
Есть объяснение всем различным магическим квадратам:
Их можно найти с помощью компьютеров. Новое свойство означает новый запрос внутри
программа.
Простые варианты наверх
Магические квадраты
в Интернете наверх
Английский
Крейг Кнехт (Мэджик
Квадратные модели)
| Вода Шаблоны удержания |
…… | Представьте, квадраты – это вершины квадратных призм с высота указана числами. Если вы нальете воду в это твердое вещество, оно останется в центре до высоты 17.Потом стекает. Количество воды равно (17-3) + (17-7) + (17-13) + (17-1) + (17-4) + (17-5) = 69. Есть приятные проблемы: Самое большое количество воды? Отдельно пруды? Остров? |
Эрик В. Вайсштейн (MathWorld)
Магия
Квадрат,
Panmagic
Квадрат,
Ассоциативный
Волшебный квадрат, Ло
Шу
Харви Д. Хайнц
магических квадратов,
Волшебные звезды и другие узоры
Хольгер Даниэльссон
Магия
Квадраты
MathTrek Иварса Петерсона
Подробнее
чем магические квадраты
Марк С.Фаррар
Магия
Квадраты
MathPages
Решение
Магические квадраты
Робин Мозли
Магия
Flexagon (файл .pdf)
Википедия
Магия
квадрат,
Самый совершенный
магический квадрат, вода
удержание на математических поверхностях, ассоциативное
магический квадрат
Немецкий
Фэн-шуй-Домашняя страница
Das magische Quadrat Lo-Shu
Герд Мюллер
Magisches
Quadrat Interaktiv
Ганс-Петер Граматке
Magische
Квадрат
Хольгер Даниэльссон
Magische Quadrate
Ян Хаазе
Das
Hexeneinmaleins aus Goethes “Faust” (Лёсунг)
Ян Теофель и Мартин Траутманн
Magische
Quadrate und Würfel
Мария Кот
Magische
Квадратный (.pdf.-Datei)
Пауль Хаймбах
Magische Quadrate
recordholder.org
Das
größte Magische Quadrat der Welt
Удо Хебиш (математическое кафе)
Magische
Квадрат
Википедия
Magisches
Квадрат, Фоллкоммен
perfektes magisches Quadrat
Список литературы наверх
(1) Bild der Wissenschaften, Heft 8/1966, Heft
6/1968, Heft 10/1976
(2) Питер ван Делфт / Джек Ботерманс: Денкспиле
der Welt, München 1980 (1998 neu aufgelegt)
(3) Максимилиан Миллер, Gelöste und ungelöste
Mathematische Probleme, Лейпциг, 1982 г.
Отзыв: Адрес электронной почты на моей главной странице
Это
страница также доступна на немецком языке
с более подробной информацией.
URL-адрес
моя домашняя страница:
http://www.mathemische-basteleien.de/
©
2000 Юрген Кёллер
верхняя
Сколько решений есть у магического квадрата 4 × 4? – AnswersToAll
Сколько решений есть у магического квадрата 4 × 4?
В отличие от магических квадратов 3 × 3, где есть только одно базовое решение головоломки, магический квадрат 4 × 4 имеет ровно 880 различных нормальных решений.
Как шаг за шагом решить магический квадрат?
Решение Magic Square
- Перечислите числа в порядке от наименьшего к наибольшему на листе бумаги.
- Сложите все девять чисел в вашем списке, чтобы получить результат.
- Разделите сумму из шага 2 на 3.
- Вернитесь к своему списку чисел, и число в самой середине этого списка будет помещено в центр магического квадрата.
Что в сумме дает магический квадрат 4 × 4?
Создание магического квадрата перед аудиторией, если все сделано правильно, может быть впечатляющей демонстрацией очевидного владения математикой более высокого уровня. Я покажу вам, как это сделать, используя, казалось бы, более сложную сетку 4 × 4.Сумма этого магического квадрата равна 34. Это наименьшая возможная сумма с использованием чисел от 1 до 16.
Почему 5 находится в центре магического квадрата?
Нечетные числа 1,3,7 и 9 встречаются дважды в сокращениях, четные числа 2,4,6,8 – трижды, а число 5 – один раз. Поэтому вы должны поместить цифру 5 в центр магического квадрата 3 × 3.
Сколько квадратов вы видите в сетке 4 × 4?
Сетка 4 × 4 будет иметь: 16 квадратов 1 × 1; 9 квадратов 2 × 2 (так как в каждом из трех верхних рядов по 3 квадрата, которые могут быть верхним правым углом квадрата 3 × 3), 4 квадрата 3 × 3 и 1 квадрат 4 × 4.
У всех магических квадратов 5 в центре?
Нечетные числа 1,3,7 и 9 встречаются дважды в сокращениях, четные числа 2,4,6,8 – трижды, а число 5 – один раз. Поэтому вы должны поместить цифру 5 в центр магического квадрата 3 × 3. Следовательно, есть только один магический квадрат 3 × 3.
Сколько прямоугольников в квадратной сетке 4 × 4?
Для квадрата 2 × 2 у нас есть в общей сложности 4 возможных прямоугольника, каждый из которых 1 × 2. Для квадрата 3×3 мы можем найти 12 квадратов 1×2, 6 квадратов 1×3 и 4 квадрата 2×3, всего 22 квадрата.Для квадрата 4 × 4 мы можем найти 24 1 × 2, 16 1 × 3, 8 1 × 4, 12 2 × 3, 6 2 × 4 и 4 3 × 4, всего 70 квадратов.
Как разгадывать магические квадраты – видео и стенограмма урока
Решение магических квадратов 3 x 3
Похоже, это может быть сложно, но если вы знаете секрет, вы можете собрать и собрать любой магический квадрат 3 x 3.
Вот секрет решения любого магического квадрата 3 x 3. Давайте посмотрим на квадрат, который складывается из 15. Есть пять простых шагов.
- Перечислите девять последовательных номеров по порядку. В этом случае 1, 2, 3, 4, 5, 6, 7, 8, 9. Обратите внимание, что во всех магических квадратах используются только последовательные числа.
- Сложите их и разделите на три. Это число, которое вы получите, сложив числа в квадрате в любом направлении. 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45. 45/3 = 15
- Самое среднее число в списке последовательных номеров – это число для среднего квадрата. Среднее число в списке последовательных номеров на самом деле называется медианой .В случае нашего списка номеров от 1 до 9, медиана – это число 5.
- Примените правила на диаграмме решения магического квадрата.
- Заполните остальные поля оставшимися числами, чтобы все строки, столбцы и диагонали добавлялись к магическому числу.
Теперь вы знаете фокус!
Создайте свой собственный магический квадрат
Если вы знаете, как собрать магический квадрат, вы также можете создать его. Для начала нужно выбрать девять последовательных чисел.Давайте использовать числа от 8 до 16. Теперь, чтобы найти число, которое будет суммой при сложении в каждом направлении, сложите числа.
8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 108
Разделите 108 на 3, и вы получите 36. Число, к которому прибавляется каждое направление, равно 36.
Вы только что совершили свое первое волшебство квадрат. Теперь, если вы хотите дать человеку подсказку, поместите медиану в средний квадрат. Помните, что медиана – это число в середине последовательности.
Если человек, решающий ее, сдается и предлагает вам это сделать, не забудьте использовать информацию из диаграммы решения магического квадрата.
Для только что использованных чисел решение находится на диаграмме.
Резюме урока
Хорошо, давайте сделаем минутку, чтобы повторить то, что мы узнали. Магический квадрат – это квадрат, в котором все числа в любом направлении – по вертикали, горизонтали и даже по диагонали – складываются в одно и то же число. После того, как вы определите медиану или среднее число в последовательности последовательных чисел и поместите его в средний квадрат, вы можете использовать уловку решения для решения любого магического квадрата 3 x 3.
Магический квадрат 4×4 в сумме 38
Вот как я бы это сделал:
Во-первых, мы хотим разделить числа на две группы, каждая из которых содержит 8 чисел, всего 76. Мы собираемся использовать одну из групп для диагоналей, а другую – для ребер. Чтобы можно было построить диагонали, по крайней мере, одна из групп должна быть разделена на две равные части по 4 числа в сумме 38.
Перед этим я бы проверил пару ограничений, основанных на четности, симметрии, а также наименьшем и наибольшем значениях.
Ограничения по четности
Поскольку все суммы четные, есть только пара возможных способов разместить четыре нечетных числа:
- по одному в каждом углу
- в четырех центральных квадратах
- по углам квадрата 3×3
- в маленьком квадрате в одном углу
- попарно на противоположных краях
Симметрии
У магического квадрата, помимо очевидного зеркального отражения и вращения, есть еще пара других симметрий, которые мы можем использовать для дальнейшего сокращения нашего дерева поиска.
Присмотревшись к возможным формам, образованным нечетными числами, мы заметим, что первый вариант фактически эквивалентен второму. Это потому, что одно можно преобразовать в другое, в то время как каждая сумма по-прежнему содержит одни и те же числа:
а б в г д е з г e f g h -> b a d c я дж к л н м п о m n o p j i l k (Каждый квадрант независимо поворачивается на 180 градусов)
Следовательно, если решение существует для конфигурации 1, симметричное решение гарантированно существует для конфигурации 2.
Аналогично, случай 3 эквивалентен случаю 4:
а б в г а в б г д е ж з -> я к дж л я j k l e g f h м н о п м о н п (Средние строки поменялись местами, затем средние столбцы поменялись местами)
Итак, достаточно протестировать конфигурации с нечетными числами 2, 4 и 5, мы не упустим никаких решений, игнорируя другие случаи. (Я придумываю все это по ходу дела, поэтому вполне вероятно, что я пропустил какую-то другую возможную конфигурацию для нечетных чисел.Будем надеяться, что нет.)
Применяя зеркальную и вращательную симметрии в дополнение к этим, и удаляя любые дубликаты, оставшееся дерево поиска начинает выглядеть довольно доступным.
(Кстати, используя те же самые симметрии, любой ответ, который мы найдем, впоследствии может быть преобразован в другие решения.)
Экстремальные значения
Тем не менее, перед тем, как начать, я бы проверил крайние значения. В среднем каждое число должно быть 9,5. Это делает посадку 4 наиболее сложной; он всегда требует 34 от своих трех спутников.Поскольку мы не можем найти три различных тройки, суммирующих до 34 в нашем числовом наборе, ясно, что мы не можем поместить 4 на диагональ. По той же причине 14 хочет пойти на край, и, вероятно, 6 и 13 тоже. ( РЕДАКТИРОВАТЬ: я, должно быть, очень устал, когда писал это. Такие тройки действительно существуют, , даже для размещения 4 по диагонали. )
Итак, наконец, давайте попробуем выбрать числа для первого разделения:
Метод проб и ошибок
Я начал с объединения всех крайних чисел 4, 6, 13 и 14 в одну группу.Поскольку 4 и 6 очень маленькие, я хотел отделить их от обеих семерок, поэтому мне нужно было поместить 11 в одну группу с 13, чтобы выровнять паритет групп. Нам все еще нужны три других числа, суммирующих до 28, и есть только один способ сделать это ( РЕДАКТИРОВАТЬ: ой, на самом деле их два. Другой не будет работать вообще, хотя ), поэтому первая попытка разделения становится
4 , 6 , 7, 7, 8 , 8, 11 , 12, 12, 13 , 14 , 10 , 10 , 10, 10, 10
Группа, выделенная жирным шрифтом, содержит 4, так что эта группа перейдет к краям.Остальное пойдет по диагоналям.
Теперь, когда есть нечетные числа как на диагоналях, так и вне их, «маленький квадрат в углу» – единственная конфигурация для нечетных чисел, которую нам нужно проверить. Оттуда и построив сначала диагонали, получим:
7 11 d (a, b, c, d: 8,10,10,10 в некотором порядке)
13 7 c (оставшиеся края: 4,6,8,10,10,14)
б 12
а 12
Наш раскол поставил семерки на диагональ в углу, что, в свою очередь, заставило двенадцать на одной диагонали.По зеркальной симметрии не имеет значения, в какую сторону мы поместим 11 и 13. Другая диагональ почти целиком состоит из десятков, и легко проверить все возможные варианты, тем более что a и c не могут быть десятками (у нас сразу закончились бы восьмерки. по краям, если они были):
7 11 10 7 11 10 13 7 10 8 13 7 8 10 10 10 12 ХХ 8 10 12 ХХ 8 12 10 12
Оба случая заканчиваются конфликтом на «XX», и нет других способов, которые можно было бы попробовать, поэтому первоначальное разделение было неправильным.
Возврат и перегруппировка
В соответствии с предыдущими предположениями, я бы попытался заменить (11, 13) другой группой. (12,12) – единственная пара в другой группе с такой же суммой, так что это то, что оттуда возвращается. Снова жирные цифры идут к краям.
4 , 6 , 7, 7, 8 , 8, 11, 12 , 12 , 13, 14 , 10 , 10 , 10, 10, 10.
Поскольку все нечетные числа теперь находятся на диагоналях, мы можем поместить их все в центр без потери общности.Семерки смежны, так как диагональная группа не имеет достаточно больших чисел для диагонали с обеими семерками. Углы тогда равны десяткам, за исключением одного угла, который равен 8. Подгонка 14 и 4 к наиболее вероятным местам (4 должны быть сгруппированы с наибольшими числами, которые они могут получить), и замечая, что этот выбор вынуждает десятки в соседних местах. угловые, остальные числа заняли свои места, и мы получаем:
10 12 6 10 14 7 7 10 4 11 13 10 10 8 12 8
Ура! Оно работает!
Итак, у нас есть рабочее решение.Но мы еще не закончили.
Примените симметрии к решениям
Применяя преобразования, описанные ранее, мы получаем следующий набор эквивалентных решений (с их зеркалами и поворотами, конечно):
10 12 6 10 7 14 10 7 10 6 12 10 13 4 10 11 14 7 7 10 12 10 10 6 4 13 11 10 6 10 10 12 4 11 13 10 8 10 8 12 14 7 7 10 12 10 8 8 10 8 12 8 11 4 10 13 10 12 8 8 7 14 10 7
Могут быть некоторые другие симметрии, которые я пропустил, и ни в коем случае это решение не гарантировано уникальным (на самом деле, в решении NetJohn по диагонали 12, поэтому оно отличается от этого), но продолжая с тем же рассуждая, осталось не так уж много вариантов, поэтому должна быть возможность провести исчерпывающий поиск даже вручную.( РЕДАКТИРОВАТЬ: после проверки этого ответа и осознания того, сколько ошибок я сделал, я действительно должен порекомендовать использовать компьютер .. )
Магические суммы и произведения
Хорошо известный магический квадрат ниже обладает тем свойством, что три числа в каждой из трех строк, трех столбцов и двух диагоналей в сумме дают одно и то же число 15 $. Это число называется магической суммой квадрата.
Менее известно, что если вы умножите три числа в каждой строке вместе и сложите три произведения:
$ 8 раз 1 раз 6 + 3 раз 5 раз 7 + 4 раз 9 раз 2 = 225 $
вы получите такую же сумму, как если бы вы умножили три числа в каждом столбце вместе и сложили три продукта:
$ 8 умножить на 3 умножить 4 + 1 раз 5 раз 7 + 6 раз 7 раз 2 = 225 $.
Это число называется магическим произведением квадрата.
Теперь возьмите «попарные произведения» в каждой строке и сложите их все:
$ (8 times 1 + 1 times 6 + 6 times 
Сделайте то же самое со столбцами:
$ (8 times 3 + 3 times 4 + 4 times 
И снова результаты такие же ! Это число называется волшебным попарным произведением квадрата.
Единственные другие магические квадраты $ 3 times 3 $, использующие числа от $ 1 $ до $ 9 $, являются просто отражениями и вращениями магического квадрата выше, например
Все эти примеры имеют ту же магическую сумму, магическое произведение и магическое попарное произведение, что и первый. Однако магические квадраты могут быть сформированы с использованием различных наборов из девяти чисел. Ниже приведены три примера.
Магическое число 18; волшебный продукт 468; магическое попарное произведение 294
Магическое число 18; волшебный продукт 414; магическое попарное произведение 285
Магическое число 24; волшебный продукт 840; магическое попарное произведение 489
Сможете ли вы найти другие магические квадраты $ 3 x 3 $?
Конечно, вы можете просто повернуть и отразить приведенные выше примеры, и вы можете умножить каждое число в квадрате на одну и ту же константу.Новые квадраты по-прежнему будут магическими, и нетрудно увидеть, что созданные вами магические квадраты снова будут иметь свойство волшебного произведения и свойство волшебного парного произведения.
Вы также можете добавить одно и то же число к каждому из девяти чисел в магическом квадрате, и в результате явно будет новый магический квадрат. В этом случае совсем не ясно, будет ли новый магический квадрат по-прежнему обладать свойствами магического произведения и магического попарного произведения.
Попробуйте составить свои собственные магические квадраты, назначив несколько чисел случайным образом некоторым ячейкам, а затем заполнив другие ячейки так, чтобы сумма строк, столбцов и диагоналей равнялась одинаковому числу.Каждый раз, когда вам удастся создать магический квадрат, вы должны проверять, работают ли также свойства волшебного продукта и волшебного парного продукта.
Проработав еще несколько примеров, вы можете заметить, что магическое число всегда в три раза больше среднего числа магического квадрата. В частности, кажется, что магическое число всегда кратно 3 долларам.
Теперь давайте разработаем систематический способ нахождения всех $ 3 times 3 $ магических квадратов.
Пусть число в середине будет $ x $, а магическая сумма каждой строки, диагонали и столбца будет $ R $.
Добавьте средний столбец и среднюю строку и обе диагонали, получив 4R $. Эта сумма включает в себя четыре раза среднее число и один раз все остальные числа, поэтому она должна составлять сумму всех чисел (3 доллара США) плюс троекратное среднее число. Итак,
$ 4R = 3R + 3x $
$ R = 3x $
Это также говорит нам, что сумма всех чисел в квадрате равна 9x $.
Теперь вы можете составлять свои собственные магические квадраты. Вы просто выбираете среднее число и два числа в других позициях, а затем заполняете весь магический квадрат, так что каждая строка добавляет в три раза больше среднего числа.
Например, с 7 долларами в середине сумма строки составляет 21 доллар, поэтому
должно быть
Если вы выберете “углы” равными $ x + a $ и $ x + b $
, тогда магический квадрат:
| х + | х – а – б | х + б |
| х – а + б | х | x + a- b |
| х – б | х + а + б | х – |
Теперь возможно, используя только элементарную алгебру, проверить, что общий магический квадрат $ 3 times 3 $ удовлетворяет свойству магического произведения и свойству магического попарного произведения.Мы оставляем это в качестве упражнения для энергичного читателя.
Что происходит с 5 умноженными на 5 $ магическими квадратами? Попробуйте пример ниже.
| 10 | 18 | 1 | 14 | 22 |
| 11 | 24 | 7 | 20 | 3 |
| 17 | 5 | 13 | 21 | 9 |
| 23 | 6 | 19 | 2 | 15 |
| 4 | 12 | 25 | 8 | 16 |
Что вы можете открыть для себя?
Волшебный квадрат 4 X 4 | MyWorldTheirWay.com
Вам понравился мой предыдущий пост о решении магического квадрата 3 х 3. Теперь у вас может возникнуть вопрос, а как насчет магического квадрата 4 х 4? Можно ли это решить таким же образом? Ну, нет, потому что, в отличие от Магического квадрата 3 х 3, в магическом квадрате 4 х 4 нет среднего столбца. Следовательно, нам нужно использовать другой подход для заполнения ячеек по часовой стрелке и против часовой стрелки. Ячейки заполнены таким образом, что числа по часовой стрелке и числа против часовой стрелки уравновешивают друг друга.
Раскрытие информации: некоторые из приведенных ниже ссылок являются партнерскими ссылками, что означает, что без дополнительных затрат для вас я получу комиссию, если вы перейдете и сделаете покупку.
Как решить Магический квадрат с четным числом ячеек
Давайте решим магический квадрат 4 X 4, который состоит из 4 строк и 4 столбцов с 4 × 4 = 16 ячеек, которые нужно заполнить. Давайте заполним квадраты от 1 до 16.
Поскольку имеется 4 ряда, разделите числа от 1 до 16 на четыре разные группы.
Математика
Вы замечаете закономерность в числах из каждой группы?
Сложите числа в Группе 1 и Группе 4, начиная с противоположного направления, и что вы видите, все они в сумме дают 17.
| 1 + 16 = 17 | 3 + 14 = 17 |
| 2 + 15 = 17 | 4 + 13 = 17 |
Аналогичным образом числа в Группе 2 и Группе 3 при сложении , первое и последнее и так далее, в сумме получается 17.
| 5 + 12 = 17 | 7 + 10 = 17 |
| 6 + 11 = 17 | 8 + 9 = 17 |
Используя полученные выше знания, мы можем заполнить первое и последнее строка квадрата с числами из группы 1 и группы 4 и вторая и третья строки с числами из группы 2 и группы 3.
Магический квадрат 4 X 4
Начиная с левой стороны квадрата, заполните ячейки в строке 1 и 4 числами из группы 1 -> 1, 2, 3, 4 против часовой стрелки.
Аналогичным образом, начиная с левой стороны квадрата, заполните ячейки в строках 1 и 4 числами из группы 4 -> 13, 14, 15, 16 по часовой стрелке.
Начиная с правой стороны квадрата, заполните ячейки в строках 2 и 3 числами из группы 2 -> 5, 6, 7, 8 против часовой стрелки.
Аналогичным образом, начиная с правой стороны квадрата, заполните ячейки в строках 2 и 3 числами из группы 3 -> 9, 10, 11, 12 по часовой стрелке.
Это магический квадрат с магической константой 34, что в два раза больше суммы первого и последнего числа в последовательности, т.е. 2 x (1 + 16) = 34. Сумма чисел в каждой строке, столбце и по диагонали равно 34.
Что такое магический квадрат
Магический квадрат – это квадрат с числами из последовательности, расположенной таким образом, что сумма всех чисел в строке, столбце и диагонали одинакова. Эта сумма называется магической постоянной. Они сгруппированы в две категории – нечетный порядок магических квадратов и четный порядок магических квадратов.В квадрате нечетной магии на каждой стороне квадрата нечетное количество клеток. Мы используем концепцию транспонирования и применяем для их решения. Точно так же в четном магическом квадрате есть четное количество ячеек с каждой стороны квадрата. И мы используем концепцию заполнения ячеек по часовой стрелке и против часовой стрелки для их решения.
Мы можем заполнить ячейки магического квадрата любой последовательностью арифметической прогрессии. Это означает, что последовательность чисел такая, что разница между последовательными членами постоянна.Например, 2,4,6, 8,…. и так далее – это серия арифметической прогрессии с разницей в 2 между каждым числом.
Как насчет того, чтобы попробовать это в другой последовательности, чтобы самому увидеть волшебство.
Вы любите изучать математические трюки, тогда посмотрите эту удивительную книгу Артура Т. Бенджамина, который увлечен двумя вещами – математикой и магией. Некоторые из его книг были бестселлерами в Нью-Йорке и победителями Американского математического общества AMA.
И пока вы здесь, ознакомьтесь с некоторыми из моих последних сообщений.