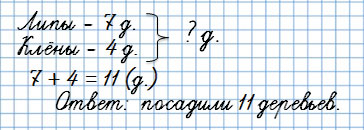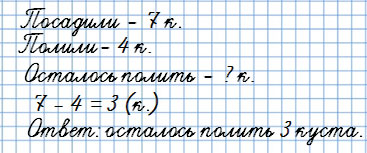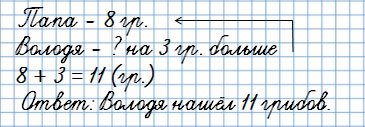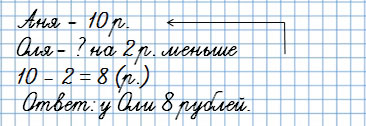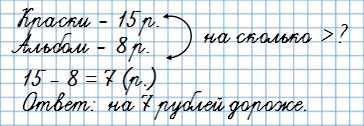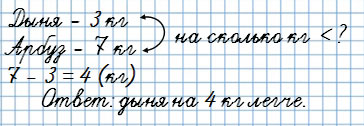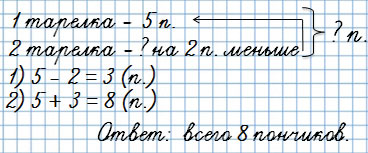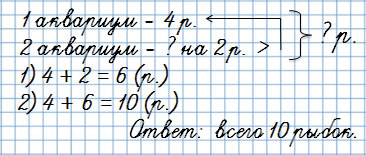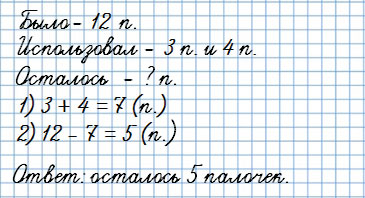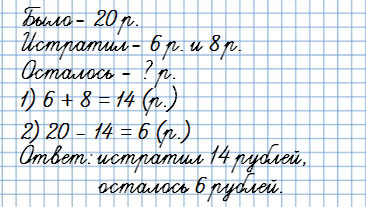Общая структура методики составления задач по математике
Математическое образование необходимо как часть общей культуры для всех учащихся, а поэтому изучение математики в колледже в группах, готовящих квалифицированных специалистов на базе основной школы с получением среднего образования и специальности, является необходимым. Уровень математического образования, обеспечиваемый введением новых программ, становится одним из важных элементов подготовки учащихся к общественно полезной деятельности. Задача для преподавателя математики в колледже непростая: в кратчайший срок, в отведенное по учебному плану время, а это в пределах 180 часов изучить программный материал в объеме математики 9 классов. И не только изучить, но и вооружить мобильными, ровными знаниями, которые при переходе на дальнейшую ступень учебы будут сразу востребованы.
Цель преподавания заключается в том, чтобы учащийся овладел математикой. Термин “овладел” очень растяжимый. Во-первых, учащийся должен нечто знать. Во-вторых, он должен на некоторую глубину понимать, т.е. под знанием подразумевается не только умение повторить формулировку, а мотивировать, почему так, а не иначе. В-третьих, учащийся должен уметь применять изученную им математику по профилю специальности.
Для достижения этих целей необходимо изучать теорию и решать задачи. Решая задачи, применяем теорию и тем самым познаем ее. Изучать математику, не решая задач, совершенно бесполезно. В этом вряд ли кто-то сомневается, но многие неправильно понимают роль задач. Обучение математике нельзя разделить на теорию и решение задач. Невозможно без решения задач усвоить теорию. Цель не в том, чтобы ученик решил задачу (т.е. получил ответ), а в том чтобы получил от этой задачи пользу, т.е. продвинулся на одну ступеньку по длинной лестнице овладения математикой. Цель не в ответе, а в процессе решения. Решая задачи учащийся приобретает новые знания и навыки, развивает в себе настойчивость, приобщается к математическому творчеству.
Наиболее эффективно и результативно развитие математического творчества проявляется при составлении математических задач преподавателем и учащимися, где отражается систематическое применение материалов по специальности, элементов производственного процесса. Математическое творчество прослеживается на всех этапах составления задач по математике. Целесообразно давать учащимся задания на составление задач, связанных с той или другой специальностью, чтобы при их решении нужно было использовать изучаемый на уроках материал. Например, предлагаются для групп по специальности “повар,кондитер” задачи на нахождение процентного содержания вещества, расчет наибольшего и наименьшего значения количества материала. Для групп по специальности “экономика и бухгалтерский учет” предлагаются задачи на определение величины дохода и возвращаемого займа, расчет прибыли, общей суммы дохода предприятия и т. д. После решения подобных задач учащиеся более подробно узнают об особенностях и значимости выбранной профессии, о трудностях в работе, об оплате.
Основным исходным положением, затрагивающим профессиональную направленность курса математики, является прикладная значимость знаний в практической деятельности. Прикладная направленность математических знаний означает осуществление реализации профессиональной подготовки. К основным направлениям этой работы в процессе обучения математике можно отнести следующие:
- усиление в аспекте прикладной ориентации взаимосвязи математики и других смежных дисциплин;
- сближение методов решения учебных задач с методами, применяемыми на практике;
- раскрытие своеобразия отражения математикой законов действительности;
- формирования у учащихся умений строить математические модели;
- изучение впечатлений учащихся, сложившихся в результате наблюдения трудового процесса, и учет обобщенных результатов при объяснении нового материала; превращение материалов наблюдения в средство повышения эффективности уроков математики;
- систематическое использование на уроках математики материала по специальности, элементов производительного процесса;
- ознакомление учащихся средствами математики с особенностями выбранной ими специальности;
Каждая решаемая задача имеет методическую цель. Поэтому преподаватель должен стремиться не к тому, чтобы задача была решена быстро и безошибочно или только на развитие тренировки, а к тому, чтобы она была решена творчески и чтобы из нее выжить как можно больше пользы для математического развития ученика.
Под составлением задачи по математике надо понимать не простую репродукцию задачи из сборника или учебного пособия, а самостоятельную постановку и решение проблемы учащимися, которая в общем случае решается с помощью логических умозаключений, математических действий на основе законов и методов математики.
Понимание взаимосвязи решения и составления задач позволит преподавателю добиться повышения эффективности и результативности составления и решения задач.
Последовательность операций в процессе составления задач сводится к следующим:
- обнаружение и наличие математической задачной ситуации;
- выявление и анализ элементов задачной ситуации (первичная модель задачи);
- краткая запись условия задачи с выполнением рисунка, чертежа, графика или схемы;
- вторичный анализ условия с выделением теории и законов, описывающих задачную ситуацию;
- упрощение условия, дополнение условия недостающими данными, постоянными;
- выбор методов, приемов, способов решения задачи;
- выделение звеньев (уравнений, выводов и т. д.);
- нахождение и осуществления решения в общем виде;
- анализ модели задачи, ее точная формулировка и корректирование;
- проверка и оценка условия задачи;
- исследование задачи, ее окончательная редакция, обсуждение, выделение и постановка новых задачных ситуаций;
Для составления и решения математических задач служат основой именно факты из практической деятельности человека для удовлетворения человеческих потребностей. Мировоззренческая направленность задачного подхода к математическому образованию требует:
- целостного видения предмета математики на каждом этапе с углублением картины математической реальности от этапа к этапу;
- “соразмерность” человеку, его потребностям, эмоциональной и интеллектуальной сферам;
- отражение мировоззренческих идей и выводов;
Можно выделить следующие виды заданий на составление задач:
- на установление аналогичных задач;
- на отыскание, составление подзадач;
- на дополнение данных по неполной ситуации;
- с другими численными данными;
- по схеме условия в общем виде;
- на отыскание, составление обратных задач;
- на отбор данных по избыточной ситуации;
- на постановку вопроса к условию;
- по схеме-решения в общем виде;
Предлагаемые учащимся преподавателем задания на составление по ситуациям в учебном материале:
- по рисункам учебника, пособия, задачника и т.д.;
- по тексту учебника, пособия;
- по материалам по профилю специальности;
- итоговое по теме, по материалам экзаменационных билетов;
- по графикам и схемам учебника, пособия задачника;
- по данной задачной ситуации;
В обучении и решении математических задач в среднем специальном заведении схемы “преподаватель-ученик”, “преподаватель-задача”, “ученик-задача” выступают в качестве составных взаимосвязанных и взаимообусловленных элементов современной концепции обучения математики: преподавания, учения и содержания изучаемого. Выделенные схемы включают в себя как прямые, так и обратные связи. Традиционное обучение решению математических задач в колледже предусматривает целенаправленное воздействие преподавателя на ученика непосредственно (“преподаватель-ученик”) или через задачу (“преподаватель–задача–ученик”). Составление математических задач позволяет осуществить эффективные и результативные обратные связи не только на уровне схемы, но и в рамках общей схемы “преподаватель-ученик-задача — преподаватель”. При этом по заданию преподавателя учащийся составляет задачу и предъявляет ее снова преподавателю. Так, в идеальном случае, ученик по требованию преподавателя составляет и решает задачу под его контролем. Но, самостоятельное, творческое составление математических задач достигается постепенным овладением всего процесса составления в ходе выполнения специальных заданий. Знания о задачах, приемах их постановки, формулировки и решения, актуализированными заданиями на составление задач, представляют собой содержание обучения составлению. Это содержание, вместе с преподаванием и учением, определяют структуру обучения составлению математических задач. Преподаватель ставит задание перед учащимися с требованием составить (полностью или частично) и решить задачу; ученик составляет и решает задачу, а саму задачу и ее решение предоставляет преподавателю для проверки с возможным последующим включением в учебно-воспитательный процесс по традиционной схеме.
В перспективе, при овладении учащимися достаточно высокого уровня в составлении математических задач, по требованию преподавателя ученик сам выбирает задачную ситуацию, составляет, решает ее, а преподаватель проверяет и осуществляет отбор для дальнейшего использования.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
В вопросе «Сколько … осталось?»
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии «на … больше»
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
В условии «на … меньше»
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
В вопросе «На сколько больше…?»
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
«На сколько меньше…?»
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было…Стало…»
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было… Осталось…»
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали… Осталось…»
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором — на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
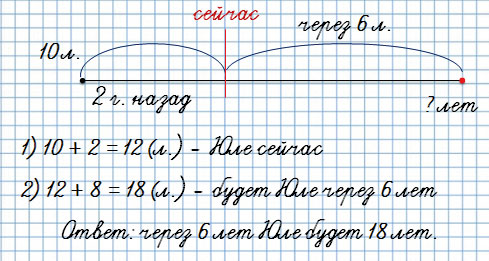
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 19,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 63. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 6,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 74. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 100,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 18,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 41,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 13,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 367,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 373,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 165,
Мерзляк, Полонский, Якир, Учебник
Номер 293,
Мерзляк, Полонский, Якир, Учебник
Номер 366,
Мерзляк, Полонский, Якир, Учебник
Номер 383,
Мерзляк, Полонский, Якир, Учебник
Номер 465,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 483,
Мерзляк, Полонский, Якир, Учебник
Номер 505,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 371,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 390,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 404,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 412,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 418,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 435,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 443,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 453,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Обучение составлению
математических задач как средство интеллектуального развития учащихся
Оглавление
ВВЕДЕНИЕ……………………………………………………………………..…3
Глава I.
Психологические и дидактические основы интеллектуального развития школьников в
процессе работы над задачей……….…………………7
§1.1 Проблема интеллектуального развития
учащихся и пути ее решения при обучении математике………………………….. ………………………………….7
§1.2 Работа над задачей как средство интеллектуального
развития учащихся .. ………………………………………………………………………………………29
§1.3 Приемы составления задач. Составление
циклов взаимосвязанных задач………………………………………………………………………………..39
Глава
II. Обучение
учащихся составлению задач при изучении темы «Прямая и плоскость в пространстве»…………………………………………………….53
§2.1 Обучение приемам составления задач на
примере применения аналогии, обобщения и конкретизации………………………………………………………53
§2.2 Логико-дидактический
анализ темы «Прямая и плоскость в пространстве» с позиции возможности обучения
составлению задач…………………………77
§2.3 Из опыта
обучения школьников составлению задач…………………….86
ЗАКЛЮЧЕНИЕ……………………………………………………………………133
СПИСОК ЛИТЕРАТУРЫ………………………………………………………..135
Введение
На
сегодняшний день проблемы, связанные с развивающим обучением, достаточно
глубоко исследованы в психологии и дидактике. Однако имеющиеся теоретические
положения развития школьников в процессе обучения пока еще не находят должного
отражения в практике работы школы и, в частности, при обучении математике.
Поэтому проблема интеллектуального развития школьников средствами математики
относится к одному из приоритетных направлений исследований в области
математического образования. Проблемой интеллектуального развития
занимались следующие психологи: Ж. Пиаже[21], Л.С.
Выготский [5], С.Л.Рубенштейн [31], Дж. Брунер [28], Б.Г. Ананьев[1]. Все
они утверждают, что в основе интеллекта лежит развитое мышление. Процесс
развития мышления методически состоит в формировании и развитии обобщенных
приемов умственных действий (сравнение, обобщение, анализ, синтез, классификация,
абстрагирование, аналогия и др.), что является общим условием функционирования
самого мышления как процесса в любой — области познания, в том числе и в
математике.
Проблема
формирования у школьников логических приемов мышления рассматривалась исследователями
в различных контекстах: формирования логических приемов мышления (Н.Н.
Поспелов, И.Н.Поспелов
[23]); формирование приемов учебно-познавательной деятельности (О.Б. Епишева,
В.И. Крупич [11]); формирование математических понятий (А.Я. Блох, Я.И. Груденов,
Н.В. Метельский, В.В. Репьев, К.А. Рупасов, З.И. Слепкань [17] ); формирование
умений и навыков применения различных приемов мыслительной деятельности (О.В.Алексеева,
Т.В. Ларионова [38] ).
Во
всех работах заявлена необходимость специального формирования приемов мышления,
в том числе логических приемов, представлены сами приемы, возможные упражнения
овладения ими, время и сроки их изучения. Однако авторы не рассматривают
проблему методики формирования логических приемов мышления. Акцент делается на
усвоение математического содержания с помощью логических приемов. Меньше
уделяется внимания формированию самих приемов посредством изучения некоторого
математического содержания.
Вышесказанное
позволяет говорить о необходимости целенаправленного формирования логических
приемов мышления, которое должно стать одной из приоритетных задач при изучении
математики.
В
организации обучения математике важнейшую роль играют задачи. В обучении
математике они являются целью, средством обучения и интеллектуального развития.
Развитие учащихся зависит от той деятельности, которую они выполняют в процессе
обучения. При этом важнейшим инструментом для развития мышления, формирования
творческой деятельности школьника служит самостоятельное составление задач. Составляя
задачи, ученик находится в позиции исследователя, первооткрывателя, проводит
анализ условий, изменяет их, устанавливает различные связи между данными,
формулирует вопросы, на которые сам отыскивает ответ. Используя упражнения на
составление задач, можно формировать и развивать такие компоненты
математических способностей, как логичность, систематичность,
последовательность словесных рассуждений и выводов и др.
Таким
образом, мы можем сделать вывод, что роль задач в интеллектуальном развитии
учащихся велика. Ученики должны не только уметь решать задачи, но и составлять
их.
К
сожалению, вследствие недостаточного владения самими учителями математики
приемами составления математических задач и технологией обучения этим приемам
школьников, упражнения на самостоятельное конструирование задач учащимися в
практике обучения математики используются редко. Поэтому и возникает проблема в
недостатке методических рекомендаций на применение и использование различных
приемов составления задач на уроках.
Таким
образом, актуальность работы обусловлена следующим:
—
процесс составления задач играет важную роль в интеллектуальном развитии
школьников;
—
к приемам самостоятельного составления задач учащимися учителя прибегают
довольно редко, так как на уроке не хватает времени;
—
процесс обучения приемам составления задач – это материал для настоящей
научно-исследовательской работы.
Объект
исследования: процесс обучения составлению задач на
уроках геометрии учащихся 10«а» класса.
Предмет
исследования: методическая система, включающая в себя
цели, содержание и технологию обучения учащихся приемам составления задач.
Целью
исследования является
разработка методических рекомендаций по обучению приемам составления задач,
направленным на развитие интеллектуальных способностей, умений и навыков
учащихся.
Можно
выдвинуть следующую гипотезу исследования: если целенаправленно обучать
школьников приемам мышления, входящим в деятельность по составлению задач, то
это будет способствовать их интеллектуальному развитию.
Для
достижения поставленной цели и проверки выдвинутой гипотезы необходимо было
решить следующие задачи:
1. На
основе анализа психологической и дидактической литературы выявить роль задач в
интеллектуальном развитии учащихся.
2. Рассмотреть
различные приемы составления задач.
3. Разработать
методические основы обучения школьников отдельным приемам мышления, входящим в
деятельность по составлению задач.
4. Разработать
конспекты и фрагменты уроков, на которых осуществляется обучение различным
приемам составления задач.
5. Опробовать
методические рекомендации в школьной практике.
Методологическая
основа:
Для
решения поставленных задач были использованы следующие методы: методы
эмпирического исследования, основанные на опыте и практике, изучение и анализ
литературы по исследуемой проблеме, беседа с учителем для определения уровня
знаний учащихся, наблюдение, личный опыт работы с учащимися.
Работа
состоит из введения, двух глав, заключения и списка литературы.
Во
введении обосновывается актуальность данной проблемы, формулируются проблема,
объект, предмет, цель исследования, гипотеза, задачи исследования, методы,
которыми решается проблема, описана структура работы.
В
первой главе излагаются психологические и дидактические основы
интеллектуального развития учащихся в процессе работы над задачей, рассмотрены
различные приемы составления задач на конкретных примерах и рассмотрена
методика обучения таким приемам как обобщения, аналогия и конкретизация.
Во
второй главе приводится логико-дидактический анализ темы «Прямая и плоскость в
пространстве» с позиции возможности обучения составлению задач, разработка
конспектов и фрагментов уроков для учащихся 10 класса, на которых осуществляется
обучение различные приемы составления задач и описана опытная проверка
результатов теоретического исследования.
В
заключении отмечены основные выводы по проделанной работе.
Список
литературы состоит из 44 наименований, которые были использованы при написании
данной работы.
Общий
объем работы – 140 страниц.
Глава
I.
Психологические и дидактические основы интеллектуального развития школьников в
процессе работы над задачей
Прежде,
чем рассмотреть проблему обучения приемам составления математических задач
необходимо выяснить основы интеллектуального развития школьников при обучении
математике, и в частности, в процессе работы над задачей. Необходимо как можно
точнее определить понятие «интеллектуальное развитие», выяснить пути развития
интеллекта, рассмотреть роль задач в обучении математике. В этой главе будут также
рассмотрены различные приемы составления задач с иллюстрацией их на конкретных
примерах из различных разделов математики.
§
1.1 Проблема интеллектуального развития учащихся и пути ее решения при обучении
математике
Проблема
развития учащихся занимает одно из центральных мест в концепции общего среднего
образования. Образовательная и воспитательная функции процесса обучения
являются основной для его развивающей функции. Вместе с тем решение проблемы
развития учащихся в процессе обучения математике важно для формирования
творческой личности даже после окончания школы. Овладение научными основами
математики, изучаемыми в школе, успешное решение математических задач
предполагают наличие у ученика определенного уровня развития его мышления.
Развитие является не только конечной целью, но и средством усвоения
математики.
Прежде
чем рассмотреть, как происходит интеллектуальное развитие школьников при
обучении математике, необходимо выяснить, что мы будем понимать под
словосочетанием «интеллектуальное развитие», что означает слово «интеллект»?
Понятия
«интеллект», «развитие», «интеллектуальное развитие» — понятия психологические.
Поэтому обратимся, сначала, к работам ученых-психологов.
В
психологическом словаре интеллект (от лат. intellectus – понимание, познание) – 1) общая способность к познанию и решению
проблем, определяющая успешность любой деятельности и лежащая в основе других
способностей; 2) система всех познавательных способностей индивида: ощущения,
восприятия, памяти, представления, мышления, воображения; 3) способность к
решению проблем без проб и ошибок «в уме». Понятие интеллекта как общей
умственной способности применяется в качестве обобщения поведенческих
характеристик, связанных с успешной адаптацией к новым жизненным задачам [27,
с. 138].
В психологической
науке выделяют ряд теоретических подходов к трактовке природы интеллекта.
В теории интеллекта,
разработанной под руководством Б.Г. Ананьева, интеллект —
интегрированная система познавательных процессов. Структура интеллекта сводится
к характеру внутрифункциональных и межфункциональных связей, выявленных с
помощью процедур корреляционного и факторного анализа (когнитивная
дифференциация-интеграция, ведущий психический процесс и т.д.). Степень
интегрированности когнитивных процессов (психомоторики, внимания, памяти,
мышления) — критерий развития интеллекта. Интеграция характеризуется
возрастанием выраженности свойств отдельных познавательных функций и усилением
межфункциональных связей между ними. Рост количества и величины корреляционных
связей интерпретируется как проявление меры интегрированности познавательных
функций и, соответственно, как показатель становления целостной структуры
интеллекта [1, c.134].
В целом критерий развития
интеллектуальных возможностей связывается с тем, насколько в познавательных
действиях субъекта реализуются доминирующие культурные ориентации. Такие
культурные факторы, как традиционный образ жизни, образование, язык унифицируют
проявления интеллектуальной активности.
В рамках
культурно-исторической теории формирования высших психических функций
интеллектуальное развитие связано с формированием в сознании ребенка системы
понятий [3, с.31]. Интеллект возникает как результат межфункциональной
интеграции познавательных процессов, перестроенных на основе понятийного
мышления. Интеллектуализация познавательных функций означает их осознанность,
произвольность, категориальность, системность, возможность протекания во
внутреннем — умственном — плане. В свою очередь регуляция собственно
интеллектуальной деятельностью осуществляется на основе усвоения т. н. «научных
понятий». Критерием развития интеллекта выступает мера общности понятия: с
точки зрения степени обобщенности его содержания и с точки зрения степени его
включенности в систему связей с другими понятиями [4, c.31].
Ключевая роль слова в
объяснении, как механизмов развития, так и механизмов функционирования
интеллекта обусловлена тем, что проблема интеллекта Л.С. Выготским решается как
проблема умственного (шире — психического) развития ребенка, а термин
«интеллект» отождествляется с понятийным мышлением. Согласно
культурно-исторической теории, главная закономерность онтогенеза психики
состоит в интериоризации ребенком структуры внешней, социально-символической
деятельности (т. е. совместно со взрослым и опосредованной знаками). В качестве
универсального орудия, изменяющего психические функции, выступает языковой знак
— слово. Поэтому основной механизм интеллектуального развития ребенка связан с
формированием в его сознании системы словесных значений, перестройка которой и
характеризует направление роста его интеллектуальных возможностей [5, c.92].
Представление об интеллекте
как предпосылке обучения разрабатывается в контексте психолого-педагогической
проблемы обучаемости (Н.А. Менчинская, З.И. Калмыкова). В этих исследованиях
природа интеллекта отождествляется с «продуктивным мышлением», сущность которого
заключается в способности к приобретению новых знаний (способности к учению или
обучаемости). Показателями обучаемости выступают уровень обобщенности знаний,
широта их применения, быстрота усвоения, темп продвижения в учебе. «Ядро»
индивидуального интеллекта составляют возможности человека к самостоятельному
открытию новых знаний и применению их в нестандартных проблемных ситуациях.
Таким образом, характеристики обучаемости определяют успешность обучения,
выступая тем самым в качестве критерия интеллектуального развития.
Операционально-процессуальный
подход в анализе интеллектуальной деятельности позволяет развести понятия
мышления и умственных способностей. Мышление — непрерывный
процесс анализа, синтеза, обобщения условий и требований решаемых задач и
способов их решения. Умственные способности — сформировавшаяся в
процессе мышления совокупность умственных операций, которые мышление порождает,
но к которым не сводится.
В контексте теории
психического развития как процесса разводятся и понятия «умственное развитие» и
«мышление». Их отождествление связано с включением в структуру мышления
совокупности умственных действий.
Известный психолог А.Н.
Леонтьев пишет: «Чтобы жить в обществе, человеку недостаточно того, что ему дает
природа при его рождении. Он должен еще овладеть тем, что было достигнуто в
процессе исторического развития человеческого общества» [18, c.50].
Для того чтобы овладеть
достижениями исторического развития, человек должен включить свои умственные
способности в деятельность, именно эту функцию и выполняет мышление. Гальперин
П.Я. отмечает «Мышление — это деятельность, чтобы узнать, а о вещах ничего
нельзя узнать, не проследив (в четко обозначенных условиях), что они делают и
что с ними делают» [6, с.33].
В процессе мышления
умственные способности реализуются через образование адекватных
действительности понятий, суждений, умозаключений. Понятия, суждения,
умозаключения есть собственно интеллект.
Понятие представляет собой
опосредованное и обобщенное знание о предмете, основанное на раскрытии его
существенных объективных связей и отношений. Понятие является отражением
наиболее существенных признаков предмета или явления и образуется на основе
представлений путем различной степени абстракции.
Суждение — утверждение или отрицание
какого-либо положения. Суждение раскрывает содержание понятия. Чтобы высказать
то или иное суждение, человек должен знать, какое понятие входит в состав
суждения.
Умозаключение — общий или частный
логический вывод, к которому приходит человек на основании сопоставления и
анализа различных суждений [2, c.514].
Изучение вопроса об
особенностях и закономерностях развития интеллекта у детей связано, прежде
всего, с именем швейцарского психолога Жана Пиаже [21, c.93]. Начиная с 20-х
гг. ХХ в. он в течение 50 лет занимался теоретическими и практическими
вопросами детского интеллекта.
По Ж. Пиаже,
«интеллект — это наиболее совершенная форма адаптации организма к
среде, представляющая собой единство процесса ассимиляции (воспроизведения
элементов среды в психике субъекта в виде когнитивных психических схем) и
процесса аккомодации (изменение этих когнитивных схем в зависимости от
требований объективного мира)».
Процесс развития интеллекта,
согласно Пиаже, состоит из трех больших периодов, в течение которых происходит
становление трех основных структур. Сначала формируются сенсомоторные
структуры, то есть системы обратимых действий, выполняемых материально и
последовательно, затем возникают и достигают соответствующего уровня структуры
конкретных операций — это системы действий, выполняемых в уме, но с опорой на
внешние, наглядные данные. После этого открывается возможность для формирования
формальных операций.
Классификация стадий развития интеллекта:
I. Сенсомоторный интеллект
А. Центрация на
собственном теле
1. Упражнение рефлексов: 0-1 мес.
2. Первые навыки и первые круговые реакции: 1-4,5 мес.
3. Координация зрения и хватания. Вторичные круговые
реакции: 4,5-9 мес.
4. Дифференциация средства и цели. Начало
практического интеллекта: 9-12 мес.
5. Дифференциация схем действия благодаря третичным
круговым реакциям.
Б. Появление новых средств для достижения
цели: 11-12-18 мес.
6. Начало интериоризации схем и решение некоторых
проблем путем дедукции: 18-24 мес.
II. Репрезентативный
интеллект и конкретные операции
А. Предоператорный
интеллект
1. Появление символической функции. Начало
интериоризации схем действия: 2-4 года.
2. Интуитивное мышление, опирающееся на восприятие:
4-6 лет.
3. Интуитивное мышление, опирающееся на более
расчлененные представления: 6-8 лет.
Б. Конкретные операции
4. Простые операции (классификация, сериация, взаимно
однозначное соответствие): 8-10 лет.
5. Система операций (система координат, проективные
понятия): 9-12 лет.
III. Репрезентативный
интеллект и формальные операции
А. Становление формальных
операций
1. Гипотетико-дедуктивная логика и комбинаторика:
12-14 лет.
Б. Достижение формальных
операций
2. Структура «решетки» и группа четырех трансформаций:
13-14 лет.
Развитие, по Пиаже, — это
переход от низшей стадии к высшей. Предыдущая стадия всегда подготавливает
последующую. Так, конкретные операции служат основой формальных операций и
составляют их часть. В развитии происходит не простое замещение низшей стадии
высшей, а интеграция ранее сформированных структур; предшествующая стадия
перестраивается на более высоком уровне.
Стадии интеллектуального
развития, согласно Пиаже, можно рассматривать как стадии психического развития
в целом.
Очевидно, что ребенок не
проходит эти стадии строго по календарю; изменения происходят постепенно и в
разные сроки у каждого ребенка. Возникает вопрос: что же является нормальным
развитием и когда можно говорить о нарушении сроков созревания тех или иных
психических процессов у ребенка? На эти вопросы в теории Пиаже ответа нет.
Несмотря на то, что его
теория внесла неоценимый вклад в понимание когнитивного развития ребенка и до
сих пор имеет большое практическое значение в области обучения и развития
познавательной сферы детей, она имеет свои слабые стороны, и прежде всего —
отсутствие у Пиаже стандартных правил проведения экспериментов с детьми, что
позволило подвергнуть сомнению полученные им результаты. Ведь изменение в
процедуре проведения опыта полностью изменяет результат тестирования. Кроме
того, в исследованиях многочисленных последователей Пиаже были показаны другие
возможные объяснения результатов решения задач детьми (например, решение детьми
задач на понимание сохранения объема и других величин основано отчасти на
языковом развитии, а не только на процессах, описанных Пиаже) [21].
На принципах Пиаже западными
психологами построены тесты для определения готовности ребенка к школе, а также
тест «Давайте посмотрим на ребенка», сочетающий в себе оценку и программу
обучения. Однако эти тесты пока не нормированы.
В теории Пиаже малое значение
придается влиянию на интеллектуальное развитие ребенка значимого взрослого. В
этом смысле представление Л.С. Выготского о развитии интеллекта у ребенка в
сотрудничестве с другими людьми является более продуктивным. Большое значение
для целей психологической диагностики и особенно психокоррекции психического
развития ребенка имеют представления Выготского о «зоне ближайшего развития»,
организации обучения и роли внутренней речи ребенка как промежуточного шага к
саморегуляции интеллектуальных навыков [4, c.216].
Согласно Ж. Пиаже, в
подростковом возрасте происходит переход от стадии конкретных операций к стадии
формальных операций. Главным результатом данной стадии является интеграция
операциональных структур интеллекта и формирование формального (рефлексивного)
мышления, что позволяет подростку решать задачи, отвлекаясь от непосредственно
воспринимаемой реальности, при меньшей зависимости от контекста, в режиме
индуктивно-дедуктивных рассуждений.
Л.С. Выготский проводит
принципиальное противопоставление между натуральными психическими функциями и
высшими психическими функциями, которые социально детерминированы и составляют
сущность человеческого сознания. К высшим психическим функциям Л.С. Выготский,
прежде всего, относит понятийное мышление, формирование которого начинается и
завершается в подростковом возрасте, полностью перестраивая всю структуру
интеллекта. С его точки зрения, обучение ведёт и определяет интеллектуальное
развитие. Это решение прямо противоположно позиции Ж. Пиаже.
На современном уровне психологических
знаний в большинстве подходов признаётся важность для становления интеллекта,
как процессов развития, так и обучения. Отмечается, что процесс обучения должен
строиться с учётом общих закономерностей умственного развития и характерных для
каждого возрастного периода особенностей интеллектуального роста. В связи с
этим перед психологией стоит задача изучения механизмов и закономерностей
интеллектуального развития на разных этапах онтогенеза, выявления того общего и
специфического, что появляется с возрастом и в процессе обучения.
Исходя из теории Ж. Пиаже,
Джером Брунер пересмотрел некоторые из его представлений об интеллектуальном
развитии. Развитие складывается не просто из ряда стадий, оно предполагает
последовательное овладение ребенком тремя сферами представлений — действием,
образом и символом (словом). Это в то же время и способы познания окружающего
мира. Сначала ребенок познает мир благодаря своим привычным действиям. Затем
мир представляется ему еще и в образах, относительно свободных от действий.
Постепенно появляется еще один новый путь — перевод действий и образов в
языковые средства [28].
Дж. Брунер не дает жесткой
периодизации интеллектуального развития. Он не указывает точные сроки появления
стадий и не выделяет переходы от одной стадии к другой. Этапы развития
интеллекта не образуют у него лестницу, каждая ступень которой поднимает
ребенка на новый, более высокий уровень, обесценивая предыдущий. Важны все три
сферы представлений, сохраняющиеся у взрослого человека. Богатство интеллекта
определяется наличием развитых представлений — действенных, образных и
символических.
Большое значение для развития
интеллекта Дж. Брунер придавал культуре общества, в котором растет ребенок,
общественному опыту, усваиваемому ребенком в процессе обучения. Ход умственного
развития представляет собой не просто «часовой механизм» последовательности
спонтанно разворачивающихся событий, он определяется также и различными
влияниями среды, особенно школьной.
Сходные взгляды на детский
интеллект высказывает С.Л. Рубинштейн [31, c.268]. По Рубинштейну,
интеллектуальная деятельность у ребенка формируется сначала в плане действия.
Она опирается на восприятие и выражается в более или менее осмысленных
целенаправленных предметных действиях. Можно сказать, что у ребенка на этой
ступени лишь «наглядно-действенное» мышление, или «сенсомоторный интеллект».
Новый этап в истории мышления связан с овладением ребенком речью. Ее обобщающая
функция опирается сначала на примитивную чувственную абстракцию, формирующуюся
в действии и оперирующую сначала в детском восприятии. Восприятие ребенка
становится все более осознанным, и в нем закладываются основы мышления. В
теснейшей взаимосвязи и взаимопроникновении с чертами, общими у него с
мышлением взрослого человека, это мышление включает и специфические черты,
которые не только количественно, но и качественно отличают его от зрелого
мышления. Специфические черты этого раннего детского мышления обусловлены тем,
что это мышление подчинено «логике» восприятия, в которое оно включено.
В
нашей работе мы рассмотрели различные взгляды на интеллект: Ч. Спирмена, Ж.
Пиаже, Л.С. Выготского, Дж. Брунера, Б.Г. Ананьева. Основываясь на их работах,
можно вывести наиболее общее определение интеллекта.
Интеллект — это
относительно самостоятельная, динамическая структура познавательных свойств
личности, возникающая на основе наследственно закрепленных
анатомо-физиологических особенностей мозга и нервной системы, во взаимосвязи с
ними формирующаяся и проявляющаяся в деятельности, обусловленной культурно-историческими
условиями, и преимущественно обеспечивающая адекватное взаимодействие с
окружающей действительностью, ее направленное преобразование [28] .
А как же развивать интеллект?
Какие пути его развития существуют?
Имеются две точки зрения на
природу интеллектуального развития. Согласно одной, интеллект, умственные
способности даны от рождения в особых психологических структурах,
обеспечивающих восприятие и переработку информации. С ростом человека
способности генетически вступают в силу, проявляются (генетическая психология
Ж.Пиаже).
Согласно другой, умственные силы на генетической основе
развиваются прижизненно под влиянием внешней среды. Для их развития требуется
специальная деятельность — обучение (Л.С.Выготский). В соответствии с этим в
отечественной педагогике разрабатывалась система умственного воспитания, задачи
которой: формирование знаний как условия умственного роста, овладение
мыслительными операциями, интеллектуальными умениями, формирование научного
мировоззрения. Основные мыслительные операции — это анализ, синтез, сравнение,
классификация, обобщение. К интеллектуальным умениям относят общие учебные
умения — читать, писать, считать, излагать свои мысли — и специальные умения:
читать карты, чертежи и т.п. К общим интеллектуальным умениям относят также
навыки самостоятельной работы, культуру умственного труда.
Развитие интеллекта
взаимосвязано с мотивационной сферой личности: потребностями, мотивами,
интересами. Средства их формирования таковы: содержание учебного и внеурочного
материала, методы его подачи и организации мыслительной деятельности, создание
положительных эмоций в деятельности детей.
В основе интеллекта лежит
развитое мышление. Процесс развития мышления методически состоит в формировании
и развитии обобщенных приемов умственных действий (сравнение, обобщение,
анализ, синтез, сериация, классификация, абстрагирование, аналогия и др.), что
является общим условием функционирования самого мышления как процесса в любой —
области познания, в том числе и в математике. Безусловным является то, что
сформированность умственных действий является абсолютной необходимостью для
развития математического мышления, не случайно эти умственные действия
именуются также приемами логических умственных действий. Их формирование
стимулирует развитие математических способностей ребенка. Одним из самых
значительных исследований в этой области явилась работа швейцарского психолога
Ж. Пиаже «Генезис числа у ребенка», в которой автор достаточно убедительно
доказывает, что формирование понятия числа (а также и арифметических операций)
у ребенка коррелятивно развитию самой логики: формированию логических структур,
в частности формированию иерархии логических классов, т.е. классификации, и
формированию асимметричных отношений, т.е. качественных сериаций. Классификация,
сериация являются приемами умственных действий, формирование которых невозможно
без предварительного развития у ребенка операций сравнения, обобщения, анализа
и синтеза, абстрагирования, аналогии и систематизации [28].
Математическое содержание
оптимально для развития всех познавательных способностей (как сенсорных, так и
интеллектуальных), приводит к активному развитию интеллектуальных способностей
ребенка.
«Математика (от греч.
mathema — знание, учение, наука), наука о количественных отношениях и
пространственных формах окружающего нас мира. Понимание самостоятельного
положения математики как особой науки возникло в Древней Греции в VI-V вв. до
нашей эры. Математика объединяет комплекс дисциплин: арифметика (теория чисел),
алгебра, геометрия, математический анализ (дифференциальное исчисление и
интегральное исчисление), теория множеств, теория вероятностей и многое другое.
Математика характеризуется: а) высокой степенью абстрактности ее понятий (точки
— без размеров, линии — без толщины, множества любых предметов и т. п.); б)
высокой степенью их общности (например, в алгебре буква обозначает любое число,
в математической логике рассматриваются произвольные высказывания и т. п.).
Абстрактность и общность понятий математики позволяют один и тот же
математический аппарат применять в различных науках» (Большая российская
энциклопедия).
В качестве
основополагающего принципа концепции школьного математического образования на
первый план выдвигается принцип приоритета развивающей функции в обучении математике.
Иными словами, обучение математике ориентировано именно на образование с
помощью математики.
В соответствии с
этим принципом главной задачей обучения математике становится не изучение основ
математической науки как таковой, а общеинтеллектуальное развитие —
формирование у учащихся в процессе изучения математики качеств мышления,
необходимых для полноценного функционирования человека в современном обществе,
для динамичной адаптации человека к этому обществу.
Пути решения задач
умственного развития — это обучение и внеклассная работа с учащимися. Проблему
умственного развития в процессе обучения разрабатывали Л.С.Выготский,
С.Л.Рубинштейн, А.Н.Леонтьев, Н.А.Менчинская, П.Я.Гальперин и др. Опорой
служили выводы Л.Выготского о том, что обучение должно ориентироваться не на
достигнутый уровень развития, а на «зону ближайшего развития»:
предъявлять ученикам задания, которые они могут выполнить при обучающей помощи
взрослых. Согласно этому подходу, умственное развитие обеспечивается, кроме содержания
обучения и воспитания, подбором заданий исследовательского характера, на
установление причинно-следственных связей, на сравнение и др. [28].
Во внеклассной работе имеются такие формы умственного
развития: научно-популярные лекции, семинары, конференции учащихся, встречи со
специалистами, выставки, организация предметных недель, игры, конкурсы,
олимпиады.
Итак, математика — это особый
язык и даже особый мир, в который мы, тем не менее «наведываемся» по сотне раз
на дню — когда ходим в магазин, готовим обед, звоним по телефону, моем полы,
купаем ребенка и т. д. Более того, стоит нам вытянуть вперед руки и взглянуть
на пальцы, мы уже оказываемся в мире математики.
Таким образом, еще до того,
как ребенок выучит первую цифру, он уже знает довольно много о базовых
математических понятиях, таких как величина, количество, прибавление и
убавление, сравнение, множество и т. д.
Упражнения, направленные на
развитие интеллекта одновременно работают на формирование всех мыслительных
приемов: сравнивать, обобщать, анализировать, синтезировать, классифицировать.
Математическое содержание
оптимально для развития интеллектуальных способностей, что приводит к активному
развитию математических способностей ребенка[28].
Главным условием эффективного
интеллектуального развития в процессе обучения математике является включение
учащихся в осознанную и целенаправленную поисковую познавательную учебную
деятельность, в качестве учебной цели выступает не только предметное содержание, но и такие
компоненты интеллектуального развития как:
— формирование основных мыслительных
операций и соответствующих им приемов мышления, общих методов рассуждений;
— развитие способности к
самостоятельной познавательной, интеллектуальной аналитико – синтетической
деятельности, усвоение отдельных элементов и процедур, целостной структуры
интеллектуальной деятельности, формирование индивидуального познавательного
опыта;
— формирование качеств
творческого мышления
Обучение
математике является одним из важнейших средств интеллектуального развития ребенка.
Моделью интеллектуальной мыслительной деятельности является процесс решения
задачи или разрешение проблемной ситуации. Математика — учебный предмет, в
котором задачи используются как цель, и как средство, и как предмет изучения.
Деятельность по решению математических задач в процессе обучения математике
является сложной интегративной
деятельностью: познавательная учебная, математическая, интеллектуальная
эвристическая, творческая.
Развитие
интеллекта зависит от тех же факторов, что и развитие других функций организма,
т.е. с одной стороны от врожденных факторов, а с другой — от окружающей среды.
Но, с каким бы потенциалом ни родился ребенок, очевидно, что необходимые ему
для выживания формы интеллектуального поведения смогут развиваться и совершенствоваться
лишь при контакте с той средой, с которой он будет взаимодействовать всю жизнь.
Эмоциональное общение новорожденного ребенка с матерью, взрослыми людьми имеет
решающее значение для интеллектуального развития ребенка. Существует тесная
связь между интеллектуальным развитием ребенка и его возможностями общаться со
взрослыми в течение достаточно длительного времени (чем меньше общения со
взрослыми, тем медленнее происходит интеллектуальное развитие). Влияет и
социальное положение семьи: обеспеченные семьи имеют более широкие возможности
для создания благоприятных условий развития ребенка, развития его способностей,
его обучения и, в конечном счете, для повышения интеллектуального развития
ребенка. Влияют и методы обучения, применяемые для развития способностей
ребенка. К сожалению, традиционные методы обучения более ориентированы на
передачу знаний ребенку и сравнительно мало внимания уделяют развитию
способностей, интеллекта, творческих возможностей человека.
Проблема
соотношения обучения и умственного развития – одна из старейших
психолого-педагогических проблем. Нет, пожалуй, ни одного сколь-нибудь
значительного теоретика дидактики или детского психолога, который не пытался бы
ответить на этот вопрос, в каком соотношении находятся эти два процесса. Этот
вопрос осложнен тем, что категории обучения и развития разные. Эффективность
обучения измеряется количеством и качеством приобретенных знаний, а
эффективность развития измеряется уровнем, которого достигают способности
учащихся, то есть тем, насколько развиты у учащихся основные формы их
психологической деятельности, позволяющие быстро, глубоко и правильно
ориентироваться в явлениях окружающей действительности. Однако до настоящего
времени результаты психолого-педагогических исследований в этой области не
находят должного отражения в практике работы школы и в частности, при обучении математике,
так как значительная часть учителей считает математику такой наукой, которая
способствует сама по себе умственному развитию учащихся. Действительно,
изучение математических понятий, установление их характеристических свойств
посредством логических умозаключений, решение большого числа задач развивают
мышление учащихся и без целенаправленной деятельности учителя в этом
направлении. Однако здесь встает вопрос о результативности такого развития.
Психологи
отмечают непрерывный процесс мыслительной деятельности школьника: ее
достигнутый уровень расширяет возможности усвоения знаний, что приводит к
необходимости их изменения, усложнения. Это, в свою очередь, служит основой для
дальнейшего развития мышления. Известный советский психолог С.Л.Рубинштейн в
своей работе «О мышлении и путях его исследования» отмечал, что такая
зависимость не односторонняя: освоение знаний и умственное развитие –
диалектический процесс, в котором причина и следствие непрерывно меняются
местами [30]. В связи с этим возникает проблема выявления дидактических
закономерностей, которые позволяют осуществлять обучение математике с позиции
диалектического единства образовательной и развивающей функций. Для этого важно
в содержание понятия «умственное развитие» вкладывать не интуитивное
представление о нем, а четко знать структурные компоненты, понимать диалектику
взаимосвязи обучения и развития и, исходя из этого, намечать пути и средства
реализации образовательной и развивающей целей в обучении [12, с.6].
Т.А.
Иванова в своей работе «Варьирование математических задач как средство развития
интеллектуальных способностей учащихся» уделила этому особое внимание. Далее
рассмотрим концепцию, которую предлагает Т.А.Иванова. Эта концепция основана на
работах В.В.Давыдова, З.И.Калмыковой, Д.Б.Эльконина, И.Я.Лернера.
Все
психологи, занимающиеся проблемой умственного развития школьников, приходят к
выводу, что ключом к ее решению служит содержание обучения[8, 15, 18, 40].
«Если мы хотим, чтобы обучение в начальных классах было развивающим, то мы
должны позаботиться, прежде всего, о научности содержания, то есть о том, чтобы
дети усваивали систему научных знаний и способы их получения», — пишет Д.Б.
Эльконин [40, с. 61]. Но это утверждение приобретает еще большее значение в
обучении математике подростков и старших школьников.
Что
входит в систему научных математических знаний? Прежде всего, это знания о
терминах и понятиях, фактах, теоремах и их доказательствах. В основном на
усвоение только этих знаний и направлены усилия значительной части учителей
математики.
Вместе
с тем ученик не только должен знать определение понятий, формулировки теорем,
но и уметь оперировать математическими фактами, переносить эти знания в новые
ситуации. Учебная деятельность школьника – это система действий (умственных и
практических), осуществление которых обеспечивает усвоение знаний, овладение
умениями и навыками. В свою очередь, действия, в зависимости от их функций и
усвоений знаний, делятся на специфические и общелогические. Специфические
учебные действия обеспечивают усвоение знаний в их конкретном предметном
содержании. Общелогические действия обеспечивают формирование общего подхода к
анализу учебного материала независимо от его содержания. К ним относятся анализ
и синтез, сравнение и аналогия, интуиция, обобщение и систематизация,
конкретизация и т.д.
Т.А.
Иванова, анализируя опыт работы учителей и личный опыт работы со студентами,
пришла к выводу, что даже математическим приемам и методам доказательства
теорем и решения задач мы не всегда обучаем школьников целенаправленно. Очень
часто приходится наблюдать, когда школьники не могут решить ту или иную задачу.
Учитель сам рассказывает решение, не акцентируя внимание учащихся ни на том,
как он пришел к этому решению (как рассуждал), ни на том, какой при этом
используется общий математический прием и как он может применяться в решении
других задач, то есть не проводится со стороны учителя целенаправленное
обучение математическим приемам. Учащиеся с высоким уровнем обучаемости
самостоятельно могут сделать соответствующее обобщение и применять этот прием в
новой и даже нестандартной ситуации. Значительная же часть школьников даже при
решении аналогичной задачи не видит способа рассуждений и не может решить
задачу без помощи учителя. Вместе с тем обобщенные приемы и методы решения
математических задач являются важнейшей составной частью математических знаний
[12, с.7].
В
систему научных знаний входят и методологические знания. «Методологические
знания включают знания о методах, процессе и истории познания, о конкретных
методах науки, о различных способах деятельности», — пишет И.Я. Лернер[19, с
11].
Применительно
к математике методологические знания включают в себя эвристические методы
познания, методы доказательств, основные черты математического стиля мышления,
логическую структуру определения понятий, формулировок теорем, аксиоматический
метод и т.д.
Таким
образом, система научных знаний, которые должны усваивать школьники, и которая
является ведущим компонентом в структуре умственного развития, включает в себя
знания в их традиционном понимании, общие способы мышления (мыслительные
операции), методологию научного поиска в математике. Все элементы этой системы
взаимосвязаны и взаимообусловлены. Усвоение способов мышления возможно только
на конкретном содержании, в которое Т.А. Иванова включает знание понятий и их
определений, теорем и их доказательств и знание способов получения этих знаний.
В процессе учебно-познавательной деятельности общие приемы мышления и методы
научного познания в математике сливаются воедино и являются движущей силой
интеллектуального развития обучаемого [14, с 13].
Обучение,
в основу которого положена методология научного поиска в математике, развивает
все основные интеллектуальные умения ученика: логические, эвристические,
речевые, формирует основные компоненты теоретического мышления, позволяет
включать школьников в самостоятельный поиск [14, с. 16].
Итак,
важнейшим компонентом умственного развития школьников является система научных
знаний, в которую органично входят и методологические знания. Однако об
умственном развитии говорит не столько наличие знаний, сколько возможность
оперировать этими знаниями. Перенос знаний в различные, в том числе и
нестандартные ситуации свидетельствует о наличии у человека общих приемов
мыслительной деятельности. В связи с этим З.И. Калмыкова вводит термин «фонд
действенных знаний», который включает в себя «содержательную сторону
(существенные признаки, входящие в содержание подлежащих усвоению понятий,
закономерностей) и операционную (приемы, способы образования понятий и их
применения на практике, оперирование ими)»[16, с. 6].
Но
ученик не пассивно поглощает преподносимые ему знания. Успешное овладение
знаниями и общими приемами мыслительной деятельности в значительной степени
зависит от индивидуальных особенностей ученика, свойств интеллекта. Поэтому в
структуру умственного развития входит, по мнению З.И.Калмыковой, понятие
обучаемости: «Под обучаемостью мы понимаем систему интеллектуальных свойств
личности, формирующихся качеств ума, от которых зависит продуктивность учебной
деятельности (при прочих равных условиях: наличии исходного минимума знаний,
положительной мотивации и т.д.)»[16, с. 7].
Чем
выше обучаемость, тем быстрее и легче приобретает человек новые знания,
свободнее оперирует ими в относительно новых условиях, тем выше темп его
умственного развития. Основными характеристиками интеллектуальных свойств
личности, качеств ума являются глубина (поверхность), гибкость (инертность) ума,
устойчивость (неустойчивость), осознанность (неосознанность) мыслительной
деятельности, самостоятельность (подражательность).
Подводя
итоги выше сказанному, Т.А.Иванова представила в виде схемы структурные
компоненты умственного развития:
Таблица 1.

Все
выделенные аспекты умственного развития, записанные в таблице 1, находятся в
сложных связях и взаимозависимостях. Их развитию способствует как
соответствующим образом подобранное содержание материала (теоретического и задачного),
так и методы обучения (проблемность, индивидуализация и дифференциация)[36].
Итак,
в этом параграфе мы рассмотрели различные подходы к определению понятий
«интеллект», «интеллектуальное развитие», выяснили основные структурные
компоненты умственного развития. Так что же, в общем представляет собой
интеллектуальное развитие? Что мы будем понимать под словосочетанием
«интеллектуальное развитие»?
Само понятие интеллектуального (умственного) развития трактуется
разными исследователями по-разному. Основываясь
на их работах, можно вывести наиболее общее определение интеллектуального
развития:
Интеллектуальное
развитие — это развитие определенных структур
интеллекта, в ходе которого мыслительные операции постепенно приобретают
качественно новые свойства: скоординированность (взаимосвязанность и
согласованность множества операций), обратимость (возможность в любой момент
вернуться к начальной точке своих рассуждений, перейти к рассмотрению объекта с
прямо противоположной точки зрения и т.д.), автоматизированность
(непроизвольность применения), сокращенность (свернутость отдельных звеньев,
«мгновенность» актуализации)[28].
Доказано,
что интеллектуальное развитие – непрерывный процесс, совершающийся в учении,
труде, играх, жизненных ситуациях, и что оно наиболее
интенсивно происходит в ходе активного усвоения и творческого применения
знаний, т.е. в актах, которые содержат особенно ценные операции для развития
интеллекта.
Успех интеллектуального
развития школьника достигается главным образом на уроке, когда учитель остается
один на один со своими воспитанниками. И от его умения «и наполнить сосуд, и
зажечь факел», от его умения организовать систематическую познавательную
деятельность зависит степень интереса учащихся к учебе, уровень знаний,
готовность к постоянному самообразованию, т.е. их интеллектуальное развитие,
что убедительно доказывает современная психология и педагогика [26].
Математическое содержание оптимально для развития всех познавательных
способностей, приводит к активному развитию интеллектуальных способностей
ребенка.
Одним из действенных средств,
способствующих умственному развитию учащихся на уроках математики, являются
задачи. Подробнее о роли задач мы остановимся в §2.
§
1.2 Работа над задачей как средство интеллектуального развития учащихся
Мы выяснили, что существуют различные пути развития интеллекта, но наиболее интенсивно это развитие происходит в ходе активного
усвоения и творческого применения знаний, т.е. на уроках, и главным образом на
уроках математики, так как математическое
содержание оптимально для развития интеллектуальных способностей.
Обучение
математике является одним из важнейших средств интеллектуального развития
ребенка. Моделью интеллектуальной мыслительной деятельности является процесс работы
над задачей. Математика — учебный предмет, в котором задачи используются как
цель, как средство, и как предмет изучения. Деятельность по решению и
составлению математических задач в процессе обучения математике является
сложной интегративной деятельностью: познавательная, учебная, математическая,
интеллектуальная, эвристическая, творческая.
Роль
задач как средства обучения и развития школьников хорошо просматривается в
технологических процессах организации усвоения основных дидактических единиц –
определений, теорем, правил. В самом деле, актуализация знаний в
мотивационно-ориентировачной части процесса предпочтительна в ходе решения
задач. Проблемная ситуация так же чаще всего возникает при выполнении
упражнений и решении задач. Даже в содержательной части иногда используются
задачи для «открытия» теоремы или правила. Рефлексивно-оценочная часть так же
строится на основе системы упражнений [36, с.161]. Роль задач на различных
этапах организации изучения определений и теорем подчеркивается также в работах
Г.И.Саранцева и А.А.Столяра. Например, в книге
«Педагогика математики» А.А. Столяра обучение через задачи представлено схемой
«задачи-теория-задачи», из которой явствует, что задачи рассматриваются автором
как источник возникновения теории, средство ее развития и применения[35]. Из работ
Г.И. Саранцева, посвященных проблеме формирования понятий, методике работы с
теоремой, можно заключить о большой роли задач в изучении теории. Он считает, что
задачи при формировании понятий призваны: способствовать мотивации введения
понятий; выявлять существенные свойства понятий; способствовать их усвоению;
способствовать усвоению терминологии, символики, пониманию смысла каждого слова
в определении; запоминанию определения; овладению объемом понятия; раскрывать
взаимосвязи понятия с другими понятиями; обучать применению понятия. Выполнение
упражнений должно обеспечить овладение умениями: распознавать объекты,
принадлежащие понятию, выводить следствия из принадлежности объекта понятию,
переходить от определения понятия к его признакам, переосмысливать объекты с
точки зрения других понятий. Введение понятия осуществляется в процессе решения
задач практического, физического и т.п. содержания. Ознакомление со многими
геометрическими понятиями возможно в процессе решения задач на построение фигур,
удовлетворяющих указанным свойствам, упражнений с моделями фигур. Усвоение
определения понятия достигается при решении задач на распознавание, на
выведение следствий, задач, требующих анализа условий, дополнения их так, чтобы
из условий вытекала принадлежность объекта понятию. Систематизация понятий
осуществляется в процессе решения задач на установление связей между понятиями,
построение схем, устанавливающих связи, на составление «родословных» понятий и
т.д.[ 33, с.129].
Задачи,
используемые для реализации различных этапов организации изучения теоремы
должны: способствовать мотивации введения теоремы; выявлять закономерности,
отраженные в теореме; способствовать усвоению содержания теоремы;
способствовать пониманию значения каждого слова в формулировке теоремы,
запоминанию ее формулировки; обеспечивать восприятие идеи доказательства,
раскрывать приемы доказательства; обучать применению теоремы; раскрывать
взаимосвязи изучаемой теоремы с другими теоремами. Первые два требования
реализуют задачи на непосредственное измерение величин, оперирование моделями
фигур, а также цепочки взаимосвязанных задач и упражнения на материале
практического содержания. Усвоению содержания теорем способствует решение задач
на выделение на чертежах и моделях фигур, удовлетворяющих условию теоремы, а
также выполнения чертежа, моделирующего условие. Восприятие доказательства
теоремы обеспечивают задачи на ознакомление со способом доказательства теоремы,
моделирующие приемы доказательства. Задачи эффективны в воспитании потребности
в обосновании утверждений, в воспитании навыков дедуктивного мышления, в
привитии взгляда на то, что справедливость утверждений выясняется рассуждением.
Усвоению логики доказательства способствует применение упражнений со
специальными карточками. На этапе применения теоремы важны задачи на
систематизацию знаний и их обобщение, на применение знаний и умений в комплексе,
на углубление и расширение знаний и умений, на составление «родословной»
доказательства теоремы, на группирование теорем по приемам их доказательства. С
помощью задач формируются умения, составляющие основу применения знаний в
конкретных ситуациях (переформулировка требования задачи, составление
промежуточных задач и т.д.) [33, с.130].
Из
сказанного легко представить роль и место задач в изучении теории. К уже
отмеченному добавим, что задачи – основное средство развития пространственного
мышления, творческой деятельности школьников, в процессе решения задач
формируется не только логическая, эвристическая, алгоритмическая составляющие
мышления, но и многие нравственные качества учащихся.
Решение математических задач требует применения многочисленных
мыслительных умений: анализировать заданную ситуацию, сопоставлять данные и
искомые, решаемую задачу с решенными ранее, выявляя скрытые свойства заданной
ситуации; конструировать простейшие математические модели, осуществляя
мысленный эксперимент; синтезировать, отбирая полезную для решения задачи
информацию, систематизируя ее; кратко и четко, в виде текста, символически,
графически и т. д. оформлять свои мысли; объективно оценивать полученные при
решении задачи результаты, обобщать или специализировать результаты решения
задачи, исследовать особые проявления заданной ситуации. Сказанное говорит о
необходимости учитывать при обучении решению математических задач современные
достижения психологической науки [29].
Исследованиями советских психологов установлено, что уже
восприятие задачи различно у различных учащихся данного класса. Способный к
математике ученик воспринимает и единичные элементы задачи, и комплексы ее
взаимосвязанных элементов, и роль каждого элемента в комплексе. Средний ученик
воспринимает лишь отдельные элементы задачи. Поэтому при обучении решению задач
необходимо специально анализировать с учащимися связь и отношения элементов
задачи. Так облегчится выбор приемов переработки условия задачи. При решении
задач часто приходится обращаться к памяти. Индивидуальная память способного к
математике ученика сохраняет не всю информацию, а преимущественно «обобщенные и
свернутые структуры». Сохранение такой информации не загружает мозг избыточной
информацией, а запоминаемую позволяет дольше хранить и легче использовать.
Обучение обобщениям при решении задач развивает, таким образом, не только
мышление, но и память, формирует «обобщенные ассоциации». При непосредственном
решении математических задач и обучении их решению необходимо все это учитывать[29].
Одно из основных назначений задач и упражнений и заключается в
том, чтобы активизировать мыслительную деятельность учеников на уроке.
Математические задачи должны, прежде всего, будить мысль учеников,
заставлять ее работать, развиваться, совершенствоваться. Говоря об активизации
мышления учеников, нельзя забывать, что при решении математических задач
учащиеся не только выполняют построения, преобразования и запоминают
формулировки, но и обучаются четкому мышлению, умению рассуждать, сопоставлять
и противопоставлять факты, находить в них общее и различное, делать правильные
умозаключения.
Правильно организованное обучение решению задач приучает к полноценной
аргументации со ссылкой в соответствующих случаях на аксиомы, введенные
определения и ранее доказанные теоремы.
Взрослому человеку, как в повседневной жизни, так и в
профессиональном труде для принятия правильных решений исключительно важно
уметь рассматривать все возможные случаи создавшейся ситуации. Это надо
разъяснять и школьникам. Важно такое умение и при изучении математики, в
противном случае неизбежны ошибки. Умение же предусмотреть все возможные
варианты некоторой ситуации свидетельствует о развитости мышления
рассматривающего эту ситуацию[29].
Умение рассуждать включает в себя и умение оценивать истинность
или ложность высказываний, правильно составлять сложные высказывания и
суждения, т. е. логически правильно употреблять союзы «и», «или», отрицание
«не». Обучение верному применению этих связок помогает воспитанию у учащихся
математически грамотной речи, а мышление, как известно, связано с языком, речью
человека.
Полезно научить школьников верно формулировать отрицания тех или
иных предложений. Такое умение особенно важно при решении задач сведением к
противоречию.
Существенно для развития математического мышления учащихся
формирование умений правильно выделять посылки и заключения. Такие умения
формируются обычно при решении задач на доказательство. На первых же порах
необходимы упражнения в расчленении некоторых предложений на посылки и
заключения.
Эффективность учебной деятельности по развитию мышления во многом
зависит от степени творческой активности учащихся при решении математических задач.
Следовательно, необходимы математические задачи и упражнения, которые бы
активизировали мыслительную деятельность школьников.
Решение математических задач приучает выделять посылки и
заключения, данные и искомые, находить общее, и особенно в данных, сопоставлять
и противопоставлять факты. При решении математических задач воспитывается
правильное мышление, и прежде всего учащиеся приучаются к полноценной
аргументации. Решение задачи должно быть полностью аргументированным, т. е. не
допускаются незаконные обобщения, необоснованные аналогии, предъявляется
требование полноты дизъюнкции (рассмотрение всех случаев данной в задаче
ситуации), соблюдаются полнота и выдержанность классификации. При решении
математических задач у учащихся формируется особый стиль мышления: соблюдение
формально-логической схемы рассуждений, лаконичное выражение мыслей, четкая
расчлененность хода мышления, точность символики [29].
Л.И.Кузнецова
отмечает, что важнейшим видом учебной деятельности, в процессе которой
школьниками усваивается математическая теория, развиваются их творческие
способности и самостоятельность мышления, является выполнение математических
упражнений и работа над задачей. Рассмотрим, как задача влияет на интеллектуальное
развитие учащихся. С понятием «задача» ассоциируется два процесса, два вида
деятельности: процесс решения и составление задачи. Эти два процесса взаимно
обратные. Они характеризуются противоположными ходами мысли. Составление задачи
есть синтез, объединение разрозненных частей в единое целое. Решение задачи,
каким бы методом оно ни осуществлялось, есть анализ, расчленение целого на
части [36, с. 166].
Известный
американский математик и педагог Д. Пойа выделяет в решении задачи четыре
этапа:
1)
понимание постановки задачи;
2)
составление плана решения;
3)
осуществление плана;
4)
взгляд назад [22] .
Л.М.Фридман
и Е.Н.Турецкий разбивают процесс решения на восемь этапов, которые содержат
перечисленные выше или детализируют их:
1)
анализ задачи;
2)
схематическая запись;
3)
поиск способа решения;
4)
осуществление решения;
5)
проверка решения;
6)
исследование задачи;
7)
формулирование ответа;

анализ решения задачи [39, с. 30].
Сущность
и назначение каждого этапа из этапов, познавательные средства, с помощью
которых они реализуются, обсуждается в работах Д. Пойа, Л.М.Фридмана и
Е.Н.Турецкого.
Л.И.Кузнецова
выделила лишь некоторые познавательные средства, которые задействованы на
этапах поиска плана решения и осуществления плана:
На
основе анализа условия и требования задач, может быть и переформулирования,
задачу необходимо отнести к тому или иному виду и осознать сущность решения
задачи данного вида. Если оказывается, что задача решается по известному
алгоритму, то план найден. Как видим здесь используется анализ, моделирование,
сравнение, аналогия.
Если
знакомого образца нет, то поиск решения идет методом анализа или методом
синтеза. При этом выполняются действия подведения под понятие, выведения
следствий, переформулирование задачи, а, следовательно, действие моделирования.
При
осуществлении плана необходимо понимание решения задач как процесса, понимание
роли законов логики в решении задач, знание и умение применять эти законы,
знание и умение применять специальные содержательные методы решения задач.
Как
подчеркивает Л.И.Кузнецова, анализ деятельностей по составлению и решению задач
показывает, что приемы и методы познания, которые осваиваются в процессе
изучения определений, правил, теорем, постигаются и в процессе работы над
задачей. Однако в освоении познавательных средств в процессе решения задач есть
своя специфика, состоящая в следующем. Даже при реализации предлагаемого
технологического процесса усвоения дидактических единиц (определения, правила,
теоремы) возникают в результате совместной деятельности учителя и учащихся при
ведущей роли учителя. При решении или составлении новой задачи в классе тоже
велика роль учителя и зачастую она является главной. Вместе с тем, при
выполнении домашней, классной, самостоятельной или контрольной, экзаменационной
и других работ ученик остается один на один с заданием и должен выполнить его
сам, без посторонней помощи. Поэтому на этапах поиска решения и анализа
решения, при составлении задач методы познания, приемы и способы мышления
осваиваются не только под воздействием учителя, но и в процессе их
самостоятельного творческого применения. Именно потому, какие задачи и как
ученик решает самостоятельно, мы судим о его умственных способностях, о
направленности его мышления, об уровне усвоения знаний, о культуре мышления [36,
с.168].
Таким
образом, анализ процессов составления и решения задач показывает, что и в том,
и в другом задействованы самые разные мыслительные операции, приемы мышления,
методы рассуждений, то есть в них участвуют и эвристические, и логические, и
речевые умения субъекта. Это с одной стороны подчеркивает роль задач в обучении
и развитии учащихся, а с другой, показывает, чему следует обучать учащихся
конкретно, если иметь в виду обучение решению задач.
Из
выше сказанного можно сделать вывод, что формирование умений решать и
составлять задачи влечет за собой развитие мышления (и логического, и
интуитивного) и целостное развитие личности, всех психических процессов (воли,
эмоций, памяти, воображения, представлений и т.д.).
Известно,
что важным направлением реализации личностно- ориентированного образования является
создание условий для развития и саморазвития обучаемых в процессе активной
учебно-познавательной деятельности. В практике обучения математике важным
средством, способствующим развитию учащихся, выступают упражнения на
самостоятельное составление школьниками задач. Еще в 1915 г. Н. Фадеев писал,
что «…придумывание задач самими учащимися развивает у них сообразительность,
воображение, способствует скорейшему уяснению ими хода решения задачи,
развивает речь и приучает детей к краткой и логической формулировке своей
мысли, вносит разнообразие и живость в урок, имеет большое психологическое
значение для учителя в смысле распознавания индивидуальности учеников» [37, с.
82]. Современная теория и методика обучения математике также считает, что
упражнения на самостоятельное составление школьниками задач есть эффективное
средство изучения предмета, которое не только вооружает учащихся необходимыми
знаниями, но и способствует формированию у них умения получать новые знания,
развивает личностные качества учащихся. Конструирование задач — это важнейшая
составляющая общего умения решать математические задачи; овладение учащимися
приемами составления новых математических задач способствует формированию у них
умения искать и находить наиболее рациональные способы решения задач, позволяет
им легче ориентироваться не только в школьном обучении, но и других сферах
теоретической и практической деятельности человека. Умение выдвигать проблемы
имеет не меньшее значение, чем умение их решать. Поэтому школа должна учить не только
отвечать на вопросы, но и задавать их, не только решать проблемы, но и ставить
их, хотя бы в виде составления задач.
Составляя
задачи, ученик находится в позиции исследователя, первооткрывателя, проводит
анализ условий, изменяет их, устанавливает различные связи между данными,
формулирует вопросы, на которые сам отыскивает ответ. Используя упражнения на
составление задач, можно формировать и развивать такие компоненты
математических способностей, как логичность, систематичность,
последовательность словесных рассуждений и выводов и др.
При
составлении задач ученик может опробовать различные стратегии и способы
действия. Для учителя важно изучить и разобрать программу действий ученика,
побудить описать ученика этот творческий акт учителю и другим ученикам,
ответить на вопросы: а как составил, увидел, вообразил? Задание,
сформулированное таким образом, превращается в задание развития личности, ее
способностей.
Заметим,
что наибольший эффект использования этих заданий достигается при гибком и
тактичном воздействии на эмоциональный мир учащегося, это делает возможным
пробуждение личной заинтересованности в получении новых знаний.
Таким
образом, мы можем сделать вывод, что роль задач в интеллектуальном развитии
учащихся велика. Ученики должны не только уметь решать задачи, но и составлять
их. В следующем параграфе мы рассмотрим некоторые приемы составления задач и
циклов взаимосвязанных задач.
§
1.3 Приемы составления задач. Составление циклов взаимосвязанных задач
Обучение
школьников решению математических задач обычно осуществляется при решении
готовых (сформулированных учителем, в учебнике, учебном пособии или в другом
литературном источнике) задач. Между тем существенную роль при этом играет их
составление учащимися. Дело в том, что составление задач часто требует
проведения рассуждений, которые при решении заданных задач не выполняются.
Стало быть, составление задач служит развитию творческого мышления учащихся. В
этом параграфе мы рассмотрим некоторые приемы составления задач.
Изучение
учебно-методической литературы позволило выделить следующие приемы составления
задач:
1.
Постановка вопроса к условию задачи;
2.
Составление задачи по готовому рисунку;
3.
Составление условия задачи по заданному
вопросу;
4.
Составление задачи, являющейся обобщением
данной;
5.
Конкретизация обобщенного способа решения
задач;
6.
Составление задачи, обратной данной;
7.
Переформулировка требования задачи;
8.
Замена части данных исходной задачи
другими данными без замены заключения задачи;
9.
Составление циклов взаимосвязанных задач.
Рассмотрим
подробнее каждый из этих приемов.
1. Постановка
вопроса к условию задачи
Данный
прием широко рассматривает Г.И.Саранцев, П.М.Эрдниев[34, 42]. Чтобы поставить
вопрос к задаче, ученик должен понять задачу. Неотъемлемой частью ознакомления
с содержанием является его анализ, который включает в себя следующие умения:
устанавливать количество элементов (ситуаций) в задаче; выделять предложения,
выражающие связи между величинами и фиксировать эти связи. Приведем примеры
задач, в которых требуется самостоятельно сформулировать вопрос (требование)
к условию задачи:
Пример задачи:
Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Сформулируйте
вопрос к задаче.
Варианты вопросов:
Найдите а) высоту цилиндра;
б) радиус цилиндра;
в) площадь основания цилиндра;
г) площадь полной поверхности цилиндра.
2.
Составление задачи по готовому
рисунку
Г.И.Саранцев в книге «Общая методика
преподавания математики» [33, с. 85] рассматривает этот метод как один из
самых важных методов составления задач. Данный прием составления задач
позволяет формировать комплекс многих действий, составляющих умение доказывать.
Составление задач предполагает анализ ситуации, заданной рисунком (выделять
объекты, отношения между ними, приводить словесную формулировку заданной
ситуации, обозначать ряд требований), выделение следствий из данных рисунка.
Учащиеся, у которых не сформированы компоненты «видения» чертежа, испытывают
трудности с его пониманием. Поэтому таким ученикам необходимы дополнительные
разъяснения. Кроме того, при выполнении таких заданий у учащихся развиваются во
взаимосвязи геометрическая и аналитическая составляющие мышления.
Пример: Составьте задачу по готовому рисунку:
Вариант
составленной задачи по данному рисунку может быть следующим:
Дан
усеченный конус с радиусами оснований 2 и 6 см. Высота конуса равна 5 см.
Найдите площадь боковой поверхности усеченного конуса.
Кроме
того, Саранцев отмечает, что решение школьных задач в учебнике геометрии
основано на трансформации словесной формулировки задач в чертеж, а обратная
трансформация не используется, что в дальнейшем ведет к значительным трудностям
у учащихся при решении геометрических задач.
3. Составление
условия задачи по заданному вопросу
Данный прием был
рассмотрен у П.М.Эрдниева в работах «Методика упражнений по математике» и
«Укрупнение дидактических единиц в обучении математики» [42, 44].
Этот прием напрямую
связан с таким свойством мышления как синтез, так как учащиеся идут от
требования задач, пытаясь тем самым составить условие задачи.
По любому разделу
математики можно сконструировать такое синтетическое упражнение, при выполнении
которого ученики выступали бы в роли исследователей.
Пример: Из
некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол
между которыми равен φ. Найдите наклонную и ее проекцию на данную плоскость.
Ученики, строя рисунок
начинают рассуждать:
Наклонная и ее образующая являются
элементами треугольника АМН, в котором известен угол. Для того чтобы
найти наклонную и ее проекцию нам необходимо знать чему равна высота. В условии
не хватает данных: высота равна какому-то числу m.
Таким образом, задача будет сформулирована так:
Из некоторой точки
проведены к данной плоскости перпендикуляр и наклонная, угол между которыми
равен φ, а высота равна m. Найдите
наклонную и ее проекцию на данную плоскость.
4.
Составление задачи, являющейся
обобщением данной
Этим приемом составления
задач глубоко занимался П.М.Эрдниев [ 42 , с.45]. Под обобщением он понимает
распространение какого-либо суждения от частного к общему (например, от
видового понятия «остроугольный треугольник» к родовому понятию «треугольник
вообще»).
Процесс обобщения
основывается на применении аналогии, но не сводится полностью к ней. Применение
обобщения связано с преобразованием мыслей, с умственным экспериментированием;
оно есть одно из самых важных средств самообучения, то есть самостоятельного
расширения и углубления имеющихся знаний.
Для достижения глубокого
усвоения нового понятия или способа решения нельзя обходиться задачами одного
уровня трудности, а нужно предложить обобщенную задачу, а еще лучше дать
учащимся возможность самим составить задачу, которая является обобщением для
только что решенной задачи.
Пример: В
конус вписана сфера радиусом равным 3. Найдите площадь полной поверхности
конуса, если угол между образующей и основанием конуса равен 45о.
Обобщение данной задачи:
В конус вписана сфера радиусом равным r.
Найдите площадь полной поверхности конуса, если угол между образующей и
основанием конуса равен α.
Чаще всего на уроках
решаются такие задачи, которые рассчитаны на средних учеников, а чтобы
расширить познавательные способности более сильных учеников необходимы
дополнительные задания по самостоятельному обобщению и решению составленных так
задач.
Если, например, готовую
задачу решают все ученики в основном одинаковой последовательностью
рассуждений, то с обобщением уже справляется не всякий. Результат обобщения
зависит не только от суммы знаний, сколько от умения комбинировать, связывать
эти знания по-новому, заглядывать за обычные пределы, то есть зависит от
индивидуальных способностей каждого человека.
Результаты обобщения
учащихся бывают различной сложности; даже при выполнении простейших
синтетических заданий проявляется резкая разница в силе воображения учащихся.
Применению аналогии и
обобщения надо учить особо, на специальных упражнениях, так же как и иным
логическим операциям: индукции и дедукции, анализу и синтезу.
Нельзя думать, будто
ознакомление с обобщением и аналогией надо вести на одних лишь положительных
примерах. Напротив, в обучении важно показывать, что истинность и ложность
суждений идут в мышлении рядом. Полезно сравнивать верные соотношения с
неверными, имеющие по форме внешнюю, неглубокую аналогию.
Упражнения по обобщению
решенных задач могут найти место при изучении самых разнообразных тем, в
особенности на факультативных или кружковых занятиях.
5.
Конкретизация обобщенного способа
решения задач
Конкретизация есть не что
иное как дедукция – движение мысли от общего к частному. Если мы заменим в
некоторой нами решенной задачи буквы на числа, то мы получим конкретизацию этой
задачи.
Пример:
Высота цилиндра равна h
, а площадь осевого сечения равна S.
Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние
между осью цилиндра и плоскостью сечения равна d.
Конкретизация этой задачи
может быть следующей:
Высота цилиндра равна 1 ,
а площадь осевого сечения равна 5. Найдите площадь сечения цилиндра
плоскостью, параллельной его оси, если расстояние между осью цилиндра и
плоскостью сечения равна 2.
Частным случаем
конкретизации является специализация задачи. Специализация задачи обратная ее
обобщению. Удобнее специализацию задачи осуществлять за счет специализации
данных или искомого.
Пример:
Доказать, что середины сторон произвольного четырехугольника являются вершинами
параллелограмма.
Для этой задачи специализация
может быть сформулирована так:
1)
Доказать, что середины сторон
параллелограмма являются вершинами другого параллелограмма.
2)
Доказать, что середины сторон ромба
являются вершинами прямоугольника.
6. Составление
задачи, обратной данной
Этот метод означает, что работу над
задачей нецелесообразно завершать получением к ней ответа; надо приемом
обобщения составлять и решать в сравнении с исходной (прямой) задачей новую,
обратную задачу, извлекая тем самым дополнительную информацию, заключающуюся в
связях между величинами решенной исходной задачи. Для этого в условии исходной
задачи вводится ее ответ, а некоторые числа из условия переводятся в разряд искомых.
Составление таких задач помогает ученикам лучше понять структуру математических
задач, приучает формулировать и доказывать теоремы, обратные изучаемым на
уроке, то есть существенно углубляет и расширяет математические представления и
знания учащихся, помогает усвоению достаточных и необходимых условий. Кроме
того, методы решения обратных задач нередко отличаются от методов решения
исходных, и хотя бы знакомство с новыми методами решения приносит пользу
обучающимся.
Приведем несколько примеров таких задач:
1)
Взаимно обратные теоремы:
Прямая
теорема:
Если
одна из двух параллельных прямых перпендикулярна к плоскости, то и другая
прямая перпендикулярна к этой плоскости.
Обратная
теорема:
Если
две прямые перпендикулярны к плоскости, то они параллельны.
2)
Задача:
Длина окружности основания прямого цилиндра С=10 м, длина образующей l =
7 м. Чему равна площадь боковой поверхности цилиндра?
Обратная задача:
Площадь боковой поверхности цилиндра равна 70 м2, а длина образующей
l =
7 м. Найдите длину окружности основания цилиндра.
Метод обратных задач был описан в работах
1953 г. (Математика в школе, 1953, №4; Начальная школа, 1953, №10).
Эффективность этого метода позднее была подтверждена также в лабораториях
Л.В.Занкова (1964), П.Я. Фридмана (1983). Позднее этот метод был рассмотрен в
работах П.М.Эрдниева (1986) и в 1991 году у Е.С.Канина [15, с. 11]. Остается
лишь сожалеть, что эта методическая находка, найдя признание в программах и
учебниках начальной школы, не находит своего места в
учебниках старших классов.
При составлении новой задачи путем обращения необходимо учитывать
и то обстоятельство, что обращается далеко не каждая задача (не для всякой
теоремы верна обратная).
Прием составления новых задач, обратных данным, приводит ученика к
постановке новых проблем, получению существенно иных разновидностей задач.
Умение решать прямую и обратную задачи является важным критерием достигнутой
учеником глубины понимания изучаемого раздела математики. Поэтому составление и
решение обратных задач является достаточно простым и удобным приемом развития
творческого мышления учащихся.
7.
Переформулировка требования задачи
Этому
приему составления задач, как говорит Г.И.Саранцев [34, с. 84], нужно учить с
первых уроков геометрии. Сущность его заключается в замене требования задачи
равносильным ему. Очевидно, использование приема предполагает владение
действиями выведения следствий, подведение под понятие, навыками анализа
ситуаций.
Пример задачи:
Решите задачу, заменив предварительно требования новыми так, чтобы из них
следовали первоначальные:
Цилиндр получен вращением квадрата со
стороной а вокруг одной из его сторон. Найдите площадь осевого сечения
цилиндра.
Требования
к этой задачи могут быть еще и следующими:
а)
Найдите площадь боковой поверхности цилиндра;
б)
Найдите площадь полной поверхности цилиндра.
8. Замена
части данных исходной задачи другими данными без замены заключения задачи
Данный
метод составления задач был рассмотрен в статье Е.С. Канина «Развитие темы
задачи» [15, с. 8].
Замена
условий задачи одних данных другими нередко приводит к применению разнообразных
приемов и методов решения, казалось бы, очень близких по содержанию задач.
Таким образом, осуществляется не отработка одного приема решения задачи, а
усвоение широкого спектра методов.
Замену одних
данных другими желательно осуществлять не беспорядочно, а придерживаясь
определенного логического плана. Для иллюстрации можно рассмотреть следующую
задачу:
1.Восстановите
равнобедренный треугольник по основаниям трех его высот.
Обозначим данные
основания высот к боковым сторонам через M
и N,
к основанию – Р, а вершины искомого треугольника – А,В (вершины при основании),
С.

M,
N,
P—
основания высот
АС=ВС
Построить:
∆АВС
Строим
прямую MN
и через точку Р проводим АВ MN.
Строим окружность О ( Р; МР). Тогда АВО
( Р; МР) = , АМ
ВN
= С.
Но параллельность АВ и MN
будет сохраняться и при любой другой заданной точке основания треугольника.
Возникает новая задача:
1а.
Восстановите равнобедренный треугольник по основаниям
высот к боковым сторонам и точке на основании треугольника.
Решается аналогично
предыдущей, лишь добавляется построение серединного перпендикуляра к отрезку MN.
Далее логично заменить
основание какой-либо высоты одной из вершин искомого треугольника:
1б. Восстановите
равнобедренный треугольник по основаниям двух его высот и одной из вершин.
Эта задача при анализе
распадается на серию задач, в которых заданы:
1) M, N, A (M, N, B); 2) M, N, C;
3) M, P, A (N, P, B); 4) N, P, A (M, P, B); 5) M, P, C (N, P, C).
Заменив теперь еще одно
из оснований высот вершиной треугольника, получим:
1в. Восстановите
равнобедренный треугольник по основанию одной из его высот и двум вершинам.
Возможны следующие
варианты данных: 6) A, C,
N
(B,
C,
M);
7) A,
B,
M
(A,
B,
N);

C,
P
(B,
C,
P);
9) A,
C,
M
(B,
C,
N);
10) A,
B,
P.
Задачи 1) – 5); 
различных вариациях могут быть решены с помощью симметрии относительно
серединного перпендикуляра СР, задачи 2) и 7) – построением прямых, содержащих
стороны треугольника и высоты к ним. Задача 9) имеет следующее решение:
Строим
отрезок АС, окружность (С; АС) и МВ АС, где В – точка пересечения
окружности и МВ (таких точек 2).
Задача 10) имеет
бесконечно много решений: условию удовлетворяет всякий треугольник, основание
которого АВ и вершина лежат на серединном перпендикуляре к АВ.
Интересные задачи
получаются, если вместо высот рассмотреть медианы или биссектрисы:
1г. Восстановите
равнобедренный треугольник по серединам его сторон.
1д. Восстановите
равнобедренный треугольник по основаниям его биссектрис.
Все предложенные выше
задачи не обязательно решать на уроке, часть задач можно предложить для решения
на внеклассных или факультативных занятиях. Указанные задачи наиболее полезны
при обобщающих уроках на геометрии.
9.
Составление циклов взаимосвязанных
задач
Каждая задача,
рассматриваемая сама по себе, обычно представляет некоторое изолированное
утверждение или требование и предполагает выполнение определенных действий для
ее решения. Между тем учитель, ставящий задачу перед учащимися, преследует, как
правило, более общие цели, для него конкретная задача является лишь одной из
многих, лишь частным средством для достижения более общих целей – формирование
или закрепление нового понятия, получения новых или активизация старых знаний,
демонстрации определенного методов доказательства теорем, изложенных в курсе, и
т.п.
В связи с этим и
возникает проблема создания циклов взаимосвязанных задач, различных по
формулировке, по сюжету, но имеющих общее дидактическое назначение, служащих
достижению поставленной цели. В теоретическом плане составление таких циклов
само по себе не является чем-то принципиально новым: именно таким циклом задач,
связанных между собой методически и математически, и является всякая система
упражнений, направленная на пропедевтику, формирование или закрепление того ли
иного понятия, утверждения или метода рассуждений.
Поэтому теоретический
аспект проблемы состоит в описании методов конструирования таких циклов, в
обобщении многочисленных отдельных приемов, используемых для их составления.
Каждая конкретная задача имеет определенный набор связанных с ней задач,
определенную окрестность – по содержанию, методам рассуждений, кругу
используемых понятий. Более того, каждая задача входит в некоторый букет
окрестностей, связанных с той или иной ее особенностью, а выбор одной из многих
окрестностей задачи для построения цикла определяется конкретной ситуацией
преподавания. Разнообразие букета окрестностей задачи предопределяет широту ее
использования и является важным критерием ее дидактической ценности.
В это же время описание
даже одной окрестности задачи представляет собой сложную проблему, решение
которой проводится на чисто интуитивном уровне и существенно зависит от опыта
учителя, от уровня его математического образования и методической подготовки.
Невозможно сформулировать
какие-либо достаточно определенные «алгоритмы» построения окрестности
конкретной задачи, и поэтому важной представляется систематизация разнообразных
приемов варьирование задач, достаточно общая в теоретическом плане и в то же
время эффективная в плане практическом.
Несколько приемов
варьирования задач рассмотрены в статье П.М. Эрдниева и др. «О постановке в
университетах спецкурса по содержанию школьных учебников» [43]. Они
сформулированы следующим образом: «рассмотрение взаимно-обратных задач»,
«обобщение вопроса задачи», «рассмотрение стереометрических аналогов»,
«изменение точки зрения на требование задачи».
Г.В. Дорофеев [10, с. 34]
проанализировал эту статью и сделал соответствующие выводы: Первый из этих
приемов хорошо известен и является эффективным средством анализа задачи,
проясняющим ее математическую сущность. Известно также, насколько важным в
дидактическом отношении является рассмотрение возможности доказательства
обратных утверждений для теорем, изучаемых в школьном курсе или содержащихся в
задачном материале. Более того полноценный анализ той или иной теоремы
непременно должен включать исследование не только обратного утверждения, то
есть необходимости условия теоремы для ее заключения, но и выяснение
существенности тех или иных ограничений, указанных в условии теоремы.
Таким образом, первый из
названных приемов с учетом указанных дополнительных вариаций представляет собой
один из самых простых приемов оптимального сочетания теоретической обобщенности
и практической эффективности. В этом плане менее удачен также хорошо известный
прием рассмотрения стереометрических аналогов – он является, по-видимому,
частным проявлением некоторого более общего приема в применении к конкретным
классам задач. Другими словами этот прием в теоретическом плане недостаточно
обобщен, хотя с практической точки зрения он является эффективным средством
варьирования задач.
Прием «обобщения вопроса
задачи» иллюстрируется авторами статьи несколько упрощенно. В теоретическом
плане для варьирования задачи применяется не столько «обобщение вопроса
задачи», сколько анализ ее условия и исследование всего комплекса вопросов,
возникающих в ситуации, описываемой условием. Имея такой набор вопросов,
учитель может использовать отдельные из них в соответствии с конкретной
методической ситуацией, создавая циклы задач специального назначения.
Можно сказать, что
существенной стороной обсуждаемого методического приема варьирования задач
является «отвлечение» от конкретного вопроса и анализ «ситуации в целом».
Рассмотрение обратной задачи также является частным случаем прояснения
«ситуации в целом», и специфика этого приема в том, что обращение задачи обычно
почти однозначно определяется именно конкретным вопросом исходной задачи; следовательно,
этот прием применим многократно при различных конкретизациях вопросов,
возникающих в связи с данной ситуацией.
Четвертый
прием, указанный авторами, — «изменение точки зрения на требование задачи» — не
представляется удачным ни с теоретической, ни с практической точки зрения. Неясен,
прежде всего, смысл самой формулировки – что вообще значит изменить точку
зрения на требование задачи? Авторы указывают, что этот прием «родственен»
постановке обратной задачи.
Одним из
действующих средств, способствующих умственному развитию учащихся является,
варьирование материала. Вместе с тем, как справедливо замечает Г.В. Дорофеев [9,
с. 35], варьирование является довольно сложной методической проблемой, как в
теоретическом, так и в практическом плане. Успех здесь зависит и от опыта
учителя и от его математической эрудиции. Поэтому учителю важно знать общие
методы варьирования.
Таким образом, включение
различных приемов составления задач в учебный процесс позволяет в комплексе
решать проблему интеллектуального развития школьников при обучении математике:
учащиеся осознано овладевают математическими знаниями, вооружаются методологией
математики, математическим стилем мышления, овладевают его операционной стороной,
развивают такие качества мышления, как гибкость, критичность,
самостоятельность, глубина, активность ума.
Составление и решение
задач — творческая деятельность учащихся. Место этой деятельности чаще всего на
стадии завершающего, обобщающего обучения при изучении различных разделов
школьного курса математики, на внеклассных и факультативных занятиях. Однако не
стоит вводить системы специальных уроков, а лучше время от времени обращаться к
составлению задач, родственных данной, при изучении различных математических
дисциплин в разных классах. Выбор места и времени составления задач, развития
темы задачи – право учителя математики. Подробнее как обучать приемам составления
задач будет рассказано во второй главе нашей работы.
Выводы по главе I
Мы
выяснили, что существуют различные пути развития интеллекта,
но наиболее интенсивно это развитие происходит в ходе активного усвоения и
творческого применения знаний, т.е. на уроках, и главным образом на уроках
математики, так как математическое содержание оптимально
для развития интеллектуальных способностей.
Обучение
математике является одним из важнейших средств интеллектуального развития
ребенка. Моделью интеллектуальной мыслительной деятельности является процесс
работы над задачей. Математика — учебный предмет, в котором задачи используются
как цель, как средство, и как предмет изучения. Деятельность по решению и
составлению математических задач в процессе обучения математике является
сложной интегративной деятельностью: познавательная, учебная, математическая,
интеллектуальная, эвристическая, творческая.
Обучение
школьников решению математических задач обычно осуществляется при решении
готовых (сформулированных учителем, в учебнике, учебном пособии или в другом
литературном источнике) задач. Между тем существенную роль при этом играет их
составление учащимися. Дело в том, что составление задач часто требует
проведения рассуждений, которые при решении заданных задач не выполняются.
Стало быть, составление задач служит развитию творческого мышления учащихся. В
работе рассмотрены некоторые приемы составления задач: постановка вопроса к
условию задачи; составление задачи по готовому рисунку; составление условия
задачи по заданному вопросу; составление задачи, являющейся обобщением данной;
конкретизация обобщенного способа решения задач; составление задачи, обратной
данной; переформулировка требования задачи; замена части данных исходной задачи
другими данными без замены заключения задачи.
Составление
и решение задач — творческая деятельность учащихся. Место этой деятельности
чаще всего на стадии завершающего, обобщающего обучения при изучении различных
разделов школьного курса математики, на внеклассных и факультативных занятиях.
Обучение
составлению задач требует немало времени и усилий, но это окупается той большой
экономией мышления, которые в последующем, достигаются благодаря единообразным
методам усвоения материала. Выбор места и времени составления задач, развития
темы задачи – право учителя математики.
Глава
II.
Обучение учащихся составлению задач при изучении темы «Прямая и плоскость в
пространстве»
§ 2.1 Обучение приемам составления задач
на примере применения аналогии, обобщения и конкретизации
Многие
ученые отмечают, что уже сам по себе процесс изучения математики приводит к
умению логически, доказательно мыслить. Математика является важнейшим средством
интеллектуального развития человека, и она же — средство измерения его уровня
интеллекта.
Очевидно, развитие мышления многократно ускоряется и усиливается, если учитель,
обучая математике, одновременно учит умелому применению различных мыслительных
приемов. Действительно, мышление учащегося проявляется в умении анализировать и
синтезировать, обобщать, конкретизировать и т. д., то есть в умении применять
различные приемы мыслительной деятельности к изучаемому материалу, к решению
задачи, к любой жизненной ситуации.
Проблема
формирования у школьников логических приемов мышления рассматривалась
исследователями в различных контекстах:
—
формирования логических приемов мышления (Н.Н. Поспелов, И.Н.Поспелов
[23] );
—
формирование приемов учебно-познавательной деятельности (О.Б. Епишева, В.И.
Крупич [11] );
—
формирование математических понятий (А.Я. Блох, Я.И. Груденов, Н.В. Метельский,
В.В. Репьев, К.А. Рупасов, З.И. Слепкань [17] );
— формирование
умений и навыков применения различных приемов мыслительной деятельности (Алексеева
О.В., Ларионова Т.В. [38] ).
Концепция Поспеловых ориентирована на
формирование мыслительных операций, которые выступают условием и средством
организации развивающего обучения. Формирование любой мыслительной операции
проходит несколько стадий:
1) стихийную, в ходе
которой ученик осуществляет операцию, но не осознает, как он это делает;
2) полустихийную, когда ученик,
совершая операцию, осознает, как он это делает, но не понимает существа этой
операции, думая, что ее применение происходит само собой, без каких-либо
правил;
3) сознательную, в процессе которой
ученик сознательно использует правила выполнения мыслительной операции и
понимает, что эти правила специально сформулированы [23].
Исходя из признанного в
психологии положения, что двумя сторонами мыслительного процесса являются
операции анализа и синтеза (Д.Н. Богоявленский, Н.А. Менчинская), Н.Н. Поспелов
отмечает, что правильный анализ любого целого — это анализ не только частей,
элементов, свойств, но и их связей и отношений. Поэтому анализ приводит не к
распаду целого, а к его преобразованию, которое и есть синтез. Задача анализа
заключается не только в разложении предмета или явления на составные части, как
это считается традиционно, но и в проникновении в сущность этих частей. Задача
синтеза состоит не только в объединении частей предмета или явления, но и в
установлении характера их изменения в зависимости от несущественных факторов,
не учтенных при анализе.
Обучение учащихся анализу и
синтезу предполагает формирование у них умений мыслить практически: разлагать
объект на составные части, выделять существенные стороны объекта, изучать
каждую часть (сторону) как элемент единого целого, соединять части объекта в
целое.
Мыслительная операция
сравнения, связанная с установлением сходства и различия в предметах, явлениях,
процессах, осуществляется в процессе анализа и синтеза.
О.Б. Епишева и В.И. Крупич занимались
проблемой формирования приемов учебной деятельности. Под приемами учебной
деятельности понимается система действий, выполняемых в определенном порядке и служащих
для решения учебных задач. Можно выделить следующие 4 группы приемов учебной
деятельности:
I. Общеучебные приемы, не зависящие от специфики предмета математики и
используемые поэтому в разных учебных предметах. Эту группу можно разделить на
две подгруппы: 1) приемы общей (внешней) организации учебной деятельности —
организация внимания, планирование, самоконтроль, работа с учебником и
справочной литературой, организация домашней работы и т. д.; их можно также
назвать приемами управления учебной деятельностью; 2) приемы мыслительной
(внутренней) деятельности — овладение и оперирование представлениями,
понятиями, суждениями, умозаключениями, мыслительными операциями.
II. Общие приемы учебной деятельности по
математике (общематематические
приемы) используются во всех математических
дисциплинах. Это: 1) приемы работы с учебником математики
и математическими таблицами, приемы организации домашней
работы по математике, ведение тетради по математике и т. д.
Они незначительно отличаются от соответствующих общеучебных приемов; 2) приемы
мыслительной деятельности в сфере
математических объектов: приемы работы с математическими
понятиями, суждениями (аксиомами и теоремами разных видов),
умозаключениями (индуктивными и дедуктивными доказательствами теорем), приемы
характерных для математики мыслительных операций (анализ, абстрагирование,
конкретизация и т. п.).
III. Специальные приемы учебной
деятельности по отдельным
математическим дисциплинам (арифметике, алгебре, геометрии,
началам анализа) — это такие общематематические приемы, которые принимают свою
особую форму в соответствии со спецификой содержания курса и особенностями его
задач. Они используются в любых разделах этого курса. Например, в школьном курсе
алгебры — это приемы тождественных преобразований выражений, приемы решения
уравнений, неравенств и их систем, приемы рационализации вычислений с
использованием алгебраических преобразований, приемы решения задач с помощью
уравнений и т. д. В курсе геометрии — это приемы построения геометрических
фигур, выполнения чертежа по условию задачи, приемы
чтения чертежа и т. д.
IV. Частные приемы
учебной деятельности – это такие
специальные приемы, которые конкретизированы для решения более узких задач и
используются в определенных темах курса [11, c. 28].
Тем самым концепцию О.Б.
Епишевой и В.И. Крупич необходимо рассмотреть в данном вопросе, т.к.
формирование логических приемов мышления осуществляется непосредственно в учебной
деятельности.
Они выделили 9 этапов
формирования приемов учебной деятельности:
I
этап – диагностика сформированности приемов
учебной деятельности.
Методы
диагностики, применяемые в обучении математике, основаны на общих методах,
разработанных дидактами (например, анализ устных ответов и письменных работ
учащихся, наблюдение за из повседневной учебной деятельностью и др.), а также
на особенностях учебной деятельности учащихся по усвоению математики (например,
учет количества решаемых учащимися за одно и то же время задач и др.).
II
этап – постановка целей учебной деятельности и
принятие их учащимися.
На
этом этапе используются методы мотивации учебной деятельности, привития
интереса к овладению приемам этой деятельности (словесные методы, наглядные методы,
проблемно-поисковые методы).
III
этап – инструктаж, введение приема учебной
деятельности.
С
позиции деятельностного подхода к обучению целесообразно не давать прием
учебной деятельности в готовом виде, а организовывать самостоятельное
нахождение его учащимися.
IV
этап – практические упражнения по отработке
введенного приема учебной деятельности.
Эти
упражнения можно разделить на 3 группы:
1.
Упражнения, направленные на усвоение
отдельных составляющих действий основного приема.
2.
Упражнения, составленные методом
варьирования, усложнением их содержания при сохранении приема решения.
3.
Обычные задачи по изучаемой теме, решаемые
«вразброс», сопровождаемые проговариванием и объяснением вслух выполняемых
действий в составе приема.
V
этап – оперативный контроль и коррекция
процесса формирования приемов учебной деятельности.
Контроль
осуществляется с помощью методов и приемов диагностики, методов взаимоконтроля
и самоконтроля.
VI
этап – применение усвоенных приемов учебной
деятельности.
На
этом этапе выделяют два основных вида деятельности учителя:
1.
Теоретические обобщения, помогающие
учащимся осознать ситуацию применения усвоенных приемов.
2.
Организация ситуаций для практического
применения усвоенных приемов учебной деятельности.
VII
этап – обобщение и перенос усвоенных приемов
учебной деятельности.
VIII
этап – закрепление обобщенных приемов учебной
деятельности.
Организуя
деятельность учащихся по самостоятельному применению приемов в повседневной
учебной деятельности, учитель акцентирует внимание учащихся на ситуациях, в
которых это можно сделать.
IXэтап
– нахождение новых приемов учебной деятельности [ 11 , с.44].
Выделенные
этапы обучения четко не отделены друг от друга и могут взаимодействовать в
разных последовательностях. Как сами приемы учебной деятельности учащихся, так
и методы их формирования в процессе обучения переплетаются в самых различных
сочетаниях.
Таким
образом, рассмотренная схема служит основным стержнем, помогающим определить
необходимые компоненты методики обучения математике на основе формирования
приемов учебной деятельности, но она может также дополняться, изменяться в
зависимости от ситуации.
Многие
исследователи считали, что основой для развития логического мышления должно
являться формирование научных понятий (А.Я. Блох, Я.И. Груденов, Н.В. Метельский,
В.В. Репьев и др.). Материал проведенных исследований свидетельствует с одной
стороны об очень тесной связи первичных обобщений и понятий с единичными
наиболее яркими и запоминающимися событиями; с другой стороны наблюдалась
тенденция к генерализации сходных признаков понятий, поляризации и симметрии
противоположных общих признаков понятий. Они обращали внимание на то, что в
процессе обучения необходимо учитывать психологию и логику формирования
понятий, способствующих развитию формально-логического мышления. Причем
развитие других видов мышления, таких как диалектическое, теоретическое даже у
старшеклассников не рассматривалось[17].
Другие авторы (Алексеева
О.В., Ларионова Т.В.) считают, что развитие мышления учащихся, то есть
формирование у них умений и навыков применения различных приемов мыслительной
деятельности, осуществляется следующими этапами:
1)
Знакомство учащихся с отдельными
мыслительными приемами. Причем они знакомятся с этими приемами обязательно в
процессе изучения соответствующего материала.
2)
Совместно с учащимися необходимо прийти к
выводу, что прием, с которым сегодня познакомились в процессе изучения новой
темы или решения задачи, не потребовал лишней траты времени. Более того, этот
прием облегчил понимание. Его использование усилило интерес к изучаемому
материалу.
3)
Выбор того или иного мыслительного приема
осуществляется в зависимости от содержания изучаемого материала. Поэтому в
дальнейшем, когда учащиеся повторно встречаются с тем или иным приемом,
напоминаем, что прием нам уже знаком. Далее выделяем те особенности данной и
ранее изученной темы, благодаря которым целесообразно использовать именно этот
прием.
4)
Учим комплексному использованию различных
мыслительных приемов во всевозможных комбинациях друг с другом.
5)
В дальнейшем вырабатываем привычку
самостоятельного применения мыслительных приемов. Для этого постоянно
обосновываем целесообразность тех или иных действий. Авторы для иллюстрации
рассматривают следующие примеры.
Прочитав в книге или услышав на уроке при объяснении, при ответе товарища
какое-либо утверждение, полезно проверить, действительно ли оно справедливо,
поставив перед собой вопросы: «Почему?», «На каком основании?» (прием
соотнесения); принимаем за правило, что преобразования, приведенные в книге,
полезно воспроизводить, по возможности видоизменяя их (приемы воспроизведения и
реконструкции).
Необходимо приучать учащихся везде, где это возможно, сопоставлять изучаемый
материал с прежними знаниями, устанавливая сходство и различия (прием
сравнения). При воспроизведении изучаемого материала необходимо требовать от
учащихся приводить свои примеры и контрпримеры (прием конкретизации).
При конспектировании материала вырабатываются у учащихся навыки расположения
записей в наиболее удобной форме с использованием всевозможных символов (прием
использования стимулирующих звеньев). Прочитав текст, учащиеся выделяют из него
главное (прием составления плана) [38].
Во
всех работах заявлена необходимость специального формирования приемов мышления,
в том числе логических приемов, представлены сами приемы, возможные упражнения
овладения ими, время и сроки их изучения. Однако авторы не рассматривают
проблему методики формирования логических приемов мышления. Акцент делается на
усвоение математического содержания с помощью логических приемов. Меньше
уделяется внимания формированию самих приемов посредством изучения некоторого
математического содержания.
Вышесказанное
позволяет говорить о необходимости целенаправленного формирования логических
приемов мышления, которое должно стать одной из приоритетных задач при изучении
математики.
В
своей работе мы будем больше придерживаться концепции О.В.Алексеевой и Т.В.
Ларионовой, так как считаем ее наиболее подходящей для формирования таких
приемов мышления, как анализ, синтез, сравнение, обобщение, конкретизация,
которые используются при составлении задач.
Инструментом
для формирования различных качеств мышления может выступать творческая задача.
Для решения таких задач характерен процесс поисковых проб. Однако гораздо более
эффективный способ — вооружить детей теми приёмами умственной деятельности,
которые необходимы для нахождения решения: анализ и синтез, сравнение,
аналогия, классификация. Предлагая учащимся занимательные задачи, мы формируем
у них способность выполнять эти операции и одновременно развиваем их.
Наибольший эффект при этом может быть достигнут в результате применения
различных форм работы над задачей — это работа над решенной задачей, решение
задач разными способами, правильно организованный способ анализа задачи, моделирование
ситуаций с помощью чертежа или рисунка, самостоятельное составление задач с
опорными словами, решение задач с недостающими данными, изменение вопроса
задачи, объяснение готового решения задачи, использование приема сравнения,
изменение условия, закончить решение задачи, составление аналогичной задачи,
решение обратных задач.
Проблеме
составления задач по математике, как главному средству развития
самостоятельного мышления учащихся, посвящены многие работы П.М.Эрдниева:
«Сравнение и обобщение в математике», «Аналогия в математике», «Укрупнение
дидактических единиц в обучении математике», «Методика упражнений по
математике»[42, 43, 44]. В своих работах он дает некоторые методические
рекомендации по обучению приемам составления задач, и главным образом приемам
обобщения и аналогии.
Насколько
важна аналогия в математике, можно судить по следующему высказыванию известного
польского математика Стефана Банаха: “Математик это тот, кто умеет находить
аналогии между утверждениями; лучший математик тот, кто замечает аналогии
теорий; но можно себе представить и такого, кто между аналогиями видит
аналогии” [38].
Эрдниев
объясняет появление аналогии как приема познания следующим образом: «В
процессе изучения окружающего мира и овладения силами природы человек
многократно замечал характерную связь: если два предмета имеют некоторые
одинаковые признаки, то очень часто (но не всегда!) оказывалось, что они имели
и некоторые другие общие признаки. На основе того, что два предмета имеют
некоторые общие признаки, и установлено, что первый из них имеет еще некоторый
признак Х, наличие которого у второго предмета пока неизвестно, делается
предположение, что второму предмету, по-видимому, тоже присущ признак Х.»
Таким образом, строятся умозаключения по аналогии. Причем, очевидно, что
истинность таких заключений должна устанавливаться посредством применения
строгих законов логики, которые могут выявить, что сделанное предположение
ошибочно. Однако, как утверждает П. Эрдниев, даже в этом случае применение
аналогии полезно, так как она обращает наше внимание на возможность необычных
связей между предметами, что расширяет представления ученого о проблеме[44].
Автор
рассматривает процесс построения аналогии и замечает, что механизм ее
умственного применения сложен и диалектичен по своей сути, так как сочетает в
себе элементы дедукции и индукции, анализа и синтеза. «В умозаключении по
аналогии, прежде всего, используется индукция, ибо переход от первого предмета
ко второму состоит в установлении связей между одними частными свойствами и
другими частными свойствами. В то же время умозаключение по аналогии тесно
связано с дедукцией, ибо истинность вывода по аналогии устанавливается
дедуктивным доказательством. Достоверный вывод, сделанный на основе аналогии,
начинается, таким образом, индукцией и завершается дедукцией. Автор
подчеркивает, что прием аналогии применяется учеными достаточно широко. Рассмотрим
схему умозаключений по аналогии:
Первая
посылка: Предмет А обладает свойствами a,
b,
c,
x.
Вторая
посылка: Предмет В обладает свойствами a,
b,
c.
Заключение:
Вероятно, предмет В обладает и свойством х.
Суждения,
полученные по аналогии, не достоверны и подлежат исследованию и доказательству.
Умозаключения
по аналогии являются непременной составной частью творческого мышления, так как
этим путем мысль человека выходит за пределы известного, пролагая путь к
неизвестному.
Выделим дидактическую
эффективность использования аналогии при обучении математике: 1)
Использование аналогии при открытии математических фактов делает учащихся «соавторами»
математической теории, знакомит учеников с мощным методом познания
действительности.
2) Аналогия интенсифицирует процесс
изучения математики, позволяя изучать сходные свойства различных математических
объектов. Примером является совместное изучение планиметрических и
стереометрических фигур. (Диагонали прямоугольника равны. Диагонали
прямоугольного параллелепипеда равны. У квадрата его измерения равны. У куба
его измерения равны). 3) Аналогия является одним из способов открытия
доказательства математических утверждений. Использование «неправильных»
аналогий формирует у учащихся потребность в доказательстве [21].
Различают несколько видов
приемов составления задач методом аналогия: аналогия по условию задачи, по
требованию и по способу решения.
Как же обучать
приему составления задач методом аналогии? Сначала происходит знакомство
учащихся с приемом аналогии в процессе изучения какой-либо темы. Почву для
применения аналогии подготавливает сравнение. Задания на сравнение
должны присутствовать на уроках постоянно. Например, при изучении нового
понятия необходимы задания на установление сходства и различия его с раннее
изученными понятиями. Устные упражнения могут содержать вопросы следующего
характера: в чем схожесть и в чем различие параллелограмма и прямоугольника,
прямоугольника и ромба, ромба и квадрата, квадрата и куба, куба и
параллелепипеда?
Интересное для
учащихся задание на сравнение может быть построено при помощи методики «Найди
лишнее»: учитель зачитывает по четыре слова, из которых три объединены общим
родовым понятием, а одно к такому понятию не относится или относится в меньшей
мере. Учащиеся должны определить это слово и записать тетради. На запись дается
10 секунд.
1) Цилиндр, шар, куб, конус. 2)
Прямоугольный параллелепипед, куб, тетраэдр, наклонный параллелепипед. 3)
Прямоугольник, треугольник, ромб, квадрат. 4) Цилиндр, куб, многоугольник шар.
5) Равнобедренный, прямоугольный, остроугольный, тупоугольный треугольник. 6)
Пирамида, параллелепипед, куб, шар. 7) Треугольник, круг, трапеция, квадрат. 
Ромб, трапеция, квадрат, прямоугольник. 9) Октаэдр, тетраэдр, икосаэдр,
параллелограмм. 10) Параллелограмм, треугольник, куб, окружность.
11) Дуга, сегмент, окружность,
прямая.
Причем в последних
примерах могут быть разные варианты ответов. В десятом «лишним» может быть или
куб или окружность, в одиннадцатом – или сегмент или прямая. Все зависит от
выбора родового понятия. Неоднозначности рассуждениях, ответах тоже надо учить.
Поэтому такие задания необходимо включать в процесс обучения с последующим
обсуждением результатов. Важно учить школьников видеть не только аналогию
геометрических объектов и их элементов, но и аналогию свойств, аналогию отношений
между объектами. Выделим некоторые виды отношений между геометрическими
объектами: часть – целое, объект – ближайший род,
плоскость – пространство, объект –
его элемент, объект – геометрическая величина, геометрическая величина –
единица измерения. Соответствующие задания могут быть следующими:
1. Замените
знак «?» геометрическим объектом из списка:
Диаметр: Радиус =
Окружность:?
а) отрезок; б) точка; в)
дуга; г) линия; д) луч.
Точка: Прямая = ? :
Пространство.
а) отрезок; б) плоскость;
в) прямая; г) луч; д) точка.
2. Укажите в
списке пары объектов, находящиеся в отношении, аналогичном отношению пары
«сторона – отрезок»: а) перпендикуляр – отрезок; б) треугольник – точка; в)
угол – фигура; г) тетраэдр – грань; д) параллелепипед – многогранник.
3. Из списка
(треугольник, прямая, точка, тетраэдр, угол, ребро, вершина, параллелепипед)
составьте пары, находящиеся в том же отношении, что и пара «сторона – грань».
Уже в младших классах второй ступени целесообразно подчеркивать
аналогию
между некоторыми плоскими и пространственными фигурами. Например, между
прямоугольником и прямоугольным параллелепипедом, между квадратом и кубом.
Аналогия между квадратом и кубом состоит в том, что у квадрата его измерения
равны и у куба его измерения равны. Учащиеся могут и сами догадаться,
что грани куба – равные квадраты, все стороны квадрата – равные отрезки. Таким
образом, учащиеся знакомятся с аналогией, но обязательно в процессе изучения
соответствующего материала.
В дальнейшем, когда учащиеся повторно встречаются с аналогией, напоминаем, что
этот прием нам уже знаком. Так, при знакомстве с понятиями площадь и объем
можно установить аналогию между единицами длины и единицами площади,
между единицами объема и единицами площади. Одновременно следует обратить
внимание на сходство в формулировках определений понятий. Например,
повторив с учащимися понятие квадратный сантиметр (квадратный сантиметр
– это площадь квадрата со стороной 1 см), можно попросить самостоятельно
дать определение понятию кубический сантиметр.
Учащиеся иногда затрудняются быстро и правильно ответить на вопросы
типа:
“ Сколько квадратных сантиметров в 1 дм2? Сколько
кубических
сантиметров
в 1 дм3?” Устранению таких трудностей способствует иллюстрация
сходства между операциями перехода от линейной единицы измерения к
квадратной или кубической. В обоих случаях вычисляется произведение
одинаковых множителей, причем число множителей в произведении равно
показателю при единице измерения: 1 дм2 = 10 * 10 см2, 1
дм3 = 10 * 10 * 10 см3.
Постепенно
задания на применение метода аналогии должны усложняться. При изучении новой
темы учащимся необходимо предлагать задания типа: Составьте задачу, аналогичную
данной, решите обе задачи.
Задачи,
аналогичные данным могут быть не только схожими по условию, по требованию, но и
по способу решения.
Типичные вопросы
учителя при решении задач методом аналогии: Не решали ли вы подобные задачи?
Какими приемами решалась подобная задача? В чем отличие новой задачи от раннее
решенной? Нельзя ли свести доказательство новой задачи к доказательству раннее
решенной?
Основным
приемом решения задачи по аналогии должен быть не переход от ранее разобранной
аналогичной задачи к данной, а от данной задачи к аналогичной. Именно такой
подход обеспечивает выявление содержательных аналогий на уровне идей и
механизмов решения, а не внешнего сходства условий и обозначений. Надо помнить,
что не во всех случаях рассуждения по
аналогии оказываются верными. Примеры
ложных аналогий:
1) Через точку на прямой в
пространстве можно провести только один перпендикуляр к этой прямой.
2) Две прямые в пространстве,
перпендикулярные к одной и той же третьей прямой, параллельны.
3) Высоты в тетраэдре пересекаются в
одной точке.
4) Из равенства 53 = 3
5 не следует что 53=35.
аb=b
a, но
log(ab)
≠ log a log
b,
аb
х=b
a
х,
но a sin bx
≠ b sin ax.
Очевидно,
некритическое использование аналогии может приводить к ошибкам, если только
забыть, что вывод, полученный по аналогии, необходимо завершать проверкой,
доказательством.
В
дальнейшем, необходимо вырабатывать у учащихся привычку самостоятельного
применения метода аналогии, с этой целью необходимо давать домашнее задание на
составление задач методом аналогия и стараться на уроках как можно чаще
прибегать к приемам составления задач учащимися.
Наиболее привычный и распространенный
способ использования аналогии – это построение обобщений на ее основе.
Процесс обобщения основывается на применении аналогии, но не сводится полностью
к ней.
Обобщение
означает переход знания на более высокий уровень на основе установления для
данных объектов общих свойств или общих отношений.
Умственное
развитее учащихся, которые должны подготавливаться уже в период школьного
обучения к роли творчески мыслящих активных деятелей, не может быть
полноценным, если их не научат в школе применению приемов аналогии и обобщения.
Виды обобщения:
1) замена
конкретных значений переменными или буквами;
2) переход
из планиметрии в стереометрию;
3) на
основе конкретных примеров выдвижение гипотез, которые в последующем
доказываются.
Применение
обобщения связано с преобразованием мыслей, с умственным экспериментированием;
оно есть одно из самых важных средств самообучения, самостоятельного расширения
и углубления имеющихся знаний [44, с.61].
Для
достижения глубокого усвоения нового понятия, способа решения нельзя обходиться
задачами одного уровня трудности, а еще лучше давать учащимся возможность самим
обобщить решенную задачу, чтобы затем решить ее, видоизменяя, если нужно,
прежний способ.
В
практике обучения общее классное задание рассчитано на среднего ученика, а для
расширения познавательных способностей более сильных учащихся необходимы
дополнительные задания по самостоятельному обобщению и решению составленных
задач.
Если,
скажем готовую задачу, решают все учащиеся в основном одинаковой
последовательностью рассуждений, то с обобщением уже справляется не всякий.
Результат обобщения зависит не столько от суммы знаний, примерно одинаковой для
всех учащихся класса, а от умения комбинировать, связывать эти знания
по–новому, заглядывать дальше обычных пределов.
Характер
упражнений, выполняемых в классе, должен отразиться и на характере контрольных
и проверочных работ; чему обучают, то и следует проверять.
Всякая
математическая задача неисчерпаема в своих связях с другими задачами; после
решения задачи почти всегда можно найти предмет размышления, найти несколько
направлений, в которых удаётся обобщить задачу, и найти затем решение созданных
таким образом новых проблем.
Время
и усилия, затраченные на обобщение знаний, окупаются той большой экономией
мышления, которые в последующем, достигаются благодаря единообразным методам
усвоения материала.
Работу
по обучению приемам обобщения удобно начинать с упражнений текстового
характера. Вот пример подобного простейшего задания, который приводит в своей
книге П.М.Эрдниев [44, с.62]:
Даны три рисунка А, Б,
а:
Требуется
нарисовать такой рисунок б, чтобы а относилось к б так же,
как А относится к Б.
Решающий
данную задачу обнаруживает для двух пар фигур сходство отношений: объемлющая
меняется местом с объемлемой.
Результаты
обобщения учащихся бывают различной сложности; даже при выполнении простейших
синтетических заданий проявляется резкая разница в силе воображения учащихся.
П.М.
Эрдниев для иллюстрации приводит следующий пример: шестиклассникам было
предложено записать выражение 6х2 в виде произведения двух
множителей. Большинство учащихся ограничилось тривиальными ответами: 2х3х; 6х2
1; 6
х2.
Лишь некоторые учащиеся, отличающиеся от своих сверстников в большей мере
комбинаторскими способностями, придумали разложения: 12х2 ;
8х2;
только один ученик «ухитрился» использовать буквенные показатели: хk
72 х2-k;
и никто не дал общей формулы разложения хотя бы в виде: 6х2 =
[41,
с.62].
На
этом простейшем примере мы видим, какой широкий диапазон комбинаций открывается
перед учащимися, когда они получают задание по синтезу тех или иных выражений.
Чтобы провести
обобщение, необходимо отвлечься от конкретного содержания и выделить сходное,
общее, существенное в структуре предмета задачи, отношений между отдельными ее
элементами, отбросить специфические, особенные, единичные признаки и сохранить
только общие для группы отдельных элементов. Способность к обобщению
математического материала можно рассматривать с двух сторон: способность
субъекта увидеть в частном уже известное ему общее (подведение частного
случая под известное общее понятие); способность увидеть в частном пока еще неизвестное
общее (вывести из частных случаев, образовать понятие). Обобщение означает
переход знания на более высокий уровень на основе установления для данных
объектов общих свойств или общих отношений.
Обобщение нередко
осуществляется путем выделения одинакового математического содержания для
различных задач. Составление математической модели – это наиболее
распространенный вид обобщения. Он состоит в переводе происходящих в
действительности процессов на язык математики. Обобщение решения конкретных
задач может дать единый метод решения целого класса однородных задач. Такой
вариант обобщения хорошо просматривается при изучении пропорциональных
зависимостей величин.
Скорость движения v
, время движения t , пройденное расстояние s связаны
формулами: s = vt , v= s/ t , t= s /v . Цена товара Ц,
количество товара К, стоимость С образуют аналогичные формулы: С=
ЦК, К =С/ Ц, Ц = С/ К. Плотность ρ , масса m,
объем вещества V вычисляются по формулам: m = ρV , V=m/ρ
, ρ=V /m. Легко заметить, что во всех рассмотренных случаях задачные
ситуации описываются с помощью всего лишь двух математических формул: y =
kx , y = k/x . Это и есть простейшие математические модели прямой
и обратной пропорциональности.
При решении и
составлении математических задач часто применяют индуктивные обобщения. Суть
индуктивного обобщения заключается в следующем. Рассматривается самый простой
частный случай задачи, когда она решается легко. Решив эту задачу, обобщают ее
на другой более сложный, но все же частный случай, используя результат
предыдущей задачи. Обобщение происходит до тех пор, пока не получится задача,
обобщающая все предыдущие. Например: 1) Докажите, что сумма расстояний от любой
точки М, находящейся на стороне правильного треугольника, до его сторон
равна длине высоты треугольника. 2) Докажите, что сумма расстояний от любой
точки М правильного треугольника до его сторон равна длине высоты
треугольника.
1)
2) Проведем через
точку М прямую SE || AC.
Тогда треугольник SBE правильный. Следовательно,
Обобщение
систематизирует знания учащихся, так как требует установления и осмысления взаимосвязи
между понятиями и отношениями, о которых идет речь в задаче. В ходе выяснения таких
взаимосвязей у учащихся составляется некий целостный образ, в котором одно
знание следует из другого и связано с ним. В конце концов, некоторая группа
знаний, расположенных в определенной последовательности по отношению друг к
другу, составит систему. В качестве примера рассмотрим обобщения при решении
задач о геометрической прогрессии. Компонентами задач о геометрической прогрессии
являются числа: b1– первый член, q – знаменатель, n
– число членов, bn – n-й член, Sn
–сумма первых n членов прогрессии. Между ними установлены два
основных соотношения:
Если заданы три
компонента из пяти, то два оставшихся могут быть вычислены. Таким образом,
возможные десять типов задач на геометрическую прогрессию определяются данными:
1) b1, q, n ; 2) b1, q,
bn; 3) b1, q, Sn;
4) b1, n , bn; 5) b
1 ,
n ,
S n;
6) b1
, bn,
Sn;
7) q,
n ,
bn;

n ,
Sn;
9) q,
b n,
S n;
10) n ,
b n,
S n.
Задачи типа 2),
3), 6), 9) приводят к системам простейших показательных уравнений, а 4), 5),
10) задачи – к системам рациональных уравнений, остальные – к системам линейных
уравнений. Таким образом, выделены три основных метода решения задач на
геометрическую прогрессию.
Обобщение может выступать
и как переход от данного множества предметов к рассмотрению более «емкого»
множества, содержащего данное. «Распространим» теорему Пифагора на
пространственный случай.
Используя
построенные ранее закономерные переходы от одного пространства к другому, длину
отрезка соотнесем с площадью фигуры, треугольник с треугольной пирамидой.
Вместо перпендикулярности сторон в пространственном случае можно рассмотреть
прямые углы при вершине пирамиды. В результате получится следующее обобщение
теоремы: «Дана треугольная пирамида, плоские углы при вершине которой прямые.
Докажите, что квадрат площади основания пирамиды равен сумме квадратов площадей
боковых граней», причем построенная пространственная теорема тоже выполняется.
Рассмотрим еще
один пример. Докажите, что , где О – произвольная точка пространства, а М
– середина отрезка АВ. Во всех учебниках геометрии эту задачу
используют в качестве иллюстрации применения векторного метода: выразив ОМ через
векторы ОА и АМ, а также через векторы ОВ и ВМ, затем,
сложив полученные векторные равенства и выполнив небольшие преобразования,
получим требуемый результат.
Замечаем, что
приведенные рассуждения можно использовать в случае замены в условии задачи
отрезка треугольником: докажите, что
,
где О – произвольная точка пространства, а М – точка пересечения
медиан треугольника АВС.
Стремление
к дальнейшему обобщению задачи приводит к замене треугольника многоугольником
или многогранником, что обусловливает и новое требование задачи: доказать, что
, где Аi – вершины многоугольника или многогранника.
Анализируя все преобразования условия задачи, видим, что они осуществляются
вокруг основной идеи: точка M должна быть центром тяжести. Это условие и
определяет направление обобщения.
Тем самым,
обобщение можно использовать при переходе от планиметрии к стереометрии, при
переходе от частных видов фигур к более сложным, общим.
Нет
ничего хуже, когда в некоторых случаях учитель отнимает у учащихся самое
интересное, а именно: опустив процесс обобщения, либо взяв его на себя,
предлагает учащимся снова задачу, которая представляет собой обобщенное
соотношение предыдущей, оставляя детям лишь концовку процесса (доказательство
или решение) [44, с.66] .
Обучение
приему обобщения происходит по той же схеме, что и методу аналогия, основываясь
на концепции Т.В.Ларионовой и О.В.Алексеевой.
Обратный процесс
по отношению к обобщению происходит при применении конкретизации. Исходная
задача – найдите длины медиан треугольника АВС, если его стороны равны a,b,c.
Конкретизируя вид треугольника (прямоугольный, равнобедренный, равносторонний),
получаем задачи, разного уровня сложности. Заметим, что по отношению к новым
задачам исходная задача является задачей-обобщением полученных. Приведем еще
один пример конкретизации. AB и CD пересекаются в точке М.
Точки A, B, C, D лежат на окружности. Доказать, что AM MB = CM
MD .
Конкретизируя – где располагается точка М – внутри или вне окружности, получим
свойства хорд и секущих. Доказательства обоих утверждений аналогичные. Совместное
решение этих задач позволит сэкономить учебное время.
Далее можно
рассмотреть частный случай первой задачи: одна из хорд (пусть АВ) является
диаметром окружности, а другая (пусть хорда СD) перпендикулярна ей.
Тогда АМ МВ = СМ 2
. Будем исследовать задачную ситуацию, взяв предельный случай, который
дает совпадение точек, например, А и В. Этот случай
трансформирует задачу в следующую: через точку М проведены касательная МА
(А – точка касания) и секущая, которая пересекает окружность в точках С и
D. Докажите, что МА2 = МС MD . Можно предложить
самим учащимся сформулировать задачу, соответствующую описанной выше ситуации.
Второй предельный случай заданной ситуации (совпадение точек С и D)
соответствует следующей задаче: из точки М проведены к окружности две
касательные МА и МС (А и С—точки касания).
Докажите, что МА=МС.
Формулировка
приведенной задачи без указания положения точки М является примером вариативной
задачи, то есть задачи, которая предполагает рассмотрение нескольких задачных ситуаций
с одинаковыми условиями, но различными вариантами чертежа.
Итак,
мы рассмотрели некоторые примеры, в которых можно использовать метод обобщения,
конкретизации и аналогии. Упражнения по обобщению решенных задач и применения
метода аналогии могут найти место при изучении самых разнообразных тем, в особенности
на факультативных занятиях или на занятиях кружка.
Обучение
приемам составления задач это долгий, целенаправленный, систематический
процесс. В этом параграфе мы рассмотрели методику обучения таким приемам
составления задач, как аналогия, обобщение и конкретизация, но эту методику
можно применять и при обучении другим приемам. Исходя из этой методики, можно
сделать вывод, что обучение приемам составления задач проходит несколько
этапов: 1) знакомство учащихся с отдельными
мыслительными приемами; 2) выделение особенностей данной и ранее изученной
темы, благодаря которым целесообразно использовать именно этот прием; 3)
комплексное использование различных мыслительных приемов во всевозможных
комбинациях друг с другом; 4) вырабатываем привычку
самостоятельного применения различных приемов составления задач, для этого
нужно и в домашнем задании давать упражнения на самостоятельное составление
задач.
Таким образом, обучать учащихся
приемам составления задач нужно постепенно, последовательно и систематично.
§ 2.2 Логико-дидактический
анализ темы
«Прямая и плоскость в
пространстве»
с позиции возможности
обучения составлению задач
[Учебник:
Геометрия. 10 кл.: учеб. для общеобразоват. учреждений с углубл. и профильным
изучением математики/ Е.В. Потоскуев, Л.И. Звавич. — М.: Дрофа, 2007, глава III.]
Выделение
и общий анализ дидактических единиц темы
а) В данной теме вводятся
определения понятий параллельности прямой и плоскости, перпендикулярность
прямой и плоскости, нормали, перпендикуляра, основания перпендикуляра,
наклонной, основания наклонной, расстояния от точки до плоскости, угла между
прямой и плоскостью, ортогональной проекции наклонной на плоскость,
ортогонального проектирования. Всем понятиям даются формально-логические
определения, через род и видовые отличия.
б)
Ведущими понятиями данной темы являются: параллельность прямой и плоскости,
перпендикулярность прямой и плоскости, расстояния от точки до плоскости, угол
между прямой и плоскостью.
в)
Логическая структура определений не нова для учащихся. Определения
параллельных прямой и плоскости и перпендикулярных прямой и плоскости
представлены в четырех формах: натуральной, графической, вербальной и
символьной. Отсюда возникает необходимость широкого использования наглядных
средств – натуральных и графических моделей. Все словесные определения должны
сопровождаться иллюстрацией на натуральных и графических моделях и обратно.
Определение
перпендикулярной прямой к плоскости содержит квантор, и в этом его сложность.
г)
Теоремы, дополняющие содержание понятий:
1.
Признак параллельности прямой и плоскости. При доказательстве этой теоремы
используется теорема о двух параллельных прямых, одна из которых пересекает
плоскость.
Из
этой теоремы, в частности, вытекает факт существования и способ построения
прямой, параллельной данной плоскости и проходящей через данную точку, не
лежащею в этой плоскости.
2.
Свойства параллельности прямой и плоскости. Метод доказательства теорем –
синтетический. При доказательстве используются определения параллельных прямых,
параллельности прямой плоскости, признак параллельности прямой плоскости и
доказанные свойства.
3.
Признак параллельности прямой и плоскости: Плоскость и не лежащая в ней прямая,
параллельные некоторой прямой, параллельны.
Этот
признак в учебнике сформулирован, но как теорема не выделен. Доказательство
предлагается провести самостоятельно. Метод доказательства – синтетический. При
доказательстве используется первый признак параллельности прямой плоскости.
4.
Признак перпендикулярности прямой и плоскости. Доказательство — дополнительные
построения.
5.
Существование перпендикулярных прямой и плоскости. Доказательство основано на
методе дополнительных построений. Единственность доказывается методом от
противного.
6.
Теоремы о связи между параллельностью прямых и их перпендикулярностью к
плоскости (признак и свойство). Доказательство признака основано на приеме
дополнительных построений, а свойство – построение и метод исключения.
7.
Теорема о трех перпендикулярах и ей обратная доказываются синтетическим методом.
8.
Свойства параллельного проектирования.
д)
Приемы доказательства теорем для учащихся не новые.
е) Теоретический материал
темы содержит большой потенциал, который может быть направлен на овладение
учащимися гипотетико-дедуктивными методами на этапе «открытия» новых фактов,
закономерностей, доказательств.
На
основе теоретического материала можно учить школьников приемам составлению
задач. Так путем обращения признаков учащиеся могут сами сформулировать
свойства. Примером может служить признак параллельности прямой к плоскости.
Учащиеся сами могут сформулировать обратную теорему к теореме о связи между
параллельностью прямых и их перпендикулярностью к плоскости, к теореме о трех
перпендикулярах и доказательство они могут провести самостоятельно. Следует
также обратить внимание учеников, что не все обратные утверждения могут быть
верны, обратив теорему, мы можем прийти и к неверному суждению.
При
изучении данной темы также можно широко использовать еще один важный прием –
обобщение. После рассмотрения конкретных примеров, учащиеся путем обобщения
приходят к формулировке некоторой теоремы. Например, так может быть получены
признак параллельности прямой и плоскости и признак перпендикулярности двух
прямых.
Так
как данная тема аналогична теме «Взаимное расположение прямых на плоскости», то
можно использовать соответственно еще один прием составления задач –
составление задачи аналогичной данной. Учащиеся, по аналогии с плоскостью, сами
могут сформулировать задачи, которые «выводят» на теоремы о связи параллельности
плоскости и их перпендикулярности к плоскости. Ученикам также можно предложить
заменить в данной теореме все прямые на плоскости, тогда аналогичная задача
будет такая:
Доказать,
что если одна из двух параллельных плоскостей перпендикулярна к третей
плоскости, то и другая плоскость перпендикулярна к этой плоскости.
Обратное
предложение: Если две плоскости перпендикулярны к некоторой плоскости, то они
параллельны.
Проанализировав
ситуацию (можно показать на натуральных моделях), учащиеся понимают, что пришли
к неверному суждению. Но устанавливается важный факт: Если две плоскости
перпендикулярны к некоторой третей плоскости, то они, либо параллельны, либо
пересекаются по прямой, перпендикулярной к третей плоскости.
Если
в теореме о связи между параллельностью прямых и их перпендикулярностью к
плоскости заменить прямые на плоскости, а плоскости на прямые, то мы получим
новую задачу: Докажите, что если одна из двух параллельных плоскостей
перпендикулярна к прямой, то и другая плоскость перпендикулярна к этой прямой.
Для этой задачи также можно сформулировать обратную, которая является корректной:
Если две плоскости перпендикулярны к некоторой прямой, то они параллельны.
Тем
самым мы пришли к выводу, что и на основе теоретического материала учащихся
можно учить приемам составления задач (используя прием аналогии, обобщения,
составление задачи, обратной данной), и эти новые задачи могут привести как к
теореме, так и к задаче, либо к неверному суждению.
При
изучении темы можно широко использовать и, следовательно, формировать у
учащихся такие познавательные средства как анализ, синтез, аналогия, обобщение
и т.д.
Примеры:
а)
определение перпендикулярных прямых на плоскости и в пространстве аналогичны,
но в этих понятиях есть и различия;
б)
связь между параллельностью двух прямых (плоскостей) и их перпендикулярностью к
плоскости (прямой);
в)
существует полная аналогия между понятиями перпендикулярность прямых на
плоскости и перпендикулярность плоскостей;
Все
эти связи нужно использовать при изучении темы и обращать также внимание на
другие познавательные средства.
Анализ задачного материала
Задачи
в данной главе разнообразны по содержанию, требованиям, функциям. И их много.
Здесь нет новых логических методов решения, но появляется новый для
стереометрии тип задач – задачи на нахождение расстояний и углов.
Рассмотрим
задачи, на основе которых можно учить учащихся составлять новые задачи. Можно
выделить следующие важные группы задач:
1. Задачи-теоремы.
В основном это задачи на
доказательство свойств и признаков параллельности и перпендикулярности прямых и
плоскостей и на доказательство существования и единственности какого-либо
объекта.
Примером таких задач
могут служить № 3.004, 3.005, 3.011, 3.014, 3.019, 3.020, 3.031, 3.048,
3.092, 3.121, 3.130.
Здесь можно использовать
прием обобщения:
№ 3.011: Через
каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой
прямой, и притом только одна.
Обобщив эту задачу
на рассмотрение различных случаев взаимного расположения прямых в пространстве,
придем к новой задаче, в которой требуется доказать существование плоскости,
параллельной данной прямой. Это есть задача №3.004: Через данную прямую а
провести плоскость, параллельную данной прямой b.
2. Задачи
на вычисление расстояний
— от точки до плоскости (№ 3.033, 3.034,
3.036, 3.070(а), 3.071, 3.074 — 3.078, 3.080, 3.093, 3.140, 3.141, 3.151,
3.153, 3.159);
— от точки до прямой (№ 3.035, 3.069,
3.070(б), 3.073, 3.079, 3.081);
— между прямыми (№ 3.136).
№ 3.034: Точка
Р удалена от каждой стороны правильного треугольника на 30 см. Найдите
расстояние от точки Р до плоскости треугольника, если площадь вписанного
в этот треугольник круга равна 576 см2.
Обобщение данной задачи:
Точка Р удалена от каждой стороны правильного многоугольника на
расстояние d.
Найдите расстояние от точки Р до плоскости многоугольника, если площадь
вписанного в этот многоугольник круга равна S.
№ 3.036: Точка О
– центроид правильного треугольника АВС; ОР – прямая,
перпендикулярная плоскости АВС; М – произвольная точка прямой ОР
(МО). Докажите, что расстояния от точки
М до вершин треугольника АВС равны.
Здесь можно использовать
прием выведения следствий из условия . Тогда на основе этой задачи можно
составить следующие:
1) Точка О –
центроид правильного треугольника АВС; ОР – прямая,
перпендикулярная плоскости АВС; М – произвольная точка прямой ОР
(МО). Докажите, что расстояния от точки
М до сторон треугольника АВС равны;
2) Точка О –
центроид правильного треугольника АВС; ОР – прямая, перпендикулярная
плоскости АВС; М – произвольная точка прямой ОР (МО). Докажите, что
;
3) Точка О –
центроид правильного треугольника АВС; ОР – прямая,
перпендикулярная плоскости АВС; М – произвольная точка прямой ОР
(МО). Докажите, что
.
№ 3.070: Расстояние
от точки М до каждой из вершин правильного треугольника АВС (АВ=6)
равно 4. Найдите расстояние от точки М: а) до плоскости треугольника АВС;
б) до каждой его стороны.
Эту задачу можно
рассмотреть и в общем виде, когда вместо треугольника будет правильный
многоугольник: Расстояние от точки М до каждой из вершин правильного
многоугольника, сторона которого а, равно 4. Найдите расстояние от
точки М: а) до плоскости многоугольника ; б) до каждой его стороны.
3. Задачи
на вычислений углов
— между прямыми (№ 3.086, 3.087, 3.135,
3.148, 3.149);
— между прямой и плоскостью (№ 3.083 —
3.085, 3.088 – 3.091, 3.094 – 3.100, 3.160);
№ 3.088: ABCD
– параллелограмм. Найдите угол между прямой АВ и плоскостью α, если
прямая CD образует с плоскостью α
угол φ.
Можно конкретизировать эту задачу,
заменив параллелограмм на прямоугольник или квадрат: ABCD
– квадрат. Найдите угол между прямой АВ и плоскостью α, если прямая CD
образует с плоскостью α угол φ.
№ 3.094:
Прямая МС перпендикулярна к плоскости треугольника АВС; ВС=МС=3;
АС=. Найдите углы, которые образуют прямые ВМ
и АМ с плоскостью треугольника.
Здесь тоже можно
использовать конкретизацию задачи, заменив произвольный треугольник на
равнобедренный, правильный или прямоугольный. Например, можно получите
следующую задачу:
Прямая МС
перпендикулярна к плоскости правильного треугольника АВС, сторона
которого равна 3, МС=3. Найдите углы, которые образуют прямые ВМ
и АМ с плоскостью треугольника.
4. Задачи
на посторенние сечений.
Это задачи, в которых необходимо
построить секущую плоскость, проходящую через некоторую прямую или точку и
перпендикулярную или параллельную некоторой плоскости или прямой. Это задача на
метрически определенном проекционном чертеже. Здесь все построения эффективные.
Примеры таких задач: №
3.015 – 3.018, 3.023 – 3.028, 3.055, 3.115, 3.116, 3.127, 3.137, 3.143, 3.147.
5. Задачи
на множество точек.
Данных задач в теме немного:
№ 3.117, 3.120, 3.150. Их можно дополнить, сформулировав им обратные или
противоположные, а лучше сформулировать в виде: найти множество точек…
Задача № 3.150:
Что представляет собой множество всех точек пространства, равноудаленных от
всех сторон данного треугольника?
(Эту задачу можно
сформулировать и так: Найдите множество точек пространства, равноудаленных от сторон
данного треугольника.)
Обобщив данную задачу на
произвольный выпуклый многоугольник, получим: Что представляет собой множество
всех точек пространства, равноудаленных от всех сторон данного выпуклого многоугольника.
Решив эти задачи,
учащимся можно предложить сформулировать аналогичную задачу, в которой
необходимо будет найти множество всех точек пространства, равноудаленных от
всех вершин данного многоугольника.
6.
Задачи на усвоение определений, признаков
и свойств:
№ 3. 002, 3.003, 3.007 – 3.010, 3.012,
3.013, 3.021, 3.029, 3.030, 3.032, 3.045. Эти задачи могут использоваться на
этапе осознания и осмысления.
7.
Задачи на установление взаимного
расположения прямых и плоскостей в пространстве:
№ 3.006, 3.022, 3.037 – 3.040, 3.042 –
3.044, 3.046, 3.047, 3.049 — 3.054, 3.058 – 3.062, 3.064, 3.082, 3.122, 3.125,
3.126, 3.128 – 3.131, 3.152.
8.
Задачи на усвоение понятий наклонная,
перпендикуляр и проекция:
№ 3.063, 3.066 – 3.068, 3.072, 3.138,
3.139, 3.142, 3.144 – 3.146, 3.155.
9.
Параллельное проектирование: №
3.101 – 3.108.
10. Ортогональное
проектирование: № 3.109 – 3.114, 3.133.
Анализ задачного
материала показывает, что в теме существуют объективные предпосылки использования
на уроках различных приемов составления задач: составление задачи, обратной
данной, конкретизация задачи, обобщение, применение аналогии, выведение новых
следствий из условия и т.д.
Учебные
задачи изучения темы
1) Формировать у учащихся
представление об основных метрических характеристиках взаимного расположения
точки и прямой (плоскости), двух прямых, прямой и плоскости, т.е. выделить пары
объектов, между которыми устанавливается отношение параллельности и
перпендикулярности, и охарактеризовать эти отношение для различных пар.
2) Формировать обобщенный
прием решения задач на вычисление расстояний и углов между пространственными
фигурами.
3) Формировать у учащихся
навыки самостоятельного составления задач.
Тема создает основу для
изучения последующих тем курса геометрии. Расстояния между простейшими фигурами
и различные виды углов в пространстве являются основными количественными
характеристиками взаимного расположения точек, прямых и плоскостей. Отработка
этих понятий до уровня навыков при решении вычислительных задач необходимы для
успешного изучения многогранников, тел вращения, векторов, метода координат,
объемов. В то же время, тема играет важную роль в формировании мышления и
пространственных представлений школьников. Поэтому в конце изучения главы о
перпендикулярности прямых и плоскостей целесообразно провести систематизацию и
обобщение знаний и умений учащихся. Систематизировать и обобщать требуется как
теоретический, так и задачный материал.
§ 2.3 Из опыта обучения школьников составлению задач
Приемам
составления задач учащихся можно учить на разных этапах изучения той или иной
темы. В качестве примеров рассмотрим конспекты уроков, которые могут быть
проведены при изучении темы «Прямая и плоскость в пространстве» в 10 классе в
соответствии с учебниками [24, 25].
Пример
1
Тема:
Прямая и плоскость в пространстве.
Учебник:
[25],
§8.
Тип
урока: урок-лекция.
Учебная
задача: Выявить особый вид отношения прямой и
плоскости в пространстве – параллельность; сформулировать определение,
«открыть» признаки и свойства параллельности прямой и плоскости на основе
графических и натуральных моделей, используя прием обобщения и формулирования
предложений, обратных данным.
Диагностируемые
цели:
В
результате ученик:
—
знает определение параллельности прямой и плоскости;
—
имеет представление о признаках и свойствах параллельности прямой и плоскости;
—
учится применять прием обобщения для составления новых задач;
—
осуществляет поиск доказательства теорем и решения задач методом восходящего
анализа и синтеза.
Структура
урока:
1)
Мотивационно – ориентировочная часть
—
на этапе актуализации ученики повторяют взаимное расположение прямой и
плоскости на конкретном примере;
—
постановка учебной задачи
2)
Содержательная часть
—
формулируется определение параллельности прямой и плоскости;
—
доказывается существование данных объектов;
—
выявляются признаки и свойства параллельности прямой и плоскости.
3)
Рефлексивно – оценочная часть
—
подводятся итоги урока, и записывается домашнее задание.
Фрагмент
урока
I.
Мотивационно-ориентировочная часть.
—
Рассмотрим следующую задачу: Средняя линия трапеции лежит в плоскости α, а
основания АВ и DC
не лежат в ней. Пересекают ли прямые, содержащие ее основания, плоскость α?
—
В каком случае прямая и плоскость называются пересекающимися?
(
если они имеют ровно одну общую точку)
—
Как расположены прямые АВ и MN?
(параллельно, т.к. MN
– средняя линия трапеции)
—
Если предположить, что прямая АВ пересекает плоскость α. Тогда что мы
получим? (тогда прямая MN
тоже должна пересекать плоскость α по свойству параллельных прямых: если одна
из двух параллельных прямых пересекает данную плоскость, то и другая прямая
пересекает эту плоскость)
—
Но это противоречит тому, что прямая MN
лежит в плоскости α. Следовательно, прямая АВ не пересекает плоскость α.
Итак,
мы знаем случаи, когда прямая и плоскость пересекаются, когда прямая лежит в
плоскости, а сейчас мы получили еще один случай взаимного расположения прямой и
плоскости – когда они не имеют общих точек. Так какая перед нами стоит задача?
(Рассмотреть
этот случай взаимного расположения прямой и плоскости)
—
По какой схеме обычно мы рассматриваем новое отношение между объектами?
(Даем
определение этого отношения, доказываем существование данных объектов, выявляем
признаки и свойства.)
—
Сегодняшний урок мы и посвятим рассмотрению этого отношения. Записи будем вести
в таблице. Таблица следующего вида:
|
Определение |
Существование |
Признак |
Свойства |
II.
Содержательная часть.
—
Введем следующее определение:
Прямая
и плоскость, не имеющие общей точки, называются параллельными.
—
Если прямая а и плоскость α параллельны, то записывают а||α
или α||а. При этом говорят, что прямая а параллельна
плоскости α или плоскость α параллельна прямой а.
—
Итак, определение мы с вами ввели, но возникает вопрос: а существует ли прямая,
параллельная плоскости? На примере мы видим — что существует, и мы это
доказали. Нам предстоит доказать это в общем случае, но на доказательстве
существования мы остановимся чуть позже.
При
решении стереометрических задач обоснование параллельности прямой и плоскости с
помощью одного определения затруднительно. В таких случаях пользуются
признаками. Как же получить признак параллельности прямой и плоскости? Давайте
вернемся к примеру: мы выяснили, что прямая АВ параллельна плоскости α.
Какой существенный факт мы использовали при доказательстве?
(прямая
АВ не лежит в плоскости и параллельна некоторой прямой MN,
лежащей в плоскости α.)
—
Подумайте, какое предположение можно получить, если обобщить данный пример?
(Если
прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в этой
плоскости, то эти прямая и плоскость параллельны.)
—
Итак, вы сформулировали признак параллельности прямой и плоскости. Давайте
запишем его в таблице и докажем.
Дано: Доказательство:
b α,
a||b,
aα.
Доказать:
a||α.
Пусть прямая а пересекает плоскость α в некоторой точке М
(аα=М).
Но по условию a||b,
тогда по свойству параллельных прямых прямая b
должна пересекать плоскость α. Это противоречит тому, что прямая b
лежит в плоскости α. Следовательно, прямая а параллельна плоскости α.
—
Итак, мы с вами сформулировали определение параллельности прямой и плоскости,
сформулировали и доказали признак. Теперь нам необходимо рассмотреть свойства.
Как же нам получить свойства параллельности прямой и плоскости? (нужно
сформулировать предложение, обратное признаку)
—
Сформулируйте обратное предложение для признака.
(Если
прямая и плоскость параллельны, то в плоскости существуют прямые, параллельные
данной прямой.)
—
На доказательстве этого свойства мы останавливаться не будем, но запишем его в
таблице как первое свойство параллельности прямой и плоскости. А сейчас мы
более подробно остановимся на тех свойствах, которые чаще используются при
решении задач.
[Далее
на уроке рассматриваются свойства параллельности прямой и плоскости.]
III.
Рефлексивно-оценочная часть.
—
Итак, сегодня на уроке мы с вами рассмотрели особый вид отношения прямой и
плоскости – параллельность. Какие прямая и плоскость называются параллельными?
(Прямая и плоскость, не имеющие общей точки, называются параллельными.)
—
Как доказать, что прямая и плоскость параллельны? (по признаку)
—
Сформулируйте признак параллельности прямой и плоскости.
(Если
прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в этой
плоскости, то эти прямая и плоскость параллельны.)
—
А как мы открыли признак параллельности прямой и плоскости?
(
обобщив рассмотренный в начале урока пример)
—
А в чем состояло обобщение?
(
Переход от конкретного примера на более общий случай)
—
То есть, рассмотрев пример, мы сформулировали гипотезу для более общего случая,
которую в последующем доказали. Это есть один из способов составления задач
методом обобщения. Обобщение нам с вами помогло не только сформулировать новую
задачу, а открыть признак параллельности прямой и плоскости.
—
Раз есть признаки, значит, есть и свойства. Мы с вами рассмотрели некоторые
свойства параллельности прямой и плоскости. А как мы получили свойство
параллельности прямой и плоскости?
(сформулировали
предложение, обратное признаку)
—
Таким образом, приемы составления задач (обобщение и формулировка предложения,
обратного данному) позволяют нам открыть новые закономерности, признаки и
свойства данных объектов, которые в дальнейшем будут полезны при решении
других, более сложных, задач.
Домашнее
задание – учить теорию — §8 (на следующем уроке будет самостоятельная работа по
теории).
Анализ урока
Учащиеся в начале
урока были подготовлены к активному и сознательному усвоению материала. На
этапе актуализации, на конкретном примере, ученики повторили взаимное
расположение прямой и плоскости в пространстве. На этапе мотивации, на этом же
примере, используя прием обобщения, пришли к еще одному случаю взаимного
расположения прямой и плоскости – параллельность. При формулировке гипотезы у
большинства учащихся не возникло проблем, так как учитель уже использовал такой
прием составления задач. Таким образом, у них возникла задача — рассмотреть
особый случай взаимного расположения прямой и плоскости в пространстве, когда
прямая и плоскость не имеют общих точек. Решению этой задачи был посвящен весь
урок. Учащиеся сами получили свойство параллельности прямой и плоскости,
сформулировав обратное предложение для признака. Рассмотрев натуральные модели,
продемонстрированные учителем, пришли к формулировкам других свойств
параллельности прямой и плоскости. При доказательстве теорем принимают активное
участие.
В
конце урока были подведены итоги, на которых еще раз вернулись к приему
обобщения, выделили его сущность и особенности, пришли к выводу, что этот прием
полезен для открытия новых фактов в математике.
Пример
2
Тема:
Прямая и плоскость в пространстве.
Учебник:
[24]
Тип
урока: урок решения ключевых задач.
Учебная
задача: Учить учащихся применять признаки и
свойства параллельности прямой и плоскости при решении задач. Рассмотреть
свойство скрещивающихся прямых, и путем обобщения перейти к задаче на доказательство
существования плоскости, параллельной данной прямой.
Диагностируемые
цели:
В
результате ученик:
—
имеет представление о свойстве скрещивающихся прямых;
—
использует прием обобщения для составления новых задач;
—
осуществляет доказательство параллельности прямой и плоскости, используя
признаки параллельности прямой и плоскости.
Фрагмент
урока
—
Когда мы рассматривали скрещивающиеся прямые, то вы оставили в таблице место
для записи свойства. Давайте рассмотрим это свойство – задача № 3.011: Через
каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой
прямой, и притом только одна.
—
Рассмотрим скрещивающиеся прямые а и b.
Докажем, что через прямую a
проходит плоскость, параллельная прямой b,
и такая плоскость только одна.
Построим
прямую b1 ,
b1
|| b и
b1
пересекает прямую а. Через прямые
а и b1
можно провести плоскость α, и притом только одну. Откуда это следует?
(следствие из аксиом)
—
Почему плоскость α будет параллельна прямой b?
(по признаку: т.к. b1
|| b,
а b1α,
значит α||b)
Дано: Доказательство:
прямые
a и
b скрещиваются.
Доказать:
существует α: α||b,
аα,
α – единственная.
1) Существует
b1
|| b
и прямая b1 пересекает
прямую а.
2) Существует
плоскость α: а⊂
α, b1⊂
α, α – единственная (по следствию из аксиом).
3) b1
|| b,
а b1α,
то α||b
по признаку параллельности прямой и плоскости.
—
Итак, мы с вами сейчас доказали, что через каждую из двух скрещивающихся прямых
проходит плоскость, параллельная другой прямой, и притом только одна. А если
рассмотреть другие случаи взаимного расположения прямых: если прямые
параллельны или пересекаются, можем ли мы в этом случае провести плоскость
через одну прямую и параллельную другой?
У
нас возникает задача на доказательство существования плоскости, параллельной
данной прямой.
Итак,
обобщив данную задачу на рассмотрение различных случаев взаимного расположения
прямых в пространстве, мы с вами пришли к новой задаче, в которой требуется
доказать существование плоскости, параллельной данной прямой.
На прошлом уроке мы с вами доказали существование прямой, параллельной
плоскости. А сейчас нужно доказать существование плоскости, параллельной данной
прямой.
Давайте
докажем это. Необходимо опять решать задачу на построение.
Рассмотрим
задачу № 3.004:
Через
данную прямую а провести плоскость, параллельную данной прямой b.
(Рассмотреть возможные случаи взаимного расположения прямых а и b.)
[Записи
будем вести в таблице, в колонке существование.]
—
Рассмотрим случай, когда прямые а и b
параллельны. Если a||b,
то через прямую а можно провести любую плоскость, кроме плоскости,
проходящей через прямые a и
b,
и она будет параллельна прямой b.
Объясните почему? (по признаку параллельности прямой и плоскости)
—
Как построить плоскость α, проходящую через прямую а?
(
Нужно взять произвольную точку А, не принадлежащую прямой а и
через прямую и точку провести плоскость.)
—
Как доказать, что плоскость α параллельна прямой b?
(a||b,
аα,
значит α||b по признаку)
—
А как вы думаете, сколько плоскостей, параллельных прямой b,
можно провести через прямую а? (Бесконечно
много, т.к. для построения плоскости мы выбрали точку произвольно.)
Дано: Построение:
прямые
a и
b. а)
a||b
Построить:
α, аα,
α||b.
1) Возьмем
точку А, не принадлежащую прямой а.
2) Существует
плоскость α: а⊂
α, А⊂
α, α – единственная (по следствию из аксиом).
3) а
|| b,
а аα,
то α||b
по признаку параллельности прямой и плоскости.
—
Рассмотри второй случай, когда прямые а и b
пересекаются в некоторой точке М.
—
Можно ли провести плоскость, проходящую через прямую а и параллельную
прямой b?
(Нет,
т.к. если мы проведем плоскость через прямую а, то прямая b будет
либо лежать в этой плоскости, либо пересекать ее.)
б)
Если прямые а и b имеют
общую точку, то любая плоскость α, содержащая прямую а, имеет с прямой b
хотя бы одну общую точку (точку М). И тогда плоскость α и прямая b
не параллельны.
—
Случай, когда прямые а и b
скрещиваются, мы с вами рассмотрели в задаче № 3.011.
—
Таким образом, мы сейчас доказали существование плоскости, параллельной данной
прямой. Как мы пришли к этой задаче?
(рассмотрели
свойство скрещивающихся прямых и обобщили его на случай различного взаимного
расположения прямых в пространстве.)
—
Итак, путем обобщения, как и на предыдущем уроке, мы с вами получили новую
задачу – задачу на построение плоскости, параллельной данной прямой.
Домашнее
задание – решить следующую задачу и сформулировать для нее обобщение: Даны
две скрещивающиеся прямые a
и b. Через каждую точку
прямой а проводится прямая, параллельная прямой b.
Докажите, что все такие прямые лежат в одной плоскости. Как расположена эта
плоскость по отношению к прямой b?
Ответ обоснуйте.
Анализ урока
На
уроке рассмотрено свойство скрещивающихся прямых, и путем обобщения учащиеся
переходят к задаче на доказательство существования плоскости, параллельной
данной прямой. Такой способ получения новых задач более интересный, так как
ученики сами принимают активное участие в формулировке задачи, а не просто
читают некоторый номер из учебника, сказанный учителем. У них повысился интерес
к решению задачи, так как она сформулирована ими.
В
домашнем задании им тоже нужно сформулировать обобщение данной задачи. Таким
образом, учитель может проверить усвоение приема обобщения каждым учеником и их
творческие способности.
Пример
3
Тема:
Перпендикулярность прямых в пространстве.
Учебник:
[25],
§7, п.7.2.
Тип
урока: урок изучение нового.
Учебная
задача: Выявить и изучить особый случай во
взаимном расположении двух прямых — перпендикулярность двух прямых в
пространстве: сформулировать определение, доказать существование данных
объектов и выявить признак перпендикулярности двух прямых. Диагностируемые
цели:
В
результате ученик:
—
знает определение перпендикулярных прямых;
—
имеет представление о признаке перпендикулярности двух прямых;
—
учится применять прием обобщения при формулировке признака перпендикулярности
двух прямых;
—
осуществляет поиск доказательства теорем и решения задач методом восходящего
анализа и синтеза.
Ход
урока
I.
Мотивационно-ориентировочная часть.
—
Рассмотрим следующий рисунок:
—
Каково взаимное расположение следующих прямых:
a) АD
и B1C1;
b) ВС
и АВ;
c) В1D
и BD;
d) В1D1
и AB;
e) DC и
B1C1.
—
Чему равен угол между прямыми АВ и ВС; АВ и СС1;
DC
и B1C1?
—
Как определяется угол между двумя прямыми в пространстве?
(
Если прямые параллельны, то величина угла между ними считается равной нулю. За
величину угла между пересекающимися прямыми принимается величина наименьшего из
углов, образованных этими прямыми. За величину угла между двумя скрещивающимися
прямыми принимается величина угла между параллельными им пересекающимися в
некоторой точке прямыми.)
—
Какой может быть величина угла между прямыми? (от 0о до 90о)
—
Как называются прямые на плоскости, угол между которыми равен 90о?
(Перпендикулярными)
—
Итак, две пересекающиеся прямые называются перпендикулярными, если угол между
ними равен 90о. Аналогичное определение перпендикулярных прямых
дается и в пространстве. Попробуйте сформулировать его.
(
Две прямые в пространстве называются перпендикулярными, если величина угла
между ними равна 90о)
—
Из примера мы видим, что перпендикулярные прямые могут пересекаться и могут
быть скрещивающимися.
Итак,
мы с вами ввели новое определение, т.е. рассмотрели новое отношение между двумя
прямыми – перпендикулярность. Изучить отношение перпендикулярности прямых это
значит доказать существование данных объектов, «выявить» и доказать признаки и
свойства. Как мы доказываем существование? (Решаем задачу на построение)
[Далее
решается задача на построение.]
—
Давайте вернемся к примеру, рассмотренному в начале урока. Мы с вами выяснили,
что угол между прямыми АВ и СС1 равен 90о.
Что мы делаем для нахождения угла между скрещивающимися прямыми?
(Строим
им параллельные прямые, которые пересекаются в некоторой точке)
—
Но в этом примере не нужно было даже строить параллельные прямые, т.к. для
прямой АВ уже есть параллельная ей прямая DC,
пересекающая прямую СС1. То есть из того, что одна из
параллельных прямых перпендикулярна к третей прямой, мы можем делать вывод, что
и другая прямая перпендикулярна к этой прямой. Что же мы такое установили?
(Признак
перпендикулярности двух прямых)
—
Давайте запишем его и докажем:
Если
одна из двух параллельных прямых перпендикулярна к третей прямой, то и другая
прямая перпендикулярна к этой прямой.
—
Что нам дано? (a||b,
ас)
Докажем,
что bс.
—
Известно, что ас,
т.е. угол между прямыми а и с равен 90о. Как мы
находим величину угла между двумя прямыми в пространстве?
(Строим
им параллельные прямые, которые пересекаются в некоторой точке)
—
Давайте построим через произвольную точку М прямые параллельные прямым а
и с: МА ||a,
MC ||
c.
Чему
равен угол АМС ? ( АМС=90о
, т.к. ас)
—
По условию известно, что a||b,
а по построению a||МА,
тогда как расположены прямые b
и МА ?
(b
параллельно АМ по свойству транзитивности параллельности прямых)
—
Итак, прямые b
и с параллельны соответственно прямым МА и МС, угол между
которыми равен 90о . Тогда как расположены прямые b
и с? (bс
)
Дано:
Доказательство:
a||b,
ас
.
Доказать:
bс.
1) Построим
МА ||a,
MC ||
c.
2) ас,
то АМС=90о
(по определению перпендикулярных прямых).
3) a||b
( по условию), a||МА
(по построению), тогда b||МА
( по свойству транзитивности параллельности прямых).
4) c
|| MC
, b||МА, АМС=90о,
тогда bс
(по определению перпендикулярных прямых).
— Итак, мы с вами доказали
признак перпендикулярности двух прямых. Сформулируйте обратное утверждение.
( Если две прямые
перпендикулярны к третей прямой, то они параллельны)
— Верно ли это обратное
утверждение? (Нет)
— Обоснуйте свой ответ.
— Таким образам, сегодня
на уроке мы рассмотрели еще один особый случай взаимного расположения двух
прямых в пространстве – перпендикулярность. Какие прямые называются
перпендикулярными?
(
Две прямые в пространстве называются перпендикулярными, если величина угла
между ними равна 90о)
—
Сформулируйте признак перпендикулярности двух прямых в пространстве.
(Если
одна из двух параллельных прямых перпендикулярна к третей прямой, то и другая
прямая перпендикулярна к этой прямой.)
—
Как мы получили признак?
(Обобщили
пример, рассмотренный в начале урока)
—
То есть на основе конкретного примера выдвинули гипотезу, которую в последующем
доказали. С таким приемом обобщения мы уже знакомы.
—
Также вы сформулировали обратное предложение для признака и убедились, что оно
не верно. То есть, не всегда обратив истинное предложение, мы получаем истинное
высказывание. Для установления истинности нужно проводить доказательство.
Анализ урока
На
данном уроке был рассмотрен особый случай взаимного расположения двух прямых в
пространстве – перпендикулярность. На этапе актуализации, на конкретном примере,
рассмотрели возможные случаи расположения прямых в пространстве. Ученики сами,
по аналогии с плоскостью, сформулировали соответствующее определение
перпендикулярных прямых в пространстве. Используя рассмотренный в начале урока
пример, пришли к формулировке признака. Ученики были активно задействованы при
открытии признака перпендикулярности двух прямых, так как прием обобщения им
уже хорошо знаком и не возникло трудностей при формулировке обобщения.
Также
на уроке ученики сформулировали обратное предложение для признака, которое
оказалось неверным. Сами же привели контрпример, показывающий, что это
утверждение не верно.
Пример
4
Тема:
Параллельные прямые, перпендикулярные к плоскости.
Учебник:
[25],
§9.
Цель:
Установить связь между параллельностью прямых и их перпендикулярностью к
плоскости.
Фрагмент урока
— На прошлом уроке вы
доказали существование прямой, перпендикулярной данной плоскости и
существование плоскости, перпендикулярной данной прямой. Также сформулировали
выводы, которые следуют из решения этих задач. Сформулируйте их.
(Через
каждую точку пространства проходит единственная плоскость, перпендикулярная
данной прямой, следовательно, две различные плоскости, перпендикулярные одной и
той же прямой, не имеют общих точек.
Через
каждую точку пространства проходит единственная прямая, перпендикулярная
данной плоскости, следовательно, две различные прямые, перпендикулярные одной и
той же плоскости, не могут пересекаться.)
—
А сегодня на уроке давайте докажем две теоремы, в которых устанавливается связь
между параллельностью прямых и их перпендикулярностью к плоскости.
Мы
знаем из планиметрии теорему, в которой устанавливается связь между
параллельностью прямых и их перпендикулярностью к третей прямой. Давайте
вспомним ее.
(Если
одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая
прямая перпендикулярна к этой прямой)
—
А если две прямые перпендикулярны не к прямой, а к плоскости? Что изменится в
формулировке теоремы? Попробуйте сформулировать аналогичное утверждение о
перпендикулярности двух прямых к плоскости.
(
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и
другая прямая перпендикулярна этой плоскости.)
-Итак,
используя прием аналогии, мы сформулировали с вами новое утверждение, но это
утверждение может оказаться и ложным. Поэтому его нужно доказать. Докажем его.
—
Что нам дано? ( l1||l2,
l1α)
—
А что требуется доказать? (l2α)
—
Как доказать, что прямая перпендикулярна плоскости?
(Нужно
использовать признак перпендикулярности прямой и плоскости: Если прямая
перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости, то
она перпендикулярна этой плоскости.)
—
То есть нам необходимо доказать, что прямая l2
перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости α.
Давайте построим две произвольные пересекающиеся прямые в плоскости α – прямые а
и b.
Тогда как расположена прямая l1
по отношению к прямым а и b?
(Перпендикулярна, по определению перпендикулярной прямой к плоскости, т.к. по
условию l1α)
—
А прямая l2?
(Тоже
перпендикулярна по признаку перпендикулярности двух прямых в пространстве:
Если одна из двух параллельных прямых перпендикулярна к третей прямой, то и
другая прямая перпендикулярна к этой прямой.)
—
Таким образом, мы получили, что прямая l2
перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости α.
Что из этого следует?
(Прямая
l2
перпендикулярна плоскости α по признаку перпендикулярности прямой и плоскости)
Дано:
Доказательство:
l1||l2,
l1α
Доказать:
l2α
1) Построим
две пересекающиеся прямые а и b в
плоскости α.
2) l1α,
тогда l1а
, l1b
(по определению перпендикулярной прямой к плоскости)
3) l1||l2
, l1а
, тогда l2а
; l1||l2
, l1b,
тогда l2b (по
признаку перпендикулярности двух прямых в пространстве)
4) l2а,
l2b,
аα,
bα,
тогда l2α
(по признаку перпендикулярности прямой и плоскости)
—
Сформулируйте обратное утверждение.
(Если
две прямые перпендикулярны к плоскости, то они параллельны.)
—
Как вы думаете, верно ли это утверждение? (Наверное, верно)
—
Надо доказать.
—
Что дано? (l1α
, l2α)
—
А что требуется доказать?( l1||l2)
—
Итак, нам нужно доказать параллельность двух прямых. А как вообще могут
располагаться две прямые в пространстве? ( Могут пересекаться, быть
скрещивающимися или параллельными)
—
Если мы докажем, что прямые не могут ни пересекаться, ни скрещиваться, то
останется только один случай взаимного расположения прямых – параллельность,
т.е. будем использовать при доказательстве метод исчерпывающих проб.
—
Почему прямые l1
и l2
не могут пересекаться?
(
В этом случае через одну точку проходит две прямые перпендикулярные плоскости.
Это противоречит единственности перпендикуляра, проведенного через точку к
данной плоскости.)
—
Предположим, что прямые l1
и l2
скрещиваются. Проведем через любую точку А прямой l1
прямую АВ, параллельную l2,
но не совпадающую с l1.
Как расположена прямая АВ по отношению к плоскости α?
(Перпендикулярна
по предыдущей теореме)
—
Мы получили два перпендикуляра (прямые l1
и АВ) к плоскости α, проходящих через точку А,
что невозможно. Следовательно, прямые l1
и l2
не могут быть скрещивающимися.
Таким
образом, остается только один случай взаимного расположения прямых –
параллельность. Теорема доказана.
—
Итак, сегодня на уроке мы доказали две теоремы, в которых устанавливается связь
между параллельностью прямых и их перпендикулярностью к плоскости.
Сформулируйте их.
(Если
одна из двух параллельных прямых перпендикулярна к плоскости, то и другая
прямая перпендикулярна этой плоскости.
Если
две прямые перпендикулярны к плоскости, то они параллельны.)
—
Чем является первая теорема?
(свойством
параллельных прямых)
-Как
мы ее получили?
(
сформулировали аналогичную теорему для теоремы из планиметрии)
—
То есть мы использовали прием аналогия для составления новой задачи. В чем
сущность этого приема?
(
Мы известные факты из планиметрии перенесли в стереометрию)
—
То есть сформулировали аналогичное утверждение для параллельных прямых в
пространстве. Этот прием можно также назвать и обобщением, так как мы обобщили
имеющиеся знания для общего случая в пространстве. Итак, использую эти приемы,
мы пришли не просто к некоторой задаче, а к теореме.
—
А как мы получили вторую теорему?
(сформулировали
предложение, обратное свойству)
—
Мы доказали истинность этого утверждения. Тем самым, получили еще один признак
параллельности двух прямых.
Таким образом,
формулируя предложение, обратное данному, составление аналогичной задачи или
используя прием обобщения, мы можем получить новую задачу, которая может
оказаться теоремой. Об этом не стоит забывать, и нужно пытаться самим, где это
возможно, использовать этот прием.
Анализ урока
В
начале урока ученики вспомнили из планиметрии теорему, в которой
устанавливается связь между параллельностью прямых и их перпендикулярностью к
третьей прямой, по аналогии попытались сформулировать теорему для пространства.
Также, без особого труда, сформулировали обратное утверждение. Принимали
активное участие в ходе доказательства теорем.
Пример
5
Тема:
Теорема о трех перпендикулярах.
Цель:
Обучение учащихся решению задач, используя теорему о трех перпендикулярах, и
обучение использованию приемов обобщения и конкретизации при составлении задач.
Учебник:
[7].
Фрагмент
урока решения задач
— Решим следующую задачу:
Задача №149:
Отрезок AD перпендикулярен к
плоскости равнобедренного треугольника АВС. Известно, что АВ=АС=5
см, ВС=6 см, AD=12
см. Найдите расстояния от концов отрезка AD
до прямой ВС.
— Что нам известно в
данной задаче? (Отрезок AD
перпендикулярен к плоскости равнобедренного треугольника АВС. АВ=АС=5
см, ВС=6 см, AD=12
см.)
— А что необходимо найти?
(расстояния от концов отрезка AD
до прямой ВС)
— Сделайте рисунок к
данной задаче:
—
Что называется расстоянием от данной точки
до прямой?
—
(Длина перпендикуляра, проведенного из
данной точки к прямой)
—
Таким образом, нам необходимо построить
перпендикуляры из точек А и D
к прямой ВС.
—
Какой перпендикуляр мы с вами точно можем
построить?
(Из точки А, т.к. треугольник
равнобедренный, а в нем высота является и медианой. Пусть Е — середина ВС.
Тогда АЕ – медиана, а следовательно и высота треугольника АВС.)
—
То есть АЕ – это расстояние от
точки А до прямой ВС. Но в задаче еще необходимо найти расстояние
от точки D до
прямой ВС. Что будет расстояние?
( DЕ–
это расстояние от точки D
до прямой ВС, т.к. прямые DЕ
и ВС перпендикулярны по теореме о трех перпендикулярах.)
—
Итак, искомые отрезки мы построили. Теперь
их надо найти.
Как мы будем искать АЕ
и DЕ
?
(Из прямоугольных
треугольников)
— Какие треугольники надо
рассмотреть? ( ∆АВЕ и ∆АDЕ)
— Рассмотрим ∆АВЕ.
Какой вид этого треугольника? (прямоугольный)
— Тогда по теореме
Пифагора найдем АЕ:
ВЕ=ВС=3см
АЕ= см
— Рассмотрим ∆АDЕ.
Какой вид этого треугольника? (прямоугольный)
DЕ=см
— Итак, мы с вами нашли
расстояния от концов отрезка AD
до прямой ВС.
АЕ=4 см, DЕ=4см
— Как можно обобщить
данную задачу? Какой прием обобщения мы уже использовали на прошлых уроках?
(На предыдущих уроках мы
получали обобщение, формулируя гипотезу на основе рассмотрения частных
примеров.)
— Здесь можно применить
такой способ обобщения?
(нет)
— Возможны и другие пути
обобщения. Обобщение может также происходить при переходе от конкретных фигур к
более общим. Какая фигура рассматривается в задаче?
(равнобедренный
треугольник)
— Какая фигура будет обобщением
для равнобедренного треугольника?
(треугольник общего вида)
— Как можно задать
треугольник?
( по трем сторонам, по
двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам)
— А в данной задаче как
задается треугольник?
(по трем сторонам)
— То есть, чтобы задать
произвольный треугольник нужно задать все его стороны.
— Сформулируйте задачу
для произвольного треугольника.
(Отрезок AD
перпендикулярен к плоскости треугольника АВС. Известно, что АВ= 4
см, АС = 5 см, ВС = 6 см, AD =12
см. Найдите расстояния от концов отрезка AD
до прямой ВС.)
— А корректна ли эта
задача? Хватит ли нам данных, чтобы ее решить? И нет ли лишних данных? В чем
будет отличаться решение данной задачи от исходной?
( АЕ уже не будет
одновременно являться и медианой, и биссектрисой и высотой в треугольнике АВС)
— И как же будем находить
АЕ?
(используя метод
площадей)
— Таким образом мы
найдем сначала АЕ, а затем и DЕ.
То есть сформулированная нами задача корректна, и мы ее можем решить. Оформите
решение данной задачи у себя в тетрадях.
[Ученики самостоятельно
оформляют у себя в тетрадях решение задачи.]
— А как еще можно
обобщить данную задачу? Существует еще один способ обобщения – замена
конкретных данных буквами. Сформулируйте обобщение исходной задачи.
(Отрезок AD
перпендикулярен к плоскости треугольника АВС, со сторонами а, b
и c.
Известно, что AD=h.
Найдите расстояния от концов отрезка AD
до прямой ВС.)
— Итак, мы с вами сформулировали
обобщения данной задачи. Обратный процесс к обобщению есть конкретизация.
— Какие задачи, конкретизируя
вид треугольника, можно составить?
(Если в задаче вместо произвольного
треугольника рассмотреть правильный, то получим: Отрезок AD
перпендикулярен к плоскости равностороннего треугольника АВС, со
стороной 5 см. Известно, что AD=12
см. Найдите расстояния от концов отрезка AD
до прямой ВС.
Или вместо
равнобедренного треугольника рассмотреть прямоугольный равнобедренный
треугольник: Отрезок AD
перпендикулярен к плоскости прямоугольного равнобедренного треугольника АВС.
Известно, что катеты равны 5 см, а гипотенуза — 6 см, AD=12
см. Найдите расстояния от концов отрезка AD
до прямой ВС.)
— Решение этих задач будет
аналогично решению исходной задачи. Решите их самостоятельно дома.
Домашнее задание —
задача № 148: Прямая АК перпендикулярна к плоскости правильного треугольника
АВС, а точка М – середина стороны ВС. Докажите, что МКВС.
Решите эту задачу и на ее
основе сформулируйте новые, используя известные вам приемы составления задач.
Анализ
урока
В
ходе урока учащиеся активно принимали участие в формулировке новых задач. На
уроке познакомились с новыми приемами обобщения и с приемом конкретизации. При
формулировке новых задач трудностей не испытывали, задачи решали с большим
интересом, так как они были сформулированы самими учащимися.
Трудности
возникли при решении обобщенной задачи, так как там нужно было уже использовать
метод площадей, а не теорему Пифагора и свойства медианы. Ученики искали
аналогию в ходе решения задач и по этому у них возникла проблема в отыскании
расстояния от точки А до точки Е.
В
целом урок прошел успешно, ученикам понравилось самим составлять задачи. Это
намного интереснее процесс, чем просто решать готовые задачи из учебника.
С домашним
заданием справились большинство учащихся. На основе задачи №148 они
сформулировали следующие задачи:
1.
Прямая АК перпендикулярна к плоскости
равнобедренного треугольника АВС, а точка М – середина основания ВС. Докажите,
что МКВС.
2.
Прямая АК перпендикулярна к плоскости
произвольного треугольника АВС, а точка М – основание перпендикуляра,
проведенного к стороне ВС. Докажите, что МКВС.
Пример
6
Тема:
Теорема о трех перпендикулярах.
Цель:
Обучение учащихся решению задач, используя теорему о трех перпендикулярах и
обучение использованию приемов аналогии и обобщения при составлении задач.
Учебник:[24].
Фрагмент
урока
— Решим следующую задачу:
№ 3.034: Точка Р удалена
от каждой стороны правильного треугольника на 30 см. Найдите расстояние от
точки Р до плоскости треугольника, если площадь вписанного в этот треугольник
круга равна 576 см2.
— Давайте сделаем рисунок
к этой задаче и запишем дано:
Дано:
∆АВС –
правильный,
ρ(Р,АВ) = ρ(Р,ВС)
= ρ(Р,АС) =30 см,
Sкр=576
см2,
Найти:
ρ(Р, АВС)
—
Что означает, что точка Р удалена от каждой стороны правильного
треугольника на 30 см?
(расстояние
от точки Р до сторон треугольника равно 30 см)
—
Что называется расстоянием от точки до прямой?
(длина
перпендикуляра, опущенного из данной точки к данной прямой)
—
То есть нужно построить из точки Р перпендикуляры к сторонам
треугольника. Построим эти перпендикуляры: РМАВ, РК
ВС, РН
АС.
—
Что известно о РМ, РК, РН?
(РМ
= РК = РН=30 см)
—
Что необходимо найти?
(расстояние
от точки Р до плоскости треугольника)
—
Что называется расстоянием от точки до плоскости?
(
расстояние от точки до плоскости – это длина перпендикуляра, опушенного из этой
точки к плоскости)
—
Построим этот перпендикуляр. Отрезок РО нам и надо найти в этой задаче.
Известно,
что РМ = РК = РН=30 см. А чем являются РМ, РК, РН по отношению к
плоскости треугольника? (наклонными)
—
А что являются проекциями этих наклонных на плоскость треугольника АВС?
(МО,
НО, КО)
—
Тогда, что мы можем сказать о проекциях наклонных на плоскость АВС, если
знаем, что наклонные равны? ( МО = НО = КО по свойству наклонных)
—
Итак, РМ – наклонная, РО – перпендикуляр, ОМ – проекция
наклонной на плоскость треугольника, РМ перпендикулярно АВ. Тогда
какой вывод мы можем сделать?
(
ОМАВ по обратной теореме о трех
перпендикулярах)
—
Аналогично, ОКВС, ОН
АС.
Таким
образом, точка О равноудалена от сторон треугольника АВС. Что это
означает?
(
О — центр круга, вписанного в треугольник АВС)
—
Какое условие задачи мы еще не использовали? (Sкр=576
см2)
—
По какой формуле вычисляется площадь круга? (Sкр=
πr2 )
—
Тогда чему равен радиус? ( r
= 24)
—
Что является радиусом в нашей задаче? (r =МО = НО = КО)
—
Тогда как мы можем найти РО?
(из
прямоугольного треугольника РОМ по теореме Пифагора РО = 18)
—
Итак, мы нашли расстояние от точки Р до плоскости АВС. Оно равно
18 см.
— К какому важному выводу
мы пришли в этой задаче?
(точка
О – центр круга, вписанного в треугольник АВС)
—
А что это за точка О?
(
О – основание перпендикуляра, опущенного из точки Р на плоскость
треугольника)
—
На каком основании мы сделали этот вывод? Что нам было известно?
(
точка Р равноудалена от каждой стороны правильного треугольника)
—
Итак, если точка равноудалена от сторон правильного треугольника, то основание
перпендикуляра, опущенного из этой точки на плоскость треугольника, есть центр
окружности, вписанной в этот треугольник.
—
Этот вывод мы сделали только для правильного треугольника. А как можно
обобщить эту задачу?
(рассмотреть
вместо правильного треугольника произвольный: Точка Р удалена от
каждой стороны треугольника на 30 см. Найдите расстояние от точки Р до
плоскости треугольника, если площадь вписанного в этот треугольник круга равна
576 см2.)
—
А верно ли это, то есть корректна ли задача?
(да,
так как окружность можно вписать в любой треугольник)
—
Итак, мы рассмотрели в данной задаче произвольный треугольник, а какие обобщения
еще возможны? Если мы отбросим ограничения на фигуру (на количество вершин,
форму), то есть рассмотрим например четырехугольник, пятиугольник или
произвольный многоугольник тогда как будет звучать задача?
(Точка
Р удалена от каждой стороны многоугольника на 30 см. Найдите расстояние от
точки Р до плоскости многоугольника, если площадь вписанного в этот
многоугольник круга равна 576 см2.)
—
Какой вывод мы сделали в первой задаче?
(Если
точка равноудалена от сторон правильного треугольника, то основание перпендикуляра,
опущенного из этой точки на плоскость треугольника, есть центр окружности,
вписанной в этот треугольник.)
—
Сформулируйте обобщенный вывод для произвольного многоугольника.
(Если
точка равноудалена от всех сторон многоугольника, то основание перпендикуляра,
опущенного из этой точки на плоскость многоугольника, есть центр окружности,
вписанной в этот многоугольник.)
—
А верно ли это?
(Нет,
так как окружность можно вписать только в правильный многоугольник и в
выпуклый четырехугольник, у которого сумма противоположных сторон равны)
-Тогда
как будет звучать задача?
(Точка
Р удалена от каждой стороны правильного многоугольника на 30 см. Найдите
расстояние от точки Р до плоскости многоугольника, если площадь
вписанного в этот многоугольник круга равна 576 см2.)
—
Итак, путем обобщения и аналогии мы с вами пришли к новым задачам, которые
позволили сделать очень важный вывод.
—
Решите следующую задачу:
Точка
Р равноудалена от всех сторон параллелограмма, одна из сторон которого равна 4
см. Найдите периметр параллелограмма.
[Ученики
решают эту задачу, используя сделанный вывод в предыдущей задаче:
—
В какой параллелограмм можно вписать окружность?
(
ромб или квадрат)
—
Тогда как найти периметр параллелограмма, зная его сторону?
(
Р =16 см) ]
-Итак,
сегодня на уроке при решении задач мы сделали важный вывод. Вспомните его.
(Если
точка равноудалена от всех сторон правильного многоугольника, то основание
перпендикуляра, опущенного из этой точки на плоскость многоугольника, есть
центр окружности, вписанной в этот многоугольник.)
—
Как мы пришли к этому выводу?
(Сначала
сформулировали аналогичные задачи, а затем обобщили полученные сведения на
более общий случай.)
-Таким
образом, прием обобщения и аналогии нам помогает открывать новые факты, которые
необходимы в дальнейшем при решении других задач.
Об этом не стоит
забывать, и нужно пытаться самим использовать эти приемы составления задач.
Домашнее задание: № 3.036: Точка О
– центроид правильного треугольника АВС; ОР – прямая, перпендикулярная
плоскости АВС; М – произвольная точка прямой ОР (МО).
Докажите, что расстояния от точки М до вершин треугольника АВС равны.
Решите
данную задачу, и на ее основе попытайтесь сформулировать новые задачи,
используя известные вам приемы составления задач.
Анализ
урока
Данный
урок был посвящен решению задач на применение теоремы о трех перпендикулярах и
ей обратной, а также обучению использованию приемов аналогия и обобщения при
составлении задач. В ходе урока все ученик были задействованы и при решении, и
при составлении задач. При решении первой задачи учащиеся повторили, что
называется расстоянием от точки до плоскости, от точки до прямой; сделали очень
важный вывод, который в последующем им пригодится при решении других более
сложных задач. При формулировке аналогичных задач и обобщенных трудностей не
возникло, так как учащиеся на прошлых уроках уже познакомились с этими
приемами и умеют их применять. Решая
последнюю на уроке задачу, ученики догадались, что нужно использовать вывод,
сделанный ими в предыдущей задаче. Поэтому решение этой задачи потребовало мало
времени и усилий.
Урок получился интересным,
динамичным и познавательным.
В домашнем задании, на
основе задачи № 3.036, ученики составили следующие задачи: Точка О – точка
пересечения диагоналей квадрата АВСD;
ОР – прямая, перпендикулярная плоскости АВСD;
М – произвольная точка прямой ОР (МО). Докажите, что расстояния
от точки М до вершин квадрата АВСD равны.
Точка О – точка
пересечения диагоналей правильного многоугольника; ОР – прямая,
перпендикулярная плоскости этого многоугольника; М – произвольная точка прямой
ОР (МО). Докажите, что расстояния от точки М
до вершин многоугольника равны.
Пример
7
Тема: Перпендикулярность
прямой и плоскости.
Учебник:
[7]
Тип урока:
урок-практикум.
Учебная задача:
Обучение приемам составления задач.
Диагностируемые цели
урока:
В результате ученик:
— знает некоторые
приемы составления задач ( составление задачи, обратной данной; выведение новых
следствий из условий);
— понимает, как
пользоваться приемами составления задач;
— учится применять
приемы составления задач.
Форма обучения:
фронтальная.
Структура урока:
1) Мотивационно –
ориентировочная часть
— на этапе актуализации
ученики повторяют теорему о трех перпендикулярах, определение двугранного угла;
— постановка учебной
задачи
2) Содержательная часть
— решение задачи №161 и
составление новых задач на ее основе.
3) Рефлексивно –
оценочная часть
— подводятся итоги
урока, и записывается домашнее задание.
Ход
урока
I.
Мотивационно – ориентировочная часть
—
На предыдущих уроках мы с вами изучили теорему о трех перпендикулярах. Давайте
вспомним формулировку этой теоремы.
(Прямая,
проведенная в плоскости через основание наклонной перпендикулярно к ее проекции
на эту плоскость, перпендикулярна и к самой наклонной)
—
Мы также изучили с вами и двугранные углы. Какие углы называются двугранными?
(Двугранным
углом называется фигура, образованная двумя полуплоскостями с общей
ограничивающей их прямой)
II.
Содержательная часть
—
Данный урок мы посвятим с вами решению одной задачи, которая является ключевой.
Откроем учебник на стр.46 и прочитаем задачу №161:
Луч
ВА не лежит в плоскости неразвернутого угла CBD.
Докажите, что если , причем
о,
то проекцией луча ВА на плоскость CBD
является биссектриса угла CBD.
—
Запишем что дано, и что требуется доказать. Сделаем рисунок к задаче.
Дано: Доказательство:
CBD – неразвернутый;
Луч ВА не
лежит в плоскости CBD;
ABC
= ABD;
ABC
<90o.
Доказать:
Проекция ВА
на плоскость CBD
есть
биссектриса CBD.
— Что нам требуется
доказать?
(
Что проекция ВА на плоскость CBD
есть биссектриса CBD)
— Для начала построим
проекцию луча ВА на плоскость CBD
.
Что будет проекцией этого луча?
(Луч с началом в точке
В)
— Построим проекцию точки
А на плоскость CBD.
Что для этого нужно сделать?
( Провести перпендикуляр
из точки А на плоскость CBD)
— Обозначим основание
этого перпендикуляра буквой О. Почему эта точка будет внутри угла CBD?
Так подсказывает наша интуиция, но нам необходимо доказать, что О –
проекция точки А на плоскость CBD,
причем точка О – внутренняя точка угла CBD.
—
Т.к. мы знаем, что ABD
– острый, то проекция точки А на прямую BD
будет находиться на луче BD.
Построим эту точку и обозначим ее буквой N.
—
Аналогично построим перпендикуляр к лучу ВС. Точка М – проекция
точки А на луч ВС. Через точку М проведем прямую m перпендикулярную
ВС, а через точку N
прямую n перпендикулярную BD.
Прямые m и n
будут пресекаться во внутренней точке О угла СBD,
т.к. СBD
– неразвернутый. Этот факт известен из планиметрии.
— Докажем, что точка О
есть проекция точки А на плоскость CBD,
т.е. докажем, что прямая АО перпендикулярна к
плоскости CBD.
Как доказать, что АО перпендикулярна CBD?
( Необходимо показать,
что АО перпендикулярна к двум пересекающимся прямым, лежащим в этой
плоскости)
— Какие прямые нужно
рассмотреть?
Мы с вами проводили
прямую m перпендикулярную
ВС и АМ перпендикулярную ВС. Какой вывод мы можем сделать?
( Прямая ВС
перпендикулярна плоскости МАО и поэтому она перпендикулярна любой прямой
лежащей в этой плоскости, а значит и прямой АО)
— Рассуждая аналогично,
мы получим, что прямая BD перпендикулярна
АО. Мы нашли с вами две пересекающиеся прямые перпендикулярные к АО.
Что из этого следует?
(АО перпендикулярна
к плоскости CBD)
— Следовательно, точка О
есть проекция точки А на плоскость CBD.
А что будет проекцией
луча ВА на плоскость CBD?
( Луч ВО)
— Итак, проекцию луча ВА
на плоскость CBD
мы нашли. Теперь нам необходимо доказать, что ВО – биссектриса угла CBD.
Как мы будем доказывать?
( Нужно доказать либо,
что углы МВО и NBO
равны, либо, что точка О равноудалена от сторон угла)
— Что нам известно в
данной задачи?
()
— Элементами каких
треугольников являются эти углы?
(Треугольников АВМ
и АВN )
— Рассмотрим треугольники
АВМ и АВN.
Какие они?
( Во-первых, они
прямоугольные, а во-вторых – равные. Они равны по гипотенузе АВ и по
острому углу)
— Что следует из того,
что эти треугольники равны?
( МВ = ВN
и АМ = АN)
— Элементами каких
треугольников являются МВ и ВN?
(Треугольников МОВ
и NОВ)
— Что следует из
равенства МВ и ВN
для этих треугольников?
( Эти треугольники равны,
т.к. они прямоугольные, ОВ – общая и МВ = ВN)
— Какие следствия мы
можем вывести?
(Либо МВО
= NBO, а
отсюда следует, что ВО – биссектриса, либо МО=NO,
т.е. точка О равноудалена от сторон угла, а следовательно, ВО –
биссектриса)
—
Итак, задача решена. Мы с вами доказали, что проекция ВА на плоскость CBD
есть биссектриса CBD.
Но из условий данной задачи можно вывести другие следствия. Подумайте какие.
— Какие следствия мы
выявили из равенства треугольников АВМ и АВN?
( МВ = ВN
и АМ = АN)
— Чем являются АМ и
АN
по отношению к сторонам угла?
(перпендикулярами)
— Да! А длины отрезков АМ
и АN
есть расстояния до сторон угла и они равны, значит, точка А равноудалена
от сторон угла. А точку А на луче мы какую брали? (произвольную)
— Таким образом, делаем
вывод: любая точка луча ВА равноудалена от сторон данного угла.
— Какие еще мы
рассматривали треугольники?
(Треугольники МОВ
и NОВ)
— Но из равенства этих
треугольников мы все полезные следствия вывели. Есть ли на рисунке еще равные
треугольники?
( Треугольники МОА
и NOA.
Они равны по трем сторонам)
— Что из этого следует?
( АМО
= АNO и
МАО = NАО
)
— А что это за угол АМО
? Как называются такие углы?
(Линейный угол
двугранного угла при ребре ВС )
— Так как линейные углы
равны, то равны и двугранные углы. То есть, грани АВС и АВD
наклонены к грани СВD
под одним и тем же углом.
— У нас было еще одно
следствие из равенства треугольников, то что
МАО
= NАО.
Это, что за углы?
( Углы, образованные перпендикуляром,
проведенным из точки А к сторонам данного угла и перпендикуляром к
плоскости CBD)
— Таким образом, перпендикуляры,
проведенные из произвольной точки луча ВА к сторонам данного угла, образуют
равные углы с перпендикуляром, проведенным из этой точки к плоскости CBD.
— Итак, не меняя условия
задачи, мы вывели с вами много следствий. Мы фактически с вами сейчас
составляли новые задачи. Сформулируйте эти задачи.
( 1. Луч ВА не
лежит в плоскости неразвернутого угла CBD.
Докажите, что если , причем
о,
то любая точка луча ВА равноудалена от сторон данного угла.
2. Луч ВА не
лежит в плоскости неразвернутого угла CBD.
Докажите, что если , причем
о,
то грани АВС и АВD наклонены
к грани СВD
под одним и тем же углом.
3. Луч ВА не
лежит в плоскости неразвернутого угла CBD.
Докажите, что если , причем
о,
то перпендикуляры, проведенные из произвольной точки луча ВА
к сторонам данного угла, образуют равные углы с перпендикуляром, проведенным из
этой точки к плоскости CBD.)
— А какой прием
использовали?
( Выводили следствия из
условия)
— На основе данной задачи
можно составить и другие задачи. А как их получить? В качестве условия можно
взять одно из следствий, которые мы с вами только что вывели, а заключение
оставить прежним, или поменять условие и заключение местами. Это что за прием?
(Составление задачи,
обратной данной)
— Составьте какую-нибудь
задачу, обратную данной.
( Луч ВА не лежит
в плоскости неразвернутого угла CBD.
Точка А равноудалена от сторон угла CBD
и о. Докажите, что
.)
— Давайте решим эту
задачу.
[ Ученик решает эту
задачу с места:
Т.к. точка А равноудалена
от сторон угла CBD,
то АМ = АN.
Треугольники МОА и NOA
равны по гипотенузе и катету. Из равенства этих треугольников следует, что МО=NO.
Рассмотрим треугольники МОВ и NОВ.
Они равны по гипотенузе и катету. Следовательно, МВ = ВN.
А значит, треугольники АВМ и АВN равны,
а отсюда следует, что.]
— Какие следствия можно
вывести из этой задачи?
( 1. Грани АВС и АВD наклонены
к грани СВD
под одним и тем же углом.
2. Перпендикуляры,
проведенные из произвольной точки луча ВА к сторонам данного угла,
образуют равные углы с перпендикуляром, проведенным из этой точки к плоскости CBD.
3. Проекцией луча ВА
на плоскость CBD
является биссектриса угла CBD.)
— То есть, брали другое
условие, а получили те же следствия.
Давайте составим еще одну
задачу.
( Луч ВА не лежит
в плоскости неразвернутого угла CBD.
Грани АВС и АВD наклонены
к грани СВD под
одним и тем же углом. Докажите, что если о
, то .)
[ Ученики с места решают
составленную задачу:
Т.к. грани АВС и АВD наклонены
к грани СВD под
одним и тем же углом, то углы АМО и АNO
равны. Эти углы являются элементами треугольников МОА и NOA.
Эти треугольники равны. Из равенства этих треугольников следует, что МО=NO.
Рассмотрим треугольники МОВ и NОВ.
Они равны по гипотенузе и катету. Следовательно, МВ = ВN.
А значит, треугольники АВМ и АВN равны,
а отсюда следует, что.]
— Из этой задачи мы тоже
можем вывести следствия. Назовите их.
( 1. Точка А равноудалена
от сторон угла CBD.
2. Перпендикуляры,
проведенные из произвольной точки луча ВА к сторонам данного угла,
образуют равные углы с перпендикуляром, проведенным из этой точки к плоскости CBD.
3. Проекцией луча ВА
на плоскость CBD
является биссектриса угла CBD.)
— Итак, в рассмотренной
конфигурации мы выделили ряд свойств. Какие это свойства?
( 1. Проекцией луча ВА
на плоскость CBD
является биссектриса угла CBD.
2. Точка А равноудалена
от сторон угла CBD.
3. Перпендикуляры,
проведенные из произвольной точки луча ВА к сторонам данного угла,
образуют равные углы с перпендикуляром, проведенным из этой точки к плоскости CBD.
4. Грани АВС и АВD наклонены
к грани СВD под
одним и тем же углом. )
— Мы показали, что если
выполняется одно из этих свойств, то выполняются и все остальные. А что это
означает?
( Эти свойства
равносильны)
— Следствия мы выводили,
заменяя только одно из условий – равенство углов. Но нам еще дано, что о. Почему это так важно? Какие
случаи еще возможны?
(о
и о)
— Если мы рассмотрим
случай, когда о, то на что
спроектируется луч ВА?
( На точку В)
— Этот случай нам не
интересен. Давайте рассмотрим случай, когда и
о. Что будет проекцией луча ВА
на плоскость CBD?
— Нам известно, что углы
ABD
и АВС тупые. Тогда какими будут углы смежные с ними?
(Острыми)
— Построим эти углы. Что
для этого нам нужно сделать?
(Построить дополнения к
лучам BD и
BC )
—
Т.е. теперь мы находимся в условиях только что решенной нами задачи:
,
причем о .
— Итак, как нам построить
проекцию луча ВА?
( Как в предыдущей
задаче)
— На что спроектируется
луч ВА?
( На биссектрису угла
вертикального с данным)
— Какую задачу мы только
что решили с вами? Сформулируйте ее.
( Луч ВА не лежит
в плоскости неразвернутого угла CBD.
Докажите, что если , причем
о,
то проекцией луча ВА на плоскость CBD
является биссектриса угла вертикального с углом CBD.)
— А при каких условиях луч
ВА спроектируется на биссектрису угла смежного с данным?
( Если сумма углов АВС и ABD
будет равна 180о)
— Но смежных углов с данным будет два. На
биссектрису какого угла спроектируется луч ВА?
(От того какой из углов будет тупой, а
какой острый будет зависеть биссектрисой какого смежного угла будет проекция
луча ВА на плоскость CBD)
III.
Рефлексивно – оценочная часть
— Итак, сегодня на уроке мы решали с
вами задачу №161, но фактически решили несколько задач, составленные на ее
основе. Таким образом, всякий раз, когда вы решаете задачу подумайте нельзя ли
на основе этой задачи составить новые, которые будут не менее интересными и
полезными.
Домашнее задание: задача № 136. Решите
данную задачу и на ее основе попробуйте сформулировать и решить новые задачи.
Анализ
урока
Он
не был реализован на практике в школе, так как он должен был проводиться после
изучения IV главы «Плоскости в
пространстве», поэтому он был проведен с магистрантами 2 курса. Это нисколько
меня не огорчило, так как и самим студентам, и мне было интересно проводить
этот урок. Студенты активно принимали участие в решении задач, в формулировках
новых задач, познакомились с различными приемами составления задач и были
удивлены, что на основе одной, на первый взгляд ничем не привлекательной
задачи, можно составить огромное число новых и интересных задач. Данной задачи
был посвящен не один урок (45 мин), а целое занятие. Это говорит о том, на
сколько интересный, творческий и довольно непростой процесс составления
задач.
Проверка
достоверности выдвинутой гипотезы исследования и эффективности разработанной
методики обучения осуществлялась в ходе опытной проверки. Он проводился в три
этапа (поисковый, констатирующий, обучающий) в период с 2009 по 2011 год.
Обучающий этап был проведен в МОУ лицей №180 г. Н. Новгорода в период
педагогической практики — с 8 ноября по 19 декабря 2010 года. В
качестве экспериментального класса был выбран 10 «А» класс, в котором
обучаются 24 человека: 14 девочек и 10 мальчиков. Данный класс
является классом с углубленным изучением математики, учитель Мартынова Ольга
Михайловна. Большинство учащихся занимаются на оценку «4». Оценку «5» имеют 4
человека. Есть неуспевающие – 3 человека.
Поисковый этап включал в себя выявление методики обучения
учащихся приемам составления задач, в частности приемам обобщения, аналогии,
конкретизации и составление задач, обратных данным. С этой целью был проведен
анализ методической и учебной литературы, сделан логико-дидактический анализ темы
«Прямая и плоскость в пространстве» с позиции возможности обучения составлению
задач и разработаны конспекты и фрагменты уроков, на которых использовались
различные приемы составления задач.
Цели
констатирующего этапа состояли в определении исходного состояния
сформированности у учащихся 10 «А» класса умения самостоятельно составлять
задачи. Для этого была проведена беседа с учителем.
Вопросы для беседы с учителем:
1)
Обучаете ли вы приемам составления задач?
2)
С какими приемами составления задач вы
познакомили учащихся?
3)
Как часто на уроках вы используете приемы
составления задач?
4)
Умеют ли учащиеся самостоятельно
составлять задачи?
5)
Какие качества мышления развиваются в
процессе составления задач?
В ходе беседы выяснилось,
что преподаватель использует приемы составления задач, но очень редко, так как
не хватает времени. Учитель познакомил учащихся со следующими приемами
составления задач: составление задач обратной данной, противоположной данной,
обратной к противоположной, составление аналогичной задачи и с использованием
приема обобщения. Не все из учащихся умеют составлять задачи, поэтому
необходима систематизация знаний. В процессе составления задач происходит
развитие всех качеств мышления: глубина ума, гибкость, критичность, самокритичность,
активность, самостоятельность, осознанность мыслительной деятельности.
Обучающий этап предполагал организацию процесса обучения
таким образом, чтобы формировать у учащихся 10 «А» класса умения
самостоятельного составления задач различными приемами: постановка
вопроса к условию задачи; составление задачи по готовому рисунку; составление
условия задачи по заданному вопросу; составление задачи, являющейся обобщением
данной; конкретизация обобщенного способа решения задач; составление задачи,
обратной данной; переформулировка требования задачи; замена части данных
исходной задачи другими данными без замены заключения задачи. Этот этап
проводился в период педагогической практики – с 8 ноября по 19 декабря 2010
года. Было проведено 10 уроков по геометрии по теме «Прямая и плоскость в
пространстве». В работе приведены конспекты уроков с последующим анализом.
После
анализа проведенных уроков можно сказать, что учащиеся научились составлять
задачи, а те знания, которые были получены до моих уроков, были приведены в
некоторую систему. Этот вывод был сделан по результатам выполнения домашней
работы и по работе на уроках. Если сравнить те умения и навыки составления
задач, которыми ученики владели до проведения опыта, то можно сделать вывод,
что приемы составления задач развивают их интеллектуальные способности, так как
в процессе составления задач задействованы самые различные мыслительные
операции: анализ, синтез, обобщение, конкретизация, аналогия и т.д.
Выводы по главе II
В
первой главе мы рассмотрели различные приемы составления задач. А проблеме
обучения этим приемам, разработке методики их обучения была посвящена вторая
глава нашей работы. На примере обучения приемам аналогии, обобщения и
конкретизации можно сделать вывод, что обучение приемам составления задач
проходит несколько стадии: на первой стадии
происходит знакомство учащихся с отдельными мыслительными приемами. Далее, совместно
с учащимися, необходимо прийти к выводу, что прием, с которым сегодня
познакомились в процессе изучения новой темы или решения задачи, не потребовал
лишней траты времени. Выбор того или иного мыслительного приема осуществляется
в зависимости от содержания изучаемого материала. Поэтому в дальнейшем, когда
учащиеся повторно встречаются с тем или иным приемом, напоминаем, что прием нам
уже знаком. Затем выделяем те особенности данной и ранее изученной темы,
благодаря которым целесообразно использовать именно этот прием. Учим
комплексному использованию различных мыслительных приемов во всевозможных
комбинациях друг с другом. На следующих уроках
необходимо вырабатывать привычку самостоятельного применения различных приемов
составления задач.
В
работе сделан логико-дидактический анализ темы «Прямая и плоскость в
пространстве» с позиции возможности обучения составлению задач. Он показал, что
данная тема имеет широкие возможности на использование различных приемов
составления задач. В работе приведены разработки конспектов и фрагментов
уроков для учащихся 10 класса, на которых используются различные приемы
составления задач и описана опытная проверка результатов теоретического
исследования.
После
проверки методических рекомендаций на практике, можно сделать вывод, что цель
работы достигнута, так как к концу практики учащиеся уже сами могли составлять
задачи и приемы составления задач они уже применяли осознанно.
Заключение
Целью
исследования было разработать методические рекомендации по обучению приемам
составления задач, направленных на развитие интеллектуальных способностей,
умений и навыков учащихся. Для ее решения необходимо было решить частные
задачи. Результатами их решения являются:
Анализ
психологической и дидактической литературы по проблеме исследования показал,
что существуют различные пути развития интеллекта,
но наиболее интенсивно это развитие происходит в ходе активного усвоения и
творческого применения знаний, т.е. на уроках, и главным образом на уроках
математики, так как математическое содержание оптимально
для развития интеллектуальных способностей.
Обучение
математике является одним из важнейших средств интеллектуального развития
ребенка. Моделью интеллектуальной мыслительной деятельности является процесс
работы над задачей. Математика — учебный предмет, в котором задачи используются
как цель, как средство, и как предмет изучения. Деятельность по решению и
составлению математических задач в процессе обучения математике является
сложной интегративной деятельностью: познавательная, учебная, математическая,
интеллектуальная, эвристическая, творческая. В
процессе составления и решения задач задействованы самые разные мыслительные
операции, приемы мышления, методы рассуждений, то есть в них участвуют и
эвристические, и логические, и речевые умения субъекта, являющиеся движущей
силой интеллектуального развития обучаемого. Поэтому очень важно научить учащихся
не только решать задачи, но и составлять задачи самостоятельно. Дело в том,
что составление задач часто требует проведения рассуждений, которые при решении
заданных задач не выполняются. Стало быть, составление задач служит развитию
творческого мышления учащихся.
В
работе рассмотрены следующие приемы составления задач: постановка вопроса к
условию задачи; составление задачи по готовому рисунку; составление условия
задачи по заданному вопросу; составление задачи, являющейся обобщением данной;
конкретизация обобщенного способа решения задач; составление задачи, обратной
данной; переформулировка требования задачи; замена части данных исходной задачи
другими данными без замены заключения задачи.
Более
подробно рассмотрены приемы аналогия, обобщения и конкретизации, разработаны
методические основы обучения школьников этим приемам.
При
обучении школьников различным приемам составления задач целесообразно
придерживаться следующих этапов:
1) Знакомство
учащихся с отдельными мыслительными приемами в процессе изучения некоторой
темы.
2)
Совместно с учащимися необходимо прийти к
выводу, что прием, с которым сегодня познакомились в процессе изучения новой
темы или решения задачи, не потребовал лишней траты времени.
3)
В дальнейшем, когда учащиеся повторно
встречаются с тем или иным приемом, напоминаем, что прием нам уже знаком. Далее
выделяем те особенности данной и ранее изученной темы, благодаря которым
целесообразно использовать именно этот прием.
4)
Учим комплексному использованию различных
мыслительных приемов во всевозможных комбинациях друг с другом.
5) Вырабатываем
привычку самостоятельного применения мыслительных приемов.
Был сделан логико-дидактический анализ темы «Прямая и плоскость в
пространстве» с позиции возможности обучения составлению задач. Он показал, что
данная тема имеет широкие возможности на использование различных приемов
составления задач. В работе приведены разработки конспектов и фрагментов
уроков для учащихся 10 класса, на которых используются различные приемы
составления задач и описана опытная проверка результатов теоретического
исследования.
После
проверки методических рекомендаций на практике, можно сделать вывод, что цель
работы достигнута, так как к концу практики учащиеся уже сами могли составлять
задачи и приемы составления задач они уже применяли осознанно. Самостоятельное
составление задач учащимися способствует их интеллектуальному развитию, т.к. в
процессе составления задач задействованы самые различные мыслительные операции:
анализ, синтез, обобщение, конкретизация, аналогия и т.д.
Список
литературы
1.
Ананьев Б.Г. Избранные психологические
труды: в 2-х т. т. II. — М.: Просвещение, 1980 — 370с.
2.
Большая Советская энциклопедия (в 30
томах)/под ред. А.М. Прохоров.- М.: Советская энциклопедия,. Т. 18 -.1974, —
632 с.
3.
Выготский Л.С. Воображение и творчество в
детском возрасте.- СПб.: СОЮЗ, 1997. — 96с.
4.
Выготский Л.С. Проблема развития
способностей. // Вопросы психологии. — 1996. — № 5. — 331c.
5.
Выготский Л.С. К вопросу о динамике
детского характера, Собр. соч. в 6 т. Т. 5. — М.: Педагогика, 1983. — 412c.
6.
Гальперин П.Я. Психология мышления и
учение о поэтапном формировании умственных действий. — М.: Просвещение, 1966. —
243с.
7.
Геометрия: Учеб. для 10– 11 кл. сред. шк./
Л.С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2005.
8.
Давыдов В.В. Проблемы развивающего
обучения: Опыт теоретического и экспериментального психологического
исследования. – М.: Педагогика, 1986. – 240 с.
9.
Дорофеев Г.В. Гуманитарно ориентированный
курс – основа учебного предмета «Математика» в общеобразовательной школе//
Математика в школе. – 1997. — №4.
10.
Дорофеев Г.В. О составлении циклов
взаимосвязанных задач // Математика в школе. – 1983. — №6.
11. Епишева
О.Б. Крупич В.И. Учить школьников учиться математике: Формирование приемов
учебной деятельности: Кн. для учителя. – М.: Просвещение, 1990.
12.
Иванова Т.А. Варьирование математических
задач как средство развития интеллектуальных способностей учащихся //Развитие
учащихся в процессе обучения математике: Межвуз. сб. науч. трудов. –
Н.Новгород: НГПУ, 1992.
13.
Иванова Т.А. Гуманитаризация общего
математического образования: Монография. – Нижний Новгород: НГПУ, 1998
14.
Иванова Т.А. Методологические знания и
умственное развитие школьников в процессе обучения математике
//Методологические знания как основа развивающего обучения математике:
Межвузовский сборник научных трудов. – Н.Новгород: Изд-во НГПУ, 1995.
15.
Канин Е.С. Развитие темы задачи //
Математика в школе. – 1991. — №3.
16.
Калмыкова З.И. Психологические принципы
развивающего обучения . – М., 1979.
17. Компетентностный
подход в формировании мыслительных операций на уроках математики. – www.oouk.vko.gov.kz/conference2_20.doc
18.
Леонтьев А.Н. О формировании способностей
// Вопросы психологии. — 1999.- №6. — С.58.
19.
Лернер И.Я. Качества знаний учащихся.
Какими они должны быть? – М., 1979.
20. Место
аналогии в обучении математике в школе
. — www.ref.by/refs/49/10050/1.html
21.
Пиаже Ж. Психология интеллекта //
Избранные психологические труды. — М.: Просвещение, 1969. — 381 с.
22.
Пойа Д. Как решать задачу. – М.,1961.
23.
Поспелов Н.Н., Поспелов И.Н. Формирование
мыслительных операций у старшекласников. — М.: Педагогика, 1989.
24.
Потоскуев Е.В. Геометрия. 10 кл.: Задачник
для общеобразоват. учреждений с углубл. и профильным изучением математики/ Е.В.
Потоскуев, Л.И. Звавич. — М.: Дрофа, 2004.
25.
Потоскуев Е.В. Геометрия. 10 кл.: учеб.
для общеобразоват. учреждений с углубл. и профильным изучением математики/ Е.В.
Потоскуев, Л.И. Звавич. — М.: Дрофа, 2007.
26.
Проблемное обучение как фактор
интеллектуального развития школьников. — http://fineref.ru/45/557/index1.1.html
27.
Психологический словарь / Под ред. В.П.
Зинченко, Б.Г. Мещерякова. – 2-е изд., перераб. и доп. – М.: Педагогика – Пресс,
1996.
28.
Развитие интеллектуальных способностей
детей средствами математики. – http//www.allbest.ru
29.
Развитие логического мышления учащихся при
решении задач. –
http://revolution.allbest.ru/pedagogics/00028649_4.html
30.
Рубинштейн С.Л. О мышлении и путях его
исследования. – М.,1958.
31.
Рубинштейн С.Л. Основы общей психологии.
изд. 4. — СПб.: Питр, 2007. — 720 с.
32.
Саввина О.А. Эстетический потенциал истории
математики // Математика в школе. – 2001. — №3.
33.
Саранцев Г.И. Общая методика преподавания
математики: Учеб. пособие для студентов мат. спец. педвузов и ун-тов. – М.:
Просвещение, 2002.
34.
Саранцев Г.И. Упражнения в обучении
математике. – М.: Просвещение, 1995.
35.
Столяр А.А. Педагогика математики. – Мн.:
Высш. школа. 1974.
36.
Теория и технология обучения математике в
средней школе: Учеб. пособие для студентов математических специальностей
педагогических вузов/ Под ред. Т.А. Ивановой. 2-е изд., испр. и доп. –
Н.Новгород: НГПУ, 2009.
37.
Фадеев Н.Ф. Придумывание задач самими
учениками // Математический вестник. — 1915. — №3.
38.
Формирование мыслительных операций на
уроках математики. — www.BestReferat.ru /referat
— 46586.htm
39.
Фридман Л.М., Турецкий Е.Н. Как научиться
решать задачи: Кн. для учащихся ст. классов сред. шк. – 3-е изд., дораб. – М.:
Просвещение, 1989.
40.
Эльконин Д.Б. Детская психология: учеб.
пособие для студ. высш. учеб. заведений/ Д.Б Эльконин ; ред.-сост. Б.Д.
Эльконин . – 5-е изд., стер. – М.: Издательский центр «Академия», 2008.
41.
Эльконин Д.Б. Психология обучения младшего
школьника. – М. , 1974.
42.
Эрдниев П.М. Методика упражнений по
математике. Изд. 2-е, доп. и переработ. Пособие для учителя. М.: «Просвещение»,
1970.
43.
Эрдниев П.М. и др. О постановке в университетах
спецкурса по содержанию школьных учебников // Математика в школе. – 1981. — №5.
44.
Эрдниев П.М., Эрдниев Б.П. Укрупнение
дидактических единиц в обучении математике: Кн. для учителя. — М.:
«Просвещение», 1986.
В процессе обучения математике в школе у учащихся формируются способности к воспроизведению знаний, а также их творческие способности. Одни сведения из курса математики должны быть усвоены прочно всеми учащимися, изучение других сведений служит целям развития. Важное значение в достижении всех этих целей имеет обучение решению задач.
Лучшему пониманию содержания задач и способов их решения содействует самостоятельное составление (придумывание) детьми задач изучаемых видов по аналогии с ранее решенной задачей: по сообщенным учителем числовым данным, по вопросу, по заданию – составить задачу, похожую на ту, которую решали, но с другими числами и о других предметах.
При организации такой работы активность учащихся проявляется с особой силой, так как им приходится самостоятельно подбирать конкретный материал, уметь использовать соответствующее правило, формулу, уравнение, которые выступают в качестве «орудия» мыслительной деятельности.
О роли самостоятельного составления задач учащимися М.Н. Скаткин писал: «Самостоятельная работа учащихся по составлению задач, выполняемая ими по заданиям различного характера и разной степени трудности, содействует закреплению умений решать задачи, формированию математических понятий, развитию мышления и укреплению связи обучения математики с жизнью» [3].
В современных учебниках редко встречаются задания, подобные следующим:
– решено иррациональное уравнение; составить аналогичное уравнение с корнями x1=–5, x2=2.
– составить тригонометрическое уравнение вида asinx–b=0, так, чтобы его решение было равно x=(–1)kπ4+πk.
– составить геометрическую прогрессию такую, чтобы сумма ее членов была равна 20.
Для успешного конструирования заданий следует:
а) изучить известные задачи и продумать способы составления аналогичных задач;
б) выяснить, каким образом могут быть реализованы общие методы составления задач применительно к изучаемой теме;
в) выявить методы составления задач, которые специфичны для изучаемой темы.
Приведем пример составления задачи по теме «Системы уравнений».
Составить и решить систему двух уравнений с двумя неизвестными, одно из которых второй степени, а другое первой, имеющую данное решение: x=-2, y=1.
Надо составить систему вида: ax2+bxy+cy2+dx+ey+f=0,mx+ny+k=0.
Составляем два тождества с учетом значений неизвестных (при произвольных коэффициентах):
(–2)2+2∙–2∙1+0∙12+0∙(–2)+3∙1=3,3∙–2+2∙1=–4.
Преобразуем: x2+2xy+3y=3,3x+2y=–4.
Решение проводится как обычно.
Самостоятельное составление учащимися задач – один из способов развития умения решать задачи, способности к творческой самостоятельности и изобретательности. Задания подобного рода становятся для учащихся стимулом показать свои знания не только в математике, но и во многих других аспектах жизни.
Литература
1. Кожухов С.К. Составление задач школьниками // Математика в школе. – 1995. – №2. – С.4-6.
2. Панина Т.С. Современные способы активизации обучения. – М.: Академия, 2008. – 176 с.
3. Скаткин М.Н. Обучение решению простых арифметических задач. – М.: Учеб. пед. изд-во, 1954, 87 с.
4. Фридман Л.М. Психолого-педагогические основы обучения математике в школе. – М.: Просвещение, 1983. – 160 с.
5. Эрдниев П.М. Методика упражнений по арифметике и алгебре. – М.: Просвещение, 1965, 327 с.
Математика, 1 класс
Урок 21. Задача. Структура задачи.
Перечень вопросов, рассматриваемых на уроке:
- Решение текстовых задач арифметическим способом.
- Структура задачи: условие, вопрос, решение, ответ.
- Решение задач в одно действие на увеличение (уменьшение) числа на несколько единиц.
- Задачи, содержащие отношения «больше (меньше) на..», «больше (меньше) в…».
- Дополнение условий задач недостающими данными или вопросом.
Глоссарий по теме
Компоненты задачи – условие, вопрос, решение, ответ.
Задачи на сложение и вычитание.
Взаимосвязь между условием и вопросом задачи.
Элементы задачи:
1. Условие (что известно в задаче).
2. Вопрос (что нужно узнать).
3. Решение (действие, нахождение неизвестного).
4. Ответ задачи (ответ на вопрос задачи).
Ключевые слова
Текстовая задача; условие задачи; вопрос задачи; решение задачи.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 1.– М.: Просвещение, 2017.– с. 88 – 89.
2. Моро М. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 1 ч.– М.: Просвещение, — с. 33 – 34.
На уроке мы узнаем, как построена задача и как называются структурные элементы задачи. Научимся решать задачи, записывать решение задачи и ответ. Сможем выделять задачи из предложенных текстов.
Основное содержание урока
Рассмотрите картинку.
Составьте задачу.
Послушайте два рассказа и сравните их:
1. В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?
2. В магазине мама купила 3 перца и 4 морковки. В овощах очень много витаминов, они очень полезные.
Какой из этих текстов мы будем изучать на уроке математики, а какой на уроке окружающего мира?
Первый текст на уроке математики, так как в нём есть вопрос, для ответа на который нужно выполнить вычисления, а второй на уроке окружающего мира.
Как называется текст с вопросом, для ответа на который нужны математические вычисления?
Такой текст называется «Задача».
Сегодня на уроке мы узнаем, какой текст называется задачей и из каких частей она состоит.
Тема нашего урока: «Задача. Структура задачи».
Посмотрите ещё раз на текст знакомой нам задачи и ответьте на вопрос.
Что в ней известно?
В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?
Что мама купила 3 перца и 4 морковки.
Это называется — условие задачи, другими словами, это то, что в задаче известно.
Что в задаче нужно узнать?
Сколько всего овощей купила мама.
Это вопрос задачи. Это о чём спрашивают в задаче, то, что нужно узнать.
Что нужно сделать, чтобы сосчитать, сколько мама купила овощей?
Нужно к трём прибавить четыре, получится семь овощей.
Это решение задачи.
Ещё раз прочитайте вопрос задачи и ответьте на него.
Мама купила семь овощей.
Это ответ задачи.
На уроке мы поймём, как построена задача – в ней есть условие и вопрос.
Будем учиться решать задачи, записывать решение задачи и ответ.
Составьте условие задачи по рисунку.
В корзинке четыре луковицы, ещё две луковицы лежат рядом.
Задайте вопрос.
Сколько всего луковиц?
Как решить такую задачу? Сложением или вычитанием?
Четыре да ещё две, задача решается сложением.
Запишем решение. К четырём прибавить два получится шесть.
Осталось записать ответ задачи. Ответим на вопрос задачи: всего шесть луковиц.
Ещё раз посмотрите внимательно на этот же рисунок:
Составьте другую задачу, которая будет решаться вычитанием:
В корзине было четыре луковицы, из неё взяли две луковицы.
Задайте вопрос.
Сколько луковиц осталось в корзине?
Как записать решение?
Из четырёх вычесть два, получится две луковицы.
Осталось записать ответ задачи.
Разбор тренировочных заданий.
Рассмотрите рисунок, дополните условие и решите задачу.
Ответ:
На огороде с одного куста сорвали 2 кабачка, а с другого куста 6 кабачков. Сколько кабачков собрали с двух кустов?
2 + 6 = 8 (к.)
Ответ: 8 кабачков.
Выберите только те тексты, которые являются математическими задачами.
Ответ:
Верные равенства обозначьте синим цветом, а неверные красным.
Ответ:
Прочитайте задачу и установите соответствия между её компонентами.

Ответ:
Попробуйте заменить овощи соответствующей цифрой.
Подсказка: у каждой цифры своя маска. На одинаковых цифрах — одинаковые маски.
Ответ:
Ответь на вопросы с помощью таблицы.
Ответ:
Покажите разным цветом, как можно получить число 6.
Ответ: