Как в математике найти ребро

Ребро куба

Куб является первым представителем в ряду правильных многогранников, благодаря тому, что все его ребра равны между собой. Все грани куба являются квадратами, в которых ребро куба становится стороной квадрата и связано отношениями с его площадью и диагональю. Найти ребро куба, зная диагональ основания, можно разделив ее на корень из двух.

Также можно найти ребро куба, зная площадь основания:

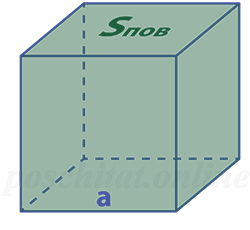
Поскольку у куба могут быть даны площади боковой и полной его поверхности, приведем необходимые формулы ребра куба и для них:

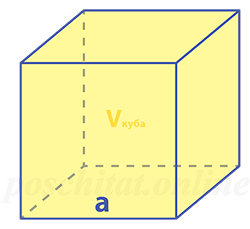
Если исходить из понятия ребра, как части объемного тела, то в таком случае становится возможным вычислить ребро куба, зная его объем:

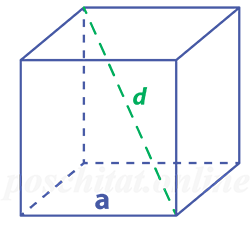
Одной из немаловажных деталей куба является его диагональ, соединяющая противоположные вершины верхнего и нижнего оснований, впрочем, для куба это могут быть любые два противоположных основания, так как все его грани конгруэнтны. Диагональ куба D , соединенная с диагональю основания d и ребром a дает прямоугольный треугольник, в котором из теоремы Пифагора можно найти ребро куба следующим образом.
a 2 +d 2 =D 2

3a 2 =D 2

Как найти ребро куба?

Куб – это один из самых простых трехмерных объектов, как в стереометрии, так и в природе. Перед тем, как найти ребро куба, необходимо напомнить о том, что такое куб. Это прямоугольный параллелепипед, имеющий равные между собой ребра. Кроме того, куб представляет собой шестигранник, гранями которого являются равные квадраты. Чтобы найти ребро куба, необходимо знать его некоторые параметры – объем куба, площадь грани, длину диагонали куба или грани.

1. В большинстве случаев встречаются задачи четырех типов, в которых находится ребро куба. Это – определить длину ребра по диагонали куба, по диагонали его грани, по объему куба и площади грани. Самая простая из них – найти ребро по площади грани. Ведь грань куба – это квадрат со стороной, которая равна ребру куба. Следовательно, площадь этой грани равна ребру куба, возведенному в квадрат. Отсюда, чтобы найти ребро, необходимо из площади грани извлечь квадратный корень. а=vS а – ребро куба (длина), S – площадь одной грани.
2. Еще проще найти грань куба исходя из его объема, так как объем куба будет равняться возведению длины ребра в 3-ю степень. Следовательно, если мы извлечем кубический корень (третью степень) из объема, то получим длину ребра а=vV (кубический корень), здесь а – ребро куба (длина), V – его объем.
3. Как найти длину ребра куба, если известны длины диагоналей. Обозначим: а – ребро куба (длина), b – диагональ грани куба (длина), c – диагональ куба (длина). Диагональ ребра и грани куба образуют между собой равносторонний прямоугольный треугольник. Применяем теорему Пифагора, где: a^2+a^2=b^2, здесь (a^ — возведение в степень) Получается: a=v(b^2/2). Извлекая корень квадратный из половины квадрата диагонали его грани, мы найдем длину ребра куба.
4. Находим длину ребра по диагонали куба, где а — ребро куба, b — диагональ грани, с — диагональ куба. Они образуют все вместе прямоугольный треугольник. Исходим из теоремы Пифагора где: a^2+b^2=c^2. Применим вышеназванную зависимость между значениями а и b, подставим их в выражение b^2=a^2+a^2. Получив: a^2+a^2+a^2=c^2, найдем: 3*a^2=c^2, получая конечное выражение; a=v(c^2/3).

Если параметры куба задаются в устаревших, национальных и других специфических единицах, тогда следует перевести их в подходящие метрические аналоги – кубические метры, дециметры, сантиметры или миллиметры.

что такое ребро куба?

поверхность куба сомтовляют одинаковые грани в форме квадрата. стоону такого квадрата называют ребро куба.

Другие вопросы из категории

маркови,по 24 кг в каждом, и 4мешка свеклы, по 15 кг в каждом,сколько всего килограммов Марков и свеклы привезли в магазин

Читайте также

4*4*4(ребро куба равно 4 см).Ответ обоснуйте.

4.Что показывает знаминатель

5.Что показывает числитель

6.Что такое отрезок

7. какие знаете треугольники

№115
Длина ребра куба 1 см 2 мм. Вычисли площадь одной грани куба. Вычисли общую площадь всех граней куба.
№116
Общая длина всех рёбер куба равна 840 см. Вычисли площадь одной грани куба. Вычисли общую площадь всех граней куба.
№117
Периметр одной грани куба равен 64 мм. Вычисли общую площадь всех граней куба.
№118
Диаметр первой окружности 1092 см, что в 14 раз больше диаметра второй окружности. Найди радиус второй окружности.
№119
Диаметр первой окружности в 2 раза больше радиуса второй окружности. Можно ли разместить эти окружности так, чтобы одна из них полностью поместилась в другой?
№120
1) Можно ли окружность радиусом 5 см разместить внутри квадрата с длиной стороны 11 см?
2) Можно ли шар радиусом 7 см разместить внутри куба с длиной ребра 15 см?

Как найти ребро куба, если есть объем

Куб — это, пожалуй, самый простой трехмерный объект, как в природе, так и в стереометрии. Кубом называется прямоугольный параллелепипед, все ребра которого равны между собой. Также куб можно представить как шестигранник, все грани которого представляют собой равные квадраты. Благодаря высокой степени симметрии, достаточно знать лишь длину ребра куба, чтобы вычислить все остальные характеристики. А для того чтобы найти ребро куба, достаточно его объема.

Вам понадобится

• калькулятор.

Инструкция

Чтобы найти ребро куба, если есть объем, извлеките корень кубический из числового значения его объема. То есть найдите такое число, куб (третья степень) которого будет равняться объему куба.

Для вычисления кубического корня воспользуйтесь калькулятором. Лучше если это будет не «бухгалтерский» калькулятор, а калькулятор, предназначенный для инженерных расчетов. Однако даже на «инженерном» калькуляторе вы вряд ли найдете отдельную кнопку для извлечения кубического корня. Поэтому используйте функцию возведения в степень. Извлечению корня кубического соответствует возведение в степень «одна третья» (1/3).

Чтобы возвести число в степень 1/3, наберите само число. Затем нажмите на кнопку «возведение в степень». В зависимости от конструкции калькулятора, она может выглядеть как x^y, или xy (у – в виде маленького значка, расположенного чуть выше). Так как большинство калькуляторов не позволяет вводить дроби, вместо 1/3 наберите 0,33. Если желаете получить большую точность вычислений, увеличьте количество троек.

Если объем куба выражен в метрических системах единиц измерения, длина ребра куба будет измеряться в соответствующей линейной единице. Так, например, если объем куба равен 8000 метров кубических (м³), то длина его ребра будет равна 20 метров (м).Если объем куба выражен в производных от нестандартных линейных единиц измерения, то длина ребра получится в соответствующих линейных единицах. Так если объем куба задан в кубических дюймах, длина ребра получится в дюймах (линейных).Если объем куба задан в национальных, устаревших, бытовых и прочих специфических единицах измерения объема, предварительно переведите этот объем в наиболее подходящий метрический аналог – кубические миллиметры, дециметры или метры.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Длина ребра куба

Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Длина ребра куба через объём

Длина ребра куба через диагональ

Длина ребра куба через площадь поверхности куба

Теория

Как найти ребро куба зная его объём

Как найти ребро куба зная его диагональ

Как найти ребро куба через площадь поверхности

См. также

Что такое ребро в геометрии для детей?

край. • сторона многоугольника или отрезка.

Что такое ребра в математике?

Край где встречаются два лица. Вершина — это угол, в котором сходятся ребра. Множественное число — вершины.

Что такое ребро в 3D-форме?

Края. Ан Край — это место, где встречаются два лица. Например, у куба 12 ребер, у цилиндра — два, а у сферы — ни одного.

Что такое примеры ребер?

Для многоугольника: Отрезок линии на границе, соединяющий одну вершину (угловую точку) с другой. Пример: Этот пятиугольник имеет 5 ребер. Для многогранника: Отрезок, на котором сходятся две грани.

Смотрите также, из чего состоят континенты.

Как найти край фигуры?

Что такое края фигуры?

Край — это место, где сходятся две грани формы. На 2D-фигурах ребра линии между каждой вершиной. В 3D-фигурах это линии, разделяющие каждую грань.

Что такое ребро в треугольнике?

Ребра — это линии, которые соединяются, образуя вершины. … У квадрата четыре стороны и четыре вершины. В треугольнике три и того, и другого. Квадратная пирамида, трехмерная фигура, имеет разное количество ребер и вершин. У него пять вершин или углов, но восемь ребер, соединяющих эти вершины вместе.

Что такое ребро куба?

Ответ: Ребро куба отрезок линии, соединяющий две вершины. Всего в кубе 12 ребер. Давайте подробно разберемся со свойствами куба. Пояснение: … Отрезок, соединяющий две вершины, называется ребром.

Что такое края и углы?

Как существительные разница между краем и углом

в том, что ребро — это граничная линия поверхности в то время как угол — это точка, где встречаются две сходящиеся линии; угол, внешний или внутренний.

Сколько ребер в конусе?

Конусы, сферы и цилиндры не имеют краев потому что у них нет плоских сторон. Место, где встречаются два или более ребра, называется вершиной. Вершина подобна углу.

Что такое края сферы?

Вот список форм вместе с количеством ребер.

Форма	Количество ребер (E)
Сфера	0 край
Цилиндр	3 ребра
Прямоугольная призма	12 ребер
Треугольная призма	9 ребер

Как рассчитать преимущество?

Что такое край в структуре данных?

край — край представляет путь между двумя вершинами или линию между двумя вершинами. В следующем примере линии от A до B, от B до C и т. д. представляют ребра.

См. Также, почему Цезарь Август приказал провести перепись

Есть ли у окружности край?

Если ребро замкнутой фигуры должно быть прямым, то круг не имеет краев, поскольку никакая часть окружности не является прямой.

Что такое ребро призмы?

То базовые края призмы – это ребра основания призмы. Вершина призмы – это точка пересечения двух ребер основания. Боковые ребра призмы — это отрезки, соединяющие соответствующие вершины оснований призмы.

Как найти ребро призмы?

Сколько ребер у трехмерного треугольника?

Треугольные призмы

Он состоит из 5 граней (2 треугольника, 3 прямоугольника). Треугольные призмы имеют 6 вершин и 9 ребер!

Как вы описываете край?

Что такое ребро 2D-формы?

Край — это место, где сходятся две грани формы. На 2D-фигурах ребра линии между каждой вершиной. В 3D-фигурах это линии, разделяющие каждую грань.

Как найти стороны треугольника?

Теорема Пифагора: длины ребер прямоугольного треугольника

Наиболее распространенное применение теоремы Пифагора состоит в том, чтобы использовать известные длины двух сторон прямоугольного треугольника, чтобы найти длину третьей стороны, используя алгебру и формула а² + b² = с².

Чему равен край прямоугольника?

четыре края

У прямоугольника четыре стороны. Прямоугольник — это двумерная фигура, имеющая четыре прямые стороны, которые пересекаются под четырьмя углами в 90 градусов. В отличие от…

Как найти ребро куба?

Чему равно ребро прямоугольной призмы?

12 ребер

Прямоугольная призма имеет 12 ребер. Край — это место, где встречаются две грани. Прямоугольная призма имеет 6 граней, каждая из которых имеет 4 ребра.

Как найти ребра куба?

12

Сколько ребер у яйца?

Доступ к ответам на вопросы по математике. Решения NCERT для класса 3 по математике. Глава 5. Формы и конструкции.

Название вещи	Есть ли у него углы	Количество ребер
Мяч	Нет
Ластик	да	12
Яйцо	Нет
Лист бумаги	да	4

См. Также, какова основная цель правительства.

Что такое ребра и вершины в графе?

На диаграмме графа вершина обычно изображается кружком с меткой, а ребро представлено линией или стрелкой, идущей от одной вершины к другой.

Какая фигура имеет ровно 9 ребер?

треугольная призма

Треугольная призма – это призма с двумя треугольными основаниями и тремя прямоугольными сторонами. У него 6 вершин, 9 ребер и 5 граней.

Сколько ребер у пирамиды?

Треугольная пирамида

Все стороны равнобедренных треугольников. Пирамида с треугольным основанием имеет 4 грани, 4 вершины, включая вершину и 6 ребер.

Сколько ребер у призмы?

Прямоугольная призма имеет 6 граней, 8 вершин (или углов) и 12 ребер.

Что такое ребро в цилиндре?

Кубы и прямоугольные параллелепипеды имеют 12 ребер. Конусы имеют 1 ребро. Цилиндры имеют 2 ребра.

Сколько ребер у куба?

12

Как найти ребра вершины?

Сумма значений степени вершины равна вдвое больше ребер, так как каждое ребро было подсчитано с обоих концов. В вашем случае 6 вершин степени 4 означают, что существует (6 × 4)/2 = 12 ребер.

Что такое процент EDGE?

Преимущество Дома — это термин, используемый для описания математическое преимущество что азартная игра и, следовательно, коммерческое место для азартных игр имеет над вами власть, когда вы играете в течение долгого времени. Это преимущество приводит к гарантированному процентному возврату в место проведения с течением времени, а для вас — к гарантированному процентному проигрышу вашей ставки.

Как использовать формулу Келли?

Формула Келли: Келли % = W – (1-W)/R, где:

1. Kelly % = процент капитала, который нужно вложить в одну сделку.
2. W = исторический процент выигрышей торговой системы.
3. R = историческое среднее соотношение выигрышей/проигрышей.

Узнайте о гранях, ребрах и вершинах — 3D-фигуры | Базовая геометрия для детей | Лапша Кидз

Грани Ребра Вершины-Трехмерные фигуры-Геометрическая формула Эйлера

Геометрия края 101

Грани, ребра и вершины | Визуализация твердых фигур | Ч-15.2 – 7-й НЦЭРТ | Эдусарал

From Wikipedia, the free encyclopedia

In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope.^[1] In a polygon, an edge is a line segment on the boundary,^[2] and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces (or polyhedron sides) meet.^[3] A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.

Relation to edges in graphs[edit]

In graph theory, an edge is an abstract object connecting two graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment.
However, any polyhedron can be represented by its skeleton or edge-skeleton, a graph whose vertices are the geometric vertices of the polyhedron and whose edges correspond to the geometric edges.^[4] Conversely, the graphs that are skeletons of three-dimensional polyhedra can be characterized by Steinitz’s theorem as being exactly the 3-vertex-connected planar graphs.^[5]

Number of edges in a polyhedron[edit]

Any convex polyhedron’s surface has Euler characteristic

where V is the number of vertices, E is the number of edges, and F is the number of faces. This equation is known as Euler’s polyhedron formula. Thus the number of edges is 2 less than the sum of the numbers of vertices and faces. For example, a cube has 8 vertices and 6 faces, and hence 12 edges.

Incidences with other faces[edit]

In a polygon, two edges meet at each vertex; more generally, by Balinski’s theorem, at least d edges meet at every vertex of a d-dimensional convex polytope.^[6]
Similarly, in a polyhedron, exactly two two-dimensional faces meet at every edge,^[7] while in higher dimensional polytopes three or more two-dimensional faces meet at every edge.

Alternative terminology[edit]

In the theory of high-dimensional convex polytopes, a facet or side of a d-dimensional polytope is one of its (d − 1)-dimensional features, a ridge is a (d − 2)-dimensional feature, and a peak is a (d − 3)-dimensional feature. Thus, the edges of a polygon are its facets, the edges of a 3-dimensional convex polyhedron are its ridges, and the edges of a 4-dimensional polytope are its peaks.^[8]

See also[edit]

• Extended side

References[edit]

External links[edit]

• Weisstein, Eric W. «Polygonal edge». MathWorld.
• Weisstein, Eric W. «Polyhedral edge». MathWorld.