Как в матрице найти базисный минор матрицы - Исправление недочетов и поиск решений вместе с Examum.ru

Ранг матрицы и базисный минор матрицы

Пусть — матрица размеров mtimes n , а — натуральное число, не превосходящее и : kleqslantmin{m;n} . Минором k-го порядка матрицы называется определитель матрицы k-го порядка, образованной элементами, стоящими на пересечении произвольно выбранных строк и столбцов матрицы . Обозначая миноры, номера выбранных строк будем указывать верхними индексами, а выбранных столбцов — нижними, располагая их по возрастанию.

Пример 3.4. Записать миноры разных порядков матрицы

$A=begin{pmatrix}1&2&1&0\ 0&2&2&3\ 1&4&3&3end{pmatrix}!.$

Решение. Матрица имеет размеры 3times4 . Она имеет: 12 миноров 1-го порядка, например, минор $M_{2}^{3}=det(a_{32})=4$ ; 18 миноров 2-го порядка, например, $M_{23}^{12}=begin{vmatrix}2&1\2&2end{vmatrix}=2$ ; 4 минора 3-го порядка, например,

$M_{{134}}^{{123}}= begin{vmatrix}1&1&0\0&2&3\ 1&3&3 end{vmatrix}=0.$

В матрице размеров mtimes n минор r-го порядка называется базисным, если он отличен от нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще не существует.

Рангом матрицы называется порядок базисного минора. В нулевой матрице базисного минора нет. Поэтому ранг нулевой матрицы, по определению полагают равным нулю. Ранг матрицы обозначается operatorname{rg}A .

Пример 3.5. Найти все базисные миноры и ранг матрицы

$A=begin{pmatrix}1&2&2&0\0&2&2&3\0&0&0&0end{pmatrix}!.$

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих определителей третья строка нулевая. Поэтому базисным может быть только минор второго порядка, расположенный в первых двух строках матрицы. Перебирая 6 возможных миноров, отбираем отличные от нуля

$M_{12}^{12}= M_{13}^{12}= begin{vmatrix}1&2\0&2 end{vmatrix}!,quad M_{24}^{12}= M_{34}^{12}= begin{vmatrix}2&0\2&3end{vmatrix}!,quad M_{14}^{12}= begin{vmatrix}1&0\0&3end{vmatrix}!.$

Каждый из этих пяти миноров является базисным. Следовательно, ранг матрицы равен 2.

Замечания 3.2

1. Если в матрице все миноры k-го порядка равны нулю, то равны нулю и миноры более высокого порядка. Действительно, раскладывая минор (k+1)-ro порядка по любой строке, получаем сумму произведений элементов этой строки на миноры k-го порядка, а они равны нулю.

2. Ранг матрицы равен наибольшему порядку отличного от нуля минора этой матрицы.

3. Если квадратная матрица невырожденная, то ее ранг равен ее порядку. Если квадратная матрица вырожденная, то ее ранг меньше ее порядка.

4. Для ранга применяются также обозначения operatorname{Rg}A,~ operatorname{rang}A,~ operatorname{rank}A .

5. Ранг блочной матрицы определяется как ранг обычной (числовой) матрицы, т.е. не обращая внимания на ее блочную структуру. При этом ранг блочной матрицы не меньше рангов ее блоков: operatorname{rg}(Amid B)geqslantoperatorname{rg}A и , поскольку все миноры матрицы (или ) являются также минорами блочной матрицы .

Теоремы о базисном миноре и о ранге матрицы

Рассмотрим основные теоремы, выражающие свойства линейной зависимости и линейной независимости столбцов (строк) матрицы.

Теорема 3.1 о базисном миноре. В произвольной матрице каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

Действительно, без ограничения общности предполагаем, что в матрице размеров mtimes n базисный минор расположен в первых строках и первых столбцах. Рассмотрим определитель

$D=left|begin{array}{ccc|c}a_{11}&cdots&a_{1r}&a_{1k}~\ ~vdots&ddots &vdots&vdots~\ ~a_{r1}&cdots&a_{rr}&a_{rk}~\hline ~a_{s1}&cdots&a_{sr}&a_{sk}end{array}right|,$

который получен приписыванием к базисному минору матрицы соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых 1leqslant sleqslant m и 1leqslant kleqslant n этот определитель равен нулю. Если sleqslant r или kleqslant r , то определитель содержит две одинаковых строки или два одинаковых столбца. Если же s>r и k>r , то определитель равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем

$a_{s1}cdot D_{r+11}+ldots+ a_{sr}cdot D_{r+1r}+a_{sk}cdot D_{r+1,r+1}=0,$

где $D_{r+1,j}$ — алгебраические дополнения элементов последней строки. Заметим, что $D_{r+1,r+1}ne0$ , так как это базисный минор. Поэтому

$a_{sk}=lambda_1cdot a_{s1}+ldots+lambda_rcdot a_{sr}$ , где $lambda_j=-frac{D_{r+1,j}}{D_{r+1,r+1}},~j=1,2,ldots,r.$

Записывая последнее равенство для s=1,2,ldots,m , получаем

$begin{pmatrix}a_{1k}\vdots\a_{mk}end{pmatrix}= lambda_1cdot! begin{pmatrix}a_{11}\vdots\a_{m1}end{pmatrix}+ldots lambda_rcdot! begin{pmatrix}a_{1r}\vdots\a_{mr}end{pmatrix}!.$

т.е. -й столбец (при любом 1leqslant kleqslant n ) есть линейная комбинация столбцов базисного минора, что и требовалось доказать.

Теорема о базисном миноре служит для доказательства следующих важных теорем.

Условие равенства нулю определителя

Теорема 3.2 (необходимое и достаточное условие равенства нулю определителя). Для того чтобы определитель был равен нулю необходимо и достаточно, чтобы один из его столбцов {одна из его строк) был линейной комбинацией остальных столбцов (строк).

В самом деле, необходимость следует из теоремы о базисном миноре. Если определитель квадратной матрицы n-го порядка равен нулю, то ее ранг меньше , т.е. хотя бы один столбец не входит в базисный минор. Тогда этот выбранный столбец по теореме 3.1 является линейной комбинацией столбцов, в которых расположен базисный минор. Добавляя, при необходимости, к этой комбинации другие столбцы с нулевыми коэффициентами, получаем, что выбранный столбец есть линейная комбинация остальных столбцов матрицы. Достаточность следует из свойств определителя. Если, например, последний столбец A_n определителя det(A_1~A_2~cdots~A_n) линейно выражается через остальные

$A_n=lambda_1cdot A_1+lambda_2cdot A_2+ldots+lambda_{n-1}cdot A_{n-1},$

то прибавляя к A_n столбец A_1 , умноженный на (-lambda_1) , затем столбец A_2 , умноженный на (-lambda_2) , и т.д. столбец $A_{n-1}$ , умноженный на $(-lambda_{n-1})$ , получим определитель $det(A_1~cdots~A_{n-1}~o)$ с нулевым столбцом, который равен нулю (свойство 2 определителя).

Инвариантность ранга матрицы при элементарных преобразованиях

Теорема 3.3 (об инвариантности ранга при элементарных преобразованиях). При элементарных преобразованиях столбцов (строк) матрицы ее ранг не меняется.

Действительно, пусть operatorname{rg}A=r . Предположим, что в результате одного элементарного преобразования столбцов матрицы получили матрицу . Если было выполнено преобразование I типа (перестановка двух столбцов), то любой минор (r+l)-ro порядка матрицы либо равен соответствующему минору (r+l)-ro порядка матрицы , либо отличается от него знаком (свойство 3 определителя). Если было выполнено преобразование II типа (умножение столбца на число lambdane0 ), то любой минор (г+l)-ro порядка матрицы либо равен соответствующему минору (r+l)-ro порядка матрицы , либо отличается от него множителем (свойство 6 определителя). Если было выполнено преобразование III типа (прибавление к одному столбцу другого столбца, умноженного на число Lambda ), то любой минор (г+1)-го порядка матрицы либо равен соответствующему минору (г+1) -го порядка матрицы (свойство 9 определителя), либо равен сумме двух миноров (r+l)-ro порядка матрицы (свойство 8 определителя). Поэтому при элементарном преобразовании любого типа все миноры (r+l)-ro порядка матрицы равны нулю, так как равны нулю все миноры (г+l)-ro порядка матрицы . Таким образом, доказано, что при элементарных преобразованиях столбцов ранг матрицы не может увеличиться. Так как преобразования, обратные к элементарным, являются элементарными, то ранг матрицы при элементарных преобразованиях столбцов не может и уменьшиться, т.е. не изменяется. Аналогично доказывается, что ранг матрицы не изменяется при элементарных преобразованиях строк.

Следствие 1. Если одна строка (столбец) матрицы является линейной комбинацией других ее строк (столбцов), то эту строку (столбец) можно вычеркнуть из матрицы, не изменив при этом ее ранга.

Действительно, такую строку при помощи элементарных преобразований можно сделать нулевой, а нулевая строка не может входить в базисный минор.

Следствие 2. Если матрица приведена к простейшему виду (1.7), то

operatorname{rg}A=operatorname{rg}Lambda=r,.

Действительно, матрица простейшего вида (1.7) имеет базисный минор r-го порядка.

Следствие 3. Любая невырожденная квадратная матрица является элементарной, другими словами, любая невырожденная квадратная матрица эквивалентна единичной матрице того же порядка.

Действительно, если — невырожденная квадратная матрица n-го порядка, то operatorname{rg}A=n (см. п.З замечаний 3.2). Поэтому, приводя элементарными преобразованиями матрицу к простейшему виду (1.7), получим единичную матрицу Lambda=E_n , так как operatorname{rg}A=operatorname{rg}Lambda=n (см. следствие 2). Следовательно, матрица эквивалентна единичной матрице E_n и может быть получена из нее в результате конечного числа элементарных преобразований. Это означает, что матрица элементарная.

Теорема 3.4 (о ранге матрицы). Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.

В самом деле, пусть operatorname{rg}A=r . Тогда в матрице имеется линейно независимых строк. Это строки, в которых расположен базисный минор. Если бы они были линейно зависимы, то этот минор был бы равен нулю по теореме 3.2, а ранг матрицы не равнялся бы . Покажем, что — максимальное число линейно независимых строк, т.е. любые строк линейно зависимы при p>r . Действительно, образуем из этих строк матрицу . Поскольку матрица — это часть матрицы , то operatorname{rg}Bleqslant operatorname{rg}A=r<p . Значит, хотя бы одна строка матрицы не входит в базисный минор этой матрицы. Тогда по теореме о базисном миноре она равна линейной комбинации строк, в которых расположен базисный минор. Следовательно, строки матрицы линейно зависимы. Таким образом, в матрице не более, чем линейно независимых строк.

Следствие 1. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов:

$operatorname{rg}A=operatorname{rg}A^T.$

Это утверждение вытекает из теоремы 3.4, если ее применить к строкам транспонированной матрицы и учесть, что при транспонировании миноры не изменяются (свойство 1 определителя).

Следствие 2. При элементарных преобразованиях строк матрицы линейная зависимость (или линейная независимость) любой системы столбцов этой матрицы сохраняется.

В самом деле, выберем любые столбцов данной матрицы и составим из них матрицу . Пусть в результате элементарных преобразований строк матрицы была получена матрица , а в результате тех же преобразований строк матрицы была получена матрица . По теореме 3.3 operatorname{rg}B'=operatorname{rg}B . Следовательно, если столбцы матрицы были линейно независимы, т.е. k=operatorname{rg}B (см. следствие 1), то и столбцы матрицы также линейно независимы, так как k=operatorname{rg}B' . Если столбцы матрицы были линейно зависимы (k>operatorname{rg}B) , то и столбцы матрицы также линейно зависимы (k>operatorname{rg}B') . Следовательно, для любых столбцов матрицы линейная зависимость или линейная независимость сохраняется при элементарных преобразованиях строк.

Замечания 3.3

1. В силу следствия 1 теоремы 3.4 свойство столбцов, указанное в следствии 2, справедливо и для любой системы строк матрицы, если элементарные преобразования выполняются только над ее столбцами.

2. Следствие 3 теоремы 3.3 можно уточнить следующим образом: любую невырожденную квадратную матрицу, используя элементарные преобразования только ее строк (либо только ее столбцов), можно привести к единичной матрице того же порядка.

В самом деле, используя только элементарные преобразования строк, любую матрицу можно привести к упрощенному виду Lambda (рис. 1.5) (см. теорему 1.1). Поскольку матрица невырожденная (det{A}ne0) , то ее столбцы линейно независимы. Значит, столбцы матрицы Lambda также линейно независимы (следствие 2 теоремы 3.4). Поэтому упрощенный вид Lambda невырожденной матрицы совпадает с ее простейшим видом (рис. 1.6) и представляет собой единичную матрицу Lambda=E (см. следствие 3 теоремы 3.3). Таким образом, преобразовывая только строки невырожденной матрицы, ее можно привести к единичной. Аналогичные рассуждения справедливы и для элементарных преобразований столбцов невырожденной матрицы.

Ранге произведения и суммы матриц

Теорема 3.5 (о ранге произведения матриц). Ранг произведения матриц не превышает ранга множителей:

operatorname{rg}(Acdot B)leqslant min{operatorname{rg}A,operatorname{rg}B}.

В самом деле, пусть матрицы и имеют размеры mtimes p и ptimes n . Припишем к матрице матрицу C=ABcolon,(Amid C) . Разумеется, что operatorname{rg}Cleqslantoperatorname{rg}(Amid C) , так как — это часть матрицы (см. п.5 замечаний 3.2). Заметим, что каждый столбец C_j , согласно операции умножения матриц, является линейной комбинацией столбцов A_1,A_2,ldots,A_p матрицы A=(A_1~cdots~A_p):

$C_{j}=A_1cdot b_{1j}+A_2cdot b_{2j}+ldots+A_{p}cdot b_{pj},quad j=1,2,ldots,n.$

Такой столбец можно вычеркнуть из матрицы (Amid C) , при этом ее ранг не изменится (следствие 1 теоремы 3.3). Вычеркивая все столбцы матрицы , получаем: operatorname{rg}(Amid C)=operatorname{rg}A . Отсюда, operatorname{rg}Cleqslantoperatorname{rg}(Amid C)=operatorname{rg}A . Аналогично можно доказать, что одновременно выполняется условие , и сделать вывод о справедливости теоремы.

Следствие. Если невырожденная квадратная матрица, то operatorname{rg}(AB)= operatorname{rg}B и operatorname{rg}(CA)=operatorname{rg}C , т.е. ранг матрицы не изменяется приумножении ее слева или справа на невырожденную квадратную матрицу.

Теорема 3.6 о ранге суммы матриц. Ранг суммы матриц не превышает суммы рангов слагаемых:

operatorname{rg}(A+B)leqslant operatorname{rg}A+operatorname{rg}B.

Действительно, составим матрицу (A+Bmid Amid B) . Заметим, что каждый столбец матрицы A+B есть линейная комбинация столбцов матриц и . Поэтому operatorname{rg}(A+Bmid Amid B)= operatorname{rg}(Amid B) . Учитывая, что количество линейно независимых столбцов в матрице не превосходит operatorname{rg}A+operatorname{rg}B , а operatorname{rg}(A+B)leqslant operatorname{rg}(A+Bmid Amid B) (см. п.5 замечаний 3.2), получаем доказываемое неравенство.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Содержание:

Формулировка теоремы о базисном миноре
Примеры решения задач

Формулировка теоремы о базисном миноре

Теорема

Столбцы матрицы $A$,
входящие в базисный минор, образуют линейно независимую
систему. Любой столбец матрицы $A$ линейно выражается через остальные столбцы
из базисного минора.

В матрице $A$ размеров
$m times n$
минор
$r$-го порядка называется базисным, если он отличен от нуля,
а все миноры
$(r + 1)$-ro порядка равны нулю или их вообще не существует.

Следствие. Если все столбцы матрицы
$A$ линейно выражаются через
$r$ столбцов
$A_{i 1}, A_{i 2}, ldots, A_{i r}$, которые образуют
линейно независимую систему, то ранг матрицы
$operatorname{rang} A=r$ .

Примеры решения задач

Пример

Задание. Найти все базисные миноры и ранг матрицы:

$$A=left(begin{array}{llll}1 & 2 & 2 & 0 \ 0 & 2 & 2 & 3 \ 0 & 0 & 0 & 0end{array}right)$$

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих
определителей
третья строка будет нулевой. Поэтому базисным может быть только минор второго порядка, который будет состоять из
элементов первых двух строк матрицы. Перебираем всевозможные миноры второго порядка, состоящие из элементов указанных строк:

$$M_{12}^{12}=left|begin{array}{cc}1 & 2 \ 0 & 2end{array}right|=1 cdot 2-0 cdot 2=2-0=2 neq 0$$
$$M_{13}^{12}=left|begin{array}{cc}1 & 2 \ 0 & 2end{array}right|=1 cdot 2-0 cdot 2=2-0=2 neq 0$$
$$M_{14}^{12}=left|begin{array}{cc}1 & 0 \ 0 & 3end{array}right|=1 cdot 3-0 cdot 0=3-0=3 neq 0$$
$$M_{23}^{12}=left|begin{array}{ll}2 & 2 \ 2 & 2end{array}right|=0$$
$$M_{24}^{12}=left|begin{array}{cc}2 & 0 \ 2 & 3end{array}right|=2 cdot 3-2 cdot 0=6-0=6 neq 0$$
$$M_{34}^{12}=left|begin{array}{cc}2 & 0 \ 2 & 3end{array}right|=2 cdot 3-2 cdot 0=6-0=6 neq 0$$

Таким образом, пять минор являются ненулевыми и каждый из них — базисный. Следовательно, так как порядок базисных миноров равен
двум, то и ранг матрицы равен двум: $operatorname{rang} A=2$ .

Ответ. Базисные миноры $M_{12}^{12}, M_{13}^{12}, M_{14}^{12}, M_{24}^{12}, M_{34}^{12} ;$ rang $A=2$ .

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

В данной публикации мы рассмотрим теорему о базисном миноре (формулировка и следствия). Также разберем пример задачи для демонстрации ее применения на практике.

Формулировка теоремы
Пример задачи

Формулировка теоремы

В произвольной матрице A столбцы/строки, входящие в состав базисного минора M (называются “базисными”), линейно независимы. Каждый столбец/строка матрицы является линейной комбинацией базисных столбцов/строк.

Допустим, дана матрица A размером mxn. Базисным называется ненулевой минор M порядка r, при этом все миноры более старшего порядка (r+1 и выше) равняются нулю или их вовсе нет. Это значит, что r равняется меньшему из чисел m или n.

Из теорему о базисном миноре следует:

Линейно независимые столбцы/строки матрицы, число которых равно рангу данной матрицы, являются базисными.
Ранг любой матрицы равняется максимальному количеству содержащихся в ней линейно независимых строк/столбцов.

Пример задачи

Давайте найдем всем базисные миноры матрицы A, представленной ниже, а также определим ее ранг.

Решение:

1. Выполним элементарные преобразования над матрицей, чтобы упростить ее. Для начала разделим третью строку на 2 и переставим ее с первой местами.

2. Отнимем из третьей строки первую.

3. Получаем матрицу с нулевой строкой, что означает, что все миноры третьего порядка равняются нулю.

4. Таким образом, базисными в нашем случае могут быть только ненулевые миноры второго порядка, состоящие из первой и второй строк полученной матрицы.

Ответ:
Все рассчитанные миноры отличны от нуля, значит, все они являются базисными. Ранг матрицы равен двум (rang A = 2), так как все миноры более высокого (третьего) порядка равны нулю.

Источник

Базисный минор матрицы. Ранг матрицы.

Как было
сказано выше, минором матрицы порядка
s называется определитель матрицы,
образованной из элементов исходной
матрицы, находящихся на пересечении
каких — либо выбранных s
строк и s
столбцов.

Определение. В
матрице порядка mn
минор порядка r называется базисным,
если он не равен нулю, а все миноры
порядка r+1
и выше равны нулю, или не существуют
вовсе, т.е. r
совпадает с меньшим из чисел m или n.
Столбцы и строки матрицы, на которых
стоит базисный минор, также называются
базисными.
В матрице может быть несколько
различных базисных миноров, имеющих
одинаковый порядок.

Определение.
Порядок базисного минора матрицы
называется рангом
матрицы и обозначается
Rg А. Очень важным свойством элементарных
преобразований матриц является то,
что они не изменяют ранг матрицы.

Определение.
Матрицы, полученные в результате
элементарного преобразования, называются
эквивалентными.
Надо
отметить, что равные
матрицы и эвивалентные
матрицы — понятия совершенно различные.

Теорема.
Наибольшее число
линейно независимых столбцов в матрице
равно числу линейно независимых строк.
Т.к. элементарные преобразования
не изменяют ранг матрицы, то можно
существенно упростить процесс нахождения
ранга матрицы. Пример. Определить
ранг матрицы. 
, RgA
= 2. Пример:
Определить ранг матрицы. 

, Rg
= 2. Пример.
Определить ранг матрицы. ,

Rg
= 2. Если с помощью элементарных
преобразований не удается найти матрицу,
эквивалентную исходной, но меньшего
размера, то нахождение ранга матрицы
следует начинать с вычисления миноров
наивысшего возможного порядка. В
вышеприведенном примере – это миноры
порядка 3. Если хотя бы один из них не
равен нулю, то ранг матрицы равен порядку
этого минора.

Теорема
о базисном миноре.
Теорема.
В произвольной
матрице А каждый столбец (строка) является
линейной комбинацией столбцов (строк),
в которых расположен базисный минор.
Таким образом, ранг
произвольной матрицы А равен максимальному
числу линейно независимых строк
(столбцов) в матрице.
Если А- квадратная матрица и detA
= 0, то по крайней мере один из столбцов
– линейная комбинация остальных
столбцов. То же самое справедливо и для
строк. Данное утверждение следует из
свойства линейной зависимости при
определителе равном нулю.

Матричный метод решения систем линейных уравнений.

Матричный
метод применим к решению систем уравнений,
где число уравнений равно числу
неизвестных. Метод удобен для решения
систем невысокого порядка. Метод
основан на применении свойств умножения
матриц. Пусть дана система уравнений:
Составим
матрицы: A
= ; B
= ; X
= .
Систему уравнений можно записать: AX
= B.
Сделаем следующее преобразование:
A^-1AX
= A^-1B,
т.к. А^-1А
= Е, то ЕХ
= А^-1В
Х = А^-1В
Для применения данного метода
необходимо находить обратную матрицу,
что может быть связано с вычислительными
трудностями при решении систем высокого
порядка.

Пример.
Решить систему уравнений: Х
= ,
B
= ,
A
= Найдем
обратную матрицу А^-1.

= det
A
= 5(4-9)
+ 1(2 – 12) – 1(3 – = -25 – 10 +5 = -30. M₁₁
= =
-5; M₂₁
= =
1; M₃₁
= =
-1; M₁₂
= M₂₂
= M₃₂
= M₁₃
= M₂₃
= M₃₃
= A^-1
= ;
Cделаем
проверку: AA^-1
= =E.
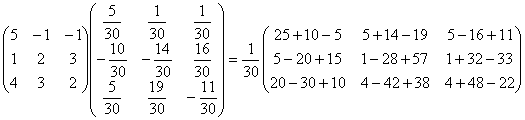
Находим матрицу Х. Х = =
А^-1В
= =
.

Итого
решения системы: x
=1; y
= 2; z
= 3. Несмотря на ограничения возможности
применения данного метода и сложность
вычислений при больших значениях
коэффициентов, а также систем высокого
порядка, метод может быть легко реализован
на ЭВМ.

Метод
Крамера. (Габриель
Крамер (1704-1752) швейцарский математик)
Данный метод также применим только в
случае систем линейных уравнений, где
число переменных совпадает с числом
уравнений. Кроме того, необходимо ввести
ограничения на коэффициенты системы.
Необходимо, чтобы все уравнения были
линейно независимы, т.е. ни одно уравнение
не являлось бы линейной комбинацией
остальных. Для этого необходимо, чтобы
определитель матрицы системы не равнялся
0. det
A

0; Действительно, если какое- либо
уравнение системы есть линейная
комбинация остальных, то если к элементам
какой- либо строки прибавить элементы
другой, умноженные на какое- либо число,
с помощью линейных преобразований можно
получить нулевую строку. Определитель
в этом случае будет равен нулю.

Теорема.
(Правило Крамера):
Теорема.
Система из n
уравнений с n
неизвестными в
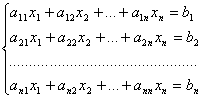
случае, если определитель матрицы
системы не равен нулю, имеет единственное
решение и это решение находится по
формулам: x_i
= _i/,
где 
= det
A,
а _i
– определитель матрицы, получаемой из
матрицы системы заменой столбца i
столбцом свободных членов b_i.
_i
=

Пример.
A
= ; ₁=
; ₂=
; ₃=
;
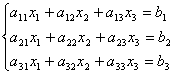
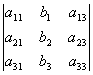
x₁
= ₁/detA;
x₂
= ₂/detA; x₃
= ₃/detA;

Пример. Найти
решение системы уравнений: 
=
= 5(4 – 9) + (2 – 12) – (3 – = -25 – 10 + 5 = -30; ₁
= =
(28 – 48) – (42 – 32) = -20 – 10 = -30. x₁
= ₁/
= 1; ₂
= =
5(28 – 48) – (16 – 56) = -100 + 40 = -60. x₂
= ₂/
= 2; ₃
= =
5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x₃
= ₃/
= 3. Как видно, результат совпадает с
результатом, полученным выше матричным
методом. Если система однородна,
т.е. b_i
= 0, то при 0
система имеет единственное нулевое
решение x₁
= x₂
= … = x_n
= 0. При 
= 0 система имеет бесконечное множество
решений. Для самостоятельного
решения: ; Ответ:
x
= 0; y
= 0; z
= -2.

Метод
Гаусса. (Карл Фридрих
Гаусс (1777-1855) немецкий математик) В
отличие от матричного метода и метода
Крамера, метод Гаусса может быть применен
к системам линейных уравнений с
произвольным числом уравнений и
неизвестных. Суть метода заключается
в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
Разделим
обе части 1–го уравнения на a₁₁

0, затем: 1) умножим на а₂₁
и вычтем из второго уравнения 2) умножим
на а₃₁
и вычтем из третьего уравнения и
т.д. Получим: , где
d₁_j
= a₁_j/a₁₁,
j
= 2, 3, …, n+1.
d_ij= a_ij
– a_i₁d₁_j
i
= 2, 3, … , n; j
= 2, 3, … , n+1.
Далее
повторяем эти же действия для второго
уравнения системы, потом – для третьего
и т.д.

Пример.
Решить систему линейных уравнений
методом Гаусса. Составим
расширенную матрицу системы. А* = Таким
образом, исходная система может быть
представлена в виде: ,
откуда получаем: x₃
= 2; x₂
= 5; x₁
= 1.

Пример.
Решить систему методом Гаусса. Составим
расширенную матрицу системы. Таким
образом, исходная система может быть
представлена в виде: ,
откуда получаем: z
= 3; y
= 2; x
= 1. Полученный ответ совпадает с
ответом, полученным для данной системы
методом Крамера и матричным методом.
Для самостоятельного решения: Ответ:
{1, 2, 3, 4}.

Предел
функции при стремлении аргумента к
бесконечности.

Определение.
Число А называется пределом
функции f(x)
при х,
если для любого числа >0
существует такое число М>0, что для
всех х, х>M
выполняется неравенство

При
этом предполагается, что функция f(x)
определена в окрестности бесконечности.

Записывают:

Графически можно представить:

Аналогично можно определить пределы
для
любого х>M
и

для
любого х<M.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.

В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.

Содержание темы:

Минор $M_{ij}$ элемента $a_{ij}$.
Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$.
Минор k-го порядка матрицы $A_{mtimes n}$. Главный минор, базисный минор, окаймляющий минор.
Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.

Минор $M_{ij}$ элемента $a_{ij}$

Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).

Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).

Для примера рассмотрим квадратную матрицу четвёртого порядка:
$A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:

Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

$$
M_{32}=left| begin{array} {ccc}
1 & -3 & 9\
2 & 11 & 5 \
3 & -5 & 58 end{array} right|=
1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579.

Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.

Часто вместо словосочетания «минор элемента матрицы» в литературе встречается «минор элемента определителя». Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя
$left| begin{array} {ccc}
-1 & 3 & 2\
9 & 0 & -5 \
4 & -3 & 7 end{array} right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:

Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:

$$
M_{12}=left| begin{array} {cc}
9 & -5\
4 & 7 end{array} right|=9cdot 7-(-5)cdot 4=83.
$$

Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.

Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$

Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).

Алгебраическое дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ находится по следующей формуле:
$$
A_{ij}=(-1)^{i+j}cdot M_{ij},
$$

где $M_{ij}$ – минор элемента $a_{ij}$.

Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:

Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=left( begin{array} {ccc}
-5 & 10 & 2\
6 & 9 & -4 \
4 & -3 & 1 end{array} right)$. Согласно формуле $A_{12}=(-1)^{1+2}cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:

Минор k-го порядка матрицы $A_{mtimes n}$

Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_{mtimes n}$, т.е. матрица, содержащая m строк и n столбцов.

Минором k-го порядка матрицы $A_{mtimes n}$ называется определитель, элементы которого расположены на пересечении k строк и k столбцов матрицы $A$ (при этом предполагается, что $k≤ m$ и $k≤ n$).

Например, рассмотрим такую матрицу:

$$A=left( begin{array} {cccc}
-1 & 0 & -3 & 9\
2 & 7 & 14 & 6 \
15 & -27 & 18 & 31\
0 & 1 & 19 & 8\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

$$
left( begin{array} {cccc}
-1 & 0 & -3 & 9 \
boldblue{2} & boldblue{7} & 14 & boldblue{6} \
15 & -27 & 18 & 31\
boldblue{0} & boldblue{1} & 19 & boldblue{8}\
0 & -12 & 20 & 14\
boldblue{5} & boldblue{3} & -21 & boldblue{9}\
23 & -10 & -5 & 58 end{array} right);;

M=left|begin{array} {ccc}
2 & 7 & 6 \
0 & 1 & 8 \
5 & 3 & 9 end{array} right|.
$$

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Минор k-го порядка матрицы $A_{mtimes n}=(a_{ij})$ называется главным, если на главной диагонали данного минора находятся только главные диагональные элементы матрицы $A$.

Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_{11}$, $a_{22}$, $a_{33}$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_{11}=-1$, $a_{22}=7$, $a_{33}=18$, $a_{44}=8$. На рисунке они выделены зелёным цветом:

$$left( begin{array} {cccc}
boldgreen{-1} & 0 & -3 & 9\
2 & boldgreen{7} & 14 & 6 \
15 & -27 & boldgreen{18} & 31\
0 & 1 & 19 & boldgreen{8}\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$

Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_{11}=-1$ и $a_{33}=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:

$$
M=left|begin{array} {cc}
boldgreen{-1} & -3 \
15 & boldgreen{18} end{array} right|
$$

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Пусть некий минор $M$ k-го порядка матрицы $A_{mtimes n}$ не равен нулю, т.е. $Mneq 0$. При этом все миноры, порядок которых выше k, равны нулю. Тогда минор $M$ называют базисным, а строки и столбцы, на которых расположены элементы базисного минора, именуют базисными строками и базисными столбцами.

Для примера рассмотрим такую матрицу:

$$A=left( begin{array} {ccc}
-1 & 0 & 3 & 0 & 0 \
2 & 0 & 4 & 1 & 0\
1 & 0 & -2 & -1 & 0\
0 & 0 & 0 & 0 & 0 end{array} right)
$$

Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):

$$
left( begin{array} {ccc}
boldpurple{-1} & 0 & boldpurple{3} & boldpurple{0} & 0 \
boldpurple{2} & 0 & boldpurple{4} & boldpurple{1} & 0\
boldpurple{1} & 0 & boldpurple{-2} & boldpurple{-1} & 0\
0 & 0 & 0 & 0 & 0 end{array} right);;

M=left|begin{array} {ccc}
-1 & 3 & 0 \
2 & 4 & 1 \
1 & -2 & -1 end{array} right|.
$$

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

$$
M=left| begin{array} {ccc}
-1 & 3 & 0\
2 & 4 & 1 \
1 & -2 & -1 end{array} right|=4+3+6-2=11.
$$

Итак, $M=11neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.

Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Пусть некий минор k-го порядка $M$ матрицы $A_{mtimes n}$ расположен на пересечении k строк и k столбцов. Добавим к набору этих строк и столбцов ещё одну строку и столбец. Полученный минор (k+1)-го порядка именуют окаймляющим минором для минора $M$.

Для примера обратимся к такой матрице:

$$A=left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & 12 & 20 & 21 & 54\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & -3 & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;

M=left|begin{array} {ccc}
-17 & 19 \
12 & 21 end{array} right|.
$$

Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:

$$
left( begin{array} {ccccc}
-1 & boldblue{2} & 0 & boldblue{-2} & boldblue{-14}\
3 & boldred{-17} & -3 & boldred{19} & boldblue{29}\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & boldblue{54}\
-7 & 10 & 14 & -36 & 79 end{array} right);;

M’=left|begin{array} {ccc}
2 & -2 & -14 \
-17 & 19 & 29 \
12 & 21 & 54 end{array} right|.
$$

Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):

$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & boldblue{-3} & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & boldblue{11} & boldblue{19} & boldblue{-20} & -98\
6 & boldred{12} & boldblue{20} & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;

M»=left|begin{array} {ccc}
-17 & -3 & 19 \
11 & 19 & -20 \
12 & 20 & 21 end{array} right|.
$$

Минор $M»$ также является окаймляющим минором для минора $M$.

Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.

Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.

Пусть задан некий минор $M$ k-го порядка матрицы $A_{ntimes n}$. Определитель (n-k)-го порядка, элементы которого получены из матрицы $A$ после вычеркивания строк и столбцов, содержащих минор $M$, называется минором, дополнительным к минору $M$.

Для примера рассмотрим квадратную матрицу пятого порядка:

$$
A=left( begin{array}{ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$

Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка. Эти элементы выделены в матрице $A$ зелёным цветом:

$$
left(begin{array}{ccccc}
-1 & boldgreen{2} & 0 & -2 & boldgreen{-14}\
3 & -17 & -3 & 19 & 29\
5 & boldgreen{-6} & 8 & -9 & boldgreen{41}\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right);;

M=left|begin{array}{cc}
2 & -14 \
-6 & 41 end{array} right|.
$$

Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (элементы убираемых строк и столбцов показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:

$$
left( begin{array}{ccccc}
boldred{-1} & boldred{2} & boldred{0} & boldred{-2} & boldred{-14}\
3 & boldred{-17} & -3 & 19 & boldred{29}\
boldred{5} & boldred{-6} & boldred{8} & boldred{-9} & boldred{41}\
-5 & boldred{11} & 16 & -20 & boldred{-98}\
-7 & boldred{10} & 14 & -36 & boldred{79} end{array} right);;

M’=left|begin{array} {ccc}
3 & -3 & 19 \
-5 & 16 & -20 \
-7 & 14 & -36 end{array}right|.
$$

Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.

Алгебраическим дополнением к минору $M$ квадратной матрицы $A_{ntimes n}$ называется выражение $(-1)^{alpha}cdot M’$, где $alpha$ – сумма номеров строк и столбцов матрицы $A$, на которых расположены элементы минора $M$, а $M’$ – минор, дополнительный к минору $M$.

Словосочетание «алгебраическое дополнение к минору $M$» часто заменяют словосочетанием «алгебраическое дополнение минора $M$».

Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка
$
M=left| begin{array} {ccc}
2 & -14 \
-6 & 41 end{array} right|
$ и дополнительный к нему минор третьего порядка:

$M’=left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:

$$
M^*=(-1)^alphacdot M’.
$$

Параметр $alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $alpha=1+3+2+5=11$. Итак:

$$
M^*=(-1)^{11}cdot M’=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|.
$$

В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:

$$
M^*=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|=-30.
$$

Источник