Как в матрице составить спираль - Исправление недочетов и поиск решений вместе с Examum.ru

Привет, мой читатель.

На днях встретил простую на вид задачу. Как оказалось, не легко решить такую задачу за пять, и даже за 50 минут. Здесь пришлось подумать и поэкспериментировать.

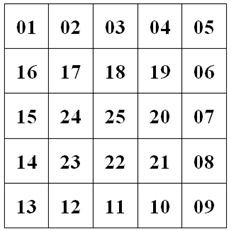
Дана матрица, или, на нашем языке, двумерный массив. Его размеры не могут превышать 10х10. Они задаются пользователем и это может быть не только квадрат, но и прямоугольник. Обозначим длины сторон через N и M. Нам необходимо заполнить эту матрицу числами от 1 и по возрастающей до M*N. Прежде, чем привести код целиком, мне хотелось бы изложить ход мыслей, чтобы стало понятно как все работает. Если же тебе просто нужно решение, то ты можешь пролистать ниже, скопировать его и закрыть страницу как больше не нужную.

Стандартно, нам нужен сам массив и переменные для хранения длин сторон прямоугольного (двумерного) массива.

    int a[10][10] = {0};
    int N, M;

Также мы будем действовать по слогике, что при заполнении мы очерчиваем прямоугольники, каждый их которых на единицу меньше с каждой стороны. Если смотреть на эти прямоугольники в декартовой системе координат, то начало каждой из сторон сдвигается на 1 вправо или вниз, а конец влево или вверх. Договоримся, что оси направлены вправо и вниз от точки [0,0].

Таким образом нам нужно знать точки начала и конца очерчиваемого прямоугольника. Это и будут точки излома (поворота). Но я еще и решил пойти следующим путем. Точки конца сторон будут равняться длине стороны первого прямоугольника минус длине текущего прямоугольника.

Обозначим их следующим образом:

int Ibeg = 0, Ifin = 0, Jbeg = 0, Jfin = 0;

Ну, и, нам нужна переменная, значением которой мы будем заполнять массив, пока она не достигнет значения M*N

int k = 1;

В цикле начинаем заполнять массив. Сначала точке a[i][j] присваиваем значение k. Это удобно тем, что если длина сторон равна 0, то мы не войдем в массив. Иначе в точку a[i][j] положим значение k, в конце же цикла инкреминируем его.

a[i][j] = k;
/**
 * Код между началом и концом цикла
 */
++k;

Далее вычисляем следующий шаг

Если у нас верхняя сторона прямоугольника и мы не достигла правой стороны, то двигаемся вправо: ++j
Если мы на правой стороне прямоугольника и не достигли нижней стороны, то двигаемся вниз: ++i
Если мы на нижней стороне прямоугольника и не достигли левой стороны, то двигаемся влево: —j
Иначе двигаемся вверх: —i

        if (i == Ibeg && j < M - Jfin - 1)
            ++j;
        else if (j == M - Jfin - 1 && i < N - Ifin - 1)
            ++i;
        else if (i == N - Ifin - 1 && j > Jbeg)
            --j;
        else
            --i;

В конце же каждого прохода проверяем, завершился ли прямоугольник и стои ли начинать прочерчивать новый — меньший:

Если мы находимся на второй строке
Если мы находимся на первом столбце
И, в случае, если чертим не прямоугльник, а вертикальную линию, если первая строка не равна последней. (этот пункт самый сложный во всем алгоритме. Его я достиг путем экспериментов)

Тогда увеличиваем отступы от краев первого прямоугольника:

        if ((i == Ibeg + 1) && (j == Jbeg) && (Jbeg != M - Jfin - 1)){
            ++Ibeg;
            ++Ifin;
            ++Jbeg;
            ++Jfin;
        }

Собственно это весь алгоритм. А ниже код всей программы:

#include 

int main()
{
    int a[10][10] = {0};
    int N, M;

    scanf("%d%d", &N, &M);
    
    int Ibeg = 0, Ifin = 0, Jbeg = 0, Jfin = 0;
    
    int k = 1;
    int i = 0;
    int j = 0;

    while (k <= N * M){
        a[i][j] = k;
        if (i == Ibeg && j < M - Jfin - 1)
            ++j;
        else if (j == M - Jfin - 1 && i < N - Ifin - 1)
            ++i;
        else if (i == N - Ifin - 1 && j > Jbeg)
            --j;
        else
            --i;

        if ((i == Ibeg + 1) && (j == Jbeg) && (Jbeg != M - Jfin - 1)){
            ++Ibeg;
            ++Ifin;
            ++Jbeg;
            ++Jfin;
        }
        ++k;
    }
    
    for (int i = 0; i < 10; ++i){
        for (int j = 0; j < 10; ++j)
            printf("%3d", a[i][j]);
        printf("n");
    }

    return 0;
}

Я видел более изящные решения данной задачи, наполненные математикой и побитовыми операциями. Но для понимания того, как последовательно наполняется пассив по спирали, достаточно данного алгоритма. Буду рад, если вы оставите в комментариях свои решения и поделитесь мыслями.

Источник

#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
#include<alloc.h>
void zapovn(int **, int);
int main()
{
    int n,i,j;
    int **arr;
    clrscr();
    printf("nn=");
    scanf("%d",&n);
    arr=(int**)calloc(n,sizeof(int*));
    for(i=0;i<n;i++)
      arr[i]=(int*)calloc(n,sizeof(int));
    zapovn(arr,n);
    for(i=0;i<n;i++){
    for(j=0;j<n;j++)
    printf("%2d  ",arr[i][j]);
    printf("n");}
    for(i=0;i<n;i++)
    free(arr[i]);
    free(arr);
    getch();
    return 0;
}
void zapovn(int **A, int m){
    int i,j,k,b,c;
    i=m/2;
    j=i;
    printf("nvvedit masivn");
    scanf("%d",&A[i][j]);
    for(k=0,j=j-1;k<2;k++,i++)
      scanf("%d",&A[i][j]);
    for(k=0,j=j+1,i=i-1;k<2;k++,j++)
      scanf("%d",&A[i][j]);
    for(k=0,j=j-1,i=i-1;k<2;k++,i--)
      scanf("%d",&A[i][j]);
    for(b=3,c=4;b<=m;b+=2,c+=2)
    {  
    if(b==m){
    b=m-1;
    for(k=0,j=j-1,i=i+1;k<b;k++,j--)
      scanf("%d",&A[i][j]);
    break;
    }
    else
    for(k=0,j=j-1,i=i+1;k<b;k++,j--)
      scanf("%d",&A[i][j]);
    for(k=0,j=j+1,i=i+1;k<b;k++,i++)
      scanf("%d",&A[i][j]);
    for(k=0,j=j+1,i=i-1;k<c;k++,j++)
      scanf("%d",&A[i][j]);
    for(k=0,j=j-1,i=i-1;k<c;k++,i--)
      scanf("%d",&A[i][j]);
}
}

Источник

Альтернативный способ заполнения «спиральной матрицы»

Время на прочтение
10 мин

Количество просмотров 26K

В процессе изучения основ алгоритмизации и программирования в качестве студента еще в середине 2000х мне попалась довольно известная всем задача по заполнению «спиральной» матрицы. Суть состоит в том, чтобы начиная с позиции [1, 1], продвигаясь по часовой стрелке, заполнить квадратную матрицу заданной величины числами в возрастающем порядке. На ее решение было потрачено около двух часов.

Собственно алгоритм заполнения был тривиален, циклы, в общей сложности состоящие из N² итерации, предполагали прохождение по всем элементам массива в требуемом порядке, при этом увеличивая значение итератора на 1 и заполняя им текущий элемент матрицы. Маршрут начинался с элемента [1, 1], далее продвигается по горизонтали до правого верхнего элемента [1, N], после – вниз до нижнего правого угла [N, N], затем до левого нижнего угла [N, 1] и завершал первый круг на столбец ниже отправной точки [2, 1]. В дальнейшем, такое же круговое движение происходило уже в следующем внутреннем круге, и так далее до центра матрицы.

Интернет, в лице различных форумов, сообществ, сайтов по посвященных данному направлению изобилует конкретными решениями на различных языках программирования, коих человечество за полвека изобрело немало. В то же время, представленный выше механизм заполнения матрицы является основным и наиболее эффективным как с точки зрения человека, так и точки зрения вычислительной машины (если она имеет точку зрения).

Через некоторое время после успешного решения задачи, на волне переоценки собственных способностей, я задумался: а возможно ли разработать универсальную формулу, позволяющей на основании размера матрицы и координат ячейки вычислить ее значение согласно условию задачи – то есть в конечном итоге заполнить массив, перебирая элементы «традиционным» путем двумя вложенными циклами от 1 до N без использования счетчика.

Но, как вы могли догадаться, ничего путного у меня не вышло, и данная затея была заброшена в пользу других, более насущных проблем в изучении программирования.

Спустя эти самые 18 лет, перебирая наиболее интересные задачи и пути их решения для обучения уже следующего поколения представителей неординарной профессии «программист», меня заинтересовала одна статья на ресурсе «Хабр» (https://habr.com/ru/post/261773), описывающая процесс создания формулы для вычисления количества дней в заданном месяце без использования каких-либо условных операторов, циклов и заранее подготовленных данных.

Автору респект, способ решения данной задачи был настолько интересен и оригинален, что мы изучили его с группой моих студентов на одном из занятий.

Именно после этого я вспомнил ту самую спиральную матрицу и решился на очередную попытку выведения универсальной формулы.

(Следует отметить, что на одном из сайтов я все же обнаружил достаточно короткое решение в виде функции, которое, однако, содержало два условных перехода).

Итак, задача: разработать алгоритм для вычисления значения элемента спиральной матрицы на основании его координат [i, j] и размера самой матрицы, пользуясь только простыми арифметическими вычислениями. Исключение составляет модуль — абсолютное значение числа.

Условие: никаких условных (прошу прощения за тавтологию) переходов или заготовленных данных в виде массивов, словарей и т.д.

Практическая полезность: никакая. Традиционным способом данная задача решается гораздо быстрее, при этом мозг программиста в процессе разработки функции не травмируется.

Очевидно, такую непростую задачу необходимо разделить на несколько этапов, или, если угодно, выделить основные элементы.

1) Найти закономерность между «координатами» ячейки и ее порядковым номером в первом внешнем «кольце», и вывести соответствующую форму.

2) Найти связь между, опять же, координатами ячейки и номером кольца, в котором она находится. Составить формулу.

3) Связать между собой два алгоритма для выведения общей формулы вычисления значения элемента массива.

Входные данные: N – размер квадратной матрицы (массива).

1 этап. Заполнение внешнего кольца. Для начала попытаемся вывести формулу вычисления значения ячейки для внешнего кольца массива, в котором отсчет начинается с ячейки [1, 1] и двигается по часовой стрелке поворачивая на углах [1, N], [N, N]. Заканчивается на строку ниже начальной точки, т.е. [2, 1].

Математический аппарат будет разрабатываться параллельно с написанием кода на языке программирования, в качестве которого выбираем C++, как наиболее распространенный и удобный язык программирования (здесь конечно читатели могут поспорить, но классика есть классика). Но, в принципе, выведенная формула не должна иметь привязки языке.

Для наглядного изучения процесса напишем соответствующий скрипт, объявив в нем массив размером 5×5 (назовем его “a”), элементы которого будем перебирать традиционным способом двумя вложенными циклами от 1 до N. На данном этапе будем работать только с внешним кольцом.

#include <iostream>
using namespace std;
int main()
{
    int N = 5;          // задаем размер матрицы
    int a[N][N];        // и инициализируем ее
    for (int ik = 0; ik < N; ik++)
        for (int jk = 0; jk < N; jk++)
            a[ik][jk] = 0;          // заполнив для удобства нулями
                                      
    for (int ik = 0; ik < N; ik++){     //назовем его "Основной цикл"
        for (int jk = 0; jk < N; jk++){
            if (!(ik == 0 || ik == N - 1 || jk == 0 || jk == N - 1)) 
                continue;      // Временное условие для фильтрации элементов внесшего "кольца"
            int i = ik + 1;     // Номера строк и столбцов приводим в удобный
            int j = jk + 1;     // в математическом плане вид (от 1 до N)  
            	//  ... здесь будем вставлять основной код вычислений
        }   
    }     

   for (int ik = 0; ik < N; ik++){          //Блок "Вывод массива"
        for (int jk = 0; jk < N; jk++){
           printf( "%02d ", a[ik][jk]);	// дополняем число ведущими нулями
        }
        cout << endl;
    }  
    return 0;
}

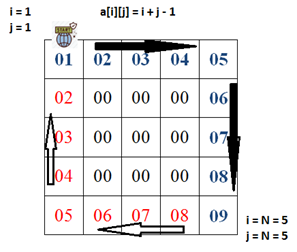
Очевидно, что, по крайней мере, до правого нижнего угла внешнего кольца суммарное значение координат (i + j) увеличивается ровно на 1 с каждым шагом. Однако первый элемент в таком случае равняется 2, E_1,2 = 3 и т.д. Поэтому необходимо уменьшить значение суммы (i + j) на один. В результате введем переменную Xs = i + j — 1, которая часто будет использоваться в дальнейших вычислениях. Пишем код:

…
int Xs = (i + j – 1);
a[ik][jk] = Xs;
…

В результате запуска первого скрипта получаем массив:

Как видим заполнение от начала до правого нижнего угла произведено корректно. Однако далее у нас происходит уменьшение шага, вместо увеличения.

Очевидно a[ik][jk] = Xsнуждается в дополнении, при котором все его значения до [5, 5] останутся неизменными, но после этой точки начнут увеличиваться на 1.

Но для начала постараемся привести в норму вторую часть кольца, которая заполнялась бы с ячейки (i = 5, j = 4) начиная со значения 10. В данном случае это легко сделать, лишь вычитая от общего количества элементов первого кольца увеличенного на два (равняется периметру первого кольца N * 4 — 4 = 16 плюс 2) значение Xs.

То есть a_1,2 = 4N – 4 + 2 – Xs = 4N – Xs — 2.

…
int Xs = i + j - 1;     
a[ik][jk] = 4 * N - Xs - 2;
…

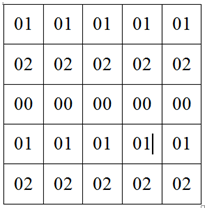
Однако теперь у нас правильно заполнилась только левая и нижняя стороны кольца, а противоположенные элементы – нет.

На текущем этапе у нас имеются две формулы, пригодные только для определенных участков массива.

1. a_i,j = Xs = i + j — 1; действует от [1, 1] до [N, N].

2. a_i,j = 4*N – 2 — X; действует от [N, N] до [2, 1].

Самым простым решением было бы использование условного перехода, однако это не соответствует нашей начальной установке. Здесь необходимо дополнительно отметить, что из всех стандартных кусочно-заданных функций, как отмечено выше, мы будем использовать только модуль (y = |x|) и формулы собственной разработки.

В этой связи, необходимо привести наше уравнение в вид:

Здесь функция F₁ принимает значение 1 при i, j между [1, 1] … [N, N] , в остальных случаях – 0. В свою очередь, F₂ , наоборот, принимает значение 1 когда ячейка находится в диапазоне [N, N — 1] … [2, 1], и 0 между [1, 1] … [N, N].

В качестве аргумента функции используется переменная switcher, вычисляемая на основе значении i и j, и опять же, принимающая различные значения в вышеуказанных диапазонах.

Неплохим вариантом выглядит идея получения значений -1, 0 и/или 1 от манипуляций с координатами элемента. Тогда F₁ и F₂ содержали бы простые арифметические операции.

Итак, мы уже использовали сложение i и j, но оно всегда дает положительное число. Почему бы сейчас не попробовать вычитание?

Заменим в нашем предыдущем листинге значение a[ik][jk].

…
int Xs = i + j - 1;     
a[ik][jk] = j – i;
…

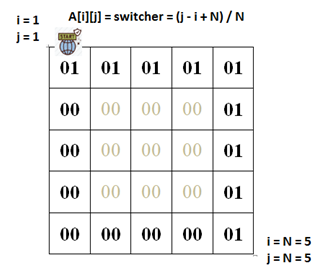
Наиболее легким вариантом видится целочисленное деление на самого себя, но в таком случае мы столкнемся с ошибкой деления на 0, поскольку а[1][1] и а[N][N] уже содержат 0. В данном случае можно прибавить ко всем значениям N и осуществить целочисленное деление на N. Введенную переменную назовем switcher.

…
int switcher =  (j - i + N) / N;
a[ik][jk] =  switcher; // временно подставим в ячейки switcher
…

Теперь осталось немногое для завершения данного этапа, а именно создать функции F₁ и F_2. F₁должна возвращать такое же значение, какое ей передали в качестве аргумента, т.е. F₁ (switcher) = switcher. В таком случае F₁ (switcher) * Xs работает только для диапазона от [1, 1] до [N, N], в остальных случаях равняется нулю. Вторая часть уравнения, должна действовать наоборот. В таком случае она должна возвращать значение по модулю switcher – 1, т.е. F_2.(switcher) = |switcher – 1|.

Итак, пишем:

…
a[ik][jk] =  switcher * Xs + abs(switcher - 1) * (4 * N - 2 - Xs);
…

Проверяем:

Отлично, этот этап завершен успешно, мы получили требуемые значения для внешнего кольца массива.

2 этап. Альтернативная система координат.

Нам удалось заполнить внешнее первое кольцо требуемыми данными. Однако, что произойдет, если мы снимем фильтр, и попытаемся вычислить данные для остальных элементов массива? Для этого необходимо удалить участок кода if (!(ik == 0 || ik == N — 1 || jk == 0 || jk == N — 1)) continue;

Чего и следовало ожидать, следующее кольцо матрицы представлено неверными значениями, что, однако, не скрывает некую системность в числах. Так, по крайней мере, сохранен возрастающий порядок. Более того, прирост значений составляет 1, за исключением стыка между нижним правым элементом и следующей ячейкой. Данный признак является благоприятным знаком того, что мы находимся на верном пути.

Очевидно, в ячейке [2, 2] вместо 03 должно находиться число 17, следующее значение после конечного элемента внешнего круга. Небольшое размышление показывает, что необходимо ввести определенный коэффициент, выправляющий значение ячейки в зависимости от «глубины залегания» кольца в котором он находится. Т.е. требуется вычислить степень удаленности элемента массива от центра (или наоборот) на основании номера строки и номера столбца.

Для этого, введем альтернативную систему координат. Так, обычная нумерация ячеек в матрице начинается с левого верхнего угла и аналогична двухмерной системе координат, с центром в указанном месте. Для тех, кто еще помнит древний Turbo Pascal с синим экраном – графики в нем чертились именно таким образом (да и в большинстве современных графических сред разработки ПО принята подобная система координат при работе с визуальными компонентами).

Мы же, перенесем начало координат в центр нашей матрицы следующим образом:

…
a[ik][jk] =  abs(N / 2 + 1 -  i);
…

Поскольку нам требуется только расстояние ячейки от центра, мы берем только абсолютные значения.

Сейчас элементы массива заполнены номерами строк относительно его центра. Если мы проделаем ту же самую операцию со стоблцами, мы получим такой же массив, только с вертикальным распределением значений.

Введем две новые переменные Ic, Jc (c обозначает center).

…
Ic = abs(i -  N / 2  - 1);
Jc = abs(j -  N / 2  - 1);
…

Теперь необходимо определить расстояние ячейки от центра, независимо в каком направлении она удалена.

Опять же, самый простой способ что-то узнать – попробовать вывести суммы номеров строк и столбцов.

…
a[ik][jk] =  Ic + Jc;
…

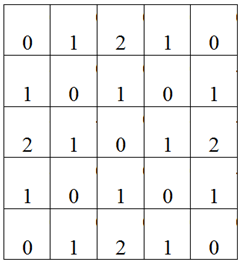
Пока ничего путного не выходит, но проявляется закономерность – чем дальше от центра, тем больше сумма. В дальнейшем это пригодится. Теперь рассмотрим, что нам даст разница между Ic и Jc.

…
a[ik][jk] =  Ic - Jc;
…

Пока также неопределенно. Но если изучить расположение чисел, и сложить поэлементно их абсолютные значения с предыдущим массивом, то получим матрицу с уникальными числами для каждого кольца.

…
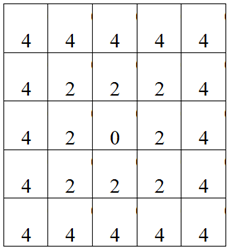
a[ik][jk] =  abs(Ic – Jc) + Ic + Jc;
…

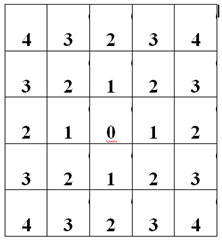
Уже проявляется верное направление. Только наши числа оказались вдвое больше и расположены в порядке возрастания с центра до краев, а не наоборот, как было бы удобно для проведения основных вычислений. К счастью решается эта проблема легко, путем целочисленного деления на два и инверсии. Проделанные вычисления запишем в новую переменную Ring.

…
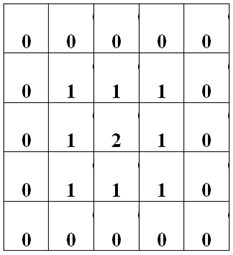
Ring = N / 2 -  (abs(Ic – Jc) + Ic + Jc) / 2; 
a[ik][jk] =  Ring;
…

Замечательно. Однако, при размере матрицы N = 6 данная формула работает не совсем корректно, так она в качестве центра считает только один элемент (что является справедливым для матриц с нечетной размерностью, как в предыдущих примерах).

N = 6

При четном размере центральный квадрат из четырех элементов должен считаться центром матрицы. Возникает вопрос: как это реализовать? Здесь к нам опять на помощь приходит целочисленное деление и кусочно-заданная функция.

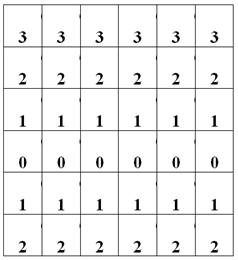
Но для этого вернемся немного назад, к вычислению Ic и Jc. Попробуем запустить наш скрипт при N = 6, и посмотрим значения Ic = |i — N / 2 — 1|.

В данный момент требуется привести массив в симметричную форму. Легче всего это сделать, увеличив значение на 1 всех строк после 3-й (то есть вторую половину).

…
Ic = abs(i - N / 2  - 1) + (i - 1) / (N /2) * ((N-1) % 2);
…

Вторая часть данного выражения работает только при четном N, и приводит номера строк в симметричный вид по горизонтали.

Тоже самое проделываем и Jc.

…
Jc = abs(j - N / 2  - 1) + (j - 1)/(N /2) * ((N-1) % 2);
…

В итоге получаем симметричную матрицу уже по вертикали. Теперь проверяем значение Ring для матрицы с размером 6.

… 
a[ik][jk] =  Ring;
…

Все работает нормально. Второй этап завершен.

3 этап. Соединение. На данном этапе мы объединим полученные данные и выведем искомую матрицу (через формулу вычисления значения заданной ячейки).

Но для начала, вернемся к первому этапу и выведем на экран:

…
a[ik][jk] =  switcher * Xs + abs(switcher - 1) * (4 * N - 2 - Xs);
…

Дальнейший порядок действий представляется следующим образом: привести значения элементов внутренних колец к «спиральному» виду (т.е. заполнить их начинания с верхнего левого угла по спирали возрастающими значениями от 1), далее вычислить коэффициент прироста, которой обеспечит нормальный переход от одного кольца к нижестоящему (в нашем примере от ячейки [1,2] к ячейке [2,2], при этом меняя значение с 16 на 17)

Описывать естественным языком или даже академическим стилем математические вычисления крайне тяжело, но еще сложнее понимать чьи-то не всегда ясные наработки изложенные подобным образом. Поэтому если вы столкнулись с определенными трудностями в понимании материала, просто читайте дальше и следите за вычислениями – скоро все будет ясно.

Поскольку при работе с кольцами нижнего уровня примерный алгоритм вычислений сохраняется, мы можем уменьшить значение Xs (содержит сумму номера строки и столбца) следующим образом, в соответствии с номером кольца в котором находится очередная ячейка.

Xs = (i – Ring) + (j – Ring) – 1.

Теперь попробуем вывести

…
a[ik][jk] =  switcher * Xs + abs(switcher - 1) * (4 * N - 2 - Xs);
…

Как вы могли заметить верхние и правые элементы внутренних колец пришли в требуемое значение. Однако нижние и левые стороны приняли гораздо большие значения, чем ожидалось. Это связано с тем, что выражение 4 * N — 2 — Xs во второй части функции вычисляет значения исходя из размера внешнего кольца, которое нужно уменьшить, заменив на N – 2 * Ring. То есть формула будет работать в соответствии с размером текущего кольца.

Итак:

…
a[ik][jk] =  switcher * (Xs) + abs(switcher - 1) * (4 * (N - 2 * Ring) - 2 - Xs); 
…

Все правильно, с первой задачей данного этапа мы справились . Остается последний шаг – вычислить коэффициент прироста, о котором говорилось выше, и связать между собой все кольца.

Как можно заметить, очередное кольцо начинается со значения равного количеству ячеек всех вышестоящих колец плюс один. Делается это очень простым способом:

Coef = N² – (N – 2Ring)²

Воспользовавшись правилами разложения квадратов разницы элементов ((a−b)²=a²−2ab+b²), можно сократить до 4Ring(N — Ring).

Теперь этот коэффициент нужно добавить к нашей основной формуле.

…
a[ik][jk] =  Coef + switcher * (Xs) + abs(switcher - 1) * (4 * (N - 2 * Ring) - 2 - Xs);
…

Требуемый результат!

Полный код участка вычисления значений представлены следующим образом:

…
int switcher =  (j - i + N) / N;
int Ic = abs(i - N / 2  - 1) + (i - 1)/(N /2) * ((N-1) % 2);
int Jc = abs(j - N / 2  - 1) + (j - 1)/(N /2) * ((N-1) % 2);
int Ring = N / 2 - (abs(Ic - Jc) + Ic + Jc) / 2;
int Xs = i - Ring + j - Ring - 1;    
int Coef =  4 * Ring * (N - Ring);
a[ik][jk] =  Coef + switcher * Xs + abs(switcher - 1) * (4 * (N - 2 * Ring) - 2 - Xs);
…

Можно конечно попробовать развернуть единую формулу, заменив дополнительные переменные выражениями, основанными только на i, j и N, и попытаться сократить ее математическими методами. Но поверьте мне, я пытался, получилось нечто такое невообразимое (на половину страницы), что я решил оставить все как есть.

(PS. Не работает только при N = 1, так как возникает ошибка деления на ноль. Но как говорится, «чуть-чуть – не считается»).

Источник

Перейти к содержимому

Как заполнить матрицу по спирали

В этой записи я продемонстрирую заполнение квадратной матрицы по спирали на языке Python. Использован Python версии 3.6

#n - размерность матрицы n x n
#mat - результирующая матрица
#st - текущее значение-счетчик для записи в матрицу
#m - коеффициент, используемый для заполнения верхней
#матрицы последующих витков, т.к. одномерные матрицы
#следующих витков имеют меньше значений
n = int(input())
mat = [[0]*n for i in range(n)]
st, m = 1, 0

# Заранее присваиваю значение центральному элементу
# матрицы
mat[n//2][n//2]=n*n

for v in range(n//2):
    #Заполнение верхней горизонтальной матрицы
    for i in range(n-m):
        mat[v][i+v] = st
        st+=1
        #i+=1
    #Заполнение правой вертикальной матрицы    
    for i in range(v+1, n-v):
        mat[i][-v-1] = st
        st+=1
        #i+=1
    #Заполнение нижней горизонтальной матрицы
    for i in range(v+1, n-v):
        mat[-v-1][-i-1] =st
        st+=1
        #i+=1
    #Заполнение левой вертикальной матрицы
    for i in range(v+1, n-(v+1)):
        mat[-i-1][v]=st
        st+=1
        #i+=1
    #v+=1
    m+=2

#Вывод результата на экран
for i in mat:
    print(*i)

Коротко объясню, для чего нужна переменная m. Обратите внимание на результирующую матрицу при n = 5:

matrix

Начиная со значения 17 мы заполняем новый виток до значения 19. То есть, имеем всего 3 значения: 17, 18, 19.
Для этого и используется коэффициент m, чтобы заново не штудировать все 5 значений.

Просмотрено:
43 488

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given two values m and n, fill a matrix of size ‘m*n’ in a spiral (or circular) fashion (clockwise) with natural numbers from 1 to m*n.

Examples:

Input : m = 4, n = 4
Output :  1  2  3  4
         12 13 14  5
         11 16 15  6
         10  9  8  7 

Input : m = 3, n = 4
Output :  1  2  3  4
          10 11 12 5
          9  8  7  6

The idea is based on Print a given matrix in spiral form. We create a matrix of size m * n and traverse it in a spiral fashion. While traversing, we keep track of a variable “val” to fill the next value, we increment “val” one by one and put its values in the matrix.

Implementation:

C++

#include <bits/stdc++.h>

using namespace std;

const int MAX = 100;

void spiralFill(int m, int n, int a[][MAX])

{

int val = 1;

int k = 0, l = 0;

while (k < m && l < n)

{

for (int i = l; i < n; ++i)

a[k][i] = val++;

k++;

for (int i = k; i < m; ++i)

a[i][n-1] = val++;

n--;

if (k < m)

{

for (int i = n-1; i >= l; --i)

a[m-1][i] = val++;

m--;

}

if (l < n)

{

for (int i = m-1; i >= k; --i)

a[i][l] = val++;

l++;

}

int main()

{

int m = 4, n = 4;

int a[MAX][MAX];

spiralFill(m, n, a);

for (int i=0; i<m; i++)

{

for (int j=0; j<n; j++)

cout << a[i][j] << " ";

cout << endl;

}

return 0;

}

C

#include <stdio.h>

const int MAX = 100;

void spiralFill(int m, int n, int a[][MAX])

{

int val = 1;

int k = 0, l = 0;

while (k < m && l < n)

{

for (int i = l; i < n; ++i)

a[k][i] = val++;

k++;

for (int i = k; i < m; ++i)

a[i][n-1] = val++;

n--;

if (k < m)

{

for (int i = n-1; i >= l; --i)

a[m-1][i] = val++;

m--;

}

if (l < n)

{

for (int i = m-1; i >= k; --i)

a[i][l] = val++;

l++;

}

int main()

{

int m = 4, n = 4;

int a[MAX][MAX];

spiralFill(m, n, a);

for (int i=0; i<m; i++)

{

for (int j=0; j<n; j++)

printf("%d ",a[i][j]);

printf("n");

}

return 0;

}

Java

import java.io.*;

class GFG {

static int MAX = 100;

static void spiralFill(int m, int n, int a[][]) {

int val = 1;

int k = 0, l = 0;

while (k < m && l < n) {

for (int i = l; i < n; ++i) {

a[k][i] = val++;

}

k++;

for (int i = k; i < m; ++i) {

a[i][n - 1] = val++;

}

n--;

if (k < m) {

for (int i = n - 1; i >= l; --i) {

a[m - 1][i] = val++;

}

m--;

}

if (l < n) {

for (int i = m - 1; i >= k; --i) {

a[i][l] = val++;

}

l++;

}

public static void main(String[] args) {

int m = 4, n = 4;

int a[][] = new int[MAX][MAX];

spiralFill(m, n, a);

for (int i = 0; i < m; i++) {

for (int j = 0; j < n; j++) {

System.out.print(a[i][j] + " ");

}

System.out.println("");

}

Python3

def spiralFill(m, n, a):

val = 1

k, l = 0, 0

while (k < m and l < n):

for i in range(l, n):

a[k][i] = val

val += 1

k += 1

for i in range(k, m):

a[i][n - 1] = val

val += 1

n -= 1

if (k < m):

for i in range(n - 1, l - 1, -1):

a[m - 1][i] = val

val += 1

m -= 1

if (l < n):

for i in range(m - 1, k - 1, -1):

a[i][l] = val

val += 1

l += 1

if __name__ == '__main__':

m, n = 4, 4

a = [[0 for j in range(n)] for i in range(m)]

spiralFill(m, n, a)

for i in range(m):

for j in range(n):

print(a[i][j], end=' ')

print('')

C#

using System;

class GFG {

static int MAX = 100;

static void spiralFill(int m, int n, int[,] a) {

int val = 1;

int k = 0, l = 0;

while (k < m && l < n) {

for (int i = l; i < n; ++i) {

a[k,i] = val++;

}

k++;

for (int i = k; i < m; ++i) {

a[i,n - 1] = val++;

}

n--;

if (k < m) {

for (int i = n - 1; i >= l; --i) {

a[m - 1,i] = val++;

}

m--;

}

if (l < n) {

for (int i = m - 1; i >= k; --i) {

a[i,l] = val++;

}

l++;

}

public static void Main() {

int m = 4, n = 4;

int[,] a = new int[MAX,MAX];

spiralFill(m, n, a);

for (int i = 0; i < m; i++) {

for (int j = 0; j < n; j++) {

Console.Write(a[i,j] + " ");

}

Console.Write("n");

}

PHP

<?php

function spiralFill($m, $n, &$a)

{

$val = 1;

$k = 0;

$l = 0;

while ($k < $m && $l < $n)

{

for ($i = $l; $i < $n; ++$i)

$a[$k][$i] = $val++;

$k++;

for ($i = $k; $i < $m; ++$i)

$a[$i][$n - 1] = $val++;

$n--;

if ($k < $m)

{

for ($i = $n - 1; $i >= $l; --$i)

$a[$m - 1][$i] = $val++;

$m--;

}

if ($l < $n)

{

for ($i = $m - 1; $i >= $k; --$i)

$a[$i][$l] = $val++;

$l++;

}

$m = 4;

$n = 4;

spiralFill($m, $n, $a);

for ($i = 0; $i < $m; $i++)

{

for ($j = 0; $j < $n; $j++)

{

echo ($a[$i][$j]);

echo (" ");

}

echo ("n");

}

?>

Javascript

<script>

const MAX = 100;

function spiralFill(m, n, a)

{

let val = 1;

let k = 0, l = 0;

while (k < m && l < n)

{

for (let i = l; i < n; ++i)

a[k][i] = val++;

k++;

for (let i = k; i < m; ++i)

a[i][n-1] = val++;

n--;

if (k < m)

{

for (let i = n - 1; i >= l; --i)

a[m-1][i] = val++;

m--;

}

if (l < n)

{

for (let i = m - 1; i >= k; --i)

a[i][l] = val++;

l++;

}

let m = 4, n = 4;

let a = Array.from(Array(MAX), () => new Array(MAX));

spiralFill(m, n, a);

for (let i = 0; i < m; i++)

{

for (let j = 0; j < n; j++)

document.write(a[i][j] + " ");

document.write("<br>");

}

</script>

Output

Time Complexity: O(m * n)
Space Complexity: O(m * n)

This article is contributed by Ayush Jauhari. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Last Updated :
12 Dec, 2022

Like Article

Save Article

Источник