Как в паскале составить блок схему функции - Исправление недочетов и поиск решений вместе с Examum.ru

Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.

В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.

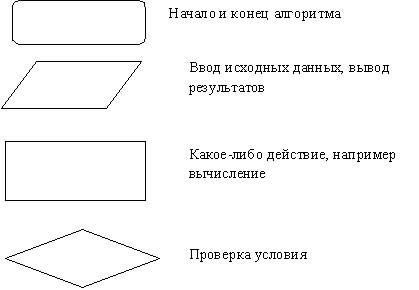
Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).

Существует несколько основных видов блоков, которые нетрудно запомнить:

Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.

Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».

Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.

Составим алгоритм решения подобных задач:

1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.

Запишем условие в более кратком виде.

Дано: a, b

Найти: S, P

Блок-схема:

Решение задачи №1

Структура программы, решающей данную задачу, тоже проста:

1) Описание переменных;
2) Ввод значений сторон прямоугольника;
3) Расчет площади прямоугольника;
4) Расчет периметра прямоугольника;
5) Вывод значений площади и периметра;
6) Конец.

А вот и решение:

Program Rectangle;
Var a, b, S, P: integer;
Begin
write('Введите стороны прямоугольника!'); 
readln(a, b);
S:=a*b;
P:=2*(a+b);
writeln('Площадь прямоугольника: ', S);
write('Периметр прямоугольника: ', P);
End.

Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.

Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:

Дано: V1, V2, S, Т
Найти: S1

Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).

Формула, используемая для решения нашей задачи, выглядит следующим образом:

S1=(V1+V2)*T+S

Следующий пункт алгоритма – блок-схема:

Решение задачи №2.

А также решение, записанное в Pascal :

Program Rasstoyanie;
Var V1, V2, S, T, S1: integer; {Ввод }
begin
write('Введите скорость первого автомобиля: '); 
readln(V1);
write('Введите скорость второго автомобиля: '); 
readln(V2);
write('Введите время: '); 
readln(T);
write('Введите расстояние между автомобилями: '); 
readln(S);
S1:=(V1+V2)*T+S;
writeln('Через ', t,'ч. расстояние ', S1,' км.');
End.

Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число! А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:

Обратите внимание в Паскале, как и в любом другом языке программирования десятичная дробь вводится с точкой, а не с запятой!

Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real. Вот, как выглядит исправленная программа:

Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

Источник

Содержание

Оформление подпрограмм в блок-схемах алгоритмов
Урок 4. Блок-схема
Блок-схема функции
Решение

Оформление подпрограмм в блок-схемах алгоритмов

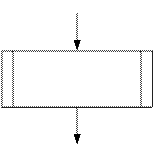
Блок-схема алгоритма подпрограммы изображается аналогично блок-схемам программ: в ней присутствуют блоки «Начало» и «Конец», между которыми заключена вся исполняемая часть подпрограммы.

Вызов подпрограммы в основной программе изображается на блок-схеме в виде блока «Предопределенный процесс»:

1.3 Пример составления алгоритма и программы на языке Pascal для обработки одномерных массивов с использованием подпрограмм.

Задание: Даны два массива вещественных чисел A(20) и F(30). Найти средние арифметические значения положительных элементов в каждом массиве и вывести на экран отношение этих значений.

Для объявления массивов A и F опишем в разделе Type тип массива из 30 вещественных чисел. Для обозначения количества элементов массива A введем переменную Na, количества элементов массива F – переменную Nf, средних арифметических значений положительных элементов массивов – переменные SrA и SrF.

Для каждого массива необходимо повторить одни и те же операции:

ввод элементов массива,
поиск среднего значения среди положительных элементов,
вывод элементов массива.

Поэтому, для выполнения этих действий удобно организовать подпрограммы. Для решения данной задачи создадим три подпрограммы: процедуру ввода элементов массива, процедуру вывода элементов массива на экран, функцию поиска среднего значения среди положительных элементов массива.

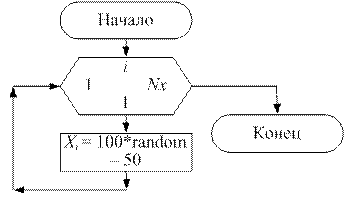
Процедуру ввода элементов массива назовем EnterMassiv, в списке формальных параметров укажем следующие переменные: массив X и количество элементов в массиве Nx. При этом в списке формальных параметров массив должен быть указан со служебным словом var, поскольку значения элементов массива изменяются в процедуре и возвращаются в основную программу. Внутри процедуры формирование элементов массива выполним с помощью генератора случайных чисел random.

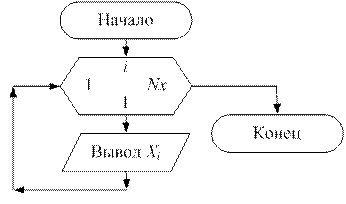
Процедуру вывода элементов массива назовем PrintMassiv, и будем в нее передавать те же переменные: массив X и количество элементов в массиве Nx. При этом в списке формальных параметров перед массивом служебное слово var можно не указывать, поскольку значения элементов массива в процедуре не изменяются, а только выводятся на экран.

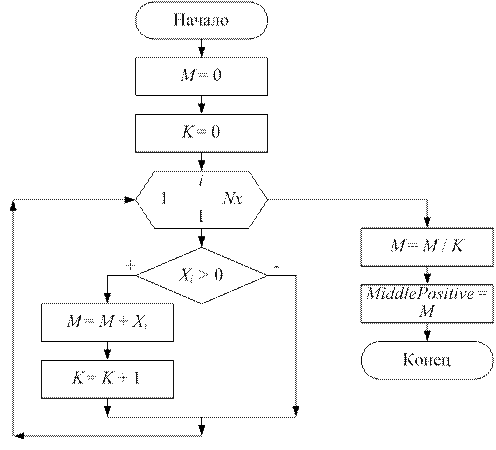
Функцию поиска среднего значения среди положительных элементов массива назовем MiddlePositive, и будем в нее также передавать массив X и количество элементов в массиве Nx. Поскольку среднее арифметическое является вещественным числом, тип функции должен быть real. Внутри функции будем использовать локальную переменную K для подсчета количества положительных элементов массива, переменную M для расчета суммы всех положительных элементов массива и их среднего значения.

1.3.1 Блок-схема алгоритма решения данной задачи выглядит следующим образом:

Блок схема подпрограммы EnterMassiv

Блок схема подпрограммы PrintMassiv

Блок схема подпрограммы MiddlePositive

Блок-схема основной программы

1.3.2 Текст программы на языке Pascal выглядит следующим образом:

Источник

Урок 4. Блок-схема

Существует несколько основных видов блоков, которые нетрудно запомнить:

Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».

Составим алгоритм решения подобных задач:

Запишем условие в более кратком виде.

Структура программы, решающей данную задачу, тоже проста:

1) Описание переменных;
2) Ввод значений сторон прямоугольника;
3) Расчет площади прямоугольника;
4) Расчет периметра прямоугольника;
5) Вывод значений площади и периметра;
6) Конец.

Формула, используемая для решения нашей задачи, выглядит следующим образом:

Следующий пункт алгоритма – блок-схема:

Решение задачи №2.

А также решение, записанное в Pascal :

Здесь понятней чем в школе.

мля… прикиньте, я узнал про этот сайт только ПОСЛЕ того как сделал программу с условием, узнавая все в инструкции

Ребята , вопрос на засыпку, как заставить «,» (введенную пользователем в числе) заменить на «.» внутри программы, что бы не вылетало юхни с ошибкой.

Взять строку введенную пользователем, заменить «,» на «.».
Если совсем гуглить не умеете, то вам сюда — http://www.cyberforum.ru/pascal/thread190664.html

>> скорость машины не обязательно круглое число!

Нет такого понятия, как «круглое число».

Обе ваши блок-схемы не соответствуют ГОСТу (сдать такие на курсовой проект не получится). ГОСТ определяет блоки начала и конца, как «прямоугольник со скругленными краями», а не «скругленными углами».

>> умение правильно и быстро составлять схемы является фундаментом, основой программирования.

Большинство программистов так не считает. Кроме того, попробуйте поспрашивать у программистов «когда они последний раз составляли блок-схему?» — окажется что в ВУЗе (когда с них зачем-то сдирали знание ГОСТа).

>> так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

Очень сложное, долгое и бесполезное занятие. Для хоть сколько-нибудь большой программы (в тысячу строк хотя бы, как курсак) блок-схемы будут огромные и их будут десятки. А что делать если они перестают соответствовать коду? — вот даже в вашей первой задаче надо будет добавить проверку, что юзер не ввел отрицательные значения сторон, что делать? — исправления кода займут 1 минуту, а исправление блок-схем 10 минут, и зачем тогда этим заниматься?

Программист не должен писать блок-схемы (он их должен читать и понимать и при необходимости исправлять). Блок-схемы это графический язык общения, который понимает как программист, так и не программист. Чтобы пользователь не общался с программистом своими «хотелками», типа я хочу, чтобы вот это правильно считалось, и это число складывалось с этим, а потом выводилось сюда (или вообще говорил — хочу что бы работало), а рисовал все в виде блок-схем с четким алгоритмом. Тогда по идее у программиста будет понимание того, что от него хотят (и он через пять минут не забудет все что ему сказали). Либо, когда общаются два программиста пишущих на разных языках программирования (LISP и Java) и одному нужно объяснить как работает его код, что бы другой переписал его на другом языке.
Как объяснить преподавателю как работает программа, если преподаватель не знает языка программирования на котором написана ваша программа? Или как преподавателю объяснить алгоритм задачи студентам пишущим и реализующим этот алгоритм или программу на разных языках программирования? Нужен какой-то универсальный язык общения и обычно это просто текст «что нужно сделать» на русском языке, а не намного облегчающая жизнь программиста блок-схема.
Вам могут сказать — сделай модуль авторизации (ты же знаешь как, ну как всегда и как везде), а могут нарисовать блок-схему модуля авторизации с учетом всех пожеланий, типа того, что пароль должен содержать не менее 6 символов и что нужно делать в противном случае т.д. То есть блок схему должен уметь рисовать тот кто ставит задачу, а не программист. Либо программист (архитектор либо менеджер проекта), который ставит задачу другим программистам.

Вы слишком придирчивы, серьезно (я говорю про последние два пункта). Понятно, что статья (как почти и весь сайт) написана почти только для школьников, которым об этом твердят в школе. Здесь же им просто объясняют те вещи, которые они на учебе недопоняли

Блок схемы всей программы могут не понадобиться. Это же тонны бумаги и много времени. И да, они устаревают и актуализировать их трудоёмко.
Но при обсуждении новых вариантов решения задачи с другими программистами удобно оперировать блоками с криво-косо нарисованными краями и линиями. Начертил на бумаге или доске и все понятно.
На практике я встречал фотографии доски с блок-схемами, прикреплённые к задачам в Jira.
Не по ГОСТу 🙂

Спасибо, теперь я напишу программу, которая делает код по блок схеме и наоборот

program Logarifm;
Var
X,y,z:real;
function Lgrfm(A,B:Real):Real;
var
Osn:Real;
begin
Osn:=ln(A)/ln(B);
Lgrfm:=Osn;
end;
begin
Write(‘Введите X = ‘);
ReadLn(X);
Write(‘Введите Y = ‘);
ReadLn(Y);
Z:=Lgrfm(X,2)+Lgrfm(Y,3);
WriteLn(‘Z = ‘,Z:10:3);
ReadLn;
end.

Отличный сайт, мне все нравится все понятно и четко, нашел нужные программы.

В блок-схемах начало и конец алгоритма обозначаются не прямоугольником со скруглёнными краями, а овалом!

Ребята, что сделали сайт молодцы)) Оч полезная инфа, что нужно поправить, чтобы сайт стал еще лучше:
1) мне не хватает структуры уроков порядковой (или хотябы под уроками чтобы была ссылка на следующий), поэтому приходится на другие уроки искать ссылки по сайту и в контексте уроков;
2)нет описания функций используемых в примерах (по крайней мере, возможно по причине отсутствия структуры, я их не нашел), поэтому беру на сторонних ресурсах описания таких функций как dec() inc() sqr() odd().
А вообще как я понял сайт составлялся школьниками «на коленках», поэтому я не придираюсь, а просто говорю им спасибо за их труд. Желаю успехов.

Источник

Блок-схема функции

Здравствуйте.
Правильно ли я сделал блок-схему функции?

И когда нужно использовать блок

когда строишь блок-схему самой функции? Или когда в основной программе вызываешь эту функцию? То есть когда пишешь summ () в основ. программе, там и используется этот блок?

процедуры и функции, блок-схема.
Здравствуйте все! У меня такой вопрос — подскажите пожалуйста- как в блок-схеме описать действие.

Блок-схема функции по госту
Здравствуйте. Как выглядит блок-схема по госту? function summ(var a: mass): single; var .

Блок-схема вычисления функции
Uses GraphABC; type mas= array of real; mas1=array of real; var ii:text; a: mas;.

Блок-схема программы вычисления функции
Помогите составить программу. Не могу понять, где у меня ошибка?

Решение

Формально почти всё верно, есть лишь одно несоответствие: в коде у Вас в 15 строке происходит печать переменных, но на блок-схеме этого не отображено. Если это — контрольная печать, тогда всё ОК. Правда, странная какая-то печать. Типа, 1 + 10 = 10.

Насчёт применения конкретных термов (символов) в блок-схеме и их соответствия ГОСТу у Вас не всё гладко (например, терм «терминатор» у Вас изображён в виде эллипса, а по стандарту должен быть прямоугольник со скруглёнными углами, радиус скругления — половина высоты прямоугольника; цикл обычно изображается, как ни странно, термом «подготовка», а не термом «граница цикла»; в тексте на блок-схемах операция присваивания стрелкой изображается редко, обычно так делается в блок-схемах, созданных в целях написания кода на ассемблере), но. Скажем так, можете считать, что «правильность» изображения блок-схемы полностью зависит от требований Вашего учебного заведения к составлению блок-схем.

Код функции у Вас оставляет желать лучшего: не нужно без особой необходимости использовать в подпрограммах глобальные переменные (у Вас это tmass), это порождает трудно локализуемые ошибки. Чего бы эту tmass не передавать в функцию по ссылке? А то как-то нелепо: функция вроде как без входных формальных параметров, хотя по факту — входной параметр функции — эта самая tmass.

Ну и. Ладно уж, что не видно толком ни tmass, ни ischo, хотя они там и есть. И как это на блок-схеме отобразить? Вот так?

А вот и нет, tmass и ischo относятся к разным предопределённым процессам, поскольку это — две разные функции, а всё остальное и вовсе не относится к какому-либо предопределённому процессу. Неувязочка, однако. Чтобы всё было корректно, в блок-схемах выражения с вызовом функций изображают с помощью терма «процесс» (это который обычный прямоугольник), а терм «предопределённый процесс» используется только для отображения процедур. Но. Бывают учебные заведения, в которых в ходу идиотское требование изображать и функцию термом «предопределённый процесс», например, так:

Но по стандарту терм в терме как-то не комильфо. Так что, на всякий случай уточните у преподавателя, нужно ли в Вашей основной блок-схеме для изображения вызова именно функции использовать прямоугольник с двойными стенками.

Источник

Подпрограммы на паскале

Цель: дать понятие о подпрограммах на паскале: процедурах и функциях. Учить использовать их при составлении более сложных программ; вводить и выполнять программы, используя компиляторы BPW или Turbo Pascal.

1. Дедуктивный метод программирования

Отвлечемся на некоторое время от составления программ и поговорим о творческом процессе вообще, не только программиста или математика, а, например, художника или архитектора.
Допустим, что художник собирается нарисовать картину: портрет человека или что-то другое. Прежде, в глубине его сознания созревает общий образ будущего произведения, затем начинается ее реальное воплощение на холсте, бумаге, дереве или на чем-то другом. И вот здесь начинается тяжелейшая работа. Художник выполняет эскизы, рисунки отдельных фрагментов картины, а потом создает единое произведение, воплощающее в красках, цвете и тени, выношенный им образ.
Архитектор задолго до создания проекта своей новой конструкции также видит его целиком, а затем воплощает по отдельным частям единый проект здания или сооружения.
Подобно им и программист должен видеть в целом программу, которая решает какую-то задачу, а потом разбивает ее на отдельные части, составляет на выбранном языке программирования эти части программы, объединяет их в единое целое и получает программу.
Итак, весь творческий процесс можно разбить (разумеется, чисто условно) на следующие этапы:

1) основная идея решения задачи;
2) общая конструкция программы;
3) выделение отдельных, элементарных частей программы;
4) практическая реализация на языке программирования этих частей программы;
5) объединение их в единую программу.

Такой процесс программирования называют структурным или нисходящим. Более подробно с этим процессом мы познакомимся позже, когда изучим хотя бы основы языка программирования, но об отдельных частях, «кирпичиках», составляющих программу узнаем на этом занятии.

Подпрограммой называется группа операторов, к которой обращаются из основной программы несколько раз. Иногда это может быть 2, 3 раза, а очень часто, каждый раз из выполняемого цикла основной программы.

Вполне понятно, что писать несколько раз одинаковые группы операторов трудно, проделывается много «технической» работы, а в некоторых случаях просто невозможно (если обращаться приходиться каждый раз при выполнении цикла).
Для облегчения такой работы и созданы подпрограммы.

Использование подпрограмм позволяет:
1) сделать основную программу более наглядной и компактной;
2) уменьшить объем используемой памяти ЭВМ;
3) сократить время отладки программы.
На языке Паскаль подпрограммы бывают двух видов, — это процедуры и функции.
2. Процедуры

Рассмотрим следующий простой пример, с помощью которого попробуем разобраться в конструкции процедур на Паскале.

Пример 1. Составить программу, которая бы проверяла, являются ли три числа взаимно простыми.

Мы знаем, что числа называются взаимно простыми, если их наибольший общий делитель (НОД) равен 1. Значит, для решения этой задачи нам придется дважды находить НОД чисел. Если заданы три числа: a, b, c, то найти НОД(a, b), а затем найти НОД(НОД(a, b), c).
Дважды писать операторы для нахождения НОД нам не хочется, поэтому оформим операторы для НОД в виде процедуры.

Блок-схема процедуры nod

Рис. 44

Блок обращения к процедуре в основной программе

Рис. 45

Блок-схема основной программы

Рис. 46

Программа
Program Problem1;
uses WinCrt;
var
a, b, c, k : integer;
{—————————————————————————————-}
Procedure nod(a, b : integer; var n : integer);
var
r : integer;
begin
repeat
r := a mod b;
a := b; b := r
until b = 0;
n := a
end;
{—————————————————————————————}
begin
nod(a, b, k);
a := k; b := c;
nod(a, b, k);
if k = 1 then writeln(«Числа взаимно простые»)
else writeln(«Числа не взаимно простые»)
end.
В разделе описаний, после описания переменных, записывается заголовок процедуры: Procedure
Это слово является служебным и зарезервировано в Паскале. В одной строке с ним, через пробел, записывается имя процедуры, которое должно удовлетворять всем требованиям, предъявляемым к именам, основными из которых являются: начинаться с буквы и не иметь пробелов, т. е., требования такие же, как и к имени программы (имя нашей процедуры — nod):
Procedure nod(a, b : integer; var n : integer);

Далее, в скобках, записываются имена переменных и их типы, значения которых будут вводиться в процедуру из основной программы, в нашем случае, их две (a, b) и они имеют тип integer.
Сразу надо заметить, что имена этих переменных могут не совпадать с именами переменных в основной программе, скажем мы могли их обозначить m, n или любыми другими именами.
После точки с запятой и зарезервированного слова var, записываются переменные и их типы, значения которых будет являться результатом работы процедуры и выводятся из нее в основную программу. Такая переменная в нашем примере одна — n. Она выведет значение НОД чисел a и b. Ее имя также может иметь одноименное в основной программе и это нисколько не отразится на работе процедуры.
Обратите внимание, что перед переменными, значения которых вводятся из основной программы, не ставится слово var, а перед переменной, значение которой выводится в основную программу, это слово записано. Это очень важное обстоятельство!
Так, если поставить var перед a и b, то компилятор будет воспринимать эти переменные как выходные и вводимые для них значения воспринимать не будет, и, наоборот, если var не будет записано перед выходной переменной, то компилятор воспримет ее как входную и выводить ее значение в основную программу не будет.
Дальнейшее построение процедуры строится также, как и основная программа на Паскале.
Описываются переменные, которые будут участвовать в ее работе, но их имена не должны повторять имена уже описанных входных и выходных параметров в заголовке программы. Далее описываются необходимые для работы операторы.
В нашем примере процедура nod будет такой:

Procedure nod(a, b : integer; var n : integer);
var
r : integer;
begin
repeat
r := a mod b;
a := b; b := r
until b = 0;
n := a
end;

Основная программа строится обычным образом, но там, где необходимо найти НОД чисел, обращается к процедуре. Как?
Для этого обращаются к ней по имени, а в скобках записывают фактические значения входных переменных (в нашем случае для переменных a и b), а также имена выходных переменных (в нашем случае k).
Из приведенного ниже участка программы видно, что при первом обращении к процедуре nod определяется НОД чисел a и b (nod(a, b, k) и результат запоминается в переменную k, далее, изменяются значения переменных a и b и снова вызывается процедура nod, которая уже находит НОД чисел k и c и результат присваивает переменной k.

Вы можете видеть основную часть программы:

begin
write(«Введите три натуральных числа «); readln(a, b, c);
nod(a, b, k);
a := k; b := c;
nod(a, b, k);
if k = 1 then writeln(«Числа взаимно простые»)
else writeln(«Числа не взаимно простые»)
end.

Сделаем общие выводы для построения и работы процедур

Процедуры помещаются в разделе описаний и начинается зарезервированным (служебным) словом
Procedure

Процедуре обязательно дается имя, которое должно удовлетворять тем же требованиям, что и имена переменных, т.е. это может быть одна или несколько букв, комбинация букв и целых чисел, но без пробелов, начинаться с буквы и т.д.
После имени, в скобках записываются переменные — параметры и их тип: входные, значения которых используются для вычисления в качестве аргументов.
Выходные параметры — это те переменные, в которых получается результат выполнения процедуры.
Входные и выходные параметры процедуры называются формальными параметрами.
Фактические, конкретные, значения формальные параметры должны получить в основной программе после обращения к ней (а пока в процедуре они являются не чем иным, как «пустышками«).
После формальных параметров, описываются переменные, которые необходимы непосредственно для работы процедуры.
Это параметры процедуры. Они нужны в ней, как и в любой другой программе и описываются также. Их имена должны отличаться от имен входных и выходных параметров.
Надо заметить, что процедура может быть такой, что в ней не будет вообще параметров, достаточно тех, которые будут введены из программы.
Описание процедуры имеет вид:

Procedure <имя> (<входные параметры>:<их тип>;
var <выходные параметры>:<их тип>);
var
(раздел описаний)
begin
(раздел операторов)
end;

Она помещается в основной программе в разделе описаний.
По входным и выходным параметрам процедуры могут быть следующих типов:

1) иметь и входные и выходные параметры:

Procedure <имя>(<входные параметры> : <их тип>;
var <выходные параметры> : <их тип>);
Мы только познакомились с программой такого типа.
2) иметь входные параметры, но не иметь выходных:
Procedure <имя>(<входные параметры> : <их тип>);
3) иметь выходные параметры, но не иметь входных:
Procedure <имя>(var <выходные параметры> : <их тип>);
4) не иметь ни входных, ни выходных параметров:
Procedure <имя>;

В зависимости от этого различаются процедуры по своей конструкции и выполняемым функциям.
Далее следует раздел операторов, который составляется по тем же правилам, как и в других программах.
Процедура описана и после этого начинается основная программа.

Вызов процедуры из программы

Как происходит вызов подпрограммы — процедуры?

Обязательно указывается имя процедуры. В скобках задаются фактические значения входных параметров и те переменные, в которые будут «запоминаться» выходные значения.

Рассмотрим пример, где может быть использована процедура второго типа: имеет входные параметры, но не имеет выходных.

Пример 2. Составить программу, которая устанавливает, какие числа из заданного промежутка [a; b] можно представить в виде суммы двух квадратов целых чисел?

В этой программе, нам придется проверять каждое из чисел промежутка [a; b] можно ли его представить в виде суммы квадратов двух чисел, поэтому было бы разумно разработать процедуру, которая бы проверяла одно число и затем обращаться к ней из основной программы для проверки каждого числа из промежутка.
Процедуру составим по следующему способу. Пусть задано число n. Нам необходимо найти такие два числа a и b, чтобы сумма их квадратов была равна n, т.е. решить в целых числах уравнение:
Возникает естественное желание испытывать натуральные числа от 1 и до …? А вот до какого значения неизвестно. Если их брать до числа n, то это будет слишком много лишней и бесполезной работы.
Чтобы выяснить этот вопрос, можно организовать цикл, в котором проверять сколько чисел a надо, чтобы выполнялось неравенство: Здесь, в качестве b взято наименьшее натуральное число 1. Организовав такой цикл, и подсчитав, сколько чисел a потребуется, мы узнаем сколько чисел надо просматривать, чтобы найти решение уравнения.
Этот цикл может быть таким:

a := 1; k := 1;
while a*a + 1<=n do
begin
k := k + 1;
a := a + 1
end;

Теперь ясно, что для испытания чисел, следует устроить цикл от 1 до k:
for a := 1 to k do
Второй цикл должен быть для значений b. Но если его организовать тоже от 1 до k, тогда могут повторяться дважды одинаковые значения, только на разных местах, например, для числа 20 могут быть выданы следующие значения:
22 + 42 = 20 и 42 + 22 = 20.
Чтобы избежать повторения чисел, цикл для чисел b можно организовать либо от 1 до a, либо от k до а.
Нами выбран первый вариант.

Блок-схема процедуры

Рис. 47

Процедура
Procedure to_square(n : integer);
label 1;
var
a, b, k : integer;
begin
a := 1; k := 1;
while a*a + 1<=n do
begin
k := k + 1;
a := a + 1
end;
for a := 1 to k do
for b := 1 to a do
if a*a + b*b = n
then
begin
writeln(n, «=», a, «*», a,» +», b, «*», b); goto 1
end;
1: end;
Процедура выполнена с досрочным прерыванием цикла, так как нет необходимости выяснять всевозможные значения пар чисел, удовлетворяющих этому уравнению, а достаточно просто выяснить возможность такого представления.
Выполнив такую процедуру, не составляет труда решить полностью задачу. Для этого в основной программе выполнить цикл для всех чисел из промежутка, и каждое из которых, с помощью процедуры проверять. Кстати говоря, эта процедура имеет только один формальный параметр — входной, — значение проверяемого числа из промежутка и не имеет выходных параметров.
Блок-схема основной программы

Рис. 48
Программа

Program Problem2;
uses WinCrt;
var
a, b, i : integer;
{—————————————————————————————}
Procedure to_square(n : integer);
label 1;
var
a, b, k : integer;
begin
a := 1; k := 1;
while a*a + 1 <= n do
begin
k := k + 1;
a := a + 1
end;
for a := 1 to k do
for b := 1 to a do
if a*a + b*b = n
then
begin
writeln(n, «=», a, «*», a, «+», b,»*», b); goto 1
end;
1: end;
{—————————————————————————————-}
begin
write(«Введите начало промежутка «); readln(a);
write(«Введите конец промежутка «); readln(b);
write(«Числа, которые можно представить в виде суммы «);
writeln(«квадратов следующих чисел»);
for i := a to b do to_square(i);
end.

Задание 1

1. Покажите, что квадрат числа, являющегося суммой двух точных квадратов, также можно представить в виде суммы двух точных квадратов. Составить блок-схемы, процедуру и программу.

2. Покажите, что произведение двух целых чисел, из которых каждое есть сумма квадратов двух целых чисел, можно представить в виде суммы двух точных квадратов. Составить блок-схемы, процедуру и программу.

Пример 3. Составить программу нахождения и вывода на экран всех простых чисел из заданного промежутка [n; m]. (Массивы не использовать.)

Следует сразу заметить, что эта задача решается иначе с помощью программы «Решето Эратосфена«, но ее мы будем разбирать при изучении работы с массивами чисел и множествами.
А сейчас приведем другой вариант решения этой задачи. Ясно, что для ее решения нам потребуется процедура, которая устанавливает, является ли число простым. На предыдущих занятиях мы уже составляли такую программу. Сейчас вспомним ее работу и возможно внесем некоторые изменения.

Алгоритм составления процедуры такой.

Во-первых, вспомним, какие числа называются простыми.
Натуральные числа, которые имеют только два делителя 1 и само себя называются простыми. Остальные называются составными.
Из их числа исключается число 1, которое не относится ни к простым, ни к составным.
Первое простое число — это 2. Если оно есть, тогда его сразу надо выводить на экран:
if p = 2 then write(p,» «)
Ясно, что все остальные четные числа являются составными, а значит их нет смысла проверять. Для исключения из рассмотренных четных чисел введем для проверки условный оператор:
else if p mod 2 <> 0 then
Если число нечетное, тогда его надо проверять. Сущность проверки будет заключаться в определении числа делителей. Но нам уже известен математический факт, что все делители некоторого натурального числа p находятся в промежутке от 1 до корня квадратного из этого числа (исключая само число). Значит, если имеются делители, в данном случае, от 3 до trunc(sqrt(p)), то оно является составным, а если таких делителей нет (четные числа мы уже исключили, а единицу и само число p не рассматриваем), тогда число будет простым.

Блок-схема процедуры

Рис. 49

Полностью процедура, устанавливающая является ли число простым, будет следующей (probleme number -простое число):

Procedure Probleme_number(p : integer);
var
i, k : integer;
begin
if p=2 then write(p, » «)
else if p mod 2<>0
then
begin
i := 3; k := 0;
while i<=trunc(sqrt(p)) do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then write(p, » «)
end
end;

Снова, эта процедура имеет только входной формальный параметр и не имеет выходных.

Блок-схема основной программы

Рис. 50

Программа

Program Problem3; { Простые числа из промежутка [n; m] }
uses WinCrt;
var
n, m, i : integer;
{—————————————————————————————-}
Procedure probleme_number(p : integer);
var
i, k : integer;
begin
if p=2 then write(p, » «)
else if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= trunc(sqrt(p)) do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then write(p, » «)
end
end;
{—————————————————————————————-}
begin
write(«Введите левую границу промежутка > 1 «); readln(n);
write(«Введите правую границу промежутка «); readln(m);
writeln(«Простые числа из промежутка [«, n, » «, m, «]»);
for i := n to m do probleme_number(i);
writeln
end.

Пример 4. Французский физик М. Мерсен (1588 — 1648) заметил, что многие простые числа имеют вид
2p — 1,

где p также простое число. Все числа такого вида называются числами Мерсена. Составить программу, которая находит числа Мерсена на заданном промежутке.

Алгоритм

Самый простейший алгоритм для составления программы, будет такой:
во-первых, необходима процедура для определения простых чисел, с которой мы уже знакомы;
во-вторых, нужна процедура, которая вычисляет степень натурального числа с натуральным показателем (эту процедуру вы уже должны были составлять при выполнении задания).

Блок-схема процедуры определения простого числа

Рис. 51

Процедура определения простого числа:

Procedure Probleme_number(p : longint; var v : longint);
var
i, k : longint;
begin
if p = 2 then v := p
else if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= trunc(sqrt(p)) do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then v := p
end
end;

Блок-схема процедуры вычисления степени натурального числа с натуральным показателем (extent — степень):

Рис. 52

Процедура вычисления степени натурального числа с натуральным показателем (extent — степень):

Procedure extent(a, n : integer; var s : longint);
var
i : integer;
begin
s := 1;
for i := 1 to n do s := s*a
end;

В основной программе надо пробовать каждое число из промежутка, является ли оно простым, а для этого необходимо обращение к процедуре probleme_number(i, p).
Если получено простое число, тогда следует 2 возвести в эту степень, а для этого следует обратиться к процедуре extent(2, p, m).
Наконец, полученный результат также надо проверить, является ли он простым числом. Если является, тогда мы получаем число Мерсена.
Казалось бы все хорошо, но нас поджидают многие неприятности.
Неприятность первая! Выбрано число 3, процедурой probleme_number(i, p) установлено, что оно простое число и его значение присвоено переменной p. Следующим числом из выбранного промежутка является 4, процедура probleme_number(i, p) установила, что оно не является простым и его значение не присваивается переменной p. Тогда возникает вопрос, а чему равно значение переменной p? Оказывается оно осталось прежним, т. е. равным 3 — предыдущему простому числу.
Если продолжать дальше процесс в программе, тогда значения будут повторяться. Аналогичное повторение будет и при проверке предполагаемого числа Мерсена, является ли оно простым?
Чтобы избежать этих неприятностей, после каждой проверки, начиная с первой, необходимо запоминать полученные значения простых чисел в новые переменные, например: p1 := p; m1 := m; n1 := n, а затем перед повторным обращением к процедурам вычисления степени и проверке простых чисел, проверять, а не являются ли эти значения повторениями предыдущих.
Эта часть основной программы такая:
for i := 2 to b do
begin
probleme_number(i, p);
if p <> p1 then extent(2, p, m);
if m <> m1 then probleme_number(m-1, n);
if n <> n1 then write(n, » «);
n1 := n; p1 := p; m1 := m
end;
Блок-схема основной программы

Рис. 53

Программа

Program Problem4; { Числа Мерсена }
uses WinCrt;
var
b, p, p1, m, m1, n, n1, i : longint;
{—————————————————————————————-}
Procedure Probleme_number(p : longint; var v : longint);
var
i, k : longint;
begin
if p = 2 then v := p
else if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= trunc(sqrt(p)) do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then v := p
end
end;
{—————————————————————————————-}
Procedure extent(a, n : integer; var s : longint);
var
i : integer;
begin
s := 1;
for i := 1 to n do s := s*a
end;
{—————————————————————————————}
begin
write(«Введите правую гран. знач. показ. степ. «); readln(b);
write(«Числа Мерсена: «);
for i := 2 to b do
begin
probleme_number(i, p);
if p <> p1 then extent(2, p, m);
if m <> m1 then probleme_number(m — 1, n);
if n <> n1 then write(n,»; «);
n1 := n; p1 := p; m1 := m
end;
writeln
end.

Замечание. В дальнейшем, при работе с массивами чисел, мы найдем более простой способ нахождения чисел Мерсена с использованием «Решета Эратосфена«.

Задание 2

Найти наименьшее натуральное число n, такое, что не делится на n, но делится на n. Составьте блок-схемы процедур и основной программы, а затем и сами процедуры и программы.

(Используйте процедуру вычисления степени натурального числа с натуральным показателем.)

Пример 5. Число, состоящее из n (n > 1) цифр, называется числом Армстронга, если сумма его цифр, возведенных в n-ю степень равна самому этому числу.
Например, числами Армстронга являются 153 и 1634, так как
153 = 13 + 53 + 33, 1634 = 14 + 64 + 34 + 44.

Составить программу, которая будет находить все n-значные числа Армстронга (n — входное данное, причем n < 10).

Математический анализ задачи

Пользователем задается, образно говоря, n — значность числа, т.е. количество цифр, которое должно быть в числе. Например, он может задать, что числа 5-ти значные. Программа должна из всех пятизначных чисел найти числа Армстронга, если, конечно, такие есть.
Для этого, в программе надо определять наименьшее n-значное число, что сделать просто, организовав цикл от 1 до n — 1 и умножая, заведомо установленную переменную (первоначальное значение которой равно 1) на 10. Чтобы установить наибольшее n-значное число, достаточно наименьшее n-значное умножить на 10 и вычесть 1. Например, для 5-значных чисел, наименьшим будет 10000, а наибольшее
Для определения наименьшего и наибольшего n-значного числа создадим такую процедуру:
Блок-схема процедуры

Рис. 54

Процедура

Procedure minmax(n : longint; var min, max : longint);
var
i : longint;
begin
min := 1;
for i := 1 to n — 1 do min := min*10;
max := min*10 — 1
end;

Каждую цифру числа придется возводить в n-ю степень, для этого снова потребуется процедура возведения в степень. Она уже нам знакома:

Procedure extent(a, n : longint; var s : longint);
var
i : longint;
begin
s := 1;
for i := 1 to n do s := s*a
end;

В основной программе придется отделять по одной цифре, мы опять-таки знакомы с этим процессом (находить остаток от деления на 10 — это последняя цифра, уменьшать число в 10 раз, отбрасывая последнюю цифру целочисленным делением на 10).
Каждая цифра возводится в степень и результат суммируется, затем происходит сравнение с исследуемым числом, если равенство выполняется, то исследуемое число — число Армстронга.

for x := min to max do
begin
p := x; s := 0;
for i := 1 to n do
begin
extent(p mod 10, n, k);
s := s + k;
p := p div 10
end;
if s = x then write(x, » «)
end;

Программа

Program Problem5; { Числа Армстронга }
uses WinCrt;
var
n, min, max, x, p, s, i, k : longint;
{—————————————————————————————-}
Procedure extent(a, n : longint; var s : longint);
var
i : longint;
begin
s := 1;
for i := 1 to n do s := s*a
end;
{—————————————————————————————-}
Procedure minmax(n : longint; var min, max : longint);
var
i : longint;
begin
min := 1;
for i := 1 to n — 1 do min := min*10;
max := min*10 — 1
end;
{—————————————————————————————}
begin
write(«Введите количество цифр числа «); readln(n);
writeln(n, «-х значные числа Армстронга»);
minmax(n, min, max);
for x := min to max do
begin
p := x; s := 0;
for i := 1 to n do
begin
extent(p mod 10, n, k);
s := s + k;
p := p div 10
end;
if s = x then write(x, » «)
end;
writeln
end.

(И эту программу, впоследствии, мы будем выполнять с использованием массивов.)

Пример 6. Напишите программу, которая для каждого из целых чисел от 1 до n напечатает все его делители. Например, 1 5 7 35 являются делителями числа 35. Аналогичный список делителей должен быть напечатан для каждого из чисел от 1 до заданного числа n.

Алгоритм

Программа составляется очень просто. Для этого, надо создать процедуру определения делителей числа (программу мы разбирали на предыдущих занятиях) и для каждого числа из данного промежутка обращаться к ней.
Получится следующая простая программа. Единственное замечание. При определении числа делителей в процедуре, проверяются делители числа до его целой половины (n div 2), хотя мы знаем, что делители числа находятся до корня квадратного из него и находили их до trunc(sqrt(n)). Такое сделано только из соображений наглядности — в первом случае делители выдаются на экран в порядке возрастания и это выглядит приятнее.
Блок-схема процедуры «Делители заданного числа n»

Рис. 56

Процедура

Procedure math_divisor(n : integer);
var
d : integer;
begin
for d := 1 to n div 2 do
if n mod d=0 then write(d, » «);
writeln(n)
end;
Блок-схема основной программы

Рис. 57
Основная программа

Program Problem6;
uses WinCrt;
var
i, n : integer;
{—————————————————————————————-}
Procedure math_divisor(n : integer);
var
d : integer;
begin
for d := 1 to n div 2 do
if n mod d=0 then write(d, » «);
writeln(n)
end;
{—————————————————————————————-}
begin
write(«Введите правую границу промежутка «); readln(n);
for i := 1 to n do
begin
write(«Делители числа «, i, » следующие: «);
math_divisor(i)
end
end.

Задание 3

1. Составьте блок-схему, напишите процедуру, которая будет вычислять сумму правильных делителей числа n. Правильными делителями числа n являются все делители этого числа, за исключением его самого. Например, если n равно 12, то сумма правильных делителей есть 1 + 2 + 3 + 4 + 6 = 16. Для проверки правильности работы этой процедуры составьте блок-схему и напишите главную программу, которая бы считывала различные значения n из заданного промежутка [a; b] и для каждого вычисляла сумму его правильных делителей.

2. Натуральное число n является точным квадратом тогда и только тогда, когда оно имеет нечетное число делителей. Доказать. Составьте блок-схемы процедур и основной программы, напишите процедуры и основную программу.

2. Вызов процедуры из процедуры

Пример 7. Нумерация книжных страниц. В книге n страниц. Составим программу, которая будет находить, сколько цифр понадобится для того, чтобы занумеровать все страницы книги.

Решение

Математическое решение рассмотрим на частном примере, а потом сделаем общий вывод.

Пусть нам требуется определить число цифр для нумерации 357 страниц.
Естественными рассуждения будут такими: однозначных цифр 9, значит они пронумеруют 9 страниц; двузначных чисел 90 — они нумеруют 90 страниц и используют 90 . 2 = 180 цифр; трехзначных чисел 900 — они пронумеруют 900 страниц и используют 2700 цифр. Следовательно, для нумерации данных 357 страниц потребуются все однозначные и двузначные числа и часть трехзначных. Чтобы узнать, сколько трехзначных чисел потребуется для нумерации, надо из заданного числа вычесть «использованные» однозначные и двузначные числа: 357 — (9 + 90) = 258.
Итак, всего потребуется цифр:

. . . . . . . . . . .

Итого: 9 + 180 + 774 = 963 цифры.
Теперь обобщим наши соображения. Пусть задано число страниц n, которое имеет c цифр. Тогда для нумерации потребуются цифры:

1 — значные; потребуется: 9 1 = 9 цифр;
2 — значные;           90 2 = 180 цифр;
3х — значные;          900 3 = 2700 цифр;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c-1 -значные;          9….0 . (c-1) . . . цифр,

а c-значных полностью не хватит, также, как не хватило полностью трехзначных для нумерации 357 страниц.
Чтобы узнать сколько потребуется c-значных цифр, надо из данного числа вычесть все число одно, -дву, -трех,- и т. д., c-1 значные, которые уже использованы: а затем полученный результат умножить на c — значность числа. Сложив израсходованные цифры, мы получим окончательный результат.
Попробуем на основе этих рассуждений составить программу.
Прежде, составим процедуру, которая определяет число цифр во введенном числе страниц. С такой программой мы уже раньше имели дело:

Блок-схема процедуры, определяющей количество цифр числа

Рис. 58

Процедура определения количества цифр введенного числа

Procedure number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;

В следующей процедуре будет находиться искомое число цифр. В ней, переменная m будет служить для указания числа цифр в одно, — двух, — трех, … c-значных числах (9, 90, 900, …, 9…0).
Переменная c покажет число цифр в числе — номере страницы, в переменной z будет накапливаться искомый результат, а сумма s даст нам сколько всего n-значных чисел было использовано для подсчета.
Первоначальные значения: m := 9; z := 0; s := 0, а число цифр числа будет получено из процедуры number(n, c) и задаст значение переменной c:
m := 9; number(n, c); z := 0; s := 0;
Теперь организуем цикл по количеству цифр введенного числа страниц, от 1 до c — 1. Переменная цикла i.

for i := 1 to c — 1 do
begin
z := z + m*i; {Сумма цифр}
s := s + m;
m := m*10
end;

В цикле подсчитывается сумма цифр (z := z + m*i), сумма использованных однозначных, двузначных и т.д. цифр.
После завершения цикла, к сумме z добавляются оставшиеся c-значные цифры:
z := z + (n — s) c {n — s оставшиеся страницы c-значными}
{цифрами}

Блок-схема процедуры нахождения искомого числа цифр

Рис. 59

Процедура

Procedure Page(n : integer; var z : integer);
var
i, m, c, s : integer;
begin
m := 9;
number(n, c);
z := 0; s := 0;
for i := 1 to c — 1 do
begin
z := z + m*i; {Сумма цифр}
s := s + m;
m := m*10
end;
z := z + (n — s)*c
end;

Блок-схема основной программы

Рис. 60

Программа
Program Problem7; { Число цифр для нумерации страниц }
uses WinCrt;
var
n, c : integer;
{—————————————————————————————-}
Procedure number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;
{—————————————————————————————-}
Procedure Page(n : integer; var z : integer);
var
i, m, c, s : integer;
begin
m := 9;
number(n, c);
z := 0; s := 0;
for i := 1 to c — 1 do
begin
z := z + m*i; {Сумма цифр}
s := s + m;
m := m*10
end;
z := z + (n — s)*c {n — s оставшиеся страницы c-значными цифрами}
end;
{—————————————————————————————-}
begin
write(«Введите число страниц «); readln(n);
page(n, c);
writeln(«Число цифр, необходимых для нумерации «, c)
end.

Задание 4

Составьте программу для решения обратной задачи: для нумерации страниц книги потребовалось k цифр (k — входное данное). Сколько страниц в книге? Если указанное число цифр не может служить для нумерации какого-либо количества страниц, то результат программы считайте равным 0.

Пример 8. Одна машинистка напечатала подряд без интервалов натуральные числа:
12345678910111213141516… .

Если подобным образом напечатать 1000 цифр, то какая цифра будет последней?

Решение

Решение будем выполнять по простой идее. Просматривать подряд числа, так как они пишутся машинисткой, подсчитывать сумму цифр каждого из чисел, находить общую сумму цифр и, когда она станет равна 1000, тогда прекратить процесс и выдать последнюю цифру на экран.
Но в этом алгоритме нас подстерегают некоторые неожиданности. Давайте проанализируем порядок записи машинисткой чисел.
Вначале пишутся однозначные числа — и здесь все в порядке, с помощью процедуру подсчитывается сумму цифр каждого однозначного числа (она равна 1), с помощью сумматора — 9 раз по 1 суммируется общее количество цифр.
Затем пишутся двузначные числа, процедура подсчета цифр будет выдавать сумму цифр 2 для каждого двузначного числа, а сумматор увеличиваться каждый раз уже сразу на 2 (90 раз), затем для трехзначных чисел — к сумматору будет прибавляться по 3 единицы. Возникает вопрос, где гарантия, что общая сумма цифр будет в точности равна 1000. Ведь очень даже может случиться, что после прибавления очередной двойки, тройки или четверки, общее число цифр «перепрыгнет» эту 1000-ю границу.
Как быть в таком случае? Это вызывает необходимость организовать цикл repeat … until … до тех пор, когда сумматор s станет больше заданной суммы цифр n Такое положение дел будет означать, что в последнем проверяемом числе (p) имеются «лишние» и ненужные нам цифры:

write(«Введите число цифр «); readln(n);
p := 1; s := 0;
repeat
number(p, v);
s := s + v; p := p + 1
until s >= n;

Выясняем сколько этих «лишних» цифр (m := s — n). Чтобы отбросить их, надо разделить последнее число p (а оно в силу инертности работы цикла увеличится еще на 1, поэтому действительное последнее число, сумма цифр которого подсчитывалась равно: p := p — 1) на 10, 100, 1000 и т. п., короче, на единицу с нулями, у которого столько нулей, сколько лишних цифр нами обнаружено, т. е. m.
С этой целью организуется цикл от 1 до м, в котором это число и строится:

m := s — n; p := p — 1; q := 1;
for i := 1 to m do q := q*10;

Теперь оно стало равно q. Далее следует разделить число p на q и «отбросить» ненужные цифры (c := p div q), а вот чтобы найти искомую цифру, надо еще найти остаток от деления c на 10 (а вдруг в оставшемся после деления на q числе еще остались не одна, а 2, 3 или более цифры, например, ).
Это выполняется последней группой операторов:
c := p div q; c := c mod 10;
Вам остается подумать, будет ли работать программа, когда сумма цифр s и число заданных цифр n окажутся равными?

Блок-схема основной программы

Рис. 61
Программа

Program Problem8; { Определение цифр в записи 1234567… }
uses WinCrt;
var
n, p, s, c, v, q, i, m : integer;
{—————————————————————————————-}
Procedure number(n : integer; var k : integer); {Число цифр}
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;
{—————————————————————————————-}
begin
write(«Введите число цифр «); readln(n);
p := 1; s := 0;
repeat
number(p,v);
s := s + v;
p := p + 1
until s >= n;
m := s — n;
p := p — 1;
q := 1;
for i := 1 to m do q := q*10;
c := p div q;
c := c mod 10;
writeln(«Последняя цифра в записи этих цифр будет: «, c);
writeln(«Она находится в числе «, p)
end.

Задание 5

Изучив две предыдущие программы, вы можете выбрать некоторый свой способ для решения такого типа задач. Попробуйте предложить свой способ для решения задачи аналогичной примеру 5. Выписать подряд все четные числа: 24681012… . Какая цифра стоит на 1971-м месте? Составьте блок-схемы процедур и основной программы, напишиет процедуры и основную программу и выполните ее.

Пример 9. Счастливые автобусные билеты.
Номера автобусных билетов представляют собой шестизначные числа. Счастливым считается тот билет, у которого сумма первых трех цифр равна сумме последних трех цифр. Например, билет 356428 считается счастливым, так как:
3 + 5 + 6 = 4 + 2 + 8 =14.
Будем считать, что номера билетов принадлежат промежутку
[100000; 999999].

Составить программу определения счастливого билета.

Алгоритм

Для программы составим две процедуры: одна — определяющая сумму цифр введенного числа, уже известную нам (sum number — сумма цифр):

Блок-схема процедуры, определяющей сумму цифр числа

Рис. 62

Процедура
Procedure sum_number(p : longint; var s : longint);
begin
s := 0;
while p <> 0 do
begin
s := s + p mod 10;
p := p div 10
end

end;

вторую — отделяющую первые и последние три цифры, а затем, с помощью вызова процедуры sum_number, устанавливает равны ли эти суммы (happiness — счастье):

Блок-схема процедуры «счастливые билеты»

Рис. 63
Процедура

Procedure happiness(x : longint);
var
l, r : longint;
begin
sum_number(x mod 1000, l);
sum_number(x div 1000, r);
if l = r then write(x,» «)
end;

x mod 1000 — отделяет последнее трехзначное число, а x div 1000 — первое трехзначное число.

Блок-схема основной программы

Рис. 64

Программа

Program Problem9; { Счастливые автобусные билеты }
uses WinCrt;
var
i : longint;
{—————————————————————————————-}
Procedure sum_number(p : longint; var s : longint);
begin
s := 0;
while p <> 0 do
begin
s := s + p mod 10;
p := p div 10
end
end;
{—————————————————————————————-}
Procedure happiness(x : longint);
var
l, r : longint;
begin
sum_number(x mod 1000, l);
sum_number(x div 1000, r);
if l = r then write(x, » «)
end;
{—————————————————————————————}
begin
writeln(«Счастливые автобусные билеты»);
for i := 100000 to 999999 do happiness(i);
writeln
end.

Этот алгоритм можно изменить, учитывая следующее. Если мы имеем некоторый «счастливый» номер, последняя цифра которого отлична от нуля, а предпоследняя — от девяти, то следующий «счастливый» номер может быть получен одновременным уменьшением последней цифры и увеличением предпоследней на единицу (эта операция эквивалентна прибавлению 9). Отсюда следует, что нет смысла перебирать все числа из указанного промежутка и для каждого из них решать, представляет ли оно «счастливый» номер.
Попробуйте составить программу, используя эти соображения.

Задание 6

Составить блок-схемы процедур и основной программы, а также процедуры и программу, печатающие все номера счастливых билетов, которые равны:
а) квадрату какого-либо натурального числа;
б) кубу какого-либо натурального числа;

в) квадрату какого-либо натурального числа и одновременно кубу какого-либо другого натурального числа.

Упражнения

Найти наибольший общий делитель всех чисел из заданного промежутка
Сократить дробь. Даны натуральные числа a и b. Сократить дробь
Найдите пять троек натуральных чисел (x; y; z), удовлетворяющих условию
Б. Кордемский указывает одно интересное число 145, которое равно сумме факториалов своих цифр: 145 = 1! + 4! + 5!. Он пишет, что неизвестно, есть ли еще такие числа, удовлетворяющие названному условию. Выясните, существуют ли еще такие числа?
Найти трехзначное число, являющееся точным квадратом числа a, и такое, чтобы произведение его цифр было равно a — 1.
Найти все натуральные решения уравнения в интервале [1; 20]

Найдите какие-нибудь три последовательных натуральных числа, каждое из которых делится на квадрат целого числа, большего единицы.
Нетрудно указать тройку квадратов целых чисел, образующих арифметическую прогрессию: 1, 25, 49. Найдите еще три такие тройки (из квадратов чисел, не имеющих общего делителя, т. е. взаимно простых).
Найти три таких простых числа, чтобы их сумма была в 5 раз меньше их произведения.
Попробуйте найти решения задачи Ферма на некотором промежутке [a, b] для показателей из промежутка [1, 30].
Попытайтесь найти пять идущих подряд целых чисел, таких, чтобы сумма квадратов двух наибольших из них равнялась сумме квадратов трех остальных?
Некоторое четное число является суммой двух точных квадратов. Докажите, что его половина является суммой двух точных квадратов.
Каждое из чисел 9, 25, 49, 81 при делении на 8 дает остаток 1. Что это: случайность или же этому закону подчинены квадраты всех нечетных чисел?

Пусть у целых чисел A и B последние k цифр одинаковы. Докажите, что у чисел и (n — любое натуральное) также k последних цифр одинаковы (ограничиться случаями n = 2, 3, 4).

3. Рекурсия

Такой процесс, когда в процедуре происходит обращение к самой себе, называется рекурсией (рекурсия — возврат). (Происходит от латинского recurreus — возвращающийся).
Теперь нам предстоит более подробно поговорить о рекурсиях.

Рекурсия — это такой способ организации подпрограммы, при котором в ходе выполнения она обращается сама к себе.

Приведем примеры, которые уже стали классическими, использования рекурсий в подпрограммах:

Пример 10. Вычисление факториала числа.

Ниже приведена программа вычисления факториала числа, в которой используется рекурсивная процедура fac:

Блок-схема процедуры вычисления факториала числа

Рис. 65
Процедура

Procedure fac(n : integer; var f : real);
begin
if (n = 0) or (n = 1)
then f := 1
else
begin
fac(n — 1, f);
f := f*n
end
end;

Разберемся детально в работе этой процедуры. Для этого снова обратимся к математике.
Для вычисления факториала числа n, т.е. n! надо умножить последовательно n натуральных чисел от 1 до n:
Так, 4! будет равно:
Это прямой путь вычисления или итеративный.
Возможен и другой путь вычисления: Этот путь можно назвать возвратным или рекурсивным.
Именно на этом принципе основана работа приведенной процедуры.
Пусть введено в программу значение 4 для вычисления факториала 4! Как будет работать процедура?
После начала ее работы, будет выполнена проверка:
if (n = 0) or (n = 1) then f := 1
Понятно, что 4 не равно 0 и не равно 1, значит будет выполняться оператор после else, т. е. fac(n — 1, f), а это означает, что снова будет вызвана также процедура, но значение n уменьшится на единицу и станет равным 3; затем снова будет выполнена проверка условия:
if (n = 0) or (n = 1) then f := 1 и переход к вызову процедуры fac(n — 1, f).
Значение n уменьшится на 1 и станет равным 2 и т. д. до тех пор, пока n не станет равным 1, а значение f получит значение 1 (надо заметить, что при всех предыдущих операциях значение f оставалось равным 0, а точнее говоря, неопределенным).
После этого, начнется обратный процесс, в котором будет выполняться команда: f := f*n. Он будет происходить так:
f := 1*4; f := 4*3; f := 12*2; f := 24*1.
Образно говоря, при первоначальном процессе, значения n от 4 до 1 «запоминаются» в стековую память «Паскаль-машины«, а при следующем процессе, значения n «считываются» из стековой памяти “Паскаль-машины” и умножаются на значения f.
Условно-схематически это можно изобразить так: значения n запоминаются в стек-память «Паскаль-машины«:

а затем начинают считываться в обратном порядке, начиная с единицы.
Обязательным элементом в описании всякого рекурсивного процесса является некоторое утверждение, определяющее условие завершения рекурсии; иногда его называют опорным условием рекурсии (или «якорем«). В нашем случае это условие:
if (n = 0) or (n = 1) then f := 1.

В опорном условии может быть задано какое-то фиксированное значение, заведомо достигаемое в ходе рекурсивного вычисления и позволяющего организовать своевременную остановку процесса; применительно к вычислению факториала им будет равенство 1! = 1. Таким образом, любое рекурсивное определение всегда содержит два элемента: условие завершения и способ выражения одного шага решения посредством другого, более простого шага.
Для четкого понимания происходящих при этом процессов необходимо иметь в виду, что:
а) при каждом вызове процедуры создается новый экземпляр f;
б) все экземпляры f накапливаются во внутреннем стеке “Паскаль-машины” и
в) в любой момент обработке доступен только один, хронологически последний экземпляр переменной f, который
г) по завершению очередного рекурсивного вызова автоматически уничтожается).

Вывод

При каждом входе в рекурсивную подпрограмму ее локальные переменные размещаются в особым образом организованной области памяти, называемой программным стеком.

Блок-схема основной программы

Рис. 66

Программа

Program Problem10;
uses WinCrt;
var
n : integer;
f : real;
{—————————————————————————————}
Procedure fac(n : integer; var f : real);
begin
if (n=0) or (n=1)
then f := 1
else
begin
fac(n — 1, f);
f := f*n
end
end;
{—————————————————————————————}
begin
write(«Введите натуральное значение n «); readln(n);
fac(n, f);
writeln(«Факториал числа «, n, » равен «, f:12:0)
end.

Турбо-Паскаль 7 или 6 дает очень удобную возможность пошаговой трассировки программы и процедуру. Для этого достаточно последовательно нажимать клавишу F7 и вы сможете полностью убедиться в правильности наших соображений.

Рекурсивная форма организации подпрограммы обычно выглядит изящнее итерационной (последовательной) и дает более компактный текст программы, но при выполнении, как правило, медленнее и может вызвать переполнение стека.

Как избавиться от этой неприятности вы узнаете позже. Но стоит знать, что при зацикливании программы следует выйти из нее нажатием <Ctrl>+<Z>+<Enter> (<Ввод>) (для Турбо-Паскаля 7 или 6).

Еще примеры с использованием рекурсивных процедур.

Пример 11. Над цепью озер летела стая белых гусей. На каждом озере садилось половина гусей и еще полгуся, а остальные летели дальше. Все гуси сели на семи озерах. Сколько гусей было в стае?

Решение

Математически задача решается устно очень остроумным способом.
Пусть вместе со стаей белых гусей все время летит еще один, Серый гусь. Если к некоторому озеру подлетит m белых гусей и Серый, то на этом озере садится — ровно половина всех гусей вместе с серым. Поэтому после каждого озера число летящих гусей уменьшается ровно вдвое. После семи озер оно уменьшится в 27 = 128 раз, а остается летящим один Серый гусь. Значит, вначале было 128 гусей, из них 127 — белых.

А теперь выполним, образно говоря, прямые рассуждения для решения задачи.
Обозначим через xk количество летящих белых гусей, когда впереди еще k озер. Тогда условие задачи записывается так:

Отсюда получаем для последовательности (xk) рекуррентное соотношение
.

Зная его, легко составить блок-схему и рекурсивную процедуру:

Рис. 67

Procedure goose(x, k : integer);
begin
if k = 1 then writeln(x)
else goose(2*x + 1, k — 1)
end;

В процедуру вводятся всего две переменные: x — искомое число гусей; k — число озер. Процедура устроена с расчетом, что гуси уже пролетели все 7 озер, значит надо вводить значение для x — один (1), а для k — семь (7). В процедуре устроено, что число k уменьшается на 1 и тогда опорным условием («якорем«) завершения процедуры является условие равенства 1 значений k и после этого на экран надо выдать значение числа гусей:
if k = 1 then writeln(x)
Опорное условие может быть и другим, если первоначальным значением k будет 1, тогда при повторном обращении к процедуре значение k надо не уменьшать, а увеличивать на 1 (k + 1), опорным условием, в этом случае, будет k = 7.

Блок-схема основной программы

Рис. 68
Ниже приводится законченная программа решения этой задачи:

Program Problem11;
uses WinCrt;
var
k : integer;
{—————————————————————————————-}
Procedure goose(x, k : integer);
begin
if k = 1 then write(x)
else goose(2*x + 1, k — 1)
end;
{—————————————————————————————-}
begin
write(«Введите число озер «); readln(k);
write(«В стае было «);
goose(1, k);
writeln(» гусей»)
end.

Придерживаясь подобных соображений, решите следующую задачу.

Задание 7

Поток студентов пять раз сдавал один и тот же зачет (не сумевшие сдать зачет приходили на следующий день). Каждый день успешно сдавала зачет треть всех пришедших студентов и еще треть студента. Каково наименьшее возможное число студентов, так и не сдавших зачет за пять раз?

Легко составлять рекурсивные процедуры, если задачи связаны с арифметическими или геометрическими прогрессиями, вообще последовательностями (к ним мы вернемся позже), заданными как формулами n-го члена, так и рекуррентными соотношениями.
Вот еще несколько простых программ с рекурсивными процедурами.

Пример 12. Мой богатый дядюшка подарил мне один доллар в мой первый день рождения. В каждый следующий день рождения он удваивал свой подарок и прибавлял к нему столько долларов, сколько лет мне исполнилось. Написать программу, подсчитывающую общую сумму денег, подаренных к N-му дню рождения и указывающую, к какому дню рождения сумма подарка превысит 100$.

Вначале напишем программу, сколько денег получит племянник к n-му дню рождения.
Снова попробуем составить рекурсивную процедуру, хотя возможен и другой путь решения.
Введем обозначения: k — число лет племянника, p — количество денег, которые дает дядя на каждом дне рождения, s — общая сумма денег, полученных племянником за все годы, n — счетчик числа дней рождения, который считает в обратном порядке от n (введенного пользователем) до 1.

Блок-схема процедуры

Рис. 69

Процедура

Procedure uncle(k, p, s, n : longint); {uncle — дядя}
begin
if n = 1
then write(s)
else
begin
k := k + 1;
p := 2*p + k;
uncle(k, p, s + p, n — 1)
end
end;

Задаются первоначальные значения формальным параметрам процедуры: n — вводится пользователем из основной программы (вы обратили внимание, что в этой, как и в предыдущей процедуре нет выходных параметров и нет переменных в самой процедуре, хотя возможны и другие варианты).

Увеличивается число лет: k := k + 1; вычисляется подарок к k-тому дню рождения: p:= 2*p + k; вызывается процедура, в которой увеличивается на p общая сумма полученных денег s и уменьшается на 1 число дней рождения:

uncle(k, p, s + p, n — 1)

Далее весь процесс повторяется, до тех пор, пока n не станет равным 1.

Блок-схема основной программы

Рис. 70

Программа

Program Rich_man1; { rich man — богатый }
uses WinCrt;
var
n : integer;
{—————————————————————————————}
Procedure uncle(k, p, s, n : longint); {uncle — дядя}
begin
if n = 1
then write(s)
else
begin
k := k + 1;
p := 2*p + k;
uncle(k, p, s + p, n — 1)
end
end;
{—————————————————————————————}
begin
write(«Введите число лет племянника «); readln(n);
write(«Я получу к «, n, «-ому дню рождения «);
uncle(1, 1, 1, n);
writeln(» долларов»)
end.

Во второй части условия требуется определить число лет, когда сумма полученных денег будет равна или превысит 100 долларов. Для этого в процедуре меняется опорное условие: if s >= 100 then write(n), а все остальное остается без изменений.

Program Rich_man2;
uses WinCrt;
var
n : integer;
{—————————————————————————————-}
Procedure uncle1(k, p, s, n : longint);
begin
if s >= 100
then write(n)
else
begin
k := k + 1;
p := 2*p + k;
uncle1(k, p, s + p, n + 1)
end
end;
{—————————————————————————————}
begin
write(«Сумма подарка превысит 100 долларов к «);
uncle1(1, 1, 1, 1);
writeln(» -ому дню рождения»)
end.

Следующие задачи решаются аналогично и особого труда не представляют, поэтому я предлагаю их для самостоятельной работы. Используйте рекурсивные процедуры.

Задание 8

1. Ежедневно Незнайка учит половину от суммы выученных за два предыдущих дня иностранных слов и еще два слова. Знайка считает, что силы Незнайки иссякнут, когда нужно будет выучить 50 слов в день. Написать программу, определяющую, через сколько дней иссякнут силы у Незнайки, если в первые два дня он выучил по одному слову.
2. Татьяна Ларина, читая очередной французский роман, подсчитала сумму номеров прочитанных страниц. Обозначим эту сумму Q. Написать программу, определяющую номер последней прочитанной страницы.
3. Царевна-лягушка съедает ежедневно на 20% комаров больше, чем в предыдущий день, и еще два комара. Написать программу, определяющую через сколько дней количество съеденных комаров превысит 100, если в первый день было съедено 12 комаров.
4. На каждом следующем дне рождения Винни Пух съедает столько же пищи, что и на двух предыдущих. На двух первых днях рождения у Пятачка и Кролика он съел по 100 г пищи. Написать программу, определяющую, сколько килограммов пищи съест Винни Пух на пятнадцатом дне рождения.
5. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько клеток будет через 3, 6, 9, 12, …, 24 часа.

6. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% от нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?

Рассмотрим более сложную задачу, для составления программы которой используется рекурсивная процедура.

Пример 13. Перемножая большие числа, можно быстро получить переполнение. Поэтому, для того чтобы напечатать произведение, превышающее наибольшее допустимое для данного целого типа (integer или longint) числа, надо применить искусственные средства.

Составим программу для печати произведения двух чисел, которое может превышать максимально допустимое целое число.

Решение

Процедура multiplication умножает число a на каждую цифру числа b, начиная с цифры единиц. Последняя цифра полученного произведения, сложенная с последней цифрой имеющегося в памяти частичного произведения, печатается, а все прочие цифры запоминаются — передаются как параметры при рекурсивном обращении к процедуре multiplication. В самом конце производится умножение на первую (левую) цифру числа b. На этом умножение заканчивается. Тогда печатается начало результата — накопившееся частичное произведение без последней цифры (s div 10), а после него при возвращении из рекурсии — все остальные цифры произведения (s mod 10) в обратном порядке по сравнению с тем, как они вычислялись при входе в рекурсию.

Блок-схема процедуры «большие произведения»

Рис. 71

Процедура

Procedure multiplication(a, b, s : longint);
begin
if b <> 0
then
begin
s := s+a*(b mod 10);
multiplication(a, b div 10, s div 10);
write(s mod 10:1)
end
else if s <> 0 then write(s)
end;

Блок-схема основной программы

Рис. 72

Программа

Program Problem13; { Большое произведение }
uses WinCrt;
var
x, y : longint;
{—————————————————————————————-}
Procedure multiplication(a, b, s : longint);
begin
if b <> 0
then
begin
s := s+a*(b mod 10);
multiplication(a, b div 10, s div 10);
write(s mod 10:1)
end
else if s <> 0 then write(s)
end;
{—————————————————————————————-}
begin
write(«Введите первый множитель «); readln(x);
write(«Введите второй множитель «); readln(y);
write(x,»*»,y:1,» = «);
if ((x < 0) and (y > 0)) or ((x > 0) and (y < 0)) then write(«-«);
multiplication(abs(x), abs(y), 0);
writeln
end.

Задание 9

1. На какое наименьшее число нужно умножить 12345679, чтобы получить число, состоящее из одних пятерок?

2. На какое наименьшее число нужно умножить 333667, чтобы получить число, состоящее из одних восьмерок?

Рекурсивный вызов может быть косвенным. В этом случае подпрограмма обращается к себе опосредованно, путем вызова другой подпрограммы, в которой содержится обращение к первой, например:
                    Procedure A(i: real);
begin
…
B(i);
…
end;
                    Procedure B(j: integer);
…
begin
…
A(j);
…
end;
Если строго следовать правилу, согласно которому каждый идентификатор перед употреблением должен быть описан, то такую программную конструкцию использовать нельзя. Для того, чтобы такого рода вызовы стали возможны, вводится опережающее описание:
Procedure B(j: integer);
forward;
A(i: real);
      Procedure
            begin
…
B(i);
…
            end;
      Procedure B;
            begin
…
A(j);
…
            end;
Как видим, опережающее описание заключается в том, что объявляется лишь заголовок процедуры B, а ее тело заменяется стандартной директивой FORWARD. Теперь в процедуре A можно использовать обращение к процедуре B — ведь она уже описана, точнее, известны ее формальные параметры и компилятор может правильным образом организовать ее вызов.
Обратите внимание: тело процедуры B начинается заголовком, в котором уже не указываются описанные ранее формальные параметры.

4. Функции

Язык программирования Паскаль допускает введение в программу функции, определяемой пользователем. Она помещается в разделе описаний основной программы.
Запись функции начинается так:
Function <имя> (<список формальных параметр.>) : <тип рез.>
       var <описание переменных, участвующих в работе функции>
Дальнейшее построение такое же, как и во всех других программах на языке Паскаль.
       begin
<операторы>
<имя> := <результат>
       end;

Обязательной является команда присваивания имени функции результата, полученного в итоге ее работы. Функция может быть использована несколько раз в программе.
Для ее вызова достаточно указать имя функции и задать значение формальных параметров: <имя> (<значение параметров>).
Например: s(2, 3) или s(n, a). Параметры и переменные функции могут иметь те же имена, что и переменные в основной программе.

Снова обратимся к наиболее типичным примерам, создаваемых функций. Как вы смогли уже убедиться, их конструкция мало чем отличается от процедур, да и существует возможность обратных преобразований функций в процедуру и процедур в функции.
Известный ряд чисел Фибоначчи имеет вид:
1, 1, 2, 3, 5, 8, 13, 21, 34, …
Каждый член этой последовательности, начиная с третьего, равен сумме двух предыдущих членов.
Если первый член последовательности обозначить f1, второй — тогда можно составить такую зависимость:

Пользуясь такой зависимостью, можно получить все члены последовательности чисел Фибоначчи.

Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro — возвращаться).

Зная зависимость между последующим и предыдущими членами, легко создать рекурсивную функцию, позволяющую найти n-е число ряда Фибоначчи:

Блок-схема рекурсивной функции «числа Фибоначчи»

Рис. 73

Рекурсивная функция

Function fib(n : integer) : longint;
begin
if (n = 1) or (n = 2)
then fib := 1
else fib := fib(n — 1) + fib(n — 2)
end;

Здесь, мы одновременно проследим и построение функции и рекурсии.

В заголовке указывается зарезервированное слово Function, далее пишется по фантазии пользователя ее имя, удовлетворяющее всем требованиям, предъявляемым к идентификаторам.

В скобках описываются, как и в процедурах, входные параметры, заметьте, в функции есть только входные параметры, в качестве выходного значения используется сама функция, поэтому обязательно указывается ее тип.

И вот теперь ее имя fib может быть использовано в программе, наряду со встроенными функциями, в различных операторах и арифметических вычислениях.

Построение самой функции начинается, как и построение любой другой программы, но обязательно надо присваивать конечное значение самой функции: fib.

Блок-схема нерекурсивной функции «числа Фибоначчи»

Рис. 74

Нерекурсивная функция

Function fib(n : integer) : longint;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1 + f2;
end;
fib := f
end;

Конечно, удобно составлять программу, когда все члены ряда вычисляются по одному правилу, но в ряде Фибоначчи выпадают из общего правила два первых члена. Если мы хотим вычислить и их по тому же правилу, тогда следует в функции fib искусственно продолжить ряд влево, пополнив его двумя фиктивными членами: f(-1) = 1 и f(0) = 0. Тогда ряд примет следующий вид:

1 0 — фиктивные члены ряда
1 1 2 3 5 … — подлинные члены ряда.

При наличии этих двух фиктивных членов все подлинные члены ряда вычисляются по тем же правилам.
Работу этой функции понять несложно, поэтому мы не будем останавливаться на детальном разборе ее работы.
Можно составить функцию для вычисления чисел Фибоначчи используя рекурсию, тогда она будет выглядеть более компактной:
Function fib(n : integer) : integer;
begin
if (n = 1) or (n = 2)
then fib := 1
else fib := fib(n — 1) + fib(n — 2)
end;

Однако, несмотря на внешнюю изысканность, эта функция крайне неэффективна.
Давайте детально проследим за ходом ее работы.
Когда n = 1 или n = 2, получаем значение функции, выполнив функцию один (первый) раз.
Когда n = 3, выполняется вторая (else) ветвь условного оператора и значение функции находится из выражения fib(2) + fib(1).
Для того, чтобы вычислить значение выражения, следует еще два раза (рекурсивно) обратиться к функции fib.
Когда n = 4, функция будет выполняться пять раз, а когда n = 5 — девять раз.
fib(4) fib(5)

fib(3) fib(2) fib(4) fib(3)

fib(2) fib(1) fib(3) fib(2) fib(2) fib(1)

fib(2) fib(1)
Таким образом, при возрастании значения параметра функции очень быстро возрастает и число обращений к функции, а тем самым увеличивается время вычисления. Это происходит от того, что вторая рекурсивная ветвь условного оператора содержит сразу два рекурсивных вызова. Поэтому эта рекурсивная функция служит примером очень часто встречаемых неэффективных рекурсивных функций.
Часто, внешняя любезность рекурсии оборачивается большими неприятностями.
Приведем и другой способ вычисления членов ряда Фибоначчи с помощью с помощью функции, построенной итеративно. Для ее построения возможны два способа.

Пример 1
Первый способ
Function Fib(n: integer):longint;
var
f1, f2, f : longint;
i : integer;
begin
f2 := 1; f := 1;
if (n = 1) or (n = 2)
then f := 1
else
for i := 3 to n do
begin
f1 := f2; f2 := f
f := f1 + f2;
end;
fib := f
end;

Второй способ

Function fib(n : integer) : integer;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1+f2;
end;
fib := f
end;

Блок-схема основной программы

Рис. 75

Основная программа:

Program Problem1;
uses WinCrt;
var
i, n : integer;
{—————————————————————————————-}
Function fib(n : integer) : integer;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1 + f2;
end;
fib := f
end;
{—————————————————————————————-}
begin
write(«Введите значение n «); readln(n);
writeln(«Числа Фибоначчи»);
for i := 1 to n do write(fib(i), » «);
writeln
end.

Пример 2. Последовательность (an) задается так: — сумма цифр квадрата числа плюс 1. Постройте эту последовательность и найдите .

Решение

При построение членов последовательности нам придется находить сумму цифр числа. Поэтому есть смысл составить функцию, которая определяет сумму цифр числа. Эта функция может быть построена так:

Блок-схема функции «сумма цифр числа»

Рис. 76

Функция

Function Sum(a : integer) : integer;
var
s : integer;
begin
s := 0;
repeat
s := s + a mod 10;
a := a div 10
until a = 0;
Sum := s
end;

Вторая функция — это функция, с помощью которой можно получить любой член последовательности:

Блок-схема функции получения любого члена последовательности

Рис. 77

Функция

Function Succ(n : integer) : integer;
var
a, i : integer;
begin
a := 7;
for i := 2 to n do a := Sum(a*a) + 1;
Succ := a
end;

Блок-схема основной программы

Рис. 78

Программа

Program Succession; { succession — последовательность }
uses WinCrt;
var
a, i, n : integer;
{—————————————————————————————-}
Function Sum(a: integer): integer;
var
s: integer;
begin
s:=0;
repeat
s := s + a mod 10;
a := a div 10
until a = 0;
Sum := s
end;
{—————————————————————————————-}
Function Succ(n : integer): integer;
var
a, i : integer;
begin
a := 7;
for i := 2 to n do a := Sum(a*a) + 1;
Succ := a
end;
{—————————————————————————————-}
begin
write(«Введите число членов последовательности «); readln(n);
for i := 1 to n do write(Succ(i), » «);
writeln;
writeln(«a[1000] = «, Succ(1000))
end.

Задание 10

1. Последовательность (an) задается так: a1 — некоторое натуральное число, — сумма квадратов цифр числа n 1.
а). Постройте эту последовательность. Будет ли она периодична?

б). Докажите, что в этой последовательности обязательно встретится одно из чисел 1 или 89 и указать номер места, на котором оно находится. Составить блок-схемы функций и основной программы, а также сами функции и программу. Выполните ее.

4.1. Применение ряда Фибоначчи

Пример 2. Определение минимума функции с помощью ряда Фибоначчи.

Ряд Фибоначчи много интересных применений в математике. О некоторых из них мы поговорим позже, а на этом занятии разберем использование этого ряда для поиска минимума функции на заданном промежутке (смотри также В.Ф. Очков, Ю.В. Пухначев, «128 советов начинающему программисту», Москва, 1991 г.).
Для примера рассмотрим функцию на промежутке (0, 2). График этой функции, а точнее, его часть на промежутка (0, 2) показан на рисунке 35.

Рис. 79

Итак, стоит задача найти минимум функции на этом промежутке, т.е. значение x, при котором получается минимум и значение функции y в этой точке. Первая мысль, которая возникает — это делить отрезок (0, 2) пополам, затем выяснять, на каком из получившихся частей может находится минимум и делить эту часть пополам и так далее. Такой процесс возможен, но имеет два существенных недостатка.
Во-первых, «приближение» к точке минимума будет очень медленным, придется испробовать много вариантов, чтобы «подобраться» к искомой точке.
Во-вторых, при даже очень большом количестве делений точность приближения будет невелика.
Поэтому, возникает необходимость как-то иначе делить отрезок (если мы избрали метод деления отрезка). Но как? Отделять от одного конца 4-ю или 3-ю части и постепенно сужать отрезок к лучшему результату не приведет, пожалуй еще и к худшему.
Улучшить процесс деления отрезка помогает ряд Фибоначчи. Может даже возникнуть впечатление, что он как будто специально создан для этой цели. Хотя ряд возник совершенно из других более естественных соображений, он показывает число появления кроликов во 2-й, 3-й, 4-й и т. д. годы, если первоначально есть только одна самка и один самец. Но многие закономерности природы прекрасно описываются математическими средствами, вот и в нашем примере ряд Фибоначчи дает очень хорошие результаты.
Для деления отрезка можно задать число делений — n, а затем в зависимости от n определить коэффициент деления, как отношение (n — 1)-го и n-го членов ряда. Если a — левый конец промежутка, b — правый, тогда разделить отрезок можно так: x2 := a + (b — a)*fib(n — 1)/fib(n); y2 := f(x2);
Для n = 10 отношение fib(9)/fib(10) = 34/55 = 0.6181818… . Тогда, правая граница станет равна: x2 := 1.236364… . Для дальнейшего процесса поиска, надо «приблизить» левый конец промежутка на такое же расстояние к правому концу ( ), затем найти соответствующее значения функции (y1 := f(x1) и определить, который из промежутков брать для дальнейшего рассмотрения.
В дальнейшем могут возникнуть несколько случаев.
Если x2 > x1 и y2 > y1, тогда в качестве правого конца промежутка принять x2 и зафиксировать его (b := x2), а x2 заменить на x1 (x2 := x1), y2 присвоить значение y1 (y2:=y1) и повторить процесс приближения левого конца к правому:
x1 := a + b — x2.
Если x2 <= x1 и y2 > y1, тогда a := x2; x2 := x1; y2 := y1 и повторить:
x1 := a + b — x2.
Если x2 > x1 и y2 < y1, тогда a := x1 и выполнить: x1 := a + b — x2.
Если x2 <= x1 и y2 <= y1, тогда b := x1 и выполнить: x1 := a + b — x2.
Если ни одно из этих условий не выполняется, тогда выполнятся оператор:
x1 := a + b — x2
и весь процесс повторяется.
Для составления программы потребуется функция, вычисляющая члены ряда Фибоначчи, уже знакомая нам:

{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1;
f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1 + f2
end;
fib := f
end;

Нужно будет вычислять значения заданной функции и для этого составим следующую функцию:

{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := x*x*x*x — 14*x*x*x + 60*x*x — 70*x
end;

Полностью программа приводится ниже:

Program Minimumfib;
uses WinCrt;
label 1;
var
a, aa, bb, x, b, x1, x2, y1, y2 : real; i, n : integer;
{—————————————————————————————-}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := x*x*x*x — 14*x*x*x + 60*x*x — 70*x
end;
{—————————————————————————————-}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real; i: integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1;
f1 := f;
f := f1 + f2
end;
fib := f
end;
{—————————————————————————————-}
{ Основная программа }
begin
write(«Введите нижнюю границу промежутка «); readln(a);
aa := a;
write(«Введите правую границу промежутка «); readln(b);
bb := b;
write(«Введите число приближений к минимуму «); readln(n);
x2 := a + (b — a)*fib(n-1)/fib(n);
y2 := func(x2);
for i := 1 to n do
begin
x1 := a + b — x2;
y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
b := x2;
x2 := x1;
y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
a := x2;
x2 := x1;
y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
b := x1; goto 1
end;
1: end;
x := (a + b)/2;
write(«Мин. значение функции на («);
writeln(aa:1:0, «,», bb:2:0, «)»);
writeln(«Значение функции равно «, func(x):6:12);
writeln(«При значении аргумента «, x:6:12)
end.

В этой программе число приближений устанавливается пользователем. Программу можно изменить, указав в условии цикла точность приближения значений аргумента x. Но тогда придется каждый раз при повторении цикла изменять коэффициент деления, так неизвестно конечное число повторений цикла. Для этого можно добавить в программу процедуру вычисления границ промежутка:

{ Процедура вычисления знач. аргумента и функции }
{ approach — приближение }
Procedure approach(a, b : real; n : integer; var x2, y2 : real);
begin
x2 := a + (b — a)*fib(n — 1)/fib(n);
y2 := func(x2)
end;

И тогда, программа станет следующей:

{Поиск минимума функции методом Фибоначчи}
Program Minimumfib;
uses WinCrt;
label 1;
var

           a, aa, bb, x, b, x1, x2, y1, y2, e : real;
           n                                                : integer;
{—————————————————————————————-}
{ Заданная исследуемая функция }
      Function func(x : real) : real;
            begin
                func := x*x*x*x — 14*x*x*x + 60*x*x — 70*x
            end;
{—————————————————————————————-}
{ Функция вычисления членов ряда Фибоначчи }
      Function fib(n : integer) : real;
            var
                f, f1, f2 : real;
                i            : integer;
            begin
                f1 := 1; f := 0;
                for i := 1 to n do
                    begin
                        f2 := f1;
                        f1 := f;
                        f := f1+f2
                    end;
                fib := f
            end;
{—————————————————————————————-}
{ Процедура вычисления знач. аргумента и функции }
{ approach — приближение }
      Procedure approach(a, b : real; n : integer; var x2, y2 : real);
            begin
                x2 := a + (b — a)*fib(n-1)/fib(n);
                y2 := func(x2)
            end;
{—————————————————————————————-}
{ Основная программа }
      begin
            write(«Введите нижнюю границу промежутка «); readln(a);
            aa := a;
            write(«Введите правую границу промежутка «); readln(b);
            bb := b;
            write(«Введите точность приближения «); readln(e); n := 3;
            approach(a, b, n, x2, y2);
            while abs(b — a) > e do
                begin
                    x1 := a + b — x2;
                    y1 := func(x1);
                    if (x2 > x1) and (y2 > y1)
                      then
                          begin
                              n := n + 1;
                              approach(a, b, n, x2, y2);
                              b := x2; x2 := x1; y2 := y1; goto 1
                          end;
                    if (x2 <= x1) and (y2 > y1)
                      then
                          begin
                              n := n + 1;
                              approach(a, b, n, x2, y2);
                              a := x2; x2 := x1; y2 := y1; goto 1
                          end;
                    if (x2 > x1) and (y2 < y1)
                      then
                          begin
                              n := n + 1;
                              approach(a, b, n, x2, y2);
                              a := x1; goto 1
                          end;
                    if (x2 <= x1) and (y2 <= y1)
                      then
                          begin
                              n := n + 1;
                              approach(a, b, n, x2, y2);
                              b := x1; goto 1
                          end;
                    n := n + 1;
                    approach(a, b, n, x2, y2);
           1: end;
           x := (a + b)/2;
           write(«Мин. значение функции на промежутке («);
           writeln(aa:1:0,»,»,bb:2:0,»)»);
           writeln(«Значение функции равно «, func(x):6:12);
           writeln(«При значении аргумента «, x:6:12)
      end.
Очень часто, при поиске минимума функции для деления отрезка используют так называемое «Золотое сечение«.
«Золотое сечение» или «золотое сечение» — деление отрезка на две части так, что большая из них есть средняя пропорциональная между меньшей частью и всем отрезком. Если a — весь отрезок, x — большая из двух частей, тогда: a : x = x : (a — x)
Решая это уравнение, получаем: получим:
(с точностью до 0.001).
Зная это, можно составить программу поиска минимума функции, используя «золотое сечение«, тогда: x1 := 0.618*a + 0.382*b, x2 := 0.382*a + 0.618*b.
Для вычисления этих значений можно составить две процедуры, которые затем использовать в программе.
Procedure gold1(a, b : real; var x1, y1 : real);
    begin
          x1 := 0.618*a + 0.382*b; y1 := fx(x1)
    end;
{——————————————————}
Procedure gold2(a, b : real; var x2, y2 : real);
    begin
          x2 := 0.382*a + 0.618*b; y2 := fx(x2)
    end;

Задание 11

Составить программу поиска минимума функции, используя «золотое сечение«. Для организации цикла используйте условие проверки приближения аргумента с заданной точностью, по аналогии со второй программой. применяющей ряд Фибоначчи.

Пример 4. От прямоугольника отрезают квадраты, стороны которых равны по длине его меньшей стороне, до тех пор, пока это возможно, и т. д.

Задание состоит в том, чтобы для произвольного натурального n, найти какие-нибудь два числа a и b, чтобы при таком разрезании прямоугольника a . b получились n квадратов разных размеров.

Общее решение

Для произвольного натурального числа n можно найти такие числа a и b, чтобы при разрезании получилось ровно n разных размеров квадратов.
В качестве таких чисел можно взять числа f2 и f1 последовательности Фибоначчи.
Если положить a = f(n + 2) и b = f(n + 1), то каждый раз от прямоугольника будет отрезаться только один квадрат со стороной длины f(k — 1) и оставаться прямоугольник .
Если взять в этой задаче f7 = 13 и f8 = 21; размеры квадратов получатся равными первым шести различным числам Фибоначчи: 1, 2, 3, 5, 8, 13.
Построенный пример прямоугольника a b имеет наименьшее возможное (при делении на n) размеры; другими словами, если числа a и b не больше f(n + 2), то алгоритм Евклида дает НОД(a, b) не больше, чем за n шагов.

Блок-схема программы

Рис. 80
Программа

Program Problem4; { Разрезание прямоугольников на квадраты }
uses WinCrt;
var
a, b, n, i : longint;
{—————————————————————————————-}
Function fib(n : longint) : longint;
var
f, f1, f2, i : longint;
begin
f1 := 1; f := 0;
for i:=1 to n do
begin
f2 := f1; f1 := f;
f := f1+f2
end;
fib := f
end;
{—————————————————————————————}
begin
write(«Введите натуральное число n «); readln(n);
a := fib(n + 2);
b := fib(n + 1);
writeln(«Прямоугольник, со сторонами «, a, » и «, b);
writeln(«Можно разделить на «,n,» квадратов со сторонами»);
for i := n+1 downto 2 do write(fib(i), » «);
writeln
end.

5. Задачи с применением НОД (Для дополнительного изучения)

Пример 5. Один мастер делает на длинной ленте пометки синим карандашом от ее начала через каждые 36 см. Другой мастер делает пометки красным карандашом от начала через каждые 25 см. Может ли синяя пометка оказаться на расстоянии 1 см от какой-нибудь красной?

Решение

Ответ: может. Например, 9-я синяя пометка и 13-я красная находятся друг от друга на расстоянии 1 см, так как 13 25 — 9 36 = 1.
В этой задаче нам фактически надо было найти какое-нибудь решение в целых числах одного из уравнений 25x — 36y = 1, 25x — 36y = — 1
или доказать, что таких решений нет. Существует стандартная процедура, с помощью которой всегда можно найти решение уравнения если Продемонстрируем ее на нашей задаче. Выпишем все шаги алгоритма Евклида для нахождения НОД(36; 25):
36 = 25 1 + 11; 25 = 11 2 + 3; 11 = 3 3 + 2; 3 = 2 1 + 1.
Перепишем эту цепочку равенств по остаткам:
11 = 36 — 25 1; 3 = 25 — 11 2; 2 = 11 — 3 3; 1 = 3 — 2 1.
Тогда получим:
1 = 3 — (11 — 3 3) = 3 4 — 11 = (25-11 2) 4 — 11 = 25 4 — 11 9 =
= 25 4 — 11 9 = 25 4 — (36 — 25) 9 = 25 13 — 36 9.
В результате получается равенство 25 13 — 36 9 = 1, дающее одно решение уравнения 25x — 36y = 1.

Определение. Неопределенные уравнения — уравнения, содержащие более одного неизвестного.

Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.

Уравнения вида ax + by = c, где a, b, c — целые числа, отличные от нуля

Теорема 1. Если НОД (a; b) = d, то существуют такие целые числа x и y, что имеет место равенство .
(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)
Теорема 2. Если в уравнении ax + by = l (a, b) = 1, то уравнение имеет по крайней мере одно целое решение.
Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + by = 1, если (а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.

Пример. Найти целое решение уравнения 15x + 37y = 1.

Решение

1) Применим алгоритм Евклида и найдем НОД(15, 37):

НОД(15, 37) = 1

2) Выразим 1 последовательно через неполные частные и остатки, используя полученные равенства, начиная с конца:
, т. е.
x0 = 5, y0 = -2.
Теорема 3. Если в уравнении ах + by = с (а, b) = d > 1 и с не делится на d, то уравнение целых решений не имеет.

Пример. Найти целое решение уравнения 16x — 34y = 7.

Решение

(16, 34) = 2, 7 не делится на 2, уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + by = с (a, b) = d > 1 и c делится на d, то оно равносильно уравнению а1х + b1у = c1, в котором (a1, b1) = 1.

Теорема 5. Если в уравнении ах + by = с (а, b) = 1, то все целые решения этого уравнения заключены в формулах:

где x0, y0 — целое решение уравнения ах + by = 1, t — любое целое число.
Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах + by = с, где (а, b) = 1:
1) находится целое решение уравнения ах + by = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
2) составляется общая формула целых решений данного уравнения:

где x0, y0 — целое решение уравнения ах + by = 1, t—любое целое число.
Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т. д.

Пример 1. Найти целые решения уравнения 407х — 2816у = 33.

Решение

1) Упрощаем данное уравнение, приводя его к виду 37х — 256у = 3.
2) Решаем уравнение 37x — 256y = 1.

. .
3) Найдем решения данного уравнения по формулам:

Ответ:

Для составления программы решения неопределенных уравнений, нам предстоит решить три задачи:
1) нахождение НОД, для последующего выяснения числа решений уравнения, — это легко сделать с помощью известной процедуры;
2) нахождение одного решения уравнения вида ах + by = 1 и
3) последующий вывод обобщенных результатов решения с учётом знаков a и b, и с учетом формулы где t — произвольное целое число.

Первую задачу можно решить с помощью рекурсивной функции:

Function nod(a, b : integer) : integer;
begin
if b = 0 then nod := abs(a)
else nod := nod(abs(b), abs(a) mod abs(b))
end;

Для решения второй задачи применять методику нахождения остатков от деления, а затем выполнять процесс в обратном порядке для компьютера нерационально. Проще составить два цикла с параметром, перебирающие числа от наименьшего (который равен наибольшему по модулю, но берётся с противоположным знаком) до наибольшего из коэффициентов (почему, будут существовать решения уравнения, меньшие или равные его коэффициентов? Докажите сами).

if abs(a) > abs(b) then max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to max do

Для вывода результатов следует рассмотреть несколько случаев, в зависимости от знаков коэффициентов a и b, а также, чтобы не получать несколько ответов, включить оператор безусловного перехода, после завершения проверки каждого условия.

Procedure The_equation(a, b : integer); {Решение уравнения ax + by = 1}
label 1;
var
max, x, y, n : integer;
begin
if (nod(a, b) <> 1) then writeln(«Уравнение не имеет решений»);
if abs(a) > abs(b) then max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to x do
begin
if (a*x + b*y = 1) and (a > 0) and (b > 0)
then
begin
writeln(«Решения уравнения x = «, x, «+», b,»*t, y = «, y, «-«, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1
end;
if (a*x + b*y = 1) and (a < 0) and (b > 0)
then
                               begin
writeln(«Решения уравнения x = «, x, «+», b,»*t, y = «, y, » «, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1
end;
if (a*x + b*y = 1) and (a > 0) and (b < 0)
then
                                begin
writeln(«Решения уравнения x = «, x, » «, b,»*t, y = «, y, «-«, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1
end;
if (a*x + b*y = 1) and (a < 0) and (b < 0)
then
                                begin
writeln(«Решения уравнения x = «, x, » «, b,»*t, y = «, y, » «, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1
end
end;
1: end;

Полностью программа решения уравнений вида ах + by = 1 будет такой:

Program Problem5;
uses WinCrt;
var
a, b : integer;
{———————————————————————————————————}
Function nod(a, b : integer) : integer;
begin
if b = 0 then nod := abs(a)
else nod := nod(abs(b), abs(a) mod abs(b))
end;
{———————————————————————————————————-}
Procedure The_equation(a, b : integer); {Решение уравнения ax + by = 1}
label 1;
var
max, x, y, n : integer;
begin
if (nod(a, b) <> 1) then writeln(«Уравнение не имеет решений»);
if abs(a) > abs(b) then max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to x do
begin
if (a*x + b*y = 1) and (a > 0) and (b > 0)
then begin writeln(«Решения уравнения x = «, x, «+», b,»*t, y = «, y, «-«, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b > 0)
then begin writeln(«Решения уравнения x = «, x, «+», b,»*t, y = «, y, » «, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end;
if (a*x + b*y = 1) and (a > 0) and (b < 0)
then begin writeln(«Решения уравнения x = «, x, » «, b,»*t, y = «, y, «-«, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b < 0)
then begin writeln(«Решения уравнения x = «, x, » «, b,»*t, y = «, y, » «, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end
end;
1: end;
{————————————————————————————————————}
begin
write(«Введите значение коэффициента при x, a «); readln(a);
write(«Введите значение коэффициента при y, b «); readln(b);
The_equation(a, b);
end.

Задание 12

1. Наберите программу и выполните ее. Проверьте работу программы для решения уравнений: 27x — 40y = 1; 54x + 37y = 1; 107x + 84 y = 1; 37x — 256y = 1/
Изменить программу решения уравнения ax + by = 1, для решения неопределенных уравнений вида ax + by = c. Проверьте работу программы для решения уравнений: 13x — 15y = 7; 81x + 52y = 5; 24x — 56y = 72; 42x + 34y = 5; 253x — 449y = 3.
2. Используя метод решения неопределенных уравнений, решить следующую задачу.

Было написано трехзначное число, затем из его цифр были составлены всевозможные двузначные числа (с неповторяющимися цифрами) и найдена их сумма. Оказалось, что она вдвое больше исходного трехзначного числа. Какое же было трехзначное число?

6. Решение уравнений с одной переменной методом половинного деления

Здесь мы очень кратко рассмотрим один из простых методов решения нелинейных уравнений — метод половинного деления, так как другие методы будут рассмотрены позже, после изучения последовательностей, массивов и множеств.
Главная цель этого небольшого раздела — показать использование функций, создаваемых пользователем в программах.
Отделение корней
Первый этап численного решения уравнения f(x) = 0 состоит в отделении корней, т.е. в установлении «тесных» промежутков, содержащих только один корень.
При отделении корней на некотором промежутке [a, b], мы потребуем, чтобы функция f(x) была непрерывна на этом промежутке и будем считать, что все интересующие нас корни находятся на промежутке [a, b], в котором f(a)*f(b) < 0.
Будем вычислять значения функции f(x), начиная с точки x = a, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений f(x), имеющих разные знаки, и функция f(x) монотонна на этом отрезке, тогда значения аргумента x (предыдущее и последующее) можно считать концами отрезка, содержащего корень. Результатом решения этой задачи будет вывод значений концов промежутка.
Очевидно, что надежность рассмотренного подхода к отделению корней зависит как от характера функции f(x), так и от выбранной величины шага h. Действительно, если при достаточно малом значении h на концах текущего отрезка функция f(x) принимает значение одного знака, естественно ожидать, что уравнение f(x) = 0 корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции f(x) на отрезке могут оказаться корни уравнения. Не один, а несколько корней могут оказаться на отрезке и при соблюдении условия Смотрите рисунки 37 и 38, иллюстрирующие эти случаи.

Рис. 81

Рис. 82

Предвидя подобные ситуации, следует выбирать при отделении корней достаточно малые значения h.
Давайте посмотрим как будет выглядеть программа отделения корней для функции на промежутке [-10; 10].
Ясно, что необходимо завести функцию, которая бы при необходимости обращения к ней вычисляла ее значения. Эту функцию мы устроим уже известным нам способом и назовем fx:
Блок-схема функции

Рис. 83

Функция

Function fx(x : real) : real;
begin
fx := cos(x) — 0.1*x
end;

В основной программе, естественно потребовать от пользователя ввода границ промежутка и шага. В качестве границ промежутка будут переменные a и b, а для шага — h (в качестве значения шага, при выполнении программы возьмем 0.1).
Для подсчета числа промежутков будет служить счетчик k. Первоначальное значение левой границы: x1:=a; а первая правая граница будет равна сумме левой границы и шага: x2:=x1+h; значение функции в левой границе первого промежутка: y1:=fx(x1).
Последовательно к левой границе добавляется шаг h и так должно продолжаться пока это значение не станет равно правой границе данного промежутка b. Значит, необходимо организовать цикл «пока«: while x2 <= b do
В цикле, вычислять значение функции в точке x2, которая уже получилась от увеличения x1 на h: y2 := fx(x2).
Теперь следует проверить знак произведения значений функций на концах промежутка (fx(x1)*fx(x2)) и, если оно отрицательно, то на этом промежутке будет существовать корень, а значит надо выдать на экран координаты этого промежутка и его номер:

     if y1*y2 < 0
        then
           begin
                k := k + 1;
                writeln(k,»-й корень на [«,x1:6:4,»; «,x2:6:4,»]»)
            end;

Далее следует продолжить движение к правой границе, а для этого выполнить следующие операторы:
x1 := x2; x2 := x1 + h; y1 := y2

Блок-схема программы «отделение корней»

Рис. 84

Программа

Program Separation_root; { Программа отделения корней }
uses WinCrt;
var
a, b, h, x1, x2, y1, y2 : real;
k : integer;
{—————————————————————————————-}
Function fx(x : real) : real;
begin
fx := cos(x) — 0.1*x
end;
{—————————————————————————————-}
begin
write(«Введите левую границу промежутка «); readln(a);
write(«Введите правую границу промежутка «); readln(b);
write(«Введите шаг «); readln(h);
k := 0;
x1 := a;
x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k+1;
writeln(k, «-й корень на [«, x1:6:4, «;», x2:6:4, «]»)
end;
x1 := x2;
x2 := x1 + h;
y1 := y2
end
end.

Следующим, естественным этапом решения, является нахождение на промежутке корень с заданной степенью точности (если, конечно, уже известно, что он существует на нем).
Для этого нетрудно сочинить простую программу вычисления корня методом половинного деления, сущность которого заключается в следующем.
Известно, что на промежутке [a; b] есть корень. Зададим необходимую точность, с которой нам необходимо его вычислить. Обозначим ее — e.
Разделим промежуток [a; b] пополам. Точкой деления будет точка (см. рис. 41) :

Рис. 85
Установим, на котором из полученных двух промежутков находится корень. Для чего найдем знак разности fx(a)*fx(c). Если этот знак отрицательный, тогда корень находится на левом промежутке. Заменив c на b (b:=c), мы получим новый промежуток, обозначенный прежними буквами (см. рис. 86):

Рис. 86
А если разность fx(a)*fx(c) не будет отрицательной, тогда корень находится на правом промежутке. Заменив c на a (a := c), мы получим новый промежуток для поиска корня, обозначенный теми же буквами (см. рис. 87):

Рис. 87

И такой процесс деления надо выполнять, пока разность между правой и левой границами по абсолютной величине будет больше заданной точности e
( .
Пользуясь этими соображениями, нетрудно составить программу, где сам процесс половинного деления будет выполняться с помощью процедуры. В качестве функции берется функция: f(x) := sin(2*x) — ln(x) и рассматривается на промежутке
После завершения основного цикла, находится окончательное значение x, и вычисляется погрешность d, .

Блок-схема процедуры уточнения корня методом половинного деления

Рис. 88
Процедура

Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b — a) > e do
begin
c := (a + b)/2;
if func(a)*func(c) < 0 then b := c else a := c
end;
x := (a + b)/2;
d := abs(b — a)/2
end;

Блок-схема программы уточнения корня методом половинного деления

Рис. 89

Основная программа уточнения корня методом половинного деления

Program Division;
uses WinCrt;
var
a, b, c, e, x, d : real;
{—————————————————————————————-}
Function func(x : real) : real;
begin
func := sin(2*x) — ln(x)
end;
{—————————————————————————————-}
Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b — a) > e do
begin
c := (a + b)/2;
if func(a)*func(c) < 0 then b := c else a := c
end;
x := (a + b)/2;
d := abs(b — a)/2
end;
{—————————————————————————————-}
begin
write(«Введите левую границу промежутка «); readln(a);
write(«Введите правую границу промежутка «); readln(b);
write(«Введите точность вычисления корня «); readln(e);
half(a, b, e, x, d);
writeln(«Значение корня равно x = «, x:6:10);
writeln(«С границей погрешности «, d:2:10)
end.

Можно объединить программы отделения корня и уточнения его методом половинного деления в одну и получить программу, которая отделяет промежутки и сразу вычисляет на каждом из них корни с заданной точностью.

Блок-схема программы отделения корней и уточнения корня методом половинного деления

Рис. 90

Программа

Program Equation;
uses WinCrt;
var
a, b, h, x1, x2, y1, y2, e, x, d : real;
k : integer;
{—————————————————————————————-}
Function fx(x : real) : real;
begin
fx := cos(x) — 0.1*x
end;
{—————————————————————————————-}
Procedure half(a, b, e : real; var x, d : real);
var
c : real;
begin
while abs(b — a) > e do
begin
c := (a + b)/2;
if fx(a)*fx(c) < 0 then b := c else a := c
end;
x := (a + b)/2;
d := abs(b — a)/2
end;
{—————————————————————————————-}
begin
write(«Введите левую границу промежутка «); readln(a);
write(«Введите правую границу промежутка «); readln(b);
write(«Введите шаг «); readln(h);
write(«Введите точность вычисления корня «); readln(e);
k := 0;
x1 := a;
x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k + 1;
half(x1, x2, e, x, d);
write(k,»-й корень равен «, x:6:6);
writeln(» с погрешностью «, d:2:10)
end;
x1 := x2;
x2 := x1 + h;
y1 := y2
end
end.

Задание 13

Составьте программы вычисления корней уравнений:
1) ; 2) ;

7. Вычисление корней уравнения нахождением минимума функции на промежутке (для дополнительного изучения)

Зная определение минимума функции на промежутке, легко применить этот метод к нахождению корней уравнения.
Для этого достаточно рассматривать на заданном промежутке не саму функцию, а ее модуль, тогда минимум функции будет находиться на оси OX , а значение аргумента в этой точке даст нам значение корня уравнения на заданном промежутке. Разумеется, функция должна удовлетворять всем вышеперечисленным требованиям.
Ниже приводятся рисунки, которые наглядно показывают механизм применения поиска минимума функции на промежутке к нахождению корней. На одном из рисунков схематически показан график заданной функции, а на втором — график абсолютного значения этой функции применительно к нахождению корня с использованием поиска минимума для нахождения корня (см. рис. 91 и 92).

Рис. 91

Рис. 92

Программа нахождения корня уравнения с использованием поиска минимума функции методом “золотого сечения” приводится ниже.

{Решение уравнений с использованием определения минимума }
{ с помощью «золотого сечения» }
Program Equation_min_gold;
uses WinCrt;
var
a, a1, b, b1, e, x : real;
{—————————————————————————————-}
{ Поиск минимума функции методом золотого сечения }
Procedure mingold(a, b, e : real; var x : real);
var
x1, x2, y1, y2 : real;

{—————————————————————————————-}

          Function func(x : real) : real;
                  begin
                      func := abs(sin(2*x) — ln(x))
                  end;
{—————————————————————————————-}
          Function f1(a, b : real) : real;
                  begin
                      f1 := 0.618*a + 0.382*b
                  end;
{—————————————————————————————-}
          Function f2(a, b : real) : real;
                  begin
                      f2 := 0.382*a + 0.618*b
                  end;
{—————————————————————————————-}
          begin
                x1 := f1(a, b); y1 := func(x1);
                x2 := f2(a, b); y2 := func(x2);
                while abs(b — a) > e do
                     if y1<y2
                       then
                           begin
                               b := x2; x2 := x1; y2 := y1;
                               x1 := f1(a, b); y1 := func(x1)
                           end
                       else
                           begin
                               a := x1; x1 := x2; y1 := y2;
                               x2 := f2(a, b); y2 := func(x2)
                           end;
                x := (a + b)/2
            end;
{—————————————————————————————-}
{ Основная программа }
      begin
          write(«Введите нижнюю границу промежутка «); readln(a);
           a1 := a;
           write(«Введите правую границу промежутка «); readln(b);
           b1 := b;
           write(«Введите точность вычисления корня «);readln(e);
           mingold(a, b, e, x);
           write(«Корень уравнения на промежутке («);
           write(a1:1:0, «; «, b1:2:0, «)»);
         writeln(» равен x = «, x:6:6);
           writeln(«с точностью до «,e:2:6)
      end.

Задание 14

Составьте программу нахождения корня уравнения, применяя поиск минимума функции с помощью ряда Фибоначчи.

Библиотека часто встречающихся процедур и функций

1. Процедуры, вычисляющая сумму цифр числа:

Procedure sum_number(n : integer; var s : integer);
begin
s := 0;
repeat
s := s + n mod 10;
n := n div 10
until n = 0
end;

Procedure sum_number(p : longint; var s : longint);
begin
s := 0;
while p <> 0 do
begin
s := s + p mod 10;
p := p div 10
end
end;

2. Процедура, вычисляющая количество цифр в числе:

Procedure quantity_number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;

3. Процедура, записывающая заданное число в обратном порядке, например, 3467 записывает так: 7643.

Procedure backwards(n : integer; var a : integer);
begin
a := 0;
repeat
a := a*10 + n mod 10;
n := n div 10
until n = 0
end;

4. Процедура перестановки первой и последней цифр числа.

Procedure first_last_number(n : integer; var n1 : integer);
var
a, i, p : integer;
begin

a := n; i := 1;
      p := n mod 10; {последняя цифра введенного числа}
      while n >= 10 do
       begin
        i := i*10;
        n := n div 10
       end;
     n1 := a — n*i — p + n + p*i
    end;

5. Процедура, определяющая, является число числом — палиндромом.

Procedure palindrom(a : integer);
var
b, c, p : integer;
begin
b := a; c := 0;
repeat
p := b mod 10;
c := c*10 + p;
b := b div 10
until b = 0;
if c = a then writeln(«Число «, a, » является палиндромом»)
else writeln(«Число «, a, » не явл. палиндромом»)
end;

6. Процедура нахождения цифрового корня числа.
Цифровым корнем числа называется сумма цифр заданного числа, затем сумма цифр полученной суммы и т.д. до тех пор, пока эта сумма не станет однозначным числом.

Procedure radical_number(n : integer; var k : integer);
var
p, s : integer;
begin
repeat
s := 0;
while n <> 0 do
begin
p := n mod 10; s := s+p; n := n div 10
end;
n := s
until n < 10;
k := n
end;

7. Процедуры нахождения наибольшего общего делителя:

1-й способ (по простому алгоритму)

Procedure nod1(a, b : integer; var n : integer);
begin
if a > b then n := b else n := a;
n := n + 1;
repeat
n := n — 1
until (a mod n = 0) and (b mod n = 0)
end;

2-й способ (по 1-му алгоритму Евклида)

Procedure nod2(a, b : integer; var n : integer);
begin
while a <> b do
begin
if a > b then a := a — b else b := b — a
end;
n := a
end;

3-й способ (по 2-му алгоритму Евклида)

Procedure nod(a, b : integer; var n : integer);
var
r : integer;
begin
repeat
r := a mod b;
a := b; b := r
until b = 0;
n := a
end;

8. Рекурсивная процедура нахождения НОД.

Procedure nod(a, b : integer; var n : integer);
begin
if b = 0 then n := a else nod(b, a mod b, n)
end;

9. Процедуры нахождения наименьшего общего кратного двух целых чисел (НОК).

1-й способ

Procedure nok(a, b : integer; var k : integer);
var
m, n : integer;
begin
k := 0;
repeat
if a > b then
begin
m := a; n := b
end
else
begin
m := b; n := a
end;
k := p + m
until k mod n = 0
end;

2-й способ (с использованием НОД).

Procedure nok1(a, b : integer; var k : integer);
var
n, c : integer;
begin
n := a*b;
repeat
c := a mod b;
a := b; b := c
until b = 0;
k := n div a
end;

10. Процедура определения всех делителей заданного числа.

1-й способ

Procedure everyone_divisor(n : integer);
var
i : integer;
begin
writeln(«Делители числа «, n);
for i := 1 to n div 2 do
if n mod i = 0 then write(i, » «);
writeln(n)
end;

2-й способ

Procedure everyone_divisor(n : integer);
var
i : integer;
begin
writeln(«Делители числа «, n);
for i := 1 to trunc(sqrt(n)) do
if n mod i = 0 then write(i, » «, n div i, » «)
end;

11. Процедура, определяющая число делителей натурального числа:

Procedure number_division(n : integer; var k : integer);
var
d : integer;
begin

     k := 0;
     for d := 1 to n div 2 do
      if n mod d = 0 then k := k + 1;
     k := k + 1
    end;

12. Процедура разложения числа на простые множители:

Procedure probleme_number(n : integer);
var
i : integer;
begin
while n mod 2 = 0 do
begin
write(2, » «);
n := n div 2
end;
i := 3;
while i <= n do
if n mod i = 0 then
begin
write(i, » «);
n := n div i
end
else
i := i + 2
end;

13. Процедура, определяющая, является ли число простым.

первый способ

Procedure probleme_number(p : integer);
var
i, k : integer;
begin
if p = 2 then write(p, » «)
else
if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= p div 2 do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then write(p, » «)
end
end;

второй способ

Procedure probleme_number(p : integer);
var
i, k : integer;
begin
if p = 2 then write(p, » «)
else if p mod 2 <> 0
then
begin
i := 3; k := 0;
while i <= trunc(sqrt(p)) do
begin
if p mod i = 0 then k := k + 1;
i := i + 2
end;
if k = 0 then write(p, » «)
end
end;

14. Процедура, определяющая, является ли число автоморфным? Автоморфным называется такое число, которое равно последним цифрам своего квадрата. Например: 52 = 25; 252 = 625.

Procedura awtomorf(x : integer);
var
d, k : integer;
begin
d := 10;
while d <= x do d := d*10;
k := x mod 10;
if (k = 1) or (k = 5) or (k = 6)
then
if x*x mod d = x then writeln(x, » «, x*x)
end;

15. Процедура, устанавливающая, равно ли заданное число сумме квадратов целых чисел и каких именно, если таковые существуют:

Procedure square(n : integer);
label 1;
var
a, b, k : integer;
begin
a := 1; k := 1;
while a*a + 1 <= n do
begin
k := k + 1; a := a + 1
end;
for a := 1 to k do
for b := 1 to a do if a*a + b*b = n then
begin
writeln(n, «=», a, «*», a, «+», b, «*», b); goto 1
end;
1: end;

16. Процедура определения Пифагоровых чисел из промежутка [n; m].

Procedure pifagor(n, m : integer);
var
a, b, c : integer;
begin
writeln(«Пифагоровы числа из промежутка [«,n, «;», m,»]»);
for a := n to m do
for b := n to a do
for c := n to m do
if a*a + b*b = c*c then writeln(a, » «, b, » «, c)
end;

17. Процедура представления числа n в виде суммы кубов двух чисел.

Procedure sum_number_cube(n : integer; var p : integer);
var
i, j, k : integer;
begin
k := 0; i := 1;
while i*i*i + 1 <= n do
begin
k := k + 1; i := i + 1
end;
p := 0;
for i := k downto 1 do
for j := 1 to i do
if i*i*i + j*j*j = n
then
begin
p := p + 1;
writeln(i, «*», i, «*», i, «+», j, «*», j, «*», j, «=», n)
end;
if p = 0
then
begin
write(«Число «, n, » нельзя представить в виде «);
writeln(«суммы кубов двух чисел»)
end
else
writeln(«Число способов равно «, p)
end;

18. Процедура представления целого числа n в виде суммы квадратов трех чисел.

Procedure sum_square_number(n : integer; var p : integer);
var

      k, x, y, z, p : integer;
    begin
     k := 0; x := 1;
     while x*x + 2 <= n do
       begin
        k := k + 1; x := x + 1
       end;
     p := 0;
     for x := 1 to k do
      for y := 1 to x do
       for z := 1 to y do
        if x*x + y*y + z*z = n
         then
          begin
            p := p + 1;
            writeln(x, «*», x, «+», y, «*», y, «+», z, «*», z, «=», n)
           end;
         if p = 0
          then
           begin
            write(«Число «,n,» нельзя представить в виде «);
            writeln(«суммы квадратов трех чисел»)
           end
          else writeln(«Число способов равно «, p)
    end;

19. Процедура определения цифры, стоящей на n-ом месте в записи подряд чисел 1234567891011121314…
Procedure location(n : integer; var c : integer);
var
p, s, v, m, q : integer;
Procedure number(n : integer; var k : integer);
begin
k := 0;
repeat
k := k + 1;
n := n div 10
until n = 0
end;
begin
p := 1; s := 0;
repeat
number(p, v);
s := s + v; p := p + 1
until s>=n;
m := s — n; p := p — 1; q := 1;
for i := 1 to m do q := q*10;
c := p div q;
c := c mod 10;
writeln(«Последняя цифра в записи этих цифр будет «, c);
writeln(«Она находится в числе «, p)
end;
20. Процедуры вычисления степени натурального числа с натуральным показателем:

с циклом repeat … until …

Procedure extent(a, n : integer; var s : integer);
var
i : integer;
begin
i := 1; s := 1;
repeat
s := s*a; i := i + 1
until i = n
end;

с циклом for … to … do …

Procedure extent(a, n : integer; var s : longint);
var
i : integer;
begin
s := 1;
for i := 1 to n do s := s*a
end;

функция вычисления степени числа:

Function extent(a, n : longint) : longint;
var
i : integer;
begin
extent := 1;
for i := 1 to n do extent := extent*a
end;

21. Процедура вычисления факториала числа:

итеративная

Procedure fac(n : integer; var f : longint);
var
i : integer;
begin
if n = 0 then f := 1 else for i := 1 to n do f := f*i
end;

рекурсивная

Procedure fac(n : integer; var f : longint);
begin
if (n = 0) or (n = 1) then f := 1
else
begin
fac(n — 1, f);
f := f*n
end
end;

22. Рекурсивная процедура умножения числа a на каждую цифру числа b, начиная с единиц:

Procedure umnogenie(a, b, s : integer);
begin
if b <> 0
then
begin
s := s + a*(b mod 10);
umnogenie(a, b div 10, s div 10);
write(s mod 10:1)
end
else
if s <> 0 then write(s)
end;

23. Функции вычисления чисел ряда Фибоначчи.

итеративная

Function fib(n : integer) : integer;
var
f, f1, f2, i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2;
end;
fib := f
end;

рекурсивная

Function fib(n : integer) : integer;
begin
if (n = 1) or (n = 2)
then fib := 1
else fib := fib(n — 1) + fib(n — 2)
end;

24. Процедура отделения корней на заданном промежутке [a; b] для заданной функции fx, т.е. определения промежутков, на которых может находиться хотя бы один корень (h — шаг), (x1, x2 — границы полученных промежутков).

Procedure separation_root(a, b, h : real);
var
x1, x2, y1, y2 : real; k : integer;
Function fx(x : real) : real;
begin
fx := ???????????
end;
begin
k := 0; x1 := a; x2 := x1 + h;
y1 := fx(x1);
while x2 <= b do
begin
y2 := fx(x2);
if y1*y2 < 0
then
begin
k := k + 1;
writeln(k, «-й корень на [«, x1:6:4, «; «, x2:6:4,»]»)
end;
x1 := x2; x2 := x1 + h;
y1 := y2
end
end;

25. Процедура уточнения корня некоторой функции func(x) методом деления пополам (a, b — границы промежутка, eps — точность вычисления, x — значение корня, d — погрешность вычисления).

Procedure half(a, b, eps : real; var x, d : real);
var
c : real;
begin
while abs(b — a) > eps do
begin
c := (a + b)/2;
if func(a)*func(c) < 0 then b := c
else a := c
end;
x := (a + b)/2;
d := abs(b — a)/2
end;

26. Процедура поиском минимума функции на промежутка с помощью ряда Фибоначчи.

{ Процедура определения минимума функции на промежутке }
Procedure minfib(a, b, e : real; var x : real);
label 1;
var
aa, bb, x1, x2, y1, y2 : real;
n : integer;
{—————————————————————————————-}
{ Заданная исследуемая функция }
Function func(x : real) : real;
begin
func := ?????????????????
end;
{—————————————————————————————-}
{ Функция вычисления членов ряда Фибоначчи }
Function fib(n : integer) : real;
var
f, f1, f2 : real;
i : integer;
begin
f1 := 1; f := 0;
for i := 1 to n do
begin
f2 := f1; f1 := f;
f := f1 + f2
end;
fib := f
end;
{—————————————————————————————-}
{ Процедура вычисления знач. аргумента и функции }
{ approach — приближение }
Procedure approach(a, b : real; n : integer; var x2, y2 : real);
begin
x2 := a + (b — a)*fib(n — 1)/fib(n);
y2 := func(x2)
end;
begin
n := 3;
approach(a, b, n, x2, y2);
while abs(b — a) > e do
begin
x1 := a + b — x2; y1 := func(x1);
if (x2 > x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 <= x1) and (y2 > y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x2; x2 := x1; y2 := y1; goto 1
end;
if (x2 > x1) and (y2 < y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
a := x1; goto 1
end;
if (x2 <= x1) and (y2 <= y1)
then
begin
n := n + 1;
approach(a, b, n, x2, y2);
b := x1; goto 1
end;
n := n + 1;
approach(a, b, n, x2, y2);
1: end;
x := (a + b)/2;
end;

27. Процедура поиском минимума функции на промежутке с помощью “золотого сечения”.

Procedure mingold(a, b, e : real; var x : real);
var
x1, x2, y1, y2 : real;
{—————————————————————————————-}
Function func(x : real):real;
begin
func := ????????????
end;
{—————————————————————————————-}
Function f1(a, b : real) : real;
begin
f1 := 0.618*a + 0.382*b
end;
{—————————————————————————————-}
Function f2(a, b : real) : real;
begin
f2 := 0.382*a+0.618*b
end;
{—————————————————————————————-}
begin
x1 := f1(a, b); y1 := func(x1);
x2 := f2(a, b); y2 := func(x2);
while abs(b — a) > e do
if y1<y2 then
begin
b := x2; x2 := x1; y2 := y1;
x1 := f1(a, b); y1 := func(x1)
end
else
begin
a := x1; x1 := x2; y1 := y2;
x2 := f2(a, b); y2 := func(x2)
end;
x := (a + b)/2
end;

28. Процедура решения неопределённых уравнений вида ax + by = c:

Procedure The_equation(a, b, c : integer); {Решение уравнения ax + by = c}
label 1;
var
max, x, y, n : integer;
begin
if (nod(a, b) <> 1) and (c mod nod(a, b) = 0)
then begin n:= nod(a,b); a := a div n; b := b div n; c := c div n end
else if (nod(a, b) <> 1) and (c mod nod(a, b) <> 0)
then writeln(«Уравнение не имеет решений»);
if abs(a) > abs(b) then max := abs(a) else max := abs(b);
for x := -max to max do
for y := -max to x do
begin
if (a*x + b*y = 1) and (a > 0) and (b > 0)
then begin writeln(«Решения уравнения x = «, x*c, «+», b,»*t, y = «, y*c, «-«, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b > 0)
then begin writeln(«Решения уравнения x = «, x*c, «+», b,»*t, y = «, y*c, » «, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end;
if (a*x + b*y = 1) and (a > 0) and (b < 0)
then begin writeln(«Решения уравнения x = «, x*c, » «, b,»*t, y = «, y*c, «-«, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end;
if (a*x + b*y = 1) and (a < 0) and (b < 0)
then begin writeln(«Решения уравнения x = «, x*c, » «, b,»*t, y = «, y*c, » «, a, «*t,»);
writeln(«где t — произвольное целое число»); goto 1 end
end;

1: end;

Автор: Тишин Владимир Иванович

Победа знаний

Победа знаний

Это было давно.
В некотором царстве, в некотором государстве на престол взошел неграмотный король: в детстве он не любил математику и родной язык, рисование и пение, чтение и труд… Вырос этот король неучем. Стыдно перед народом. И порешил король: пусть все в этом государстве будут неграмотными. Он закрыл школы, но разрешил изучать только военное дело, чтобы …

Окрестности Млечного Пути

Ядро нашей Галактики (направление на созвездие Стрельца, на фото справа) в 1948-м году впервые удалось сфотографировать в тепловых лучах советским астрономам В.Б.Никонову, В.И.Красовскому и А.А.Калиняку в Крымской обсерватории. От Солнца ядро закрыто скоплениями газа и пыли, но тепловые лучи их с потерями преодолевают. Изучение ядра с помощью инфракрасных, рентгеновских …

Modal verb Make

Make — заставить/ сделать(создать) : когда ‘make’ используется в предложении, то глагол идущий после него пишется без ‘to’ :
What makes you think so? = Что заставляет вас так думать?

Вместо глагола может быть прилагательное :
He made me angry = Он разозлил меня.
You made me happy = Ты меня осчастливел.

В некоторых случаях ‘make’ имеет значение ‘сделать’ заменяя глагол ‘to do’ и иногда трудно определить, что надо вставить …

Involved turns with participle 1 and 2 in function of definition

Примеры причастных оборотов с причастием 1 :
The rising sun = Восходящее солнце.
The approaching train = Приближающийся поезд.
The woman, standing at the window is my sister = Женщина, стоящая у окна, моя сестра.
I recognized the boy, playing near us = Я узнал игравшего около нас мальчика.
The man, writing something at the table, is my brother = Человек, что-то пишущий за столом, мой брат.

Определительный причастный оборот должен следовать за тем существительным …

Источник

Оксана Богуцкая

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Определение 1

Блок-схема – это графический метод представления алгоритма, в котором его шаги изображаются в виде определенных блоков разной формы, соединенных между собой стрелками.

Введение

В шестидесятых годах двадцатого века, началась работа по созданию нового языка программирования и уже к началу семидесятых специалисты закончили работу над первым вариантом языка Pascal и его программой компиляции. Затем фирма Borland International существенно улучшила исходную версию этого языка и выпустила в свет новую среду программирования, названную Turbo Pascal. Этот вариант программы раздвинул границы её применения и создал основу для её дальнейших модификаций. Программные приложения, сформированные на Паскале, проходят следующие основные шаги:

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Процесс занесения и редакции текстового варианта программы.
Выполнение транслятором перевода программы в машинные коды.
Процедура отладки программного приложения.

Все вышеперечисленные операции осуществляются при помощи предназначенных для этого средств:

Программа, предназначенная для коррекции текстов (текстовый редактор).
Программа, которая осуществляет процесс компиляции. В её составе есть программа компоновки, которая предназначена для создания программного объекта компьютера.
Отладочная программа, которая применяется программистом для обнаружения и исправления ошибок.

Блок-схема и программа Паскаль

Проектирование программного продукта в Турбо Паскале следует начинать с формирования алгоритма и отображения его в формальной записи в формате блок-схемы. Блок-схема является набором процедур или операций, которые представлены в виде геометрических фигур. Очерёдность действий, то есть завершение одного действия и начало другого, следует обозначать линией, имеющей направление. При формировании блок-схемы следует прибавлять компоненты сверху вниз поочерёдно один за другим. Если необходимо выполнять проверку условий, то следует соблюсти древовидность иерархии. Блок-схема обязана начинаться компонентом «Начало» и оканчиваться компонентом «Конец», при этом они должны обязательно присутствовать в единственном числе. Сформированная блок-схема должна соответствовать всем ГОСТ и другим регламентирующим документам. В частности, это ГОСТ 19.003-80, который регламентирует формат схем алгоритмов и программ, а также условные графические обозначения.

«Блок-схема и программа Паскаль » 👇

Согласно этим документам главными компонентами блок-схемы являются следующие:

Рисунок 1. Терминатор. Автор24 — интернет-биржа студенческих работ

Терминатор. Он призван обозначить начало или окончание программы. А также определяет зону взаимообмена с окружающим пространством. Применяется, как правило, с командами, записанными внутри, «Начало», «Конец», или «Пуск» и «Стоп», и обязательно только один раз.

Рисунок 2. Процесс. Автор24 — интернет-биржа студенческих работ

Процесс. Обозначает какую-либо функцию или операцию. Это может быть арифметическая, логическая или какая-либо другая операция, которая в итоге как-то изменяет данные. Допускается соединение операционного набора в одном блоке.

Рисунок 3. Решение. Автор24 — интернет-биржа студенческих работ

Решение. Осуществляется выбор одного из допустимых продолжений алгоритма. В компоненте располагается проверяемое условие, которое определяет дальнейшее направление алгоритма. Этих направлений всего два и они выходят в виде стрелок, обозначенных как «Да» и «Нет», то есть проверяемое условие истинно или ложно. Чтобы было удобно читать блок-схему, путь, отвечающий истинности условия, должен выходить снизу ромба, а путь «нет» должен выходить из бокового. Данные компонент применяется для задания некоторых циклов, таких как, repeat..until и while..do.

Рисунок 4. Модификация. Автор24 — интернет-биржа студенческих работ

Модификация. Служит для осуществления команд цикла типа for. Команды и функции цикла должны располагаться под элементом. После каждого прохождения цикла выполняется возврат программы к началу по стрелке, расположенной слева. Цикл заканчивается выходом в направлении стрелки, расположенной справа.

Рисунок 5. Предопределённый процесс. Автор24 — интернет-биржа студенческих работ

Предопределённый процесс. Обозначает процедуру, функцию или модуль, которые являются элементами программы. Располагаются они вне текущего последовательного кода.

Рисунок 6. Данные. Автор24 — интернет-биржа студенческих работ

Данные. Выполнение информационного обмена, то есть ввода или вывода данных. Служит обобщённым отображением информационного обмена без указания конкретного вида носителя.

Рисунок 7. Документ. Автор24 — интернет-биржа студенческих работ

Документ. Является обозначением вывода данных на печать.

Рисунок 8. Обозначение ручного ввода. Автор24 — интернет-биржа студенческих работ

Обозначение ручного ввода. Подразумевается ввод информации с клавиатуры.

Рисунок 9. Перфокарта. Автор24 — интернет-биржа студенческих работ

Перфокарта. Обозначение чтения или записи данных с перфокарт.

Рисунок 10. Перфолента. Автор24 — интернет-биржа студенческих работ

Перфолента. Обозначение чтения или записи данных с использованием перфоленты.

Рисунок 11. Устройство памяти, имеющее последовательный доступ. Автор24 — интернет-биржа студенческих работ

Устройство памяти, имеющее последовательный доступ. Предполагается информационный обмен с носителями на магнитной ленте.

Рисунок 12. Устройство памяти, имеющее прямой доступ. Автор24 — интернет-биржа студенческих работ

Устройство памяти, имеющее прямой доступ. Имеется в виду информационный обмен с магнитным барабаном.

Рисунок 13. Магнитный диск. Автор24 — интернет-биржа студенческих работ

Магнитный диск. Информационный обмен с носителем на магнитном диске.

Рисунок 14. Оперативная память. Автор24 — интернет-биржа студенческих работ

Оперативная память. Предполагается информационный обмен с оперативным запоминающим устройством.

Рисунок 15. Режим ручного управления. Автор24 — интернет-биржа студенческих работ

Режим ручного управления. Отображается процесс, который выполняет человек.

Рисунок 16. Сохранение данных. Автор24 — интернет-биржа студенческих работ

Сохранение данных. Информационный обмен с применением устройства памяти, которое управляется напрямую процессором.

Рисунок 17. Монитор. Автор24 — интернет-биржа студенческих работ

Монитор. Вывод информации на дисплей, визуальные индикаторы.

Рисунок 18. Извлечь. Автор24 — интернет-биржа студенческих работ

Извлечь. Выделить одно или набор множеств из определенного множества.

Рисунок 19. Слияние. Автор24 — интернет-биржа студенческих работ

Слияние. Соединение одного или набора множеств в единое множество.

Рисунок 20. Группирование. Автор24 — интернет-биржа студенческих работ

Группирование. Слияние множеств и выделение каких-либо других.

Рисунок 21. Выполнение сортировки. Автор24 — интернет-биржа студенческих работ

Выполнение сортировки. Осуществление упорядочения множеств по определённым признакам.

Рисунок 22. Соединение. Автор24 — интернет-биржа студенческих работ

Соединение. Обозначение применяется, чтобы оборвать связующую линию в одном месте и продолжить её в другом. В этом компоненте блок-схемы указывается уникальная идентификация.

Рисунок 23. Межстраничное соединение. Автор24 — интернет-биржа студенческих работ

Межстраничное соединение. Является аналогом предыдущего компонента блок-схемы. Выполняет перенос линии связи с окончания исходной страницы к началу следующей.

Рисунок 24. Комментарий. Автор24 — интернет-биржа студенческих работ

Комментарий. С его помощью помечается неактивный участок программы.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Конструирование блок-схем алгоритмов

Рассмотрим
несколько типов задач, которые понадобятся
Вам при решении контрольной работы. За
основу построения блок-схем возьмем
алгоритмы, построенные в разделе
«Алгоритмы».

1.
Разветвляющиеся алгоритмы.

Составить
алгоритм вычисления следующей функции:

a=2,68;
b=1,75.

х=1,27.

Решение.

Как
уже говорилось, сам алгоритм и принцип
его построения приведет в разделе
«Алгоритмы». Поэтому здесь мы приведем
лишь готовую блок-схему, сконструированную
на основе алгоритма приведенного выше.

астала
очередь приступить к составлению
программы. Но прежде посмотрим, как
должна выглядеть программа, написанная
на Паскале. Оказывается текст программы
имеет довольно жесткую структуру блоков,
которые следуют в определенном порядке.
Основные разделы и подразделы этого
текста — заголовок, раздел описаний
(состоит из раздела констант, переменных,
процедур и функций) и раздел операторов.
В общем случае его можно представить
следующим образом:

PROGRAM
<имя>; {Заголовок программы}

{РАЗДЕЛ
ОПИСАНИЙ}

CONST —
раздел констант

VAR —
раздел переменных

PROCEDURE,
FUNCTION
— раздел описания собственных процедур
и функций

{РАЗДЕЛ
ОПЕРАТОРОВ ИЛИ ТЕЛО ПРОГРАММЫ}

BEGIN

оператор
1;

оператор
2;

…

оператор
n

END.

При
написании программы нужно помнить, что
жестко задаются только названия и
последовательность разделов. Причем
разделы CONST,
VAR
и PROCEDURE-FUNCTION
вовсе не обязательны. Операторы не
привязаны к определенной позиции в
строке и могут начинаться после нескольких
пробелов. Каждый оператор заканчивается
символом «;». В одной строке можно указать
несколько операторов или описаний.
Допускается перенос с одной строки на
другую частей описания или операторов,
но не разрешается разделять слова,
константы и составные символы.

Прежде,
чем начать писать программу, мы предлагаем
ознакомиться с еще один разделом, который
поможет немного глубже понять структуру
программы.

Типы данных и операторы

Все
переменные, которые вы собираетесь
использовать в своей программе, должны
быть описаны в разделе описаний. В
большинстве случаев при написании
программ для представления информации
используются следующие основные типы:

целые
числа (integer);
вещественные
числа (real)
— числа, имеющие дробную часть. В
математике Вы наверняка изучали
стандартную форму представления
дробного числа (числа с плавающей
точкой): например, 3,456х10²³
или 3,14159 или 6,12х10²⁵;
символы
(char)
— это любые символы алфавита языка, а
также любые символы, которые Вы можете
ввести с клавиатуры;
строки
(string)
— символы могут объединяться в символьные
строки.

Примеры
описания переменных:

VAR

X
: INTEGER;

Y,Z,T
: REAL;

C1,C2
: CHAR;

S1
: STRING;

I,
J, K : INTEGER;

Кроме
основных типов, в Паскале используется
зарезервированной слово для организации
массивов переменных — ARRAY.
Примеры описания массивов:

X
: ARRAY
[1..5] OF
INTEGER;
— одномерный массив из 5 целых чисел,

Y
: ARRAY
[1..5,1..10] OF
REAL
— двухмерный массив вещественных чисел
размером 5×10.

Для
того, чтобы обратиться к элементу массива
с определенным номером, используются
квадратные скобки: X[2]
— второй элемент массива X,
Y[3,7]
— элемент массива Y
из строки 3 с номером 7.

Единственная
оговорка при задании имен в Паскале
состоит в том, что имя должно начинаться
с латинской буквы и содержать только
латинские символы и цифры.

И
последний момент перед написанием
программы. Мы уже можем задавать
переменные и выполнять над ними
арифметические действия. Для обработки
данных в Паскале (как и в других языках
программирования) используются операторы
и процедуры.

Оператор
присваивания.
Основной операцией в программе, как
правило, является операция присваивания.
В Паскале этот оператор обозначается
символом «:=».

Примеры.

X
:= 5;

Y
:= SQRT(X+10);

После
выполнения этого оператора, переменной,
стоящей слева от оператора (всегда
одна!) присваивается значение выражения,
записанного справа от знака присваивания.

Операторы
арифметических операций.

сложение
(+);
вычитание
(-);
умножение
(*);
деление
(/);
деление
целых чисел без остатка (DIV);
остаток
от деления целых чисел (MOD).

Приоритет
выполнения операций в выражении точно
такой же, как и в арифметике, изучаемой
Вами в школе: сначала выполняются
операции *, /, затем — +, -. Изменить приоритет
операций можно с помощью круглых скобок.

Операторы
отношения.

Операторы
данного класса сравнивают два значения,
возвращая в результате одно из двух
значений: TRUE
или FALSE
(истина или ложь, в блок-схемах алгоритмов
мы обозначали эти значения соответственно
«да» или «нет»).

>
— больше, чем;
>=
— больше или равно;
<
— меньше,
чем;
<=
— меньше или равно;
=
— равно;
<>
— не равно.

Логические
операторы.

Если
Вам потребовалось в Паскале проанализировать
несколько условий, то можно воспользоваться
логическими операторами AND
и OR
— соответственно «И» и «ИЛИ». Каждое
условие при этом берется в круглые
скобки.

Примеры:

IF
(X<>0)
AND
(X<10)
THEN
Y
:= 6; — если Х не равен нулю и меньше 10 — то
Y
присвоить значение 6;

IF
(A[1]=0)
OR
(A[10]=0)
THEN
X
:= 10; — если первый или десятый элемент
массива A
равны нулю, то Х присвоить значение 10.

Вывод.

После
того, как Вы выполните расчет нужных
элементов, Вам потребуется вывести
информацию о результатах на экран
компьютера. Самый распространенный
способ — использование стандартной
процедуры вывода на экран — WRITELN.

Формат
команды: WRITELN(выражение
1, выражение 2, …, выражение n);

Выражением
может быть любая константа или переменная,
строка (для вывода строки ее надо взять
в одинарные кавычки, например
WRITELN(‘Привет’);).
Нужно помнить, что при выводе нескольких
элементов пробелы между ними не
проставляются, поэтому их надо учитывать
самим.

Иногда
для вывода информации используется
процедура WRITE.
Ее отличие видно из примеров, приведенных
ниже

Примеры
использования процедуры WRITELN
для различных типов переменных:

VAR

A,
B, C : INTEGER;

X
: REAL;

NAME
: STRING;

BEGIN

A
:= 15; B := 2; C := 32;

X
:= 15.5678;

NAME
:= ‘СВЕТА’;

WRITELN(A,
B, C); 15232

WRITELN(A,’
‘,B,’ ‘,C); 15 2 32

WRITELN(A:2,
B:2,
C:2); 15
232 { — с заданием позиций вывода для
каждого числа}

WRITELN(A:3,
B:3, C:3); 15 2 32

WRITELN(A,
B:2, C:3); 15 2 32

WRITELN(‘ПРИВЕТ’,NAME); ПРИВЕТСВЕТА

WRITELN(‘ПРИВЕТ,
’,NAME); ПРИВЕТ,
СВЕТА

WRITELN(X); 1,5567800000E+02
{ — такой вид имеет число внутри машины}

WRITELN(X:4); 1,5567E+02

WRITELN(X:4:3); 15,567

WRITELN(X:5:2); 15,567

WRITELN(X:7:6); 15,567800

WRITELN(A);WRITELN(B);WRITELN(C); 15

WRITE(A);WRITE(B);WRITE(C); 15232

END.

Ввод.

В
Паскале существует стандартная процедура
ввода любой переменной с клавиатуры —
READLN.

Пример.

READLN(X);

READLN(A);

Итак,
мы ознакомились со всеми основными
элементами языка программирования
Паскаль и можем теперь смело приступать
к созданию собственных программ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник