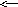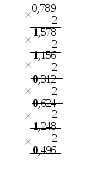Как в системе счисления найти порядок числа

Основы систем счисления

Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.

Введение

Система счисления — это способ записи (представления) чисел.

Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палецзарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки

Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.

Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.

Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.

Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.

Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.

Непозиционные системы

Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.

Единичная система счисления

Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.

Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.

Древнеегипетская десятичная система

В Древнем Египте использовались специальные символы (цифры) для обозначения чисел 1, 10, 10², 10³, 10⁴, 10⁵, 10⁶, 10⁷. Вот некоторые из них:

Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.

Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:

Вавилонская шестидесятеричная система

В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:

Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:

Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:

Теперь число 3632 следует записывать, как:

Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.

Римская система

Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.

Методы определения значения числа:

1. Значение числа равно сумме значений его цифр. Например, число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2=32
2. Если слева от большей цифры стоит меньшая, то значение равно разности между большей и меньшей цифрами. При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
3. Значение равно сумме значений групп и цифр, не подходящих под 1 и 2 пункты.

Помимо цифирных, существуют и буквенные (алфавитные) системы счисления, вот некоторые из них:
1) Славянская
2) Греческая (ионийская)

Позиционные системы счисления

Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.

Десятичная система счисления

Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.

Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10² + 0*10¹ + 3*10⁰ = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 503₁₀.

Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.

Двоичная система счисления

Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.

Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.

Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 101₂ = 1*2² + 0*2¹ + 1*2⁰ = 4+0+1 = 5₁₀.

Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?

Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 101100₂. В восьмеричной — это 101 100 = 54₈, а в шестнадцатеричной — 0010 1100 = 2С₁₆. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.

Восьмеричная система счисления

8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.

Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8ⁿ, где n — это номер разряда. Получается, что 254₈ = 2*8² + 5*8¹ + 4*8⁰ = 128+40+4 = 172₁₀.

Шестнадцатеричная система счисления

Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.

В качестве примера возьмем число 4F5₁₆. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F5₁₆ = (100 1111 101)₂. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2ⁿ, где n — номер разряда: (0*2²+1*2¹+0*2⁰) (0*2²+1*2¹+1*2⁰) (1*2²+1*2¹+0*2⁰) (1*2²+0*2¹+1*2⁰) = 2365₈.

Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная

Позиционные системы подразделяются на однородные и смешанные.

Однородные позиционные системы счисления

Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.

Смешанные системы счисления

К уже приведенному определению можно добавить теорему: “если P=Qⁿ (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”

Опираясь на теорему, можно сформулировать правила перевода из P-й в Q-ю системы и наоборот:

1. Для перевода из Q-й в P-ю, необходимо число в Q-й системе, разбить на группы по n цифр, начиная с правой цифры, и каждую группу заменить одной цифрой в P-й системе.
2. Для перевода из P-й в Q-ю, необходимо каждую цифру числа в P-й системе перевести в Q-ю и заполнить недостающие разряды ведущими нулями, за исключением левого, так, чтобы каждое число в системе с основанием Q состояло из n цифр.

Яркий пример — перевод из двоичной системы счисления в восьмеричную. Возьмем двоичное число 10011110₂, для перевода в восьмеричное — разобьем его справа налево на группы по 3 цифры: 010 011 110, теперь умножим каждый разряд на 2ⁿ, где n — номер разряда, 010 011 110 = (0*2²+1*2¹+0*2⁰) (0*2²+1*2¹+1*2⁰) (1*2²+1*2¹+0*2⁰) = 236₈. Получается, что 10011110₂ = 236₈. Для однозначности изображения двоично-восьмеричного числа его разбивают на тройки: 236₈ = (10 011 110)_2-8.

Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева

Перевод из одной системы счисления в другую

Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.

Преобразование в десятичную систему счисления

Имеется число a₁a₂a₃ в системе счисления с основанием b. Для перевода в 10-ю систему необходимо каждый разряд числа умножить на bⁿ, где n — номер разряда. Таким образом, (a₁a₂a₃)_b = (a₁*b² + a₂*b¹ + a₃*b⁰)₁₀.

Пример: 101₂ = 1*2² + 0*2¹ + 1*2⁰ = 4+0+1 = 5₁₀

Преобразование из десятичной системы счисления в другие

Целая часть:

1. Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
2. Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.

Дробная часть:

1. Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
2. Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.

Пример: переведем 15₁₀ в восьмеричную:
158 = 1, остаток 7
18 = 0, остаток 1

Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 15₁₀ = 17₈.

Преобразование из двоичной в восьмеричную и шестнадцатеричную системы

Для перевода в восьмеричную — разбиваем двоичное число на группы по 3 цифры справа налево, а недостающие крайние разряды заполняем ведущими нулями. Далее преобразуем каждую группу, умножая последовательно разряды на 2ⁿ, где n — номер разряда.

В качестве примера возьмем число 1001₂: 1001₂ = 001 001 = (0*2² + 0*2¹ + 1*2⁰) (0*2² + 0*2¹ + 1*2⁰) = (0+0+1) (0+0+1) = 11₈

Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.

Преобразование из восьмеричной и шестнадцатеричной систем в двоичную

Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.

Для примера рассмотрим число 45₈: 45 = (100) (101) = 100101₂

Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.

Преобразование дробной части любой системы счисления в десятичную

Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.

Пример: 101,011₂ = (1*2² + 0*2¹ + 1*2⁰), (0*2^-1 + 1*2^-2 + 1*2^-3) = (5), (0 + 0,25 + 0,125) = 5,375₁₀

Преобразование дробной части двоичной системы в 8- и 16-ую

Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.

Пример: 1001,01₂ = 001 001, 010 = (0*2² + 0*2¹ + 1*2⁰) (0*2² + 0*2¹ + 1*2⁰), (0*2² + 1*2¹ + 0*2⁰) = (0+0+1) (0+0+1), (0+2+0) = 11,2₈

Преобразование дробной части десятичной системы в любую другую

Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.

Для примера переведем 10,625₁₀ в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,625₁₀ = (1010), (101) = 1010,101₂

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

 
2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Содержание:

1. Системы счисления в математике
2. Непозиционные системы счисления
3. Позиционные системы счисления
4. Двоичная система счисления
5. Восьмеричная система счисления
6. Шестнадцатеричная система счисления
7. Переведение чисел из одной системы в другую
8. Перевод чисел системы в систему с помощью арифметики системы
9. Перевод целых чисел
10. Переведение правильных дробей

Системы счисления в математике

Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр). Системы счисления бывают: непозиционными (в этих системах значение цифры не зависит от ее позиции — положения в записи числа).

Непозиционные системы счисления

Непозиционными называются такие системы счисления, в которых каждая цифра сохраняет своё постоянное значение независимо от того места, которое она занимает в записи числа.

Примером непозиционной системы счисления, которая дошла до наших дней и иногда используется, является римская система счисления. В этой системе для записи чисел используется такие цифры: I, V, X, C, D, M и т.д., они обозначают числа один, пять, десять, пятьдесят, сто, тысяча и т.д. Запись любых других чисел производится на основе определённых правил: несколько одинаковых цифр, стоящих рядом, отображают число, равное сумме чисел, которые соответствуют этим цифрам, например III — три, XX — двадцать, пара цифр в которой младшая цифра (которая обозначает меньшее число) стоит слева от старшей (которая обозначает большее число), отображает разность соответствующих чисел, например IV — четыре, XL — сорок, пара цифр, в которой младшая цифра стоит справа от старшей, отображает сумму соответствующих чисел, например XI — одиннадцать, VI — шесть, и т.п. 

Позиционные системы счисления

Позиционными называются такие системы счисления, в которых значение каждой цифры определяется не только самой цифрой, но и тем местом (позицией), которое она занимает в записи числа.

Основой позиционной системы счисления называется число , которое показывает, сколько необходимо единиц любого разряда для получения единицы старшего разряда. Систему счисления с основой  будем обозначать через . Очевидно, что основой системы счисления определяется количество цифр, которые используются для записи чисел в данной системе счисления. Основой десятичной системы счисления является число десять, для записи любых чисел используется только десять разных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

В позиционной системе счисления с основой  используются  разных целых чисел , которые называются базой системы счисления. Различаются позиционные системы счисления с неотъемлемой и симметричной базой. В позиционных системах счисления с неотъемлемой базой цифры означают последовательные целые числа начиная с нуля; в позиционных системах счисления с симметричной базой цифры обозначают последовательные целые числа, симметрично расположенные относительно нуля и ноль. Как правило, цифры 0, 1 в позиционных системах счисления обозначают число ноль и единицу.

Числа в позиционной системе счисления с основой  записывают как последовательность цифр системы , разделённых запятой на целую и дробную части. Если буквы  обозначают цифры системы, то последовательность цифр означает число .

Арифметические действия над числами в любой позиции системы счисления выполняются по тем же правилам, что и в десятичной системе. Однако, при выполнении действий над числами системы, необходимо пользоваться таблицами сложения и умножения этой системы.

Чтобы различать в какой системе счисления записано то или другое число, договоримся обозначать через  число х, записанное в системе счисления .

Рассмотрим наиболее внедрённые в ЭВМ системы счисления.

Двоичная система счисления

Эта система счисления использует две цифры 0, 1, которые обозначают числа ноль и единицу соответственно. Основой этой системы является число два.

Ниже дано изображения некоторых чисел в двоичной системе счисления:

 

При добавлении двух чисел, записанных в двоичной системе счисления, следует пользоваться таблицей сложения:

Таблица умножения в двоичной системе счисления также очень простая:

Примеры

Восьмеричная система счисления

Эта система счисления использует цифры 0, 1, 2, 3, 4, 5, 6, 7 для обозначения последовательных чисел от нуля до семи включительно. Основой этой системы является число 8. Запись произвольного числа в этой системе основывается на его разложении по степеням числа восемь с указанными выше коэффициентами.

Запишем некоторые числа в восьмеричной системе счисления:

Восьмеричные таблицы сложения и умножения имеют вид:

Примеры

Шестнадцатеричная система счисления

Эта система счисления использует шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, которые обозначают последовательно целые числа, начиная с нуля заканчивая числом «пятнадцать». Основой этой системы счисления является число шестнадцать. 

Запишем некоторые числа в шестнадцатеричной системе счисления:

Примеры

Переведение чисел из одной системы в другую

При решении задач на ЭВМ начальные данные, как правило, задаются в десятичной системе счисления, в той же системе необходимо получить результат. Однако почти все машины работают не в десятичной системе, а в какой-нибудь другой, например в двоичной. Поэтому возникает необходимость переведения чисел из одной системы в другую. При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только системами счисления с неотъемлемой базой. Поскольку переведение отрицательных чисел сводится к переводу абсолютных величин и приписыванием им знака минус, то достаточно рассмотреть перевод положительных чисел.

Перевод чисел системы в систему  с помощью арифметики системы .

Такой перевод будем обозначать символами .

Для того, чтобы число , записанное в системе . 

перевести в систему , пользуясь арифметикой системы , необходимо:

а) записать число  в виде:

б) заменить основу 10 и все цифры  системы  их изображениями в системе ;

в) сделать вычисления, пользуясь арифметикой системы .

Примеры:

Проведя вычисления, пользуясь арифметикой десятичной системы счисления, получаем число 22,75₁₀.

Следовательно,

10110,11₂  = 22,75₁₀.

б) Перевести число 27,5₁₀ из десятичной системы счисления в двоичную 

Поскольку

то, заменив основу 10 и цифры 2, 7, 5 их изображением в двоичной системе счисления, получаем:  

Сделав вычисления, пользуясь арифметикой двоичной системы счисления, получим число .

Следовательно, 

в) Перевести число 634,52₈ из восьмеричной системы счисления в десятичную (8 → 10(10)).

Подав это число в виде

и заменив основу 10 — числом 8 (цифры 6, 3, 4, 5, 2 имеют тот же вид в десятичной системе счисления) получаем:

Сделав вычисления, пользуясь арифметикой десятичной системы счисления, получаем число 412,93750₁₀.

Следовательно, 634,52_{8 =} 412,93750_10.

г) Перевести число 98,6₁₀ из десятичной системы счисления в восьмеричную (10 →8(8)).

Представив это число в виде 

и заменив основу числа 10 и цифры 9, 8, 6 их видом в восьмеричной системе счисления, получим:

Сделав вычисления, руководствуясь арифметикой восьмеричной системы счисления получим число 142,4₈. Следовательно, 98,6₁₀ = 142,4₈.

Перевод чисел системы в систему с помощью арифметики системы

Перевод чисел системы в систему  с помощью арифметики системы .

Такой перевод будем обозначать символами . Поскольку для перевода любого числа достаточно уметь переводить его дробную и целую части, то можно рассмотреть эти оба случая отдельно.

Перевод целых чисел

Пусть целое число , записанное в системе , необходимо перевести в систему . Поскольку  — целое число, то его вид в системе  будет таким:

то есть 

где цифры системы , которые необходимо определить, а 10 — основа системы .

Заменим цифры  и основу 10 системы  их видом в системе . Пусть является изображением цифры  изображением основы системы  в системе .

Тогда 

Разделив обе части полученного равенства на , получим остаток  и частное 

Если теперь частное   разделить на , то получим остаток  и частное

Повторяя этот процесс  раз, мы последовательно найдём все числа , причём последнее частное  Деление выполняем, пользуясь арифметикой системы .

Таким образом, при последовательном делении числа и частных, которые получаем при делении, на основу системы, записанную в системе, то есть на , получим в виде остатков от деления цифры, необходимое для изображения числа  в системе , записанные в системе . Последовательное деление производится до тех пор, пока не одержим частное, меньше чем . Это последнее частное даст нам цифру числа , записанную в системе. При делении пользуются арифметикой системы .

Примеры

а) Перевести число 65₁₀ из десятичной системы счисления в двоичную (10 → 2(10)).

и десятичные цифры 0, 1 имеют тоже самое изображение в двоичной системе счисления, то 65₁₀ = 1000001₂

б) Перевести число 325₁₀ из десятичной системы счисления в восьмеричную (10 → 8(10)).

и десятичные цифры 5, 0 имеют тоже самое изображение в восьмеричной системе счисления, то 325₁₀ = 505₈.

в) Перевести число 3060₁₀ из десятичной системы в шестнадцатеричную (10→16(10)).

Поскольку: 

а десятичные цифры 15, 11 изображаются в шестнадцатеричной системе счисления как F и B, 3060₁₀ = BF4₁₆.

г) Перевести число 111011₂ из двоичной системы счисления в десятичную (2→10(2)).

Пользуясь арифметикой двоичной системы счисления, получим: 

Двоичные числа 101 и 1001 в десятичной системе счисления имеют изображение 5 и 9 соответственно, 111011₂ = 59₁₀.

Переведение правильных дробей

Пусть D — правильная дробь, записанная в системе P. Допустим, что необходимо перевести дробь в систему . Пусть изображение D в системе  найдём и она имеет изображение 

то есть 

Умножим две части полученного равенства на . Получим число, целая часть которого  и дробная часть 

Умножим  на , получим число, целая часть которого  и дробная 

Повторяя умножение необходимое нам количество раз, мы найдём одну за одной цифры, необходимые нам для изображения числа D в системе . При умножении пользуемся арифметикой системы P.

Таким образом, при последовательном умножении числа D и дробных частей произведения, которые получаются при умножении на основу , записанную в системе P, то есть на , получим в виде целых частей произведений цифры, необходимые для изображения числа D в системе . Умножение выполняем, пользуясь арифметикой системы P.

Примеры:

а) Перевести число 0,5625₁₀ из десятичной системы исчисления в восьмеричную (10→8(10)).

Поскольку: 

и десятичная цифра 4 имеет то же самое изображение в восьмеричной системе счисления, то 0,5625₁₀ = 0,44₈.

б) Перевести число 0,375₁₀ из десятичной системы исчисления в двоичную (10→2(10)).

Поскольку:

и десятичные цифры 0, 1 имеют то же самое изображение в двоичной системе счисления, то 0,375₁₀ = 0,0012.

в) Перевести число 0,5B4₁₆  из шестнадцатеричной системы исчисления в десятичную (16→10(16)).

Поскольку:

и шестнадцатеричные цифры 5, 5, 5, 6, 0, 1, 2 имеют то же самое изображение в десятичной системе счисления, то 0,5B4₁₆ = 0,3569015625₁₀.

Замечание: Удобнее всего, при переводе чисел из системы счисления P в систему , пользоваться арифметикой системы P, если 

Перевод чисел системы  в систему  и наоборот, если .

Пусть , где  целые положительные числа. В этом случае общие правила перевода значительно упрощаются.

Для того, чтобы перевести число системы  в систему  при , достаточно каждую цифру этого числа заменить соответствующим -разрядным числом в системе .

Для того, чтобы перевести число системы  в систему  при , достаточно, двигаясь от запятой влево и вправо, разбить все цифры числа на группы по  цифр в каждой (крайние группы дополняются нулями, если это необходимо) и каждую группу заменить соответствующей цифрой системы .

Примеры:

Трёхразрядное двоичное число, которое соответствует определённой восьмеричной цифре, называется триадой. Соответствие между восьмеричными цифрами и триадами такое:

Системы счисления и простейшие числовые коды

Каждый
человек в повседневной деятельности
сталкивается с вычислениями (счетом).
Однако, получив, например, в результате
вычисления число 1234,56, многие и не
подозревают, что пользовались десятичной
системой счисления, а само это число
есть сокращенная запись полинома 1
^. 10³
+ 2 ^.
10²
+ 3 ^.
10¹
+ 4 ^.
10⁰
+ 5 ^.
10^-1
+ 6 ^.
10^-2.

Число
— это действительная величина в
определенной системе счисления,
выражающая количество однородных
объектов. Системой
счисления называется
совокупность правил записи любых чисел
ограниченным количеством символов,
называемых цифрами, позволяющая
установить взаимнооднозначное
соответствие между любым числом и его
представлением и наименованием. Цифра
— это
символ, изображающий конкретное число.
Разрядом
числа называется позиция цифры в
изображении числа. Основанием
или базой
(p)
системы счисления называется количество
различных цифр, применяемых для написания
числа: 0,
1,…, p
– 1.

Система
счисления называется позиционной,
если количество, определяемое каждой
цифрой, входящей в запись числа, зависит
от ее положения (позиции) в ряду цифр,
изображающих это число. Число, на которое
умножается цифра данного разряда, чтобы
получить это количество, называется
весом
разряда. Среди позиционных систем особое
значение имеют системы счисления, в
которых веса отдельных разрядов
представляют собой геометрическую
прогрессию со знаменателем, равным
основанию системы счисления p.
В этом случае говорят о системах счисления
с естественным
порядком весов.
Например, разряды десятичного числа
1234,56 имеют веса 10³
= 1000; 10²
= 100; 10¹
= 10; 10⁰
= 1; 10^-1
= 0,1; 10^-2
= 0,01. Существуют системы счисления с
искуственным порядком весов.
Позиционные системы счисления с общим
основанием для всех разрядов называются
однородными.
Они характеризуются тем, что цифры во
всех разрядах используются из одного
и того же множества 0,
1,…, p
– 1. Наибольшее
распространение получили позиционные
однородные системы
счисления, для которых можно сформулировать
три важные характеристики:

• количество
  используемых цифр равно основанию
  системы счисления;

• наибольшая
  цифра на единицу меньше основания;

• каждая
  цифра в числе умножается на основание
  в степени, значение которой определяется
  позицией цифры в числе.

Широко
распространенная десятичная система
счисления p
= 10 (по-видимому
ее основой явились 10 пальцев на руках
человека) изобретена в Индии около 400
-х г. н. э. В 800-х г. н. э. она получила широкое
распространение в арабских странах,
откуда приблизительно в начале XIII века
попала в Европу, поэтому цифры десятичной
системы счисления 0, 1, … , 9 традиционно
(но ошибочно) называют арабскими.

Если
позиционная система для каждой цифры
имеет отдельный символ, то она называется
системой
с непосредственным представлением
чисел.
Таковой является, например, десятичная
система счисления. Позиционная система
называется системой
с кодированным представлением чисел,
когда количество символов меньше, чем
количество цифр, а каждая цифра кодируется
определенной комбинацией из нескольких
символов. Таковой является, например,
двоично-десятичная система счисления
(0 = 0000, 1 = 0001, … , 9 = 1001), в которой десять
цифр, но только два символа.

До
изобретения позиционных систем счисления
использовались непозиционные
системы счисления,
в которых значение цифры не зависит от
ее положения в ряду цифр, изображающих
число. Среди них наиболее известны
римская
система счисления,
унитарная,
а также современная система
счисления в остаточных классах.

В
римской системе счисления используют
следующие цифры: I = 1, V = 5, X = 10, L =
50, C = 100, D =
500, M = 1000. В этой системе число 1997 будет
записано как MCMXCVII. Римские цифры в
настоящее время в основном используются
для обозначения юбилейных дат, нумерации
в книгах страниц введения, глав, строф
в стихотворениях, на циферблатах часов
и т. п.

В
унитарной системе число представляется
общей совокупностью однородных объектов
(палочек, черточек, импульсов и т. п.)
Такая система используется в
электромеханических городских часах,
в аналого-цифровых преобразователях и
др.

В
системе остаточных классов числа
представляются своими остатками от
деления на выбранную систему взаимно
простых оснований [1] .

Достоинства
и недостатки различных систем счисления,
используемых при технической реализации
цифровых устройств, могут быть выявлены,
исходя из следующих практически важных
требований:

• возможность
  представления любого числа в заданном
  диапазоне;

• единственность
  представления, когда любой числовой
  код соответствует только одному числу;

• простота
  выполнения арифметических и логических
  операций над числами.

Главным
преимуществом
позиционных
систем
счисления
по сравнению с непозиционными является
удобство представления чисел и простота
выполнения арифметических и логических
операций.

Недостатком
позиционных систем счисления
является наличие межразрядных связей
(переносов и заемов) при выполнении
арифметических операций над числами,
то есть невозможность выполнения
арифметических операций как поразрядных
(когда результат операции не зависит
от ее результата в остальных разрядах).

Недостатками
непозиционных систем счисления являются
неудобство выполнения арифметических
и логических операций и трудности при
записи и восприятии больших чисел.

В
системе остаточных классов все операции
могут выполняться параллельно над
цифрами каждого разряда в отдельности.
Однако ей присущ и ряд недостатков:
ограниченность действия этой системы
полем целых положительных чисел,
трудность определения соотношения
чисел по величине, определения выхода
результата операции из диапазона,
отсутствие наглядной связи между числом
и его представлением, не позволяющем
оценить величину числа без перевода
его в позиционную систему счисления,
трудность выполнения операций деления
и округления и др.

Несмотря
на то, что в практике ручных вычислительных
работ наибольшее распространение
получила десятичная позиционная
однородная система счисления, она не
является удобной для использования в
цифровых устройствах, в частности в
электронных вычислительных машинах
(ЭВМ). Это связано прежде всего с трудностью
технической реализации десяти различных
уровней сигналов при одновременном
обеспечении высокой помехоустойчивости.

Минимальное
количество цифр, которое может быть
принято в позиционной системе счисления,
равно двум (0
и 1).
Именно двоичная система счисления и
нашла самое широкое применение в цифровых
устройствах и ЭВМ в силу следующих
очевидных преимуществ:

• простота
  технической реализации двух сигналов,
  кодирующих числа 0
  и 1,
  которые в большинстве случаев отличаются
  друг от друга не столько количественно,
  сколько качественно;

• обеспечиваются
  высокие помехоустойчивость, надежность
  и быстродействие;

• легко
  выполняются арифметические и логические
  операции, что значительно упрощает
  схемотехнику арифметических и логических
  узлов, а их анализ и синтез просто
  выполняется на основе аппарата булевой
  алгебры и теории конечных автоматов;

• экономичность.

Эти
преимущества полностью перекрывают
такие недостатки двоичной (а также
двоично-кодированной) системы счисления,
как:

• длинная
  запись числа;

• необходимость
  преобразования входных и выходных
  данных из привычной человеку десятичной
  системы счисления в двоичную;

• трудность
  чтения и восприятия чисел.

Сокращение
длины записи двоичных чисел легко
обеспечивается применением систем
счисления с кратным основанием. Если
для оснований систем счисления p₁
и p₂
справедливо соотношение p₂
= p₁^k,
где k
– цeлое положительное число, то такие
системы называются системами
счисления с кратными основаниями.
Примером таких систем являются двоичная,
восьмеричная и шестнадцатеричная
системы (2³
= 8; 2⁴=16).
Хорошее знание этих систем счисления
является обязательным для каждого, кто
решил серьезно заняться изучением
цифровой техники. Восьмеричная и
шестнадцатеричная системы счисления
в основном используются как вспомогательные
для сокращения трудоемкости ручной
обработки кодов чисел, команд и т. п. при
подготовке программ, чтобы избежать
чтения и записи громоздких двоичных
чисел.

Хотя
перевод чисел из десятичной системы
счисления в двоичную и обратно в ЭВМ
осуществляется автоматически (аппаратно
или программно), надо знать и ручные
методы таких переводов. Наиболее
распространены два метода перевода
чисел из одной системы счисления в
другую: табличный
и
расчетный.

При
первом методе используются специальные
таблицы соответствия чисел в различных
системах счисления. Этот метод громоздкий,
но применим как к позиционным, так и к
непозиционным системам. Такие таблицы
очень удобны на начальном этапе
ознакомления с новой системой. Например,
полезно запомнить четырехразрядные
двоичные эквиваленты десятичных цифр
(см. табл.1).

Расчетный
метод универсальнее и удобнее, но
применим он только к позиционным системам
счисления. В практике встречаются три
случая перевода: целых чисел, правильных
дробей и неправильных дробей. Правильной
дробью называется
дробь, у которой числитель меньше
знаменателя, то есть число, меньшее
единицы (например: 0,6; 3/7;
0,33…).
Неправильной
дробью называется
дробь, у которой числитель равен или
больше знаменателя, то есть число большее
или равное единицы (например:
3/3;
7/3;
1,23;
15,36).

Таблица 1.
Десятичное число	Двоичное число	Восьмеричное число	Шестнадцатиричное число
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Алгоритмы
перевода чисел в другую систему счисления,
использующие арифметику исходной
системы счисления (p).

Правило
перевода целых чисел.
Будем обозначать целое число X
по основанию p
как
X_(p).
Если основание p
не указывается,
то, по умолчанию, считают, что число
представлено в десятичной системе
счисления.

Для
перевода целого числа
X_(p)
в систему счисления с основанием q
необходимо
по правилам арифметики исходной p-системы
делить данное число X_(p)
на новое
основание q_(p)
до получения целого остатка, меньшего
q.
Полученное частное необходимо снова
делить на основание q
до получения
целого остатка, меньшего q,
и т. д. до тех пор, пока последнее частное
будет меньше нового основания q.
Число X_(q)
в системе счисления с основанием q
представляется последовательностью
остатков деления в порядке, обратном
их получения, причем старшую цифру в
числе X_(q)
дает
последний остаток (метод
последовательного деления).
Поскольку используется арифметика
исходной системы, то таким способом
удобно переводить из десятичной системы
счисления в другие системы.

Пример.
Перевести число 181 в систему счисления
с основанием 2.

_181	2
180	_90	2
1	90	_45	2
	0	44	_22	2
	1	22	_11	2
	0	10	_5	2
	1	4	_2	2
	1	2	1	Старший разряд числа
	0		в двоичной системе

Ответ:
181 = 10110101₍₂₎.

Правило
перевода правильной дроби.
X_(p)X_(q).
Перевод
правильной дроби X_(p)
в систему
счисления с основанием q
заключается
в последовательном умножении этой дроби
на новое основание q_(p)
(по правилам исходной p—системы),
причем перемножению подвергаются только
дробные части. Дробь X_(q)
в системе счисления с новым основанием
представляется в виде последовательности
целых частей произведений в порядке их
получения, причем старший разряд является
целой частью первого произведения. Если
требуемая точность перевода есть q^-k
, то число указанных последовательных
произведений равно k
(метод
последовательного умножения).

Пример.
Перевести
десятичную дробь 0,789 в двоичную с
точностью 2^-6.
Заданное число умножаем последовательно
6
раз на 2:

Ответ:
0,789 = 0,110010₍₂₎.

Правило
перевода неправильной дроби.
Для чисел, имеющих как целую, так и
дробную части, перевод из одной системы
счисления в другую осуществляется
отдельно для целой и дробной части по
правилам, указанным выше.

Алгоритмы
перевода чисел в другую систему счисления,
использующие арифметику новой системы
счисления (q).

Для
перевода чисел в десятичную систему из
любой другой удобно пользоваться
арифметикой десятичной системы. В этих
случаях используются алгоритмы перевода
целых и дробных чисел, представленных
в виде полинома, причем веса разрядов
и все цифры надо представлять в новой
системе счисления и все арифметические
операции выполнять по правилам новой
системы счисления.

Пример.
10110101₍₂₎
= 1^.2⁷
+ 0^.2⁶
+ 1^.2⁵
+ 1^.2⁴
+ 0^.2³
+ 1^.2²
+ 0^.2¹
+ 1^.2⁰
= 181.
0,110010₍₂₎
= 1^.2^-1
+ 1^.
2^-2
+ 0^.2^-3
+ 0^.2^-4
+ 1^.2^-5
+ 0^.2^-6
= 0,78125.

Перевод
чисел в системах счисления с кратными
основаниями.

Перевод чисел
в системах с кратными основаниями не
требует выполнения арифметических
действий и выполняется с использованием
табличной шифрации (см. табл. 1).

Первый
случай.
X_(p)X_(q);
p
= q^k.
Каждая
цифра числа X_(p)
заменяется своим k—разрядным
представлением в q—системе.

Пример.
p
= 8; q
= 2; k
= 3. Исходное число: 123,4566₍₈₎.

1	2	3,	4	5	6	6
001	010	011,	100	101	110	110

Каждая
восьмеричная цифра заменена двоичной
триадой (см.
выделенную штриховой линией часть табл.
1).

Примечание:
незначащие нули в старших и младших
разрядах двоичного числа можно опустить.
Ответ: 1010011,10010111011₍₂₎.

Пример.
p = 16; q
= 2; k
= 4. Исходное
число: 79A,2C₍₁₆₎.

7	9	А,	2	С
0111	1001	1010,	0010	1100

Каждая
шестнадцатеричная цифра заменена
двоичной
тетрадой.

Ответ:
11110011010,001011₍₂₎.
Здесь также опущены незначащие нули в
младших и старших разрядах при записи
двоичного числа.

Второй
случай.
X_(p)
X_(q);
q
= p^k.
Число в
исходной p—системе
разбивается на группы по k
разрядов
вправо и влево от запятой, причем в
неполные группы добавляются нули (справа
— для дробной части, слева — для целой).
Каждая группа из k
цифр p—системы
заменяется одним эквивалентным ей
символом q—системы.

Пример.
Перевести двоичное число 1010011,10010111011
в восьмеричную систему.

001	010	011,	100	101	110	110
1	2	3,	4	5	6	6

Ответ:
123,4566₍₈₎.

Пример.
Перевести двоичное число 11110011010,001011
в
шестнадцатеричную систему.

0111	1001	1010,	0010	1100
7	9	A ,	2	C

Ответ:
79A,2C₍₁₆₎.

Приведенные
примеры показывают, что представление
двоичного числа в восьмеричной
(шестнадцатеричной) системе счисления
сокращает длину записи в три (четыре)
раза.

Рассмотрение дальнейшего материала
будет вестись для двоичных чисел, так
как в большинстве случаев в цифровых
устройствах используется двоичная
система счисления.

Разрядность
операционных устройств, регистров и
ячеек памяти фиксирована, что ограничивает
как диапазон представления, так и
точность чисел. Количество разрядов
ограничено длиной разрядной
сетки, под
которой понимается фиксированная
совокупность двоичных разрядов,
предназначенных для приема, обработки,
хранения и выдачи данных
в виде
двоичных кодов. Данные — это обобщающее
понятие для содержимого разрядной
сетки, в качестве которого могут быть:

1. числа
   без знака;

2. числа
   со знаком, представленные в различных
   формах и форматах;

3. алфавитно-цифровые
   (текстовые) коды символов;

4. системная
   информация о состоянии аппаратных и
   программных средств, представленная
   в регистре состояния (перенос,
   переполнение, знак числа, нулевое
   состояние, режим работы и т.д.);

5. команды;

6. адреса;

7. константы;

8. маски;

9. смещение
   и т.п.

В
каждом такте машинного времени все
разряды сетки обрабатываются одновременно.
Доступность для пользователя данных,
обрабатываемых в разрядной сетке,
определяет два вида кодов: параллельный,
когда в каждый момент времени все разряды
сетки доступны, и последовательный,
когда в каждый момент времени доступен
только либо младший, либо старший разряды
сетки. Говорят, что данные, представленные
параллельным кодом, доступны за один
такт, а данные, представленные
последовательным кодом, доступны за n
тактов, где n
— разрядность сетки. Если разрядность
данных превышает длину сетки, то их
обработка ведется по частям.

Рассматривая
данные как
целые числа без знака,
(так называемый натуральный
код) (см.
рис. 1, а)
, можно ввести следующие важные параметры
разрядной сетки:

• емкость
  сетки М
  — это максимальное количество различных
  чисел, представимых в ней (для двоичных
  чисел М = 2ⁿ);

• максимальное
  число N_max,
  представимое в ней (для двоичных чисел
  N_max
  = 2ⁿ
  –1);

• минимальное
  число N_min
  = 1;

• динамический
  диапазон разрядной
  сетки d = (N_max)/(N_min)
  = 2ⁿ
  –
  1.

Очевидно,
что относительная
точность
представления целого числа зависит от
его абсолютной величины и может меняться
в широких пределах.

Р

а) Число без
знака б) Прямой код

128 64 32 16 8 4 2 1

нет
64 32 16 8 4 2 1

	b7	b6	b5	b4	b3	b2	b1	b0		+122	0	1	1	1	1	0	1	0
122	0	1	1	1	1	0	1	0		–122	1	1	1	1	1	0	1	0

в) Обратный
код г) Дополнительный код

–127
64 32 16 8 4 2 1
–128
64 32 16 8 4 2 1

+122	0	1	1	1	1	0	1	0		+122	0	1	1	1	1	0	1	0
–122	1	0	0	0	0	1	0	1		–122	1	0	0	0	0	1	1	0

д)
Смещенный код с “+0” е) Смещенный
код с “–0”

64
32 16 8 4 2 1
64
32 16 8 4 2 1

+122	1	1	1	1	1	0	1	0		+122	1	1	1	1	1	0	0	1
–122	0	0	0	0	0	1	1	0		–122	0	0	0	0	0	1	0	1

ис. 1. Числовые
коды в восьмиразрядной сетке,

где
=–(1–
b₇)128;
=–(1–
b₇)128+1.

Эти
же числовые параметры справедливы и
для представления чисел
со знаком в естественной форме (с
фиксированной запятой (точкой)).
Эта форма представления чисел предполагает,
что положение запятой, отделяющей целую
часть числа от дробной, фиксировано в
разрядной сетке (запятая подразумевается,
но аппаратно не реализуется).

Для
представления знака выделяется
специальный знаковый разряд сетки,
причем обычно это левый (старший) ее
разряд. Используются два основных
способа расположения фиксированной
запятой: перед старшим разрядом — для
правильных дробей или после младшего
разряда — для целых чисел.

Возможность
построения сравнительно несложных
операционных устройств с высоким
быстродействием — одно из важных свойств
представления чисел в форме с фиксированной
запятой. Представление чисел в этой
форме используется как основное и
единственное лишь в специализированных
ЭВМ и сравнительно небольших по своим
вычислительным возможностям машинах,
применяемых в системах передачи данных,
для управления технологическими
процессами и обработки измерительной
информации в реальном масштабе времени.

Наибольшее
распространение получило представление
целых чисел со знаком как целых, что и
используется в дальнейшем изложении
материала. Выбор числовых кодов для
представления целых чисел со знаком
осуществляется с учетом следующих
факторов: общее количество положительных
и отрицательных чисел не может превышать
емкость разрядной сетки; целесообразно,
чтобы количество положительных и
отрицательных чисел было бы одинаковым;
для выполнения основных арифметических
и логических операций над числовыми
кодами желательно использовать одну и
ту же аппаратуру.

Число
со знаком изображается знаком числа
(“+” — для положительных чисел, “–”
— для отрицательных) и модулем числа.
Полезно помнить также, что знаки “+” и
“–” используются и для обозначения
арифметических операций “сложение”
и “вычитание” соответственно.

Поскольку
аппаратура ЭВМ выполняется на элементах
булевой алгебры и для представления
двоичных состояний применяют символы
0
и 1,
то эти же символы следует использовать
и для обозначения знака числа.

Конкретную
иллюстрацию примеров различных числовых
кодов будем вести для разрядной сетки
с n =
8. Сетку с
такой длиной называют байтом.
Байт является основной единицей для
двоичного кодирования текстовой
(литерной) информации не только в ЭВМ,
но и в системах передачи данных, а также
является наименьшей адресуемой единицей
данных в большинстве ЭВМ. Отдельные
разряды сетки обозначим индексированной
буквой b_i,
i
= 0,…, n-1
(bit
— binary
digit),
причем 2ⁱ
будет являться весом двоичного разряда.
Полезно помнить, что число без знака
(см. рис. 1, а)
имеет положительные веса 2ⁱ
во всех разрядах сетки. Для сетки с n
= 8 имеем: М
= 256₍₁₀₎
= 100000000₍₂₎;
N_max
= 255₍₁₀₎
= 11111111₍₂₎.
B дальнейшем индексы 10 и 2 опустим из-за
очевидности записи чисел. Обратите
также внимание, что для записи ‘М’
в виде двоичного числа требуется девять
разрядов, то есть такое число нельзя
представить в 8-ми разрядной сетке
(емкость разрядной сетки равна весу
разряда, следующего за ее старшим
разрядом).

Кодируя
разряд b₇
символом 0
для знака “+” и символом 1
для знака ”–”,
а в разрядах b₆,…,b₀
помещая модуль числа, получим представление
чисел со знаком в прямом
коде (см.
рис. 1, б).
Важной особенностью прямого кода
является то, что цифру знакового разряда
и цифровую часть числа нельзя рассматривать
как единое целое, так как кодируется
только знак числа. Максимальное
положительное число равно +127 = 01111111,
то есть (2^n–1
–1).
Минимальное (максимальное по модулю)
отрицательное число равно –127
= 11111111.
Нуль имеет два представления: положительный
нуль +0=
00000000
и отрицательный нуль –0
= 10000000.

Достоинства
прямого кода:
цифровые разряды содержат модуль
представляемых чисел, что обеспечивает
наглядность их считывания в этом коде;
просто осуществляется сложение чисел,
имеющих одинаковые знаки, а также деление
и умножение, когда операции со знаками
и модулями ведутся раздельно; количество
положительных и отрицательных чисел
одинаково.

Недостатки
прямого кода:
сложно
складывать и вычитать числа с разными
знаками, так как, например при сложении,
приходится определять большее по модулю
число, производить вычитание чисел и
присваивать результату знак большего
по модулю числа; нуль имеет два
представления.

Прямой
код широко используется для хранения
чисел в памяти, в устройствах ввода-вывода,
в цифроаналоговых и аналогоцифровых
преобразователях (ЦАП и АЦП).

В
общем случае представление прямого
двоичного кода в n—разрядной
сетке определяется как

где
А — величина, равная весу старшего разряда
сетки (А = 2^n–1
для целых чисел и А =1
для правильных дробей), а |Х|
≤
А–1
= 2^n–1
–1.

Рассмотрим
теперь следующий пример. Пусть требуется
вычислить разность двух чисел 126 = 1111110
(уменьшаемое) и 122 = 1111010
(вычитаемое). Здесь двоичные числа
представлены пока как семиразрядные,
так как разряд b₇
кодирует
знак числа. Очевидно, что модуль
положительного и отрицательного числа
не может быть больше 2^n–1
–1,
что при n =
8 дает 127, а как кодируется знак будет
ясно чуть ниже.

Разность
указанных чисел можно представить как

126
–
122 = 126 + (255 — 122) — 255,

где
255 = 11111111 = N_max
для n
= 8.

Выражение
в скобках (255 — 122) называется дополнением
отрицательного числа –122
до N_max,
а численное значение разности 133 =
10000101
обратным
кодом
отрицательного двоичного числа
–122₍₁₀₎
(см. рис. 1, в).
Наличие 1
в знаковом разряде обратного кода
отрицательного числа говорит о том, что
знак “–”
кодируется единицей, а “+” нулем. Итак,
обратный код отрицательного двоичного
числа представляет собой дополнение
исходного числа до наибольшего числа
без знака, размещаемого в разрядной
сетке, а получение обратного кода
отрицательного числа сводится к
поразрядному
инвертированию
n—разрядного
двоичного кода модуля этого числа (в
том числе и знакового разряда). Отсюда,
в частности, ясно происхождение термина
“обратный”, то есть инверсный. Проведем
теперь вычисление 126 + 133 — 255, представив
числа в двоичных кодах:

Так
как выделенная единица результата
первого суммирования выпадает из 8-ми
разрядной сетки, то она уменьшает
полученный результат на 256,
(вес девятого разряда), а нам надо было
уменьшить результат на 255,
следовательно для получения правильного
результата нужно к первой сумме добавить
единицу (это делается с помощью так
называемого циклического
переноса
аппаратными средствами, когда перенос
в несуществующий девятый разряд
прибавляется в младший разряд сумматора
чисел). Наличие нуля в знаковом разряде
суммы говорит о том, что результат
положительный, а сама разность равна
4.

Рассмотренный
пример показывает, что вычитание числа
(или сложение с отрицательным числом)
можно заменить сложением с обратным
кодом отрицательного числа с прибавлением
в младший разряд результата единицы.

Достоинства
обратного кода:
простота его получения; легко осуществляется
сложение чисел с разными знаками;
количество отрицательных и положительных
чисел одинаково; так как для отрицательных
чисел здесь кодируются и знак числа, и
его модуль, то при выполнении арифметических
операций сложения и вычитания цифру
знакового разряда и цифровую часть
числа можно рассматривать как единое
целое и обращаться со знаковым разрядом
так же, как и с разрядами цифровой части
числа. Причем веса цифровых разрядов
положительные и равны 2ⁱ,
а вес знакового разряда отрицательный
и равен 2^n–1
–1
(см. рис.1, в).

Недостатки
обратного кода:
нуль имеет два представления: положительный
+0
= 00000000
и отрицательный –0
= 11111111;
требуется аппаратная реализация
циклического переноса.

В
общем случае представление обратного
двоичного кода в n-разрядной
сетке определяется как:

где
В — наибольшее число без знака, размещающееся
вn-разрядной
сетке (В
= 2^n–1
–1
для целых чисел и В = 2 – 2^–(n–1)
для правильных дробей), а |Х|
≤
2^n–1
–1.

Соседние файлы в папке vorob

• #
• #

  17.04.20134.47 Кб20Vorob01.htm

• #

  17.04.201343.77 Кб22VOROB02.HTM

• #
• #
• #
• #
• #
• #
• #
• #

Информатика, 10 класс. Урок № 8.

Тема — Представление чисел в позиционных системах счисления

Урок посвящен теме «Представление чисел в позиционных системах счисления и переводу чисел из одной позиционной системы счисления в другую». В ходе урока школьники научатся различать позиционные и непозиционные системы счисления, узнают о развернутой форме числа. А также научатся переводить числа из одной системы счисления в другую.

Ключевые слова: Системы счисления, позиционная система счисления, непозиционная система счисления, базис системы счисления, схема Горнера, триада, тетрада, «компьютерные» системы счисления, «быстрый» перевод.

Учебник: Босова Л. Л, Босова А. Ю. Информатика 10 класс базовый уровень — БИНОМ Лаборатория знаний 2016 г.

Федерального центра информационных образовательных ресурсов:

http://fcior.edu.ru/

Мы постоянно оперируем числами, ежедневно, не слишком задумываясь о том, что они из себя изначально представляют. 

Счет появился тогда, когда человеку потребовалось информировать своих сородичей о количестве обнаруженных им предметов. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов свидетельствуют о том, что первоначально число предметов отображали равным количеством каких-либо значков:

точки, черточки. Такая система записи чисел называется единичной (унарной), т.к. любое число в ней образуется путем повторения одного знака, символизирующего единицу. Самым простым инструментом счета были пальцы на руках человека

Унарная система — не самый удобный способ записи чисел: при написании больших чисел получается очень длинная запись. С течением времени возникли иные, более удобные и экономичные системы: Вавилонская, Египетская, Славянская, Римская и другие. Рассмотренные записи чисел называются системами счисления.

Система счисления — это способ записи чисел.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемые цифрами.

Алфавит системы счисления — это используемый в ней набор цифр.

Основание системы счисления — это количество цифр в алфавите (мощность алфавита).

Различают непозиционные и позиционные системы счисления.

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения этой цифры в числе.

Примером непозиционной системы, которая сохранилась до наших дней, может служить система Древнего Рима.

Римская система счисления. В качестве цифр использовались большие латинские буквы. А остальные числа записываются комбинациями этих знаков. Число формировалось из цифр, а также с помощью групп: Группа 1-го вида — несколько одинаковых подряд идущих цифр: XX = 20 (не более трёх одинаковых цифр); Группа 2-го вида — разность значений двух цифр, если слева стоит меньшая: СМ = 1000 – 100 = 900 (может стоять только одна цифра). Величина числа суммируется из значений цифр и групп 1-го или 2-го вида.

Позиционные системы счисления.

Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (места, позиции) в записи числа. Основное достоинство любой позиционной системы счисления — возможность записи произвольного числа ограниченным количеством символов. Пример этой системы — привычная нам десятичная система счисления. Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q>1, называемым основанием системы счисления. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр. В q-ичной системе счисления q единиц какого-либо разряда образуют единицу следующего разряда. Последовательность чисел, каждое из которых задает «вес» соответствующего разряда, называется базисом позиционной системы счисления. Представление числа в виде суммы разрядных слагаемых называется развёрнутой формой записи числа в системе счисления с основанием q. Свёрнутой формой представления числа называется его запись в виде:

Свернутой формой записи числа мы пользуемся в повседневной жизни. Развёрнутая форма записи чисел также всем хорошо известна. Ещё в начальной школе дети учат записывать числа в виде суммы разрядных слагаемых. Если представить разряды в виде степеней основания, то получим:

Иногда бывает полезно преобразовывать развернутую форму записи числа так, чтобы избежать возведения основания в степень. Такую формулу представления числа называют схемой Горнера.

В наши дни большой практический интерес представляют двоичная, троичная, восьмеричная и шестнадцатеричная системы счисления. Двоичная система счисления — самая важная для компьютеров. В двоичной системе счисления основание — 2, а алфавит состоит из двух цифр 0 и 1.

Перевод числа, записанного в системе счисления с основанием q, в десятичную систему счисления основан на использовании развёрнутой формы записи чисел.

Алгоритм перевода в 10-ю систему счисления:

1. Записать развёрнутую форму числа.
2. Представить все числа, фигурирующие в развёрнутой форме, в 10-й системе счисления.
3. Вычислить значение полученного выражения.

Перевод в десятичную систему счисления целых двоичных чисел будет значительно проще, если вспомнить и использовать уже знакомую вам таблицу степеней двойки.

Рассмотрим пример:

Для перевода двоичного числа в десятичную систему счисления можно воспользоваться схемой Горнера.

1. Возьмем 1, соответствующую самому старшему разряду числа, и умножим её на 2.
2. Прибавим следующую цифру.
3. Умножим результат на 2.
4. Прибавим следующую цифру.
5. Умножим результат на 2.
6. Прибавим следующую цифру.
7. Умножим результат на 2.

Рассмотрим несколько примеров решения задач.

Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления. Решение: поскольку в записи числа 212_q есть цифра 2, то можно сказать, что q>2. Представим число 212_q в развёрнутой форме и приравняем к 57.

Решим уравнение: это квадратное уравнение, его корни Х₁ = –5,5; Х₂ = 5. Так как основание системы счисления должно быть натуральным числом, то q = 5

Перевод целого десятичного числа в систему счисления с оcнованием q

Для перевода целого десятичного числа в систему счисления с основанием q следует:

1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю.
2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Для перевода целого десятичного числа в двоичную систему счисления можно воспользоваться таблицей степеней двойки. Рассмотрим пример: переведем число 529 в двоичную систему счисления.

Представим число в виде суммы степеней двойки, для этого:

— возьмем максимально возможное значение, не превышающее исходное число (512 < 529);

— найдем разность между исходным числом и этим значением (17);

— выпишем степень двойки, не превышающее эту разность и т. д. Когда исходное число было представлено в виде суммы, мы построили его двоичное представление, записав 1 в разрядах, соответствующих слагаемых, вошедшим в сумму, и 0 – во всех остальных разрядах.

529₁₀ = 512 + 17 = 512 + 16 +1 = 2⁹ + 2^{4 +} 2⁰ = 1000010001₂

Перевод десятичной дроби в систему счисления с основанием q

Для перевода конечной десятичной дроби в систему счисления с основанием q следует:

1. Последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа.
2. Полученные целые части (цифры числа) привести в соответствие алфавиту новой системы счисления.
3. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

При необходимости перевод целого числа А из системы счисления с основанием p в систему счисления с основанием q можно свести к хорошо знакомым действиям в десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления.

Быстрый перевод чисел в компьютерных системах счисления

Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q=2ⁿ) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод. Для этого:

1. Данное двоичное число надо разбить справа налево на группы по n цифр в каждой.
2. Если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2ⁿ.

Рассмотрим перевод целых чисел между двоичной и 16-ной системами счисления

Рассмотрим перевод дробной части между двоичной и восьмеричной системами

Чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2ⁿ, достаточно:

двоичное число разбить слева направо на группы по n цифр в каждой; если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов; рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой.

Итак, сегодня вы узнали, что существуют разные системы счисления: непозиционные и позиционные. Позиционные системы счисления имеют алфавит и основание и его можно представить в развернутом виде. Научились переводить из 10 с.с в любую другую систему счисления. Научились переводить из 2, 8, 16 сс в 10 с.с. Узнали, как быстро можно переводить числа между системами.