Как в трапеции найти угол сад - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти угол в трапеции

Трапеция — это плоский четырехугольник, у которого две противолежащие стороны параллельны. Они называются основаниями трапеции, а две другие стороны — боковыми сторонами трапеции.

Инструкция

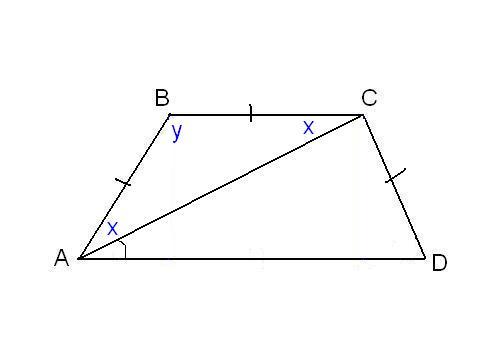
Задача нахождения произвольного угла в трапеции требует достаточного количества дополнительных данных. Рассмотрим пример, в котором известны два угла при основании трапеции. Пусть известны углы ∠BAD и ∠CDA, найдем углы ∠ABC и ∠BCD. Трапеция обладает таким свойством, что сумма углов при каждой боковой стороне равна 180°. Тогда ∠ABC = 180°-∠BAD, а ∠BCD = 180°-∠CDA.

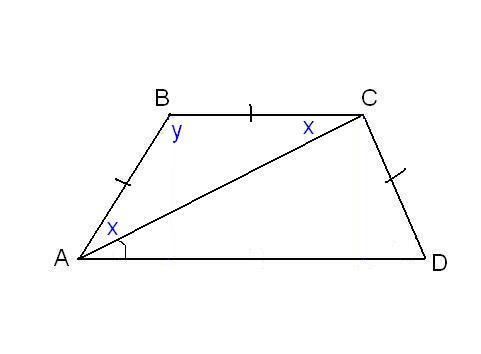
В другой задаче может быть указано равенство сторон трапеции и какие-нибудь дополнительные углы. Например, как на рисунке, может быть известно, что стороны AB, BC и CD равны, а диагональ составляет с нижним основанием угол ∠CAD = α.Рассмотрим треугольник ABC, он равнобедренный, так как AB = BC. Тогда ∠BAC = ∠BCA. Обозначим его x для краткости, а ∠ABC — y. Сумма углов любого треугольника равна 180°, из этого следует, что 2x + y = 180°, тогда y = 180° — 2x. В то же время из свойств трапеции: y + x + α = 180° и следовательно 180° — 2x + x + α = 180°. Таким образом, x = α. Мы нашли два угла трапеции: ∠BAC = 2x = 2α и ∠ABC = y = 180° — 2α.Так как AB = CD по условию, то трапеция равнобокая или равнобедренная. Значит, диагонали равны и равны углы при основаниях. Таким образом, ∠CDA = 2α, а ∠BCD = 180° — 2α.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.

Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.

Угол трапеции при основании через высоту и прилегающую
боковую сторону
Угол трапеции через нижнее основание, боковую сторону и
диагональ
Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону
Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону
Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания
Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону

Угол трапеции при основании через высоту и прилегающую боковую сторону

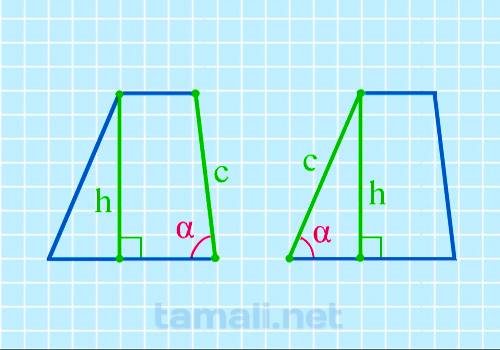
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы

sin α = h/с

где: h — высота трапеции, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.

Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции

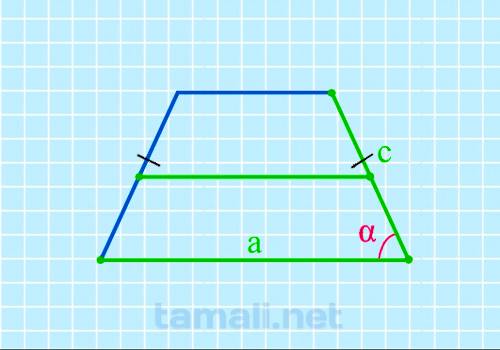
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:

cos α = (2a-2m) / 2c

где а — нижнее основание, m — средняя линия, с — боковая сторона.

Цифр после
запятой:

Результат в:

Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.

Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали

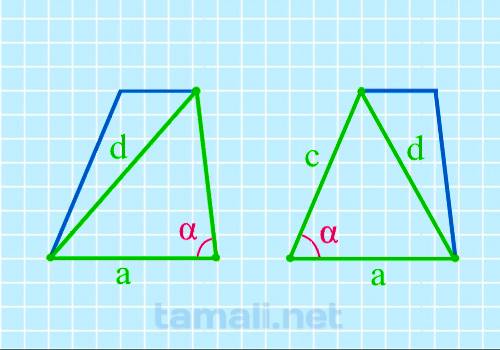
Если известны эти величины, воспользуемся формулой:

cos α= (a²+c²-d²) / 2ac

где а-нижнее основание, d-диагональ, с-боковая сторона.

Цифр после
запятой:

Результат в:

Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.

Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции

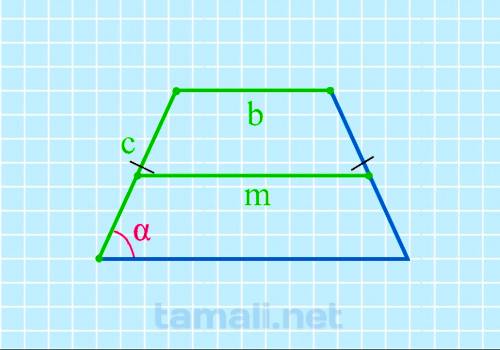
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:

cos α = (2m-2b) / 2c

где m — средняя линия, b — верхнее основание, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции

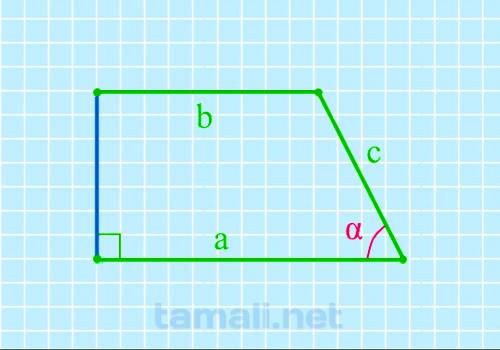
Находится по формуле

cos α = (a — b) / c

где a,b — основания, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º

Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции

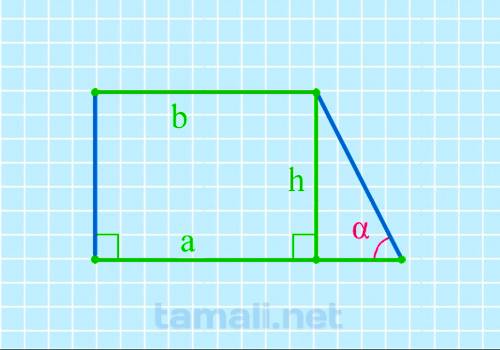
При известных указанных величинах воспользуемся следующей формулой:

tg(α) = h / (a-b)

где h — высота, a,b — верхнее и нижнее основания.

Цифр после
запятой:

Результат в:

Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.

Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.

Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.

Источник

Из треугольника АСД: уголД=60гр., Угол АСД=90гр., отсюда угол САД=30гр.
Так, как АС это биссектриса угла ВАД, то угол ВАД=САД+ВАС=30гр.+30гр.=60гр.
Отсюда можно сделать вывод, что трапецыя АВСД- равнобедренная.
Из треугольника АВС:
Угол ВСА=ВСД-АСД=120гр.-90гр.=30гр.; уголВАС=углуВСА, отсюда треугольникАВС-равнобедренный.
Отсюда АВ=ВС=СД.
Проведем высоты ВЛ и СМ.
Треугольник АВЛ = треугольнику СМД, за тремя сторонами равными.
Так, как МД лежит против угла 30гр., в прямоугольном треугольнике, то 2МД=ДС.
Пускай МД=АЛ=х, ЛМ=ВС=АВ=СД=2х. Так, как сума всех этих сторон равна 35 см., то имеем уравнение:
2х+2х+2х+2х+х+х=35
10х=35
Х=35/10
Х=3,5
Значит АВ=2х=2*3,5=7см.
Ответ:7см.
это проверенныый ответ

Источник

Какими могут быть углы трапеции?

рисунок 1

Как и все другие четырехугольники и многоугольники, которые изучаются в школьном курсе, трапеция — выпуклый четырехугольник. Поэтому сумма углов трапеции равна 360º (речь идет о внутренних углах).

То есть для трапеции ABCD ∠A+∠B+∠C+∠D=360º.

Поскольку основания трапеции лежат на параллельных прямых, сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусам.

Для трапеции ABCD (рисунок 1)

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),

∠C+∠D=180º (как внутренние односторонние при AD ∥ BC и секущей CD).

Следовательно, если один из углов, прилежащих к одной боковой стороне, острый, то другой — тупой. Если один из этих углов прямой, другой — тоже прямой.

Суммы углов, прилежащих к боковым сторонам трапеции, равны:

∠A+∠B=∠C+∠D

Могут ли углы трапеции, взятые в последовательном порядке, относиться как

1) 7:3:5:2?

Нет, поскольку 7k+3k≠5k+2k и 7K+2k≠3k+5k.

2) 5:4:6:3?

5k+4k=6k+3k, следовательно, углы трапеции могут быть пропорциональны этим числам.

На рисунке 1 углы прилежащие к основанию AD, оба острые, углы, прилежащие к основанию BC, оба тупые. В паре противолежащих углов ∠A и ∠С, ∠B и ∠D один — острый, другой — тупой.

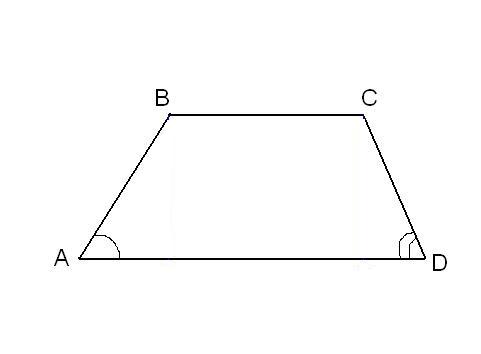
Существует ли трапеция, у которой два противолежащих угла обо тупые или оба острые?

рисунок 2

Да, такая трапеция существует.

Например, трапеция, изображенная на рисунке 2.

Существует ли трапеция, у которой два противоположных угла оба прямые? Противоположные углы равны?

Нет, такой трапеции не существует (противоположные углы равны у параллелограмма).

Источник

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Углы при параллельных прямых и секущей

Пусть прямая пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна $180^{circ}$ .

Углы 3 и 5 (а также 1 и 7, 2 и 8, 4 и 6) — накрест лежащие.

Накрест лежащие углы равны.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна $180^{circ}$ , то есть

$angle 1+angle 6=180^{circ}$ ,

$angle 4+angle 7=180^{circ}$ .

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и называются соответственными.

Соответственные углы равны, то есть

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач по геометрии, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть две параллельных прямые и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это – один из шагов, из которых и состоит решение.

В этой статье – полезные теоремы и примеры решения задач ЕГЭ и ОГЭ по теме «Углы при параллельных прямых и секущей».

Этот материал можно использовать для проектов по геометрии, в работе на уроке и самостоятельно.

Теорема 1.

Углы с соответственно параллельными сторонами равны, если они оба острые или тупые.

Доказательство:

Дано два острых угла: и Известно, что их стороны параллельны: и

Докажем, что

Пусть

Тогда как соответственные углы при параллельных прямых CA и NF и секущей CB.

как соответственные углы при параллельных прямых CB и NM и секущей NF.

Отсюда следует, что что и требовалось доказать.

Аналогично и для тупых углов.

Теорема 2.

Углы с соответственно параллельными сторонами в сумме составляют $180{}^circ ,$ если один из них острый, а другой тупой.

Доказательство:

Дано: – острый, а – тупой. Известно, что их стороны параллельны: и

Докажем, что сумма углов и равна $180{}^circ .$

Пусть Продолжим луч NM за точку N и получим прямую MK.

Получили два острых угла, и с параллельными сторонами. Согласно теореме 1, они равны, т. е.

$angle MNF+angle FNK=180{}^circ$ как смежные. Значит, $angle MNF+angle ACB=180{}^circ.$

Теорема доказана.

Теорема 3.

Если накрест лежащие углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей AB накрест лежащие углы равны:

Докажем, что Если углы 1 и 2 прямые, то прямые и перпендикулярны к прямой AB и, следовательно, параллельны.

Рассмотрим случай, когда углы 1 и 2 не прямые.

Из середины О отрезка АВ проведем перпендикуляр OH к прямой

На прямой от точки В отложим отрезок ${BH}_1$ равный отрезку AH

по двум сторонам и углу между ними, поэтому и Из равенства следует, что точка H_1 лежит на продолжении луча OH, т. е. точки H, O и H_1 лежат на одной прямой, а из равенства следует, что угол 6 – прямой (так как угол 5 – прямой). Итак, прямые и перпендикулярны к прямой HH_1, поэтому они параллельны. Теорема доказана.

Теорема 4.

Если соответственные углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей соответственные углы равны, например

Так как углы 2 и 3 – вертикальные, то Из этих двух равенств следует, что . Но углы 1 и 3 – накрест лежащие, поэтому прямые и параллельны. Теорема доказана.

Теорема 5.

Если сумма односторонних углов равна 180 градусов, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей сумма односторонних углов равна $180{}^circ ,$ например $angle 1+angle 4=180{}^circ.$

Так как углы 3 и 4 – смежные, то Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые и параллельны. Теорема доказана

И самое главное. Подборка примеров заданий ОГЭ и ЕГЭ по темам: углы при параллельных прямых и секущей, внешние накрест лежащие и внутренние накрест лежащие углы, односторонние углы.

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

Задача 1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.

Решение:

Стороны BC и AD параллелограмма параллельны, АК – секущая. Углы и равны как накрест лежащие.

– равнобедренный треугольник.

Мы доказали важное утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

AB=BK=5.

$P_{ABCD}=left(AB+BCright)cdot 2;$

$P_{ABCD}=left(5+19right)cdot 2=48.$

Ответ: 48.

Задача 2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F.

Найдите AB, если AF=24, BF=10.

Решение:

Основания трапеции АD и ВС параллельны, поэтому углы BAD и АВС – односторонние при параллельных прямых АD и ВС и секущей АВ. Сумма односторонних углов равна

Сумма углов, прилежащих к боковой стороне трапеции, равна $180{}^circ .$

Мы получили, что

AF — биссектриса угла А,

BF — биссектриса угла В, поэтому

$angle FAB=frac{1}{2}angle BAD;; angle ABF=frac{1}{2}angle ABC,$ тогда

Из треугольника AFB получим, что $AFB=90{}^circ .$

Мы доказали теорему:

Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AFB – прямоугольный.

По теореме Пифагора, ${AB}^2={AF}^2+{BF}^2Rightarrow AB=sqrt{{24}^2+{10}^2}=sqrt{676}=26.$

Ответ: 26.

Задача 3. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=16, MN=12. Найдите AM.

Решение:

Пусть М – середина АВ, N – середина ВС. Тогда MN – средняя линия треугольника АВС,

Значит, как односторонние углы при параллельных прямых и и секущей АВ.

по двум углам.

Отсюда $displaystyle frac{AB}{BM}=displaystyle frac{AC}{MN}Rightarrow BM=displaystyle frac{ABcdot MN}{AC}$ ;

$BM=displaystyle frac{28cdot 12}{16}=21.$

Ответ: 21.

Задача 4. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108 ${}^circ.$ Найдите угол B этой трапеции. Ответ дайте в градусах.

Решение:

ABCD – трапеция, – основания, AB – секущая.

Значит, angle A и angle B – внутренние односторонне углы.

Отсюда $angle B=180{}^circ -108{}^circ =72{}^circ.$

Ответ: 72.

Задача 5. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.

Решение:

Сумма углов, прилежащих к боковой стороне параллелограмма, равна $180{}^circ .$

Это значит, что $angle BAD +angle ABC = 180{}^circ.$

AК — биссектриса угла А,

BК — биссектриса угла В, поэтому

$angle KAB=frac{1}{2}angle BAD; ; angle ABK=frac{1}{2}angle ABC,$ тогда

$angle KAB+angle ABK= 90{}^circ .$

Из треугольника AKB получим, что $angle ABK= 90{}^circ .$

Мы доказали теорему:

Биссектрисы углов параллелограмма, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AKB – прямоугольный.

Расстояние от точки K до стороны AB – это длина перпендикуляра, проведенного из точки на прямую АВ, т.е. KH=4.

по гипотенузе и острому углу

Аналогично, по гипотенузе и острому углу

Получили:

Тогда $S_{ABCD}=ADcdot MN$ ; $S_{ABCD}=8cdot 7=56.$

Ответ: 56.

Задача 6. На плоскости даны четыре прямые. Известно, что $angle 1=120{}^circ ,$ $angle 2=60{}^circ ,$ $angle 3=55{}^circ .$ Найдите Ответ дайте в градусах.

Решение:

angle 1 и angle 2 – это внутренние односторонние углы,

$angle 1+angle 2=120{}^circ +60{}^circ =180{}^circ.$

Отсюда следует, что прямые параллельны, т.е.

Рассмотрим углы при параллельных прямых и секущей d.

angle 3 и angle 4 – это односторонние углы, а значит, они равны: $angle 3=angle 4=55{}^circ.$

Ответ: 55.

Задача 7. Прямые m и n параллельны. Найдите если $angle 1=22{}^circ ,$ $angle 2=72{}^circ .$ Ответ дайте в градусах.

Решение:

$mparallel nRightarrow angle 1=angle 4=22{}^circ$ как односторонние углы.

Сумма углов треугольника равна $180{}^circ .$

Для треугольника на рисунке:

$angle 2+angle 3+angle 4=180{}^circ Rightarrow angle 3=180{}^circ -72{}^circ -22{}^circ =86{}^circ .$

Ответ: 86.

Задача 8. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30 ${}^circ$ и 45 ${}^circ.$ Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение:
$angle A=angle BAC+angle CAD=30{}^circ +45{}^circ =75{}^circ ,$

angle A и angle B – это внутренние односторонние углы при параллельных прямых.

и секущей АВ, их сумма равна $180{}^circ .$

Тогда $angle B=180{}^circ -angle A=180{}^circ -75{}^circ =105{}^circ .$

Это и есть наибольший угол параллелограмма.

Ответ: 105.

Задача 9. Найдите величину тупого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15 ${}^circ.$ Ответ дайте в градусах.

Решение:

AK – биссектриса угла А параллелограмма ABCD, $angle A=30{}^circ.$

angle A и angle B – внутренние односторонние углы при параллельных прямых.

и секущей АВ. Их сумма равна $180{}^circ ,$ значит, $angle B=180{}^circ -30{}^circ =150{}^circ.$

Ответ: 150.

Задача 10. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и $angle ACD=169{}^circ .$ Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение: тогда – равнобедренный, в нем OC= CD. Значит, $angle COD=angle CDO=displaystyle frac{180{}^circ -169{}^circ }{2}=5,5{}^circ .$

Ответ: 5,5.

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

Задача 1, ЕГЭ. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Решение:

Напомним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Пусть BM – биссектриса тупого угла B. По условию, отрезки MD и AB равны 3x и 4x соответственно.

Рассмотрим углы CBM и BMA. Поскольку AD и BC параллельны, BM – секущая, углы CBM и BMA являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник ABM – равнобедренный, следовательно, AB = AM = 4x.

Периметр параллелограмма – это сумма всех его сторон, то есть

7x+7x+4x+4x=88.

Отсюда x=4, 7x=28.

Ответ: 28.

Задача 2, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $50{}^circ$ ? Ответ дайте в градусах.

Решение:

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на рисунок. По условию, $alpha -beta =50{}^circ ,$ то есть $alpha =beta +50{}^circ .$

Углы alpha и beta – односторонние при параллельных прямых и секущей, следовательно,

$alpha +beta =180{}^circ ,$ по свойству односторонних углов.

Итак, $2beta +50{}^circ =180{}^circ.$

$beta =65{}^circ ,$ тогда $alpha =115{}^circ .$

Ответ: 115.

Задача 3, ЕГЭ. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Решение:

angle B и angle C – внутренние односторонние углы и при параллельных прямых

и и секущей BC; их сумма равна $180{}^circ .$

BE – биссектриса угла В, значит как накрест лежащие углы при и секущей BE. Тогда – равнобедренный,

Аналогично, CE – биссектриса угла С, значит как накрест лежащие углы при и секущей CE. Тогда – равнобедренный и

Значит

Ответ : 10.

Задача 4, ЕГЭ. В ромбе ABCD угол ABC равен 122 ${}^circ.$ Найдите угол ACD. Ответ дайте в градусах.

Решение:

angle B и angle C – это внутренние односторонние углы при параллельных прямых.

и секущей BC, их сумма равна $180{}^circ .$

Значит, $angle C=180{}^circ -angle B=180{}^circ -122{}^circ =58{}^circ .$

ABCD – ромб, диагонали ромба делят его углы пополам.

Тогда $angle ACD=58div 2=29{}^circ .$

Ответ: 29.

Задача 5, ЕГЭ. Угол между стороной и диагональю ромба равен $54{}^circ .$ Найдите острый угол ромба.

Решение:

Диагональ ромба делит его угол пополам, то есть является биссектрисой угла ромба. Поэтому один из углов ромба равен градусов, и это тупой угол ромба. Тогда острый угол ромба равен $180{}^circ -108{}^circ =72{}^circ .$

Ответ: 72.

Задача 6, ЕГЭ. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 ${}^circ.$ Найдите площадь трапеции.

Решение:

Пусть $angle D=150{}^circ ; AB=18; DC=6; AD=7.$

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними при и секущей BC. Их сумма равна $180{}^circ .$

Тогда $angle A=30{}^circ .$ Построим высоту из вершины Получим прямоугольный треугольник с острым углом в 30 ${}^circ .$

Высота трапеции DH – это катет, лежащий напротив угла в $30{}^circ$ и равный половине гипотенузы, т. е.

Отсюда $S_{ABCD}=displaystyle frac{DC+AB}{2}cdot h;$ $S_{ABCD}=displaystyle frac{6+18}{2}cdot 3.5=12cdot 3.5=42.$

Ответ: 42.

Задача 7, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $50{}^circ$ ? Ответ дайте в градусах.

Решение:

У равнобедренной трапеции углы при основании равны т.е.

По условию, $angle D-angle B=50{}^circ Rightarrow angle C-angle B=50{}^circ ;$

angle C и прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых
и и секущей BC. Их сумма равна $180{}^circ .$

$angle C+angle B=180{}^circ.$

Получили:

$left{ begin{array}{c}angle C-angle B=50{}^circ \angle C+angle B=180{}^circ end{array}right. .$

Сложив два уравнения, получим: $2angle C=230{}^circ ,$ тогда $angle C=115{}^circ.$

Ответ: 115.

Задания ЕГЭ Базового уровня, геометрия. Свойства углов при параллельных прямых и секущей.

Задание 1. Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол $150{}^circ .$ Найдите площадь трапеции.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных основаниях трапеции и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол трапеции равен 30 ${}^circ .$ Построив высоту, мы увидим, что она лежит против прямого угла в прямоугольном треугольнике. Значит, высота равна половине боковой стороны, т.е. h=4.

Отсюда

Ответ: 60.

Задание 2. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен $135{}^circ .$ Найдите меньшую боковую сторону.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол равен $45{}^circ .$

Вторая высота отсекает равнобедренный прямоугольный треугольник с катетом, равным разности оснований. Значит, высота равна: 7–4=3.

Отсюда

Ответ: 16,5.

Задание 3. В трапеции ABCD известно, что AB = CD, $angle BDA=40{}^circ$ и $angle BDC=30{}^circ .$ Найдите угол ABD. Ответ дайте в градусах.

Решение:

$angle D=angle BDA+angle BDC=40{}^circ +30{}^circ =70{}^circ .$ Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна $180{}^circ .$ Значит, острый угол равен $110{}^circ .$

Нам дана трапеция, в которой AB=CD. Очевидно, что это боковые стороны, и трапеция равнобедренная с основаниями и .

и параллельны, BD секущая, тогда $angle ADB=angle DBC=40{}^circ .$

$angle ABD=angle ABC-angle DBC=110{}^circ -40{}^circ =70{}^circ.$

Ответ: 70.

Задание 4. В параллелограмме ABCD проведена биссектриса угла A, пересекающая сторону BC в точке K. Найдите KC, если AB = 4, а периметр параллелограмма равен 20.

Решение:

ABCD – параллелограмм, тогда AB = DC = 4.

AK – биссектриса угла А, значит,

как накрест лежащие углы при параллельных прямых и и секущей AK.

Получили, что – равнобедренный и

$P_{ABCD}=left(AB+ADright)cdot 2=20,$ значит

Ответ: 2.

Задание 5. Прямые m и n параллельны (см. рисунок). Найдите если $angle 1=117{}^circ ,$ $angle 2=24{}^circ .$ Ответ дайте в градусах.

Решение:

$angle 2=angle 4=24{}^circ$ (как накрест лежащие углы).

$angle 1+angle 4+angle 3=180{}^circ$ (развернутый угол).

Тогда $angle 3=180{}^circ -left(angle 1+angle 4right)=180{}^circ -left(117{}^circ +24{}^circ right)=39{}^circ .$

Ответ: 39.

Задание 6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и $angle ACD=104{}^circ .$ Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение:

Пусть диагонали пересекаются в точке О, т.е.

$AC=2ABRightarrow AB=displaystyle frac{1}{2}cdot ACRightarrow AB=AO=OC=CD.$

и параллельны, АС – секущая, $Rightarrow angle BAC=angle ACD=104{}^circ .$

– равнобедренный, отсюда угол между диагоналями равен:

$angle BOA=displaystyle frac{180{}^circ -104{}^circ }{2}=38{}^circ .$

Ответ: 38.

Если вам понравился наш материал на тему «Углы при параллельных прямых и секущей» — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Как найти угол в трапеции

Угол трапеции при основании через высоту и прилегающую боковую сторону

Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции

Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали

Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой стороны в прямоугольной трапеции

Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Углы при параллельных прямых и секущей

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции