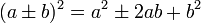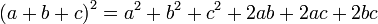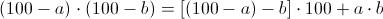Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей.
В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.
Квадрат суммы и квадрат разности
Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:
Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:
- 372 = (30+7)2 = 302 + 2*30*7 + 72 = 900+420+49 = 1 369
- 942 = (90+4)2 = 902 + 2*90*4 + 42 = 8100+720+16 = 8 836
Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.
Квадрат близкий к известному квадрату
Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:
На 1 больше:
Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.
- 312 = 302 + 31 + 30 = 961
- 162 = 152 + 15 + 16 = 225 + 31 = 256
На 1 меньше:
Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.
- 192 = 202 – 19 – 20 = 400 – 39 = 361
- 242 = 252 – 24 – 25 = 625 – 25 – 24 = 576
На 2 больше
Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.
- 222 = 202 + 2*(20+22) = 400 + 84 = 484
- 272 = 252 + 2*(25+27) = 625 + 104 = 729
На 2 меньше
Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.
- 482 = 502 – 2*(50+48) = 2500 – 196 = 2 304
- 982 = 1002 – 2*(100+98) = 10 000 – 396 = 9 604
Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).
Квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
- 152 = (1*(1+1)) 25 = 225
- 252 = (2*(2+1)) 25 = 625
- 852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
- 1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Квадрат чисел близких к 50
Посмотрите работу алгоритма на примерах:
- 442 = (25-6)*100 + 62 = 1900 + 36 = 1936
- 532 = (25+3)*100 + 32 = 2800 + 9 = 2809
Квадрат трехзначных чисел
Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:
Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:
4362 = (400+30+6)2= 4002 + 302 + 62 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Время на прочтение
3 мин
Количество просмотров 115K
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
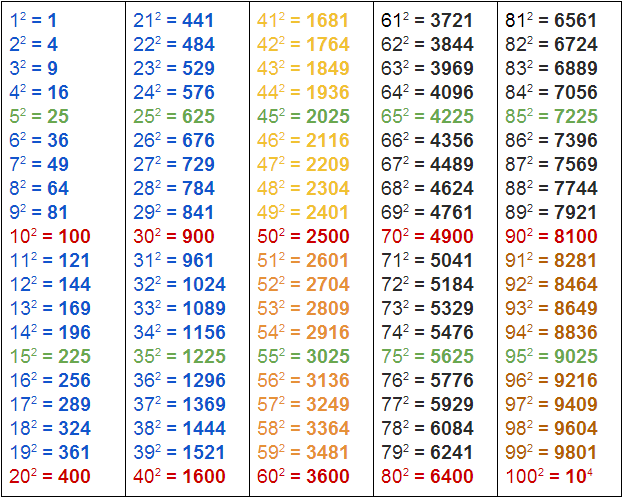
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
75 * 75 = 7 * 8 = 56 … 25 = 5625.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
XX * XX = 1500 + 100 * вторую цифру + (10 - вторая цифра)^2
Достаточно трудно, верно? Давайте разберем пример:
43 * 43 = 1500 + 100 * 3 + (10 - 3)^2 = 1500 + 300 + 49 = 1849.
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
XX * XX = 2500 + 100 * вторую цифру + (вторая цифра)^2
Тоже достаточно трудно для восприятия. Давайте разберем пример:
53 * 53 = 2500 + 100 * 3 + 3^2 = 2500 + 300 + 9 = 2809.
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
XX * XX = 8000+ 200 * вторую цифру + (10 - вторая цифра)^2
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
93 * 93 = 8000 + 200 * 3 + (10 - 3)^2 = 8000 + 600 + 49 = 8649.
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
XX * XX = 100(XX - 25) + (50 - XX)^2
Например:
37 * 37 = 100(37 - 25) + (50 - 37)^2 = 1200 + 169 = 1369
Для чисел от 50 до 100
XX * XX = 200(XX - 50) + (100 - XX)^2
Например:
67 * 67 = 200(67 - 50) + (100 - 67)^2 = 3400 + 1089 = 4489
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
(a+b)^2 = a^2 + 2ab + b^2.
56^2 = 50^2 + 2*50*6 + 6*2 = 2500 + 600 + 36 = 3136.
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
92*92 = (92-8)*100+8*8 = 8464
(от sielover)
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Быстрое возведение чисел в квадрат без калькулятора
21 сентября 2013
Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.
Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:
[{{34}^{2}}=times frac{34}{frac{34}{+frac{136}{frac{102}{1156}}}}]
1156 — это и есть квадрат 34.
Проблему данного способа можно описать двумя пунктами:
1) он требует письменного оформления;
2) в процессе вычисления очень легко допустить ошибку.
Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.
Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:
[{{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]
[{{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}]
Что нам это дает? Дело в том, что любое значение в пределах от 10 до 100 представимо в виде числа $a$, которое делится на 10, и числа $b$, которое является остатком от деления на 10.
Например, 28 можно представить в следующем виде:
[begin{align}& {{28}^{2}} \& 20+8 \& 30-2 \end{align}]
Аналогично представляем оставшиеся примеры:
[begin{align}& {{51}^{2}} \& 50+1 \& 60-9 \end{align}]
[begin{align}& {{42}^{2}} \& 40+2 \& 50-8 \end{align}]
[begin{align}& {{42}^{2}} \& 40+2 \& 50-8 \end{align}]
[begin{align}& {{77}^{2}} \& 70+7 \& 80-3 \end{align}]
[begin{align}& {{21}^{2}} \& 20+1 \& 30-9 \end{align}]
[begin{align}& {{26}^{2}} \& 20+6 \& 30-4 \end{align}]
[begin{align}& {{39}^{2}} \& 30+9 \& 40-1 \end{align}]
[begin{align}& {{81}^{2}} \& 80+1 \& 90-9 \end{align}]
Что дает нам такое представление? Дело в том, что при сумме или разности, мы можем применить вышеописанные выкладки. Разумеется, чтобы сократить вычисления, для каждого из элементов следует выбрать выражение с наименьшим вторым слагаемым. Например, из вариантов $20+8$ и $30-2$ следует выбрать вариант $30-2$.
Аналогично выбираем варианты и для остальных примеров:
[begin{align}& {{28}^{2}} \& 30-2 \end{align}]
[begin{align}& {{51}^{2}} \& 50+1 \end{align}]
[begin{align}& {{42}^{2}} \& 40+2 \end{align}]
[begin{align}& {{77}^{2}} \& 80-3 \end{align}]
[begin{align}& {{21}^{2}} \& 20+1 \end{align}]
[begin{align}& {{26}^{2}} \& 30-4 \end{align}]
[begin{align}& {{39}^{2}} \& 40-1 \end{align}]
[begin{align}& {{81}^{2}} \& 80+1 \end{align}]
Почему следует стремиться к уменьшению второго слагаемого при быстром умножении? Все дело в исходных выкладках квадрата суммы и разности. Дело в том, что слагаемое $2ab$ с плюсом или с минусом труднее всего считается при решении настоящих задач. И если множитель $a$, кратный 10, всегда перемножается легко, то вот с множителем $b$, который является числом в пределах от одного до десяти, у многих учеников регулярно возникают затруднения.
Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:
[{{28}^{2}}={{(30-2)}^{2}}=200-120+4=784]
[{{51}^{2}}={{(50+1)}^{2}}=2500+100+1=2601]
[{{42}^{2}}={{(40+2)}^{2}}=1600+160+4=1764]
[{{77}^{2}}={{(80-3)}^{2}}=6400-480+9=5929]
[{{21}^{2}}={{(20+1)}^{2}}=400+40+1=441]
[{{26}^{2}}={{(30-4)}^{2}}=900-240+16=676]
[{{39}^{2}}={{(40-1)}^{2}}=1600-80+1=1521]
[{{81}^{2}}={{(80+1)}^{2}}=6400+160+1=6561]
Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.
Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.
Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:
[{{50}^{2}}=2500]
Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:
[{{51}^{2}}=2500+50+51=2601]
И так со всеми числами, отличающимися на единицу.
Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:
[{{21}^{2}}=400+20+21=441]
[{{39}^{2}}=1600-40-39=1521]
[{{81}^{2}}=6400+80+81=6561]
Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:
[begin{align}& {{26}^{2}}=625+25+26=676 \& 26=25+1 \end{align}]
При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.
Ключевые моменты
С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!
Для начала запомните квадраты значений, кратных 10:
[begin{align}& {{10}^{2}}=100,{{20}^{2}}=400,{{30}^{2}}=900,…, \& {{80}^{2}}=6400,{{90}^{2}}=8100. \end{align}]
Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:
[begin{align}& {{34}^{2}}={{(30+4)}^{2}}={{30}^{2}}+2cdot 30cdot 4+{{4}^{2}}= \& =900+240+16=1156; \end{align}]
[begin{align}& {{27}^{2}}={{(30-3)}^{2}}={{30}^{2}}-2cdot 30cdot 3+{{3}^{2}}= \& =900-180+9=729. \end{align}]
Как считать еще быстрее
Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:
[begin{align}& {{14}^{2}}={{15}^{2}}-14-15= \& =225-29=196. \end{align}]
Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:
[begin{align}& {{31}^{2}}={{30}^{2}}+30+31= \& =900+61=961. \end{align}]
Почему так происходит? Давайте запишем формулу квадрата суммы (и разности). Пусть $n$ — наше опорное значение. Тогда они считаются так:
[begin{align}& {{(n-1)}^{2}}=(n-1)(n-1)= \& =(n-1)cdot n-(n-1)= \& =={{n}^{2}}-n-(n-1) \end{align}]
— это и есть формула.
[begin{align}& {{(n+1)}^{2}}=(n+1)(n+1)= \& =(n+1)cdot n+(n+1)= \& ={{n}^{2}}+n+(n+1) \end{align}]
— аналогичная формула для чисел, больших на 1.
Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!
Смотрите также:
- Решение ЕГЭ-2011: вариант 1, часть B
- Задача B1 — время, числа и проценты
- Комбинаторика в задаче B6: легкий тест
- Интегрирование по частям
- Нестандартная задача B2: студенты, гонорары и налоги
- Особенности решения неравенств с радикалами
Несколько рекомендаций как быстро и просто возвести числа в квадрат (умножить число само на себя).
Вариант 1. Двухзначное число, заканчивающееся на 5
Например, найдем квадрат числа 35
Шаг 1: Умножьте первую цифру числа на цифру, которая стоит выше в ряду с ней: 3 х 4 = 12
Шаг 2: К числу, которое получилось припишите в конце число 25.
Ответ: 1225
Вариант 2. Любое двухзначное число
Например, найдем квадрат числа 47
Шаг 1: Возьмем ближайшее число, кратное 10. В нашем примере это число 50 Разница составит 3
Шаг 2: Теперь найдем нижнее число с разницей 3 от нашего числа. В нашем примере 47 — 3 = 44
Шаг 3: Умножим два полученных одно на второе. 44 х 50 = 2200
Шаг 4: Находим квадрат нашей разницы 3, квадрат 3 = 9
Шаг 5: Прибавляем число полученное в шаге 5 к числу шага 4. 2200 + 9 = 2209.
Ответ: 2209
При желании всегда быстро общаться, обмениваться мнениями или просто болтать можно просто скачать аську и наслаждаться общением. Аська самый простой и быстрый способ онлайн общения
людей нашли эту статью полезной. А Вы?