Время на прочтение
3 мин
Количество просмотров 74K
Дано: 12 монет, одна из них фальшивая, отличается только весом. Неизвестно легче или тяжелее. Даны рычажные весы, которые показывают, что груз с одной из сторон тяжелее. За 3 взвешивания необходимо найти фальшивую монетку.
Из опыта советую не спешить, решать письменно. Головоломка «12 монет, 3 взвешивания» несколько раз возникала в моей жизни. Первый раз ее задал мне мой товарищ-олимпиадник, решил я ее после олимпиады и пришлось пару часиков поломать голову. И через несколько лет она далось мне не сразу. Если желаете решить самим — делайте на листочке.
Ниже будет разбор и этапы решения. Этапы проведут по универсальной методике решения задач, которая применима как к программированию, так и к жизни. Благодаря подходу решение головоломки станет простым.
Предлагаю вам, прежде чем читать предложить решение. У вас есть ответ? Проверенный?
Если бы это было программного обеспечения вопросы были бы следующие: «Вы запрограммировали, протестировали алгоритм? Рассмотрели тестовые случаи и проверили их?».
Как показывает опыт, чтобы решить требуется нарисовать дерево решений и проверить все 12 случаев.
1. Подсказки
В процессе решения поможет:
1) Понижение энтропии (меры неопределенности) и ответы на вопросы:
- Что узнали на предыдущем шаге?
- Что снижает неопределённость?
- Какой информацией располагаем?
- Что еще нужно узнать?
Вопросы подходят для любой задачи, проектов. Ответы на них помогают в снижении рисков срыва сроков, перерасхода бюджета и получения нагоняя от начальства.
2) Декомпозиция. Подход от простого к сложному. Если подготовить решение простейших случаев, затем использовать их для решения задачи (алгоритм разделяй и властвуй) то, будет проще, чем представлять всю ситуацию в голове.
Алгоритмы «разделяй и властвуй» разбивают задачу на две или более подзадачи того же типа, но меньшего размера до элементарных задач и объединяют их решения для получения ответа к исходной задаче.
Составьте вопросы для декомпозиции. Какие бы вы предложили?
2. Декомпозиция
Какие вопросы вы сформулировали для декомпозиции? Есть совпадения?
1) Какая ситуация самая элементарная? Что можем сделать за одно взвешивание?
За одно взвешивание можем определить, какая монета тяжелее, равен ли вес монет.
2) Если у нас 2 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо взвесить монеты, и в зависимости от стрелки весов определить фальшивую.
3) Если у нас 2 монеты, и, не известно, фальшивая тяжелее или легче, как за одно взвешивание определить фальшивую?
Взвесив одну из 2-х представленных монет с третьей монетой, про которую известно, что она подлинная.
4) Если у нас 3 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо сравнить любые две из этих монет, если они равны, фальшивой является третья монета.
5) Если у нас 3 монеты, и, неизвестно, фальшивая тяжелее или легче. Можно ли определить фальшивую за одно взвешивание?
К сожалению, нет.
6) Если у нас 4 монеты, и, неизвестно фальшивая тяжелее или легче, можно определить фальшивую за одно взвешивание?
К сожалению, нет.
7) Если у нас 4 монеты, и, неизвестно, фальшивая тяжелее или легче, за сколько взвешиваний можно определить фальшивую?
За два взвешивания.
Далее из элементарных случаев соберем ситуации из 8, 9, 10, 11 и 12 монет. Как вы видите решение?
Ниже полное решение.
3. Решение
Первый шаг: разделим монеты на 3 группы по 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Сравним первые две группы. Возможны три варианта:
- первая группа тяжелее;
- вторая группа тяжелее;
- равны.
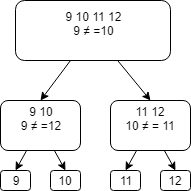
1) Если группы равны, то фальшивая монета находится в третьей группе. Необходимо найти фальшивую монету из 4 монет за два взвешивания.
Делим третью группу на две: 9 10 11 12
Сравниваем 9 и 10:
- если они равны, то фальшивая монета во второй группе – сравниваем 9 и 11. Если 9 и 11 равны — то фальшивая – 12, если нет -11
- если они не равны, то фальшивая в первой группе – сравниваем 10 и 12. Если 10 и 12 равны – фальшивая – 9, если нет – 10.
Таким образом мы нашли фальшивую монету.
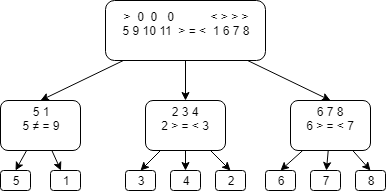
2) Рассмотрим второй случай. Если первая группа тяжелее второй, то присваиваем первой группе знак «>», второй группе знак «<», третьей группе – «0».
Делим монеты на группы 1 9 10 11 и 5 2 3 4, взвешиваем. Возможны три варианта:
- Равны. Фальшивая монета находится среди чисел: 6 7 8. Сравниваем 6 и 7, если равны – фальшивая — 8, если 6 больше, то фальшивая – 7, если 7 больше, то фальшивая – 6, так как в данном случае фальшивая монета легче.
- Первая группа тяжелее, то фальшивая монета либо 1, либо 5. Сравниваем 1 и 9, если они равны – фальшивая монета — 5, если нет — 1.
- Первая группа легче, то фальшивая среди монет 2 3 4, так как известно, что 9, 10 и 11 настоящие, и перевесить вторая группа может только за счет монет 2, 3 и 4. Сравниваем 2 и 3, если равны – фальшивая 4, если 2 тяжелее, то фальшивая – 2, иначе 3-я является фальшивой.
3) Случай когда вторая группа тяжелее первой, аналогичен второму.
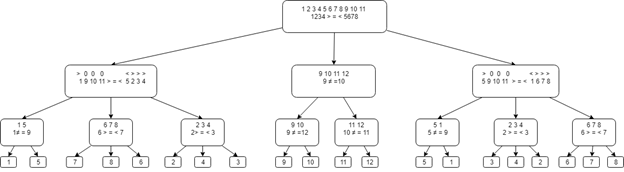
Общая диаграмма «Дерева решений» представлена ниже.
Заключение
При поступлении задачи на доработку или отладку хорошо применить рассмотренный выше подход:
- Определиться, что дано?
- На какие элементарные случаизадачи можно разложить?
- Что неизвестно для решения задачи? Какие эксперименты нужно провести, чтобы снизить энтропию?
- Выполнить.
- Задача решена? Нет? Вернуться к шагу 1.
Успешных решений.
Есть 12 монет, одна из которых фальшивая. При этом неизвестно, в какую сторону она отличается от настоящих, т.е. она может быть как легче, так и тяжелее. В вашем распоряжении чашечные весы без гирь, как в аптеке. Нужно за три взвешивания найти фальшивую монету, а также выяснить, тяжелее она или легче.
Решение
Для удобства пронумеруем монеты от 1 до 12.
Первым взвешиванием сравним две группы по четыре монеты: 1, 2, 3, 4 и 5, 6, 7, 8.
Случай I: первое взвешивание показало равенство
Если весы покажут равенство, то фальшивая монета находится среди оставшихся четырёх монет. Тогда вторым взвешиванием мы сравним три монеты 9, 10, 11 с заведомо настоящими 1, 2, 3.
Если и в этот раз весы покажут равенство, то фальшивка — монета номер 12, и третьим взвешиванием мы сравним её с настоящей и узнаем, легче она или тяжелее.
Если же три монеты 9, 10, 11 оказались легче (тяжелее), то третьим взвешиванием сравним друг с другом монеты 9 и 10. Если они равны, то монета 11 — фальшивая, и она легче (тяжелее) настоящей. Иначе заключаем, что из монет 9 и 10 фальшивая та, которая легче (тяжелее) другой.
Случай II: первое взвешивание показало неравенство
Теперь предположим, что первое взвешивание показало, что монеты 1, 2, 3, 4 тяжелее, чем 5, 6, 7, 8. Случай, когда первые монеты оказались легче, симметричен.
Во втором взвешивании на одну чашу поместим монеты 1, 2, 5, а на другую — монеты 3, 4, 9 (монета 9 — заведомо настоящая).
Если второе взвешивание показало равенство, то у нас остаются три монеты 6, 7, 8, одна и которых легче остальных. Третьим взвешиванием сравниваем монеты 6 и 7. Если они равны, то монета 8 легче остальных. Иначе фальшивой является та, которая легче другой.
Теперь предположим, что во втором взвешивании монеты 1, 2, 5 оказались тяжелее, чем 3, 4, 9. Это означает, что фальшивка находится среди монет 1 и 2, причём она тяжелее остальных. Сравнив в третьем взвешивании эти две монеты друг с другом, мы определим фальшивую.
Предположим, что во втором взвешивании монеты 1, 2, 5 оказались легче, чем 3, 4, 9. Это означает, что либо монета 5 легче остальных, либо одна из монет 3 и 4 тяжелее остальных. Третьим взвешиванием мы сравним друг с другом монеты 3 и 4 и найдём ответ.
Разминка для мозга: сможете решить задачу про фальшивую монету? Проверьте!
25 августа 2020
Отдых
Есть 12 монет, среди них одна поддельная. Помогите математику обнаружить её всего за три взвешивания.
Анастасия Сукманова
Избранное
За критику налоговой системы император заточил в темницу величайшего математика страны. Но однажды пленнику представился шанс вновь обрести свободу. Один из 12 наместников императора уплатил налог фальшивой монетой, которая уже попала в казну. Император пообещал освободить математика, если тот сумеет найти подделку.
Перед пленником поставили стол, на котором были чашечные весы, карандаш и 12 одинаковых на вид монет. А потом сказали, что фальшивка отличается от остальных денег по весу в большую или меньшую сторону. Взвесить монеты разрешили лишь трижды. Как математику вычислить подделку?
Показать ответ
Скрыть ответ
Читайте также ✅
- Сложная задачка про голубоглазых пленников, которые застряли на острове
- Задача про пленников и колпаки, цвет которых нужно определить
- Задача про тайник Леонардо да Винчи, в который не так-то легко пробраться
Как тремя взвешиваниями найти фальшивую монету
Это достаточно популярная логическая задачка. Есть двадцать одинаковых с виду монет, одна из которых фальшивая, и весы с чашками без гирь. Известно, что фальшивая монета весит меньше чем настоящая. Необходимо найти фальшивую монету за три взвешивания.

Вам понадобится
- — двадцать монет;
- — чашечные весы.
Инструкция
Разделите монеты на три части: в двух будет по семь монет, и в оставшейся – шесть. На чашечные весы положите две равные кучки. Если весы уравновешены, значит, в двух кучках по семь монет все монеты настоящие, а фальшивая находится среди оставшихся шести монет. Если же равновесие нарушилось, пропустите следующий пункт решения.
Возьмите кучку из шести монет, разделите ее на три части. В каждую чашку весов положите по 2 монеты, еще 2 оставьте. Это второе взвешивание. Если весы уравновешены, значит, фальшивая монета осталась среди двух, лежащих на столе. Если равновесие нарушилось, значит, фальшивая монета среди тех двух монеток, которые оказались легче. Таким образом, вы обнаружили пару монет, одна из которых фальшивая, и ее легко найти третьим взвешиванием, просто положив в каждую чашку весов по одной монете.
Возьмите ту часть из семи монет, которая оказалась легче. Напомним, что это вы делаете в том случае, если при первом взвешивании равновесие на весах нарушилось. Разделите монеты на три части: в двух будет по три монеты и в оставшейся – одна. В каждую чашку весов положите по три монеты. Это второе взвешивание. Если равновесие весов не нарушено, значит, оставшаяся монета и есть фальшивая. Задача решена даже быстрее благодаря везению! Если же одна чашка весов оказалась легче, проведите последнее взвешивание.
Положите в каждую чашку весов по одной монете из той части, которая оказалась легче. Третья монета останется лежать на столе. Если весы уравновешены, значит, оставшаяся монета и есть фальшивая. Если же одна из чашек весов легче, то фальшивая монета находится в ней.
Полезный совет
Вы можете столкнуться с разными вариантами подобной задачи: монет может быть сколько угодно, и определить фальшивую нужно будет за минимальное число взвешиваний. Хитрость решения состоит в том, что делить монеты нужно не на две, а на три части, так как уравновешивание чашек весов позволяет сделать определенный вывод не только о тех монетах, которые лежат на весах, но и о тех, которые остались на столе.
Источники:
- Логические задачи и головоломки
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Для начала «лемма»: как за одно взвешиваени найти одну фальшивую монету из трёх, если ИЗВЕСТНО, что она тяжелее или легче. Для этого надо взять две любые из трёх и взвесить их. Если весы в равновесии, то фальшивая — третья. Если нет, то они и покажут фальшивую.
Теперь собсно к задачке. Разбиваем монетки на группы 3, 3, 3 и 1.
Взвешиваем 3 и 3 (первое взвешивание). Если весы в равновесии, то фальшивая монета среди оставшихся четырёх, про это мы потом поговорим.
Если весы НЕ в равновесии, то заменяем одну из троек, для определённости возьмём более тяжёлую, на другую и снова взвешиваем (второе взвешивание). Если весы ТЕПЕРЬ в равновесии, то фальшивая монета среди убранной тройки, и уже известно, что она тяжелее. А одна монет из трёх находится одним взвешиваением (см. лемму). Если же весы снова не в равновесии, то фальшивая монета в оставшейся на весах тройке, и опять же становится известно, легче она или тяжелее. Так что опять третье взвешивание её обнаружит.
Ну и вернёмся к случаю равновесия троек при первом взвешивании. Тут у нас задачка найти фальшивую среди четырёх за ДВА оставшихся взвешивания. Причём по условию ваще-то по фигу, легче она или тяжелее. Её надо просто найти. Значит, берём две любые и взвешиваем (второе взвешивание для этого варианта развития событий). Если весы в равновесии, то заменяем одну из монет на одну из оставшихся и взвешиваем (третье взвешивание). Если весы вышли из равновесия, то фальшивая монета найдена. Если весы остались в равновесии, то фальшивая та, что осталась на столе.
Если при втором взвешивании весы НЕ в равновесии, то две оставшиеся монеты точняк настоящие. Так что опять же заменяем любую из двух на одну настоящую и взвешиваем (третье взвешивание). Предлагаю самому рассмотреть оба варианта и догадаться, что к чему…