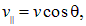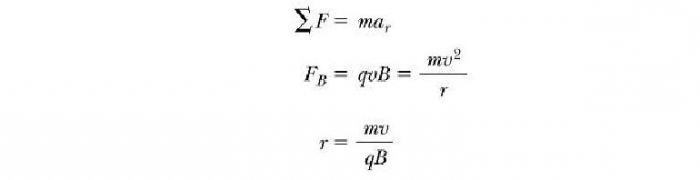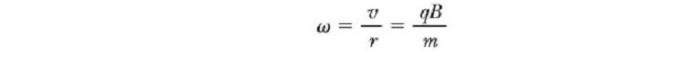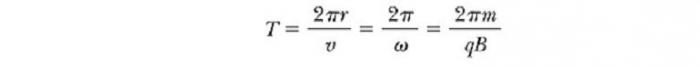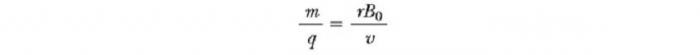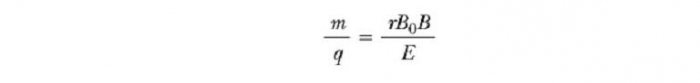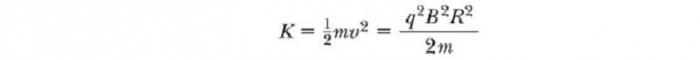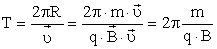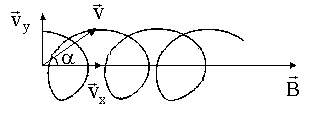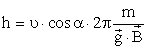Кинетическая энергия альфа частицы как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Альфа–частица, вылетевшая из ядра радия со скоростью 15 Мм/с, пролетев в воздухе 3,3 см, остановилась. Найти кинетическую энергию частицы, время торможения и ускорение.

Спрятать решение

Решение.

Кинетическая энергия альфа–частицы находится по формуле

Из формулы перемещения при равноускоренном движении находим время торможения

Из формулы перемещения при равноускоренном движении находим ускорение

Ответ: 4,7 МэВ; 4,4 нс; 3,4 · 10¹⁵ м/с².

Источник: Рымкевич А. П. Сборник задач по физике для 9−11 классов, М.: «Просвещение», 1990 (№ 1164)

Источник

Кинетическая энергия движения частицы по окружности

2017-05-20
Кинетическая энергия частицы, движущейся по окружности радиуса $R$, зависит от пройденного пути $s$ по закону $T = as^<2>$, где $a$ — постоянная. Найти силу, действующую на частицу, в зависимости от $s$.

Дифференцируя уравнение (1) по времени

Следовательно, искомое ускорение частицы

Следовательно, искомая сила $F = mw = 2as sqrt<1 + (s/R)^<2>>$

Кинетическая энергия движения частицы по окружности

Протоны в однородном магнитном поле между полюсами магнита движутся по окружностям радиусом R под действием силы Лоренца. После замены магнита по окружностям тем же радиусом между полюсами стали двигаться α-частицы, обладающие такой же кинетической энергией, как и протоны. Как изменились индукция магнитного поля и скорость движения α-частиц по сравнению со скоростью протонов?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Индукция

магнитного поля
Скорость α-частиц

При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями

Индукция магнитного поля равна

Кинетическая энергия частицы выражается как Масса альфа-частицы в четыре раза больше массы протона, следовательно, при сохранении кинетической энергии, скорость альфа-частиц меньше скорости протонов в два раза. Заряд альфа-частицы в два раза больше заряда протона, тогда из формулы для индукции магнитного поля получаем, что индукция магнитного поля не изменилась.

Движение заряженных частиц по окружности

5.3. Движение заряда в однородном магнитном поле

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

из которого легко получить выражение для угловой скорости частицы

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

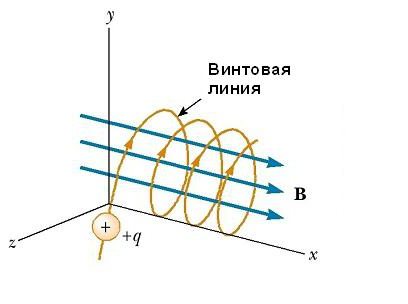
Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

Кинетическая энергия протона будет

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.

Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.

Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).

Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.

Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.

Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

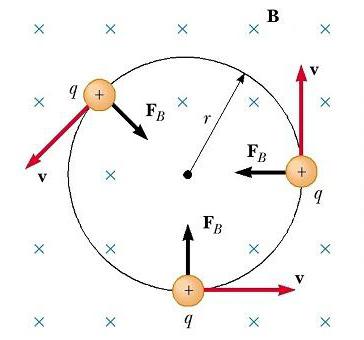
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

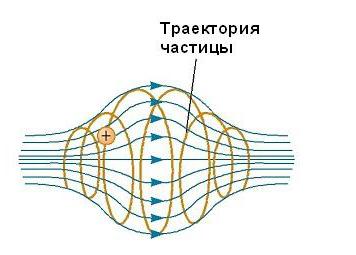
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

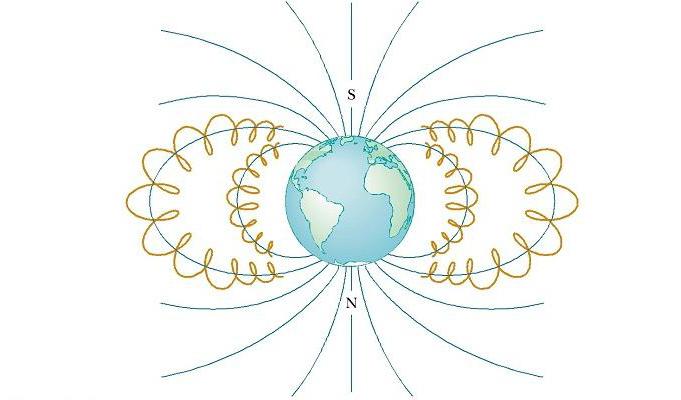
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

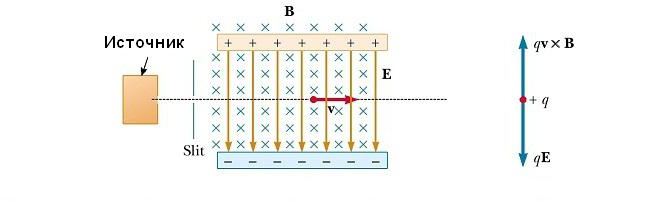
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

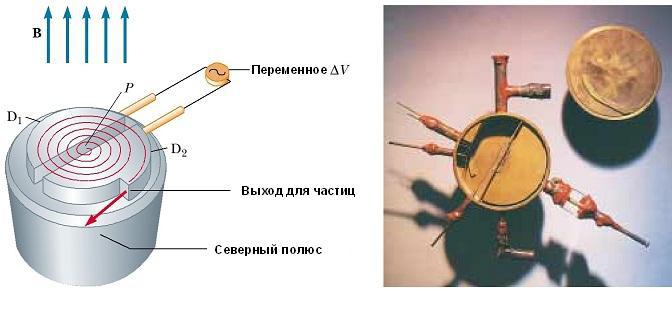
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Движение заряженной частицы в магнитном поле.

Для вывода общих закономерностей движения заряженной частицы в магнитном поле будем считать магнитное поле однородным, электрические поля на частицу не действуют. При этом учтем очевидное:

а) Если заряженная частица движется в магнитном поле вдоль силовой линии, сила Лоренца, действующая на неё, равна нулю

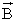
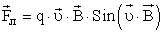
б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярно к вектору , то сила Лоренца, равная постоянна по модулю и перпендикулярна к траектории частицы.

Согласно второму закону Ньютона, эта сила создаёт центростремительное ускорение. Поэтому частица будет двигаться по окружности, радиус которой определяется из условия:

, , ,

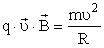
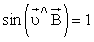
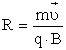
период вращения частицы, т. е. время, затрачиваемое ею на один полный оборот,

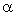
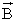
в) Если скорость заряженной частицы направлена под углом к вектору то её движение можно представить в виде двух движений: 1) равномерного прямолинейного движения вдоль поля, 2) равномерного движения по окружности в плоскости перпендикулярной полю (Рис. 23).

В результате этих двух движений возникает движение по винтовой линии, ось которой параллельна вектору 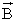. Шаг винтовой линии:

Направление, в котором закручивается частица, зависит от знака её заряда.

Действие магнитного поля на движущиеся заряженные частицы. Действие магнитного поля на проводник с током означает, что магнитное поле действует на движущиеся электрические заряды. Найдем силу, действующую на электрический заряд q при его движении в однородном магнитном поле с индукцией .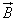
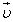
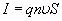
Сила тока I в проводнике связана с концентрацией n свободных заряженных частиц, скоростью их упорядоченного движения и площадью S поперечного сечения проводника следующим выражением:

,(1)

где q — заряд отдельной частицы.

.

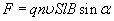
Так как произведение nSl равно числу свободных заряженных частиц в проводнике длиной l

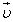
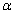
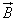
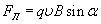
то сила, действующая со стороны магнитного поля на одну заряженную частицу, движущуюся со скоростью под углом к вектору индукции, равна

.(2)

Эту силу называют силой Лоренца.
Направление вектора силы Лоренца 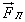определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.

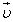
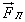
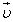
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила , постоянная по модулю и направленная перпендикулярно вектору скорости (рис. 187).

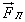
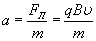
В вакууме под действием силы Лоренца частица приобретает центростремительное ускорение

(3)

и движется по окружности. Радиус r окружности, по которой движется частица, определяется из условия

, .(4)

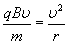
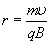
Период обращения частицы в однородном магнитном поле равен

.(5)

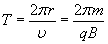
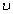
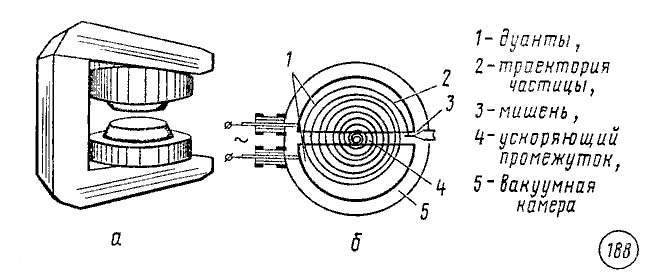
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле при постоянной массе не зависит от скорости и радиуса r траектории ее движения. Этот факт используется, например, в ускорителе заряженных частиц — циклотроне.

Циклотрон. В этом ускорителе заряженные частицы — протоны, ядра атомов гелия — разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами — дуантами. Дуанты находятся между полюсами постоянного электромагнита (рис. 188, а).

Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту времени, когда они совершают половину оборота и подходят к зазору между дуантами, направление вектора напряженности электрического поля между дуантами изменяется на противоположное и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности все большего радиуса (рис. 188, б), но период их обращения остается неизменным. Поэтому для ускорения частиц на дуанты подается переменное напряжение с постоянным периодом.
Ускорение частиц в циклотроне с постоянным периодом возможно лишь до значений скоростей, значительно меньших скорости света. С приближением скорости частицы к скорости света в вакууме, равной c = 300000 км/с, масса частицы возрастает, вследствие чего увеличивается период ее обращения в магнитном поле. Равенство периода обращения частицы и периода изменения электрического поля нарушается, ускорение прекращается.

топлива по сравнению с обычной тепловой электростанцией.

В заключение, по традиции, предлагаем Вашему вниманию шпаргалку по этой теме:

источники:

http://phys-ege.sdamgia.ru/problem?id=17662

http://b4.cooksy.ru/articles/dvizhenie-zaryazhennyh-chastits-po-okruzhnosti

Источник

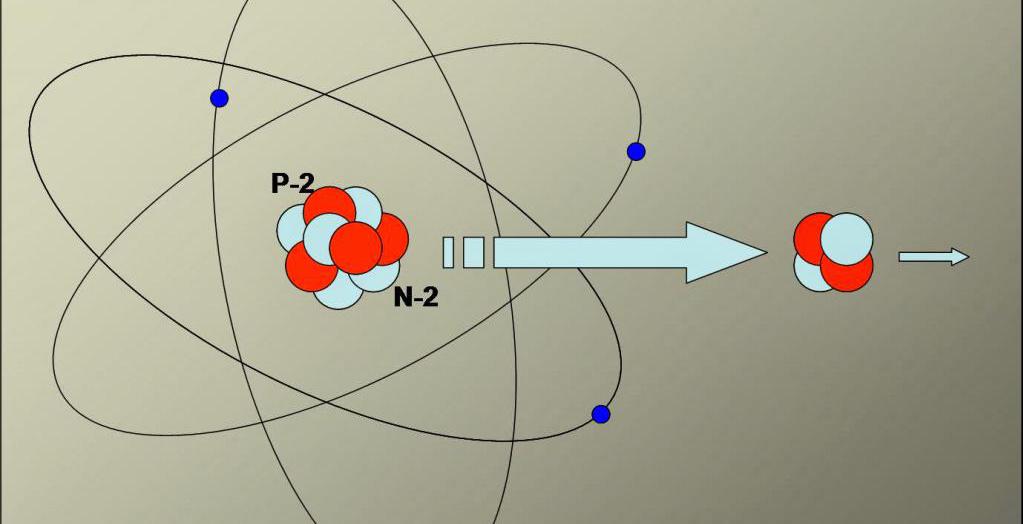
Альфа-частица представляет собой ядро гелия. Если у атома гелия убрать электронную оболочку, то останется эта частица. Она состоит из двух протонов и двух нейтронов, имеет сферическую форму с радиусом 10^-5 метра. Масса альфа-частицы составляет 6,68 * 10^-27 килограмм.

История открытия

На рубеже XIX-XX веков два физика с мировым именем открыли существование альфа-частиц. Это были новозеландский физик Эрнест Резерфорд, который работал в Канаде в городе Монреале, и французский химик и физик Поль Вийяр, который ставил свои эксперименты в Париже. Эти два ученых изучали различные виды радиации по их свойствам проникать через различные среды, а также по их взаимодействию с искусственным магнитным полем.

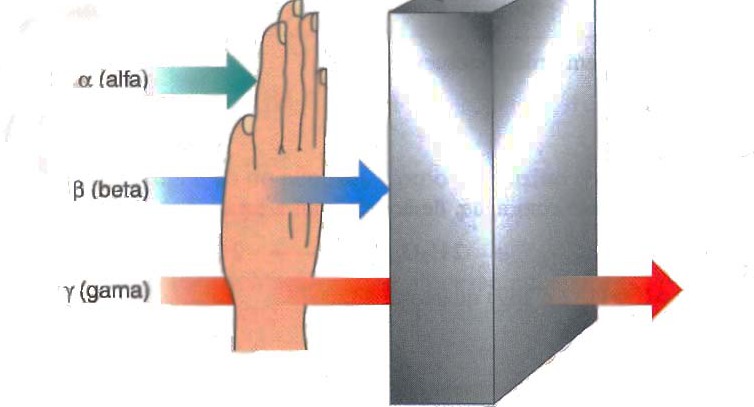
В результате этих экспериментов Резерфорд выделил три типа радиоактивного излучения: альфа, бета и гамма. Альфа-лучи были определены как лучи, имеющие наименьшую проникающую способность через различные предметы среди изучаемых видов радиации.

Элементарные частицы: протоны и нейтроны

В физике любой частице принято приписывать две основные характеристики — электрический заряд и массу, так как эти критерии определяют во многом ее свойства и поведение в конкретных физических условиях.

Как было сказано выше, альфа-частица состоит из двух протонов и двух нейтронов. Протон представляет собой элементарную частицу, имеющую массу 1,6726 * 10^-27кг и заряд +1,602 * 10^–19 Кл. Что касается нейтрона, то его масса в 1,00137 раз больше, чем у протона, то есть составляет 1,67489*10^-27кг. Заряд нейтрона равен нулю, то есть эта частица является электрически нейтральной (отсюда и название — «нейтрон»).

Альфа-частицы и их заряд

Заряд и массу альфа-частицы можно определить, если принимать во внимание названные выше цифры, а также учитывать, что сама частица состоит из двух протонов и двух нейтронов. Заряд альфа-частицы является положительным и равен +3,204 * 10^–19 Кл. Отметим, что значение +1,602 * 10^–19 Кл принято в физике называть элементарным зарядом, поскольку он равен по модулю этим же величинам у протона и электрона. Таким образом, заряд альфа-частицы равен +2 элементарных заряда.

Масса альфа-частицы

Если учитывать аддитивное свойство физической величины «масса», то можно рассчитать самостоятельно, сколько весит альфа-частица. Приведенные выше цифры для протонов и нейтронов говорят, что масса альфа-частицы равна 6,69498 * 10^-27кг. Получается эта цифра, если сложить массы в покое двух протонов и двух нейтронов. В итоге отношение масс протона и альфа-частицы приблизительно составляет 1/4. То есть альфа-частица в четыре раза тяжелее протона.

Однако множество проведенных экспериментов по установлению точной массы этой частицы говорят, что масса покоя альфа-частицы составляет 6,68 * 10 * 10^-27кг, то есть она меньше на 0,015 * 10^-27кг полученного выше значения. Куда же девается разница? Ответ на этот вопрос достаточно прост — она переходит в энергию. Дело в том, что при образовании альфа-частицы из протонов и нейтронов в результате ядерных взаимодействия между ними выделяется энергия в виде электромагнитного излучения, два протона и два нейтрона переходят в более выгодное энергетическое состояние — нашу альфа-частицу.

Энергия образования

Чтобы рассчитать энергию образования альфа-частицы, следует воспользоваться знаменитым уравнением Эйнштейна, которое связывает массу и энергию через одну из фундаментальных постоянных нашей Вселенной — скорость света. Это уравнение имеет вид: E = mc², где E — энергия, m — масса, c — скорость света в вакууме.

Зная, что при образовании альфа-частицы масса ее компонентов уменьшается на 0,015 * 10^-27 кг, а также зная, что скорость света составляет 3 * 10⁸ м/с, получаем энергию, которая выделяется во время этого процесса. Она равна E = 0,015 * 10^-27* 9 * 10¹⁶ = 1,35 * 10^-12 Дж. В физике элементарных частиц принято энергии записывать в электрон-вольтах (эВ). Один электрон-вольт равен 1,602177 * 10⁻¹⁹ Дж. Тогда энергия образования альфа-частицы равна 8,426 * 10⁶ эВ, или 8,426 МэВ (мегаэлектрон-вольт).

Чтобы понять, насколько велика эта энергия, можно провести простой расчет. Представим, что вся энергия образования альфа-частицы переводится на ее ускорение. Пользуясь уравнением Лоренца для нерелятивистских скоростей, то есть полагая, что кинетическая энергия-альфа частицы равна mv²/2, где v — скорость ее движения, получаем, что этой энергии образования будет достаточно, чтобы разогнать альфа-частицу до скорости 2 * 10⁷ м/c, что составляет 6,7 % от скорости света в вакууме. Отметим, что задавать вопрос о том, на сколько увеличится масса альфа-частицы при таких скоростях, не имеет смысла, поскольку увеличением ее массы можно пренебречь, так как она составит всего 0,015/6,68 * 100 = 0,2 %.

Основные физические свойства

Альфа-частица тяжелее в 4 раза протона и в 8000 раз — электрона, то есть для мира элементарных частиц она обладает большой массой. Напомним, что масса одного протона или одного нейтрона в атомных единицах (а.е.м.) равна 1, а заряд протона равен +1 в единицах элементарного заряда, то есть альфа-частица имеет заряд +2, а массу — 4. Тогда отношение заряда к массе альфа-частицы равно +1/2 = +0,5.

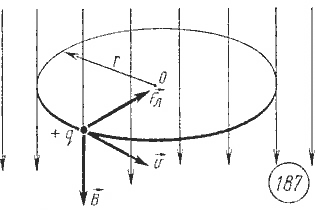
Поскольку она обладает электрическим зарядом, пролетая через электрическое или магнитное поле, она взаимодействует с ним. Чтобы определить направление силы, которая действует на альфа-частицу в магнитном поле, необходимо воспользоваться так называемым правилом левой руки: четыре пальца следует расположить вдоль вектора движения альфа частицы, а ладонь повернуть таким образом, чтобы линии магнитной индукции входили в нее. Тогда оттопыренный под прямым углом большой палец укажет направление действующей силы на движущуюся заряженную частицу.

Альфа-частицы могут разгоняться до больших скоростей, достигающих величин 15 млн км/с, то есть 5 % от скорости света. Ввиду большой массы и огромных скоростей они приобретают значительную кинетическую энергию, которая может составлять до 10 МэВ.

Проникающая способность

Поскольку альфа-частица обладает значительной массой (по сравнению с массой электрона), а также электрическим зарядом, который по модулю превышает заряд электрона в 2 раза, то ее проникающая способность, то есть способность проходить через слой вещества, является незначительной.

Во время своего движения альфа-частица испытывает столкновения с атомами, передавая им значительное количество энергии, которая приводит к ионизации атомов, то есть к отрыву электронов от них. Например, проходя всего 5 см в воздухе, альфа-частица испытывает огромное число столкновений и практически полностью теряет свою кинетическую энергию.

Любое твердое вещество легко задерживает альфа-частицу. Так, она не может пройти через слой из нескольких листов бумаги, а алюминиевая пластина толщиной всего 0,1 мм задерживает поток любой интенсивности из альфа-частиц. Еще раз отметим, хотя проникающая способность этой частицы мала, она очень сильно ионизирует всякое вещество, через которое движется.

Альфа-частица — продукт радиоактивного распада

Несмотря на то что альфа-частица состоит из протонов и нейтронов, из этих элементарных частиц она в природе не образуется, а получается в результате радиоактивного альфа-распада некоторых химических элементов.

Альфа-распад является одним из видов радиоактивного распада, в результате которого атомное ядро некоторого химического элемента, испуская альфа-частицу, превращается в ядро другого элемента, масса которого на 4 а.е.м. меньше, чем эта величина у родительского ядра, а порядковый номер в таблице Менделеева на 2 единицы меньше, чем у исходного элемента.

Альфа-распад бывает спонтанным (происходит произвольным образом в природе) и вынужденным (вызван в результате какого-либо специального воздействия на атомное ядро). Спонтанный распад характерен только для очень тяжелых атомных ядер. Так, самым легким элементом, который испытывает спонтанный альфа-распад, является теллурий 106. Уран 238 также претерпевает альфа-распад с образованием технеция 234.

Поскольку альфа-частица обладает двойным положительным элементарным зарядом, она при распаде радиоактивного ядра быстро захватывает электроны, образуя при этом атом гелия. Именно по этой причине во многих породах с большим содержанием альфа-радиоактивных элементов имеются полости, заполненные газом гелием, например в минералах, богатых ураном или торием. Основным источником альфа-частиц на Земле является благородный газ радон, который находится в почве, воде, воздухе и различных типах горных пород.

Источник

2021-03-26

Определите минимальное значение кинетической энергии $alpha$-частицы, необходимое для осуществления реакции

$^{4} He + ^{7} Li rightarrow ^{10} B + n$,

если реакция идет с поглощением энергии $Q = 2,85 МэВ$. Ядро лития неподвижно.

Решение:

До реакции мы имеем $alpha$-частицу, или ядро атома гелия, и ядро лития, а после реакции образуются ядро бора и нейтрон. Если мы подсчитаем суммарные энергии покоя частиц до реакции и после реакции, то увидим, что энергия покоя ядра бора и нейтрона больше, чем энергия покоя а -частицы и ядра лития. Эта разность как раз и равна поглощаемой энергии $Q$ при данной реакции. Такие ядерные реакции, проходящие с поглощением энергии, называют эндотермическими реакциями. Реакции, идущие, наоборот, с выделением энергии, называют экзотермическими. Отсюда понятно, что если исходные частицы неподвижны, то эндотермическая реакция не пойдет. Значит, налетающая на мишень частица должна обладать некоторой минимальной энергией, при которой начнется реакция. Величину этой энергии называют пороговой.

Наиболее удобно рассмотреть процесс неупругого взаимодействия частиц в системе отсчета, связанной с центром масс системы. Обозначим скорость $alpha$-частицы в лабораторной системе отсчета через $v_{ alpha}$. Тогда скорость движения центра масс равна

$u = frac{m_{ alpha }v_{ alpha } }{m_{ alpha } + m_{Li} }$,

где $m_{ alpha }$ и $m_{Li}$ — массы $alpha$-частицы и ядра лития. Скорость $alpha$-частицы в системе центра масс составляет

$v_{ alpha ц} = v_{ alpha } — u = frac{m_{Li}v_{ alpha } }{m_{ alpha }+ m_{Li} }$

— здесь за положительное направление выбрано направление скорости $alpha$-частицы в лабораторной системе отсчета. Скорость ядра лития в системе центра масс равна

$v_{Liц} = — u = — frac{m_{ alpha } v_{ alpha } }{m_{ alpha } + m_{Li} }$.

В этой системе отсчета при пороговой скорости $alpha$-частицы образовавшееся ядро бора и нейтрон должны покоиться. Запишем закон сохранения полной энергии до реакции и после реакции:

$m_{ alpha }c^{2} + frac{m_{ alpha }v_{ alpha ц}^{2} }{2} + m_{Li}c^{2} + frac{m_{Li} v{Liц}^{2} }{2} = m_{B}c^{2} + m_{n}c^{2}$

— энергии частиц здесь записаны для нерелятивистского случая. Подставляя в это уравнение выражения для $v_{ alpha ц}$ и $v_{Li ц}$ и учитывая, что

$m_{B}c^{2} + m_{n}c^{2} — ( m_{ alpha} c^{2} + m_{Li}c^{2}) = Q$,

получим

$frac{m_{ alpha }m_{Li} v_{ alpha }^{2} }{2(m_{ alpha} + m_{Li} ) } = Q$.

Отсюда находим минимальную кинетическую энергию $alpha$-частицы в лабораторной системе отсчета:

$E_{k} = frac{m_{ alpha}v_{ alpha }^{2} }{2} = left ( 1 + frac{m_{ alpha } }{m_{Li} } right )Q = 4,48 МэВ$.

Источник

Символическая
запись атомного ядра

где
— символ химического элемента,— зарядовое число, совпадающее с атомным
номером (число протонов в ядре),— массовое число (сумма числа протонов
и нейтронов в ядре).

Разность суммы
масс покоя входящих в ядро нуклонов и
массы покоя ядра называется дефектом
массы

где
— масса протона,— масса нейтрона,— масса ядра.

Энергия связи ядра
вычисляется по формуле

где при практических
расчетах удобно использовать массу,
выраженную в атомных единицах массы, а
квадрат скорости света
.

Для расчетов
энергии связи (дефекта масс) удобнее
пользоваться выражением, куда входят
не массы ядер, а массы нейтральных
атомов:

где
— масса атома водорода,— масса атома данного химического
элемента.

Удельная энергия
связи (энергия связи на нуклон)

Энергия, выделяющаяся
(поглощающаяся) в ходе ядерной реакции,
вычисляется по формуле

где в первой скобке
стоит сумма масс покоя частиц, вступающих
в реакцию, а во второй – сумма масс покоя
продуктов ядерной реакции.

Символическая
запись ядерной реакции может быть дана
в развернутом виде, например,

или в сокращенном
виде

В ходе любой ядерной
реакции должны выполняться законы
сохранения зарядового и массового
чисел.

Символические
обозначения некоторых частиц, участвующих
в ядерных реакциях:
— протон,— нейтрон,— дейтрон (ядро изотопа водорода),— тритон (ядро изотопа водорода),— альфа-частица (ядро изотопа гелия),— электрон,— позитрон,— нейтрино,— антинейтрино,— гамма-квант.

Закон радиоактивного
распада

где
— число радиоактивных атомов в начальный
момент времени,— число нераспавшихся атомов к моменту
времени,— постоянная радиоактивного распада.

Период полураспада
(промежуток времени, в течение которого
распадается половина первоначального
количества радиоактивных атомов) связан
с постоянной распада соотношением

Величина, обратная
постоянной распада

называется средним
временем жизни радиоактивного атома.

Активность
радиоактивного образца определяется
как отношение числа
ядер, распавшихся в изотопе, к промежутку
времени,
за которое произошел распад

Примеры решения задач

Задача 1. Определить
энергию, которая может выделиться при
образовании из протонов и нейтронов
одного моля гелия
.

Решение

Вычислим дефект
массы процесса, в ходе которого из двух
протонов и двух нейтронов образуется
ядро атома гелия. Поскольку в таблицах
приведены массы покоя атомов, а не ядер,
добавим к каждому протону по электрону
(в результате получится атом водорода),
а к ядру атома гелия добавим два электрона
(в результате получится атом гелия). В
результате получим

.
(2.3.1)

Используя табличные
данные (,,),
находим

(2.3.2)

При помощи (2.3.2)
определяем энергетический эффект от
слияния протонов и нейтронов в атом
гелия

Как известно, число
частиц в одном моле любого вещества
равно постоянной Авогадро, поэтому при
образовании из протонов и нейтронов
одного моля гелия должна выделиться
энергия

Задача 2. Под
действием протонов могут происходить
реакции термоядерного деления:

а)
;
б).

Какие изотопы
используются в качестве мишеней в этих
реакциях? Определить энергию
,
выделяющуюся в ходе реакций.

Решение

Для ответа на
первый вопрос воспользуемся законами
сохранения зарядового и массового
чисел. Для первой реакции это позволяет
записать уравнения

,
,

решая которые
получаем

,
,

что позволяет при
помощи таблицы Менделеева определить
первую мишень:

Аналогичные
вычисления для второй реакции дают
ответ:

Теперь аналогично
задаче 1 определяем энергетический
выход реакция, предполагая, что
кинетической энергией бомбардирующих
мишени протонов можно пренебречь:

а)
;

б)
.

Сравнение полученных
значений с энергией покоя протона
,
показывает, что использованное при
решении пренебрежение кинетической
энергией протона справедливо только
для нерелятивистских протонов.

Задача 3. Протоны
с кинетической энергией
бомбардируют литиевую мишень, в результате
чего наблюдается ядерная реакция.
Найти кинетическую энергию каждой
альфа-частицы и угол между направлениями
их разлета, если разлет происходит
симметрично по отношению к направлению
налетающих протонов.

Решение

Воспользуемся для
решения задачи законами сохранения
импульса и энергии. Суммарная кинетическая
энергия альфа-частиц очевидно равняется
сумме кинетической энергии протона и
энергетическому выходу ядерной реакции:

.
(2.3.3)

Обозначая угол,
который образует импульс альфа-частицы
с импульсом протона через
,
и проектируя закон сохранения импульса
на направление движения протона, получаем

.
(2.3.4)

Используя
классическую формулу связи кинетической
энергии и импульса (это оправдано, так
как рассматриваемые в задаче энергии
намного меньше энергий покоя участвующих
в реакции частиц)

(2.3.5)

и формулу
энергетического выхода ядерной реакции

,
(2.3.6)

из (2.3.3), (2.3.4) находим

,
(2.3.7)

.
(2.3.8)

Подстановка в
(2.3.7), (2.3.8) числовых значений с учетом
найденного при решении предыдущей
задачи энергетического выхода реакции
дает:

Задача 4. За время
начальное количество некоторого
радиоактивного изотопа уменьшилось враза. Во сколько разоно уменьшится за время?

Решение

Воспользуемся
законом радиоактивного распада

.
(2.3.9)

Согласно условию
задачи

,
.
(2.3.10)

Логарифмируя
первое из уравнений (2.3.10), получаем

что после подстановки
во второе уравнение (2.3.10) дает

Задача 5. Известно,
что из радиоактивного полония
массойза времядня в результате его распада образуется
гелий объемомпри нормальных условиях. Определить по
этим данным период полураспада данного
изотопа полония.

Решение

Начальное число
атомов полония найдем из формулы
молекулярно-кинетической теории

.
(2.3.11)

Число распавшихся
атомов полония в предположении, что не
происходит других реакций альфа-распада,
будет равно образовавшемуся числу
атомов гелия, которое можно определить
при помощи уравнения состояния идеального
газа

.
(2.3.12)

Из закона
радиоактивного распада находим

,
(2.3.13)

что после подстановки
(2.3.11), (2.3.12) дает уравнение

.
(2.3.14)

Учитывая формулу
связи постоянной распада и периода
полураспада
и решая уравнение (2.3.14) с учетом,
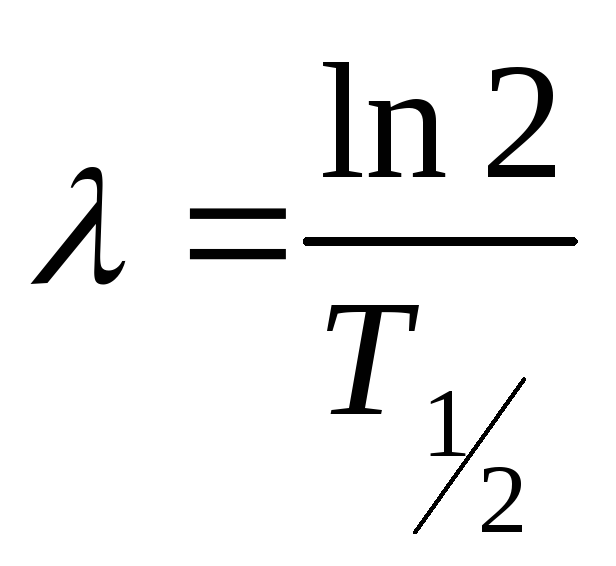
находим значение периода полураспада

Источник