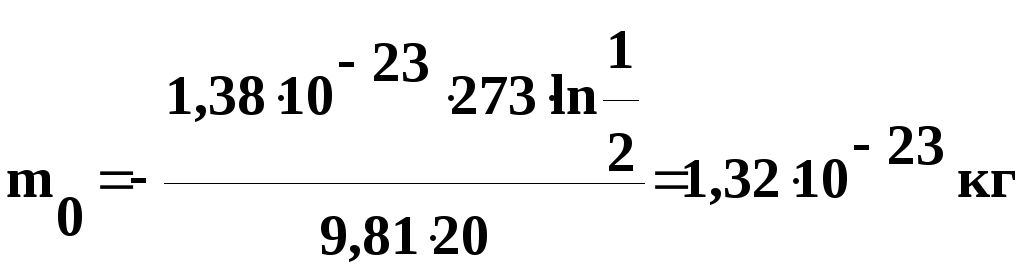Калькулятор расчётов массы, скорости, кинетической энергии
Условные обозначения формулы: m — масса тела, V — скорость, E — кинетическая энергия.
Формула расчёта кинетической энергии: E=m*V2/2. Масса тела, умноженная на скорость в квадрате и разделённая на два.
Формула расчёта массы : m=E/V2*2. Кинетическая энергия, разделённая на скорость в квадрате и умноженное на два.
Формула расчёта скорости: V=[квадратный корень][E/(1/2*m)]. Кинетическую энергию, делим на половину массы и извлекаем квадратный корень.
Заполните поля, оставив, пустым, только поле которое вы хотите узнать. Например: чтобы узнать кинетическую энергию, заполните массу и скорость.
Калькулятор расчёта массы, скорости, кинетической энергии, онлайн
Потенциальная энергия тела
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Как найти массу, зная кинетическую энергию и скорость?
(Выразите пожалуйста массу!
).
На этой странице вы найдете ответ на вопрос Как найти массу, зная кинетическую энергию и скорость?. Вопрос
соответствует категории Физика и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Как найти массу,если известна скорость и кинетическая энергия?
-
- 0
-
-
- 0
-
2*кин.єнергия и разделить на квадрат скорости
-
Комментариев (0)
Ваш ответ
В предыдущих статьях мы видели как найти массу с ускорением и силой и без ускорения и силы. Итак, в этом посте мы рассмотрим, как рассчитать массу по силе и скорости, используя несколько подходов и задач.
Существуют различные подходы к нахождению массы, но второй закон Ньютона самый простой. Это поможет вам найти массу, используя силу и скорость. Более того, формула центростремительной силы, теорема работы-энергии и кинематические уравнения движения также помогают нам найти массу, используя силу и скорость.
Масса, сила и скорость — это слова физики, которые мы также используем в нашей повседневной жизни, и они каким-то образом взаимосвязаны.
Сила — это не что иное, как физический эффект, вызывающий изменение состояния движения объекта или тела. Масса, фундаментальное свойство любого физического тела, говорит нам, сколько вещества содержится в этом конкретном теле. Фактически, он ведет себя как сопротивление, оказываемое телом, когда оно вынуждено изменить свое состояние с точки зрения движения или положения. Когда объект или тело меняют свое положение со временем под действием силы, это измерение относится к скорости объекта.

Рассмотрим каждый метод вычисление массы с помощью силы и скорость один за другим.
Как рассчитать массу по силе и скорости, используя Второй закон Ньютона:
Второй закон Ньютона можно выразить по-разному. В утверждении говорится, что когда сила действует на возражающую частицу, эта сила равна изменение импульса со временем. Следующее уравнение можно использовать для выражения этого утверждения:
Здесь буква p может использоваться для обозначения импульса объекта или частицы. Однако мы знаем, что это произведение массы и скорости объекта. В результате это записывается математически как:
р = мв
Когда мы подставляем указанное выше уравнение количества движения в уравнение силы, мы получаем следующее:
Теперь масса увеличивается только тогда, когда скорость объекта достигает скорости света. Однако здесь дело обстоит иначе. Поскольку скорость частицы или объекта не очень высока, то есть близка к скорости света, масса объекта остается постоянной. В результате мы предполагаем, что со временем изменяется только скорость, а не масса. В результате приведенное выше уравнение можно представить в виде:
………. (1)
Или,
F = ma ………. (2)
Таким образом, с точки зрения силы и скорости масса объекта может быть рассчитана следующим образом:
………. (3)
Таким образом, из уравнения (3), если мы знаем силу, действующую на тело, и то, как скорость изменяется со временем, легко вычислить массу, используя второй закон Ньютона.
Проблема: при приложении силы 25 Н скорость объекта изменяется на 5 м / с каждую секунду. Какой была бы масса объекта?
Данный:
Сила, действующая на объект F = 25 Н
Изменение скорости dv = 5 м / с
Изменение во времени dt = 1 с
Найти:
Масса объекта m =?
Решение:
Масса объекта:
∴ м = 5 кг
Таким образом, применяя силу 25 Н на объект массой 5 кг, его скорость меняется на 5 м / с каждую секунду.
Как рассчитать массу по силе и скорости с использованием центростремительной силы:
Когда тело движется по изогнутой траектории, на него действует центростремительная сила, имеющая направление внутрь, или, можно сказать, к центру.. Центростремительная сила, действующая на тело, движущееся по круговой траектории радиуса R, определяется выражением:
………. (4)
Таким образом, масса объекта, движущегося по круговой траектории, определяется как:
………. (5)
Здесь Fc используется для центростремительной силы.
Так может быть измерена масса объекта, движущегося по круговой траектории. cрассчитано с использованием центростремительная сила, скорость и радиус пути.
Проблема: Под действием центростремительной силы 3 Н шар, прикрепленный к концу струны, вращается по горизонтальной окружности с угловой скоростью 5 рад / с.-1. Какая масса у мяча, если длина шнура 60 см?
Данный:
Центростремительная сила Fc = 3 Н
Угловая скорость ⍵ = 5 рад / с
Длина шнура (радиус шнура) r = 60 см = 0.6 м.
Найти:
Масса шара m =?
Решение:
Прежде чем найти массу шара, мы находим скорость.
Скорость в терминах угловых скорость определяется выражением:
v = ⍵r
∴ v = 5 Х 0.6
∴ v = 3 м / с
Таким образом, масса мяча:
∴ м = 0.2 кг = 200 г
Таким образом, масса мяча составляет 200 граммов.
Как рассчитать массу по силе и скорости, используя Третье кинематическое уравнение движения:
Ниже приводится третье кинематическое уравнение движения:
v2 = ты2 + 2ad ………. (6)
Он показывает соотношение между начальной и конечной скоростью. Теперь мы можем применить Второй закон Ньютона (уравнение (2)) к этому уравнению и получить:
v2 = ты2 + 2 (Ф / м) д
v2 — ты2 = 2 (Ф / м) d ………. (7)
Таким образом, используя третье кинематическое уравнение, массу объекта можно рассчитать следующим образом:
………. (8)
Если вы знаете расстояние (d), которое проходит объект, когда его скорость v отличается от его начальной скорости u в результате действия силы F. В этом случае мы можем использовать третье кинематическое уравнение движения для вычисления его массы.
Проблема: предположим, что объект движется со скоростью 3 м / с. Когда к объекту прилагается сила 20 Н, он перемещается на 5 м со скоростью 7 м / с. Определить массу объекта.
Данный:
Начальная скорость объекта u = 3 м / с
Конечная скорость объекта v = 7 м / с
Сила, приложенная к объекту F = 20 Н
Расстояние, пройденное объектом под действием силы d = 5 м
Найти:
Масса объекта m =?
Решение:
Масса объекта:
∴ м = 5 кг
Таким образом, масса объекта составляет 5 кг.
Как рассчитать массу по силе и скорости, используя теорему об энергии работы:
Когда к объекту прикладывается сила, он перемещается на определенное расстояние. В результате, согласно теореме об энергии работы, работа, совершаемая объектом для перемещения на это расстояние, равна кинетической энергии, полученной объектом. Одним словом, работа превращается в энергию. Выражаясь математически:
W = KE ………. (9)
Однако работа, проделанная с объектом для перемещения на расстояние d, выглядит следующим образом:
W = F ᐧ d ………. (10)
А кинетическая энергия объекта со скоростью v равна:
………. (11)
Из уравнений (9), (10) и (11):
………. (12)
Таким образом, используя теорему об энергии работы, масса объекта определяется как:
………. (13)
Таким образом, мы можем утверждать, что нахождение массы из теоремы о работе энергии является частным случаем нахождения массы из третьего кинематического уравнения, где начальное значение объекта скорость равна нулю, подразумевая, что изначально считается, что он находится в состоянии покоя.
Проблема: предположим, что коробка лежит на горизонтальной поверхности. При толкании с силой 60 Н он скользит по поверхности на 15 м со скоростью 30 м / с. Определите массу объекта.
Данный:
Усилие, приложенное к коробке F = 60 Н
Расстояние, пройденное коробкой под действием силы d = 15 м.
Скорость объекта на этом расстоянии v = 30 м / с
Найти:
Масса ящика m =?
Решение:
Масса ящика:
∴ м = 2 кг
Таким образом, масса ящика 2 кг.
• Основное уравнение
кинетической теории газов
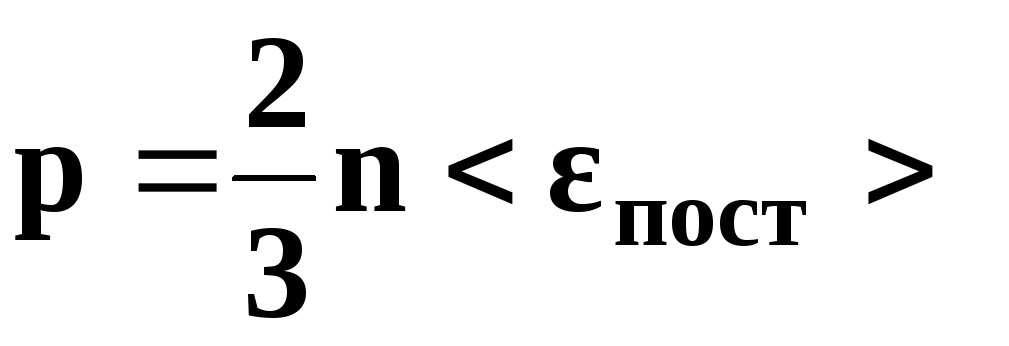
где
р — давление
газа, n
– концентрация
молекул (число молекул в единице объема),
—
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по
большому
ансамблю частиц, m0
– масса
молекулы,
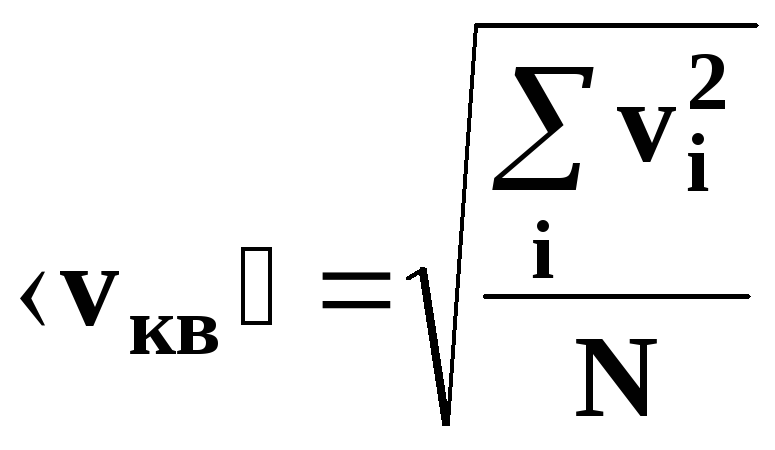
средняя квадратичная скорость движения
молекул.
• Средняя
кинетическая энергия поступательного
движения одной молекулы
,
где
k
=
1,38·10-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.
•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):
,
где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.
• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (iпост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
iвр
= 2, у
многоатомных iвр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.
• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
.
• Средняя
кинетическая энергия вращательного
движения одной молекулы:
•
Средняя суммарная
кинетическая энергия одной молекулы:
,
где
i
– число степеней свободы молекулы
(i=iпост+
iвр).
• Средняя
квадратичная скорость молекулы:
• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:
,
где m0
– масса одной молекулы, М
– молярная масса вещества, причем
,
NA=
6,023·1023
1/моль –
число Авогадро.
• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:
или
,
где
p
– давление
на высоте h
над уровнем
моря, p0
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.
•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:
,
где
n
– концентрация частиц, обладающих
потенциальной энергией Wп
, n0
— концентрация
частиц в точках поля с Wп
= 0.
Примеры
решения задач
Задача
1. Найти
среднюю кинетическую энергию
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
вращательного движения всех молекул
кислорода массойm
= 4 г.
Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.
Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:
Подставим
в полученную формулу значения k
= 1,38·10-23
Дж/К, и Т
= 350 К, получим
Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:
Число
всех молекул газа можно вычислить по
формуле:
,
где NA
– число
Авогадро,
—
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:
Подставляем
числовые значения: NA
= 6,023·1023
1/моль ; m
= 4 г = 4·10-3
кг ; М
= 32·10-3
кг/моль;
=
4,83·10-21
Дж:
Выведем
размерность полученной величины:
Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.
Решение.
Воспользуемся формулой распределения
Больцмана:
,
где
Wп
= m0gh
– потенциальная
энергия частицы в поле сил тяжести.
Подставив
это выражение в формулу распределения
Больцмана, получим:
Логарифмируем
обе части уравнения по основанию е,
тогда:
,
откуда
Подставив
числовые значения в полученную формулу,
найдем
Выведем
размерность полученной величины:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #