Основной
закон взаимодействия электрических
зарядов был найден Шарлем Кулоном в
1785 г. экспериментально. Кулон установил,
что сила
взаимодействия
между двумя небольшими заряженными
металлическими шариками обратно
пропорциональна квадрату расстояниямежду ними и зависит от величины зарядов
и
:
,
где
—коэффициент
пропорциональности
.
Силы,
действующие на заряды,
являются центральными,
то есть они направлены вдоль прямой,
соединяющей заряды.
-
Для
одноименных зарядов произведение
и сила
соответствует взаимному отталкиванию
зарядов, -
для
разноимнных зарядов
,
и силасоответствует взаимному притяжению
зарядов.
Закон
Кулона
можно записать в
векторной форме:,
где
—вектор
силы, действующей на заряд
со стороны заряда
,
— радиус-вектор,
соединяющий заряд
с зарядом
;
— модуль радиус-вектора.
Сила,
действующая на заряд
со стороны
равна
,
.
Закон Кулона в
такой форме
-
справедлив
только
для взаимодействия точечных электрических
зарядов,
то есть таких заряженных тел, линейными
размерами которых можно пренебречь по
сравнению с расстоянием между ними. -
выражает
силу взаимодействия
между неподвижными электрическими
зарядами, то есть это электростатический
закон.
Формулировка
закона Кулона:
Сила
электростатического взаимодействия
между двумя точечными электрическими
зарядами прямо пропорциональна
произведению величин зарядов и обратно
пропорциональна квадрату расстояния
между ними.
Коэффициент
пропорциональности
в законе Кулоназависит
-
от свойств среды
-
выбора единиц
измерения величин, входящих в формулу.
Поэтому
можно
представить отношением,
где
—коэффициент,
зависящий только от выбора системы
единиц измерения;
— безразмерная
величина, характеризующая электрические
свойства среды, называется относительной
диэлектрической проницаемостью среды.
Она не зависит от выбора системы единиц
измерения и равна единице в вакууме.
Тогда
закон Кулона примет вид:,
для
вакуума
,
тогда
—относительная
диэлектрическая проницаемость среды
показывает, во сколько раз в данной
среде сила взаимодействия между двумя
точечными электрическими зарядами
и
,
находящимися друг от друга на расстоянии,
меньше, чем в вакууме.
В
системе СИ коэффициент
,
и
закон
Кулона имеет вид:.
Это
рационализированная
запись закона Кулона.
— электрическая
постоянная,
.
В
системе СГСЭ
,
.
В
векторной форме закон Кулона
принимает вид
где
—вектор
силы, действующей на заряд
со стороны заряда
,

радиус-вектор, соединяющий заряд
с зарядом
(рис. 1.2),
r
–модуль радиус-вектора
.
Всякое
заряженное тело состоит из множества
точечных электрических зарядов, поэтому
электростатическая
сила, с которой одно заряженное тело
действует на другое, равна векторной
сумме сил, приложенных ко всем точечным
зарядам второго тела со стороны каждого
точечного заряда первого тела.
1.3.Электрическое поле. Напряженность.
Пространство,
в котором находится электрический
заряд, обладает определенными физическими
свойствами.
-
На
всякий
другой заряд,
внесенный в это пространство, действуют
электростатические силы Кулона. -
Если в каждой
точке пространства действует сила, то
говорят, что в этом пространстве
существует силовое поле. -
Поле наряду с
веществом является формой материи. -
Если
поле стационарно, то есть не меняется
во времени, и создается неподвижными
электрическими зарядами, то такое поле
называется электростатическим.
Электростатика
изучает только электростатические поля
и взаимодействия неподвижных зарядов.
Для
характеристики электрического поля
вводят понятие напряженности.
Напряженностью
в каждой точке электрического поля
называется вектор
,
численно равный отношению силы, с которой
это поле действует на пробный положительный
заряд, помещенный в данную точку, и
величины этого заряда, и направленный
в сторону действия силы.
Пробный
заряд,
который вносится в поле, предполагается
точечным и часто называется пробным
зарядом.
— Он
не участвует в создании поля,
которое с его помощью измеряется.
—
предполагается, что этот заряд не
искажает исследуемого поля,
то есть он достаточно мал и не вызывает
перераспределения зарядов, создающих
поле.
Если
на пробный точечный заряд
поле действует силой
,
то напряженность.
Единицы напряженности:
СИ:
СГСЭ:
В
системе СИ выражение
для
поля точечного заряда:
.
В векторной форме:
Здесь
– радиус-вектор, проведенный из зарядаq
, создающего поле, в данную точку.
Т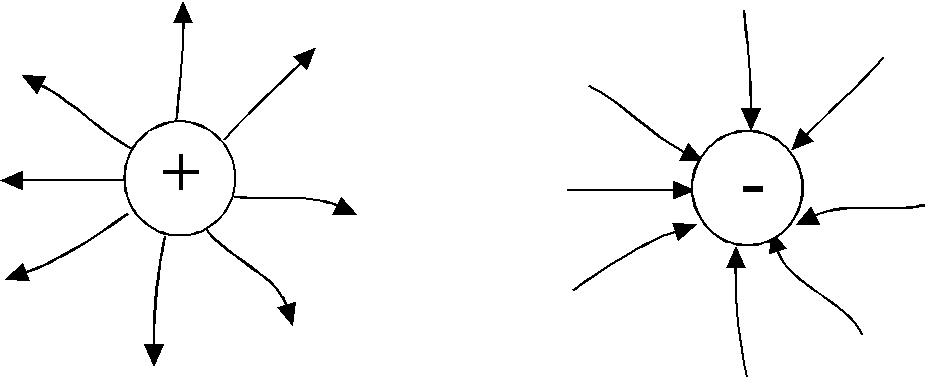
образом,векторы
напряженности электрического поля
точечного заряда q
во всех точках поля направлены радиально
(рис.1.3)
— от
заряда, если он положительный, «исток»
— и
к заряду, если он отрицательный
«сток»
Для
графической интерпретации
электрического поля вводят понятие
силовой линии или линии
напряженности.
Это
-
кривая,
касательная в каждой точке к которой
совпадает с вектором напряженности. -
Линия напряженности
начинается на положительном заряде и
заканчивается на отрицательном. -
Линии напряженности
не пересекаются, так как в каждой точке
поля вектор напряженности имеет лишь
одно направление.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.
История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).
У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10-9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1º. Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r2
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 — 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 1018 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10-12 Кл2/Н∙м2. Выполнив несложные вычисления, мы находим: k = 9×109 H*м2 / Кл2. В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Использованная литература:
- Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004.
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов.
- Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм.
Видео по теме
The magnitude of the electrostatic force F between two point charges q1 and q2 is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them. Like charges repel each other, and opposite charges mutually attract.
Coulomb’s inverse-square law, or simply Coulomb’s law, is an experimental law[1] of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is conventionally called electrostatic force or Coulomb force.[2] Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb, hence the name. Coulomb’s law was essential to the development of the theory of electromagnetism, maybe even its starting point,[1] as it made it possible to discuss the quantity of electric charge in a meaningful way.[3]
The law states that the magnitude of the electrostatic force of attraction or repulsion between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them.[4] Coulomb studied the repulsive force between bodies having electrical charges of the same sign:
It follows therefore from these three tests, that the repulsive force that the two balls – [that were] electrified with the same kind of electricity – exert on each other, follows the inverse proportion of the square of the distance.[5]
Coulomb also showed that oppositely charged bodies obey an inverse-square law of attraction:
Here, ke is the Coulomb constant (ke ≈ 8.988×109 N⋅m2⋅C−2),[1] q1 and q2 are the assigned magnitudes of the charges, and the scalar r is the distance between the charges.
The force is along the straight line joining the two charges. If the charges have the same sign, the electrostatic force between them is repulsive; if they have different signs, the force between them is attractive.
Being an inverse-square law, the law is analogous to Isaac Newton’s inverse-square law of universal gravitation, but gravitational forces are always attractive, while electrostatic forces can be attractive or repulsive; also gravitational forces are extremely weak as compared to electrostatic forces.[2] Coulomb’s law can be used to derive Gauss’s law, and vice versa. In the case of a single stationary point charge, the two laws are equivalent, expressing the same physical law in different ways.[6] The law has been tested extensively, and observations have upheld the law on the scale from 10−16 m to 108 m.[6]
History[edit]
Charles-Augustin de Coulomb
Ancient cultures around the Mediterranean knew that certain objects, such as rods of amber, could be rubbed with cat’s fur to attract light objects like feathers and pieces of paper. Thales of Miletus made the first recorded description of static electricity around 600 BC,[7] when he noticed that friction could render a piece of amber magnetic.[8][9]
In 1600, English scientist William Gilbert made a careful study of electricity and magnetism, distinguishing the lodestone effect from static electricity produced by rubbing amber.[8] He coined the Neo-Latin word electricus («of amber» or «like amber», from ἤλεκτρον [elektron], the Greek word for «amber») to refer to the property of attracting small objects after being rubbed.[10] This association gave rise to the English words «electric» and «electricity», which made their first appearance in print in Thomas Browne’s Pseudodoxia Epidemica of 1646.[11]
Early investigators of the 18th century who suspected that the electrical force diminished with distance as the force of gravity did (i.e., as the inverse square of the distance) included Daniel Bernoulli[12] and Alessandro Volta, both of whom measured the force between plates of a capacitor, and Franz Aepinus who supposed the inverse-square law in 1758.[13]
Based on experiments with electrically charged spheres, Joseph Priestley of England was among the first to propose that electrical force followed an inverse-square law, similar to Newton’s law of universal gravitation. However, he did not generalize or elaborate on this.[14] In 1767, he conjectured that the force between charges varied as the inverse square of the distance.[15][16]
In 1769, Scottish physicist John Robison announced that, according to his measurements, the force of repulsion between two spheres with charges of the same sign varied as x−2.06.[17]
In the early 1770s, the dependence of the force between charged bodies upon both distance and charge had already been discovered, but not published, by Henry Cavendish of England.[18] In his notes, Cavendish wrote, «We may therefore conclude that the electric attraction and repulsion must be inversely as some power of the distance between that of the 2 + 1⁄50 th and that of the 2 − 1⁄50 th, and there is no reason to think that it differs at all from the inverse duplicate ratio».
Finally, in 1785, the French physicist Charles-Augustin de Coulomb published his first three reports of electricity and magnetism where he stated his law. This publication was essential to the development of the theory of electromagnetism.[4] He used a torsion balance to study the repulsion and attraction forces of charged particles, and determined that the magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
The torsion balance consists of a bar suspended from its middle by a thin fiber. The fiber acts as a very weak torsion spring. In Coulomb’s experiment, the torsion balance was an insulating rod with a metal-coated ball attached to one end, suspended by a silk thread. The ball was charged with a known charge of static electricity, and a second charged ball of the same polarity was brought near it. The two charged balls repelled one another, twisting the fiber through a certain angle, which could be read from a scale on the instrument. By knowing how much force it took to twist the fiber through a given angle, Coulomb was able to calculate the force between the balls and derive his inverse-square proportionality law.
Scalar form[edit]
Coulomb’s law can be stated as a simple mathematical expression. The scalar form gives the magnitude of the vector of the electrostatic force F between two point charges q1 and q2, but not its direction. If r is the distance between the charges, the magnitude of the force is

The constant ke is called the Coulomb constant and is equal to 1/4πε0, where ε0 is the electric constant; ke ≈ 8.988×109 N⋅m2⋅C−2. If the product q1q2 is positive, the force between the two charges is repulsive; if the product is negative, the force between them is attractive.[19]
Vector form[edit]
In the image, the vector F1 is the force experienced by q1, and the vector F2 is the force experienced by q2. When q1q2 > 0 the forces are repulsive (as in the image) and when q1q2 < 0 the forces are attractive (opposite to the image). The magnitude of the forces will always be equal.
Coulomb’s law in vector form states that the electrostatic force 




where 





The vector form of Coulomb’s law is simply the scalar definition of the law with the direction given by the unit vector, 








The electrostatic force 


System of discrete charges[edit]
The law of superposition allows Coulomb’s law to be extended to include any number of point charges. The force acting on a point charge due to a system of point charges is simply the vector addition of the individual forces acting alone on that point charge due to each one of the charges. The resulting force vector is parallel to the electric field vector at that point, with that point charge removed.
Force 



where 





Continuous charge distribution[edit]
In this case, the principle of linear superposition is also used. For a continuous charge distribution, an integral over the region containing the charge is equivalent to an infinite summation, treating each infinitesimal element of space as a point charge 
For a linear charge distribution (a good approximation for charge in a wire) where 


For a surface charge distribution (a good approximation for charge on a plate in a parallel plate capacitor) where 


For a volume charge distribution (such as charge within a bulk metal) where 


The force on a small test charge 

where it the «continuous charge» version of Coulomb’s law is never supposed to be applied to locations for which 

Coulomb constant[edit]
The Coulomb constant is a proportionality factor that appears in Coulomb’s law as well as in other electric-related formulas. Denoted 





Prior to the 2019 redefinition of the SI base units, the Coulomb constant was considered to have an exact value:
Since the 2019 redefinition,[25][26] the Coulomb constant is no longer exactly defined and is subject to the measurement error in the fine structure constant. As calculated from CODATA 2018 recommended values, the Coulomb constant is[27]
With electric charge defined as in the Gaussian and Heaviside–Lorentz systems, the corresponding constant has different, dimensionless values.
In the Gaussian system (as for the electrostatic system), the unit charge (esu or statcoulomb) is defined in such a way that the Coulomb constant disappears, as it has the value of one and becomes dimensionless:[28]
In the Heaviside–Lorentz system, also called rationalized units, the Coulomb constant is dimensionless:
Limitations[edit]
There are three conditions to be fulfilled for the validity of Coulomb’s inverse square law:[29]
- The charges must have a spherically symmetric distribution (e.g. be point charges, or a charged metal sphere).
- The charges must not overlap (e.g. they must be distinct point charges).
- The charges must be stationary with respect to each other.
The last of these is known as the electrostatic approximation. When movement takes place, Einstein’s theory of relativity must be taken into consideration, and a result, an extra factor is introduced, which alters the force produced on the two objects. This extra part of the force is called the magnetic force, and is described by magnetic fields. For slow movement, the magnetic force is minimal and Coulomb’s law can still be considered approximately correct, but when the charges are moving more quickly in relation to each other, the full electrodynamics rules (incorporating the magnetic force) must be considered.
Electric field[edit]
If two charges have the same sign, the electrostatic force between them is repulsive; if they have different sign, the force between them is attractive.
An electric field is a vector field that associates to each point in space the Coulomb force experienced by a unit test charge.[20] The strength and direction of the Coulomb force 



If the field is generated by a positive source point charge 

The magnitude of the electric field E can be derived from Coulomb’s law. By choosing one of the point charges to be the source, and the other to be the test charge, it follows from Coulomb’s law that the magnitude of the electric field E created by a single source point charge Q at a certain distance from it r in vacuum is given by
A system N of charges 

Atomic forces[edit]
Coulomb’s law holds even within atoms, correctly describing the force between the positively charged atomic nucleus and each of the negatively charged electrons. This simple law also correctly accounts for the forces that bind atoms together to form molecules and for the forces that bind atoms and molecules together to form solids and liquids. Generally, as the distance between ions increases, the force of attraction, and binding energy, approach zero and ionic bonding is less favorable. As the magnitude of opposing charges increases, energy increases and ionic bonding is more favorable.
Relation to Gauss’s law[edit]
Deriving Gauss’s law from Coulomb’s law[edit]
Gauss’s law can be derived from Coulomb’s law and the assumption that electric field obeys the superposition principle, which says that the resulting field is the vector sum of fields generated by each particle (or the integral, if the charges are distributed in a region of space).
Outline of proof
Coulomb’s law states that the electric field due to a stationary point charge is:
where
- er is the radial unit vector,
- r is the radius, |r|,
- ε0 is the electric constant,
- q is the charge of the particle, which is assumed to be located at the origin.
Using the expression from Coulomb’s law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give
where ρ is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem[30]
where δ(r) is the Dirac delta function, the result is
Using the «sifting property» of the Dirac delta function, we arrive at
which is the differential form of Gauss’ law, as desired.
Note that since Coulomb’s law only applies to stationary charges, there is no reason to expect Gauss’s law to hold for moving charges based on this derivation alone. In fact, Gauss’s law does hold for moving charges, and in this respect Gauss’s law is more general than Coulomb’s law.
Deriving Coulomb’s law from Gauss’s law[edit]
Strictly speaking, Coulomb’s law cannot be derived from Gauss’s law alone, since Gauss’s law does not give any information regarding the curl of E (see Helmholtz decomposition and Faraday’s law). However, Coulomb’s law can be proven from Gauss’s law if it is assumed, in addition, that the electric field from a point charge is spherically symmetric (this assumption, like Coulomb’s law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Outline of proof
Taking S in the integral form of Gauss’ law to be a spherical surface of radius r, centered at the point charge Q, we have
By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is
where r̂ is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get
which is essentially equivalent to Coulomb’s law. Thus the inverse-square law dependence of the electric field in Coulomb’s law follows from Gauss’ law.
In relativity[edit]
Coulomb’s law can be used to gain insight into the form of the magnetic field generated by moving charges since by special relativity, in certain cases the magnetic field can be shown to be a transformation of forces caused by the electric field. When no acceleration is involved in a particle’s history, Coulomb’s law can be assumed on any test particle in its own inertial frame, supported by symmetry arguments in solving Maxwell’s equation, shown above. Coulomb’s law can be expanded to moving test particles to be of the same form. This assumption can be justified by obtaining the correct form of field equations, that is with respect to agreement with Maxwell’s equations. Considering the charge to be invariant of observer, the electric and magnetic fields of a uniformly moving point charge can hence be derived by the Lorentz transformation of the four force on the test charge in the charge’s frame of reference, given by Coulomb’s law and attributing magnetic and electric fields by their definitions given by the form of Lorentz force.[31] The fields hence found for uniformly moving point charges are given by:[32]
where 






This form of solutions need not obey Newton’s third law as is the case in the framework of special relativity (yet without violating relativistic-energy momentum conservation).[33] Note that the expression for electric field reduces to Coulomb’s law for non-relativistic speeds of the point charge and that the magnetic field in non-relativistic limit (approximating 
Coulomb potential[edit]
Quantum field theory[edit]
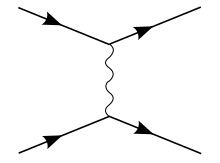
The most basic Feynman diagram for QED interaction between two fermions
The Coulomb potential admits continuum states (with E > 0), describing electron-proton scattering, as well as discrete bound states, representing the hydrogen atom.[35] It can also be derived within the non-relativistic limit between two charged particles, as follows:
Under Born approximation, in non-relativistic quantum mechanics, the scattering amplitude 
This is to be compared to the:
where we look at the (connected) S-matrix entry for two electrons scattering off each other, treating one with «fixed» momentum as the source of the potential, and the other scattering off that potential.
Using the Feynman rules to compute the S-matrix element, we obtain in the non-relativistic limit with 
Comparing with the QM scattering, we have to discard the 
where Fourier transforming both sides, solving the integral and taking 
as the Coulomb potential.[36]
However, the equivalent results of the classical Born derivations for the Coulomb problem are thought to be strictly accidental.[37][38]
The Coulomb potential, and its derivation, can be seen as a special case of the Yukawa potential, which is the case where the exchanged boson – the photon – has no rest mass.[35]
Simple experiment to verify Coulomb’s law[edit]
Experiment to verify Coulomb’s law.
It is possible to verify Coulomb’s law with a simple experiment. Consider two small spheres of mass 





|
|
(1) |
and
|
|
(2) |
Dividing (1) by (2):
|
|
(3) |
Let 

|
|
(Coulomb’s law) |
so:
|
|
(4) |
If we now discharge one of the spheres, and we put it in contact with the charged sphere, each one of them acquires a charge 

|
|
(5) |
We know that 
Dividing (4) by (5), we get:
|
|
(6) |
Measuring the angles 



|
|
(7) |
Using this approximation, the relationship (6) becomes the much simpler expression:
|
|
(8) |
In this way, the verification is limited to measuring the distance between the charges and checking that the division approximates the theoretical value.
See also[edit]
- Biot–Savart law
- Darwin Lagrangian
- Electromagnetic force
- Gauss’s law
- Method of image charges
- Molecular modelling
- Newton’s law of universal gravitation, which uses a similar structure, but for mass instead of charge
- Static forces and virtual-particle exchange
References[edit]
- ^ a b c Huray, Paul G. (2010). Maxwell’s equations. Hoboken, New Jersey: Wiley. pp. 8, 57. ISBN 978-0-470-54991-9. OCLC 739118459.
- ^ a b Halliday, David; Resnick, Robert; Walker, Jearl (2013). Fundamentals of Physics. John Wiley & Sons. pp. 609, 611. ISBN 9781118230718.
- ^ Roller, Duane; Roller, D. H. D. (1954). The development of the concept of electric charge: Electricity from the Greeks to Coulomb. Cambridge, Massachusetts: Harvard University Press. p. 79.
- ^ a b Coulomb (1785). «Premier mémoire sur l’électricité et le magnétisme» [First dissertation on electricity and magnetism]. Histoire de l’Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 569–577.
- ^ Coulomb (1785). «Second mémoire sur l’électricité et le magnétisme» [Second dissertation on electricity and magnetism]. Histoire de l’Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 578–611.
Il résulte donc de ces trois essais, que l’action répulsive que les deux balles électrifées de la même nature d’électricité exercent l’une sur l’autre, suit la raison inverse du carré des distances.
- ^ a b Purcell, Edward M. (21 January 2013). Electricity and magnetism (3rd ed.). Cambridge. ISBN 9781107014022.
- ^ Cork, C.R. (2015). «Conductive fibres for electronic textiles». Electronic Textiles: 3–20. doi:10.1016/B978-0-08-100201-8.00002-3. ISBN 9780081002018.
- ^ a b Stewart, Joseph (2001). Intermediate Electromagnetic Theory. World Scientific. p. 50. ISBN 978-981-02-4471-2.
- ^ Simpson, Brian (2003). Electrical Stimulation and the Relief of Pain. Elsevier Health Sciences. pp. 6–7. ISBN 978-0-444-51258-1.
- ^ Baigrie, Brian (2007). Electricity and Magnetism: A Historical Perspective. Greenwood Press. pp. 7–8. ISBN 978-0-313-33358-3.
- ^ Chalmers, Gordon (1937). «The Lodestone and the Understanding of Matter in Seventeenth Century England». Philosophy of Science. 4 (1): 75–95. doi:10.1086/286445. S2CID 121067746.
- ^ Socin, Abel (1760). Acta Helvetica Physico-Mathematico-Anatomico-Botanico-Medica (in Latin). Vol. 4. Basileae. pp. 224–25.
- ^ Heilbron, J.L. (1979). Electricity in the 17th and 18th Centuries: A Study of Early Modern Physics. Los Angeles, California: University of California Press. pp. 460–462 and 464 (including footnote 44). ISBN 978-0486406886.
- ^ Schofield, Robert E. (1997). The Enlightenment of Joseph Priestley: A Study of his Life and Work from 1733 to 1773. University Park: Pennsylvania State University Press. pp. 144–56. ISBN 978-0-271-01662-7.
- ^ Priestley, Joseph (1767). The History and Present State of Electricity, with Original Experiments. London, England. p. 732.
- ^ Elliott, Robert S. (1999). Electromagnetics: History, Theory, and Applications. ISBN 978-0-7803-5384-8.
- ^ Robison, John (1822). Murray, John (ed.). A System of Mechanical Philosophy. Vol. 4. London, England: Printed for J. Murray.
- ^ Maxwell, James Clerk, ed. (1967) [1879]. «Experiments on Electricity: Experimental determination of the law of electric force.». The Electrical Researches of the Honourable Henry Cavendish… (1st ed.). Cambridge, England: Cambridge University Press. pp. 104–113.
- ^ «Coulomb’s law». Hyperphysics.
- ^ a b c Feynman, Richard P. (1970). The Feynman Lectures on Physics Vol II. ISBN 9780201021158.
- ^ a b c Fitzpatrick, Richard (2006-02-02). «Coulomb’s law». University of Texas.
- ^ «Charged rods». PhysicsLab.org.
- ^ Walker, Jearl; Halliday, David; Resnick, Robert (2014). Fundamentals of physics (10th ed.). Hoboken, NJ: Wiley. p. 614. ISBN 9781118230732. OCLC 950235056.
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, p. 15, ISBN 978-92-822-2272-0
- ^ BIPM statement: Information for users about the proposed revision of the SI (PDF)
- ^ «Decision CIPM/105-13 (October 2016)». The day is the 144th anniversary of the Metre Convention.
- ^ Derived from ke = 1 / (4πε0) – «2018 CODATA Value: vacuum electric permittivity». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ Jackson, John D. (1999). Classical Electrodynamics. p. 784. ISBN 9788126510948.
- ^ Discussion on physics teaching innovation: Taking Coulomb’s law as an example. Education Management and Management Science. CRC Press. 2015-07-28. pp. 465–468. doi:10.1201/b18636-105. ISBN 978-0-429-22704-2.
- ^ Griffiths, David J. (2013). Introduction to Electrodynamics (4th ed.). Prentice Hall. p. 50.
- ^ Rosser, W. G. V. (1968). Classical Electromagnetism via Relativity. pp. 29–42. doi:10.1007/978-1-4899-6559-2. ISBN 978-1-4899-6258-4.
- ^ Heaviside, Oliver (1894). Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge.
- ^ Griffiths, David J. (1999). Introduction to electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. p. 517. ISBN 0-13-805326-X. OCLC 40251748.
- ^ Purcell, Edward (2011-09-22). Electricity and Magnetism. Cambridge University Press. doi:10.1017/cbo9781139005043. ISBN 978-1-107-01360-5.
- ^ a b Griffiths, David J. (16 August 2018). Introduction to quantum mechanics (Third ed.). Cambridge, United Kingdom. ISBN 978-1-107-18963-8.
- ^ «Quantum Field Theory I + II» (PDF). Institute for Theoretical Physics, Heidelberg University.
- ^ Baym, Gordon (2018). Lectures on quantum mechanics. Boca Raton. ISBN 978-0-429-49926-5. OCLC 1028553174.
- ^ Gould, Robert J. (21 July 2020). Electromagnetic processes. Princeton, N.J. ISBN 978-0-691-21584-6. OCLC 1176566442.
[edit]
- Coulomb, Charles Augustin (1788) [1785]. «Premier mémoire sur l’électricité et le magnétisme». Histoire de l’Académie Royale des Sciences. Imprimerie Royale. pp. 569–577.
- Coulomb, Charles Augustin (1788) [1785]. «Second mémoire sur l’électricité et le magnétisme». Histoire de l’Académie Royale des Sciences. Imprimerie Royale. pp. 578–611.
- Coulomb, Charles Augustin (1788) [1785]. «Troisième mémoire sur l’électricité et le magnétisme». Histoire de l’Académie Royale des Sciences. Imprimerie Royale. pp. 612–638.
- Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- Tamm, Igor E. (1979) [1976]. Fundamentals of the Theory of Electricity (9th ed.). Moscow: Mir. pp. 23–27.
- Tipler, Paul A.; Mosca, Gene (2008). Physics for Scientists and Engineers (6th ed.). New York: W. H. Freeman and Company. ISBN 978-0-7167-8964-2. LCCN 2007010418.
- Young, Hugh D.; Freedman, Roger A. (2010). Sears and Zemansky’s University Physics: With Modern Physics (13th ed.). Addison-Wesley (Pearson). ISBN 978-0-321-69686-1.
External links[edit]
- Coulomb’s Law on Project PHYSNET
- Electricity and the Atom—a chapter from an online textbook
- A maze game for teaching Coulomb’s law—a game created by the Molecular Workbench software
- Electric Charges, Polarization, Electric Force, Coulomb’s Law Walter Lewin, 8.02 Electricity and Magnetism, Spring 2002: Lecture 1 (video). MIT OpenCourseWare. License: Creative Commons Attribution-Noncommercial-Share Alike.
Между заряженными телами существует сила взаимодействия, благодаря которой они могут притягиваться или отталкиваться друг от друга. Закон Кулона описывает данную силу, показывает степень её действия в зависимости от размеров и формы самого тела. Об этом физическом законе пойдёт речь в данной статье.
Содержание
- 1 Неподвижные точечные заряды
- 2 Крутильные весы Шарля Кулона
- 3 Коэффициент пропорциональности k и электрическая постоянная
- 4 Направление силы Кулона и векторный вид формулы
- 5 Где закон Кулона применяется на практике
- 6 Направление сил в законе Кулона
- 7 История открытия закона
Неподвижные точечные заряды
Закон Кулона применим к неподвижным телам, размер которых намного меньше их расстояния до других объектов. На таких телах сосредоточен точечный электрический заряд. При решении физических задач размерами рассматриваемых тел пренебрегают, т.к. они не имеют особого значения.
На практике покоящиеся точечные заряды изображаются следующим образом:
В данном случае q1 и q2 — это положительные электрические заряды, и на них действует сила Кулона (на рисунке не показана). Размеры точечных объектов не имеют значения.
Обратите внимание! Покоящиеся заряды располагаются друг от друга на заданном расстоянии, которое в задачах обычно обозначается буквой r. Далее в статье данные заряды будем рассматривать в вакууме.
Крутильные весы Шарля Кулона
Это прибор, разработанный Кулоном в 1777 году, помог вывести зависимость силы, названной в последствии в его честь. С его помощью изучается взаимодействие точечных зарядов, а также магнитных полюсов.
Крутильные весы имеют небольшую шёлковую нить, расположенную в вертикальной плоскости, на которой висит уравновешенный рычаг. На концах рычага расположены точечные заряды.
Под действием внешних сил рычаг начинает совершать движения по горизонтали. Рычаг будет перемещаться в плоскости до тех пор, пока его не уравновесит сила упругости нити.
В процессе перемещений рычаг отклоняется от вертикальной оси на определённый угол. Его принимают за d и называют углом поворота. Зная величину данного параметра, можно найти крутящий момент возникающих сил.
Крутильные весы Шарля Кулона выглядят следующим образом:
Коэффициент пропорциональности k и электрическая постоянная 
В формуле закона Кулона есть параметры k — коэффициент пропорциональности или — электрическая постоянная. Электрическая постоянная
представлена во многих справочниках, учебниках, интернете, и её не нужно считать! Коэффициент пропорциональности в вакууме на основе
можно найти по известной формуле:
Здесь — электрическая постоянная,
— число пи,
— коэффициент пропорциональности в вакууме.
Дополнительная информация! Не зная представленные выше параметры, найти силу взаимодействия между двумя точечными электрическими зарядами не получится.
Формулировка и формула закона Кулона
Чтобы подытожить вышесказанное, необходимо привести официальную формулировку главного закона электростатики. Она принимает вид:
Сила взаимодействия двух покоящихся точечных зарядов в вакууме прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Причём произведение зарядов необходимо брать по модулю!
В данной формуле q1 и q2 — это точечные заряды, рассматриваемые тела; r2 — расстояние на плоскости между этими телами, взятое в квадрате; k — коэффициент пропорциональности ( для вакуума).
Направление силы Кулона и векторный вид формулы
Для полного понимания формулы закон Кулона можно изобразить наглядно:
F1,2 — сила взаимодействия первого заряда по отношению ко второму.
F2,1 — сила взаимодействия второго заряда по отношению к первому.
Также при решении задач электростатики необходимо учитывать важное правило: одноимённые электрические заряды отталкиваются, а разноимённые притягиваются. От этого зависит расположение сил взаимодействия на рисунке.
Если рассматриваются разноимённые заряды, то силы их взаимодействия будут направлены навстречу друг другу, изображая их притягивание.
Формула основного закона электростатики в векторном виде можно представить следующим образом:
— сила, действующая на точечный заряд q1, со стороны заряда q2,
— радиус-вектор, соединяющий заряд q2 с зарядом q1,
Важно! Записав формулу в векторном виде, взаимодействующие силы двух точечных электрических зарядов надо будет спроецировать на ось, чтобы правильно поставить знаки. Данное действие является формальностью и часто выполняется мысленно без каких-либо записей.
Где закон Кулона применяется на практике
Основной закон электростатики — это важнейшее открытие Шарля Кулона, которое нашло своё применение во многих областях.
Работы известного физика использовались в процессе изобретения различных устройств, приборов, аппаратов. К примеру, молниеотвод.
При помощи молниеотвода жилые дома, здания защищают от попадания молнии во время грозы. Таким образом, повышается степень защиты электрического оборудования.
Молниеотвод работает по следующему принципу: во время грозы на земле постепенно начинают скапливаться сильные индукционные заряды, которые поднимаются вверх и притягиваются к облакам. При этом на земле образуется немаленькое электрическое поле. Вблизи молниеотвода электрическое поле становится сильнее, благодаря чему от острия устройства зажигается коронный электрический заряд.
Далее образованный на земле заряд начинает притягиваться к заряду облака с противоположным знаком, как и должно быть согласно закону Шарля Кулона. После этого воздух проходит процесс ионизации, а напряжённость электрического поля становится меньше возле конца молниеотвода. Таким образом, риск попадания молнии в здание минимален.
Обратите внимание! Если в здание, на котором установлен молниеотвод, попадёт удар, то пожара не произойдёт, а вся энергия уйдёт в землю.
На основе закона Кулона было разработано устройство под названием “Ускоритель частиц”, которое пользуется большим спросом сегодня.
В данном приборе создано сильное электрическое поле, которое увеличивает энергию попадающих в него частиц.
Направление сил в законе Кулона
Как и говорилось выше, направление взаимодействующих сил двух точечных электрических зарядов зависит от их полярности. Т.е. одноимённые заряды будут отталкиваться, а разноимённые притягиваться.
Кулоновские силы также можно назвать радиус-вектором, т.к. они направлены вдоль линии, проведённой между ними.
В некоторых физических задачах даются тела сложной формы, которые не получается принять за точечный электрический заряд, т.е. пренебречь его размерами. В сложившейся ситуации рассматриваемое тело необходимо разбить на несколько мелких частей и рассчитывать каждую часть по отдельности, применяя закон Кулона.
Полученные при разбиении вектора сил суммируются по правилам алгебры и геометрии. В результате получается результирующая сила, которая и будет являться ответом для данной задачи. Данный способ решения часто называют методом треугольника.
История открытия закона
Взаимодействия двух точечных зарядов рассмотренным выше законом в первый раз были доказаны в 1785 Шарлем Кулоном. Доказать правдивость сформулированного закона физику удалось с использованием крутильных весов, принцип действия которых также был представлен в статье.
Кулон также доказал, что внутри сферического конденсатора нет электрического заряда. Так он пришёл к утверждению, что величину электростатических сил можно менять путём изменения расстояния между рассматриваемыми телами.
Таким образом, закон Кулона по-прежнему является главнейшим законом электростатики, на основе которого было сделано немало величайших открытий. В рамках данной статьи была представлена официальная формулировка закона, а также подробно описаны его составляющие части.
Два неподвижных тела, обеспеченные определенным зарядом, взаимодействуют.
Они притягиваются либо отталкиваются. И математическое описание той самой величины действия и является законом Кулона.
Но речь идет именно о точечном заряде, когда отсутствуют сторонние источники электромагнитных полей и не учитывается стороннее воздействие.
Закон Кулона же описывает ту самую силу, исходя из формы и размеров тех самых тел.
Где F — сила воздействия, q1 b q2 — уровень заряда (в кулонах), r — расстояние (от центра тел, в метрах), k — индекс пропорциональности.
Содержание
- История открытия
- Формулировка
- Коэффициент пропорциональности K и электрическая постоянная с точки зрения физики
- Направление силы Кулона и векторный вид формулы
- Устройство крутильных весов Шарля Кулона
- Закон Кулона для зарядов в вакууме
- Закон Кулона для зарядов в веществе
- Закон Кулона в диэлектриках
- Где применяется на практике
- Ограничение в применении
- Прямая и обратная пропорциональность
- Закон Амонтона-Кулона
История открытия
Физическое свойство открыто в 1785 году Шарлем Кулоном.
Точнее, он его подтвердил, а в дальнейшем — вывел математическую зависимость.
Опыты он проводил с помощью обычных металлических шариков.
Итоговое заключение: сила взаимодействия в условиях безвоздушного пространства имеет прямую зависимость от произведения этих модулей и обратную пропорциональность корню расстояния.
И на основе этого в дальнейшем был выведен закон сохранения точечного электрического заряда закон Кулона, что сейчас является основной электростатики.
Кстати, воздействие зарядов ранее на протяжении 20 лет изучал английский физик-теоретик Кавендиш.
И именно он предложил теорию, что два не движущихся тела с имеющимся точечным зарядом взаимодействуют между собой.
Но какая именно сила действует при этом, в каком направлении и от каких параметров она может меняться — он не определил (точнее, не опубликовал информацию о своих выводах).
Математического обоснования он также не предоставил.
Аналогичные исследования проводил и Бернулли, и Робинсон, и Пристли.
Но никто из них не смог вывести окончательную математическую формулу для расчета взаимодействия и перевести её в общепринятую меру.
Формулировка
Текущее формулирование закона Кулона звучит следующим образом:
Но есть условия, при которых получается рассчитать взаимодействие двух точечных зарядов по закону:
- В пространстве расстояние между зарядами должно существенно превышать их физические габариты.
- Тела — статичны относительно окружающей среды.
- Тела расположены в вакууме (нивелируется возможное воздействие окружающей среды).
Но в теории, закон Кулона можно применять и для расчета электростатического взаимодействия между двумя точечными движущимися телами.
В итоговую формулу лишь потребуется добавить вектор от заряда q1 к q2.
Но расчет взаимодействия между собой точечных зарядов актуален только если тела находятся в условиях вакуума.
Для движущихся тел, находящихся в окружении определенной среды, применять радиус-вектор не представляется возможным, так как при смене положения меняется также и направление внешних действующих сил.
То есть в данном случае невозможно определить статический коэффициент зависимости.
Коэффициент пропорциональности K и электрическая постоянная с точки зрения физики
Рассчитывается сила взаимодействия при помощи индекса k, который по СГСЭ обозначает единицу заряда.
Его рассчитывать не нужно, так как с математической точки зрения он всегда равен 1 (при условии, что заряды расположены в условиях вакуума).
А вот индекс К — постоянный для заданных условий.
Это не статический показатель, заблаговременно его рассчитать невозможно.
Но для двух тел в одной среде значение К всегда остается одинаковым.
Направление силы Кулона и векторный вид формулы
Направление действующей силы Кулона зависит от того, одноименные или разноимённые точечные заряды взаимодействуют между собой.
Здесь действует основное правило электростатики, согласно которому два тела с одинаковым потенциалом отталкиваются, с разным — притягиваются.
Заряд при этом не имеет значения, учитывается именно потенциал (положительный или отрицательный).
Соответственно, в векторном виде формула выглядит так:
Где q — это электрический заряд (в кулонах), r — радиус-вектор (1/с), ℇ — постоянная (≈ 8,85 Ф/м).
Устройство крутильных весов Шарля Кулона
Для опытов Кулон использовал так называемые «крутильные весы».
Их основа — это шелковая нить (в безвоздушном пространстве).
На ней — уравновешенный рычаг, на краях которого — заряды (аналогично помещенные в вакуум).
При возникновении внешней движущей силы рычаг двигается по горизонтали. И смещается он до уравновешивания силой упругости имеющейся шелковой нити.
Рычаг при этом отклоняется от оси (обозначается как d). И зная это отклонение можно рассчитать крутящий момент кулоновского взаимодействия.
Допускается замена нити на любой другой материал, главное — рассчитать её обратное сопротивление, которое и уравновешивает всю конструкцию.
Но это — уже современная вариациях весов.
Непосредственно Шарль Кулон опыт проводил иначе.
Сперва фиксировалось положение горизонтального рычага, когда оба тела — не заряжены.
Далее одному из шариков придавался определенный заряд. По возвращению обратно в вакуум тела между собой начинали взаимодействовать.
С какой именно силой — как раз и показывала шкала отклонения (с поправкой на силу упругости нити, которая и удерживала всю конструкцию).
Данное физическое явление и позволило определить, что сила прямо пропорциональна заряду.
Чем выше потенциал тел — тем больше отклонение по шкале.
В дальнейшем аналогичный опыт проводился и в условиях воздуха.
Разница в результатах — минимальная, поэтому условно считается, что закон Кулона действует как для вакуума, так и для воздуха (за счет схожей диэлектрической проводимости пространства в единицу).
Поэтому опыт Шарля вполне реально повторить в домашних условиях при наличии источника тока и высокоточного измерительного прибора (мультиметра).
В качестве тел можно использовать все те же металлические шарики.
Закон Кулона для зарядов в вакууме
Сила отталкивания в вакууме рассчитывается с учетом эффекта поляризации (по квантовой электродинамике).
Что это означает? Что необходимо учитывать условное сопротивление электронно-позитронных пар, экранирующих непосредственно заряд.
И оно увеличивается при большем расстоянии.
То есть эффективный заряд электрона считается убывающей функцией по логарифмическому соотношению к расстоянию.
Но при этом формой, массой и габаритами точечного заряда в данном правиле также пренебрегают, оценивая их в условную единицу.
На практике, поправку с учетом эффекта поляризации делать не нужно, так как она играет роль только для микрочастиц размером в несколько атомов.
Закон Кулона для зарядов в веществе
Действие тел друг на друга, размещенных в каком-нибудь веществе, будет ниже, чем в вакууме.
Сила взаимодействия точечных зарядов рассчитывается аналогично, но добавляются 2 дополнительные составляющие:
- объем вещества (который условно взаимодействует с телами);
- проницаемость вещества (диэлектрическая).
Закон Кулона в диэлектриках
Диэлектрик приравнивается к среде, в которой из-за поляризации он снижает силу Кулона.
Уменьшение F пропорционально диэлектрической проницаемости.
Для воздуха он близок к 1, поэтому закон в этом случае рассчитывается точно так же, как и для вакуума.
Но нивелируется факт, что модуль рассматриваемого заряда может передавать заряженные частицы непосредственно диэлектрику (процесс формирования статического заряда).
И это актуально только в том случае, если данный процесс постоянный.
Если же телу придали заряд, а в дальнейшем извлекли из электромагнитного поля, то уровень заряженности постепенно меняется.
Соответственно, если между телами находится диэлектрик, чья проницаемость близка или равна бесконечности, то взаимодействия между ними не будет.
Увеличение заряда до бесконечности тоже не меняет данную формулу.
Где применяется на практике
Основной действующий закон электростатики как раз и выстроен на базовых понятиях кулоновской силы и взаимодействия электромагнитных полей.
Даже самая обычная молния — это ничто иное, как процесс формирования определенной силы взаимодействия между землей и грозовой тучей (где каждое из «тел» снабжено определенным зарядом).
И на основании этого и был придуман громоотвод, так как его потенциал всегда выше, чем у земли и других окружающих тел (даже если это антенна для приема и передачи сотового сигнала).
Схожим образом работает и защита от возможного попадания молнии в летательных аппаратах.
Там имеется специальный громоотвод (выступающая металлическая часть, имеющая больший заряд, чем корпус) и среда, поглощающая электромагнитное поле.
Также адронный коллайдер в своей работе тоже использует закон Кулона.
С его помощью рассчитывается потенциально возможное высвобождение кинетической энергии при движении или столкновении двух заряженных частиц.
Таким образом, например, удалось в 2014 году рассчитать потенциальную силу действия двух атомов в момент соприкосновения, когда у них световая скорость движения (порядка 300000 километров в секунду).
Ещё закон используется в производстве конденсаторов, кремниевых транзисторов (включая все компьютерные и мобильные процессоры), антистатических материалов (рассеивающих попадающий на них заряд), специализированной защитной одежды (для работы в условиях активных электромагнитных полей).
Также распространенный вариант использования закона Кулона — в промышленном оборудовании для очистки зерна.
Есть 2 основных их варианта:
- когда вся масса получает определенный статический заряд и при прохождении через электромагнитное поле — разделяется (по уровню силы взаимодействия);
- когда в массу добавляют металлическую стружку, а после — просеивают через сепаратор на основе электромагнита (железные опилки притягивают к себе остаточный мусор и «связываются» с ним).
Ещё одна сфера использования — это производство электромагнитных накопителей (карты памяти, жесткие диски, ленточные носители).
В них информация сохраняется в двоичном виде (0 и 1) при помощи так называемых «ячеек», взаимодействующих с точечными заряженными частицами.
И именно за счет диэлектрических свойств основания накопителя потенциальный срок хранения данных составляет более 5 лет (далее требуется либо повторно сформировать заряд, либо обеспечить установленный уровень намагниченности).
Схожая технология применяется ещё в производстве квантовых компьютеров.
Ограничение в применении
Закон Кулона является основной любых электромагнитных взаимодействий.
Но действует только на сравнительно небольших расстояниях.
Минимальное — это 10-16 метров, максимальное — несколько километров.
И рассчитывается только для не движущихся тел, расстояние между которыми не меняется.
И условное действие всех окружающих сил приравнено к нулю (за исключением поляризации среды, в которой и находятся тела с зарядом).
Соответственно, сумма моментов тоже приравнивается к нулю и не учитывается в формуле.
Но также известно, что при избыточно высоких зарядах (когда между телами формируется облако плазмы) сила взаимодействия растет в геометрической прогрессии.
Но по какой именно формуле — ученым ещё не удалось установить.
И здесь же можно заметить практическое значение силы Кулона.
Молния возникает только между землей и грозовыми тучами, которые расположены над уровнем почвы менее чем в 2 километра.
Тогда как поля заряженных ионов, находящихся в более высоких слоях атмосферы, взаимодействуют только между собой.
В противном бы случае Земля являлась бы необитаемой планетой.
Также закон не может применяться, если заряды помещаются в среду, не являющейся диэлектриком, так как имеющийся потенциал мгновенно нивелируется.
Поэтому его нельзя использовать, к примеру, для расчета потенциально опасного расстояния между трансформатором и человеком.
Прямая и обратная пропорциональность
Под пропорциональностью в данном случае необходимо понимать зависимость одной действующей силы от иной.
Взаимодействие между телами производно от их текущего заряда (чем выше — тем больше сила действует).
Обратная же пропорциональность актуальна по отношению к расстоянию: чем оно больше, тем сила меньше.
Но это актуально только для тех расстояний, при котором закон действует.
Если выполняется расчет для зарядов, расположенных в веществе или диэлектрике, то здесь тоже наблюдается обратная пропорциональность.
Чем выше показатель диэлектрической проницаемости — тем сила меньше, так как среда «поглощает» часть электромагнитного поля и рассеивает его.
Закон Амонтона-Кулона
Шарль Кулон известен не только своими открытиями в электростатике.
Он также сформулировал закон, описывающий линейную связь между силой трения, и действием (нормальной реакцией), оказываемым на тело со стороны поверхности.
Первичную формулировку предложил Гийом Амонтон ещё в 1699 году.
Кулон же подтвердил закон и описал его математической формулой F=A+ μN, где А — условный показатель «сцепления» поверхности, по которой и производится скольжение (трение), N — сила нормальной реакции, μ — коэффициент трения поверхностей.
А согласно 3 закону Ньютона, сила Амонтона-Кулона — взаимодействующая.
То есть она актуальна и в отношении статического, и динамичного тела.
И действие оказывается одновременно также на саму поверхность.
Данный закон активно используется при производстве смазочных материалов.
С его помощью можно также рассчитать условную устойчивость и эксплуатационный ресурс материалов.
Кулон, в свою очередь, только сформулировал математическое описание открытия Амонтона, без определения статических индексов.
Итого, закон Кулона — это фундаментная сила в электростатике в целом.
И на её основе было сделано множество новых открытий, связанных с электромагнитным воздействием.
Вся современная электроника, компоненты печатных плат — всё это прямо связано с законом Кулона.
















































![{displaystyle {frac {frac {L_{1}}{2ell }}{frac {L_{2}}{2ell }}}approx 4{left({frac {L_{2}}{L_{1}}}right)}^{2}Rightarrow {frac {L_{1}}{L_{2}}}approx 4{left({frac {L_{2}}{L_{1}}}right)}^{2}Rightarrow {frac {L_{1}}{L_{2}}}approx {sqrt[{3}]{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62ed1b16522d9823535ec4bef15b8def28943175)















