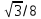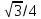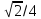Коэффициент упаковки как найти

From Wikipedia, the free encyclopedia

In crystallography, atomic packing factor (APF), packing efficiency, or packing fraction is the fraction of volume in a crystal structure that is occupied by constituent particles. It is a dimensionless quantity and always less than unity. In atomic systems, by convention, the APF is determined by assuming that atoms are rigid spheres. The radius of the spheres is taken to be the maximum value such that the atoms do not overlap. For one-component crystals (those that contain only one type of particle), the packing fraction is represented mathematically by

where N_particle is the number of particles in the unit cell, V_particle is the volume of each particle, and V_unit cell is the volume occupied by the unit cell. It can be proven mathematically that for one-component structures, the most dense arrangement of atoms has an APF of about 0.74 (see Kepler conjecture), obtained by the close-packed structures. For multiple-component structures (such as with interstitial alloys), the APF can exceed 0.74.

The atomic packing factor of a unit cell is relevant to the study of materials science, where it explains many properties of materials. For example, metals with a high atomic packing factor will have a higher «workability» (malleability or ductility), similar to how a road is smoother when the stones are closer together, allowing metal atoms to slide past one another more easily.

Single component crystal structures[edit]

Common sphere packings taken on by atomic systems are listed below with their corresponding packing fraction.

• Hexagonal close-packed (HCP): 0.74^[1]
• Face-centered cubic (FCC): 0.74^[1] (also called cubic close-packed, CCP)
• Body-centered cubic (BCC): 0.68^[1]
• Simple cubic: 0.52^[1]
• Diamond cubic: 0.34

The majority of metals take on either the HCP, FCC, or BCC structure.^[2]

Simple cubic[edit]

For a simple cubic packing, the number of atoms per unit cell is one. The side of the unit cell is of length 2r, where r is the radius of the atom.

Face-centered cubic[edit]

For a face-centered cubic unit cell, the number of atoms is four. A line can be drawn from the top corner of a cube diagonally to the bottom corner on the same side of the cube, which is equal to 4r. Using geometry, and the side length, a can be related to r as:

Knowing this and the formula for the volume of a sphere, it becomes possible to calculate the APF as follows:

Body-centered cubic[edit]

The primitive unit cell for the body-centered cubic crystal structure contains several fractions taken from nine atoms (if the particles in the crystal are atoms): one on each corner of the cube and one atom in the center. Because the volume of each of the eight corner atoms is shared between eight adjacent cells, each BCC cell contains the equivalent volume of two atoms (one central and one on the corner).

Each corner atom touches the center atom. A line that is drawn from one corner of the cube through the center and to the other corner passes through 4r, where r is the radius of an atom. By geometry, the length of the diagonal is a√3. Therefore, the length of each side of the BCC structure can be related to the radius of the atom by

Knowing this and the formula for the volume of a sphere, it becomes possible to calculate the APF as follows:

Hexagonal close-packed[edit]

For the hexagonal close-packed structure the derivation is similar. Here the unit cell (equivalent to 3 primitive unit cells) is a hexagonal prism containing six atoms (if the particles in the crystal are atoms). Indeed, three are the atoms in the middle layer (inside the prism); in addition, for the top and bottom layers (on the bases of the prism), the central atom is shared with the adjacent cell, and each of the six atoms at the vertices is shared with other six adjacent cells. So the total number of atoms in the cell is 3 + (1/2)×2 + (1/6)×6×2 = 6. Each atom touches other twelve atoms. Now let be the side length of the base of the prism and be its height. The latter is twice the distance between adjacent layers, i. e., twice the height of the regular tetrahedron whose vertices are occupied by (say) the central atom of the lower layer, two adjacent non-central atoms of the same layer, and one atom of the middle layer «resting» on the previous three. Obviously, the edge of this tetrahedron is . If , then its height can be easily calculated to be , and, therefore, . So the volume of the hcp unit cell turns out to be (3/2)√3 , that is 24√2 .

It is then possible to calculate the APF as follows:

See also[edit]

• Crystal
• Packing density
• Random close packing
• Cubic crystal system
• Diamond cubic
• Percolation threshold

References[edit]

Further reading[edit]

• Schaffer; Saxena; Antolovich; Sanders; Warner (1999). The Science and Design of Engineering Materials (2nd ed.). New York, NY: WCB/McGraw-Hill. pp. 81–88. ISBN 978-0256247664.
• Callister, W. (2002). Materials Science and Engineering (6th ed.). San Francisco, CA: John Wiley and Sons. pp. 105–114. ISBN 978-0471135760.

Под коэффициентом упаковки, или компактностью, /ш решетки понимают отношение объема, занимаемого шарами в элементар ной ячейке, ко всему объему элементарной ячейки.  [c.33]

Так как кубическая и гексагональная решетки отвечают наиболее плотной упаковке шаров, то 0,74 следует считать наивысшим значением коэффициента упаковки.  [c.34]

Очевидно, что коэффициент упаковки — величина безразмерная.  [c.238]

Следует отметить, что коэффициент упаковки не зависит от слойности плотной упаковки.  [c.164]

Такой высокий коэффициент упаковки, отличающийся от КУ для ГЦК и ГПУ структур всего на 8%, при формально существенно меньшем координационном числе (8 против 12) объясняется близостью к центральному атому шести атомов второй координационной сферы. Легко видеть, что размеры второй и первой координационных сфер различаются всего на 2/уЗ—1 = 15%. Поэтому часто координационное число этой структуры обозначают 8- 6 или 14.  [c.165]

Вычислить коэффициент упаковки для кристаллов с алмазной структурой, составленной из равновеликих шаров.  [c.186]

Современные методы моделирования основываются на том, что составленная тем или иным способом аморфная глобула с СПУ-структурой подвергается процедуре статической релаксации, при которой с помощью подходящего парного потенциала последовательно вычисляются коллективные локальные смещения атомов по принципу энергетической минимизации (модель мягких сфер). Релаксационные модели обеспечивают повышенное значение коэффициента упаковки атомов и прекрасное соответствие характера синтезированной функции парного распределения экспериментально определенной. Следует особо отметить, что процедура статической релаксации существенно меняет локальную структуру  [c.14]

Введем количественную меру плотности упаковки— коэффициент упаковки т], равный доле пространства, занятого твердыми шарами. Вычислим его, например, для ГЦК структуры. Объем элементарного кубика, содержащего четыре атома (убедитесь в этом сами), — а . Диаметр шара равен расстоянию между ближайшими узлами в решетке, т. е.  [c.93]

Следовательно, коэффициент упаковки равен  [c.93]

Аналогичным образом вычисляются коэффициенты упаковки и для других структур.  [c.93]

Из табл. 4 видно, что три характерные для металлов решетки (ГЦК, ГПУ, ОЦК) имеют достаточно высокие коэффициенты упаковки. Намного выше, чем у приведенной для сравнения простой кубической (ПК) решетки.  [c.93]

Таблица 4 Коэффициент упаковки в разных решетках

Так как вязкость жидкости явно определяется главным образом прочностью межатомной связи и коэффициентом упаковки атомов, то зависимость вязкости от состава в бинарной системе могла бы дать хорошее качественное указание, как средняя прочность межатомной связи изменяется в зависимости от структуры.  [c.87]

В равновесных условиях свободная поверхность не является источником вакансий, т. е. повышенная плотность вакансий в приповерхностных слоях устойчива. При трении в контактной зоне возникают значительные деформации и высокие температуры, способствующие образованию множества дополнительных центров активации, главным образом, на свободной поверхности твердого тела и границах зерен (причем скорость активации на поверхности металла и границах его зерен примерно одинаковая). При внешнем воздействии активированные атомы занимают более поверхностные положения и позволяют проникать вглубь имеющимся на поверхности вакантным узлам. Этот механизм образования вакансий в металле известен как процесс растворения в кристалле окружающей пустоты. По такому механизму преимущественно образуются вакансии в металлах с гранецентрированной плотноупакованной решеткой (коэффициент упаковки 0,74). Таким образом, при одновременном повышении температуры и степени деформации в тонких поверхностных слоях металла толщиной от размера атома в равновесных условиях до нескольких микрометров в результате трения накапливаются вакансии. Кроме того, тетра- и октаэдрические поры, имеющиеся в металлах с ЩК решеткой, расширяясь при повышении температуры, могут превращаться в дырки .  [c.116]

У.6.6. Коэффициент упаковки (упаковочный коэффициент, упаковочный множитель)  [c.72]

Формообразование должно придать изделию заданную форму и обеспечить возможно более плотную и равномерную упаковку частиц во всем объеме. Плотность упаковки характеризуется коэффициентом упаковки /Суп, т. е. отношением веса неорганических частиц Р , фактически находящихся в единице объема отпрессованного изделия, к удельному весу материала v , из которого состоят неорганические частицы  [c.119]

От величины коэффициента упаковки и от постоянства его по объему зависят коробление, усадка, появление трещин. При прессовании в закрытых пресс-формах, когда весь помещенный в матрицу материал под действием пуансона принимает форму внутреннего рабочего объема матрицы, внешнее давление от пуансона передается на верхний ряд частиц с передачей этого давления в нижние д ряды от частицы к частице (рис.  [c.120]

При мундштучной протяжке коэффициент упаковки уменьшается к центру сечения, так как силы формирования в этом случае приложены радиально.  [c.120]

В случае формования трубок коэффициент упаковки получается более стабильным по объему, чем при сплошных стержнях, но до диаметра 4 мм еще можно считать, что при мундштучной протяжке стержней /Суп равномерен по объему.  [c.120]

При наличии упорядоченного расположения частиц, которое характеризуется параметром ближнего порядка Р (коэффициентом упаковки частиц), интенсивность рассеяния имеет вид  [c.817]

Таким образом, коэффициент упаковки при идеальной у кладке шаров в поверхностном слое равен 0,604, в то время как в объеме соответствующий коэффициент к равен 0,740.  [c.355]

Другой очень важный параметр — атомный объем (т. е. объем, приходящийся на один атом). Для системы твердых шаров его лучше всего выразить через коэффициент упаковки т]. Последний определяется как часть полного объема, заключенная внутри шаров. Для упорядоченной плотной упаковки т) = 0,74. Учет случайности приводит к расширению системы все исследования случайных плотно упакованных структур сходятся на том, что средняя плотность упаковки составляет т) = 0,637. Одно из наиболее важных утверждений, относяш ееся к жидкому состоянию, принадлежит Берналу [78] оно гласит, что, как следует из опыта, абсолютно невозможно создать однородную (нерегулярную) систе-  [c.104]

Здесь т], как и прежде, означает коэффициент упаковки Отсюда, обращая уравнение Орнштейна — Цернике (2.42), мы можем получить и другие корреляционные функции и функции распределения типа К К) и g (i ) они, однако, не будут иметь столь простого вида. Для сравнения с экспериментом зачастую гораздо проще иметь дело с самой функцией с (Н) или с ее фурье-образом, который непосредственно получается из дифракционных опытов (см. 4.1). Точная функция с Щ для плотной жидкости из твердых шаров представляет собой, в сущности, сглаженный вариант прямоугольной функции, получающейся из формулы (2.43), и ее фурье-образ можно написать сразу. Таким образом, мы здесь имеем полезную, хотя и грубую модель жидкости, которой удобно пользоваться для оценки на обороте конверта .  [c.112]

Равенства (2.56) и (2.57) представляют собой не более чем матричное обобщение соотношений (2.42) и (2.44) для системы твердых шаров здесь также можно найти точное решение. Все парциальные прямые корреляционные функции представляются в виде конечных полиномов по степеням R [110 111] коэффициенты их суть рациональные функции парциальных коэффициентов упаковки  [c.119]

Плотноупакованные решетки — такие решетки, для которых коэффициент упаковки, определяемый как отношение полезного объема, занимаемого атомами, к полному объему элементарной ячейки, оказывается близким к предельному значению 0.74 для трехмерной решетки.  [c.32]

Коэффициент упаковки в структуре типа алмаза (плотность упаковки) мал — 0.34. Такая неплотная упаковка решетки, обусловленная направленностью связей, существенно сказывается на особенностях образования точечных дефектов, растворимости и диффузии примесей в алмазоподобных полупроводниках.  [c.43]

Кроме понятий энергии связи, удельной энергии связи на нуклон и коэффициента упаковки, в ядерной физике пользуются также понятием энергии связи или энергии присоединения последнего нейтрона и соответственно последнего протона. Энергия связи последнего нейтрона больше энергии связи последнего протона ё . Так, например, в диапазоне значений массового числа 84 -< < 104 средняя энергия связи последнего нейтрона при Z четном равна 8,480 Мэе, а при Z нечетном — 8,440 Мэе, т. е. примерно одинакова. Для энергии связи последнего протона имеем совершенно иное положение в этом же диапазоне А при четном Z средняя ёр = 8,960 Мэе, а при нечетном Z средняя Sp = 6,380 /И/, разница составляет — 2,580 Мэе. На рисунке 32 приведены значения как функции N—Z при Z = onst для четных и нечетных Z. Ядра с четным N имеют всегда большие значения энергии связи последнего нейтрона, чем соседние ядра с нечетным Л/. С увеличением числа нейтронов N в ядре величина (з уменьшается как по четным, так и по нечетным Z. На рисунке 33 приведена зависимость энергии связи последнего протона ёр от числа протонов при N = onst. Заметно монотонное уменьшение ёр с увеличением Z.  [c.97]

Кокрофта—Уолтона реакция 263 Комплексный потенциал 198 Комптоновская длина волны 35, 367 Комптононское рассеяние 33—35 Конверсия внутренняя 258 Космические лучи 73 Коэффициент упаковки 93  [c.393]

Коэффициент упаковки /—отношение отпоситель-пого избытка массы к массовому числу  [c.238]

Относительная плотность минерального вещества в отлитой заготовке, или, как ее иногда называют, коэффициент упаковки является важной характеристикой, прямо или косвенно связанной с некоторыми технологическими свойствами шликера или отливки. Относительная плотность твердой фазы в отливке указывает на степень заполнения единицы объема твердыми частицами и, следовательно, ожет быть выражена в долях единицы или процентах.  [c.59]

Изменение частоты колебаний может внести значительный вклад в Ср, если сильно меняется природа межатомной связи после смешения (как в системе Hg—К), приводя к большим изменениям длины или прочности связи. Это приводит к отрицательным отклонениям от закона Неймана — Коппа и, следовательно, делает 5 более отрицательной. Заметное влияние коэффициента упаковки при смешении возможно в результате значительного различия в атомных размерах компонентов. Оно может оказывать аналогичное воздействие и может быть значительным в системах, содержащих очень большие атомы щелочных металлов. велико и отрицательно во многих из этих систем (см. раздел 2.2 и приложение XXVII).  [c.40]

Молекулярная структура. Основные особенности жидкого агрегатного состояния вещества — способность сохранять объем, существование свободной поверхности и текучесть под действием небольшого давления. Свойства жидкостей определяются прйродой атомов, входящих в состав молекул, взаимным расположением молекул в пространстве и расстояниями между ними, от которых зависят энергия межмолекулярного взаимодействия и подвижность элементов структуры. В твердых и жидких телах существует внутренний ( свободный ) объем Vf, равный разности внешнего объема тела V и собственного объема его молекул Dq (для одного моля вещества). Отношение к = VojV, называемое коэффициентом упаковки, для низкомолекулярных органических кристаллов составляет 0,68 — 0,80, для аморфных полимеров 0,625-0,680, для жидкостей 0,5 [81]. Структуру жидкости можно представить в виде множества определенным образом организованных молекулярных комплексов (роев), совершающих тепловое движение, в которых и между которыми спонтанно возникают  [c.21]

Структурная формула повторяющегося звена nonHMqia О ьём звена, см /моль Коэффициент упаковки к  [c.44]

Для этого расс штаем значения удельного оСь ма полимера в предположении, что он имеет тот же коэффициент упаковки, rro и мономер т.е.  [c.60]

Здесь 5/ = ( 0 — / h (ki — парциальный коэффициент упаковки /-го атома) Уу- инкременты, учитывающие вклад сильных межмолекуляриых взаимодействий А = kgl к(1 — kg) = 10,418 смысл всех остальных обозначений тот же, что и в соотношении (82 ). Значения 6, и у, приведены в табл. 21.  [c.207]

He трудно увидеть, что соотношение (387) по форме близко к эмпирической форм> ле (383). Однако сомножитель, стоящий перед величиной (у/И ), не является константой, а зависит от химического строения органических жидкостей, поскольку от него зависит величина коэффициента упаковки В первом приближении Аюжно принять, что для рассматриваемых выше групп органических соединений величины к колеблются в небольших пределах и можно использовать среднее их значение. Проведенные расчеты показывают, что для группы I органргческих жидкостей ] = 0,580, для группы II к 2 0,601, для группы III А-(.р 3 = 0,586. Тогда на основе форму лы (387) запишем  [c.361]

Коэффициент упаковки. Показать, что относительная доля объема, занимаемого твердыми шарами, моделирующими атомы, при образовании перечисленных ниже структур имеет следующие значения для простой кубпческой 0,52, для объемноцентрированной кубической 0,68, для гранецентрированной кубической 0,74.  [c.57]

Плотнейшая упаковка волокон. Найти плотноупаковаицос расположение идентичных бесконечных прямых волокон в круглом поперечном сечении. Определить коэффициент упаковки для этой системы.  [c.58]

---

Основы ядерной физики (1969) — [
c.93
]

Физические величины (1990) — [
c.238
]

---

Коэффициент — упаковка

Cтраница 2

Значения коэффициентов упаковки весьма чувствительны к изменению параметров ячейки. Ошибка определения параметра 0 5 — 0 6 % меняет вторую цифру коэффициента упаковки на единицу. Такая точность хотя и вполне достижима, но имеет место не во всех работах. Поэтому к подбору материала, привлекаемого для подсчета k, следует относиться весьма осторожно.
 [16]

Под коэффициентом упаковки, или компактностью, / ш решетки понимают отношение объема, занимаемого шарами в элементар ной ячейке, ко всему объему элементарной ячейки.
 [18]

Контракции, коэффициенты упаковок и их разности рассчитаны на основании данных плотностей гидрированных мономерных соединений и плотностей полимеров.
 [19]

Чему равен коэффициент упаковки для структуры алмаза.
 [20]

Астон, определивший коэффициент упаковки многих атомных ядер, установил, что эта величина быстро растет от водорода до железа, а затем медленно уменьшается до самого конца перио дической таблицы. Значит, энергия связи ядер выше в элементах средней части периодической таблицы. Поэтому превращение тяжелых элементов в средние по массе элементы должно сопровождаться выделением энергии.
 [21]

Следовательно, коэффициенты упаковки большого числа кристаллических полимеров колеблются около этого значения. Особое внимание следует обратить на возможность весьма рыхлой упаковки макромолекул в кристалле. Естественно, что это не может противоречить принципу [1] наиплотнейшей упаковки молекул в кристалле, поскольку необходимость соблюдения симметрии, а также неудобства, возникающие при укладке асимметрично построенных молекул ( в нашем случае повторяющихся звеньев), должны приводить к появлению достаточно больших пустот.
 [23]

Для расчета коэффициентов упаковки k в ряде работ [2 — 10] были вычислены инкременты ван-дер-ваальсовых объемов ДУг большого числа атомов, валентно связанных с самыми разнообразными атомами.
 [24]

При расчете коэффициентов упаковки аморфных монолитных полимеров оказалось [2, 6], что независимо от химического строения полимера значения коэффициентов упаковки для них приблизительно одинаковы и составляют около 0 681 при 20 С.
 [25]

С ростом А коэффициент упаковки Р вначале быстро убывает и принимает отрицательные значения.
 [26]

Очевидно, что коэффициент упаковки — величина безразмерная.
 [27]

Аналогичным образом вычисляются коэффициенты упаковки и для других структур.
 [29]

Установлено, что коэффициент упаковки ароматических молекул колеблется в пределах от 0 6 до 0 8 и при / С 0 595 образование кристаллов вообще невозможно.
 [30]

Страницы:  

   1

   2

   3

   4

Содержание

• Формула коэффициента упаковки
• Простая кубическая
• Телоцентрированный кубический
• Определение объема клеток
• Определение коэффициента упаковки
• Гранецентрированная кубическая
• Определение объема клеток
• Определение коэффициента упаковки
• Компактный шестигранник
• Определение высоты ячейки
• Определение объема клеток
• Определение коэффициента упаковки
• использованная литература

Фактор упаковки — это доля, которая указывает, какой объем частицы, будь то атомы, ионы или молекулы, занимают во внутреннем пространстве кристалла. Его значение всегда меньше 1, что составляет 100% объема кристалла; точнее, его элементарная ячейка, которая представляет собой наименьшее представление всего кристалла.

Фактор упаковки 100% означает, что частицы занимают весь объем элементарной ячейки. Физически это невозможно, потому что это, например, означало бы, что атомы деформируют свои радиусы и растворяются, как если бы они были «электронной жидкостью». Геометрия атомов, сферическая для удобства, всегда приводит к образованию пустых пространств во время упаковки.

Как и в автоматах для раздачи конфет, коэффициент упаковки говорит нам, насколько «плотно» частицы находятся в кристалле: чем он больше, тем больше жевательной резинки или атомов будет в космосе.

При определении коэффициента упаковки предполагается, что атомы состоят из твердых сфер, подобных шарикам жевательной резинки или конфет из раздаточной машины (изображение выше). Между сферами всегда будут полые пространства, через которые можно заливать более мелкие сферы (примеси или добавки).

Если увеличить коэффициент упаковки, сферы будут сжаты, что сделает кристалл более компактным и плотным; или, с другой стороны, более деформируемый, как это бывает с ковкими и пластичными металлами.

Фактор упаковки применяется к любому типу стекла. Однако его расчет может быть немного утомительным, поэтому здесь он будет рассматриваться только для атомных кристаллов с простой структурой.

Указатель статей

• 1 Формула коэффициента упаковки
• 2 Простая кубическая
• 3 Объемный кубический
  • 3.1 Определение объема клеток
  • 3.2 Определение коэффициента упаковки
• 4 Гранецентрированный кубик
  • 4.1 Определение объема клеток
  • 4.2 Определение коэффициента упаковки
• 5 компактных шестигранников
  • 5.1 Определение высоты ячейки
  • 5.2 Определение объема клеток
  • 5.3 Определение коэффициента упаковки
• 6 источников

Формула коэффициента упаковки

Фактор упаковки обычно выражается в процентах. Например, если его значение составляет 40%, это означает, что частицы занимают только 40% от общего пространства элементарной ячейки; или что то же самое, что утверждать, что 60% стакана «пусто».

Сказанное выше поясняет, по какой формуле рассчитывается этот коэффициент:

• FEA = (объем атомов) / (объем элементарной ячейки)

Где FEA означает Фактор атомной упаковки, которые являются простейшими кристаллами.

Объем элементарной ячейки зависит от ее параметров (таких как длина ее сторон), с которыми мы исходим из простой геометрии, чтобы вычислить ее объем. С другой стороны, атомы определяют указанную ячейку, поэтому ее размеры можно выразить по атомным радиусам, как будет показано в следующих разделах.

Что касается объема атомов, необходимо учитывать их общее количество в элементарной ячейке (1, 2, 3 и т. Д.), А также их сферическую геометрию. Итак, формула немного изменена:

FEA = (Кол-во атомов) (Объем атома) / (Объем элементарной ячейки)

Затем, чтобы рассчитать FEA, мы должны определить No., V_атом и V_ячейка.

Простая кубическая

Простая кубическая элементарная ячейка.Источник: CCC_crystal_cell_ (непрозрачный) .svg: * Cubique_centre_atomes_par_maille.svg: Cdang (исходная идея и исполнение в SVG), Самуэль Дюпре (3D-моделирование с помощью SolidWorks), производная работа: Даниэле Пуглиси (доклад), производная работа: Даниэле Пульези 3.0 https://creativecommons.org/licenses/by-sa/3.0>, через Wikimedia Commons

Самая простая элементарная ячейка — простая кубическая. В нем у нас есть по несколько частей атомов в каждом из углов. Если мы увидим, то заметим, что длинный к этой ячейки равно 2r, поскольку именно атомы определяют ячейку. Таким образом, объем элементарной ячейки будет равен:

V_ячейка = к³ (объем куба)

= (2r)³

= 8r³

При этом объем атома будет равен:

V_атом = (4/3) πr³ (объем шара)

Каждый из углов является общим для 8 других соседних элементарных ячеек. Следовательно, у нас есть доля 1/8 в каждом углу, и поскольку их 8, мы не равняем 1 атому на элементарную ячейку (1/8 x 8 = 1).

Фактор упаковки:

FEA = (1) (4/3) πr³ / 8r³

= π/6 ≈ 52%

То есть в простой кубической ячейке атомы занимают 52% всего объема кристалла.

Телоцентрированный кубический

Определение объема клеток

Объемно-центрированная кубическая элементарная ячейка. Источник: Cubique_centre_atomes_par_maille.svg: Cdang (исходная идея и исполнение SVG), Samuel Dupré (3D-моделирование с SolidWorks), производная работа: Даниэле Пуглиси, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0> , через Wikimedia Commons

Теперь посмотрим на объемно-центрированную кубическую ячейку. Сторона к он больше не может быть равен 2r, потому что у нас есть пустое пространство между двумя атомами в углах. Следовательно, мы должны рассматривать диагональ d равный 4r (зеленый цвет), который пересекает ячейку через центр и касается противоположных углов, и другой диагонали d лица (черный цвет).

Стороны к, d и 4r нарисуйте прямоугольный треугольник, к которому мы можем применить тригонометрию, чтобы вычислить значение к:

(4р)² = d² + а²

Но с другой стороны, в основании элементарной ячейки мы имеем еще один треугольник (к, к а также d), к которому можно вычислить гипотенузу:

d²  = а² + а²

= 2a²

После подстановки получим:

(4р)² = (2a²) + а²

(4р)² = 3a²

а = (4 / √3) г

V_ячейка равно:

V_ячейка = а³

= ((4 / √3) г)³

Определение коэффициента упаковки

Обратите внимание, что относительно количества атомов у нас есть 1 атом в этой ячейке, следуя тому же выводу, сделанному для простой кубической ячейки, и еще один дополнительный атом, который расположен в центре ячейки. Таким образом, на каждую кубическую ячейку с центром в теле приходится всего 2 атома.

Тогда коэффициент упаковки становится:

FEA = (2) (4/3) πr³ / ((4 / √3) г)³

= (√3/8) π ≈ 68%

Другими словами, в кубической ячейке с центром в теле 68% объема кристалла занято атомами. Следовательно, это кристаллическое устройство более компактное (или плотное), чем простое кубическое.

Гранецентрированная кубическая

Определение объема клеток

Гранецентрированная кубическая элементарная ячейка. Источник: Cdang, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0>, через Wikimedia Commons

Давайте теперь посмотрим на гранецентрированную кубическую элементарную ячейку, очень часто встречающуюся в неорганических солях и некоторых металлах, таких как золото и серебро. Чтобы определить его коэффициент упаковки, мы должны начать, следуя предыдущим примерам, с определения объема его элементарной ячейки. Поэтому необходимо снова вычислить сторону к и так объем куба к³.

На этот раз процедура проще и прямее, так как у нас диагональ d перед которой вместе с боковыми к, сформируйте прямоугольный треугольник, к которому мы можем применить тригонометрию:

d² = а² + а²

= 2a²

Расчистка к у нас будет:

к = d / √2

Но визуально мы замечаем, что d равно 4r, поэтому сделаем замену:

к = 4r / √2

= 2r 2^1-1/2

= (2√2) г

Быть V_ячейка равно:

к³ = ((2√2) г)³

= (16√2) г³

Что касается количества атомов в ячейке, у нас снова есть восемь частей атома в каждом углу, а также одна половина атома для каждой из шести граней, которая является общей для другой соседней ячейки. Следовательно, количество атомов равно:

Кол-во атомов = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Определение коэффициента упаковки

Учитывая, что в каждой кубической ячейке с центрами на гранях по 4 атома, а также ее объем, равный (16√2) r³, затем мы можем рассчитать коэффициент упаковки:

FEA = (Кол-во атомов) (Объем атома) / (Объем элементарной ячейки)

= (4) (4/3) πr³ / (16√2) г³

= π/(3√2) ≈ 74%

Отметим, что эта ячейка даже более компактна, чем предыдущие: 74% от общего объема ячейки занято атомами. В идеальном и чистом кристалле это было бы равносильно утверждению, что 26% его объема доступно для размещения других атомов хозяина.

Компактный шестигранник

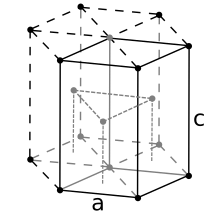
Компактная шестиугольная ячейка и ее ромбоэдрическая примитивная ячейка. Источник: Оригинал: Dornelf Вектор: DePiep, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0>, через Wikimedia Commons

Наконец, среди самых простых и компактных элементарных ячеек мы имеем компактную гексагональную ячейку. В отличие от предыдущих, расчет его объема немного сложнее. Как видно, он не кубический, поэтому имеет два параметра к а также c, последнее — высота ячейки.

Определение высоты ячейки

Гексагональную ячейку можно разложить на три ромбоэдрические ячейки, и по одной из них переходим к вычислению к а также c. Сторона к, хотя на изображении выше это не так очевидно, оно равно 2r. Вычислять cВместо этого мы используем красный треугольник и скалярное произведение внутренней треугольной призмы той же ячейки.

Нам нужно рассчитать расстояние d чтобы определить, сколько это стоит c. На полу красный треугольник равносторонний, с углом 60º. Но если вы рассмотрите другой внутренний прямоугольный треугольник со сторонами к/ 2 и d, и угол 30º (половина), то по тригонометрии мы можем определить d:

Cos (30º) = (к/2) / d

d = к/√3

А теперь рассмотрим прямоугольный треугольник, составленный из сторон c/ 2 (зеленый), к (черный и d (пунктирный):

к² = (к/√3)² + (с / 2)²

Расчистка c мы бы хотели иметь:

c = √(8/3) к

И подставив к по 2r:

c = √ (8/3) (2r)

 = √ (4 · 2/3) (2r)

= 4√ (2/3) г

Определение объема клеток

Чтобы определить объем шестиугольной ячейки, умножьте площадь шестиугольника на его высоту. Зная, что у равносторонних треугольников есть стороны к, его высота рассчитывается час. Таким образом, найдя площадь треугольника, которая в данном случае равна √3 / 4к², мы умножаем это значение на 6, чтобы получить площадь шестиугольника: 3 (√3 / 2)к²

Таким образом, объем составляет:

V_ячейка = Площадь шестиугольника x Высота

= 3(√3/2)к² х 4√ (2/3) г

И подставляя еще раз к по 2r:

V_ячейка = 3 (√3 / 2) (2r)² х 4√ (2/3) г

= 24√2 г³

Определение коэффициента упаковки

В гексагональной ячейке по углам 12 атомов, внутри которых находится 1/6 своего объема. Точно так же есть 3 внутренних атома, объемы которых являются полными, и еще 2 атома на верхней и нижней гранях, половина их объемов которых находится внутри ячейки.

Следовательно, количество атомов равно:

№ атом = 1/6 (12) + 1 (3) + 1/2 (2) = 6 атомов

И, наконец, коэффициент упаковки становится:

FEA = (Кол-во атомов) (Объем атома) / (Объем элементарной ячейки)

= (6) (4/3) πr³ / 24√2 г³

= π/(3√2) ≈ 74%

Обратите внимание, что коэффициент отсека для гексагональной ячейки такой же, как для гранецентрированной кубической ячейки. То есть оба одинаково компактны.

использованная литература

1. К. Барри Картер и М. Грант Нортон. (2007). Керамическое материаловедение и инженерия. Springer.
2. Дрожь и Аткинс. (2008). Неорганическая химия. (Четвертое издание). Мак Гроу Хилл.
3. Уиттен, Дэвис, Пек и Стэнли. (2008). Химия. (8-е изд.). CENGAGE Обучение.
4. Википедия. (2021 г.). Фактор атомной упаковки. Получено с: en.wikipedia.org
5. Брэндон. (2021 г.). Что такое атомный коэффициент упаковки (и как его рассчитать для SC, BCC, FCC и HCP)? Студент материаловедения и инженерии. Получено с: msestudent.com

Плотность
упаковки
– это доля объема кристаллической
решетки, занятая атомами.

Плотность
упаковки можно рассчитать как отношение
объема касающихся шароподобных атомов,
приходящихся на элементарную ячейку,
к объему всей ячейки; обычно плотность
упаковки выражают в процентах.

Кратчайшее
расстояние между центрами двух шаров
в элементарной ячейке равно двум радиусам
шара – 2r.
Объем шара V
= 4/3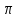r³,
объем шаров, входящих в элементарную
ячейку, V_n
= 4/3nr³,
где n
– кратность элементарной ячейки. Если
объем элементарной ячейки V₀,
то плотность упаковки равна Р = (V_n/V₀)·100
%.

Если
период решетки равен а, то V₀
= а³,
решение задачи сводится к выражению
атомного радиуса через период решетки,
для конкретной структуры следует
определить кратчайшее межатомное
расстояние, например, в алмазе 2r
= a
/4
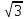
(кратчайшее расстояние, равное двум
атомным радиусам, составляет четверть
пространственной диагонали куба).

В
табл. 2.3
приведены результаты расчета плотности
упаковки для различных структур.

Таблица
2.3

Плотность
упаковки для различных структур

Тип решетки	К. ч.	Атомный радиус r	Кратность ячейки n	Р, %
Алмаз	4	а	8	34
Кубическая примитивная	6	а/2	1	52
ОЦК	8	а	2	68
ГЦК	12	а	4	74
ГПУ	12			74

С
повышением координационного числа
плотность упаковки растет.

Заполнение
междоузлий в ГЦК решетке, что соответствует
повышению кратности элементарной
ячейки, приводит к менее плотным
упаковкам.

2.8. Связь между типом структуры, координационным числом и электрофизическими свойствами

Плотнейшие
и плотные упаковки (Р = 68 – 74 %) с к.ч. 8/8
и 12/12 типичны для металлов (структуры
ОЦК, ГЦК, ГПУ) .

Наименее
плотные упаковки (Р = 34 % и подобными) с
к.ч. 4/4 (структуры алмаза, сфалерита,
вюрцита), 4/2 (куприт), 2/2 (селен) типичны
для полупроводников.

Структуры
с промежуточными значениями к.ч. 6/6 и
плотности Р
67 %, например, типаNaCl,
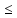
могут иметь и проводниковые свойства
(TiO,
TiN,
VN,
TiC
и др.), и полупроводниковые свойства
(PbS,
PbSe,
PbTe),
и диэлектрические (NaCl,
MgO,
CaO,
BaO).

Металлические
вещества могут кристаллизоваться и в
структуры с низкими к.ч., например, в
графите к.ч. равно 4, как и в алмазе.

Важнейшие
полупроводники образуют следующие
структуры:

алмаза:
Si,Ge,
α-Sn;

сфалерита:
ZnS,
HgS,
CdTe,
AlP,
AlAs,
AlSb,
GaP,
GaAs,
GaSb,
InP,
InAs,
InSb,
SiC,
ZnSe,
HgSe,
ZnTe,
HgTe;

куприта:
Cu₂O,
Ag₂O;

флюорита:
Mg₂Si,
Mg₂Ge;

вюрцита:
ZnS,
ZnO,
CdS,
CdSe;

хлорида
натрия: PbS,
PbSe,
PbTe;

арсенида
никеля: VS,
VSe,
FeS,
FeSe.

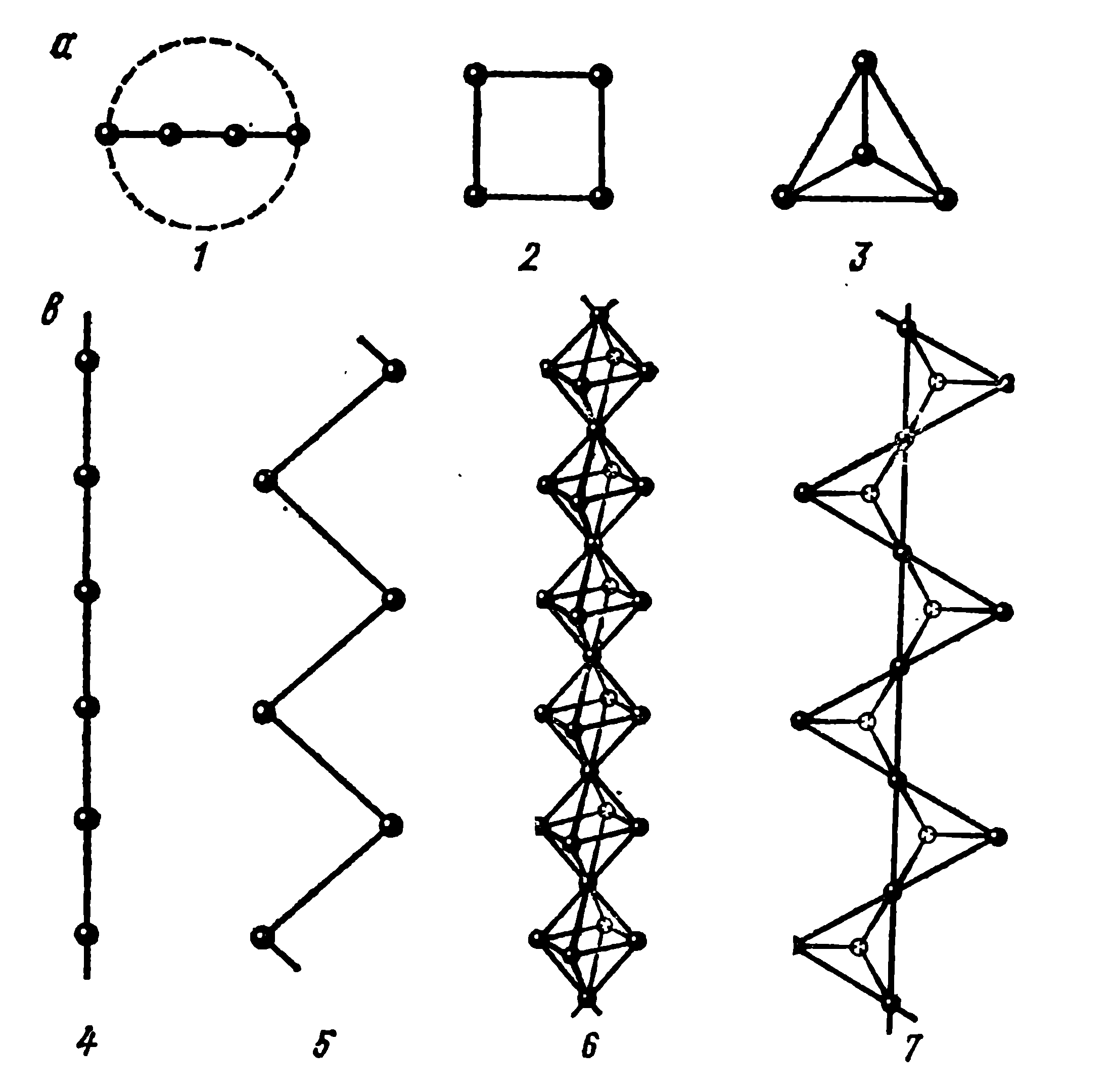
2.9. Островные, цепные и слоистые структуры

Кроме
координационных структур, в которых
межатомные расстояния между всеми
структурными единицами одинаковы (один
тип связи), в островных, цепных и слоистых
структурах (рис.2.15) могут быть выделены
группы атомов, которые образуют «острова»
(молекулы), непрерывно простирающиеся
в одном направлении (цепи), или бесконечные
в двух (слои) или трех (каркасы) измерениях.
Такие структуры являются молекулярными.

На
рис. 2.15 а изображены островные структуры:
1 — линейные, 2 – двумерные (квадрат), 3 –
трехмерные (тетраэдр). На рис. 2.15 b
показаны цепные структуры: 4 – линейная,
5 – цигзагообразная, 6 и 7 – звенья из
октаэдров и тетраэдров.

Рис.2.15.
Островные и цепные структуры

Контрольные
вопросы

1. Какая
   решетка называется простой, сложной?

2. Чем
   поликристалл отличается от монокристалла?

3. Что
   обозначает запись: (hkl),
   {hkl},
   < hkl>,
   [hkl]?

4. Какие
   значения могут принимать индексы
   Миллера?

5. Запишите
   индексы Миллера плоскостей, перпендикулярных
   ребрам куба.

6. Запишите
   индексы Миллера плоскостей, перпендикулярных
   диагоналям граней куба.

7. Запишите
   индексы Миллера плоскостей, параллельным
   граням куба.

8. Запишите
   индексы Миллера направлений,
   перпендикулярных граням куба.

9. В
   чем отличие (110), {110 }, < 110>, [110]?

10. Какое
    явление называется полиморфизмом?

11. Что
    такое изоморфизм?

12. Чем
    отличается строение стекол от строения
    кристаллов?

13. Каковы
    особенности строения аморфных тел?

14. Какие
    структуры относятся к плотным упаковкам?
    Как расположены в них атомы?

15. В
    чем отличие ГПУ от ГЦК?

16. Чему
    равны координационные числа в плотных
    упаковках?

17. Где
    расположены тетраэдрические междоузлия
    в ГЦК решетке?

18. Где
    расположены октаэдрические междоузлия
    в ГЦК решетке?

19. Что
    называется политипизмом?

20. Что
    называется кратностью элементарной
    ячейки?

21. Как
    рассчитать число атомов, приходящихся
    на элементарную ячейку?

22. Чем
    отличаются различные типы кубических
    структур?

23. Изобразите
    элементарные ячейки меди, кремния,
    NaCl,
    CsCl,
    сфалерита.

24. Поясните
    расположение атомов в решетке вюрцита.

25. На
    основе какой плотной упаковки строится
    решетка вюрцита?

26. На
    основе какой плотной упаковки строится
    решетка сфалерита?

27. Сколько
    атомов приходится на элементарную
    ячейку вюрцита?

28. Как
    рассчитывается плотность упаковки
    кристаллических структур?

29. Какие
    кристаллические решетки имеют
    максимальную плотность упаковки?

30. Какие
    кристаллические решетки имеют минимальную
    плотность упаковки?

31. Как
    связана плотность упаковки с
    координационным числом?

32. Можно
    ли отнести цепные структуры к
    координационным? Почему?

33. В
    чем разница между дальним и ближним
    порядком в твердых телах?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #