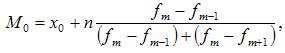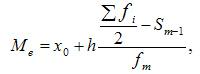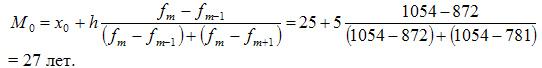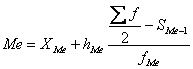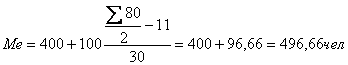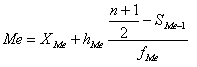Кумулята как найти медиану - Исправление недочетов и поиск решений вместе с Examum.ru

Структурные
средние величины

Мода —
это наиболее часто встречающийся вариант
ряда. Мода применяется, например, при
определении размера одежды, обуви,
пользующейся наибольшим спросом у
покупателей. Модой для дискретного ряда
является варианта, обладающая наибольшей
частотой. При вычислении моды для
интервального вариационного ряда
необходимо сначала определить модальный
интервал (по максимальной частоте), а
затем — значение модальной величины
признака по формуле:Кроме степенных
средних в статистике для относительной
характеристики величины варьирующего
признака и внутреннего строения рядов
распределения пользуются структурными
средними, которые представлены ,в
основном, модой и медианой.

где:

—
значение моды

—
нижняя граница
модального интервала

—
величина интервала

—
частота модального
интервала

—
частота интервала,
предшествующего модальному

—
частота интервала,
следующего за модальным

Медиана
— это значение признака, которое
лежит в основе ранжированного ряда и
делит этот ряд на две равные по численности
части.

Для
определения медианы в дискретном
ряду при наличии частот сначала
вычисляют полусумму частот ,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:

М_е =
(n_{(число

признаков в совокупности)} +
1)/2,

в
случае четного числа признаков медиана
будет равна средней из двух признаков
находящихся в середине ряда).

При
вычислении медианы для интервального
вариационного ряда сначала определяют
медианный интервал, в пределах которого
находится медиана, а затем — значение
медианы по формуле:

где:

—
искомая медиана

—
нижняя граница
интервала, который содержит медиану

—
величина интервала

—
сумма частот или
число членов ряда

—
сумма накопленных частот интервалов,
предшествующих медианному

—
частота медианного
интервала

Пример.
Найти моду и медиану.

Возрастные группы	Число студентов	Сумма накопленных частот ΣS
До 20 лет	346	346
20 — 25	872	1218
25 — 30	1054	2272
30 — 35	781	3053
35 — 40	212	3265
40 — 45	121	3386
45 лет и более	76	3462
Итого	3462

Решение:
В
данном примере модальный интервал
находится в пределах возрастной группы
25-30 лет, так как на этот интервал приходится
наибольшая частота (1054).

Рассчитаем
величину моды:

Это
значит что модальный возраст студентов
равен 27 годам.

Вычислим
медиану. Медианный интервал находится
в возрастной группе 25-30 лет, так как в
пределах этого интервала расположена
варианта, которая делит совокупность
на две равные части (Σf_i/2
= 3462/2 = 1731). Далее подставляем в формулу
необходимые числовые данные и получаем
значение медианы:

Это
значит что одна половина студентов
имеет возраст до 27,4 года, а другая свыше
27,4 года.

Кроме
моды и медианы могут быть использованы
такие показатели, как квартили, делящие
ранжированный ряд на 4 равные части,
децили -10 частей и перцентили — на 100
частей.

Определение
моды и медианы графическим методом

Моду
и медиану в интервальном ряду можно
определить графически.
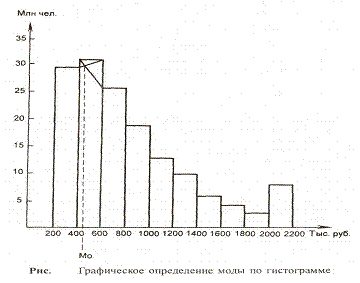
Мода определяется по гистограмме
распределения. Для этого выбирается
самый высокий прямоугольник, который
является в данном случае модальным.
Затем правую вершину модального
прямоугольника соединяем с правым
верхним углом предыдущего прямоугольника.
А левую вершину модального прямоугольника
– с левым верхним углом последующего
прямоугольника. Из точки их пересечения
опускаем перпендикуляр на ось абсцисс.
Абсцисса точки пересечения этих прямых
и будет модой распределения (рис.
5.3).

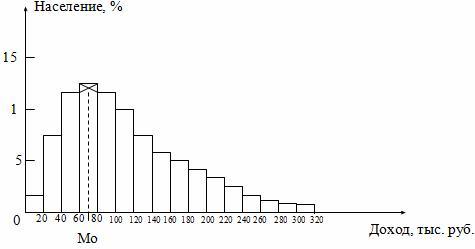
Рис.
5.3. Графическое определение моды по
гистограмме.

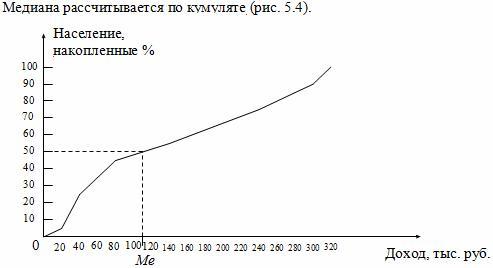
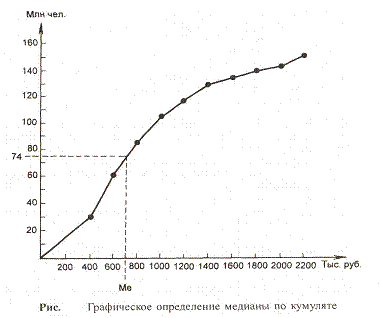
Рис.
5.4. Графическое определение медианы по
кумуляте
Для
определения медианы из точки на шкале
накопленных частот (частостей),
соответствующей 50 %, проводится прямая,
параллельная оси абсцисс до пересечения
с кумулятой. Затем из точки пересечения
опускается перпендикуляр на ось абсцисс.
Абсцисса точки пересечения является
медианой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Дискретный вариационный ряд и его характеристики

Классификация рядов распределения
Дискретный вариационный ряд, полигон частот и кумулята
Выборочная средняя, мода и медиана
Степень асимметрии вариационного ряда
Выборочная дисперсия и СКО
Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Алгоритм исследования дискретного вариационного ряда
Примеры

п.1. Классификация рядов распределения

Статистический ряд распределения – это количественное распределение единиц совокупности на однородные группы по некоторому варьирующему признаку.

В зависимости от природы признака различают атрибутивные и вариационные ряды.
Атрибутивный ряд распределения построен на качественном признаке.
Вариационный ряд распределения построен на количественном признаке.

Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.

По упорядоченности вариационные ряды делятся на упорядоченные (ранжированные) и неупорядоченные. Упорядочить ряд можно по возрастанию или убыванию исследуемого признака.

По характеру непрерывности признака вариационные ряды делятся на дискретные и интервальные.

Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.

Варианты – это отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариант.

Например:

Распределение учеников по оценкам за контрольную работу

Оценка, (x_i)	2	3	4	5	Всего
К-во учеников, (f_i)	3	15	10	5	33

В данном ряду признак – это оценка, варианты признака (x_i) – это множество {2;3;4;5}, частоты (f_i) – это количество учеников, получивших каждую из оценок.

п.2. Дискретный вариационный ряд, полигон частот и кумулята

Дискретный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся прерывно и принимающему конечное множество значений.

Общий вид дискретного вариационного ряда

Варианты, (x_i)	(x_1)	(x_2)	…	(x_k)
Частоты, (f_i)	(f_1)	(f_2)	…	(f_k)

Здесь k — число вариант исследуемого признака.
Тогда общее количество исходов (число единиц в совокупности): (N=sum_{i=1}^k f_i)

Полигон частот – это ломаная, которая соединяет точки ((x_i,f_i)).

Например:

Для распределения учеников по оценкам из нашего примера получаем такой полигон:

Относительная частота варианты (x_i) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$ Относительная частота (w_i) является эмпирической оценкой вероятности варианты (x_i) в исследуемом ряду.

Полигон относительных частот – это ломаная, которая соединяет точки ((x_i,w_i)).
Полигон относительных частот является эмпирическим законом распределения исследуемого признака.

Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)).
Ступенчатая кривая (F(x_i)), построенная по точкам ((x_i,S_i)), является эмпирической функцией распределения исследуемого признака.

Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.

Оценка, (x_i)	2	3	4	5	Всего
К-во учеников, (f_i)	3	15	10	5	33
(w_i)	0,0909	0,4545	0,3030	0,1515	1
(S_i)	0,0909	0,4545	0,8485	1	—

Полигон относительных частот (эмпирический закон распределения)

Кумулята (красная ломаная) и эмпирическая функция распределения (ступенчатая синяя кривая).

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 2\ 0,0909, 2lt xleq 3\ 0,5455, 3lt xleq 4\ 0,8485, 4lt xleq 5\ 1, xgt 5 end{cases} $$

п.3. Выборочная средняя, мода и медиана

Выборочная средняя дискретного вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$

Мода дискретного вариационного ряда – это варианта с максимальной частотой: $$ M_o=x*, f(x*)=underset{i=overline{1,k}}{max}f_i $$ Мод может быть несколько. Тогда говорят, что ряд мультимодальный.

На полигоне частот мода – это абсцисса самой высокой точки.

Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.

Алгоритм:
1. Отсортировать ряд по возрастанию.
2а. Если общее количество измерений N нечётное, найти (m=lceilfrac N2rceil) и округлить в сторону увеличения. (M_e=x_m) — искомая медиана.
2б. Если общее количество измерений N чётное, найти (m=frac N2) и вычислить медиану как среднее (M_e=frac{x_m+x_{m+1}}{2}).

На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:

Оценка, (x_i)	2	3	4	5	Всего
К-во учеников, (f_i)	3	15	10	5	33
(x_if_i)	6	45	40	25	116

$$ X_{cp}=frac{6+45+40+25}{33}=frac{116}{33}approx 3,5 $$ Средняя оценка за контрольную – 3,5.
2) Найдем моду. Максимальная частота – 15 человек – у троечников. Значит: (M_o=3).
3) Найдем медиану. Общее количество измерений N=33 — нечетное.
Находим: (m=lceilfrac N2rceil=17)
Смотрим на ряд слева направо. Сначала у нас идет 3 двоечника, затем 15 троечников.
Вместе их 18, и 17-й человек в ряду — троечник. Группа троечников является медианной: (M_e=3).
Также, медиану можно найти по графику кумуляты. (3;0,5455) – это первая слева точка, в которой ордината больше 0,5. Значит, медиана равна абсциссе этой точки, т.е. (M_e=3).

п.4. Степень асимметрии вариационного ряда

В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.

Мода, медиана и выборочная средняя совпадут, если вариационный ряд является симметричным: $$ X_{cp}=M_o=M_e $$ Если вершина распределения сдвинута влево и правая часть ветви длиннее левой (длинный правый хвост), такая асимметрия называется правосторонней. При правосторонней асимметрии: $$ M_olt M_elt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_ogt M_egt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}geq 3 $$

Например:
Для распределения учеников по оценкам мы получили (X_{cp}=3,5; M_o=3; M_e=3).
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{0,5}{0,5}=1lt 3), т.е. распределение умеренно асимметрично.

п.5. Выборочная дисперсия и СКО

Выборочная дисперсия дискретного вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac{(x_1-X_{cp})^2 f_1+(x_2-X_{cp})^2 f_2+…+(x_k-X_{cp})^2 f_k}{N}=\ =frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$

Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$

Например:
1) Найдем выборочную дисперсию для распределения учеников по оценкам:

Оценка, (x_i)	2	3	4	5	Всего
К-во учеников, (f_i)	3	15	10	5	33
(x_i^2)	4	9	16	25	—
(x_i^2 f_i)	12	135	160	125	432

$$ D=frac{12+135+160+125}{33}-3,5^2=frac{432}{33}-3,5^2approx 0,73 $$ 2) Значение СКО: (sigma=sqrt{D}approx 0,86)

п.6. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации

Исправленная выборочная дисперсия дискретного вариационного ряда определяется как: begin{gather*} S^2=frac{1}{N-1}sum_{i=1}^k(x_i-X_{cp})^2 f_i=frac{N}{N-1}D end{gather*}

В теоретической статистике доказывается, что выборочная дисперсия D является смещенной оценкой дисперсии при распространении на генеральную совокупность.
А именно, выборочная дисперсия D всегда меньше математического ожидания для дисперсии генеральной совокупности.
Исправленная выборочная дисперсия S² является несмещенной оценкой.

Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$

Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$

Если показатель вариации V<33%, то выборка считается однородной, т.е. большинство полученных в ней вариант находятся недалеко от средней, и выборочная средняя хорошо характеризует среднюю генеральной совокупности.
В противном случае, выборка неоднородна. Варианты в выборке находятся далеко от средней, есть выбросы. А значит, и в генеральной совокупности они возможны. Т.е., распространять результаты выборки на генеральную совокупность нельзя.

Внимание!

Если исследуется не выборка, а вся генеральная совокупность, дисперсию «исправлять» не нужно.

Например:
Для распределения учеников по оценкам получаем:
1) Исправленная выборочная дисперсия $$ S^2=frac{N}{N-1}D=frac{33}{32}cdot 0,73approx 0,76 $$ 2) Стандартное отклонение $$ x=sqrt{S^2}approx 0,87 $$ 3) Коэффициент вариации: $$ V=frac{0,87}{3,5}cdot 100text{%}approx 24,8text{%}lt 33text{%} $$ Выборка является однородной.
Это означает, что согласно коэффициенту вариации полученные результаты контрольной работы можно рассматривать в качестве «типичных» и распространить их на генеральную совокупность, т.е. на всех школьников, которые будут писать эту работу.

п.7. Алгоритм исследования дискретного вариационного ряда

На входе: таблица с вариантами (x_i) и частотами (f_i, i=overline{1,k})
Шаг 1. Составить расчетную таблицу. Найти (w_i,S_i,x_if_i,x_i^2,x_i^2f_i)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.

п.8. Примеры

Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:

Число постоянных заказчиков	0	1	2	3	4	5
Число фрилансеров	22	35	27	11	3	1

Исследуйте полученный вариационный ряд.

1) Вариационный ряд является дискретным.
Исследуемый признак – «число постоянных заказчиков».
Варианты признака (x_iinleft{0;1;..;5right}). Количество вариант k=6.
Составим расчетную таблицу:

(x_i)	0	1	2	3	4	5	∑
(f_i)	23	35	27	11	3	1	100
(w_i)	0,23	0,35	0,27	0,11	0,03	0,01	—
(S_i)	0,23	0,58	0,85	0,96	0,99	1	—
(x_if_i)	0	35	54	33	12	5	139
(x_i^2)	0	1	4	9	16	25	—
(x_i^2f_i)	0	35	108	99	48	25	315

2) Полигон относительных частот (эмпирический закон распределения):

Кумулята и эмпирическая функция распределения:

$$ F(x)= begin{cases} 0, xleq 0\ 0,23, 0lt xleq 1\ 0,58, 1lt xleq 2\ 0,85, 2lt xleq 3\ 0,96, 3lt xleq 4\ 0,99, 4lt xleq 5\ 1, xgt 5 end{cases} $$ 3) Выборочная средняя: $$ X_{cp}=frac1Nsum_{i=1}^k x_if_i= frac{1}{100}cdot 139=1,39 $$ Мода (абсцисса самой высокой точки на полигоне частот): (M_0=1).
Медиана (абсцисса первой слева точки на кумуляте, где значение превысило 0,5): точка (1;0,58), (M_e=1).

(X_{cp}gt M_e=M_0) – распределение асимметрично, с правосторонней асимметрией.
При этом (frac{|M_0-X_{cp}|}{|M_e-X_{cp}|}=frac{0,39}{0,39}=1lt 3), т.е. распределение умеренно асимметрично.

4) Выборочная дисперсия: $$ D=frac1Nsum_{i=1}^k x_i^2f_i-X_{cp}^2=frac{1}{100}cdot 315-1,39^2=1,2179approx 1,218 $$ CKO: $$ sigma=sqrt{D}approx 1,104 $$
5) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{100}{99}cdot 1,218approx 1,230 $$ Стандартное отклонение выборки: $$ s=sqrt{S^2}approx 1,109 $$ Коэффициент вариации: $$ V=frac{s}{X_{cp}}cdot 100text{%}=frac{1,109}{1,39}cdot 100text{%}approx 79,8text{%}gt 33text{%} $$ Представленная выборка неоднородна. Полученное значение средней (X_{cp}=1,39) не может быть распространено на генеральную совокупность всех фрилансеров.

Источник

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.

Расчёт структурных характеристик
вариационного ряда распределения.

Студент
должен:

знать:

— область применения и методику расчёта структурных
средних величин;

уметь:

— исчислять структурные средние величины;

— формулировать вывод по полученным результатам.

Методические указания

В
статистике исчисляются мода и медиана, которые относятся к структурным средним,
так как их величина зависит от строения статистической совокупности.

Расчёт моды

Модой называется значение признака
(варианта), чаще всеговстречающееся в изучаемой
совокупности. В дискретном ряду распределения модой будет варианта с наибольшей
частотой.

Например: Распределение проданной женской обуви по размерам характеризуется
следующим образом:

Размер обуви	34	35	36	37	38	39	40	41
Количество проданных пар	8	19	34	108	72	51	6	2

В этом ряду
распределения модой является 37 размер,
т.е. Мо=37 размер.

Для
интервального ряда распределения мода определяется по формуле:

где Х_Mo —
нижняя граница модального интервала;

h_Mo — величина модального интервала;

f_Mo –
частота модального интервала;

f_Mo_{—1 и}
f_Mo₊₁ – частота интервала соответственно

предшествующего модальному и следующего за ним.

Например:
Распределение рабочих по стажу работы характеризуется следующими данными.

Стаж работы, лет	до 2	2-4	4-6	6-8	8-10	10 и более
Число рабочих, чел.	4	23	20	35	11	7

Определить моду
интервального ряда распределения.

Мода интервального ряда составляет

Мода всегда бывает
несколько неопределённой, т.к. она зависит от величины групп и точного
положения границ групп. Мода широко применяется в коммерческой практике при
изучении покупательского спроса, при регистрации цен и т.п.

Расчёт медианы

Медианой в статистике называется варианта,
расположенная в середине упорядоченного ряда данных, и которая делит
статистическую совокупность на две равные части так, что у одной половины
значения меньше медианы, а у другой половины – больше её. Для определения
медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания
или убывания индивидуальных значений признака.

В дискретном
упорядоченном ряду с нечётным числом членов медианой будет варианта,
расположенная в центре ряда.

Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7
лет, т.е. Ме=7 лет

Если дискретный
упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя
арифметическая из двух смежных вариант, стоящих в центре ряда.

Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду
имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя
арифметическая из этих значений и будет медианой ряда

Чтобы определить медиану для
сгруппированных данных, необходимо считать накопленные частоты.

Например: По имеющимся данным определим медиану размера обуви

Размер обуви	Количество проданных пар	Сумма накопленных частот
34	8	8
35	19	8+19=27
36	34	27+34=61
37	108	61+108=169
38	72	—
39	51	—
40	6	—
41	2	—
Итого	300

Для
определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание
итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот
ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная
сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е.
37 и есть медиана ряда.

Если
же сумма накопленных частот против одной из вариант равна точно половине суммы
частот ряда, то медиана определяется как средняя арифметическая этой варианты и
последующей.

Например: По имеющимся данным определим медиану заработной платы рабочих

Месячная заработная плата, тыс.руб.	Число рабочих, чел.	Сумма накопленных частот
14,0	2	2
14,2	6	2+6=8
16,0	12	8+12=20
16,8	16	—
18,0	4	—
Итого:	40	—

Медиана будет равна:

Медиана
интервального вариационного ряда распределения определяется по формуле:

Где Х_Ме – нижняя граница медианного интервала;

h_Me –
величина медианного интервала;

∑f
— сумма частот ряда;

f_Ме – частота медианного интервала;

Например: По имеющимся данным о распределении предприятий по численности
промышленно – производственного персонала рассчитать медиану в интервальном
вариационном ряду

Группы предприятий по численности ППП, чел.	Число предприятий	Сумма накопленных частот
100-200	1	1
200-300	3	1+3=4
300-400	7	4+7=11
400-500	30	11+30=41
500-600	19	—
600-700	15	—
700-800	5
Итого:	80

Определим, прежде всего,
медианный интервал. В данном примере сумма накопленных частот, превышающих половину
суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный
интервал, т.е. интервал, в котором находится медиана ряда. Определим её
значение

Если же сумма накопленных частот
против одного из интервалов равна точно половине суммы частот ряда, то медиана
определяется по формуле:

где n – число
единиц в совокупности.

Например: По имеющимся данным о распределении предприятий по
численности промышленно – производственного персонала рассчитать медиану в
интервальном вариационном ряду

Группы предприятий по численности ППП, чел.	Число предприятий	Сумма накопленных частот
100-200	1	1
200-300	3	1+3=4
300-400	6	4+6=10
400-500	30	10+30=40
500-600	20	40+20=60
600-700	15	—
700-800	5
Итого:	80

чел

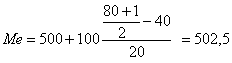
Моду и медиану в
интервальном ряду можно определить
графически:

моду
в дискретных рядах — по полигону распределения, моду в интервальных рядах — по
гистограмме распределения, а медиану — по кумуляте.

Мода интервального ряда распределения
определяется по гистограмме распределения определяют
следующим образом. Для этого выбирается самый высокий прямоугольник, который
является в данном случае модальным. Затем правую вершину модального
прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.

Медиана рассчитывается по
кумуляте. Для её определения из точки на шкале
накопленных частот (частостей), соответствующей 50%,
проводится прямая, параллельная оси абсцисс, до
пересечения с кумулятой. Затем из точки пересечения
указанной прямой с кумулятой опускается перпендикуляр
на ось абсцисс. Абсцисса точки пересечения является медианой.

Кроме моды и медианы в вариантных рядах могут быть
определены и другие структурные характеристики – квантили. Квантили
предназначены для более глубокого изучения структуры ряда распределения.

Квантиль – это значение
признака, занимающее определенное место в упорядоченной по данному признаку
совокупности. Различают следующие виды квантилей:

— квартили – значения признака, делящие упорядоченную
совокупность на четыре
равные части;

— децили
– значения признака, делящие упорядоченную совокупность на десять
равных частей;

— перцентели —
значения признака, делящие упорядоченную совокупность на сто равных частей.

Таким образом, для характеристики положения центра ряда распределения
можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя
центра распределения необходимо исходить из следующих рекомендаций:

—
для устойчивых социально-экономических
процессов в качестве показателя центра используют среднюю
арифметическую. Такие процессы характеризуются симметричными распределениями, в
которых ;

—
для неустойчивых процессов положение
центра распределения характеризуется с помощью Mo
или Me. Для асимметричных процессов предпочтительной
характеристикой центра распределения является медиана, поскольку занимает
положение между средней арифметической и модой.

Источник

Интервальный ряд

Условие:

Имеются данные о возрастном составе рабочих (лет):

18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24,
30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 25, 29, 29.

1.
Построить интервальный ряд
распределения.

2.
Построить графическое изображение
ряда.

3.
Графически определить моду и
медиану.

Решение.

1) По формуле Стерджесса совокупность надо разделить на

1 + 3,322 lg 30 = 6 групп.

Максимальный возраст – 38, минимальный – 18.

Ширина интервала

.
Так как концы интервалов должны быть целыми числами, разделим

совокупность на 5 групп. Ширина интервала – 4.

Для облегчения подсчетов расположим данные в порядке
возрастания

18, 22, 22, 23, 24, 24, 25, 25, 26, 26, 27, 27, 28, 28, 28, 29,
29, 29, 29, 29, 30, 30, 31, 32, 32, 33, 34, 35, 38, 38.

Распределение возрастного состава рабочих

№ пп	Возраст х	Частота f	Накопленная частота S
1	18-22	3	3
2	23-26	7	10
3	27-30	12	22
4	31-34	5	27
5	35-38	3	30
	Всего	30

Графически ряд можно изобразить в виде гистограммы или полигона.
Гистограмма – столбиковая диаграмма. Основание столбика – ширина
интервала. Высота столбика равна частоте.

Полигон (или многоугольник распределения) – график частот. Чтобы его
построить по гистограмме, соединяем середины верхних сторон
прямоугольников. Многоугольник замыкаем на оси Ох на
расстояниях, равных половине интервала от крайних значений х.

Мода (Мо) – это величина изучаемого признака, которая в данной
совокупности встречается наиболее часто.

Чтобы определить моду по гистограмме, надо выбрать самый высокий
прямоугольник, провести линию от правой вершины этого
прямоугольника к правому верхнему углу предыдущего
прямоугольника, и от левой вершины модального прямоугольника
провести линию к левой вершине последующего прямоугольника. От
точки пересечения этих линий провести перпендикуляр к оси х.
Абсцисса и будет модой. Мо ≈ 27,5. Значит, наиболее часто
встречаемый возраст в данной совокупности 27-28 лет.

Медиана (Mе) – это величина изучаемого
признака, которая находится в середине упорядоченного
вариационного ряда.

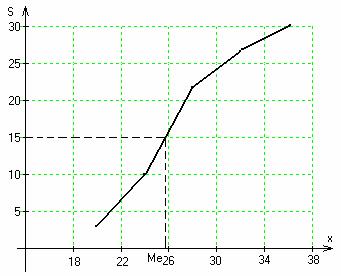
Медиану находим по кумуляте. Кумулята – график накопленных частот.
Абсциссы – варианты ряда. Ординаты – накопленные частоты.

Для определения медианы по кумуляте находим по оси ординат точку,
соответствующую 50% накопленных частот (в нашем случае 15),
проводим через неё прямую, параллельно оси Ох, и от точки её
пересечения с кумулятой проводим перпендикуляр к оси х. Абсцисса
является медианой. Ме ≈ 25,9. Это означает, что половина
рабочих в данной совокупности имеет возраст менее 26 лет.

Источник

Элементы математической статистики. Выборочный метод

Генеральная и выборочная совокупности. Статистические распределения выборок. Кумулята и ее свойства. Гистограмма и полигон статистических распределений. Числовые характеристики: выборочная средняя; дисперсия выборки; среднеквадратическое отклонение; мода и медиана для дискретных и интервальных статистических распределений выборки; эмпирические начальные и центральные моменты, асимметрия и эксцесс.

Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении статистических данных — результатах наблюдений. Первая задача математической статистики — указать способы сбора и группировки (если данных очень много) статистических сведений. Вторая задача математической статистики — разработать методы анализа статистических данных в зависимости от цели исследования. Изучение тех или иных явлений методами математической статистики служит средством решения многих вопросов, выдвигаемых наукой и практикой (правильная организация технологического процесса, наиболее целесообразное планирование и др.).

Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Генеральная и выборочная совокупности

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, для партии деталей качественным признаком может служить стандартность детали, а количественным — контролируемый размер детали. Иногда проводят сплошное обследование, т. е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяется сравнительно редко. Например, если совокупность содержит большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то случайным образом отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых проводится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда для упрощения вычислений или для облегчения теоретических выводов, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки.

Статистические распределения выборок

В результате статистической обработки материалов можно подсчитать число единиц, обладающих конкретным значением того или иного признака. Каждое отдельное значение признака будем обозначать x_1,x_2,ldots,x_n и называть вариантой, а абсолютное число, показывающее, сколько раз встречается та или иная варианта, — частотой и обозначать m_1,m_2,ldots,m_n .

Если отдельные значения признака (варианты) расположим в возрастающем или убывающем порядке и относительно каждой варианты укажем, как часто она встречается в данной совокупности, то получим статистическое распределение признака, или вариационный ряд. Он характеризует изменение (варьирование) какого-нибудь количественного признака. Следовательно, вариационный ряд представляет собой две строки (или колонки). В одной из них приводятся варианты, в другой — частоты.

Вариация признака может быть дискретной и непрерывной. Дискретной называется вариация, при которой отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число); Например: количество детей в семье; оценки, полученные студентами на экзамене; размеры обуви, проданной за день фирмой.

Непрерывной называется вариация, при которой значения признака могут отличаться одно от другого на сколь угодно малую величину. Например: стоимость реализованной продукции; уровень рентабельности предприятия; процент занятости трудоспособного населения; депозитная ставка коммерческих банков.

При непрерывной вариации распределение признака называется интервальным. Частоты относятся не к отдельному значению признака, а ко всему интервалу. Часто значением интервала принимают его середину, т. е. центральное значение.

Пример 1. Уровень рентабельности предприятий легкой промышленности характеризуется следующими данными.

Сводная таблица рентабельности предприятий легкой промышленности

Нередко вместо абсолютных значений частот используют относительные. Для этого можно использовать долю частоты того или иного варианта (а также интервала) в сумме всех частот. Такая величина называется относительной частотой и обозначается . Для получения относительных частот необходимо соответствующую частоту разделить на сумму всех частот:

$w_1=dfrac{m_1}{sumlimits_{i=1}^{n}m_i};~~~w_2=dfrac{m_2}{sumlimits_{i=1}^{n}m_i};~~~ldots,$

где w_1,~w_2 — относительная частота варианты или интервала соответственно первой, второй и т. д.

Сумма всех относительных частот равна единице:

$sumlimits_{i=1}^{n}w_1=1.$

Относительные частоты можно выражать и в процентах (тогда их сумма равна 100%).

В интервальном вариационном ряду в каждом интервале различают нижнюю и верхнюю границы интервала: нижняя граница интервала $x_{min}$ ; верхняя граница интервала $x_{max}$ величина интервала $k=x_{max}-x_{min}$ . Как правило, при построении интерваль-ных вариационных рядов в каждый интервал включаются варианты, числовые значения которых больше нижней границы и меньше или равны верхней границе. Интервальные вариационные ряды бывают с одинаковыми и неодинаковыми интервалами. В последнем случае чаще всего встречаются последовательно увеличивающиеся интервалы. Для выбора оптимальной величины интервала, т. е. такой, при которой вариационный ряд не будет громоздким и будут сохранены особенности явления, можно рекомендовать формулу

$kapproxfrac{x_{max}-x_{min}}{1+3,!2lg{n}},$ где — число единиц в совокупности.

Так, если в совокупности 200 единиц, наибольший вариант равен 49,961, а наименьший — 49,918, то

$kapproxfrac{49,!961-49,!918}{1+3,!2lg200}approxfrac{0,!043}{8,!36}approx0,!005.$

Следовательно, в данном случае оптимальной величиной интервала может служить 0,005.

Гистограмма и полигон статистических распределений. Кумулята

Для наглядного представления вариационного ряда большое значение имеют его графические изображения. Графически вариационный ряд может быть изображен в виде полигона, гистограммы и кумуляты.

Полигон распределения (дословно — многоугольник распределения) строится в прямоугольной системе координат. Величина признака откладывается на оси абсцисс, частоты или относительные частоты — по оси ординат. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но их можно применять также для интервальных рядов. В этом случае на оси абсцисс откладываются точки, соответствующие серединам данных интервалов.

Гистограмма распределения строится аналогично полигону в прямоугольной системе координат. В отличие от полигона при построении гистограммы на оси абсцисс выбирают не точки, а отрезки, изображающие интервал, а вместо ординат, соответствующих частотам или относительным частотам отдельных вариант, строят прямоугольники с высотой, пропорциональной частотам или относительным частотам интервала. В случае интервалов различной длины гистограмма распределения строится, не по частотам или относительным частотам, а по плотности интервалов (абсолютной или относительной). При этом общая площадь гистограммы равна численности совокупности, если построение проводится по абсолютной плотности, или единице, если гистограмма построена по относительной плотности.

Если соединить прямыми линиями середины верхних сторон прямоугольников, то получим полигоны распределения.

Разбивая интервалы на несколько частей и исходя из того, что вся — площадь гистограммы должна остаться при этом неизменной, можно получить мелкоступенчатую гистограмму, которая при уменьшении величины интервала будет приближаться к плавной кривой, называемой кривой распределения.

Пример 2. По данным примера и построить полигон распределения и гистограмму.

Решение см. на рисунке 28.

Полигон распределения и гистограмма

Кумулятивная кривая (кривая сумм — кумулята) получается при изображении вариационного ряда с накопленными частотами или относительными частотами в прямоугольной системе координат, Накопленная частота определенной варианты получается суммированием всех частот вариант, предшествующих данной, с частотой этой варианты. При построении кумуляты дискретного признака по оси абсцисс откладывают значения признака (варианты), Ординатами служат вертикальные отрезки, длина которых пропорциональна накопленной частоте или относительной частоте той или иной варианты. Соединением вершин ординат прямыми линиями получаем ломаную (кривую) кумуляту.

При построении кумуляты интервального вариационного ряда нижней границе первого интервала соответствует частота, равная нулю, а верхней — вся частота интервала. Верхней границе второго интервала соответствует накопленная частота первых двух интервалов (т. е. сумма частот этих интервалов) и т. д. Верхней границе последнего (максимального) интервала соответствует накопленная частота, равная сумме всех частот.

Пример 3. По данным примера 1 построить кумуляту распределения.

Решение cм. на рисунке 29.

Кумулята распределения

Числовые характеристики выборки

В качестве одной из важнейших характеристик вариационного ряда применяют среднюю величину. Математическая статистика различает несколько типов средних величин: арифметическую, геометрическую, гармоническую, квадратическую, кубическую и др. Все перечисленные типы средних могут быть рассчитаны для случаев, когда каждая из вариант вариационного ряда встречается только один раз (тогда средняя называется простой, или невзвешенной) и когда варианты или интервалы повторяются. При этом число повторений вариант или интервалов называют частотой, или статистическим весом, а среднюю, вычисленную с учетом статистического веса, — взвешенной средней.

Для характеристики вариационного ряда один из перечисленных типов средних выбирается не произвольно, а в зависимости от особенностей изучаемого явления и цели, для которой среднее исчисляется.

Практически при выборе того или иного типа средней следует исходить из принципа осмысленности результата при суммировании или при взвешивании. Только тогда средняя применена правильно, когда в результате взвешивания или суммирования получаются величины, имеющие реальный смысл.

Обычно затруднения при выборе типа средней возникают лишь в использовании средней арифметической, или гармонической. Что же касается геометрической и квадратической средних, то их применение обусловлено особыми случаями (см. далее).

Следует иметь в виду, что средняя только в том случае является обобщающей характеристикой, если она применяется к однородной совокупности. В’ случае использования средней для неоднородных совокупностей можно прийти к неверным выводам. Научной основой статистического анализа является метод статистических группировок, т. е. расчленения совокупности на качественно однородные группы.

Все указанные типы средних величин можно получить из формул степенной средней. Если имеются варианты x_1,x_2,ldots,x_n , то среднюю из вариант можно рассчитать по формуле простой невзвешенной степенной средней порядка :

$overline{x}=sqrt[LARGE{LARGE{z}}]{frac{1}{n}sumlimits_{i=1}^{n}x_{i}^{z}}.$

При наличии соответствующих частот m_1,m_2,ldots,m_n средняя рассчитывается по формуле взвешенной степенной средней:

$overline{x}=sqrt[LARGE{LARGE{z}}]{dfrac{sumlimits_{i=1}^{n}x_{i}^{z}m_i}{sumlimits_{i=1}^{n}m_i}}.$

Здесь overline{x} — степенная средняя; — показатель степени, определяющий тип средней; x_i — варианты, m_i — частоты или статистические веса вариантов.

Средняя арифметическая получается из формулы степенной средней при подстановке z=1 :

незвешенная $overline{x}_{text{ar}}=frac{1}{n}sumlimits_{i=1}^{n}x_i$ ; взвешенная $overline{x}_{text{ar}}=dfrac{sumlimits_{i=1}^{n}x_{i}m_i}{sumlimits_{i=1}^{n}m_i}$

Средняя гармоническая получается при подстановке в формулу степенной средней значения z=-1 :

незвешенная $overline{x}_{text{gr}}=dfrac{n}{sumlimits_{i=1}^{n}frac{1}{x_i}}$ ; взвешенная $overline{x}_{text{gr}}=dfrac{sumlimits_{i=1}^{n}m_i}{sumlimits_{i=1}^{n}frac{1}{x_i}}$

Средняя гармоническая вычисляется тогда, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, т. е. когда суммированию подлежат не сами варианты, а обратные им величины $frac{1}{x_1},frac{1}{x_2},ldots,frac{1}{x_n}.$ .

Средняя квадратическая получается из формулы степенной средней при подстановке z=2 :

незвешенная $overline{x}_{text{kv}}=sqrt{frac{1}{n}sumlimits_{i=1}^{n}x_i^2}$ ; взвешенная $overline{x}_{text{kv}}=sqrt{dfrac{sumlimits_{i=1}^{n}x_i^2}{sumlimits_{i=1}^{n}m_i}}$

Средняя квадратическая используется только тогда, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.

Средняя геометрическая получается из формулы степенной средней при предельном переходе zto0 :

незвешенная $overline{x}_{text{gm}}=sqrt[LARGE{LARGE{n}}]{prodlimits_{i=1}^{n}x_i}$ ; взвешенная $overline{x}_{text{gm}}=sqrt[LARGE{LARGE{sumlimits_{i=1}^{n}m_i}}]{prodlimits_{i=1}^{n}x_i^{m_i}}$

Вычисления средней геометрической в значительной мере упрощаются применением логарифмирования:

незвешенная $lgoverline{x}_{text{gm}}=frac{1}{n}sumlimits_{i=1}^{n}lg{x_i}$ ; взвешенная $lgoverline{x}_{text{gm}}=dfrac{sumlimits_{i=1}^{n}m_ilg{x_i}}{sumlimits_{i=1}^{n}m_i}.$

Таким образом, логарифм средней геометрической есть средняя арифметическая из логарифмов вариантов. Средняя геометрическая используется главным образом при изучении динамики. Средние коэффициенты и темпы роста рассчитывают по формулам средней геометрической.

Если вычислить различные типы средних для одного и того же вариационного ряда, то числовые их значения будут различаться. При этом средние по своей величине расположатся в определенном порядке. Наименьшей из перечисленных средних окажется средняя гармоническая, затем геометрическая и т. д., наибольшей будет средняя квадратическая. При этом порядок возрастания средних определяется показателем степени z в формуле степенной средней. Так, при z=-1 получаем среднюю гармоническую, при z=0 — геометрическую, при z=1 — арифметическую, при z=2 — квадратическую:

$overline{x}_{text{gr}}<overline{x}_{text{gm}}<overline{x}_{text{ar}}<overline{x}_{text{kv}}$

В качестве характеристики вариационного ряда используют медиану (M_e) , т. е. такое значение варьирующего признака, которое приходится на середину упорядоченного вариационного ряда. Если в вариационном ряду 2m+1 случаев, то значение признака у случая m+1 будет медианным. Если в ряду четное число случаев, то медиана равна средней арифметической из двух срединных значений. При нечетном количестве вариантов медиана рассчитывается по формуле

$M_e=x_{m+1}$ ; при чётном $M_e=frac{x_m+x_{m+1}}{2}.$

При расчете медианы интервального вариационного ряда сначала находят интервал, содержащий медиану, путем использования накопленных или относительных частот. Медианному интервалу соответствует первая из накопленных или относительных частот, превышающая половину всего объема совокупности. Для нахождения медианы при постоянстве плотности внутри интервала, содержащего медиану, используют формулу

$M_e=x_{M_e(min)}+frac{k}{m_{M_e}}left(frac{1}{2}sumlimits_{i=1}^{n}m_i-V_{M_e-1}right)$

где $x_{M_e(min)}$ — нижняя граница медианного интервала; — величина медианного интервала; $V_{M_e-1}$ — накопленная частота интервала, предшествующего медианному; $m_{M_e}$ –частота медианного интервала.

Медиану можно определить также графически по кумуляте. Для этого последнюю ординату, пропорциональную сумме всех частот или относительных частот, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения — значение медианы (см. рис. 29).
Медиана обладает таким свойством: сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):

$sumlimits_{i=1}^{n}|x_i-M_e|=min.$

Это свойство медианы можно использовать при проектировании расположения трамвайных и троллейбусных остановок, бензоколонок и т. д.

Пример 4. На шоссе длиной 100 км имеется 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых поездок на заправку с каждого гаража. Результаты обследования приведены в таблице.

Таблица расположения гаражей вдоль шоссе

Бензоколонку нужно поставить так, чтобы общий пробег машин на заправку был наименьшим.

Решение.

Вариант 1. Если бензоколонку поставить на середине шоссе, т. е. на 50-м километре (средняя арифметическая), то пробеги с учетом числа поездок составят:

в одном направлении

43cdot10+24cdot15+22cdot5+13cdot20+10cdot5+4cdot25=1310 км;

в противоположном

10cdot15+28cdot30+36cdot10+42cdot65=4080 км;

Общий пробег в оба направления окажется равным 5390 км.

Вариант 2. Уменьшения пробега можно достичь, если бензоколонку поставить на 63,85-м километре, т. е. на среднем участке шоссе с учетом числа поездок (средняя арифметическая взвешенная). В этом случае пробеги составят по 2475,75 км в оба направления, т. е. общий пробег составит 4951,5 км и окажется меньше, чем при первом варианте, на 438,5 км.

Вариант 3. Наилучший результат, т. е. минимальный общий пробег, получим, если поставим бензоколонку на 78-м километре, что будет соответствовать медиане. Тогда пробеги составят 3820 км и 990 км. Общий пробег равен 4810 км, т. е. он оказался меньше, общих пробегов, рассчитанных по предыдущим вариантам.

Модой M_0 называется варианта, наиболее часто встречающаяся в данном вариационном ряду. Для дискретного ряда мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариант и соответствует варианте с наибольшей частотой. В случае интервального распределения с равными интервалами модальный интервал (т. е. содержащий моду) определяется по наибольшей частоте, а при неравных интервалах — по наибольшей плотности. Мода рассчитывается по формуле

$M_0=x_{M_0(min)}+kcdotfrac{m_{M_0}-m_{M_0-1}}{(m_{M_0}-m_{M_0-1})+(m_{M_0}-m_{M_0+1})},$

где $x_{M_0(min)}$ — нижняя граница модального интервала; — величина модального интервала; $m_{M_0}$ — частота модального интервала; $m_{M_0-1}$ частота интервала, предшествующего модальному; $m_{M_0+1}$ — частота интервала, следующего за модальным.

Вариационные ряды, в которых частоты вариант, равноотстоящих от средней, равны между собой, называются симметричными. Особенность симметричных вариационных рядов состоит в равенстве трех характеристик — средней арифметической, моды и медианы:

$overline{x}=M_0=M_e.$

(это необходимое условие симметричности вариационного ряда, но не достаточное).

Вариационные ряды, в которых расположение вариант вокруг средней не одинаково, т. е. частоты по обе стороны от средней изменяются по-разному, называются асимметричными, или скошенными. Различают асимметрию — левостороннюю и правостороннюю.

Средние величины, характеризуя вариационный ряд одним числом, не учитывают вариацию признака, между тем эта вариация существует. Для измерения вариации признака в математической статистике применяют ряд способов.

Вариационный размах , или широта распределения, есть разность между наибольшим и наименьшим значениями вариационного ряда:

$R=x_{max}-x_{min}.$

Вариационный размах представляет собой величину неустойчивую, чрезвычайно зависящую от случайных обстоятельств; применяется для приблизительной оценки вариации.

Среднее линейное отклонение, или простое среднее отклонение (обозначается ) представляет собой среднюю арифметическую из абсолютных значений отклонений вариант от средней. В зависимости от отсутствия или наличия частот вычисляют среднее линейное отклонение невзвешенное или взвешенное:

$d=frac{1}{n}sumlimits_{i=1}^{n}|x_i-overline{x}|;~~~~~d=dfrac{sumlimits_{i=1}^{n}|x_i-overline{x}|m_i}{sumlimits_{i=1}^{n}m_i}.$

Средний квадрат отклонения, или дисперсия (обозначается ) наиболее часто применяется как мера колеблемости признака. Дисперсии невзвешенную и взвешенную вычисляют по формулам

$D=frac{1}{n}sumlimits_{i=1}^{n}(x_i-overline{x})^2;~~~~~D=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^2m_i}{sumlimits_{i=1}^{n}m_i}.$

Таким образом, дисперсия есть средняя арифметическая из квадратов отклонений вариант от их средней арифметической.
Квадратный корень из дисперсии sqrt{D} называется среднеквадратическим отклонением.

Обобщающими характеристиками вариационных рядов являются моменты распределения. Характер распределения можно определить с помощью небольшого количества моментов.

Средняя из k-х степеней отклонений вариант от некоторой постоянной величины называется моментом k-го порядка:

$M_k=overline{(x-A)^k}$

При расчете средних в качестве весов можно использовать частоты, относительные частоты или вероятности. При использовании в качестве весов частот или относительных частот моменты называются эмпирическими, а при использовании вероятностей — теоретическими. Порядок момента определяется величиной . Эмпирический момент k-го порядка находится как отношение суммы произведений k-х степеней отклонений вариант от постоянной величины на частоты к сумме частот:

$M_k=dfrac{sumlimits_{i=1}^{n}(x_i-A)^km_i}{sumlimits_{i=1}^{n}m_i}.$

В зависимости от выбора постоянной величины различают следующие моменты.

1. Если A=0 , то моменты называются начальными, обозначаются nu_k и вычисляются по формуле

$nu_k=dfrac{sumlimits_{i=1}^{n}x_i^km_i}{sumlimits_{i=1}^{n}m_i}.$

Тогда при k=0 получаем начальный момент нулевого порядка:

$nu_0=dfrac{sumlimits_{i=1}^{n}x_i^0m_i}{sumlimits_{i=1}^{n}m_i}=1.$

при k=1 получаем начальный момент первого порядка:

$nu_1=dfrac{sumlimits_{i=1}^{n}x_im_i}{sumlimits_{i=1}^{n}m_i}=overline{x}.$

при k=2 получаем начальный момент второго порядка:

$nu_2=dfrac{sumlimits_{i=1}^{n}x_i^2m_i}{sumlimits_{i=1}^{n}m_i}=overline{x^2}.$

при k=3 получаем начальный момент третьего порядка:

$nu_3=dfrac{sumlimits_{i=1}^{n}x_i^3m_i}{sumlimits_{i=1}^{n}m_i}=overline{x^3}.$

при k=4 получаем начальный момент четвёртого порядка:

$nu_4=dfrac{sumlimits_{i=1}^{n}x_i^4m_i}{sumlimits_{i=1}^{n}m_i}=overline{x^4}.$

и т.д. Практически используют моменты первых четырёх порядков.

2. Если не равно нулю, а некоторой произвольной величине x_0 (начало отчёта), то моменты называются начальными относительно x_0 , обозначаются nu'_k и рассчитываются по формуле

$nu'_k=dfrac{sumlimits_{i=1}^{n}(x_i-x_0)^km_i}{sumlimits_{i=1}^{n}m_i}.$

3. Если за постоянную величину взять среднюю A=overline{x} , то моменты называются центральными, обозначаются mu_k и вычисляются так

$mu_k=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^km_i}{sumlimits_{i=1}^{n}m_i}.$

Тогда при k=0

$mu_0=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^0m_i}{sumlimits_{i=1}^{n}m_i}=1,$

то есть центральный момент нулевого порядка, равный единице;

при k=1

$mu_1=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})m_i}{sumlimits_{i=1}^{n}m_i}=0,$

то есть центральный момент первого порядка равен нулю;

при k=2

$mu_2=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^2m_i}{sumlimits_{i=1}^{n}m_i}=D,$

то есть центральный момент первого порядка равен дисперсии и служит мерой колеблемости признака;

при k=3

$mu_3=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^3m_i}{sumlimits_{i=1}^{n}m_i},$

в этом случае центральный момент третьего порядка служит мерой асимметрии распределения признака.

Если распределение симметрично, то mu_3=0 ;

при k=4

$mu_4=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^4m_i}{sumlimits_{i=1}^{n}m_i},$

получаем центральный момент четвёртого порядка.

Коэффициентом асимметрии A_s называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:

$A_s=frac{mu_3}{sigma^3}=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^3m_i}{sigma^3sumlimits_{i=1}^{n}m_i}.$

Если полигон вариационного ряда скошен, то есть одна из его ветвей начиная от вершины зримо короче другой, то такой ряд называется асимметричным.

Эксцессом (E) называется уменьшенное на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения:

$E=frac{mu_4}{sigma^4}-3=dfrac{sumlimits_{i=1}^{n}(x_i-overline{x})^4m_i}{sigma^4sumlimits_{i=1}^{n}m_i}-3.$

Кривые распределения, у которых E<0 , менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых E>0 , более крутые, имеют острую вершину и называются островершинными.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник